The airborne transmission of infection between flats in high-rise residential buildings: Tracer gas simulation

Abstract

Airborne transmission of infectious respiratory diseases in indoor environments has drawn our attention for decades, and this issue is revitalized with the outbreak of severe acute respiratory syndrome (SARS). One of the concerns is that there may be multiple transmission routes across households in high-rise residential buildings, one of which is the natural ventilative airflow through open windows between flats, caused by buoyancy effects. Our early on-site measurement using tracer gases confirmed qualitatively and quantitatively that the re-entry of the exhaust-polluted air from the window of the lower floor into the adjacent upper floor is a fact. This study presents the modeling of this cascade effect using computational fluid dynamics (CFD) technique. It is found that the presence of the pollutants generated in the lower floor is generally lower in the immediate upper floor by two orders of magnitude, but the risk of infection calculated by the Wells–Riley equation is only around one order of magnitude lower. It is found that, with single-side open-window conditions, wind blowing perpendicularly to the building may either reinforce or suppress the upward transport, depending on the wind speed. High-speed winds can restrain the convective transfer of heat and mass between flats, functioning like an air curtain. Despite the complexities of the air flow involved, it is clear that this transmission route should be taken into account in infection control.

Nomenclature

a

thermal diffusivity (m²/s)

A

window opening area (m²)

C

number of new cases

C_d

discharge coefficient

c_p

specific heat of air (J/kg K)

C₀

initial indoor tracer gas concentration (ppm)

C_τ

tracer gas concentration at time τ (ppm)

D

depth of the room (m)

e

base of natural logarithms

Fr

Froude number

g

gravity acceleration (m/s²)

g′

reduced gravity to describe buoyancy force, g′=g  Δρ/ρ=g  ΔT/T (m/s²)

g_i

component of the gravitational vector in the ith direction (m/s²)

G_b

generation of turbulence kinetic energy due to buoyancy

h

window height (m)

H

height of the insulated cavity (m)

I

number of infectors

k_i,j

fraction of exhaust air from the flat i which re-enters the flat j

p

pulmonary ventilation rate of susceptible individuals (m³/h)

P

the probability of infection for susceptible individuals

PS_i

generation rate of pollutants in the flat i (g/s)

Pr_t

turbulent Prandtl number

q

number of infectious “quanta” produced per hour by infectors

Q

absolute room ventilation rate (m³/h)

S

number of susceptible individuals exposed

t

exposure time (h)

T

air temperature (K)

T_c

cavity core temperature (K)

T_cold

cold wall surface temperature (K)

T_h

hot wall surface temperature (K)

T_i

the average inside air temperature (K)

T_o

outside air temperature (K)

T_ref

reference air temperature (293 K)

U

the wind speed at the building height (m/s)

U₀

reference velocity in the calculation of inlet streamwise velocity, 1.068 m/s

V

volume of the building model (m³)

V_met

meteorological wind speed (m/s)

V_y

wind speed at the height of y (m/s)

x_i

the ith coordinate

y

height above the ground in the calculation of wind speed (m)

y₀

reference height in the calculation of inlet streamwise velocity, 0.005 m

Greek symbols

β

thermal expansion coefficient (K⁻¹)

κ

Von Karman's constant, 0.41

μ_t

turbulent viscosity (g/ms)

ρ

air density (kg/m³)

ρ₀

the density of outside air (kg/m³)

ρ_ref

reference air density (1.205 kg/m³)

υ

kinetic viscosity (m²/s)

τ

time (s)

Δp

pressure difference across the opening (Pa)

ΔT

temperature difference between indoor and outdoor (°C)

1. Introduction

Airborne transmission is known to be the route of infection for a number of diseases including smallpox, tuberculosis, and severe acute respiratory syndrome (SARS). Beggs's study in hospital buildings concluded that the contribution of airborne micro-organisms to the spread of infection is likely to be underestimated currently although contact-spread is the principal route of transmission for most infections [1]. Airborne transmission is deemed as long-range aerosol transmission, which refers to the situation that agents can be carried long distances (within a room or between rooms, generally greater than 1 m) by air flows [2]. With the lessons from SARS outbreak in 2003 and the threats from a possible approaching avian influenza pandemic, our concern about aerosol-transmitted infections in hospitals buildings, residential buildings, and even in transportation vehicles has been refreshed. Li et al. [3] reviewed over 40 studies on the relationship between the transmission of infection and ventilation systems in hospitals, offices, aircraft cabins, etc. This interdisciplinary review found that there was sufficient evidence to demonstrate the association between ventilation, indoor air movements and the transmission of infection diseases. In a hospital environment, on the basis of the principle of diluting contaminated air using fresh air, a ventilation rate of at least 12 air changes per hour is recommended for new isolation rooms (constructed since 2001) equipped with mechanical ventilation systems [4]. To restrict virus transmission between wards, negative pressure ventilation systems are used. However, Escombe et al.'s measurements in eight hospitals using a carbon dioxide tracer gas technique found that opening windows and doors provided median ventilation of 28 air changes per hour (ACH), more than double that of mechanically ventilated rooms [5]. The airborne infection probability for 24 h exposure to tuberculosis predicted by the Wells–Riley model was reduced from 39% in mechanically ventilated rooms to 33% in naturally ventilated rooms. They suggested that in resource-limited settings where negative-pressure isolation rooms were difficult to implement, natural ventilation may be a low-cost alternative.

On the other hand, anecdotal evidence in Hong Kong during the SARS outbreak in the spring of 2003 shows that in certain high-rise residential buildings, adjacent upper floor residents were infected after those on the lower floor. In addition, the SARS virus was found within the deposits on the windowsill and floors on two other upper floors, where residents on floors immediately beneath had been infected with SARS. Prompt investigations upon the occurrences ruled out the possibilities of the spread via unsealed U-traps of the drainage systems in the building. These blocks have rectangular plan layouts and have common corridors separating the two sides, each of which has a flat-façade with operable windows. With doors closed, the flats become single-sided naturally ventilated, and the open windows function as both inlet and outlet of air. Room exhaust air, which is typically not centralized and not stacked, is left to drift freely around the building. Therefore, the exhaust air of one flat may become the intake of the adjacent upper flat. Under normal circumstances, one can detect from the smell of the air what one's neighbor is cooking. This fact arouses our concern about the vertical upward transport of contaminants between flats in high-rise residential buildings with natural ventilation, i.e., there may be a cascade effect, which has been over-looked so far in both building design and infection control.

In recent years, natural ventilation has attracted considerable interest in the designs of green buildings [6]. There are two major forms of natural ventilation: single-sided and cross flow. Cross ventilation generally promotes a robust airflow through an internal space via multiple openings on different facades. However, in densely occupied urban environments, there may be only one external façade for small cellular rooms. The design of buildings thus often adopts single-sided natural ventilation. In this configuration, wind turbulence and temperature differences between indoor and outdoor areas are the main driving forces. Although the uncertainty of these driving forces makes natural ventilation not as controllable as mechanical ventilation, a well-designed natural ventilation system is not only energy efficient compared with mechanical ventilation systems, but also able to provide a comfortable and healthy indoor environment. Temperature-driven single-sided natural ventilation through large openings has been fully studied in regard to air change rate [7] and the resulting indoor air quality and comfort level [8] by experimental works [9], theoretical predictions [10], and computational fluid dynamics (CFD) simulations [11]. However, less consideration has been given to the fate of the exhaust air so far, and on whether it will re-enter the upper floor with the same mechanism. Allocca et al. [12] simulated pure buoyancy-driven single-sided natural ventilation through a lower and upper opening in a three-storey building. They found that although the flats were physically and thermally isolated from one another, the indoor temperature level in each flat increased slightly with height, which they attributed to the outside thermal plume from the openings underneath. In their configurations, the distance between upper openings of one space and lower openings of the above space was small. Unfortunately, this cascade effect of energy is not elaborated in detail in their study, nor the transport of contaminants.

From the point of view of infection control, this cascade air flow is undesirable. Earlier special onsite investigations after the SARS outbreak revealed that the room immediately upstairs could contain up to 7% of the exhaust air from the lower floor [13]. Our previous simulations also exhibited this cascade effect in windless cases [14]. This study applies the CFD method to investigate the combined effect of wind and buoyancy on the upward contaminant transport. The investigation is focused on the passive tracer gas concentration field and infection risks. Some of the results are compared with the earlier on-site measurements [13]. Considering that the sizes of human-generated aerosols typically range from 5 to 100 μm, using a tracer gas to represent their aerodynamic behaviors by neglecting the gravity effect on the aerosols can reasonably give meaningful results, especially for those fine droplets. The aerosols’ movement modeling, which can more accurately capture the dispersion characteristics of sneezed/coughed virus-containing droplets, will be studied and reported in a separate paper.

2. CFD methods validation

The computations are carried out by using a commercial program, Fluent [15]. This program solves the governing equations in a finite-volume procedure with a staggered grid system. The turbulent effect is simulated by the re-normalization group (RNG) k–ε model. All thermophysical properties are assumed to be constant except for density, which is treated with the Boussinesq model. The Boussinesq model approximates density in the buoyancy term in the momentum equation by the following equation:

$$(\rho -{\rho }_{\mathrm{ref}})g\approx -{\rho }_{\mathrm{ref}}\beta (T-T_{\mathrm{ref}})g$$ (1)

The generation of turbulence due to buoyancy in the transport equations for k and ε equations is included by

$$G_{\mathrm{b}}=\beta g_i\frac{{\mu }_{\mathrm{t}}}{P{r}_{\mathrm{t}}}\frac{\mathit{\partial }T}{\mathit{\partial }{x}_i}$$ (2)

The convection terms are discretized by second order upwind scheme and the diffusion term by central differences and with second-order accuracy. The SIMPLE algorithm [16] is adopted as pressure–velocity coupling method. The elementary flow characteristics involved in the present study are natural convection flows in a cavity and forced convection flows over a bluff body. As validations of the above model, the simulations on natural convection and forced convection are compared with the measured data from the literature. In particular, the experimental data from Denmark Aalborg University [17] are also used to validate the modeling of pure buoyancy-driven single-sided natural ventilation.

2.1. Natural convection in a cavity

Cheesewright et al. [18] measured a two-dimensional buoyancy flow in an enclosed cavity (Fig. 1 ). The temperature difference between the vertical opposite walls is 45.8 K, corresponding to a Rayleigh number ($\mathit{Ra}=(g\beta (T_{\mathrm{h}}-T_{\mathrm{c}})H^3)/(\upsilon \times a)$) of 2.8×10¹⁰. Because this cavity flow is relatively stable and the flow characteristics are similar to indoor airflows, the experimental data have been widely used to validate the computation of Reynolds-stress models [19], large eddy simulation [20], and low-Reynolds-number k–ε model [21]. Here the RNG k–ε model including low-Reynolds-number effect is adopted since the flow pattern consists of both turbulent and laminar flow. For improving the simulation of the boundary layer and convective heat transfer from the walls, a two-layer wall function is used [14]. The first grids are located within the viscous sub-layer with y ⁺<1. The overall grids number is 273 (H)×74 (L) (Fig. 1).

Fig. 1.

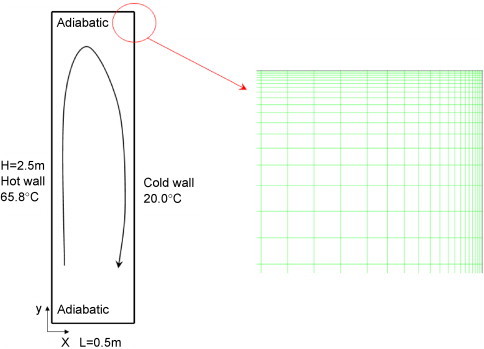
Sketch of the air cavity with natural convection.

The mean velocity distribution at the middle height and the vertical dimensionless core temperature (defined as (T−T _cold)/(T _h−T _cold) are shown in Fig. 2, Fig. 3 , respectively. The prediction of mean velocity agrees well with the experiment, whereas the temperature profile is higher than the experimental data. Heat loss due to imperfect insulation at the top and bottom walls in the experiment reduces the core temperature at any level [18]. The linear vertical gradient of the dimensionless temperature is represented well by RNG k–ε model, and the relaminarization effect at the bottom of the hot wall and the top of the cold wall is clearly captured in this simulation. The value of convective heat transfer coefficient based on the wall-to-cavity-center temperature difference is 3.51 W/m²  K. It is very close to the simulation by Chen et al. [22] using low-Reynolds-number k–ε models (3.8 W/m²  K). This shows that the two-layer wall function can effectively correct the generally over-predicted convective heat transfer by the standard wall function.

Fig. 2.

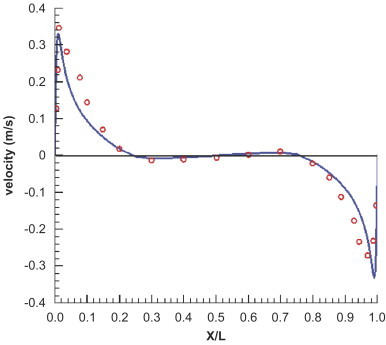
Profile of the vertical velocity at the middle height (Y=1.25 m): (—) simulations; (○) experimental data.

Fig. 3.

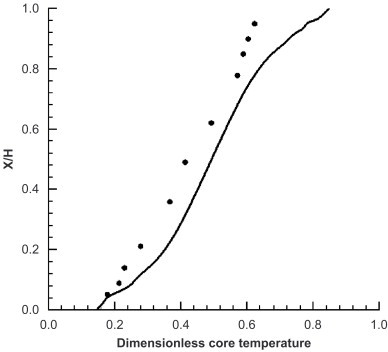
Profile of the dimensionless core temperature (X=0.25 m): (—) simulations; (●) experimental data.

2.2. Air flow around a bluff body

Jiang et al. [23] carried out wind tunnel tests to investigate the airflow around a building-like model, whose dimensions are 250 mm (H)×250 mm (L)×250 mm (W) with a wall thickness of 6 mm (Fig. 4a ). The mean air velocity and its fluctuation along 10 vertical lines were measured by a laser Doppler anemometer. The mean air velocities at four of these lines, ranging from 25 to 500 mm in height, are selected for comparisons with the current simulation (Fig. 4b). In the isothermal simulation, the computational domain have a downstream length of 8H, an upstream of 4H, a lateral length of 4W on both sides, and a height of 4H. The domain inlet velocity profile in the x direction follows a logarithmic law ($U(y)=(U_0/\kappa )\ln (y/y_0)$), and the velocity components in y and z directions are zero.

Fig. 4.

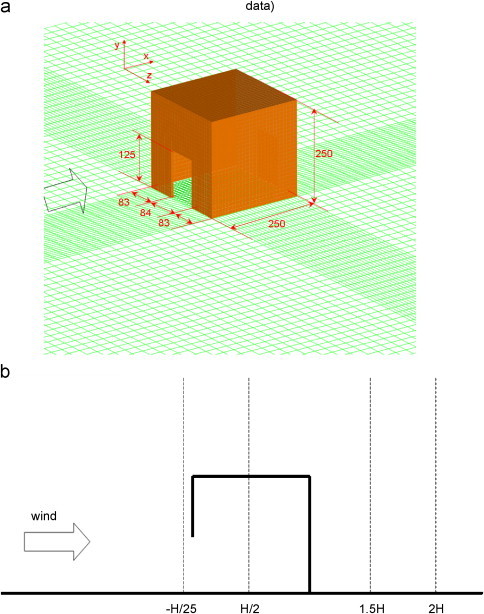
A schematic view of the building model and the numerical grids on the ground surface (a), and the locations where air velocities were measured (b).

The velocity vector at the middle section is illustrated in Fig. 5 , and mean velocity distributions at different height levels are shown in Fig. 6 . It is well known that the flowfield around a surface-mounted cube involves impingement, separation, and vortex shedding, etc. The use of isotropic k–ε models and wall functions has revealed deficiencies in this situation, with Reynolds-stress model performing better and large eddy simulation being the best. In Fig. 5, the recirculation zones before and after the cubic are reproduced by the RNG model. However, the small reverse flow above the cubic is not captured. Murakami et al. [24] attributed this error to the over-prediction of turbulent kinetic energy in the stagnant impingement region, which consequently produced large eddy viscosity and the reverse flow on the cubic roof was negated by this large viscosity. The simulated velocity agrees well with the measurement except at the line H/2 above the cubic and line 2H behind the cubic (Fig. 6). The negative simulated velocity at the lower part of the line 2H means the RNG model predicts a larger separation region. In its wake the vortex-shedding effects, which promote momentum exchange and thereby shorten the separation region, are ignored by the steady-state k–ε models. Despite the inaccuracies of k–ε models in the calculation of flow around a bluff body, the simulation of flow field inside the building and at the windward close to the opening is satisfactory. It justifies our application of the RNG model in the study of the cascade effect on a moderate day without wind or with a gentle breeze.

Fig. 5.

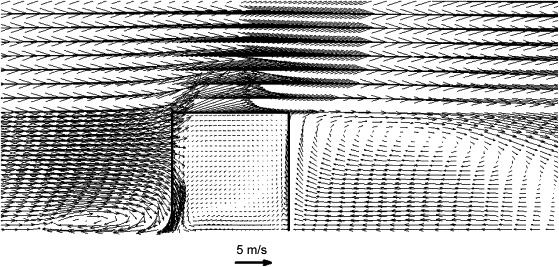
Air velocity field at the middle section.

Fig. 6.

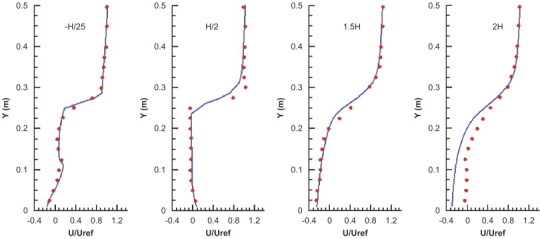
Mean velocity distribution for the single-sided, windward ventilation: (—) simulation; (●) experiment.

Another concern is the method to estimate the ventilation rate through the opening. The ventilation rate can be calculated by several methods, including the use of empirical models, integration of the velocity across the opening, and tracer gas concentration decay calculation. We adopted the tracer gas step-down method, i.e., the tracer gas decay method, by monitoring the transient evolution of the volume-averaged concentration indoors. This method is believed to be more rational than integration of air velocities because the outdoor air seems to form a short circuit at the opening and the effective depth of fresh air is very limited. Table 1 summarizes the ventilation rates. Because turbulent fluctuation contributes mainly to the air exchange in the wind-driven single-sided natural ventilation, Jiang and Chen [26] concluded that the time-averaged velocity field from k–ε model significantly cancels out the instantaneous air exchange between the indoor and outdoor flows. Therefore, the mean ventilation rate is much smaller than the average of instantaneous values from large eddy simulation. In Table 1, the ventilation rate from large eddy simulation is the highest. However, the result from the tracer gas decay method based on the airflow field predicted by the RNG model agrees with the empirical values. It cannot be judged which method is the best since no credible experimental data are available here.

Table 1.

Ventilation rate of wind-driven single-sided natural ventilation

	Ventilation rate, Qss (m3/s)	Remarks
Empirical method [25]	2.20×10−3	Qss=0.025AU, U is the wind velocity at the height of 125 mm (opening height)
	1.73×10−3	Qss=0.025AU, U is the wind velocity at the height of 62.5 mm (half of the opening height)
Integration of velocity from LES [23]	2.70×10−3	$Q_{\mathrm{ss}}=0.5{\mathit{\int }}_0^A|U_x|\mathrm{d}A$
Tracer gas step-down method (present study)	1.88×10−3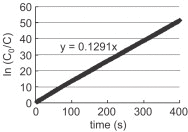
		$\frac{Q_{\mathrm{ss}}}{V}=\ln \left(\frac{C_0}{C_{\tau }}\right)\times \frac{1}{\tau }$

2.3. Pure buoyancy-driven single-sided natural ventilation through a large opening

Heiselberg et al. [17] performed pure buoyancy-driven single-sided natural ventilation experiments at Aalborg University. A constant temperature difference was maintained between a large full-scale chamber, which simulated the outdoor cool environment (13 °C), and a smaller test room inside the chamber, which was heated to a high temperature (33 °C) by electrical floor heating (Fig. 7 ). There was a window opening (width 1.0 m×height 1.6 m) in one of the test room walls at a height of 0.9 m. For measuring the air change rate, a tracer gas (N₂O) was uniformly released in the test room with an initial average concentration of less than 100 ppm. After the stable temperature fields were reached, the window was quickly opened. Then the temperature field, velocity field, and concentration field were continuously monitored.

Fig. 7.

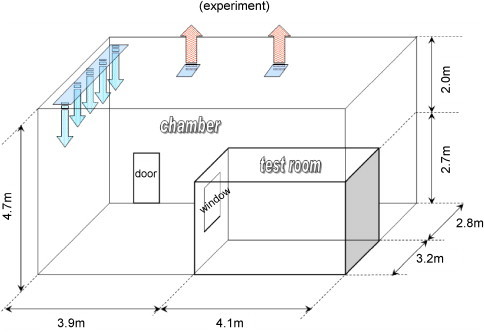
A schematic view of the full-scale test chamber and the test room.

For a single large opening, using Bernoulli and mass conservation equations, the volume flow rate is approximated at [27]

$$V=C_{\mathrm{d}}A\sqrt{\frac{2\mathrm{\Delta }p}{{\rho }_0}=}\frac{C_{\mathrm{d}}A}{3}\sqrt{\mathit{gh}\frac{T_{\mathrm{i}}-T_{\mathrm{o}}}{T_{\mathrm{o}}}}$$ (3)

The discharge coefficient, C _d, is a characteristic parameter for a specific window. It is influenced by window thickness, window height, aspect ratio, room depth and width, and indoor-to-outdoor temperature difference, etc. Generally speaking, a value of 0.6 is a proper approximation. The temporal evolution of air change rate per hour (ACH) and tracer gas decay is compared in Fig. 8(a) and (b) , respectively. The air change rate is derived from two approaches: integrating the normal air velocity across the window and calculation from Eq. (3). The predicted average concentration is in line with the experimental value, both of which accord with the exponential decay law. The air change rate reduces as the indoor–outdoor temperature difference decreases. In both approaches, the ACH is under-predicted. It is suspected that the temperature on the surface of the floor heater is still higher than 33 °C in experiments after electrical heating is turned off so causing a higher indoor air temperature and consequently a higher ACH.

Fig. 8.

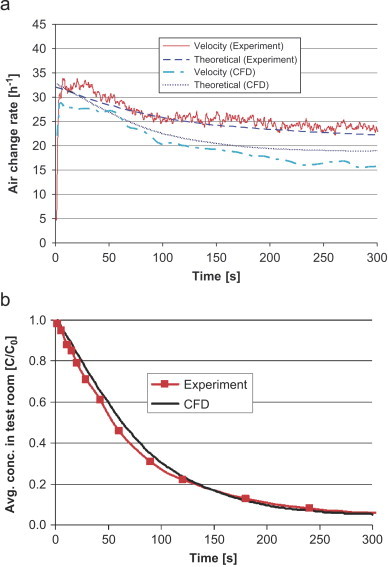
Air change rate per hour (a) and average tracer-gas concentration in the test room (b) in the simulations and experiments. (In the legend of (a), “velocity” means that the ACH is calculated from integration of the normal air velocity across the window; “theoretical” means the ACH is calculated from Eq. (3).)

It is observed, in both the current simulations (Fig. 9 ) and the flow visualization in the experiments that the cold outdoor air pours into the room and spreads over the floor, behaving like the airflow from a low-velocity diffuser in displacement ventilation. The room air is displaced from the bottom to the top, with a vertical temperature gradient. Compared with upper and lower openings on one façade, single openings normally generate low ventilation rates, and the effective depth of fresh air is not as far into the space [8]. However, in this case the outdoor air is able to reach the opposite wall along the floor, indicating an effective depth of fresh air distribution higher than the room length. Thus, a good indoor air quality is ensured. The net heat flow across the window is around $(V\rho c_{\mathrm{p}}\mathrm{\Delta }T=1000\mathrm{W})$, which represents a cooling power of 76.7 W/m² (based on the floor area). This cooling capacity may provide a high level of thermal comfort because it exceeds the cooling load in many offices. Therefore, we can confidently expect that single-sided natural ventilation through a large opening in this case can provide adequate ventilation.

Fig. 9.

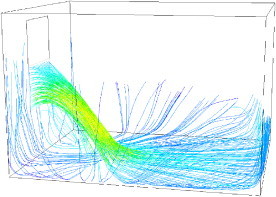
Pathline description of the fresh outdoor air flowing into the room.

3. Configuration of simulation

To study the possible cross contamination of ventilation air via open windows in multi-family buildings, a four-storey building is adopted (Fig. 10 ). Windows are opened at the windward end on the second and third floor. The room dimension is height (Y)×length (X)×width (Z)=2.7 m×3.1 m×2.4 m and the window height (Y)×width (Z)=1.2 m×0.75 m. The bottom of the window is 0.8 m above the room floor. These dimensions are identical with those in our field study. This building is placed in a computational domain, as illustrated in Fig. 10. According to the experiences by Schaelin et al. [28] and Allocca et al. [12], this domain is large enough to obtain the true results. The domain boundary at x–y plane is defined as symmetry. It means that the building and its surroundings are extended in the negative and positive z direction. This treatment is based on the fact that in many high-rise residential blocks in Hong Kong the shape of the whole building is like a vertical slab.

Fig. 10.

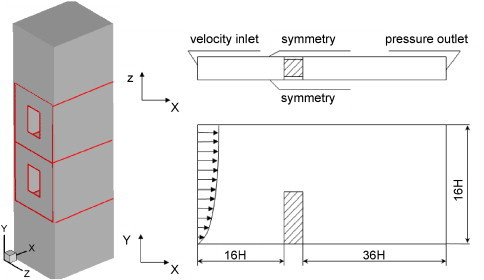
Description of the building model and the computational domain.

Heat is released only from the internal walls on the second and third floors. The atmospheric air temperature is 20 °C and the indoor wall surface temperature is 25 °C. In the simulation of a low wind day, a uniform velocity profile (0.1 m/s) is set at the domain inlet, in place of pressure boundary. This is because we found it is difficult to reach convergence if using pressure boundary at the domain inlet as well as outlet. For this building configuration and an indoor–outdoor temperature difference of 5 °C, a very gentle wind at a speed less than 0.2 m/s will make the wind force and buoyancy force comparable, indicating an Archimedes number, Ar,

$$\mathit{Ar}=\frac{\mathit{Gr}}{R{e}^2}=\frac{\beta \mathrm{\Delta }Tg{h}^3/{\upsilon }^2}{(\mathit{UD}/\upsilon {)}^2}=1$$ (4)

In a normal urban environment, even on a windless day in meteorology, the wind speeds are usually higher than this value (0.2 m/s). Therefore, a small meteorological wind speed, V _met (wind speed usually taken at 10 m above the ground level), at 0.5, 1.0, 2.0, and 4.0 m/s is considered. The wind profile in an urban environment is calculated by the following equation [27]:

$$V_y=0.35V_{\mathrm{met}}{y}^{0.25}$$ (5)

The turbulence on the inlet boundary is characterized by turbulence intensity and length scale, which are 8% and 1 m, respectively. Carbon dioxide (CO₂), as a tracer of indoor pollutants, is generated at a rate of 8 mg/s in the middle of the second floor at the height of 1.6 m. The governing equation of this tracer gas is solved alone after the convergence of air flow field.

4. On-site field study

On-site measurements were carried out at Wing Shui House in the spring from January to February of 2005 [13]. It was in spring that the SARS outbreak happened in 2003 in Hong Kong. During the period of measurement, the outdoor temperature varied from 10.6 to 24.0 °C and indoor temperature from 12.8 to 23.3 °C. Two units located adjacently at the second and third floor were rented. SF₆ were used as a tracer of indoor pollutant originating from the second floor at 3 ml/s and CO₂ as a tracer for determining the ventilation rate. SF₆ concentrations at six points (three points in the second floor and the other three points in the third floor) within the two rooms were monitored by B&K 1302 and INNOVA-1412. CO₂ concentrations were logged by TSI Q-Trak Model 8851. The wind speed components in the U, V, and W direction outside the window were measured using a YOUNG GILL UVW Anemometer (Model 27005). Indoor and outdoor temperatures were recorded simultaneously by StowAway Temperature Loggers.

One index, the re-entry ratio, was defined as the fraction of exhaust air from the lower source room which re-enters the adjacent upper room. It was found that on a windless day the ratio of the SF₆ concentration in the upper room to the lower room ranged from 3% to 7%, depending on the locations. The re-entry ratio is 4.8%, warning us of a high cross-infection probability by the upward cascade effect. Smoke visualization revealed this phenomenon qualitatively as well. Outside wind speed, when increased from 0–0.03 to 2.48 m/s, could lower the maximum concentration ratio to 3.6% and re-entry ratio to 0.6%.

5. Results and discussions

In the iterations of numerical simulation, it was noticed that a steady quasi-periodic variation appears after around 8000 iterations, especially in the pure buoyancy-driven windless case. The residuals no longer decrease but are maintained at an acceptable level. The velocity and concentration fluctuate significantly, and the fluctuation amplitude is over 20% of the mean values. In principle, the thermal plume above a heat source is not stable because it may laterally oscillate at a certain frequency. In our investigation of the cascade effect, two-dimensional simulations are also performed, and it was found that if there is a wind outside the window blowing vertically upward, alternating indoor air flow patterns were observed at certain critical points of the iterations where aiding force and counter-aiding force are equivalent. The multiple numerical solutions of unstable airflows are not taken into account due to the limited computation resources. Large eddy simulation and transient simulation using two equation models are expected to perform better in these situations. However, they are much more time-consuming. The following results are from the converged field after 15,000 iterations in each case.

5.1. Air change rate per hour (ACH)

Tracer gas decaying as a function of time is plotted in Fig. 11 . At time=0 s, the room is uniformly filled with tracer gas. Then the air exchange through the window is permitted and the normalized volume-average concentration is monitored. Given the previous discussion on pure buoyancy-driven natural ventilation in the validation section, here the emphasis is to explore the combined effect of weak wind and buoyancy on the ACH. As seen from Fig. 11, a gentle wind up to 1.0 m/s normal to the window has little or no influence on the ACH. However, if the normal wind speed increases to 2.0 and 4.0 m/s, the ACH is remarkably lowered. This finding is supported by the experiment by Wilson and Kiel [29]. In their measurements, at small temperature differences less than 10 °C, a wind speed of 20 km/h measured 10 m above the ground produced flow rates through a sheltered doorway that were about 25% smaller than calm conditions. Based on our present simulations and previous studies, we find that the effects of weak wind are multiple and complicated. Firstly, as explained by Wilson and Kiel [29], wind increases the intensity of outdoor turbulence, and further increases the interfacial mixing at the middle height of the opening between incoming and outgoing airstreams (Fig. 12 ). This mixing lowers the net flow rate. It is the re-entrainment by interfacial mixing that produces the gradual profile of velocity and temperature along the height of the opening. The effect of wind could be evaluated by the Froude number, $\mathit{Fr}=U/(g^{\prime }h{)}^{1/2}$. Davies and Linden's [30] measurement showed that the ACH decreased with increasing Fr. In current cases, Froude number at 3–4 would produce significant reduction on the ACH. Secondly, approaching wind speed profile may attenuate the net pressure difference across the opening (Fig. 13 ). Wind and stack forces counteract each other. The combined effect of opposing wind and buoyancy forces is widely studied in cross ventilation. Nevertheless, there are few reports of single-sided ventilation. Thirdly, turbulent fluctuations in wind contain high frequency energy, which could strengthen the air exchange through the opening [6]. The frequency of turbulence energy for wind-driven flow is one order of magnitude higher than that for buoyancy-driven flow [11], [14]. In buoyancy-driven cases, mean pressure differences across the opening impels airflow while, on the other hand, pressure fluctuation plays an important role in wind-driven natural ventilation. In Fig. 11, the ACH is higher on the second floor than on the third floor at a wind speed of 1.0, 2.0, and 4.0 m/s. This discrepancy was observed in our field study as well. One possible explanation is that the wind speed at the height of the upper window is higher than at the lower window.

Fig. 11.

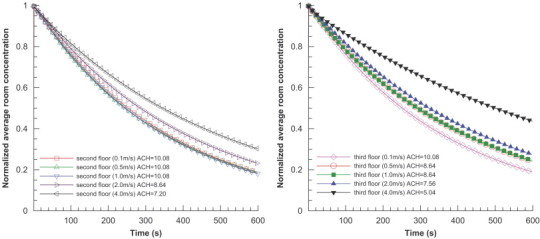
Decaying curves of normalized average indoor CO₂ concentration.

Fig. 12.

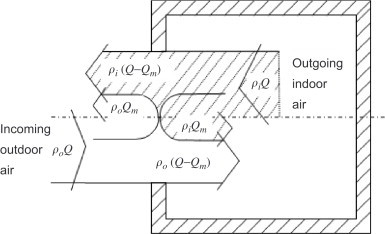
Re-entrainment by cross-stream interfacial mixing between counterflowing streams [29].

Fig. 13.

The combined effect of wind and stack forces.

It should be borne in mind that although both existing studies from literature and our simulation results find the counteraction between wind and stack forces in single-side natural ventilation, due to the inherent inability of the k–ε models, this finding still needs more experimental validations.

5.2. Cascade effect

Mass fractions of the tracer gas at the middle section in z direction are shown in Fig. 14 . In the windless condition, the warm plume emitted from the upper part of the lower window drifts upward. Due to the horizontal momentum when leaving the lower window, the central region of this plume is apart from the upper window. The re-entry ratio is 7.5% (Table 2 ). The average concentration in the upper room is two orders of magnitude lower than in the lower room. As wind speed ascends from 0.5 to 2.0 m/s, the plume is forced to approach the upper window by the impingement of the normal wind. The re-entry ratio increases to up to 16.3% as a result. The wind assists in the cascade effect. If the wind speed increases further to 4.0 m/s, the development of the warm plume from the lower window is confined. The air velocity levels in the two rooms (mean value 0.08 m/s) are quite lower than in the windless case, which results in a diffusion-dominated spread of pollutants. The re-entry ratio is the lowest (3.5%). It seems that strong normal wind will act as an air curtain. This curtain helps to block the heat and mass transfer between flats.

Fig. 14.

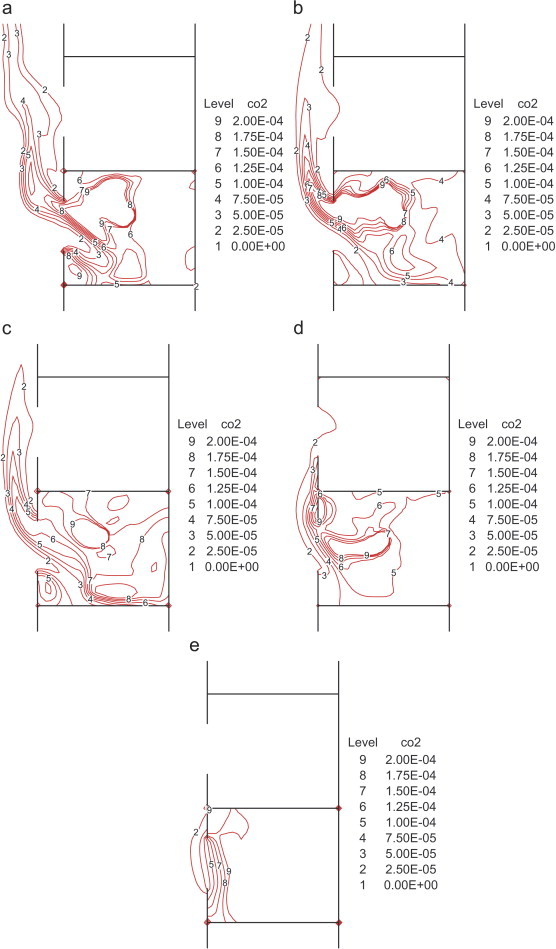
Distribution of mass fraction (kg/kg) of tracer gas CO₂ which is generated in the middle of the second floor at a rate of 8 mg/s.

Table 2.

Mean risk of infection from Wells–Riley equation and re-entry ratio in various cases

	0.1 m/s	0.5 m/s	1.0 m/s	2.0 m/s	4.0 m/s
Mean risk of infection (second floor) (%)	30	28	29	31	46
Mean risk of infection (third floor) (%)	2.0	3.4	3.5	6.6	1.7
Re-entry ratio (%)	7.5	9.6	10.9	16.3	3.5

In this article only the transmission between two adjacent flats is discussed. Actually, the pollutants from the second floor may enter into the fourth floor and floors further above. By defining the re-entry ratio, k_{i , j} as the fraction of exhaust air from the flat i which re-enters the flat j (i<j), and assuming that the pollutant source strength in the ith room is PS_i, we can calculate the total mass of pollutants in the jth flat $={\sum }_{i-1}^{j-1}{\mathrm{PS}}_i\times k_{i,j}$. On the other hand, only the wind normal to the window is taken into account. In fact, the wind direction varies randomly, as confirmed in our field study. The wind which is parallel with the window in the horizontal plane can easily blow away the warm exhaust foul air from the window. In this scenario, the cascade transport is destroyed. However, the adjacent rooms on the same floor may be contaminated, giving birth to another problem.

Based on the knowledge of infection dose (the number of organisms required to cause infection), the risk of airborne infection and ventilation rate per person can be correlated by Wells–Riley equation [31]:

$$P=\frac{C}{S}=(1-{\mathrm{e}}^{-\mathit{Iqpt}/Q})$$ (6)

The quantum, q, represents the generation rate of infectious doses. Exposure to one quantum gives an average infection probability of (1−e⁻¹). The Wells–Riley equation is set up on the assumption of a well-mixed and steady-state condition. Here using CFD we can get the concentration of infectious particles at a certain point, which allows derivation of spatial distribution of infection risk. It does not require the assumption of well-mixed conditions. The spatial variance of infection probability is similar with the distribution of mass fraction of the tracer gas (Fig. 14). A high mass fraction denotes a high risk. Supposing one patient standing in the middle of the second floor producing 13 infectious quanta per hour (q=13), pulmonary ventilation rate at 0.6 m³/h (p=0.6), and exposure time of 8 h (t=8), the calculated mean infection probabilities are listed in Table 2. These probabilities can give a rough estimation of the infection risk level although the occupants may move in the room sometimes. The mean infection risk is highest in the case of 2.0 m/s due to the highest re-entry ratio. A probability as high as 6.6% on the third floor alerts us that the upward transport of infectious diseases in high-rise residential buildings is worthy of due consideration in infection control. As one of the effective intervention measures is to isolate and quarantine the close-contacts, the upstairs household residents may be included in the close-contact list in case of a highly infectious disease.

6. Conclusions

SARS case clusters in several high-rise residential buildings in Hong Kong in 2003 have motivated the authors to seriously evaluate the degree to which the airborne virus can be transported by natural ventilative airflows through open windows between flats in high-rise residential buildings in crowded urban environments. As a counterpart of the field study, which revealed qualitatively and quantitatively that the vertical upward re-entry into the upper room of exhaust air from the lower adjacent room is a reality, the present study employs CFD technique to quantify the infection risks. Comparisons with experimental data of some elementary flows including the natural convection in a cavity, air flow around a bluff body, and pure buoyancy-driven natural ventilation through a large opening help to enhance the confidence level of modeling the cascade effect in windless and gentle-wind conditions.

It is found that, on a windless day, around 7.5% of the exhaust air can be re-entrained into the upper room. The concentration level is generally 2 orders of magnitude lower in the adjacent upper room than in the lower source room, but the risk of infection is only 1 order of magnitude lower and is still significantly high when it is assessed using the Wells–Riley TB infection model. One of the parameters is the long time that residents would spend at their own homes. The effect of wind blowing perpendicularly to the window is rather complicated. It may reinforce or prevent the upward transport, depending on the wind speed. A gentle-wind forces the warm polluted plume to enter into the upper window by its horizontal momentum. But high-speed winds may function like an air curtain, suppressing the convective spread of pollutants between flats. In spite of these complexities, the vertical spread risks should not be overlooked from the perspective of infection control, especially when an emerging infectious disease is dealt with.

Present simulations using the RNG k–ε model are not able to reveal the turbulent fluctuations and instantaneous air exchanges through the opening, especially in wind-driven single-sided natural ventilation, although we find the value of ACH from the RNG k–ε model is acceptable. The symmetrical boundary conditions imposed on the pollutant concentration equations in the horizontal directions may have overestimated the vertical transmission, but the effects are expected to be small, and will be examined in our further studies.