Waveform changes with the evolution of beta bursts in the human subthalamic nucleus

Abstract

Objective

Phasic bursts of beta band synchronisation have been linked to motor impairment in Parkinson’s disease (PD). However, little is known about what terminates bursts.

Methods

We used the Hilbert–Huang transform to investigate beta bursts in the local field potential recorded from the subthalamic nucleus in nine patients with PD on and off levodopa.

Results

The sharpness of the beta waveform extrema fell as burst amplitude dropped. Conversely, an index of phase slips between waveform extrema, and the power of concurrent theta activity increased as burst amplitude fell. Theta activity was also increased on levodopa when beta bursts were attenuated. These phenomena were associated with reduction in coupling between beta phase and high gamma activity amplitude. We discuss how these findings may suggest that beta burst termination is associated with relative desynchronization of the beta drive, increase in competing theta activity and increased phase slips in the beta activity.

Conclusions

We characterise the dynamical nature of beta bursts, thereby permitting inferences about underlying activities and, in particular, about why bursts terminate.

Significance

Understanding the dynamical nature of beta bursts may help point to interventions that can cause their termination and potentially treat motor impairment in PD.

1. Introduction

Untreated Parkinson’s disease (PD) is characterized by excessive beta frequency band (13–30 Hz) synchronization in the basal ganglia (Hammond et al., 2007). In particular, the reduction in mean beta power of the local field potential (LFP) in the subthalamic nucleus (STN) with dopaminergic medication or deep brain stimulation (DBS) correlates with the improvement in motor impairment achieved with these interventions (Kühn et al., 2006, 2008, 2009; Ray et al., 2008; Özkurt et al., 2011; Neumann et al., 2016; Oswal et al., 2016). More recently, pathological LFP beta activity has been suggested to consist of phasic bursts lasting several hundred milliseconds or longer (Deffains et al., 2018), with the percentage of long bursts correlating with motor impairment (Tinkhauser et al., 2017a, 2017b). Beta-amplitude triggered adaptive DBS curtails long duration bursts and improves motor function (Tinkhauser et al., 2017b). Dopaminergic medication also shifts the distribution of burst durations in favour of shorter bursts with this correlating with the improvement in motor impairment (Tinkhauser et al., 2017a). In addition, studies measuring the kinematics of individual ballistic movements have demonstrated motor slowing when beta bursts precede movement (Torrecillos et al., 2018; Tinkhauser et al., 2019), while studies examining repetitive movements have linked the occurrence of beta bursts to the progressive bradykinesia over time that characterises PD (Lofredi et al., 2019). Although these studies are only correlative, they suggest that the incidence of beta bursts in the LFP may be more strongly linked to bradykinesia than mean LFP beta power (Deffains et al., 2018; Torrecillos et al., 2018; Lofredi et al., 2019).

Evidence is therefore growing that beta bursts in the LFP, particularly longer duration beta bursts, may play a central role in Parkinsonian motor dysfunction. Recent work in the 6-hydroxydopamine rodent model of PD suggests that phase slips occur in the locking between neural activities in the cortex and different basal ganglia sites just before bursts develop (Cagnan et al., 2019). However, the mechanisms leading to the termination of beta bursts in the basal ganglia are unclear, and could provide clues as to potential therapeutic interventions. Here we seek to shed light on these mechanisms through consideration of the dynamics in the shape of beta bursts. This approach is motivated by recent observations that the shape of beta oscillations in the primary motor cortex of patients with PD carries information about the motor state. Thus, the sharpness of cortical beta oscillations correlates with rigidity (Cole et al., 2017), and is reduced during conventional DBS (Cole et al., 2017) and after dopaminergic medication (Swann et al., 2015; Jackson et al., 2019). Such sharpness of the LFP activity is increasingly thought to be associated with the tight synchronisation of a regular input or drive, so that the temporal summation of synapticly driven polarisation changes gives sharp transients (Sherman et al., 2016; Burke et al., 2015; Lozano-Soldevilla et al., 2016; Cole et al., 2017; Cole and Voytek, 2017; Vaz et al., 2017). In the case of the STN, the beta input is likely to originate from the cerebral cortex, given that STN beta is coherent with and phase lags cortical beta (Williams et al., 2002; Fogelson et al., 2006). Here we consider the shape of waveforms in STN beta bursts in detail. These beta bursts are approximately spindle shaped, with an initial rising slope, followed by a descending slope (Tinkhauser et al., 2017a). Our results provide evidence, albeit indirect, to support the hypothesis that the descending slope of beta bursts might reflect desynchronization and disorganisation of the beta drive to the STN, and the rise of competing inputs.

2. Materials and methods

2.1. Subjects and surgery

We investigated waveform changes within beta bursts before and after administration of levodopa in nine patients (6 males, 18 hemispheres, age 62 ± 3 years, disease duration 12.6 ± 1.4 years) with advanced PD undergoing DBS surgery targeting the STN. Patients were bilaterally implanted with the Medtronic 3389 DBS lead (Medtronic Neurological Division) with four platinumiridium cylindrical surfaces. The subjects have been previously reported and the clinical and operative details described within these earlier reports (Kühn et al., 2006 reports all 9 subjects, but only data from 17 hemispheres; Tinkhauser et al., 2017a reports 8 subjects and data from 16 hemispheres. Here we report data from the complete 18 sides, as exclusion criteria were not applied in the current study). All experimental protocols were approved by the local ethics committee (at the Charité, University Medicine Berlin, Campus Virchow, Berlin, Germany) and all participants gave their written informed consent.

2.2. Experiments and recordings

DBS electrodes were externalized prior to connection to the implantable pulse generator. LFPs were recorded 3–6 days after lead implantation following overnight withdrawal of antiparkinsonian medication before and, again, after administration of levodopa. LFPs were recorded from adjacent bipolar contact pairs (C01, C12, C23), while patients sat quietly. Signals were amplified and bandpass filtered between 1–250 Hz using an INA 128 instrumentation amplifier (Texas Instruments), and then transferred through a 1401 analogue/digital converter (Cambridge Electronic Design) onto a computer with Spike2 software (Cambridge Electronic Design). The sampling rate was 1 kHz. The Unified Parkinson’s Disease Rating Scale (UPDRS) was used to score motor symptoms before and after administration of levodopa (ON 23.2 ± 4.5, OFF 45.7 ± 5.7). All data were analyzed in Matlab (version R 2018a; MathWorks, Natick, MA).

2.3. Contact localisation

To visualize the distribution of the DBS lead contacts in the STN we used the Lead-DBS Matlab toolbox (version 2.1.6) (Horn et al., 2019). Preoperative MRI and postoperative CT scans were coregistered using Advanced Normalization Tools (ANTs, Avants et al., 2008; http://stnava.github.io/ANTs/) and normalised into the ICBM 2009b NLIN asymmetric MNI space using the symmetric diffeomorphic image registration approach implemented in ANTs (Avants et al., 2008). Electrode trajectories were then automatically detected and manually refined to define exact lead contacts location.

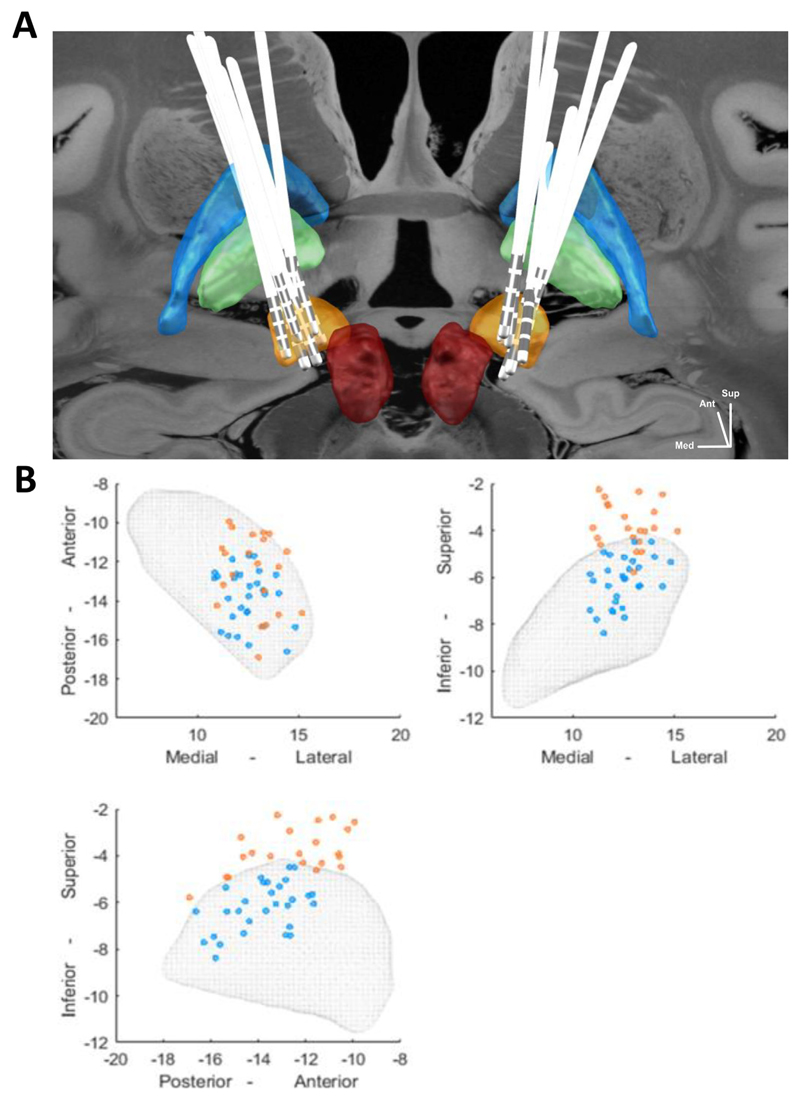
Given that LFPs were registered from adjacent bipolar contact pairs (C01, C12, C23), the x, y and z coordinates were derived for the center point of the upper, middle and lower bipolar contact pairs. All contact pairs, both from the left and right STN, were projected on to the right STN of the DISTAL Atlas (Ewert et al., 2018) using a nonlinear flip function (Lead-DBS Matlab toolbox). We then determined whether the contact pairs were localized inside or out-side the STN (Fig. 1)

Fig. 1.

Spatial representation of electrodes and recording sites. (A) Localisation of deep brain stimulation (DBS) leads in Montreal Neurological Institute (MNI) space (posterior view). Subthalamic nucleus (STN; yellow), red nucleus (red), globus pallidus interna (green) and globus pallidus externa (blue). Backdrop is the 100 lm postmortem magnetic resonance image (MRI) warped to MNI space and released in Lead DBS (Edlow et al., 2019). (B) Spatial distribution of all the bipolar contact pairs of all 9 subjects relative to the midcommissural point (mm) in the MNI space. The STN is depicted as mesh and data are illustrated in all 3 planes. The blue dots indicate the contact pairs localised inside of the STN and the orange dots indicate contacts pairs localised outside the STN. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.4. Determination of bursts

The raw signals were notch filtered at 50 Hz and its harmonics, and high-pass filtered at 1 Hz. Beta bursts were determined using methods that have been previously outlined (Tinkhauser et al., 2017a). LFP signals were first decomposed using Wavelet transformation (fieldtrip-function ft_freqanalysis, Morlet Wavelet, width = 10, gwidth = 5) into frequencies ranging from 1 to 40 Hz with a resolution of 1 Hz (Oostenveld et al., 2011). The 40 Hz cut-off was only used here and did not affect the empirical mode decomposition. The frequency of the maximum amplitude bin in the beta frequency range (1-Hz bins between 13 and 30 Hz from the three bipolar contacts) was selected in the OFF medication state for each electrode and the corresponding time evolved wavelet amplitude (bandwidth = 5 Hz) was smoothed (0.2 s) and DC corrected (non-overlapping 20 s moving average) to eliminate potential baseline shifts in amplitude. Time points at which the time evolved wavelet amplitude exceeded a fixed amplitude threshold were determined as samples within beta bursts. The threshold was defined as the average of the 75th percentile amplitude distributions in the ON and OFF conditions. As we were particularly interested in the evolution of activities during beta bursts, we selected for further analysis bursts with a minimum duration of 400 ms. This also served to limit contributions from noise-induced spontaneous fluctuations in signal amplitude. The selected beta bursts were split at the point of their peak amplitude into an initial 200 ms duration segment with a rising slope (ending at the point of the beta burst’s peak amplitude) and a later 200 ms duration segment with a descending slope (beginning at the point of the beta burst’s peak amplitude).

2.5. Empirical mode decomposition

The focus of our investigation was the shape of the waveforms comprising beta bursts in the STN. To this end, we used the Hilbert–Huang transform (HHT), which is the result of empirical mode decomposition (EMD) and Hilbert spectral analysis (Huang et al., 1998). The HHT uses the EMD method to decompose a signal into elementary signals referred to as intrinsic mode functions (IMFs), and applies Hilbert spectral analysis to obtain instantaneous frequency data for these components (Fig. 2A). These IMFs are virtually free from harmonic artifacts, an important characteristic when evaluating phase-amplitude coupling (Wu and Huang, 2004; Shi et al., 2018; Yeh et al., 2016). The intra-wave frequency modulation (FM) can be used to define the degree of nonlinearity (DoN) of each IMF decomposed through the EMD method (Wang et al., 2012; Huang et al., 2014), and to extract wave shape functions (Wu, 2013; Hou and Shi, 2016). As the DoN defines the deviation of instantaneous frequency cycle-by-cycle it is not affected by any changes in frequency between cycles, as, for example, may occur as an oscillation becomes less well tuned. The DoN has been used to assess the sparsity, or otherwise, of instantaneous frequencies as a nonlinear property in irregular oscillations (Veltcheva and Soares, 2016; Tsai et al., 2016).

Fig. 2.

Intrinsic mode functions (IMFs) and dependency of Degree of Non-linearity (DoN) on signal noise levels. (A) The beta peaking-IMF (β IMF, red line) retains the nonlinear elements of the test beta waveform (black line) and hence the amplitude of the test waveform better than a standard Butterworth IIR filter (order = 6, blue line). The low-frequency peaking-IMF (LF IMF, green line) captured components with peak frequency around 4 Hz. The power spectral densities of the different components were estimated using Welch’s power spectral density. (B) DoN of nonlinear waveforms with different degrees of polynomial for phases (inverse nonlinear level). The synthetic signals also have a component of Gaussian white noise with the standard deviation relative to the oscillatory component (noise level). Four lines include beta peaking-IMFs with (red track) or without (blue track) averaging by autocorrelation, Butterworth IIR filter in the beta band (order = 6, band = 18–22 Hz, green track), and DoN of the original signal without Gaussian white noise as control (black interrupted track). Autocorrelation serves to reduce the effects of increasing noise levels. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

We implemented the fast EMD for computational efficiency (Wang et al., 2014). The Matlab code used is available (https://data.mrc.ox.ac.uk/mrcbndu/data-sets/search). The raw signals were notch filtered at 50 Hz and its harmonics, and highpass filtered at 1 Hz. Fig. 3 summarises the steps in the EMD algorithm for a given signal $\stackrel{\rightharpoonup }{\chi }$. (1) Generating local mean curve: the algorithm begins with identifying all the local maxima and minima. The upper envelope $\stackrel{\rightharpoonup }{e_u}$ is generated by connecting all the local maxima using a cubic spline curve. Likewise, all the local minima are connected to create the lower envelope $\stackrel{\rightharpoonup }{e_l}$. Then the mean $\stackrel{\rightharpoonup }{m}$ of these two envelopes is computed. (2) Sifting process: the first component $\stackrel{\rightharpoonup }{h^{(1)}}$ is obtained by subtracting $\stackrel{\rightharpoonup }{m^{(1)}}$ from x. The sifting process is repeated on $\stackrel{\rightharpoonup }{h^{(1)}}$ while $\stackrel{\rightharpoonup }{h^{(1)}}$ still possesses multiple extrema between zero crossings. After recursively applying this step on $\stackrel{\rightharpoonup }{h^{(1)}}$, the sifting process stops once the shortest period component of the signal (here we take the first IMF $\stackrel{\rightharpoonup }{c_1}$ as an example) is obtained. The sifting process stops when the sum of the difference (SD) is zero; however, to avoid local wiggles in IMFs due to oversifting, the maximum sifting number is 10 (Wu and Huang, 2004). Then c ₁(t) is separated from the data to obtain the residue r ₁(t). The extracted IMFs would have the same numbers of zero-crossings or differ by one at most, and have almost symmetrical envelopes defined by local maxima and minima respectively (Huang et al., 1998). (3) Generating all IMFs: If the residue r ₁(t) still contains information about larger scales, it is treated as a new input and the sifting process is repeated again. This process is repeated on all IMFs $\stackrel{\rightharpoonup }{c_j}$ (j^th IMFs) with the subsequent residues. The whole procedure is terminated once the residue r(t) is a constant or monotonic slope, or a function with only one extremum.

Fig. 3.

Empirical mode decomposition (EMD) algorithm. Terms are described in the methods.

We found 10 IMFs in our analysis of LFPs; the first two IMFs with the highest peak frequencies were summed as a high gamma peaking-IMF (peak frequency > 60 Hz), the 3rd and the 4th IMFs with their peak frequencies within the beta band were summed as a beta peaking-IMF, the 5th IMF had a peak frequency in the high alpha band (12 Hz), and the 6th and the 7th IMFs had peak frequencies in the theta band and were summed as a theta peaking-IMF. Finally, the 8th to the 10th IMFs had peak frequencies below 2 Hz and were not analysed further. The retained IMFs with peaks at different frequencies may be interpreted as broad frequency spectra due to the dyadic filter bank, in which within cycle sharpening and other within-cycle waveform distortions, and inter-cycle non-stationarities, contribute to the artificial harmonics and broad frequency spectral components in the Fourier decomposition, respectively. Fig. 4 demonstrates that the beta IMF, in particular, serves to capture beta bursts, which were therefore missing when this IMF was subtracted from the raw signal.

Fig. 4.

Beta bursts were identified from the time evolving wavelet amplitudes in the beta band (13–30 Hz). Two sets of time evolving wavelet amplitudes were estimated from (A) the raw signal and (B) from the same raw signal after subtracting the beta-peaking intrinsic mode function (IMF). The beta-peaking IMF is shown to capture beta bursts, which are missing from the signal in (B). The horizontal dotted line is the 75% percentile threshold derived from the time evolving wavelet amplitude of the raw signal. Threshold crossings had to be sustained for at least 100 ms to be considered as significant. The peaks of events satisfying these criteria are marked by red dots. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.6. Oscillation sharpness

In this study we estimate several measures from the beta IMF during bursts; extremata sharpness in the oscillations, phase slips and degree of non-linearity (Supplementary Fig. 3). To obtain a measure of oscillation sharpness, the beta IMF was first extracted using ensemble EMD (level of added noise = 0.1, ensemble number = 100) with the influences from the added noise less than a fraction of 1% of the standard deviation (Wu and Huang, 2009). Next, we implemented the concept of the order-statistic filter, which is used in imaging denoising to identify peaks and troughs (Cheng and Venetsanopoulos, 1992). Briefly, this consists of weighting IMFs with a sliding Tukey window and setting the maxima as output (Lin et al., 2019). The procedure for estimating the sharpness of beta oscillations was introduced by Cole et al. (2017). This was applied to the beta peaking-IMF. The sharpness of each extrema is defined as the average of the two absolute voltage differences between the extrema and the 5 ms either side of the peak or trough. Note that here we considered the sharpness of extrema (peaks and troughs) independently of their polarity, as the latter is determined by the orientation of the contact pair used to record the LFP with respect to the generator. Accordingly, sign may flip between recordings in an unconstrained way, so here we averaged the sharpness of trough and peaks.

In order to ratify our measure of sharpness we created a family of normal probability densities in which the standard deviation of the distribution (sigma) ranged from 0.2 to 1 in steps of 0.1 (Fig. 5A). Lower sigma values and sharper waveforms corresponded to higher oscillation sharpness (Fig. 5B).

Fig. 5.

Simulations showing how sharpness and Degree of Non-linearity (DoN) vary with known waveform distortions. (A) Normal probability densities with standard deviation of the distribution (sigma) ranging from 0.2 to 1 in steps of 0.1 were designed. (B) Lower sigma values correspond to higher sharpness. (C) A series of simulated oscillatory signals with different phase slips were designed, where n controls the level of phase slips (see equation in sub-section “Non-sinusoidal features”). n = 1 gives a linear phase change over time whereas n = 0.5 is the least linear phase plotted. (D) Higher averaged phase slips are associated with higher DoN estimates.

2.7. Non-sinusoidal features

An important feature of brain waves is the time evolving instantaneous frequency (IF). IFs were derived from dyadic IMFs (Flandrin et al., 2004). The IF is defined as the time derivative of the Hilbert phase function θ(t) (Huang et al., 2009), and provides insight into intra-wave frequency modulations including phase slips. Huang has used intra-wave frequency modulation to estimate the degree of nonlinearity (DoN) in nonlinear oscillations as follows (Huang et al., 2014).

$${\text{DoN}}_i=std\langle \frac{{(IF)}_i-{(I{F}_z)}_i}{{(I{F}_z)}_i}\rangle$$

where IF is the instantaneous frequency and IF_z is the zero-crossing frequency. This measure has previously been used to characterize neurophysiological and other signals (Tsai et al, 2016; Veltcheva and Soares, 2016).

Both the sharpness around the extrema of the beta peaking-IMFs and the intra-wave instantaneous frequency variations of the gaps between these extrema (DoN_gap) contribute to the nonlin-earity. In this work, the DoN, DoN_gap and sharpness of beta peaking-IMFs in the 1st and the 2nd halves of beta bursts were estimated. The two beta burst halves were separated by the peak of each burst. The DoN is affected by the signal-to-noise ratio so by contrasting values from the two halves of each approximately amplitude symmetrical spindle-shaped beta burst we partially controlled for this. In addition, we performed autocorrelation within each half before estimating the DoN and DoN_gap. Fig. 2B provides evidence through simulations that autocorrelation is able to limit the effects of relative increases in noise. In Fig. 2B we designed a series of simulated nonlinear oscillatory signals with different degrees of nonlinearity. To generate nonlinear waveforms, we designed time-varying phase as

$$\text{Ph}(\text{t})=2\pi {\left(\frac{t}{t_0}\right)}^n$$

where n controls the nonlinear level, and t₀ is the period length. We constructed synthetic signals with these time-varying phases but with constant amplitude. All oscillatory cycles by default had the same frequency (20 Hz). To test the effects of noise, we added a random white-noise component with its standard deviation (SD) as a fraction of that of the raw signal. Fractions varied from 0.1 to 0.5 in steps of 0.1. For each synthetic signal, the sampling frequency was 600 Hz and data length was 10 s. From Fig. 2B it is clear that the dynamic range of the EMD-based DoN is progressively limited by increasing noise levels. However, autocorrelation of the IMF prior to estimation of the DoN reduces the effects of noise and affords a more robust estimate of DoN despite increasing noise levels.

Finally, we estimated the sharpness at the autocorrelated peaks and troughs, the DoN of a 200 ms period of the rising and descending slopes of the beta burst and the DoN_gap that was similar to the former but excluded the periods of the signal that were used to estimate the sharpness. In the case of the high gamma peaking-IMF, we also contrasted the amplitude in 5 ms periods centred on the extrema with that estimated as for the same period as the DoN_gap.

In order to ratify our DoN measure we simulated a series of oscillatory signals with different levels of phase slips, where n controlled the latter. The higher the averaged phase slips the higher was the DoN (Fig. 5C and D).

2.8. Phase-amplitude coupling

To calculate the phase-amplitude coupling (PAC) between the beta peaking-IMF and gamma peaking-IMF, we first obtained the beta phase and gamma amplitude from the analytic form using Hilbert transform (Pittman-Polletta et al., 2014; Yeh and Shi, 2018). Next, we divided each phase cycle into 20 bins, and then assigned the gamma amplitude at each time point to a corresponding beta phase bin. By averaging the amplitudes in each bin, we derived the beta phase to gamma amplitude distribution. Then, the modulation index (MI) was used to quantify the coupling between beta phase and gamma amplitude (Tort et al., 2010). Briefly, we inversely normalise the Shannon entropy of the beta phase to gamma amplitude distribution by the maximum possible entropy, yielding a quantity between zero and one.

2.9. Statistical analysis

Results are reported as mean ± standard error and two-tailed p value < 0.05 considered statistically significant (α = 0.05 for all hypothesis testing). Repeated measures ANOVAs were performed as described in the results and pairwise t-tests used for post-hoc comparisons. Hemispheres were treated as independent variables, as in the previous reports describing these patients. All statistical analyses were conducted using JMP software (SAS, NC, USA).

3. Results

3.1. Characteristics of Beta-peaking IMFs during beta bursts

Beta bursts with a duration greater than 400 ms were identified in the time-evolved wavelet amplitude of the STN LFP, as previously (Tinkhauser et al, 2017a, 2017b). These were split at the point of the beta burst’s peak amplitude into an initial 200 ms duration segment with a rising slope and a later 200 ms duration segment with a descending slope. The average number of bursts analysed per subject were 230.97 ± 9.11 and 222.14 ± 8.57 before and after administration of levodopa, respectively. On average beta amplitude rose by 1.27 ± 0.05 a.u./s in the rising segment of beta bursts and fell by 1.19 ± 0.05 a.u./s in the decreasing segment of beta bursts.

The IMFs peaking in the theta (5–8 Hz), alpha (8–13 Hz), beta (13–30 Hz) and high gamma bands (60–250 Hz) were extracted in nine patients (18 hemispheres) with PD (Supplementary Fig. 1) and their spectral power estimated (Fig. 6). We began by testing whether the power of the IMF peaking in the beta band was modulated by the segment of the burst, levodopa treatment or electrode contact pair. The ANOVA summarised in Table 1A demonstrates that there was a significant effect of levodopa (F(1, 159.3) = 11.49, p = 0.0009) and a trend towards an effect of contact pair (F(2,158.4) = 2.84, p = 0.0616) whereby beta peaking-IMF power at contact pair 12 tended to be greater than at 01. Post-hoc tests indicated that the power of beta bursts averaged across all contact pairs was greater off compared to on levodopa (DF = 17, t = -1.78, p = 0.0466). However, there was no difference in the beta power between the two segments of the bursts, consistent with an approximately symmetrical spindle shape.

Fig. 6.

Intrinsic mode function (IMF) spectra. (A) Theta peaking-IMF power. Power is greater in the descending segment than in the rising segment and higher on levodopa. See Table 2A for statistical evaluation of power differences. (B) Alpha peaking-IMF power. There is a clear increase in power on levodopa (see Table 2A). (C) Beta peaking-IMF power. Power tends to be greater off levodopa (see Table 1A). (D) Gamma peaking-IMF power. No clear differences in gamma peaking-IMF power were seen between burst segments (see Table 2A). Mean shown in bold and ± standard error in shading.

Table 1.

Beta peaking-intrinsic mode function (IMF) characteristics during beta bursts. Analysis of variance (ANOVA) results for (A) beta peaking-IMF power, (B) beta peaking-IMF Degree of Non-linearity (DoN), (C) beta peaking-IMF sharpness, (D) beta peaking-IMF Degree of Non-linearity in the gaps between extrema (DoNgap), (E) beta peaking-IMF averaged zero-crossing frequency, and (F) variation of beta peaking-IMF zero-crossing frequency from the 200 ms rising and falling segments bordering the peak of each phasic burst. Factors include burst segments (two levels; rising and descending segments of phasic bursts), levodopa (two levels; OFF and ON medication), and contact pairs (three levels; C01, C12 and C23). Significant p values and those showing a trend are emboldened.

A: beta IMF power
Factor	DF	F-value	P-value
Segments	(1,158.8)	1.06	0.3052
Levodopa	(1,159.3)	11.49	0.0009
Contacts	(2,158.4)	2.84	0.0616
Segments*Levodopa	(1,158.7)	0.23	0.6290
Levodopa*Contacts	(2,158.6)	0.53	0.5909
B: beta DoN
Factor	DF	F-value	P-value
Segments	(1,160.1)	7.96	0.0054
Levodopa	(1,161.2)	1.42	0.2360
Contacts	(2,159.4)	0.92	0.4003
Segments*Levodopa	(1,160.0)	0.03	0.8542
Segments*Contacts	(2,159.7)	0.17	0.8424
Levodopa*Contacts	(2,159.9)	0.44	0.6464
C: beta IMF Sharpness
Factor	DF	F-value	P-value
Segments	(1,156.9)	4.62	0.0332
Levodopa	(1,157.4)	0.08	0.7722
Contacts	(2,156.6)	8.21	0.0010
Segments*Levodopa	(1,156.9)	0.49	0.4844
Segments*Contacts	(2,156.7)	0.01	0.9895
Levodopa*Contacts	(2,156.8)	1.01	0.3684
D: beta IMF DoNgap
Factor	DF	F-value	P-value
Segments	(1,159.6)	10.36	0.0016
Levodopa	(1,160.6)	3.28	0.0722
Contacts	(2,159.0)	0.34	0.7113
Segments*Levodopa	(1,159.6)	0.09	0.7644
Segments*Contacts	(2,159.3)	0.15	0.8614
Levodopa*Contacts	(2,159.5)	0.81	0.4483
E: beta IMF averaged zero-crossing frequency
Factor	DF	F-value	P-value
Segments	(1,155.4)	1.58	0.2109
Levodopa	(1,156.5)	1.12	0.2925
Contacts	(2,154.6)	2.94	0.0560
Segments*Levodopa	(1,155.5)	0.01	0.9039
Segments*Contacts	(2,154.8)	0.84	0.4355
Levodopa*Contacts	(2,155.3)	0.83	0.4401
F: variation of beta IMF zero-crossing frequency
Factor	DF	F-value	P-value
Segments	(1,159.2)	1.06	0.3041
Levodopa	(1,161.2)	2.19	0.1404
Contacts	(2,157.9)	0.17	0.8447
Segments*Levodopa	(1,159.4)	1.67	0.1981
Segments*Contacts	(2,158.4)	0.63	0.5321
Levodopa*Contacts	(2,158.9)	1.60	0.2042

Hemispheric sides as random factor.

Variable is box-cox transformed.

Post-hoc analysis: C12 > C01.

Post-hoc analysis: C23 & C12 > C01.

We then examined whether the DoN of the beta peaking-IMF was modulated by burst segment, levodopa treatment or electrode contact pair. The ANOVA summarised in Table 1B demonstrates that the only significant effect was that of burst segment (F (1,160.1) = 7.96, p = 0.0054). The effect size for the factor burst segment, in the form of partial eta squared, was 0.09, indicating that almost 10% of the total variance in the DoN could be attributed to the factor burst segment. A post-hoc test indicated that the DoN was greater in the later, descending segment of the beta burst, suggesting that the shape of the beta waveforms was, overall, less sinusoidal in the descending segment (DF = 17, t = 2.73, p = 0.0141; Supplementary Fig. 2A).

Next we explored the distribution of nonlinearities in the structure of beta bursts in greater detail, beginning by deriving an estimate of the sharpness of the extrema of the oscillations in the beta peaking-IMF. As noted earlier, this sharpness feature is thought to be associated with tight synchronisation in the inputs carrying the beta oscillation. The ANOVA summarised in Table 1C examines whether sharpness was modulated by burst segment, levodopa treatment or electrode contact pair. Both burst segment and contact influenced sharpness (F(1,156.9) = 4.62, p = 0.0332 and F (2,156.6) = 8.21, p = 0.0010, respectively), although these factors did not interact. The partial eta squared for the factor burst segment was 0.06, indicating that 6% of the total variance in sharpness could be attributed to the factor burst segment. Post-hoc tests indicated that sharpness was greater in the first, rising segment of the beta burst than in the second, descending segment (DF = 17, t = - 2.36, p = 0.0304; Supplementary Fig. 2B), and was greater at electrode contacts 23 and 12 than at contact 01, regardless of the segment of the beta burst, or drug state (DF = 17, t = 3.38, p = 0.0036 between contact 12 and 01; DF = 17, t = 2.25, p = 0.0377 between contact 23 and 01, paired t-tests). To explore localisation still further, we plotted the contact pair with the greatest sharpness index versus the contact pair in the same electrode with the greatest beta band power (Fig. 7). This revealed that the contact pair with the greatest sharpness tended to be more dorsal than that with the highest beta power.

Fig. 7.

Distribution of beta peaking-intrinsic mode function (IMF) power and sharpness across the three bipolar contacts of each electrode (OFF levodopa). Points indicate 18 electrodes/hemispheres. Sharpness tends to be more superior than peak beta in the same hemisphere.

The fact that the DoN was greater in the second, descending segment of the beta burst, and yet sharpness, which itself is a nonlinear feature, was more marked in the initial, rising segment of the beta burst, suggested that there might be a higher DoN in between the extrema of the beta burst in the later, descending segment. The ANOVA in Table 1D considered whether the DoN between extrema (DoN_gap) was modulated by burst segment, levodopa treatment or electrode contact pair. Only burst segment was a significant factor (F(1,159.6) = 10.36, p = 0.0016; Supplementary Fig. 2C) and the partial eta squared was 0.13, indicating that 13% of the total variance in DoN_gap could be attributed to the factor burst segment. Post-hoc testing confirmed that DoN_gap was greater in the later, descending segment than the initial, rising segment of the beta burst (DF = 17, t = 2.91, p = 0.0097). Thus, although the rising segment of the beta bursts had sharper extrema, the descending segment departed more from sinusoidal form between extrema, consistent with the higher overall DoN in the descending segment.

Next we explored whether there was a progression in the DoN_gap within the rising or descending segment of the beta bursts. Specifically, we hypothesized that the DoN_gap might be greatest towards the end of the descending segment, as the afferent beta drive becomes the DoN_gap over 100 ms periods, giving data for two sub-segments each for the rising and descending segments of the beta bursts. An ANOVA of DoN_gap with factor sub-segment revealed a significant effect (F(3,337.8) = 2.73, p = 0.0440). A planned simple contrast with the last sub-segment as reference demonstrated that there was a significant increase in DoN_gap in the (last) second sub-segment of the descending section of the beta burst (DF = 17, t = 2.39, p = 0.0290 compared to the second sub-segment of the rising section; Fig. 8A).

Fig. 8.

Finer structure of beta bursts. (A) Degree of Non-linearity in the gaps between extrema (DoN_gap) was estimated over 100 ms periods, giving data for two sub-segments each for the rising and descending segments of the beta bursts. The analysis of variance (ANOVA) of DoN_gap revealed a significant effect of sub-segment. A planned simple contrast with the last sub-segment as reference demonstrated that there was a large increase in DoN_gap in the (last) second sub-segment of the descending section of the beta burst (DF = 17, t = 2.39, p = 0.0290 compared to the second sub-segment of the rising section). (B) Beta sharpness was estimated over 100 ms periods, giving data for two sub-segments each for the rising and descending segments of the beta bursts. The ANOVA of beta sharpness revealed a significant effect of sub-segment. A planned simple contrast with the last sub-segment as reference demonstrated that there was a large decrease in sharpness in the (last) second sub-segment of the descending section of the beta burst (DF = 17, t = -3.40, p = 0.0034 compared to the second sub-segment of the rising section; DF = 17, t = -2.68, p = 0.0157 compared to the first sub-segment of the descending section). (C) The high gamma peaking-intrinsic mode function (IMF) difference inside and outside of extrema of the beta peaking- IMF was estimated over 100 ms periods, giving data for two sub-segments each for the rising and descending segments of the beta bursts. The ANOVA of high gamma peaking-IMF power difference revealed a significant effect of sub-segment. A planned simple contrast with the last sub-segment as reference demonstrated that there was a sharp fall-off in high gamma peaking-IMF difference inside and outside of extrema in the (last) second sub-segment of the descending section of the beta burst (DF = 17, t = -2.18, p = 0.0436 compared to the second sub-segment of the rising section). Mean ± standard errors are shown. Q1 and 2 refer to the first and last 100 ms periods of the rising segment of bursts and Q3 and 4 to the first and last 100 ms periods of the descending segment of bursts.

The DoN evaluates intra-wave frequency modulation rather than the effects of inter-wave frequency modulation. However, it is susceptible to changes in frequency. We therefore checked whether the above findings with respect to the rising DoN_gap towards the end of beta bursts might be confounded by a change in frequency. Neither the beta peaking-IMF averaged zero-crossing frequency (Table 1E), nor the variation in this beta peaking-IMF zero-crossing frequency (Table 1F) varied with burst segment, levodopa treatment or electrode contact pair.

Finally, we also explored whether there was a progression in sharpness within the rising or descending segment of the beta bursts. Specifically, we hypothesized that sharpness might fall off towards the end of the descending segment, as the afferent beta drive becomes less synchronised. To this end, we estimated the sharpness over 100 ms periods, giving data for two sub-segments each for the rising and descending segments of the beta bursts. An ANOVA of sharpness with factor sub-segment revealed a significant effect (F(3,310.3) = 3.05, p = 0.0288). A planned simple contrast with the last sub-segment as reference demonstrated that there was a significant decrease in sharpness in the (last) second sub-segment of the descending section of the beta burst (DF = 17, t = -3.40, p = 0.0034 compared to the second sub-segment of the rising section; DF = 17, t = -2.68, p = 0.0157 compared to the first sub-segment of the descending section; Fig. 8B).

3.2. IMFs in other frequency bands during beta bursts

We also investigated if IMFs outside of the beta range were disproportionately represented in one or other segment of the beta bursts. The ANOVA of IMF power with factors frequency (3 levels; high gamma peaking-IMF, alpha peaking-IMF and theta peaking-IMF), levodopa state and burst segment is shown in Table 2A. The high gamma peaking-IMF included the high frequency oscillatory activity reported in the STN of patients off-medication (López-Azcárate et al., 2010; Özkurt et al., 2011; van Wijk et al., 2016). Both burst segment (F(2,181.5) = 3.68, p = 0.0272) and levodopa state (F(2,181.5) = 12.30, p < 0.0001) showed significant interaction with frequencies. Post-hoc testing showed that alpha power was higher on levodopa than off levodopa (DF = 17, t = 2.00, p = 0.0308). Post-hoc testing also showed that theta peaking-IMF power was greater in the later, descending segment of beta bursts then in the initial rising segment (DF = 17, t = 2.55, p = 0.0207) and that theta power was higher on levodopa than off levodopa (DF = 17, t = 2.59, p = 0.0190). Post-hoc testing also showed that high gamma peaking-IMF power was higher off levodopa than on levodopa (DF = 17, t = -2.71, p = 0.0149).

Table 2.

Intrinsic mode function (IMF) characteristics of frequency bands other than beta during beta bursts. (A) Analysis of variance (ANOVA) of IMF power with factors burst segments (two levels; 1st and 2nd half of the burst), levodopa (two levels; OFF and ON medication), and frequency (three levels; high gamma peaking-IMF, alpha peaking-IMF and theta peaking-IMF). (B) ANOVA of high gamma peaking-IMF power with factors extrema (two levels; extrema or between extrema) and burst segment. Significant p values and those showing a trend are emboldened.

A: theta/alpha/gamma IMF power
Factor	DF	F-value	P-value
Segments	(1,181.8)	6.72	0.0103
Levodopa	(1,181.8)	11.48	0.0009
Frequencies	(2,181.3)	601.66	0.0000
Segments*Levodopa	(1,181.6)	0.31	0.5770
Segments*Frequencies	(2,181.5)	3.68	0.0272
Levodopa*Frequencies	(2,181.5)	12.30	0.0000
B: gamma IMF power distribution
Factor	DF	F-value	P-value
Extrema	(1,113.9)	38.14	0.0000
Segments	(1,113.3)	0.31	0.5793
Levodopa	(1,114.0)	36.05	0.0000
Extrema*Segments	(1,113.3)	0.05	0.8269
Extrema*Levodopa	(1,114.0)	0.66	0.4166
Segments*Levodopa	(1,113.3)	0.28	0.5963

Hemispheric sides as random factor

Variable is box-cox transformed

Post-hoc analysis:

1) Theta-IMF shows higher power in the descending segment.

2) Alpha-IMF and gamma-IMF show no differences in segments.

3) Theta-IMF and alpha-IMF show higher power in the ON medication.

4) Gamma-IMF shows higher power in the OFF medication.

Post-hoc analysis:

1) Extrema > between extrema

2) OFF > ON medication

3.3. Phase-amplitude coupling

Finally, we investigated whether the amplitude of the high gamma peaking-IMF in the STN might be increased around extrema in the beta peaking-IMF. An ANOVA of high gamma peaking-IMF power with factors extrema (two levels; beta extrema and between beta extrema), levodopa state and burst segment showed that the factor extrema was significant (F(1,113.9) = 38.1 4, p < 0.0001; Table 2B). This provides evidence of an interaction between distinct oscillatory processes (the beta peaking-IMF and high gamma peaking-IMF), independently of changes in the shape of the beta peaking-IMF waveform.

We also explored whether there was a change in the difference between high gamma peaking-IMF power in extrema and non-extrema over the course of beta bursts. Specifically, we hypothesized that this difference might fall off towards the end of the descending segment of bursts, as the afferent beta drive becomes more and more disorganized, theta power increases and entrainment of multi-unit activity by the beta afferent drive fails. To this end, we estimated the high gamma peaking-IMF difference inside and outside of extrema of the beta peaking-IMF over 100 ms periods, giving data for two sub-segments each for the rising and descending segments of the beta bursts. An ANOVA with factor sub-segment showed a significant effect (F(3,338.0) = 3.04, p = 0.0293). A planned simple contrast with the last sub-segment as reference demonstrated that there was a sharp fall-off in the difference in high gamma peaking-IMF inside and outside of the extrema of the beta peaking-IMF in the (last) second sub-segment of the descending section of the beta burst (DF = 17, t = -2.18, p = 0.0436 compared to the second sub-segment of the rising section; Fig. 8C). This suggests a failure of phase-amplitude coupling between the beta and high gamma activities towards the end of beta bursts.

4. Discussion

We have demonstrated a systematic pattern of evolution of nonlinear features during beta bursts recorded from the STN in PD patients. Overall, there was no difference in the power of beta peaking-IMFs between the rising and descending segments of the beta bursts, consistent with a roughly symmetrical spindle-form. However, the nature of the beta peaking-IMFs differed between the two segments of beta bursts. The rising segment was characterized by sharper beta oscillations at their extrema, whilst the descending segment was characterized by increased nonlinearities between the extrema and an increase in theta band activity. Beta bursts were of elevated amplitude off medication, whereas the theta power during beta bursts increased on medication.

4.1. Methodological considerations

We used the Hilbert–Huang transform to decompose the LFP signal into elementary IMF signals (Huang et al., 1998; Lopes-Dos-Santos et al., 2018; van Ede et al., 2018). Computation of the EMD, unlike convolution filters such as Fourier and Wavelet decompositions, captures intra-waveform changes in IMFs without dispersing their waveform characteristics into higher-frequency decompositions (Wu et al., 2007; Yang et al., 2018; Yeh et al., 2016). This feature of IMFs enables decompositions that are virtually free from harmonic artifacts, an important characteristic when evaluating PAC (Lopes-Dos-Santos et al., 2018; Shi et al., 2018; Yeh et al., 2016; Nguyen et al., 2019; Pittman-Polletta et al., 2014; Aru et al., 2015). The broadband nature of IMFs which follows the dyadic filter bank also ensures that higher-frequency IMFs include information about amplitude modulation indicative of PAC (Flandrin et al., 2004; Pittman-Polletta et al., 2014).

Irregular waveform changes in IMFs give broadband spectral components when using linear decomposition. These IMF spectra need not therefore be restricted to traditional frequency bands. However, here we made the assumption that IMFs peaking in the beta band captured the behavior of the beta bursts. This assumption was reasonable given our simulation in which the time evolving wavelet beta amplitude of the STN LFP lost its beta bursts when the beta-peaking IMF was subtracted. IMFs also retain characteristics due to intra-wave variations and this enables the computation of sharpness (Cole et al., 2017) and of the DoN (Huang et al., 2014). Sharpness highlights sharp changes around waveform extrema and the DoN measures how instantaneous frequency deviates away from the zero-crossing frequency and therefore considers phase slips over all intra-wave time points. The estimation of instantaneous frequency is made through the derivative of the Hilbert phase with respect to time, and such estimations can be noisy due to the derivation step (Huang et al., 2009). The effects of noise on the DoN were tested in simulations, and autocorrelation introduced to minimize its consequences (Fig. 2B).

4.2. Significance of sharper extrema in the rising segment of beta bursts

It is interesting to speculate on what can be inferred from the sharpness of oscillation extremata, especially in the context of recent interest in PAC. Inferences are necessarily indirect and based on the extent to which the LFP can be relied upon to reflect the pattern of underlying synchronization, and the hypotheses generated should be tested in the future with direct recordings of activity across neurons in the STN.

Sharpness of oscillatory LFP activity is thought to be associated with tight synchronisation in rhythmic inputs, albeit at the cortical level and on theoretical rather than empirical grounds (Sherman et al., 2016; Burke et al., 2015; Lozano-Soldevilla et al., 2016; Cole et al., 2017; Cole and Voytek, 2017; Vaz et al., 2017). Tight synchronisation may or may not be suprathreshold and sufficient to cause local spiking, which may, in turn, be evident as high frequency oscillations (Özkurt et al. 2011). The potential for sharpened oscillations to drive output is exemplified by cortical myoclonus, where rhythmic cortical waves with sharp troughs can drive highly synchronized alpha motor neuron discharges (Thompson et al., 1994; Brown and Marsden, 1996). In the case of the beta activity recorded in the STN, this input is also believed to be driven mainly from the cerebral cortex (Williams et al., 2002; Fogelson et al., 2006), with the oscillations perhaps being amplified by recurrent activity between the STN and globus pallidus externa (Leblois et al., 2006; Holgado et al., 2010; Marreiros et al., 2013). The inference from the present results is therefore that the rising segment of STN beta bursts is associated with a more tightly synchronized beta drive than the descending segment. The results also suggest a tendency for beta oscillations with sharper extrema to be maximal more dorsally in the STN than overall beta power. This distribution concurs with that in a previous report of the distribution of phase-amplitude coupling (PAC) in the STN (van Wijk et al., 2017), given that PAC may, in part, reflect sharpness (Cole et al., 2017; Cole and Voytek, 2017; Vaz et al., 2017; Yeh et al., 2016).

The relationship between extrema sharpness and PAC deserves further comment. PAC estimated using convolution filters like the fast Fourier Transform can reflect waveform distortion, the real amplitude modulation of one signal by the phase of another, or both. PAC has been reported between the beta phase and the amplitude of the high-frequency oscillation (HFO, ~ 200 Hz) in the STN, linked to symptom severity and demonstrated to be attenuated by movement and dopaminergic replacement therapy (López-Azcárate et al., 2010; van Wijk et al., 2016). Evidence suggests that the PAC in the STN at the upper range of the high gamma activity defined here reflects the locking of (possibly bursting) unit activity to input beta-oscillations (Meidahl et al. 2019). However, whether waveform distortion contributes to beta-high gamma PAC in the STN has yet to be established. This may, in part, be because the polarity of the sharpened extrema is not fixed in bipolar recordings of LFPs, as this depends on the orientation of the contact pair with respect to the generator. We allowed for this by averaging sharpness estimates across the peaks and troughs of beta oscillations, and confirmed increased sharpness during the rising segment of beta bursts. This in-of-itself could explain beta-high gamma PAC in the STN, at least over the lower frequencies in our high gamma band (60–250 Hz). However, we also found that high gamma peaking-IMFs were increased in amplitude at the peaks and troughs of the beta oscillations, indicative of the genuine amplitude modulation of one process by the phase of another. The fact that nonlinear features were estimated by EMD means that the high gamma peaking-IMFs were most unlikely to be due to filtering artifacts, such as harmonics, related to waveform sharpness and caused by the convolution filters usually used in PAC analysis (Pittman-Polletta et al., 2014; Shi et al., 2018; Yeh et al., 2016; Yeh and Shi, 2018). Our data therefore suggest that beta-high gamma PAC within the STN reflects both distortion of the beta oscillation and interactions between the beta and high gamma oscillations. As our low pass filter was at 250 Hz our signal extended to the middle of the range of high frequency oscillations recorded in the off medication state (López-Azcárate et al., 2010; Özkurt et al. 2011; van Wijk et al., 2017). These oscillations are thought to relate to multi-unit activity in the STN of PD patients off levodopa (Sanders, 2016; Meidahl et al., 2019), so that the component of PAC involving these high frequencies may index entrainment of STN output to bursts of cortical drive to STN (Meidahl et al., 2019). Nevertheless, we did not capture the whole range of high frequency activity thought to reflect aspects of multi-unit activity, and which extends to even higher frequencies on levodopa (Özkurt et al. 2011). As such our 250 Hz low-pass filter may have led us to under-estimate the contribution from amplitude modulation of multi-unit activity.

4.3. Significance of the increased DoN, decreased sharpness and increased theta activity in the descending segment of beta bursts

The elevated DoN in the later, descending segment of beta bursts is evidence that, overall, beta oscillations were less sinusoidal than in the ascending segment, despite the greater sharpness in the latter. The inference is that other frequency components contaminate the beta oscillation and are not limited to the extrema in the descending segment of bursts. We confirmed this by estimating the DoN_gap which was higher in the later, descending segment of the beta burst. This change in the relative purity of the beta oscillation in the later part of the burst may stem from an increase in phase slips which give changes in instantaneous frequency. Thus the beta drive becomes progressively more disorganized during the descending slope of the beta burst, and this change may be linked to the loss of extrema sharpness of the beta peaking-IMF in the latter half of the descending phase of the beta burst. The latter might suggest a progressive loss of tight synchronization within the beta afferent drive to STN, predisposing the descending segment to phase slips in the face of spontaneous stochastic events (Hurtado et al., 2005) and competing oscillations. With respect to the latter, the theta band contamination in the descending segment of the beta burst may reflect a relatively time delayed input to the STN, that possibly competes with the beta drive and progressively helps degrade entrainment to the original beta oscillation. Its origin is unknown, but it is interesting that theta activity in the STN LFP was elevated by treatment with levodopa in our study (see also Rodriguez-Oroz et al., 2011), and the same treatment shortens beta burst duration (Tinkhauser et al., 2017a). Finally, we suggest that the drop in the relative locking of high gamma peaking-IMF activity to the extrema of the beta peaking-IMF in the latter half of the descending segment of the beta burst could be taken as evidence for the failing entrainment of multi-unit activity (and hence STN output) by the beta afferent drive.

4.4. Possible confounds and conclusions

We assessed the dynamics in the waveform within beta bursts with a minimum duration of 400 ms in patients with PD. As such it remains to be proven if our observations apply, or not, to briefer beta bursts whether recorded in patients or healthy humans and other animals (Leventhal et al., 2012; Feingold et al., 2015; Shin et al., 2017; Little et al., 2019). In addition, as we recorded LFPs a few days after electrode implantation, temporary stun effects may have influenced our findings through the suppression of beta-band phenomema (Chen et al, 2006). The dependency of non-linear measures on signal-to-noise ratios also impacts on our results. However, our main contrast was between the rising and descending segments of beta bursts that tend to be spindle-shaped and approximately matched in beta power. In addition, we performed autocorrelation within each burst segment before estimating the DoN and DoN_gap, to limit the noise sensitivity of these measures. Importantly, our inferences principally relate to changes in synchronization during the evolution of bursts, and it should be stressed that more definitive conclusions would require the simultaneous recording of two or more neurons during bursts in the LFP. Finally, our patient sample was relatively small and, moreover, we treated recordings from different hemispheres as independent variables. In particular, we recorded too few patients to examine any association between our findings and particular phenotypic patterns.

With the above caveats in mind, we were able to show an evolution in the organization of subthalamic beta bursts as they passed through rising and decreasing segments. The change in nonlinear features was compatible with progressive entrainment of local neurons by a tightly synchronised extrinsic beta drive during the rising amplitude segment, followed by the loss of such entrainment in the face of weakening of the tight synchronization in the afferent drive, multiple phase slips and the rise of a competing theta drive in the falling amplitude segment of the beta burst. Levodopa was found to increase this theta drive, which may help explain why beta bursts tend to be shorter in duration in the levodopa-treated state.

5. Conclusions

Phasic bursts of beta band synchronisation are linked to motor impairment in Parkinson’s disease. We provide evidence that suggests progressive entrainment of local neurons by a tightly synchronised afferent beta drive during the rising amplitude segment of bursts, followed by the loss of such entrainment in the face of weakening synchronization in the afferent beta drive, multiple phase slips and the rise of a theta drive in the falling amplitude segment of beta bursts. Levodopa increases the theta drive. These insights help explain how beta bursts pattern subthalamic outflow and why they terminate. Moreover, they motivate a search for the source of theta activity that increases as bursts fail, least this can be further manipulated for therapeutic purposes.

highlights.

• Bursts of beta activity have been linked to motor impairment in Parkinson’s disease.

• Termination of bursts is associated with characteristic changes in oscillation shape.

• These suggest input drive desynchronization, increased theta activity and phase slips.

Abbreviations used

AU

arbitrary unit

DoN

Degree of Non-linearity

EMD

Empirical mode decomposition

IMF

Intrinsic mode function

PD

Parkinson’s disease

LFP

local field potentials

STN

subthalamic nucleus

UPDRS

Unified Parkinson’s Disease Rating Scale