Model Choice, Missing Data and Taxon Sampling Impact Phylogenomic Inference of Deep Basidiomycota Relationships

Abstract

Resolving deep divergences in the tree of life is challenging even for analyses of genome-scale phylogenetic datasets. Relationships between Basidiomycota subphyla, the rusts and allies (Pucciniomycotina), smuts and allies (Ustilaginomycotina) and mushroom-forming fungi and allies (Agaricomycotina) were found particularly recalcitrant both to traditional multigene and genome-scale phylogenetics. Here, we address basal Basidiomycota relationships using concatenated and gene-tree based analyses of various phylogenomic datasets to examine the contribution of several potential sources of bias. We evaluate the contribution of biological causes (hard polytomy, incomplete lineage sorting) versus unmodeled evolutionary processes and factors that exacerbate their effects (e.g. fast-evolving sites and long-branch taxa) to inferences of basal Basidiomycota relationships. Bayesian MCMC and likelihood mapping analyses reject the hard-polytomy with confidence. In concatenated analyses, fast-evolving sites and oversimplified models of amino acid substitution favored the grouping of smuts with mushroom-forming fungi, often leading to maximal bootstrap support in both concatenation and coalescent analyses. On the contrary, the most conserved data subsets grouped rusts and allies with mushroom-forming fungi, although this relationship proved labile, sensitive to model choice, to different data subsets and to missing data. Excluding putative long branch taxa, genes with high proportions of missing data and/or with strong signal failed to reveal a consistent trend toward one or the other topology, suggesting that additional sources of conflict are at play. While concatenated analyses yielded strong but conflicting support, individual gene trees mostly provided poor support for any resolution of rusts, smuts and mushroom-forming fungi, suggesting that the true Basidiomycota tree might be in a part of tree space that is difficult to access using both concatenation and gene-tree based approaches. Inference-based assessments of absolute model fit strongly reject best fit models for the vast majority of genes, indicating a poor fit of even the most commonly used models. While this is consistent with previous assessments of site-homogenous models of amino acid evolution, this does not appear to be the sole source of confounding signal. Our analyses suggest that topologies uniting smuts with mushroom-forming fungi can arise as a result of inappropriate modeling of amino acid sites that might be prone to systematic bias. We speculate that improved models of sequence evolution could shed more light on basal splits in the Basidiomycota, which, for now, remain unresolved despite the use of whole genome data.

Introduction

Accurately resolving phylogenetic relationships across the Tree of Life is one of the central challenges for evolutionary biologists. Phylogenetic datasets relying on one to a few genes have left many phylogenetic questions open, for which the use of genomic data appeared to be a magic bullet (Gee 2003; Rokas et al. 2003; Delsuc et al. 2005; Philippe et al. 2005; Misof et al. 2014; Prum et al. 2015). Genome-scale datasets are 10–1000 times larger than the size of traditional phylogenetic datasets, virtually eliminating data availability and stochastic error as the limiting factor for resolving phylogenetic questions and eliminating the impact of stochastic error, offering great promise for resolving several historically recalcitrant nodes (Rokas et al. 2003; Niehuis et al. 2012; Misof et al. 2014; Telford et al. 2015). Despite the early promise of initial genome-scale studies, phylogenomic datasets present fundamentally new challenges in terms of dataset assembly, effects of missing data and the strength and sources of incongruence (Soltis et al. 2004; Philippe et al. 2005; Jeffroy et al. 2006; Galtier and Daubin 2008; Philippe et al. 2011; Kumar et al. 2012).

Compared to traditional phylogenetics, phylogenomic datasets often yield highly resolved, often maximally supported trees. Increasing the amount of data alleviates some sources of error, but not others: inadequate modeling of the data can lead to systematic biases in the estimation procedure (Philippe et al. 2005; Jeffroy et al. 2006; Philippe et al. 2011; Kumar et al. 2012). In such cases, there is no guarantee that the true phylogenetic signal dominates the inferred topology, even if it is strongly supported, as systematic errors can inflate support values for incorrect topologies under some circumstances (Phillips et al. 2004; Philippe et al. 2005; Rodriguez-Ezpeleta et al. 2007; Philippe et al. 2011; Parks et al. 2012; Sharma et al. 2014). Systematic error can arise as a result of improper modeling of biological phenomena (e.g. heterotachy, compositional bias, rate heterogeneity, incomplete lineage sorting (ILS), horizontal gene transfer, etc.) (Phillips et al. 2004; Rodriguez-Ezpeleta et al. 2007; Hallstrom and Janke 2010; Parks et al. 2012; Szollosi et al. 2012; Sharma et al. 2014; Sharma et al. 2015; Smith et al. 2015; Whelan et al. 2015; Li et al. 2016; Romiguier et al. 2016) or technical problems (e.g. poor model fit, biased taxon or gene sampling, orthology inference) (Dunn et al. 2008; Hejnol et al. 2009; Simon et al. 2012; Misof et al. 2013; Dell’Ampio et al. 2014; Lanfear et al. 2014; Yang and Smith 2014; Chen et al. 2015; Pisani et al. 2015; Smith et al. 2015; Whelan et al. 2015; Hosner et al. 2016), both of which can lead to biased or incorrect parameter estimates in phylogenomic analyses, including topology (Philippe et al. 2011; Kumar et al. 2012). Furthermore, effects of taxa on long branches, heterotachy, or fast-evolving sites may be exacerbated by systematic errors, again, leading to biased estimates of topology and/or other parameters.

Fungi have been at the forefront of phylogenomics due to the ease of sequencing their relatively small and non-repetitive genomes (Grigoriev et al. 2014), and have been among the first groups to be subjected to phylogenomic analyses (Rokas et al. 2003; Fitzpatrick et al. 2006; Robbertse et al. 2006; Aguileta et al. 2008), yet, several deep divergences in the fungal tree remain unresolved. Basal relationships of the Basidiomycota have been particularly recalcitrant (Padamsee et al. 2012; Aime et al. 2006; Hibbett 2006; Hibbett et al. 2007; Matheny et al. 2007; Kohler et al. 2015; Nagy et al. 2016) and recent phylogenomic treatments have recovered strongly supported contradicting relationships (Nagy and Szollosi 2017). The basal divergence of Basidiomycota was estimated at ca. 450 - 530 Ma (Taylor and Berbee 2006; Floudas et al. 2012; Chang et al. 2015) and comprises three subphyla, the Pucciniomycotina (rusts and allies), the Ustilaginomycotina (smuts and allies) and the Agaricomycotina (mushroom-forming fungi and allies). For simplicity, these will be referred to as the rust lineage (abbreviated ‘R’), the smut lineage (‘S’) and the mushroom-forming lineage (‘M’), respectively, in this paper. Ultrastructural characters can be difficult to interpret (Lutzoni et al. 2004), but seem to favor the grouping of smuts with mushroom-forming fungi, based on the development of membrane-bounded septal pores, and swollen pore margins in both. Traditional multilocus studies have generally found weak support for various groupings of these clades (Swann and Taylor 1993; Berres et al. 1995; Aime et al. 2006; James et al. 2006; Hibbett et al. 2007; Matheny et al. 2007), whereas genome-scale studies have provided often strongly supported but conflicting relationships. In most previous studies, smuts and mushroom-forming fungi grouped together to the exclusion of rusts (referred to as R(S,M) topology hereafter) (Padamsee et al. 2012; Ebersberger et al. 2012; Zajc et al. 2013; Toome et al. 2014; Kohler et al. 2015; Sharma et al. 2015, Zhao et al 2017), although rusts as the sister group of smuts (hereafter: M(R,S) topology) (Kohler et al. 2015) and rusts as the sister group of mushroom-forming fungi (hereafter: S(R,M) topology) (Medina et al. 2011; Nagy et al. 2014; Riley et al. 2014) have also been reported. Furthermore, analyses of the same datasets under different models or methods have yielded contradicting results (Kohler et al. 2015), suggestive of evolutionary processes not captured by the models or methods used. For example, taxon sampling was biased towards mushroom-forming fungi in most previous phylogenomic studies, with only 1–2 exemplars from the rust and smut lineages included. Biased taxon sampling can compromise phylogenomic inference (Dunn et al. 2008; Philippe et al. 2011; Simon et al. 2012; Pisani et al. 2015) and has been suggested as a potential factor underlying the difficulty of resolving basal Basidiomycota relationships (Nagy et al. 2016). Notably, members of both the rust and smut lineages have experienced massive gene losses compared to mushroom-forming fungi and Ascomycota (Nagy et al. 2014; Toome et al. 2014; Kijpornyongpan et al. 2018), which may impact the number of genes available for phylogenetic inference and thus the reconstructed relationships. It has also been suggested that basal relationships of the Basidiomycota might have been shaped by fast successive diversification events and thus be better described as a hard polytomy (Kohler et al. 2015).

The selection of orthologous groups of genes is one of the most important determinants of dataset quality (Dunn et al. 2008; Simon et al. 2012; Yang and Smith 2014; Smith et al. 2015; Whelan et al. 2015). Unwanted inclusion of non-orthologous genes (e.g. deep paralogs, horizontally acquired genes) can introduce both noise and incongruence in a dataset, whereas the inclusion of too many (non-random) missing data in concatenated analyses can influence phylogenetic signal (Hejnol et al. 2009; Misof et al. 2013; Dell’Ampio et al. 2014; Chen et al. 2015; Hosner et al. 2016; Streicher et al. 2016; Xi et al. 2016, Lemmon et al 2009). It is widely accepted that tree-based methods are most accurate for determining ortholog/paralog relationships (Gabaldon 2008; Kristensen, et al. 2011; Boussau et al. 2013; Kocot et al. 2013; Yang and Smith 2014; Kocot et al. 2017), however, they have rarely been the choice in phylogenomic dataset assembly in favor of simpler, blast- or similarity-based methods (for exceptions see Dunn et al. 2008; Hejnol et al. 2009; Smith et al. 2011).

In this study we set out to identify the principal causes of phylogenetic uncertainty among the three Basidiomycota subphyla. We explore two major sources of topological uncertainty: biological reality and systematic bias. We considerably increase the number of sampled rust and smut species and employ a gene-tree-based orthogroup inference pipeline that minimizes the chance for including non-orthologous genes and thus technical sources of gene tree conflict. Among the biological explanations, we test the hypothesis that the observed topological variation is indicative of a near simultaneous divergence at the base of Basidiomycota. We also explore contradicting or weak signal in the sampled genes and compare concatenation to species-tree methods to assess the role of ILS. Among sources of systematic error, we consider long-branch attraction, heterotachy, and model violation in shaping topological inferences. We assess the fit of site-homogenous models with fixed matrices of amino acid frequencies and compare inferences to those from site-heterogenous models and those that allow lineage-specific evolutionary rates. Our analyses detect multiple sources of bias in the datasets that complicate accurate resolution of ancient Basidiomycota relationships and highlight several general challenges of phylogenetic inference from genomic data.

Materials and Methods

Data Assembly - Taxon sampling, selection of orthologous groups, and alignment uncertainty

We used complete genome sequences of 67 species, representing the three subphyla of Basidiomycota plus 10 representatives of the Ascomycota and three representatives of Mucoromycota as outgroups (Table S1, see Supplementary Material at doi:10.5061/dryad.g0db883). The Basidiomycota included 54 species: 32 mushroom-forming fungi (Agaricomycotina, including representatives of the earliest-diverging lineage, Wallemiomycetes, fide Padamsee et al. 2012 and Dentinger et al. 2016), 12 species from 9 orders from across the rust lineage (Pucciniomycotina, selected fide Aime et al. 2014) and 10 species from 6 orders across the smut lineage (Ustilaginomycotina, selected fide Kijpornyongpan et al. 2018). We performed all-vs-all BLAST on non-redundant predicted protein sequences in the 67 input genomes using mpiblast 1.6.0 (Darling et al 2004). Proteins showing significant hits were clustered based on similarity using the Markov clustering algorithm implemented in Mcl 14-137 (van Dongen 2000) with an inflation parameter of 2.0. Clusters containing 33 to 134 proteins (50 to 200% of the number of species analyzed) were further analyzed as these are most likely to contain conserved, single-copy genes for the highest number of species. We hereafter refer to these single-copy clusters of genes simply as ‘genes’. Multiple sequence alignments and gene trees were estimated for each of these genes using PRANK v.140603 (Loytynoja and Goldman 2008) and RAxML 7.2.3 (Stamatakis 2014), respectively (both with default parameters). The WAG model of protein sequence evolution with gamma-distributed rate heterogeneity was used in RAxML. We then screened the resulting genes trees for gene duplications and retained only those that had no duplications at all (only a single protein per species) or terminal duplications only (i.e. inparalogs), using a customized perl script (available from the authors upon request). Genes containing deep paralogs were discarded. Of inparalogs, we retained the one with the shortest root-to-tip patristic distance. From the resulting gene families we further excluded ones that contained overly divergent, potentially non-orthologous proteins by calculating the contribution of each terminal branch length to the total tree length; gene trees in which a single terminal accounted for >60% of the total tree length were eliminated (dos Reis et al. 2012).

We used GBlocks 0.91b (Castresana 2000) to remove poorly aligned regions from the alignments using three levels of stringency: first, with default parameters, second with ’-b2=50 -b3=10 -b4=5’ and third with ’-b2=40 -b3=20 -b4=2’. For comparison, we also analyzed the original gene alignments (no sites removed). Next, we concatenated gene families that had representatives in >50% of the species and a final trimmed length >50 amino acid sites. This resulted in three trimmed datasets (referred to as 314G, 824G and 901G datasets) corresponding to three levels of stringency applied in GBlocks and the untrimmed data (referred to as the 950G dataset).

Initial phylogenetic analyses

All datasets were analyzed using the PTHREADS version of RAxML 7.2.3 (Stamatakis 2014) and MrBayes 3.2.6 (Ronquist and Huelsenbeck 2003). For maximum likelihood and Bayesian (MrBayes) analysis we partitioned the dataset by gene and used the best fit model selected by Prottest (version 3.4.2) (Abascal et al. 2005) for each partition with gamma-distributed rate heterogeneity. Bootstrap analyses were run with 100 replicates. The 950G dataset was not subjected to bootstrapping due to the prohibitive run time of the analysis. MrBayes was run with 2 independent replicates with 4 chains each, for 1,000,000 generations and a partitioned model (best fit for each partition) with 250,000 generations as burn-in. Convergence was assessed by inspecting clade posterior probabilities and by the bpcomp and tracecomp functions of Phylobayes.

Gene content based phylogeny

We also reduced the variability in our dataset by constructing a matrix based on gene presence/absence data in the 67 fungal genomes and assessed support for each of the three alternative conformations of rusts, smuts and mushroom-forming fungi. A binary presence-absence (PA) matrix was constructed for each of the protein clusters (50,971) against all the species (67). No distinction was made in the coding between single-copy and multicopy genes. Next, a maximum likelihood tree was inferred using RAxML 7.2.3 with a GAMMA model of rate heterogeneity and 1000 bootstrap replicates. We calculated the number of gene family origins and losses needed to explain the data under the two competing conformations as an independent test of topologies. To this end, we manually rearranged the ML tree in Mesquite 4 (Maddison and Maddison 2009) to create trees with two alternative topologies: S(R,M) (union of Pucciniomycotina + Agaricomycotina) and R(S,M) (union of Ustilaginomycotina + Agaricomycotina). We then mapped gene family gains and losses using Dollo parsimony, recording the total number of gains and losses. The two competing topologies were then compared using the approximately unbiased test as implemented in CONSEL (Shimodaira and Hasewaga 2001).

Biological sources of topological uncertainty – Information content, hard polytomy, and incomplete lineage sorting

We tested the hypothesis that the Pucciniomycotina, Ustilaginomycotina and Agaricomycotina diverged from each other in fast successive diversification events and thus, their relationships would be best described by multifurcation, using two approaches. We first used four-quartet likelihood mapping (FcLM) (Strimmer and von Haeseler 1997), which examines the dispersion of information content among three possible topologies at a given node using all possible splits in the alignment. FcLM yields, for each four-taxon subset of the data, information on which resolution it supports in a likelihood framework. Support in each quartet is visualized as a triangle, in which three angles correspond to three resolved trees, whereas regions between angles reflect cases in which it is difficult to distinguish between topologies. This was done under the WAG model with gamma-distributed rate heterogeneity (4 categories) and examined 100,000 quartets. To address saturation levels of the datasets, we calculated uncorrected and patristic distances from the trimmed single-gene alignments and corresponding ML gene trees using the ‘dist.hamming’ and ‘cophenetic.phylo’ functions of the phangorn 2.1.1 (Schliep 2011) and ape 4.0 (Paradis et al. 2004) R packages, respectively. We also summarized information content by gene, using two metrics, and assessed the relationship between information content and topology. The first metric is based on the number of parsimony-informative characters (PIC) per alignment and the second is a Bayesian approach (BI) for summarizing information content (Lewis et al. 2016). The latter is based on measuring the change in entropy between the prior and posterior marginal distributions of topologies as implemented in Galax v. 1.1 (Lewis et al. 2016). We then determined the correlation between information content and mean support for each hypothesis under each model using the Pearson product-moment correlation coefficient.

. Phycas 2.2.0 (Lewis et al. 2010) was used to run Bayesian Markov Chain Monte Carlo (MCMC) analyses that allows the prior on tree topologies to include polytomous trees. We ran 100,000 cycles with 25,000 cycles as burn-in and an unpartitioned GTR+G model of sequence evolution on the 314G dataset (our attempts to run partitioned analyses failed due to the prohibitive memory requirements of the analyses). We ran analyses under a range of flat to polytomy-friendly priors, including polytomy and resolution class priors by setting the mcmc.topo_prior_c parameter between 1 and 3. Analyses were run in triplicate.

To account for gene tree incongruence (e.g. resulting from incomplete lineage sorting) we used the Accurate Species Tree Algorithm (ASTRAL-II), to estimate species trees from individual gene trees (Mirarab and Warnow 2015; Mirarab et al. 2016). We inferred gene trees from each of the trimmed gene alignments for the 314G, 824G and 901G gene datasets in RAxML under the WAG+G model with 100 bootstrap replicates. Astral-II 4.7.8 was used to summarize gene trees into a species tree with 100 multi-locus bootstrap replicates.

Methodological sources of topological uncertainty – fast-evolving sites, long-branch attraction, heterotachy, and absolute model fit

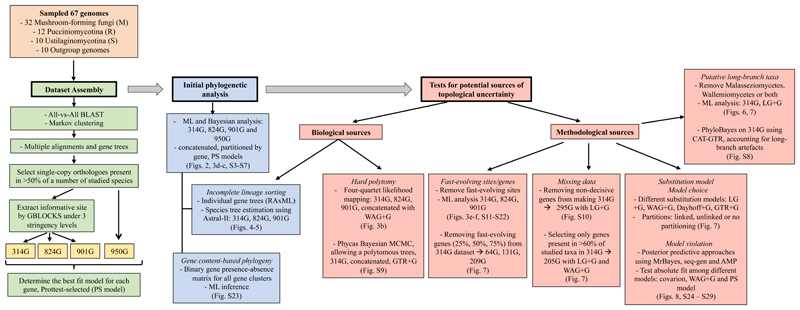
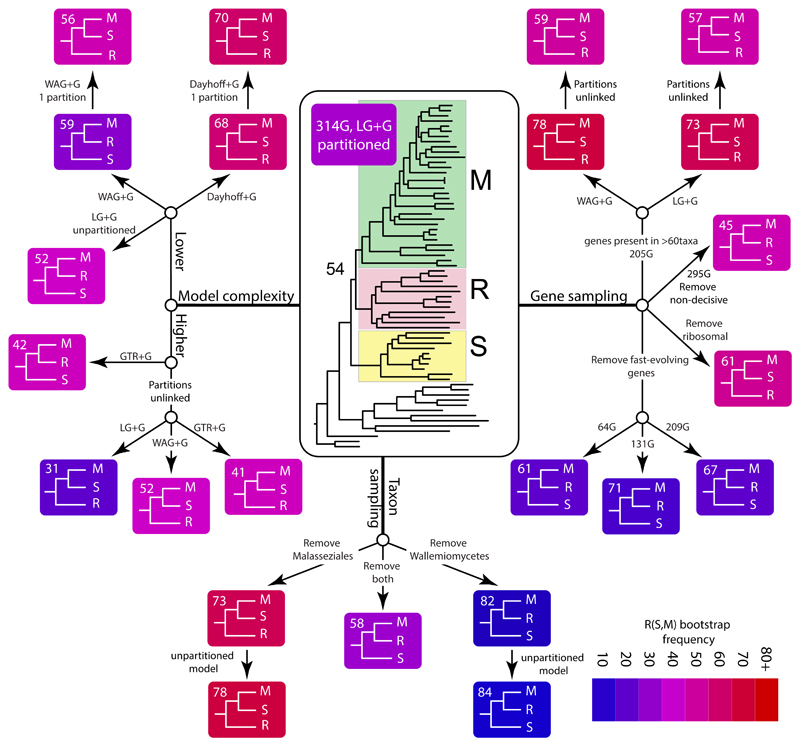
We performed several modifications to the original datasets to examine the sensitivity of the results to removing various data subsets (see Fig 1).

Figure 1.

Overview of the analytical strategy followed and the major hypotheses tested in this paper. Yellow boxes are the major datasets used in the study.

Fast evolving sites

In order to determine the influence of fast-evolving sites on phylogenetic inferences, we used TIGER 1.02 (Cummins and McInerney 2011) to sort amino acid sites into 20 rate categories. Next, we sequentially removed the fastest evolving sites from each concatenated dataset and inferred ML trees with 100 bootstraps (as above) for each dataset for the 901G, 824G and 314G datasets. We removed additional rate categories until rusts, smuts, mushroom-forming fungi and Ascomycetes were not monophyletic, which presumably marked the loss of a significant portion of the phylogenetic signal in the dataset.

Missing data

We assessed the impact of missing data in two ways. First, we identified genes that are decisive with respect to the relationships of rusts, smuts, and mushroom-forming fungi. Genes decisive for basal Basidiomycota relationships are defined as ones with at least one representative from each of the three subphyla (Dell’Ampio et al. 2014). Indecisive genes were first excluded from concatenated datasets and ML bootstrap analyses were run as described above. Second, to produce a dataset with a much lower amount of missing data than in the original 314G dataset, we excluded genes that were present in <60 species, and re-run ML bootstrap analyses, as above.

Putative long branch taxa

Based on our initial phylogenetic analyses (Fig. 2), we identified two particularly divergent classes, the Wallemiomycetes and the Malasseziomycetes, that may be impacted by substitutions unaccounted for by standard models. We took two approaches for assessing the impact of these taxa, and long-branch attraction in general, on topological inferences. We focused on the 314G dataset and alternately removed the Wallemiomycetes, the Malasseziomycetes, and both from each alignment and reanalyzed the resulting alignments. In addition, we ran PhyloBayes 4.1 (Lartillot et al. 2013) under the CAT-GTR model, which has been shown to better account for long-branch attraction artifacts (Lartillot et al. 2007). Each analysis was run with 2 independent replicates of 8,000 cycles with one chain each. The first 1,000 cycles were discarded as burn-in.

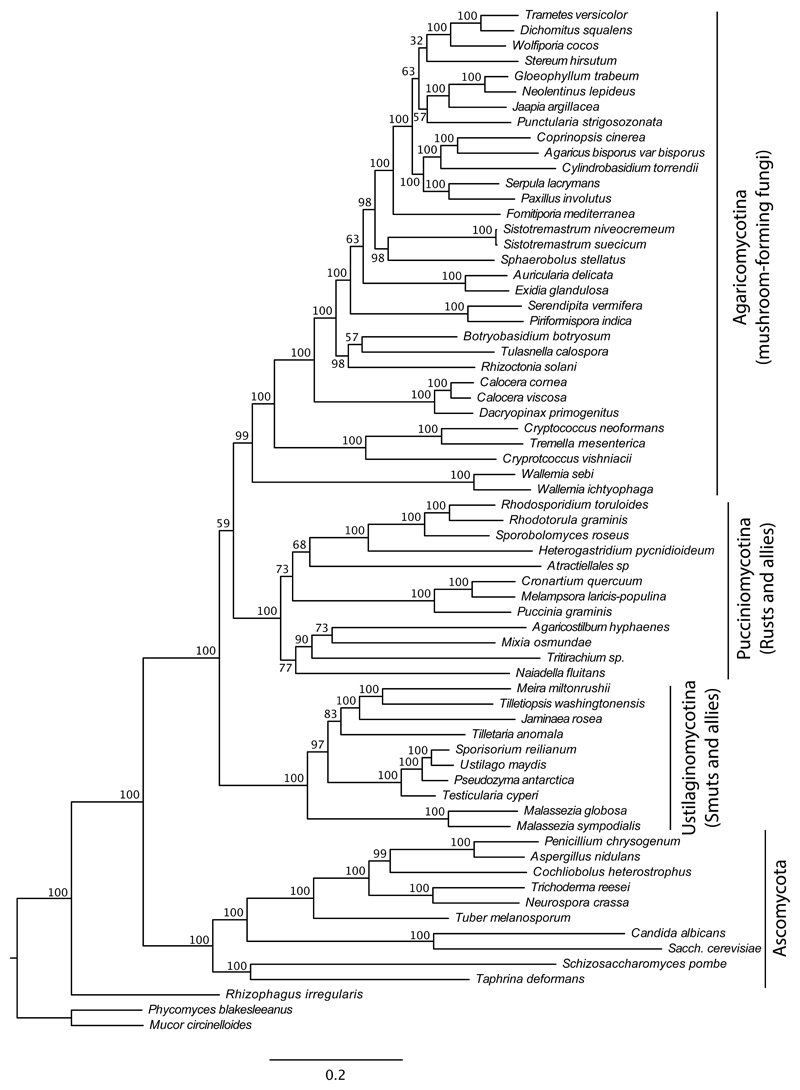
Figure 2.

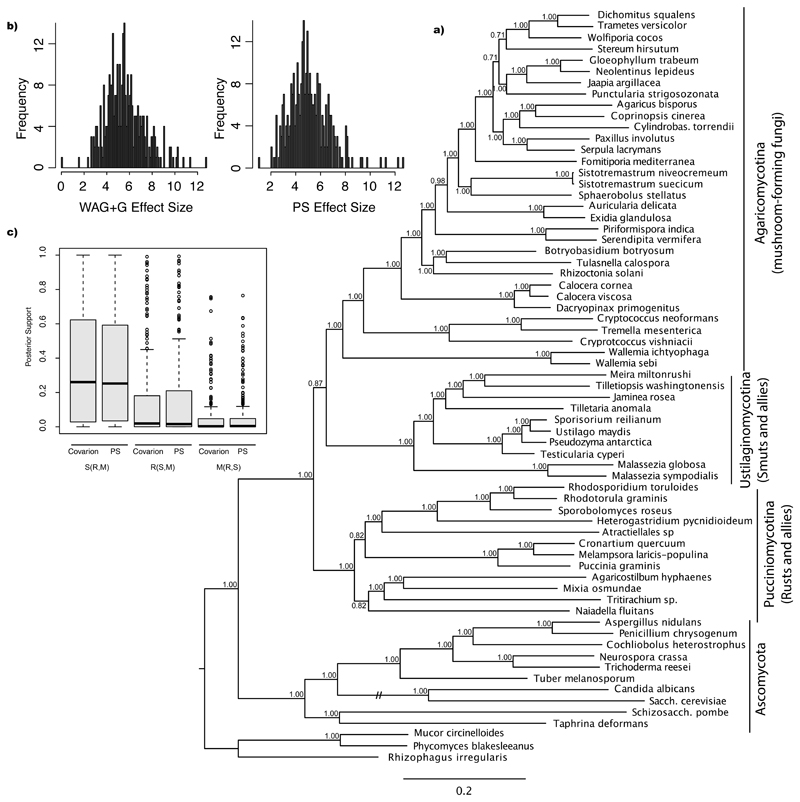
Maximum Likelihood phylogeny inferred from the concatenated 314G dataset. ML bootstrap percentages are shown above branches.

Assessments of absolute model fit

In order to determine the absolute fit of the data to the WAG+G model (a commonly used model in concatenated phylogenomics) and the best fit models, hereafter referred to as PS (Prottest-selected), we used a posterior predictive approach following (Doyle et al. 2015). We chose to focus on the most conservative dataset (314G) to understand the impact of model violation on topological variation. We also attempted to assess the absolute fit of the data to the covarion model (Huelsenbeck 2002) but were unable to simulate data in seq-gen as described below under the covarion model. The alignment of each gene/protein was analyzed under the WAG+G model and the PS model using MrBayes v.3.2.5 (Huelsenbeck and Ronquist 2001; Ronquist and Huelsenbeck 2003; Ronquist et al. 2012) with the joint posterior distribution of topologies and parameter values estimated with a chain length of 2 million generations, 4 replicate MCMC runs, and 4 Metropolis-coupled chains per run. Samples were drawn every 800 generations for a total of 2500 samples from each MCMC run. Runs were considered converged if the average standard deviation of split frequencies was below 0.05, the minimum ESS values for all parameters was greater than 200 and the Potential Scale Reduction Factor (PSRF) was close to 1 after discarding the first 25% of samples as burn-in.

One hundred generations were sampled evenly across the posterior distribution of each empirical analysis. A posterior predictive dataset was simulated with seq-gen v 1.3.3 (Rambaut and Grassly 1997) according to the model under which the empirical data were analyzed (WAG+G or PS) using the topology and parameter values sampled from the posterior. Four genes were excluded because the PS model is not one of the simulation models available in seq-gen. This resulted in 100 posterior predictive datasets per alignment per model (62,400 posterior predictive datasets). The resulting posterior predictive datasets were analyzed in the same manner as the empirical datasets, but reducing the number of generations to 1 million, the sampling frequency to every 400 generations, and the number of replicate runs to 2.

To determine the degree to which model violation might be impacting topological inferences, we calculated several test statistics using AMPv0.99e (Brown 2014). We then used one of these, the 9999th 10,000 quantile in the ordered vector of pairwise symmetric differences (unweighted Robinson-Foulds distances; (Robinson and Foulds 1981)) to detect deviations between inferences drawn from the empirical data and those drawn from the posterior predictive data. We calculated two-tailed P-values as well as effect sizes to determine the degree to which the empirical values fall outside of the distribution of the posterior predictive test statistic. The difference between the median value of the test statistic from the posterior predictive inferences and the empirical value divided by the standard deviation of the posterior predictive test statistics is the effect size. The effect size represents the degree to which inferences drawn from the empirical data deviate from those expected under the respective model, with an effect size of zero representing perfect fit between the model and the data.

Heterotachy

We also assessed the impact of heterotachy, i.e. site-specific rate variation over time, on topological variation by analyzing each alignment under the covarion model in MrBayes v. 3.2.5. Unable to test absolute fit of the covarion in a posterior predictive framework as described above, we opted to test the relative fit of the WAG+G, PS, and the PS + covarion models using the harmonic mean estimator of the marginal log-likelihood to calculate the log of the Bayes Factors (ln(BF)) (attempts were made to calculate BF using a stepping stone analysis, but these gave nonsensical likelihoods under the covarion). The relative fit for each competing model was approximated by the difference between the marginal log-likelihood of M₀ and of M₁. Values of ln(BF) greater than 0 represent support for M₁ over M₀ (Kass and Raftery 1995).

In order to determine the impact of model choice on support for basal Basidiomycota relationships, we compared the mean posterior support across genes for each of the three topological hypotheses analyzed under the PS model selected on the basis of Bayes Factor comparisons. To estimate the impact of heterotachy on topological inferences, we examined the mean support for each topological hypothesis under the covarion versus support for each hypothesis under the PS model using a Student’s t-test for those genes that best fit the covarion. We also determined if there was a greater than expected increase in mean support from those genes that best fit the covarion model and were analyzed under the covarion by comparing mean support to a null distribution of expected support under the covarion model. We randomly selected sets of posterior support values equal in size to the number of genes that best fit the covarion and calculated the mean support for each hypothesis and repeated the procedure one million times. An increase in mean support for a given hypothesis under the covarion was considered significant if it was in the upper 5% of the null distribution.

While the best fit model may provide the best available means to account for the evolutionary complexity that have generated the data, the increased complexity of the covarion model may lead to a decrease in topological support when information content is low compared to the number of parameters to be estimated. Under this scenario, we might expect increased support for particular relationships when using the simpler model. In order to test this hypothesis, we compared the mean support values for each topological hypothesis under the PS model to that under the covarion model using a Student’s t-test for those genes that best fit the PS model. We also determined if there was a greater than expected increase in mean support from those genes that best fit the PS model and were analyzed under the PS model by comparing mean support to a null distribution of expected support under the PS model. We randomly selected sets of posterior support values equal in size to those that best fit the PS model and calculated the mean support for each hypothesis and repeated the procedure 1x10⁶ times. An increase in mean support for a given hypothesis under the PS model was considered significant if it was in the upper 5% of the null distribution.

Information content

Finally, we assessed the impact that variable information content has on our ability to detect model violation based on posterior prediction. As above, we used both parsimony informative characters and Bayesian information content to quantify phylogenetic information across alignments and determined the correlation between information content and posterior predictive effect sizes using the Pearson product-moment correlation coefficient.

Results

Overview of the datasets and initial phylogenetic analyses

Clustering with an inflation parameter of 2.0 yielded 5,257 clusters that contained 33 to 134 proteins (50–200% of the number of species), of which 1,327 clusters contained a single gene per species or inparalogs only. The alignments of three genes containing overly divergent sequences (contributing >60% of total tree length) were excluded from further analyses. Of the remaining clusters, 950 contained more than 33 species, corresponding to at least half of the species in the analyses. We removed ambiguously aligned regions using three stringency levels in GBlocks, and retained the trimmed alignments if they contained >50 amino acid characters. This resulted in three sets of trimmed alignments comprising 314, 824 and 901 genes, which we designate as the 314G, 824G and 901G datasets. We hereafter refer to the 950 untrimmed alignments as the 950G dataset. The concatenated 314G, 824G, 901G and 950G datasets comprised 46,573, 165,465, 241,004 and 704,775 amino acid residues, respectively (Table 1). Overall, the 314G dataset was the most conserved (mean pairwise ML distance 0.406) followed by the 824G (0.537), 901G (0.616) and 950G (0.962) datasets. Taxon occupancy was even across datasets (82% to 86%) with the 314G dataset having the fewest missing genes (14%), followed by the 824G, 901G and 950G datasets (all with 18% of the genes missing) (Fig S1). Mushroom-forming fungi were best represented in all datasets, with 89% - 92% of the orthologs present per species, followed by rusts (78% - 83%), smuts (74% - 82%) and Ascomycota (70% - 77%). The Malasseziomycetes and Wallemiomycetes, two classes containing species with reduced genomes were represented by 60-80% and 74-88% of genes, respectively. Of the four datasets, the 314G dataset is the most conserved on average and is the least saturated, followed by the 824G, 901G and 950G datasets (Fig S2).

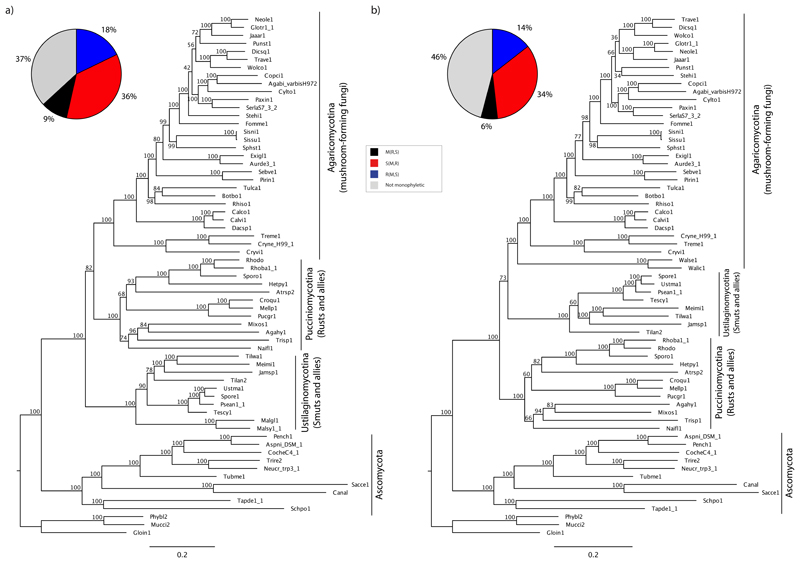
Maximum likelihood trees inferred for the four datasets resembled each other very closely (Table 1, Fig 2, Fig S3-S6), but differed in the relationships of the smut, rust and mushroom-forming lineages. The 314G dataset placed rusts as the sister group to mushroom-forming fungi (referred to as the S(R,M) hypothesis) with moderate support (54%), whereas the other three datasets placed smuts and mushroom-forming fungi as sister (referred to as the R(S,M) hypothesis) (Fig 3a,c, Table 1). Bootstrap support for the R(S,M) topology showed a positive correlation with alignment length but an inverse relationship with the conservation of the concatenated alignments (Fig 3d-f). Bayesian analyses of the 314G dataset under partitioned best fit models and an unpartitioned CAT model placed smuts as the sister group to mushroom-forming fungi (Fig S7-S8), with low support values (BPP: 0.85).

Table 1. Summary of phylogenetic analyses performed in this study.

Dataset	#char	Analysis/Model	ML topology	(R,M)/(S,M)bootstrap
314 Gene Dataset
314G	46,573	ML/WAG+G, partitioned	S(R,M)	59/37
314G	46,573	ML/Dayhoff+G, unpartitioned	R(S,M)	30/70
314G	46,573	ML/Dayhoff+G, partitioned	R(S,M)	32/68
314G	46,573	ML/GTR+G, partitioned	S(R,M)	42/54
314G	46,573	ML/LG+G, partitioned	S(R,M)	54/44
314G	46,573	ML/WAG+G, unpartitioned	R(S,M)	44/56
314G	46,573	ML/WAG+G, partitioned, b-lengths unlinked	R(S,M)	41/52
314G	46,573	ML/LG+G, partitioned, b-lengths unlinked	R(S,M)	60/31
295G	43,662	ML/WAG+G, partitioned	S(R,M)	45/55
64G	11,622	ML/WAG+G, partitioned	S(R,M)	61/30
131G	23,180	ML/WAG+G, partitioned	S(R,M)	71/26
209G	34,944	ML/WAG+G, partitioned	S(R,M)	67/29
314G	46,573	Bayes/LG+G, partitioned (MrBayes)	S(R,M)
314G	46,573	Bayes/unpartitioned CAT-GTR (Phylobayes)	R(S,M)
314G	46,573	Bayes,/unpartitionedGTR+G (Phycas)	R(S,M)	0.01/0.99
314G	NA	Astral	R(S,M)	55/NA
314G-no-Wallemia	46,573	ML/WAG+G, partitioned	S(R,M)	82/18
314G-no-Wallemia	46,573	ML/WAG+G, unpartitioned	S(R,M)	84/16
314G-no-Wallemia	46,573	ML/LG+G, partitioned	S(R,M)	82/18
314G-no-Malassezia	46,573	ML/WAG+G, partitioned	R(S,M)	27/73
314G-no-Wall./Mal.	46,573	ML/LG+G, partitioned	S(R,M)	58/42
314G/c20	38,456	ML/WAG+G, partitioned	S(R,M)	55/45
314G/c19-20	31,234	ML/WAG+G, partitioned	M(S,R)	43
314G/c18-20	29,543	ML/WAG+G, partitioned	NA	NA
205G	30,896	ML/LG+G, partitioned, b-lengths unlinked	R(S,M)	43/57
205G	30,896	ML/WAG+G, partitioned, b-lengths unlinked	R(S,M)	41/59
205G	30,896	ML/LG+G, partitioned	R(S,M)	27/73
205G	30,896	ML/WAG+G, partitioned	R(S,M)	22/78
824 Gene Dataset
824G	165,465	ML/WAG+G, partitioned	R(S,M)	5/95
824G/c20	137,702	ML/WAG+G, partitioned	R(S,M)	16/84
824G/c19-20	81,981	ML/WAG+G, partitioned	NA	20/19
824G/c18-20	56,149	ML/WAG+G, partitioned	NA	2/3
824G/c17-20	43,218	ML/WAG+G, partitioned	NA	2/0
824G	165,465	Bayes/model, partitioned (MrBayes)	R(S,M)
824G	NA	Astral	R(S,M)	NA/95
824G-no-Wallemia	165,465	ML/WAG+G, partitioned	R(S,M)	1/99
824G	165,465	ML/WAG+G, partitioned + b-lengths unlinked (Iq-Tree)	R(S,M)	1/75
901 Gene Dataset
901G	241,004	ML/WAG+G, partitioned	R(S,M)	1/99
901G/c20	202,598	ML/WAG+G, partitioned	R(S,M)	2/98
901G/c19-20	128,347	ML/WAG+G, partitioned	NA	3/2
901G/c18-20	95,197	ML/WAG+G, partitioned	NA	3/2
901G/c17-20	80,230	ML/WAG+G, partitioned	NA	0/0
901G	NA	Astral	R(S,M)	99/NA
Other
950G	704,775	ML/WAG+G, partitioned	R(S,M)	NA
Gene content	50,971	ML/Mk2	S(R,M)	98/2

Notes: The Maximum likelihood topology and support values are shown as a function of dataset name, number of characters and the methods and model employed. NA for topology means the monophyly of one of more of the subphyla broke down. Removal of the fast-evolving amino acid categories are indicated by c20 … c17-20, corresponding to the removal of the fastest, to the four fastest rate categories.

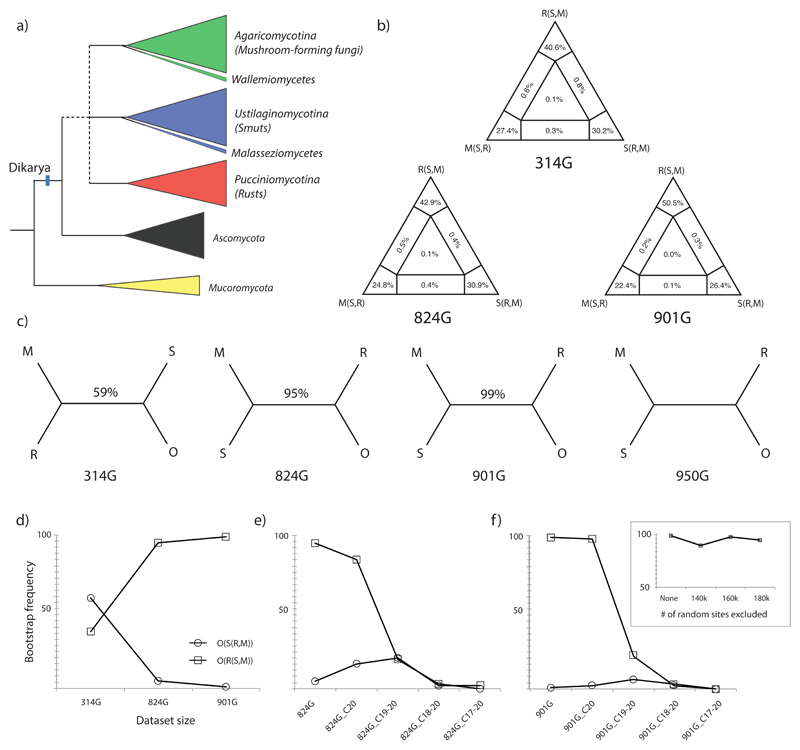
Figure 3.

Summary of dataset properties and results of initial concatenated analyses. (a) schematic tree showing the position of basal Basidiomycota splits and the Agaricomycotina (mushroom-forming fungi), Ustilaginomycotina (smuts and allies) and Pucciniomycotina (rusts and allies) in the fungal tree. The unresolved branching order of rusts, smuts and mushroom-forming fungi are shown by a dashed line. The early-diverging classes Malasseziomycetes and Wallemiomycetes are highlighted as suspected long branch taxa. (b) Results of four quartet likelihood mapping (FcLM) for the 314G, 824G and 901G datasets. For all three datasets, the vast majority of quartets map to angular regions of the triangles, suggesting a strong tree-like pattern in the data. Percentages indicate the proportion of quartets mapping to the given topology. (c) Simplified tree topologies inferred from the three aforementioned datasets plus the 950G dataset. Bootstrap percentages obtained from concatenated ML analysis are shown above branches. (d) The relationship between dataset size and bootstrap proportions for smuts sister to mushroom-forming fungi (squares) and rusts sister to mushroom forming fungi (circles). These proportions change in a complementary manner when a number of categories of the fastest-evolving sites are removed from the 824G (e) and the 901G (f) datasets. Inset at (f) shows the bootstrap proportions for the grouping of smuts with mushroom-forming fungi when equal numbers of random sites were removed from the 901G dataset.

Gene content-based phylogeny

Scoring gene family presence/absence across the 67 genomes resulted in a binary matrix with 50,971 characters. The ML tree inferred from this dataset was very similar to the concatenation topologies and supported the S(R,M) hypothesis with strong bootstrap support (98%, Table 1, Fig S9). Interestingly, the Wallemiomycetes were inferred as the sister group of smuts (93%), which might be related to the reduced gene content of both groups. Using the reverse approach, we asked which of the three competing topologies is better explained by gene presence/absence information in a parsimony context. All other branches being equal, the S(R,M) topology required 36 fewer steps than the R(S,M) one, which might appear marginal, is highly significant when tested in a likelihood framework (p<0.00001, approximately unbiased test).

Biological sources of topological uncertainty – Information content, hard polytomy, and incomplete lineage sorting

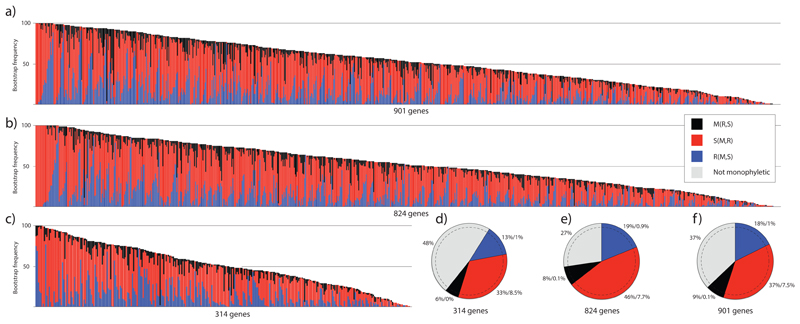
Most gene trees did not resolve the individual subphyla as monophyletic, suggesting that the phylogenetic signal of individual genes is generally weak (Fig 4). The S(R,M) topology was most common among gene trees in all three datasets, followed by the R(S,M) hypothesis. Average bootstrap percentages remained low, 33–46% for the S(R,M) and 13–19% for the R(S,M) topology. Further, on 27–48% of the bootstrap trees, one or more subphyla were not resolved as monophyletic. We did not find a significant correlation between the strength of signal in individual gene trees (measured by percentages of bootstrap trees) for either the S(R,M) or R(S,M) topologies and alignment length, taxon number or evolutionary rate (results not shown).

Figure 4.

Frequencies of competing tree topologies in bootstrap samples of individual gene trees (a-c) and ML gene trees (d-f) from the 314G, 824G and 901G datasets. (a-c) the S(R,M) topology is most frequent among resolved bootstrap replicates across individual genes in all three datasets. The bootstrap frequency of the S(R,M), R(S,M) and M(R,S) topologies are shown on the y axis. Each column of the x axis corresponds to a single gene. White section of each column represents the number of gene trees on which one or more of the large clades (rusts, smuts and mushroom-forming fungi) were not resolved as monophyletic (d-f) proportions of alternative tree topologies in ML bootstrap trees. Percentages correspond to the proportion of gene trees showing the given topology followed by the proportion of gene trees that resolved the positions of rusts, smuts and mushroom-forming fungi with >70% bootstrap support. As in the case of bootstrap trees, most genes did not resolve one or more of the large clades as monophyletic (grey section). S = smuts (Ustilaginomycotina), R = rusts (Pucciniomycotina) and M = mushroom-forming fungi (Agaricomycotina).

The first hypothesis we tested was that of a hard polytomy, which assumes a (near) simultaneous divergence of descendant lineages, in which case we do not expect bifurcating trees to provide a reasonable biological explanation of the data. Bayesian MCMC analyses that allow sampling polytomic trees yielded fully resolved trees for the 314G dataset under both polytomy-friendly and neutral priors. These trees supported the R(S,M) hypothesis with strong support (BPP: 0.99, Fig S10), consistent with the results of other unpartitioned analyses. Because of potential bias in unpartitioned analyses, we regard these topologies as moderately informative as to the biological question at hand. In agreement, FcLM analyses of the 314G dataset suggest a strong bifurcating pattern pertaining to the split of the rust, smut and mushroom-forming lineages, with 98.2% of the splits supporting resolved topologies (Fig 3b). The R(S,M), S(R,M) and M(R,S) topologies were supported by 40.6%, 30.2% and 27.4% of the splits, respectively. Similar patterns were obtained for the 824G and 901G datasets (Fig 3b), with the R(S,M) topology receiving increasing support in order from the 314G to the 901G dataset. Collectively, these results suggest that the datasets contain tree-like signal with regard to early Basidiomycota relationships, and that a hard polytomy does not plausibly explain the origin of three subphyla therein. Nevertheless, the even distribution of supporting quartets among the three angles of the triangle indicates that no single topology is clearly preferred by the alignments.

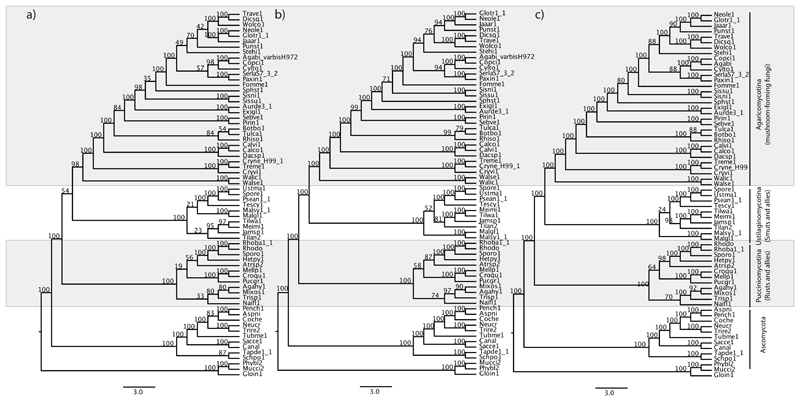
Coalescent-based species trees estimated by ASTRAL-II for all three datasets (314G, 824G and 901G) recovered the R(S,M) topology, i.e. smuts as the sister group of mushroom-forming fungi, although similarly to the concatenated analyses, bootstrap support for this configuration increased with decreasing conservation of the input alignments (Fig ,5 Table 1). Although ASTRAL-II is designed to account for ILS, whether this is a contributor of uncertainty in our data remains to be understood.

Figure 5.

Species trees obtained using Astral-II for the 314G (a), 824G (b) and 901G (c) datasets. Numbers on nodes indicate support values from multilocus bootstrapping in 100 replicates.

Methodological sources of topological uncertainty – fast-evolving sites, long-branch attraction, heterotachy, and absolute model fit

The influence of dataset composition on topologies and support values

Most of the genes in the three datasets were decisive (sensu (Dell’Ampio et al. 2014)), i.e. had representatives in all three subphyla. Smuts had the highest number of indecisive families (65–91, i.e. not represented in the gene family), followed by rusts (11–14), whereas mushroom-forming fungi had representatives in all of the gene clusters. Restricting the 314G dataset to only decisive genes yielded a marginally more conserved dataset comprising 295 genes and 43,662 amino acids (295G dataset, mean pairwise genetic distance 0.404) with slightly less missing data (11.9% vs. 13% in the original 314G dataset). The tree inferred from this alignment was topologically identical (an S(R,M) topology) with very similar support values to the tree inferred from the original 314G dataset (Fig S11), however, the bootstrap support for the node uniting rusts and mushroom-forming fungi decreased from 54% to 45% (Table 1, Fig 7). This suggests that indecisive genes are not the major source of uncertainty in basal Basidiomycota relationships. On the other hand, when we increased dataset completeness by concatenating only gene families that had representatives in at least 60 taxa (instead of 35), the resulting 205 gene dataset (205G, 30,896 sites, 4.9% missing data) yielded the R(S,M) topology, with 73% bootstrap support.

Figure 7.

Summary of the effects of model complexity, taxon and gene sampling on topologies and bootstrap values for the relationships of rusts, smuts and mushroom-forming fungi. Boxes are colored according to the strength of bootstrap support for the grouping of smuts and mushroom-forming fungi (note that this is basically complementary to the bootstrap of rusts + mushroom forming fungi, because bootstrap trees grouping smuts with rusts had negligible frequency). Best fit partitioned models were used unless indicated otherwise.

Long branch attraction

We identified two clades that could potentially be affected by long-branch attraction (LBA), the Wallemiomycetes (2 species, Agaricomycotina) and the Malasseziomycetes (2 species, Ustilaginomycotina). The deletion of one or both of these classes from the 314G dataset had a major impact on topologies and bootstrap support (Fig 6). Elimination of the Wallemiomycetes resulted in an (S(R,M) topology whereas the removal of Malasseziomycetes from the same dataset gave an R(S,M) topology with 73% bootstrap (Table 1, Fig 7). Removal of both groups, however, essentially returned the original S(R,M) topology and support values (Table 1). Remarkably, the removal of either group yielded two of the highest bootstrap values during this study, although for conflicting topologies. Although both Malasseziomycetes and Wallemiomycetes seem to impact the analyses, we conclude that LBA alone can’t explain the observed uncertainty.

Figure 6.

The effects of removing putative long-branch taxa. Topologies and ML bootstrap values in (a) and (b) were inferred from the 314G dataset with removing the Wallemiomycetes and the Malasseziomycetes, respectively. The distribution of individual gene tree topologies in the two modified datasets (pie charts) resemble closely that of the original 314G dataset.

Removal of fast-evolving regions

The gradual removal of the fastest evolving categories of sites sharply decreased bootstrap support for the grouping of the smut lineage with the mushroom-forming fungi (R(S,M)) in the 901G and 824G datasets (Fig 3e-f, Table 1). On the other hand, support for the grouping of the rust lineage with the mushroom-forming fungi (S(R,M)) increased in both datasets (Fig 3d-f, Fig S12-S23). Removal of the fastest rate category did not appreciably affect the topology and support values in the 314G dataset (S(R,M)), whereas removing the two fastest categories resulted in a M(R,S) topology with 43% bootstrap. The exclusion of further sites resulted in poorly supported topologies and the degradation of the monophyly of subphyla in all three datasets, probably due to the removal of many of the phylogenetically informative sites. Consistent with results of site-wise removal, eliminating the fastest evolving genes favored the S(R,M) topology. By ranking genes according to their substitution rate and removing top 25%, 50% and 75% fastest genes, we created three subsets of the 314G dataset: 209G, 131G and 64G (Table 1). Analyses of these yielded trees on which rusts grouped with mushroom-forming fungi with 61% to 71% bootstrap support (Table 1). Taken together, eliminating fast-evolving regions of the datasets increased support for the S(R,M) hypothesis, suggesting that support for the R(S,M) topology is driven, at least in part, by fast evolving, potentially noisy sites.

Effects of model complexity

The Le & Gascuel model (LG+G) (Le et al. 2008) was selected as the best fit model for most of the partitions in all three datasets, based on BIC values. In the case of the 314G dataset, LG+G was preferred for 304 genes followed by RtREV+G (4 genes), MtArt+G (3 genes), WAG+G (1 gene), MtREV+G (1 gene) and CpREV+G (1 gene). After initial ML partitioned analyses under the best fit model for each gene (see Fig 1-2, Figure S3-S8) we performed ML bootstrapping under modified versions of the original partitioned models on the 314G dataset (Fig 7). First, we treated all genes as a single partition and used the LG+G model that was found to fit most individual genes the best. This was found to have a minor effect on the topology and support values. Next, we substituted the LG+G model by the WAG+G and Dayhoff+G models in partitioned, then unpartitioned analyses. Analyses under a partitioned WAG+G model yielded the S(R,M) topology with 59% bootstrap similarly to the original partitioned analysis under LG+G. Under the Dayhoff+G model, however, the ML topology was R(S,M) with 68% bootstrap support. Unpartitioned versions of both the WAG+G and Dayhoff+G analyses also gave the R(S,M) topology with 56% and 70% bootstrap support, respectively. Unpartitioned version of the analysis omitting the Wallemiomycetes or the Malasseziomycetes yielded the same topologies as their partitioned ones with increased bootstrap values (Fig 7).

To increase model complexity we unlinked model parameters across partitions. Analyses under unlinked versions of both the LG+G and WAG+G models resulted in R(S,M) topologies, with 31% and 52% bootstrap, respectively (Fig 7). Analyses of the more complete 205G dataset under unlinked best fit and WAG+G matrices also yielded R(S,M) topologies, although bootstrap support decreased relative to analyses in which model parameters were linked. Using linked and unlinked, partitioned GTR+G models we obtained the S(R,M) and R(S,M) topologies with 42% and 41% bootstrap support, respectively (Fig 7). These analyses revealed a strong relationship between model complexity and support for alternative hypotheses: simpler models favored the R(S,M) topology, whereas more complex models yielded S(R,M) topologies. Bootstrap support remained moderate to low in all cases.

The Bayesian consensus tree inferred for the 314G dataset under the covarion model (accounting for heterotachy) (Tuffley and Steel 1998) weakly supports the grouping of smuts with mushroom-forming fungi (Fig 8a), whereas other parts of the tree are topologically identical to those found in analyses under other models.

Figure 8.

Absolute model fit and the impact of the implementation of covarion-like models to basal Basidiomycota relationships. a) Distribution of posterior predictive effect sizes representing degree of model violation for WAG+G and Prottest-selected (PS) models. Scatterplot of posterior predictive effect sizes by gene index. The larger the value the poorer the fit between the data and the selected model. The horizontal line represents the median effect size (WAG+G: 5.481, PS: 4.903). b) Distribution of posterior probabilities for S(R,M), R(S,M), and M(R,S) topologies for genes that best fit the covarion model analyzed under the covarion and PS model. c) 50% majority rule consensus tree inferred for the 314G dataset under the covarion-like model.

Tests of model adequacy reject best fit models in all cases

Because of the inconsistent results under different models, we aimed to assess absolute model fit for each gene in the 314G dataset. Posterior predictive tests for absolute model-fit showed both the WAG+G and PS models to be a poor fit to the majority of genes. Using the 9,999–10,000^th quantile of ordered unweighted RF distances among topologies in the posterior distribution as a test statistic for inference-based assessment of model fit, both the WAG+G model and PS models were a poor fit for all but three and four gene families (Fig 8b-c), respectively, and were rejected on the basis of a two-tailed test (P=0.05). However, as noted in Doyle et al. (2015), we used effect sizes to assess the degree of model violation among genes because P-values do not allow for the differentiation of empirical values that lay near the posterior predictive distribution versus those that represent extreme deviations. Both models appear to fit the data poorly, with effect sizes being also similar for the WAG+G (ranging from 0 to 12.776, median: 5.481; Fig 8b) and the PS models (1.056 to 12.601, median: 4.903; Fig 8b).

Although measurements of absolute model fit are not available for the covarion model (Tuffley and Steel 1998), it relatively fits most genes better than either the WAG+G or the PS models. The covarion model was preferred over the PS model for 260 genes (82%; Fig S24) with a median ln(BF) of 13.7, whereas the WAG+G model was rejected in favor of the covarion model for 311 genes (99%; median ln(BF)=59.8; Fig S24). Accounting for heterotachy by using the covarion model (Huelsenbeck 2002), however, does not appear to have a significant impact on the mean support for any of the three topological hypotheses we explored. No significant increases in mean support were observed for S(R,M) (t(515) = 0.174, P = 0.8623), R(S,M) (t(515) = -0.330, P = 0.7414), or M(R,S) (t(515) = -0.133, P = 0.8945) topologies, among trees inferred from those genes that best fit the covarion model when analyzed under the covarion versus the PS model (Fig 8c). We also did not see a greater than expected increase in support when comparing mean support for each topology among those genes that best fit the covarion to a null distribution of expected support under the covarion model (Fig S25). Similarly, we do not see any changes in posterior support among trees inferred from those genes that best fit the PS model when analyzed under the PS and covarion models for each of the S(R,M) (t(103)=-0.089, P = 0.9291), R(S,M) (t(103)=0.039, P = 0.9686), and M(R,S) (t(103)=0.019, P = 0.985) topologies (Fig S26). We also did not see a greater than expected increase in support when comparing mean support for each hypothesis among those genes that best fit the PS model to a null distribution of expected support under the PS model (Fig S27).

Posterior support for a particular hypothesis does not seem to be impacted by information content (Fig S28), in contrast to our ability to reject a model in a posterior predictive framework (Fig S29). Neither parsimony informative characters (PIC, Fig S28a-c) nor Bayesian information content (Fig S28d-f) are significantly correlated with posterior probabilities for each of R(S,M) (PIC: r(311) = 0.0920, P = 0.1043; BI: r(311) = 0.0494, P = 0.3842), S(R,M) (PIC: r(311) = -0.0038, P = 0.9461; BI: r(311) = 0.0483, P = 0.3942), and M(R,S) (PIC: r(311) = -0.0225, P = 0.6917; BI: r(311) =-0.0075, P = 0.8954) topologies.

With measurements of absolute model fit available for each of the genes in the 314G dataset, we asked what topology do genes that fit the model least poorly prefer. To this, we concatenated the 100 and 200 genes that showed the least evidence of poor model fit and analyzed the resulting datasets using ML bootstrapping. The resulting 100- and 200-gene datasets 10,023 and 22,285 characters and yielded R(S,A) topologies, with 66% and 52% bootstrap, respectively (Figs S30-31). Interestingly, support for the R(S,A) is higher in the 100-gene dataset, which is the reverse pattern as we usually saw when gradually removing sites in previous analyses.

Discussion

Gene tree based selection of orthogroups

Data collection is one of the primary determinants of the outcome of bioinformatic analyses. Distinguishing orthologues from paralogues is a central task in phylogenomics, as unwanted inclusion of paralogous genes confers incorrect topological signal and can have a large impact on inferred trees (Dunn et al. 2008; dos Reis et al. 2012; Whelan et al. 2015; Brown and Thomson 2017). Our orthology detection strategy explicitly scores internal nodes of gene trees as duplication or speciation and only considers gene families not affected by deep duplication. Although this strict orthogroup selection strategy resulted in fewer orthogroups than more relaxed methods usually do (e.g. those based on best reciprocal hits), the set of gene families can be expected to virtually be devoid of contamination by deep paralogs.

Taxon sampling and putative long-branch taxa

Limited (≤ 2 species) sampling from the smut and rust lineages in previous phylogenomic studies was hypothesized to underlie the difficulties in resolving the basal split in the Basidiomycota (Nagy et al. 2016). In this study we increased taxon sampling density across all Basidiomycota, with special emphasis on Pucciniomycotina and Ustilaginomycotina. We included whole genome sequences from 10 Ustilaginomycotina, 12 Pucciniomycotina and 32 Agaricomycotina species, representing most of the known orders of these taxa. Even with this improved sampling, the branching order of the subphyla remained equivocal. It is noteworthy, however, that we identified the Wallemiomycetes (Agaricomycotina) and Malasseziomycetes (Ustilaginomycotina) as potentially problematic classes, which is consistent with the unstable placement of these taxa in rDNA and multigene phylogenies (Padamsee et al. 2012; Matheny et al. 2007; Kijpornyongpan et al. 2018). Removing these lineages resulted in the largest influence on topologies and support values observed in this study, suggesting they might be affected by long branch attraction: without the Malasseziomycetes bootstrap support for R(S,M) increased to 73%, whereas without the Wallemiomycetes support increased to 82% for the S(R,M) topology. Because the effect of LBA can get more more pronounced if the chosen model fits the data poorly, these clades are likely problematic in our datasets, where the best-fit models were found to provide a poor overall fit. Such mutually exclusive strongly supported hypotheses are unsettling not only from a biological but also a methodological point of view. Whether sampling more early-diverging species in these lineages could improve topological inferences needs to be seen, nevertheless, these observations also highlight the importance of careful taxon sampling and analyses of the contributions of individual taxa to the inferred relationships.

Could the grouping of smuts with mushroom-forming fungi be a result of model violation?

We observed a remarkable relationship between data subsets, evolutionary models and the inferred phylogenetic relationships. First, longer and less conserved concatenated alignments favored the grouping of smuts with mushroom forming fungi, whereas more conserved subsets preferred the grouping of rusts with mushroom-forming fungi (Fig S3-S5). This observation prompted us to examine whether fast evolving sites favored the R(S,M) topology. Gradual elimination of the fastest-evolving sites decreased bootstrap support for the R(S,M) topology rapidly (but not for other nodes in the tree), whereas that of the S(R,M) topology increased slightly, until most phylogenetic signal was removed and support generally declined across the whole tree. In a complementary set of analyses, we eliminated the fastest-evolving genes to create increasingly more conserved versions of the 314G dataset, which slightly increased support (61-71%) for the S(R,M) hypothesis. We speculate that the stronger support by the less conserved datasets can be related to the inadequate modeling of fast-evolving amino acid sites in the alignment. Decreasing model complexity consistently led to increased bootstrap proportions in favor of the R(S,M) topology: analyses under unpartitioned and the poorly-fitting Dayhoff model grouped the smut and mushroom-forming lineages with up to 70% bootstrap support. On the other hand, under the most parameter-rich models (GTR, or LG+G with parameters unlinked across partitions), both the smuts and the rusts were inferred as the sister lineage of the mushroom-forming fungi with bootstraps between 45-55%.

These observations might indicate that poor model fit favors the R(S,M) topology whereas partitioned best fit models and more complex models are inconclusive with regard to the branching order of the three subphyla. As in all empirical studies, the true model of evolution remains unknown and thus to what extent the data violate the assumptions of the models used here is difficult to address. Nevertheless, assessments of absolute model fit strongly rejected the best fit models for each individual gene, suggesting that even best fit models fail to adequately describe the processes of evolution that have generated our data. While these models are commonly used for phylogenetic analysis, our finding of widespread model inadequacy is not unprecedented in data-based posterior predictive tests (Lartillot et al. 2007). However, our inference-based posterior predictive analyses are a more direct look at the impact of model violation on topological inferences. Interestingly, Lartillot et al. (2007) show that a site-heterogeneous model, such as the CAT model, provides a better fit to the data than site-homogeneous models, such as WAG. Several other papers reach a similar conclusion: site-homogeneous models are inadequate for accounting for saturation. However, recent work (Whelan and Halanych 2017) suggests that partitioning by gene using a site-homogeneous model and the CAT+GTR+G model perform similarly. In contrast, we find that inferences under a site-homogenous partitioned model and the CAT+GTR model differ with respect to basal relationships in the Basidiomycota, suggesting these models are interpreting the data in different ways. The covarion model that accounts for heterotachy (Tuffley and Steel 1998) fits most genes better than either the best fit or WAG+G models, although accounting for rate variation among lineages had a minor effect on the topologies of both gene trees and a concatenated tree. However, while we focus here on topological results, other evolutionary parameters of interest are the focus of many phylogenomic studies and our results indicate model choice may have a significant impact on these parameter estimates. For example, we observed generally higher evolutionary rates estimated under the PS model as compared to those estimated under the covarion for the 314G dataset, which may have a significant impact on divergence time estimation depending on the selected model. These results, combined with the results obtained using the more variable 824G and 901G datasets and by removing the fastest-evolving sites are consistent with reports of strong support for incorrect topologies arising from dataset-wide model violation (Jeffroy et al. 2006; Philippe et al. 2011; Kumar et al. 2012; Roch and Steel 2015; Mendes and Hahn 2017). If true, however, this alerts against recognizing the >95% bootstraps obtained for the R(S,M) topology in this and most previous studies.

Analyses of individual genes revealed that gene tree bootstraps most frequently supported the S(R,M) topology while coalescent-based methods using Astral-II recovered R(S,M). It is known that under some circumstances (e.g. short internal nodes) the most common gene tree topology might differ from the true species tree, a part of the tree space known as the anomaly zone (Degnan 2013; Mendes and Hahn 2017). This might explain the discrepancy between the most common gene tree topology and the Astral tree. Similar to concatenated analyses, multilocus bootstrap support increased as a function of the number of genes and their rate of evolution. This is surprising given that no such trend was observed in individual gene tree bootstraps. In general, most gene trees were poorly supported, with the rust, smut and mushroom-forming lineages paraphyletic on >40% of the bootstrap trees. Species tree estimation from poorly estimated gene trees represent a challenging situation for gene tree-based methods (Roch and Warnow 2015), suggesting that our dataset might be hard to tackle for gene tree-based coalescent methods.

Basal Basidiomycota relationships remain an enigma

We performed several analyses to understand basal Basidiomycota relationships. These uncovered multiple sources of biases that complicate phylogenomic inference in this region of the fungal tree of life, including model choice, taxon and gene sampling, and the inclusion of fast-evolving sites. A sister-group relationship between the smut and mushroom-forming fungi was the most commonly recovered relationship (R(S,M) topology) followed by rusts and allies as the sister group of the mushroom-forming fungi (S(R,M) topology). The rust and smut lineages as sister groups (M(S,R) topology) can be rejected with confidence. Smuts as the sister group to the mushroom-forming fungi is the most common topology in both our analyses and in the literature (Padamsee et al. 2012; Ebersberger et al. 2012; Floudas et al. 2012; Toome et al. 2013; Zajc et al. 2013; Kohler et al. 2015; Sharma et al. 2015; Nagy et al. 2016, Nagy and Szollosi 2017), however, it should be emphasized that we found evidence for this grouping to arise also as a result of model violation and in the presence of fast-evolving sites. This cautions against conclusively considering smuts as the sister group to mushroom-forming fungi. On the other hand, the grouping of rusts and allies with mushroom-forming fungi is less frequent both in our analyses and the literature, was poorly supported and found to be unstable, sensitive to model choice, taxon and gene sampling.

Despite detailed examinations of the sources of incongruence, and occasional strong support for either topology, we consider basal basidiomycete relationships unresolved. Yet, analyses of information content and rejection of the hard polytomy hypothesis suggest that there is considerable signal pertaining to the branching of basidiomycete subphyla. Whether and how this signal can be accessed using contemporary phylogenetic methods and models is not clear and needs further research. We speculate that the true tree topology could be restricted to a region of the parameter space that is difficult to access in the presence of patterns not captured by current models of sequence evolution. A deeper understanding of the evolutionary processes shaping fungal genomes and/or more biologically realistic models might help confidently reconstructing basal relationships in the Basidiomycota.

The relationships among rusts, smuts and mushroom-forming fungi have important implications for understanding some of the defining traits of fungi. For example, the structure of the septal pore apparatus (which blocks septal pores of hyphae) shows great diversity among these clades, ranging from simple pores (Pucciniomycotina and Ascomycota) to pores with membrane-bounded but structurally diverse pore caps in the smuts and mushroom-forming fungi (Lutzoni et al. 2004). Members of Agaricomycotina and some Ustilaginomycotina also produce swollen pore margins, called dolipores. If dolipores and membrane bound caps are homologous in the smuts and mushroom-forming fungi then these two being sister groups implies a single origin for this trait, whereas S(R,M) implies these traits arose in the last common ancestor (LCA) of the Basidiomycota and were then lost in the LCA of the rust lineage. This and the morphology of spindle pole bodies (Aime et al. 2006) have been used as an argument for the sister group relationship between smuts and mushroom-forming fungi. However, this hypothesis has its own challenges. For example, septal pore anatomy can be subject to convergent evolution (Sharma et al. 2015; Nguyen et al. 2017); it is not known whether the structurally different membrane caps are homologous and even losses would not be surprising given the extent of gene loss some Pucciniomycotina have experienced during their evolution (Nagy et al. 2014). Similarities between the Pucciniomycotina and mushroom-forming fungi exist in a number of lesser-known characters. Some Pucciniomycotina share with Tremellomycetes (an early-diverging class of Agaricomycotina) the ability to form a specialized type of mycoparasitic interaction with their hosts through tremelloid haustorial cells (Zugmaier and Oberwinkler 1995; Oberwinkler et al. 1999). Mycoparasitism itself is a life history strategy shared by many Tremellomycetes and some Pucciniomycotina but not, to our knowledge, any Ustilaginomycotina. Further, several Pucciniomycotina species (e.g. Helicogloea) produce gelatinous cushion-like basidiocarps (sexual fruiting bodies) similar to those of simple Tremellomycetes and Dacrymycetes. Finally, members of Atractiellomycetes (Pucciniomycotina) form mutualistic plant-root associations (Aime et al. 2018), a character found repeatedly throughout Agaricomycotina but not within Ustilaginomycotina. Taken together, consistent with phylogenomic results, conflict is observed in ultrastructural and life history traits too; understanding how these evolved and how they can be used to distinguish between phylogenetic hypotheses for early Basidiomycota evolution will require further research.

Conclusions

Ancient divergences in basidiomycete fungi represent a classic example of historically recalcitrant nodes (Lutzoni et al. 2004) that pose a challenge even for genome-enabled phylogenetics (Hibbett et al. 2013). In this study we examined biological and technical sources of incongruence around basal Basidiomycota nodes in concatenation and gene tree-based analyses. We have demonstrated that dataset composition, taxon sampling, fast-evolving sites and the choice of analytical method and model all have an impact on resolving contentious relationships and that the difficulty of resolving basal Basidiomycota relationships might stem from a combination of these factors. Although we have not identified the relative contributions of these factors, our analyses reveal a complex interaction between the data and the analytical tools. These results further suggest that including all data without careful selection of genes/sites in phylogenomic analyses can result in incorrect estimates of support values and even tree topologies. Despite identifying several sources of incongruence, however, we consider basal Basidiomycota relationships as unresolved. We have ruled out the possibility of a hard polytomy and could conclusively reject the M(R,S) topology, while the R(S,M) and S(R,M) topologies remained both plausible resolutions of early Basidiomycota relationships. While this is not satisfying from the perspective of fungal biology, it highlights important limitations of genome-scale phylogenetics.

Although several of our analyses yielded apparently robust phylogenies, the pervasive conflict among trees, in our opinion, merely revealed robust incongruence rather than conclusive evidence for one or the other hypothesis. It is becoming more and more obvious that, despite initial expectations of genome-scale datasets erasing incongruence completely from phylogenetic studies (Gee 2003; Rokas et al. 2003), phylogenomic datasets bring about new types of challenges that may be even more difficult to resolve than those we faced in the age of multi-gene phylogenetics. One such challenging situation is when individual gene trees are poorly supported, but supermatrix analyses suffer from systematic biases; in these cases both concatenation and gene tree-based analyses can perform poorly (Kubatko and Degnan 2007; Warnow 2015). We conjecture that such a situation underlies the failure to resolve basal Basidiomycota relationships, creating a landscape in which the true tree topology is hidden behind complex model-data interactions. A higher density of sequenced genomes, better understanding of the evolutionary processes shaping fungal genomes and, in particular, more biologically realistic models might be needed to tackle recalcitrant phylogenetic questions either at the level of single genes or in concatenation methods.

Supplementary Material

Supplementary material, including data files and/or online-only appendices, can be found in the Dryad data repository at http://datadryad.org, doi: 10.5061/dryad.g0db883.