Preferential Presentation of High-Affinity Immune Complexes in Germinal Centers Can Explain How Passive Immunization Improves the Humoral Response

Summary

Passive immunization (PI) with external antibodies has been used classically for rapid but temporary alleviation of disease. Transcending this role, recent studies have shown PI to induce lasting improvements in natural antibody production, suggesting that PI could become a powerful tool to engineer humoral responses. We propose a mechanism with which PI can alter the humoral response. Antigen-specific B cells evolve and get selected in germinal centers (GCs) on the basis of their ability to acquire antigen from antibody-antigen complexes presented in GCs. When external antibodies of high affinity for antigen are used, they form the majority of the complexes in GCs, letting only B cells with even higher affinities be selected. Using an in silico GC reaction model, we show that this mechanism explains the improved humoral responses following PI. The model also synthesizes several independent experimental observations, indicating the robustness of the mechanism, and proposes tunable handles to optimize PI.

Introduction

Passive immunization (PI) is a century-old strategy where antibodies (Abs) generated externally are administered to achieve rapid control of disease (Slifka and Amanna, 2018). The external Abs neutralize and clear antigen (Ag), alleviating disease (Beck et al., 2010; Baxter, 2014; Salazar et al., 2017; Brekke and Sandlie, 2003). The power of PI is evident from the array of Ab therapeutics currently in use against pathogens, such as HIV-1 (Salazar et al., 2017; Nishimura and Martin, 2017), influenza (Salazar et al., 2017; Nachbagauer and Krammer, 2017; Sparrow et al., 2016), and respiratory syncytial virus (RSV) (Salazar et al., 2017; Storey, 2010), and against auto-immune disorders (Chan and Carter, 2010) and cancer (Weiner et al., 2010; Baxter, 2014). PI is also what results in the acquisition of immunity by infants from mothers by the transfer of Abs through the placenta or breast milk (Baxter, 2014). The influence of PI, however, is temporary. PI is a drug-like therapy with exogenous Abs targeting specific Ag; its effect wanes once the administered Abs are cleared from circulation (Baxter, 2014).

Surprisingly, recent studies have found effects of PI that transcend this canonical, drug-like mechanism. First, PI with Ag-specific Abs was found to modulate the evolution of endogenous Ab responses to the Ag (Visciano et al., 2008; Ng et al., 2010; Jaworski et al., 2013; Zhang et al., 2013; Schoofs et al., 2016). For instance, HIV-1-infected individuals infused with a single dose of the broadly neutralizing antibody (bNAb) 3BNC117 developed endogenous serum Ab responses with significantly improved breadth and potency compared to untreated individuals (Schoofs et al., 2016). Second, the influence on endogenous Ab responses lasted well beyond the expected duration of the drug-like effect of PI. The improved humoral response was found 24 weeks after PI with 3BNC117, which was well after 3BNC117 was cleared from circulation (Schoofs et al., 2016). Similarly, passive administration of low-dose neutralizing Abs to newborn macaques before simian/human immunodeficiency virus (SHIV) challenge improved the production of endogenous neutralizing Abs, the presence of which correlated with low set-point viremia and 100% survival (Jaworski et al., 2013). These effects suggest that PI could be developed into a strategy to elicit potent, lasting humoral responses, akin to vaccination with Ag. PI could then, remarkably, exert the combined effects of drugs and vaccines.

Although the drug-like effect of PI is well understood, its influence on endogenous Ab production is less clear. It signals a gap in our understanding of host humoral responses and precludes the rational development of PI as a tool to engineer them. Here, to address this limitation, we elucidate a mechanism with which external Abs can alter endogenous Ab production.

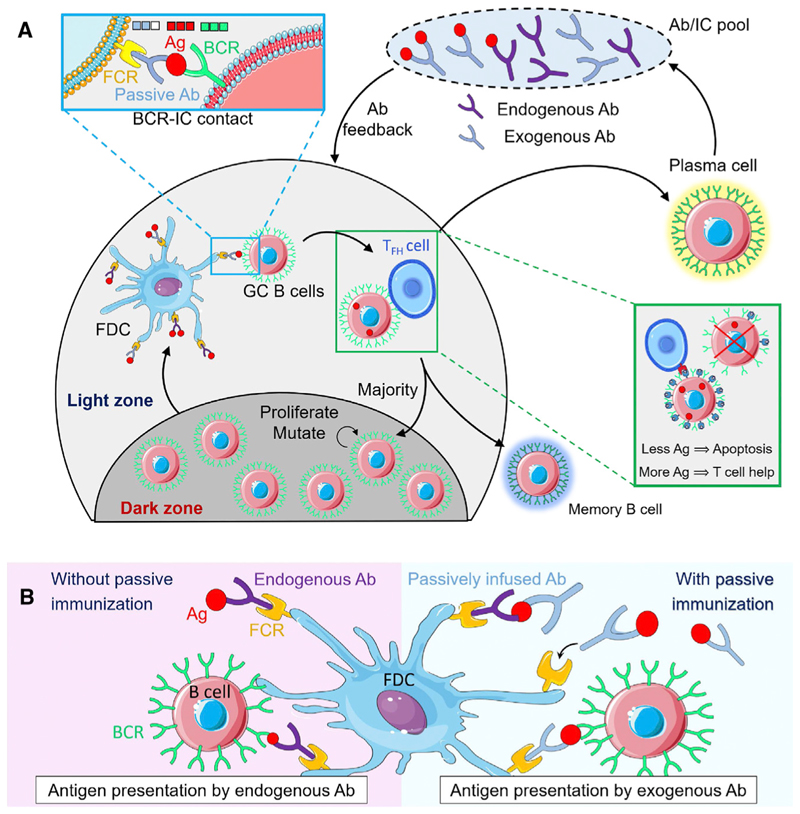
B cells that can produce Abs of high affinity for a target Ag evolve and get selected in germinal centers (GCs) (Figure 1A), which are temporary structures formed in lymphoid organs during an infection (Victora and Nussenzweig, 2012; Shlomchik and Weisel, 2012; Zhang et al., 2016). Each GC is divided into a light zone, where B cells interact with other cells and get selected, and a dark zone, where the selected B cells proliferate and mutate (Victora and Nussenzweig, 2012). GC B cells exist in a default pro-apoptotic state and must receive two signals sequentially in the light zone to survive (Victora and Nussenz-weig, 2012; Shlomchik and Weisel, 2012): first, they must acquire Ag presented as Ag-Ab immune complexes (ICs) on follicular dendritic cells (FDCs). Second, they must present the acquired Ag to and receive help from follicular T helper (T_fh) cells. The chances of receiving each of these signals depend on the affinity of the B cell receptor (BCR) for the Ag. The higher the affinity, the greater the likelihood of a BCR acquiring Ag from an IC (Batista and Neuberger, 2000). Each B cell has a single type of BCR (Victora and Nussenzweig, 2012). Thus, B cells with higher affinity BCRs would acquire more Ag on average than those with lower affinity BCRs. B cells present Ag as peptides on major histocompatibility complex II (pMHCII) on their surfaces in amounts proportional to the quantum of acquired Ag (Victora and Nussenzweig, 2012). T_fh cells form larger synapses with B cells displaying relatively high amounts of pMHCII, eventually leading to their selection (Cyster and Allen, 2019). Most B cells thus selected migrate to the dark zone of the GC, where they proliferate and mutate their BCR sequences, altering their affinities for the Ag (Victora and Nussenzweig, 2012; Shlomchik and Weisel, 2012). They then return to the light zone, a phenomenon termed cyclic re-entry, and get subjected to the same selection process again (Victora and Nussenzweig, 2012; Shlomchik and Weisel, 2012; Oprea and Perelson, 1997; Kepler and Perelson, 1993). Gradual selection of B cells with BCRs of increasingly higher affinities for Ag ensues, a process termed affinity maturation (AM). A small minority of B cells selected exits the GC and differentiates into plasma and memory B cells (Victora and Nussenzweig, 2012; Li et al., 2018). Mature plasma cells produce Abs in the serum and mount the humoral response.

Figure 1. Schematic of the Mechanism with which Exogenous Abs Influence the GCR.

(A)Schematic of the GCR: GC B cells in the light zone interact with Ag-presenting FDCs, forming BCR-IC contacts (left zoom). BCRs with greater affinity for Ag than the complexed Ab rupture the IC and internalize Ag.Acquisition of more Ag results in an increased probability of binding with T_fh cells and survival (right zoom). A majority of the selected B cells migrate to the dark zone and the remaining differentiate into Ab-producing plasma cells and memory B cells. Endogenous Abs, produced by plasma cells, and infused exogenous Abs diffuse into the GC and capture Ag from existing ICs to form new ICs or form higher affinity ICs in the serum and enter the GC, altering the selection stringency for B cells.

(B)Schematic of B-cell-FDC interaction. Without passive immunization (left), endogenous Abs present Ag to B cells as ICs on FDCs. With passive immunization (right), administered exogenous Abs with higher affinity for Ag either capture Ag from pre-existing lower affinity ICs or react with Ag molecules in serum to form new ICs that are trafficked on to FDCs. B cells must thus acquire Ag from these stronger ICs, increasing B cell selection stringency.

We hypothesized that PI influences endogenous Ab production by altering the ICs presented in GCs. Abs in circulation can enter GCs (Zhang et al., 2013, 2016; Toellner et al., 2018). When exogenous Abs have a higher affinity for Ag than endogenous Abs, they become the preferred Abs with which Ag forms ICs. The exogenous Abs could thus bind free Ag or acquire Ag from ICs containing endogenous, lower affinity Abs on FDCs, and themselves then be displayed as ICs on FDCs (Figure 1B). Indeed, ICs with higher Ab-Ag affinity have been shown to rapidly replace ICs with lower Ab-Ag affinity on FDCs (Zhang et al., 2013, 2016; Toellner et al., 2018). BCRs would then have to acquire Ag from these more stable ICs, which raises the selection stringency in the GC, potentially expediting and enhancing AM and modulating the humoral response.

To test this hypothesis, we constructed an in silico model of the GC reaction (GCR) in the presence of passively administered Abs and compared its predictions to available experimental observations. In silico models have proven to be a powerful tool to test hypotheses, often using available experimental observations (Kepler and Perelson, 1993; Oprea and Perelson, 1997; Wang et al., 2015a; Luo and Perelson, 2015; De Boer and Perelson, 2017), and to make predictions that could be evaluated in future experiments, as was done, for instance, with the cyclic re-entry model (Kepler and Perelson, 1993; Oprea and Perelson, 1997; Victora et al., 2010; Victora and Nussenzweig, 2012). Our model recapitulated the observed improvements in the humoral response following PI. Further, it unraveled a quality-quantity trade-off that constrains the GC response: increasing selection stringency in the GC improves the affinity of the Abs produced for the target Ag but reduces the amount of the Abs produced. The model also showed that the quality-quantity trade-off could be tuned by altering the availability of Ag in GCs. Manifestations of the quality-quantity trade-off as well as the influence of Ag availability have been observed in independent experiments (Zhang et al., 2013; Tam et al., 2016). Our model thus synthesizes diverse observations of the GC response using a single framework, indicating the robustness of our hypothesis and the model. Finally, we predict, using the model, that the affinity of exogenous Abs and Ag availability could be used as handles to optimize PI protocols.

Results

In Silico Model of the GCR and the Influence of PI

The GCR is complex, involving the interactions between several cell types, proteins, cytokines, and Ag, together culminating in the selection of B cells with high affinity for target Ags and the mounting of an Ab response (Victora and Nussenzweig, 2012; Cyster and Allen, 2019). Here, we abstracted key aspects of the GCR that are essential to understanding the role of PI in modulating the Ab response into an in silico stochastic simulation model. We briefly describe the model here; details are presented in STAR Methods.

We focused on individual GCs from the time when the GC is assembled and AM has commenced. We considered the GCR in response to a single, non-mutating antigenic epitope, representative of simple immunogens, such as haptens, employed widely (Tas et al., 2016; Gitlin et al., 2014; Zhang et al., 2013; Victora et al., 2010; Schwickert et al., 2007; Dal Porto et al., 1998; Jacob et al., 1991; Weiss and Rajewsky, 1990; Eisen and Siskind, 1964). We modeled evolutionary processes in the GCR using spatially homogeneous, discrete generation Wright-Fisher simulations, commonly used in population genetics (Hartl and Clark, 2007; Figure 1A; STAR Methods). We initiated the GCR with 1,000 GC B cells expressing BCRs with low affinity for the Ag, similar to previous studies (Wang et al., 2015a). We represented BCR paratopes and the antigenic epitope as bit strings of a fixed length (L), with an alphabet of size 4 representing the classification of amino acids into positively charged, negatively charged, polar, and hydrophobic groups (Luo and Perelson, 2015). In each generation, also called a GC cycle, we let each B cell interact with η ICs on FDCs on average. η was thus a surrogate for Ag availability in the GC; higher values of η indicated greater Ag levels. The affinity of a BCR for Ag was set proportional to the extent of the match between the two sequences. We defined the match length, ɛ, as the length of the longest sub-string common to the two sequences. Similarly, the strength of the Ag-Ab interaction in an IC, ω, was set proportional to the match length of the two corresponding sequences. In each B cell-IC encounter, the probability that the B cell acquired Ag was set proportional to ε − ω. As this difference increased, the difference in the affinities of the BCR and the Ab in the IC for the Ag increased; the BCR then had a higher chance of disrupting the IC and acquiring the Ag.

Following Ag acquisition, B cells competed for T_fh help. The probability that a B cell received T_fh help was proportional to the relative amount of Ag it acquired (Victora and Nussenzweig, 2012); we set the probability to 0 for a B cell that acquired less than a minimum level of Ag and to 1 for a B cell that acquired the maximum Ag in the cycle. Accordingly, B cells with high amounts of internalized Ag relative to their peers were preferentially selected. Of the selected B cells, which we restricted to a maximum of 250, 10% differentiated equally into plasma and memory B cells and 90% migrated to the dark zone, where they proliferated and mutated. Each B cell proliferated twice in one cycle. We let 10% of the daughter cells harbor a single, random mutation in their BCR sequences that could either increase, retain, or decrease affinity for Ag. The B cells then migrated to the light zone and formed the pool of cells that competed for selection in the next cycle. A cycle was assumed to last 12 h (Jacob et al., 1991; Victora and Nussenzweig, 2012). The rationale behind the parameter settings used here is provided in the STAR Methods.

In the absence of PI, the ICs on FDCs comprise endogenous Abs. As AM progresses, ICs containing lower affinity Abs are continuously replaced by those containing higher affinity Abs via the trafficking of secreted Abs back into the GC (Zhang et al., 2013, 2016; Figure 1B). To model this Ab feedback and IC turnover, we chose plasma cells from a previous GC cycle randomly and let Abs produced by them form the ICs for the present cycle.

With PI, because IC turnover is fast (Zhang et al., 2013), until endogenous Abs of higher affinity than the administered Abs for Ag are formed, ICs are expected predominantly to contain administered Abs. We therefore let, as an approximation, all ICs contain administered Abs, which we assumed were not limiting, until the average BCR affinity in a cycle exceeded the affinity of the administered Abs for the Ag, at which point, we switched to “natural AM,” i.e., AM in the absence of PI.

The GCR ended when B cells with BCRs of the highest match length (ε = L) were produced, marking completion of AM, or if all the B cells in a cycle died, representing GC collapse. In simulations where we let the Ag availability vary with time, the GCR could also end if no Ag was left.

With this in silico model, we performed stochastic simulations of the GCR and examined AM with and without PI.

Model Recapitulates Natural AM

We first examined whether the model recapitulated known features of the GCR in the absence of PI. We set L = 3 for ease of computation and so that the BCR/Ab paratopes could be classified as having low, intermediate, or high affinity (match length, ε, of 1, 2, or 3, respectively) for the Ag. We initiated the GCR with a random mixture of all types of B cells with low affinity for Ag. Note that there are 27 types of low-affinity B cells, given the 3 different mutations possible from the defined Ag sequence for an alphabet of size 4 at each of the L = 3 positions. We performed simulations with η = 10, mimicking scenarios where Ag availability is not limiting (see below).

Upon initiation of the GCR, the low-affinity GC B cell counts dropped and gave way to the fitter, intermediate affinity B cells (Figure 2A). The intermediate affinity B cells rose in number but soon let mutations give rise to the even fitter, high-affinity B cells, which eventually dominated the GC B cell population. The average affinity of the B cell population for Ag increased gradually, showing AM (Figure 2B). Concomitantly, the average affinity of the Abs in the ICs presented on the FDCs increased, indicating increasing selection stringency (Figure 2B). The plasma cell output, which included B cells of intermediate and high affinity for Ag, also increased and saturated (Figure 2C, inset). For the parameters chosen, AM reached completion in 2 to 3 weeks, in agreement with the observed temporal evolution of Ab affinity for haptens during natural AM (Dal Porto et al., 1998; Weiss and Rajewsky, 1990; Havenar-Daughton et al., 2017; Zhang et al., 2013). The humoral response mounted by the GC, characterized by the instantaneous and cumulative affinity-weighted Ab output from the GC (STAR Methods), intensified with time (Figure 2C). The long plasma cell half-life (~23 days; Kepler and Perelson, 1993; Tam et al., 2016) implied that the humoral response would take longer to saturate than the duration studied in our simulations. Our focus was on AM; we therefore ignored processes beyond the completion of AM, including the eventual extinguishing of GCs due to Ag decay (Wang et al., 2015a). The above predictions matched previously observed characteristics of natural AM (Eisen and Siskind, 1964; Berek et al., 1991; Wang et al., 2015a; Zhang et al., 2013), indicating that the essential features of the GCR were captured by our simulations.

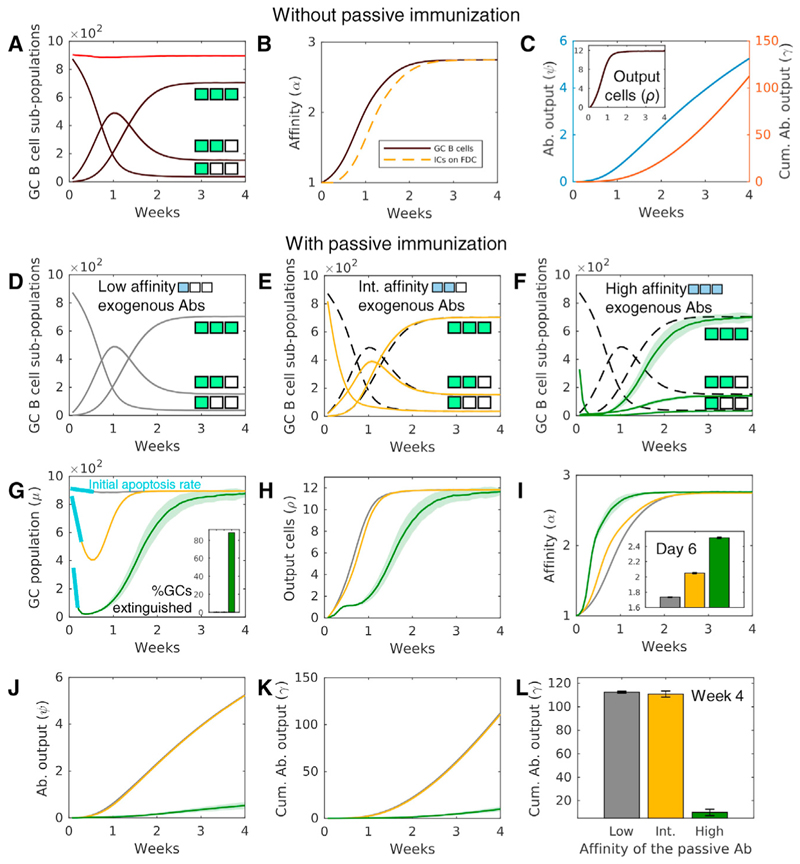
Figure 2. Passive Immunization Alters Affinity Maturation and the Quality-Quantity Trade-Off Constraining the GCR.

(A–C) Natural AM. Temporal evolution of (A) low- (ε = 1), intermediate- (ε = 2), and high (ε = 3)-affinity GC B cell sub-populations and overall GC size, μ(t) (red); (B) the average affinity of GC B cells (black) and of the Abs in ICs (dashed orange); and (C) the plasma cell output (inset), instantaneous Ab production from GCs, and the cumulative Ab output from GCs. The match length, e, is illustrated with colored positions in box strings.

(D-K) AM with passive immunization. Evolution of GC B cell sub-populations upon passive immunization with Abs of (D) low (ω = 1, gray), (E) intermediate (ω = 2, yellow), or (F) high (ω = 3, green) affinity is shown. Dashed lines represent natural AM, shown for comparison. The match lengths are illustrated with green (endogenous) or blue (exogenous) colored positions in box strings. Temporal evolution of GC attributes upon immunization with low- (gray), intermediate- (yellow), and high (green)-affinity Abs is as follows: (G) size (μ(t); % GCs extinguished over the course of 4 weeks shown in inset and initial apoptosis rates in blue); (H) plasma cell output (ρ(t)); (I) affinity (α(t)); (J) instantaneous Ab output (ψ(t)); and (K) overall Ab output (γ(t)).

(L) Comparison of λ at week 4 shows that intermediate affinity Abs maximized the quality-quantity trade-off. Lines and bars represent meansof50 ensemble means, with each ensemble comprising 100 realizations, and shaded regions and error bars represent SEMs STAR Methods.

See also Figures S1 and S2.

AM with PI Reveals a Quality-Quantity Trade-Off Constraining the GCR

We examined next how PI altered the GCR. We performed simulations with passively administered Abs of low, intermediate, or high affinity (match length, ω, of 1, 2, or 3, respectively) for Ag, which we assumed were available from the start of the simulations. With low-affinity passive Abs, no IC turnover with exogenous ICs was possible. The GCR was thus indistinguishable from natural AM (Figure 2D). With intermediate affinity passive Abs, AM proceeded faster than natural AM. Low-affinity B cell counts declined faster than with natural AM because of the greater selection stringency imposed by the administered Abs (Figure 2E). The decline was even sharper with high-affinity passive Abs (Figure 2F). Correspondingly, the overall GC B cell population initially declined, with the decline being steeper with higher passive Ab affinity. With intermediate passive Ab affinity, the population was rescued with the emergence of B cells with intermediate affinity BCRs (ε = 2). Although such BCRs did not have a fitness advantage over the passive Abs, they had a 50% chance of acquiring Ag in an encounter with an IC. Such B cells therefore had a significant chance of receiving the requisite survival signals. Their populations thus rose. The lower population of low-affinity B cells present compared to natural AM implied that fewer intermediate affinity B cells could be produced, resulting in the net fewer intermediate affinity B cells with PI with intermediate affinity passive Abs than natural AM (Figure 2E). The intermediate affinity B cells gave rise to high-affinity B cells, which eventually dominated the B cell population (Figure 2E). With PI with high-affinity passive Abs, however, the intermediate affinity B cells too had a strong selective disadvantage imposed by the higher affinity ICs. The intermediate affinity B cell population thus rose at a very low rate, based on chance events where BCRs acquired Ag from ICs with a probability far smaller than 50% (Figure 2F). Lower affinity B cells acquiring Ag from higher affinity ICs has been observed in vitro (Batista and Neuberger, 2000). Mutations eventually yielded BCRs with high affinity, following which the GC B cell population was rescued and AM reached completion.

These results revealed a fundamental constraint on the GC response: a quality-quantity trade-off. As the selection stringency (defined by the affinity of the passive Abs, ω) increased, the GCs experienced greater apoptosis of the lower affinity B cells (Figures 2D–2G). Indeed, with high-affinity passive Abs, a majority of the GCs were extinguished (Figure 2G, inset). The overall plasma cell output thus suffered as selection stringency increased (Figure 2H). However, the GC B cells selected were of higher affinity (Figure 2I). The difference was evident from the average affinity of the GC B cells at day 6 (Figure 2I, inset). Thus, as selection stringency increased, the average affinity for Ag, or quality, of the GC B cells selected increased, but the number, or quantity, of the GC B cells selected suffered. This quality-quantity trade-off implied that intermediate selection stringencies would maximize the GC response. The instantaneous and cumulative Ab outputs were thus significantly higher with ω = 2 than ω = 3 Figures 2J–2L). The small L makes it difficult to distinguish between the cumulative outputs with low and intermediate ω; the difference is evident with L = 8 (Figure S1). Furthermore, these results are robust to modest depletion of Ag during AM, which could occur due to Ag clearance by the administered Abs and/or host immune responses as well as due to Ag uptake by GC B cells (Figure S2).

Importantly, these results recapitulate the improvement in the humoral response due to PI seen experimentally (Jaworski et al., 2013; Schoofs et al., 2016). If passive Abs mimicking the intermediate affinity Abs were used in the experiments, they would lead to an improved overall Ab response. Furthermore, the higher affinity endogenous Abs generated during PI determine the selection stringency in the GCs after the clearance of the administered Abs and thus can sustain the improved response long term.

The results also indicate that, if passive Abs of high or low affinity for Ag were to be used, the gain in the overall Ab response would be compromised because of the quality-quantity tradeoff. Given the fundamental nature of the quality-quantity tradeoff, we asked next whether evidence of the trade-off could be found in experiments and whether our model was consistent with the evidence.

Model Captures Experimental Observations of the Quality-Quantity Trade-Off

Recent experiments do present evidence of the quality-quantity trade-off constraining the GC response. In Ag-primed mice, passively administered Abs of high affinity for the Ag at the start of the GCR enhanced AM but also resulted in amplified GC B cell apoptosis and lower plasma cell output, whereas low-affinity exogenous Abs maximized the GC B cell population and plasma cell output but resulted in relatively poor AM (Zhang et al., 2013). Further, the effects of PI were lost when the immunization was delayed. To test whether our model was consistent with these observations, we performed two sets of simulations: (1) GCs were started with low-, intermediate-, or high-affinity exogenous Abs to mimic early PI and (2) GCs were allowed to undergo natural AM for 2 weeks and then the ICs were turned over with administered Abs of low, intermediate, or high affinity to mimic delayed PI. GC responses were calculated 2 and 4 days after PI, following the experimental protocol (Zhang et al., 2013).

We found that early (week 0) PI decreased the GC B cell population, and hence GC size, as the affinity of the administered Abs for Ag increased (Figure 3A). The decrease was due to increased GC B cell apoptosis (Figure 3B), which in turn resulted in decreased plasma cell output (Figure 3C). The affinity of the GC B cells, however, increased (Figure 3D), consistent with the quality-quantity trade-off. Late PI, at week 2 from the start of the GCR, resulted in negligible differences in GC attributes (Figures 3E–3H). By week 2, natural AM had nearly reached completion, so that endogenous Abs had affinities on par with, if not higher than, the administered Abs. The latter thus could not induce IC turnover and alter selection stringency. Our simulations thus reproduced qualitatively all the above observations (Zhang et al., 2013), reaffirming the quality-quantity trade-off constraining the GC response.

Figure 3. Simulations Recapitulate Experiments of the Quality-Quantity Trade-Off.

(A-H) Point measurements (left; 2 and 4 days after passive immunization) and temporal evolution of GC attributes (right), after (A-D) immunization with GC initiation and (E-H) immunization 2 weeks after GC initiation. Attributes include GC size (A and E), extent of apoptosis (B and F), plasma cell output (C and G), and affinity (D and H). Red and gray vertical dashed lines in all the temporal trends indicate the times of passive immunization and measurement of GC characteristics, respectively. The results are consistent with recent experimental observations (Zhang et al., 2013). Shaded regions and error bars represent SEMs.

The quality-quantity trade-off limits the extent to which PI can improve the GC response. We therefore examined next ways in which the constraint imposed by the quality-quantity trade-off could be overcome.

Ag Availability Tunes the Quality-Quantity Trade-Off

In the simulations above, as the selection stringency increased, more B cell apoptosis occurred because B cells with low-affinity BCRs failed to acquire Ag from ICs of higher affinity passive Abs. Each B cell had η attempts, on average, to acquire Ag from FDCs. η was a surrogate for the amount of Ag available, assuming all other factors were not limiting. We reasoned that if more Ag were available, leading to higher η, each B cell would have more chances to acquire Ag and therefore survive. The probability of Ag acquisition per attempt would remain unaltered, still favoring higher affinity B cells. Thus, higher GC output quantities could potentially be realized without severely compromising quality.

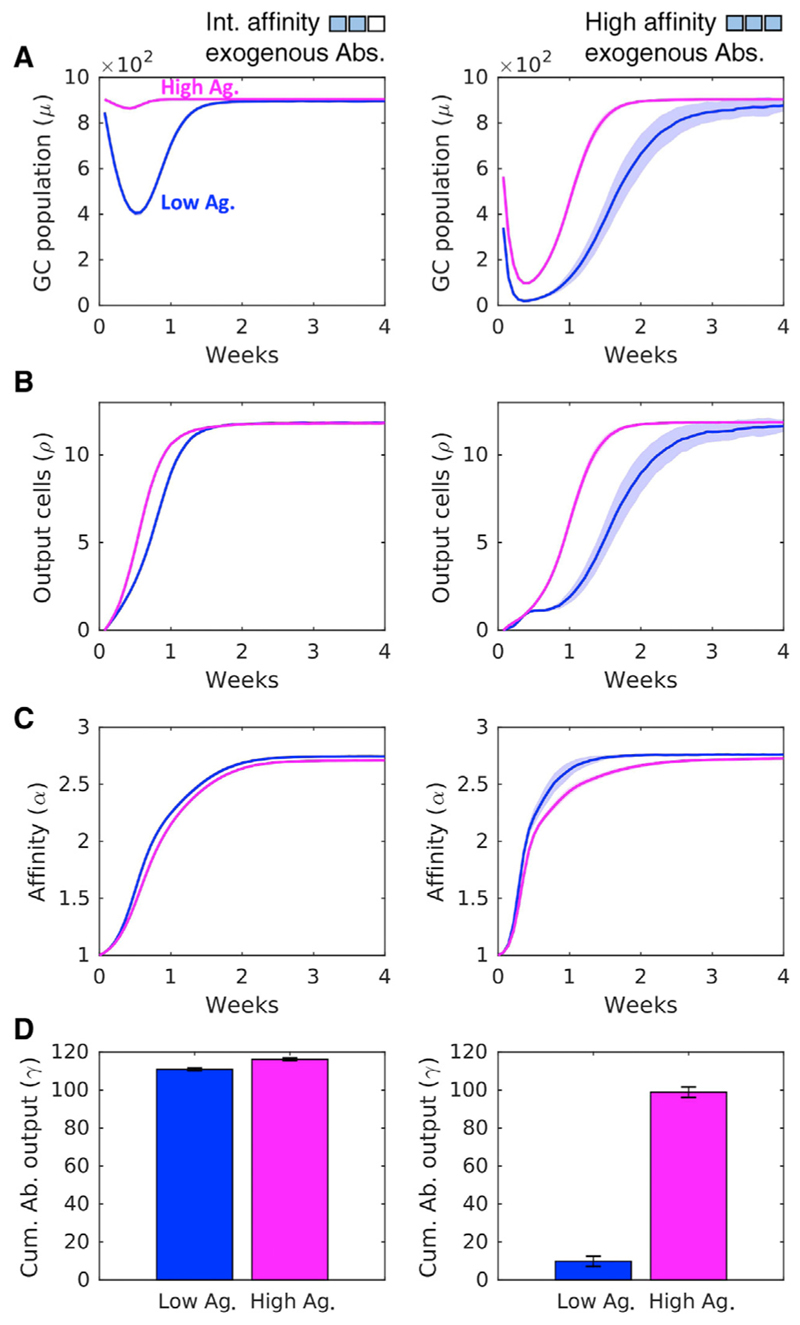
To test this hypothesis, we performed simulations with different values of η. We note first that, in the absence of PI, greater Ag availability leads to increased survival of lower affinity B cells, which improves the quantity of the GC output but compromises its quality (Figure S3). This result is consistent with the long-standing observation of increased Ag availability compromising the overall extent of AM (Eisen and Siskind, 1964; Siskind and Benacerraf, 1969; Wang et al., 2015a). We next performed simulations with two different levels of Ag availability (η = 10 and η = 14) and with PI with Abs of intermediate and high affinity for Ag (Figure 4). We found again that higher h resulted in higher GC B cell populations, indicating greater B cell survival (Figure 4A). This in turn resulted in increased plasma cell output (Figure 4B). The mean affinity of the GC B cells was weakly affected by η, indicating that AM and the quality of the GC response was marginally compromised by Ag availability for the parameters used (Figure 4C). AM was influenced by the affinity of the passively administered Abs, in keeping with our results above (Figures 2 and 3). The cumulative Ab output at week 4 was reduced by higher affinity passive Abs but was restored by increasing Ag levels: the high Ag regime resulted in a nearly 10-fold higher Ab output than the low Ag regime upon PI with high-affinity Abs (Figure 4D). Ag availability thus tuned the quality-quantity trade-off; increased Ag availability offset the adverse effects of selection stringency on the quantity of the GC output, albeit with some cost to its quality.

Figure 4. Ag Availability Tunes the Quality-Quantity Trade-Off in the GCR.

(A-D) GC characteristics: (A) size; (B) plasma cell output; (C) affinity of GC B cells; and (D) cumulative Ab output at week 4 upon passive administration of exogenous Abs with intermediate (left column) and high (right column) affinity for Ag under low (η = 10, blue) and high (η = 14, magenta) Ag availability regimes. Shaded regions and error bars represent SEMs. See also Figure S3.

One way to tune Ag availability is to administer controlled doses of Ag as part of a vaccine, a strategy showing great promise in recent studies (Tam et al., 2016; Boopathy et al., 2019; Cirelli et al., 2019). We therefore asked whether signatures of our findings of Ag availability tuning the quality-quantity trade-off were evident in studies that controlled Ag availability.

Model Recapitulates Experimental Observations of the GC Response with Varying Ag Availability

In a recent study, Ag availability was modulated by administering varying doses of Ag during the GCR in the absence of PI (Tam et al., 2016). Exponentially increasing, constant, or exponentially decreasing Ag doses were administered while keeping the total amount of infused Ag the same. Interestingly, the exponentially increasing Ag dosage, which mimics the way Ag levels rise due to pathogen replication following an infection, was found to induce GC responses with higher Ab titers than the other scenarios (Tam et al., 2016). These experiments were motivated by predictions of a simplified mathematical model of the GCR with time-varying Ag levels (Tam et al., 2016). Here, we examined whether our simulations, which include a more comprehensive description of the GCR, could recapitulate these observations.

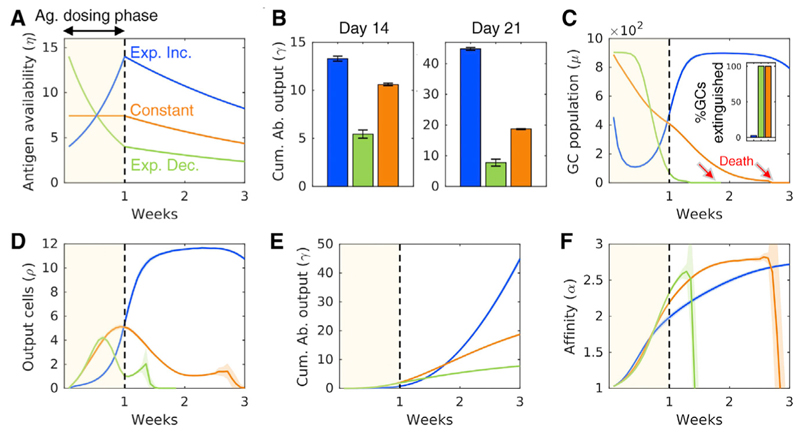
To mimic the experiments, we performed simulations of natural AM with η varying within each simulation following the patterns of the doses employed but with a constant area under the curve until day 7, when Ag loading ended (Figure 5A). η was subsequently assumed to decay exponentially at a rate commensurate with IC turnover on FDCs. We found that the exponentially increasing η, which ensured adequate Ag availability in GCs throughout, yielded the highest cumulative Ab output on day 14 (Figure 5B), in agreement with experiments (Tam et al., 2016). Constant and exponentially decaying Ag dosing protocols led to progressive apoptosis, GC collapse, and abrogation of plasma cell output by week 3, although exponentially increasing Ag ensured GC survival and robust plasma cell outputs (Figures 5C and 5D). The exponentially increasing dosing also yielded the highest overall Ab output (Figure 5E). However, consistent with our results above, AM progressed more slowly because of the relatively improved survival of low-affinity B cells (Figure 5F). The predicted dependence of the GC output on the Ag loading profile was consistent with experimental observations (Tam et al., 2016). Importantly, the predictions show how Ag availability can tune the quality-quantity trade-off and help overcome this intrinsic constraint on the GC response.

Figure 5. Simulations Recapitulate Experiments with Varying Ag Availability.

(A)Time evolution of Ag availability, η (see text), mimicking the exponentially increasing, constant, or exponentially decreasing Ag dosage till day 7 (Ag dosing phase) and exponential decline afterward. The latter decline occurs with the rate constant of 0.018 generation^-1 (ICs on FDCs are lost by turnover with an estimated rate constant of 0.012 generation^-1; Tam et al., 2016; Kepler and Perelson, 1993. We let an additional 50% loss occur, as an approximation, due to Ag acquisition by B cells.).

(B)GC responses elicited by the three Ag dosing profiles in terms of the cumulative Ab output on day 14 and day 21.

(C-F) Temporal evolution of the GC size (% GCs extinguished by week 3 in inset) (C), plasma cell output (D), cumulative Ab output (E), and GC B cell affinity (F), respectively. The results are consistent with corresponding experiments (Tam et al., 2016). Shaded regions and error bars represent SEMs.

Our model thus recapitulated and synthesized several independent and diverse experiments (Zhang et al., 2013; Tam et al., 2016; Schoofs et al., 2016; Eisen and Siskind, 1964) using a single framework, suggesting that our formalism accurately captured the essential features of the GCR and the role of passively administered Abs. The model could thus be applied to inform the design of optimal PI protocols. We present such an application next.

In Silico Identification of Optimal Sequential Passive Immunization Protocols

Numerous choices must be made in defining a PI protocol. For instance, the number of Ab infusions, the timings of the infusions, the dosages, the affinities of the exogenous Abs for a target Ag, and the use of Ag dosing to modulate Ag availability must all be determined. Given the huge resulting parameter space, searching for optimal PI protocols experimentally is prohibitive. Our model can help narrow this search space. The model has the flexibility to be tailored to any dosing protocol involving the above determinants and can then predict the resulting GC response. The protocols that predict the best responses could form candidates for future experimental verification. Here, we explored this idea with a dosing protocol used in recent PI studies, where 3 Ab infusions were administered with a fixed interval between doses (Nishimura et al., 2017).

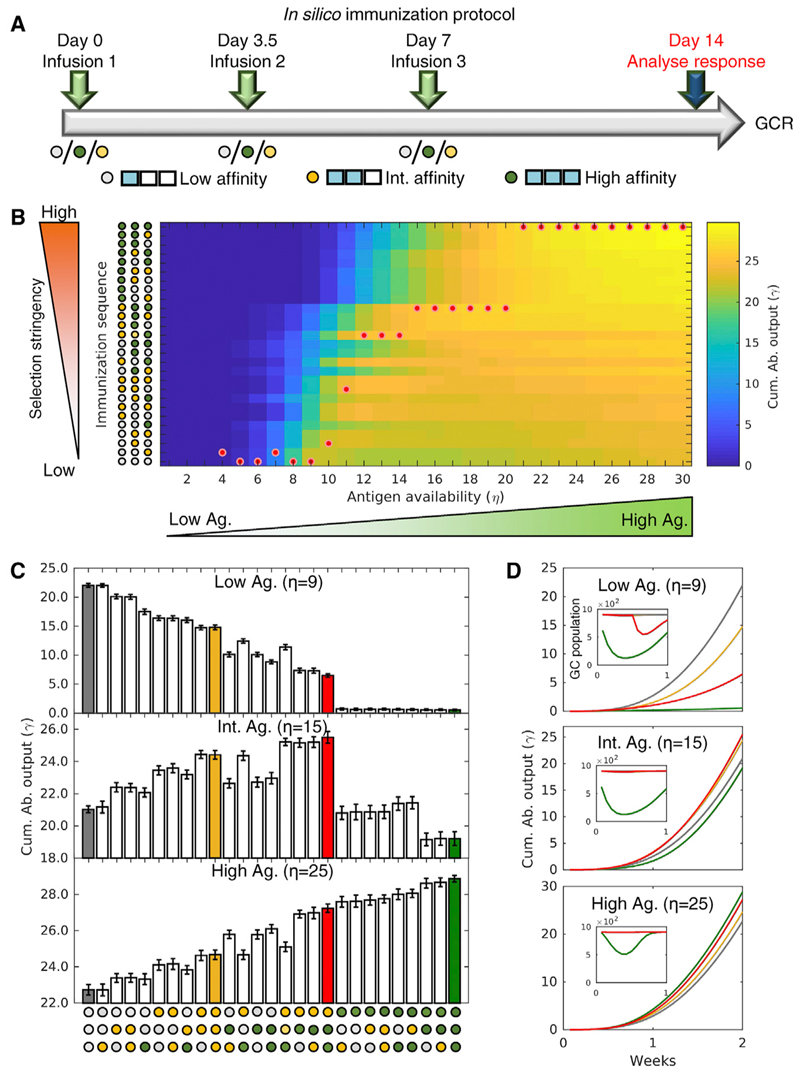
We assumed, following recent experiments (Zhang et al., 2013), that Abs with low, intermediate, and high affinity for the target Ag were available. These could then be administered in different sequences in the 3 doses. We let them be administered on day 0 (start of the GCR), day 3.5 (cycle 7), and day 7 (cycle 14) of the GCR (Figure 6A; a cycle typically lasts 12 h; Jacob et al., 1991; Victora and Nussenzweig, 2012). Each dose could be of low-(denoted as “L”), intermediate-(denoted as “I”), or high (denoted as “H”)-affinity Abs. For example, the combination H-I-L referred to the infusion of high-affinity Abs at cycle 0, intermediate-affinity Abs at cycle 7, and low-affinity Abs at cycle 14. The 3-dose protocol allowed 27 unique passive Ab administration sequences, from the all low, L-L-L, to the all high, H-H-H, affinity sequence. The Ag availability in the GC could vary depending, among other factors, on the pathogen load. We therefore performed simulations over a wide range of (constant) Ag availability, from η = 1 to η = 30, exploring each of the 27 Ab sequences for every integral η in the range. We calculated the affinity-weighted cumulative Ab output at day 14 (cycle 28) as a measure of the humoral response.

Figure 6. Optimization of Ab Combinations for Sequential Passive Immunization.

(A) Schematic of the in silico passive immunization protocol, with 3 doses of either low- (gray dot), intermediate- (yellow dot), or high (green dot)-affinity Abs on days 0,3.5, and 7 after initiation of the GCR and measurement of response on day 14.

(B) The cumulative Ab outputs at day 14 elicited by all possible passive Ab administration sequences as functions of Ag availability, η.

(C) Cumulative Ab outputs for all possible passive Ab administration sequences for low- (η = 5), intermediate- (η = 8), and high (η = 18)-Ag availability. The responses to the sequences L-L-L, I-I-I, H-H-H, and I-H-H (see text) are colored gray, yellow, green, and red, respectively.

(D) Temporal evolution of the cumulative Ab output (see Figure S4 for evolution of plasma cells and affinity) and GC size (inset) for the latter sequences. Error bars represent SEMs.

See also Figure S4.

The humoral responses elicited are summarized as a heatmap (Figure 6B). The Ab sequence eliciting the best response for each η is indicated by a red dot. For example, the best sequences for low (η = 9), intermediate (η = 15), and high (η = 25) Ag availability were L-L-L, I-H-H, and H-H-H, respectively. To understand these optimal combinations, we examined the simulated humoral responses at day 14 to each of the 27 sequences for these values of η (Figure 6C). Selection stringency increased as the usage of high-affinity Abs increased in the sequences. We found, interestingly, that the response gradually weakened as the selection stringency increased for η = 9. With η = 25, the opposite happened, with the response the best when selection stringency was the highest. With η = 15, an intermediate level of selection stringency elicited the best response. These results were in keeping with our observations above where increasing Ag availability helped overcome the constraint imposed by the quality-quantity trade-off, allowing better overall responses despite higher selection stringency. To elucidate these findings further, we examined the dynamics of the GCR for four different dosing sequences, L-L-L (gray), I-I-I (yellow), H-H-H (green), and I-H-H (red), for the three values of η above (Figures 6D and S4). With η = 9, L-L-L resulted in weak selection pressure and maintained the plasma cell output, although the harsher selection imposed by higher affinity passive Abs in the other combinations led to reduced Ab output, GC size, and plasma cell output (Figures 6D and S4). With η = 15 and η = 25, however, the GCs withstood higher selection stringencies, yielding better outputs with immunization sequences containing higher affinity Abs. In all cases, the quality of the GC response, defined by the average GC B cell affinity, increased with the usage of higher affinity passive Abs (H-H-H > I-H-H > I-I-I > L-L-L; Figure S4).

In summary, dosing sequences containing lower affinity Abs were optimal when Ag availability was low, whereas sequences containing higher affinity Abs elicited the best response with high Ag availability. Validation of these predictions, in part, comes from observations of the improvement in the humoral response in chronically HIV-1-infected individuals administered the HIV-1 bNAb 3BNC117 (Schoofs et al., 2016). Although PI with 3BNC117 improved the endogenous Ab response overall, the improvement was significantly greater in individuals not on antiretroviral therapy (ART) than in those on ART prior to the PI. ART suppressed viremia. Individuals on ART thus had lower plasma viremia, and hence potentially lower Ag availability in the GCs, than individuals not on ART. Based on our model predictions, optimal PI should have employed lower affinity Abs in the former than in the latter. The use of the same bNAb and dosing protocol in both the patient groups thus resulted in the disparate outcomes, consistent with our predictions.

Discussion

With growing evidence of its ability to elicit improved and lasting humoral responses, PI is poised to transcend its classical role as a strategy for the temporary alleviation of disease burden and emerge as a potent tool to engineer host humoral responses. Here, we elucidated a mechanism with which administered Abs can influence endogenous Ab production, addressing a fundamental knowledge gap that has precluded the rational deployment of PI to engineer humoral responses. We hypothesized that administered Abs raise the selection stringency in GCs by preferentially forming ICs and preventing GC B cells with low affinities for Ag from acquiring Ag and receiving survival cues. Stochastic simulations of the GC reaction based on this hypothesis captured several independent experimental observations. The simulations unraveled a quality-quantity trade-off constraining the GC reaction and showed how optimal passive immunization protocols can be designed to exploit this trade-off and maximize the GC output.

Previous mathematical models and stochastic simulations of AM have presented important insights into the GCR, such as the cycling of B cells between the light and dark zones (Oprea and Perelson, 1997; Kepler and Perelson, 1993) and the limiting nature of T_fh help (Meyer-Hermann et al., 2006; Figge et al., 2008), and have suggested vaccination protocols that could guide the GCR into eliciting desired Ab responses (Tam et al., 2016; Wang et al., 2015a; Shaffer et al., 2016; Wang, 2017). Models have also explored the evolution of B cells yielding bNAbs of HIV-1 and the reasons impeding their selection (Luo and Perelson, 2015; Zarnitsyna et al., 2016; De Boer and Perelson, 2017). The influence of passive immunization on the GCR has been less well explored. One study, where passive administration of bNAbs to HIV-1-infected individuals improved humoral responses, speculates that the bNAbs may have altered the viral quasispecies and selected for viral variants that robustly stimulated GC responses and/or formed more immunogenic ICs with Ag (Schoofs et al., 2016). Although the first possibility exists in the context of mutating HIV-1 virions, it cannot explain the enhanced rates of AM observed with non-mutating Ag, such as haptens following passive immunization. The second possibility may explain higher rates of Ag clearance and increased immune activation but leaves unclear how the ICs of higher immunogenicity could specifically modulate GC B cell selection. An earlier study argued that passive immunization increases the selection stringency in GCs via epitope masking, where administered Abs bind Ag in ICs already presented on FDCs and block BCRs from accessing Ag (Zhang et al., 2013). A model based on this mechanism made predictions consistent with the quality-quantity trade-off. The model, however, had a limitation. Although it let the binding of administered Abs to the ICs be reversible, it did not account for the possibility that Ag could be tugged away by the dissociating Abs based on the relative affinities of the endogenous and exogenous Abs for Ag. If Ag is thus tugged away, as is expected from energetic considerations, epitope masking may cease to be the predominant mechanism increasing selection stringency. Our model accounted for the latter possibility of Ag being tugged away by administered high-affinity Abs and explained not only the quality-quantity trade-off but also other independent observations discussed below. A more robust conceptual view of the selection forces driving AM in GCs and the influence PI has on these forces thus emerges.

Our findings synthesize several independent experimental observations. By showing how AM is influenced not only by the affinity of the administered Abs for Ag but also by Ag availability, our findings recapitulated observations of the GC response with PI using Abs of different affinities (Zhang et al., 2013) as well as with active immunization using Ag dosing protocols that tuned Ag availability (Tam et al., 2016). In the former experiments (Zhang et al., 2013), PI with low-affinity Abs did not alter AM significantly, whereas PI with high-affinity Abs improved AM but compromised the quantum of Abs produced. Our simulations recapitulated this quality-quantity tradeoff. The preferential presentation of Ag by the high-affinity administered Abs raised the selection stringency in the GCs, leading to the selection of fewer but higher affinity B cells, explaining the trade-off. The trade-off is tuned by Ag availability. Indeed, going all the way back to the early experiments of Eisen and coworkers, enhanced Ag availability has been shown to compromise AM, allowing the increased selection of lower affinity B cells (Eisen and Siskind, 1964; Siskind and Benacerraf, 1969). Our model recapitulates this behavior, as do previous models of the GCR (Wang et al., 2015a). In more recent experiments (Tam et al., 2016), exponentially increasing Ag availability as the GC progresses, mimicking the natural expansion of pathogen following the onset of an infection, was found to yield better Ab responses than constant or exponentially decreasing Ag availability. In our simulations, the increased Ag availability as the GCR progressed offset the increasing selection stringency and hence improved the overall Ab response, consistent with the latter experiments. Our findings are also consistent with improvements in the endogenous Ab response elicited by PI in several studies. For instance, in the newborn or 1-month-old rhesus macaque model of SHIV infection, administration of neutralizing Abs enhanced endogenous neutralizing Ab production, which suppressed set-point viremia, delayed disease progression, and enhanced survival (Ng et al., 2010; Jaworski et al., 2013). Similarly, PI of mice with anti-CD4 binding site Abs enhanced the production of Abs targeting the CD4 binding site of HIV-1 gp120 (Visciano et al., 2008). More recently, improved neutralization breadth and potency of endogenous Abs was observed following PI of HIV-1-infected individuals with the HIV-1 bNAb 3BNC117 (Schoofs et al., 2016). Furthermore, the improvement was greater in individuals not on ART and hence with higher plasma viremia prior to PI than in those on ART, an observation again in accordance with our findings.

This synthesis of diverse experiments presents a strong test of our model and of our hypothesis of the influence of exogenous Abs on the GC response. Models have been constructed previously that separately describe several of the observations, including the quality-quantity trade-off (Zhang et al., 2013), the influence of varying Ag availability (Tam et al., 2016), and other features of the GCR (Kepler and Perelson, 1993; Luo and Perelson, 2015; Wang et al., 2015a). Our model, for the first time, recapitulates all of these observations using a single framework. Thus, each of these independent observations can be viewed as a different manifestation of the same underlying process, captured in our model, when subjected to different external inputs, such as passively administered Abs or varying doses of Ag. The agreement between our model predictions and the several corresponding experimental observations indicates the robustness of our model.

Consistent with previous studies (Zhang et al., 2013; Tam et al., 2016; Cirelli et al., 2019; Boopathy et al., 2019), the affinity of administered Abs for Ag and the availability of Ag emerge as potentially tunable handles to engineer the host humoral response using PI strategies. Although Ag availability within GCs remains difficult to estimate (Tam et al., 2016), it is likely to be proportional to the pathogen load. Pathogen loads can vary widely across individuals; for instance, the set-point viral load varies by 4 orders of magnitude across HIV-1-infected individuals (Fraser et al., 2014). Our simulations suggest that PI protocols must be personalized based on the pathogen load. By comprehensively spanning parameter space, the simulations showed that PI with Abs of low affinities for Ag were optimal when Ag availability in the GCs was low, whereas higher affinity Abs were best suited when Ag availability was high. Future studies may also examine whether simultaneously tuning Ag availability, using suitable Ag administration patterns (Tam et al., 2016), and selection stringency in the GCs, using passive immunization with Abs of suitable affinities (Zhang et al., 2013), may be a more powerful strategy than PI alone. Our simulations present a framework for the design of such PI protocols. Finally, because passively administered Abs alter AM by forming ICs in our simulations, our simulations can also be applied to define optimal strategies of immunization with ICs, which have been argued to improve the humoral response more than with the uncomplexed Ag (Lambour et al., 2016; Kumar et al., 2012; Chen et al., 2016).

Our simulations have been restricted to describing the GCR with a single, non-mutating antigenic epitope. With rapidly evolving pathogens, such as HIV-1, B cell evolution is expected to occur in the presence of multiple epitopes in a GC. Accounting for this diversity would be an important extension of our formalism, especially given that the strength of the endogenous response following passive immunization was found to correlate with antigenic diversity (Schoofs et al., 2016). Further, our simulations did not include T cell receptor specificity that allows interactions of T_fh cells only with cognate GC B cells. Both multiple epitopes and T cell receptor specificity may be important to the development of breadth in Ab responses (Wang et al., 2015a; Luo and Perelson, 2015; De Boer and Perelson, 2017). We employed approximate descriptions of the fitness of B cells based on the energetics of BCR-IC interactions, following previous studies (Luo and Perelson, 2015). More detailed descriptions based on intracellular signaling following BCR stimulation (Kwak et al., 2019), leading to B cell proliferation and differentiation or apoptosis, may yield more reliable fitness landscapes. Such landscapes would be important to understanding recent observations where stronger immune responses were elicited by upregulating the inhibitory receptors on B cells and raising the signaling threshold for B cell selection (Wang et al., 2015b).

In summary, our simulations present a mechanistic understanding of the influence of passive immunization on the GCR, capture independent experimental observations, and facilitate optimization of passive immunization protocols to engineer the humoral response.

Star★Methods

Key Resources Table.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
Germinal center simulation code	This paper	N/A.
MATLAB 2018a	MathWorks	https://in.mathworks.com

Lead Contact and Materials Availability

Further information and requests can be addressed to Narendra M. Dixit (narendra@iisc.ac.in). This study did not generate new unique reagents.

Method Details

In Silico Stochastic Simulation Model of the GCR

We present details of the model formulation and the simulation protocol we employed to describe the GCR including the role of passively administered Abs.

Initialization

Low affinity seeder B cells initiate the GCR and proliferate rapidly until the GC population reaches a steady state of ~ 1000 cells, at which point somatic hypermutation of the immunoglobulin genes of the GC B cells switches on (De Silva and Klein, 2015; Robert et al., 2017; Wang et al., 2015a; Jacob et al., 1991). We thus initiate our simulations with N = 1000 low affinity B cells. We consider AM of the B cells in response to a single, non-mutating antigenic epitope, representative of haptens or other simple Ags employed widely (Zhang et al., 2013; Gitlin et al., 2014; Victora et al., 2010; Schwickert et al., 2007; Jacob et al., 1991; Dal Porto et al., 1998; Weiss and Rajewsky, 1990; Tas et al., 2016; Eisen and Siskind, 1964). The Ag epitope and BCR/Ab paratopes are represented as bit-strings of length L and an alphabet of size 4, similar to previous AM models (Robert et al., 2018; Luo and Perelson, 2015; Wang et al., 2015a). We first choose a randomly assembled string to represent the Ag. We then choose a BCR paratope for each cell in the initial B cell pool by randomly mutating the Ag sequence at L - 1 randomly chosen positions. We subject the B cell pool to selection, mutation, and proliferation in discrete generations, described below.

Antigen acquisition and T_fh cell help

Let N_GC(t) be the GC B cell population in the t^th generation, or cycle. We let the B cells acquire Ag as follows. In each generation, B cells are selected randomly for interaction with ICs on the FDC for antigen acquisition. Depending on the affinity of the BCR for the antigen, the interaction could result in successful antigen acquisition with the probability f_Ag, defined below. For these interactions, we randomly choose B cells N_GC(t)×η times with replacement, so that each B cell has an average of η chances to acquire Ag in each generation. We thus use the number of attempts, η, as a surrogate of the amount of antigen available in the GC. In each generation, we track the number of successful attempts of every B cell and define the maximum number of successful attempts by any Bcell(s) as the maximum antigen acquired in the generation. The B cells are then subjected to competition for T_fh cell help. A B cell is chosen at random for T_fh help, and allowed to survive with a probability f_Tfh, also defined below. This process is repeated N_GC(t) times or until $N_{max}^T$ B cells are selected, whichever is earlier. This ensures, given that each selected B cell proliferates twice, that the GC B cell population remains within the cap of 1000 cells, consistent with experimental estimates (~ 1300 B cells in a day 12 GC; Jacob et al., 1991), and similar to the sizes used in previous GC models (~ 1500 cells; Wang et al., 2015a).

Proliferation, evolution, and GC exit

Of the selected cells, we randomly select 90% for proliferation (in the dark zone) and let the remaining 10% differentiate equally into plasma and memory B cells and exit the GC (Wang et al., 2015a). Each B cell selected for proliferation proliferates twice (Gitlin et al., 2014; Wang et al., 2015a). We then select ξ = 10% of the daughter cells and introduce single random point mutations in each of their BCR sequences. The resulting B cells form the pool for the next GC cycle. This mutation rate, or percentage, X, was chosen because the somatic hypermutation rate of Ig variable regions was estimated to be ~ 10³/base pair/generation and the order of the number of nucleotides involved is ~ 10² (Victora and Nussenzweig, 2012; Luo and Perelson, 2015). This suggests that on average, ~ 1 in 10 B cells would be mutated per generation in their Ig variable regions, similar to other GC models (probability of ~ 0.14 per sequence per generation; Wang et al., 2015a). Further, we note that most mutations in our simulations are either neutral or deleterious. This is because in our simulations, fitness gain happens when mutations, implemented in an unbiased manner, drive an Ab sequence toward that of the Ag. Because the alphabet is of size 4, there are in general far more ways to mutate (or stay) away from the target (Ag) sequence than move toward it. Most mutations, therefore, are either neutral or result in fitness penalties and only a small percentage would lead to fitness gain, as is expected. Because many mutations can be neutral, ξ = 10% marks an upper bound on the rate of affinity affecting mutations. Variations in ξ did not significantly affect AM (Figures S5A–S5C).

IC turnover

FDCs mainly present ICs of Ag bound to Abs on FC_γ or complement receptors (Toellner et al., 2018; Zhang et al., 2016; Heyman, 1990; Noris and Remuzzi, 2013; Batista and Harwood, 2009). Previous studies have shown that Ag by itself may not bind with high affinity to Fcγ or complement receptors (Nimmerjahn and Ravetch, 2008; Chan et al., 2015) and therefore may not be efficiently presented on FDCs. Indeed, humoral responses were found to be significantly better when ICs were used for PI compared to uncomplexed Abs (Kumar et al., 2012; Lambour et al., 2016; Chen et al., 2016). Upon Ag stimulation, low affinity ICs are initially formed by endogenous broadly-reacting immunoglobulin M (IgM) Abs with Ag, which initiate the GCR (Boes, 2000; Tam et al., 2016). As the GCR proceeds, these low affinity ICs are replaced by higher affinity ICs by a process of Ab feedback. Endogenous Abs produced by plasma cells in the vicinity of the GC may re-enter the GC (Zhang et al., 2013, 2016) and capture Ag from existing ICs to form new ICs (Figure 1). ICs presented on cell surfaces could dissociate spontaneously, leading to the release of Ag (Boder et al., 2000), which Abs of higher affinity would preferentially acquire. This dissociation and acquisition may be accelerated if the higher affinity Abs could bind Ag in ICs on the FDCs and destabilize the ICs. While BCRs destabilize ICs by the application of force (Batista and Neuberger, 2000; Natkanski et al., 2013; Kwak et al., 2018), Ag acquisition by BCRs has been argued to still depend on the intrinsic quality of the Ag-Ab interaction (Batista and Neuberger, 2000). Higher affinity Abs are thus expected to similarly bind and acquire Ag from ICs presented on FDCs. Abs may also bind Ag in the serum and form ICs which are then deposited on the FDC via sub-capsular sinus macrophages and marginal zone B cells (Victora and Nussenzweig, 2012; Batista and Harwood, 2009; Phan et al., 2009; Roozendaal et al., 2009; Noris and Remuzzi, 2013). Finally, higher affinity Abs may competitively displace low affinity Abs in existing serum ICs and be trafficked similarly on to FDCs. IC turnover from low to high affinities has been observed experimentally (Zhang et al., 2013).

We implement IC turnover as follows. For natural AM, we let affinity matured endogenous Abs secreted by the plasma cells in the j^th generation form the ICs presented on FDCs in the (j + τ)^th generation. In agreement with reported IC turnover timescales (Zhang et al., 2013), we let τ be 2 generations. We base this assumption on experiments (Zhang et al., 2013) of temporal imaging of ICs on the FDC network before and after passive immunization in mice. Within two hours of passive immunization, exogenous ICs localized in the marginal zone, and by 24 hours the majority (approximately two-thirds) of the endogenous ICs on the FDC network were turned over and replaced by exogenous ICs. AM is not sensitive to variations in τ (Figures S5D–S5F).

With PI, we let exogenous Abs form the ICs on FDCs until endogenous ICs of the same average affinity for Ag as exogenous Abs are formed, at which point we implement turnover akin to natural AM. Higher affinity exogenous ICs show higher residence times on FDCs than lower affinity exogenous ICs (Zhang et al., 2013, 2016). IC turnover was thus affinity dependent. If the administered ICs were low affinity complexes, they were turned over rapidly, whereas if they were of high affinities, they remained presented on FDCs for several days. Long turnover times are consistent thus with high affinity ICs. In our simulations too, turnover of low affinity ICs is quick and that of high affinity ICs more difficult. We note that FDCs can often retain ICs in non-degradative endosomal compartments for many months, which is much longer than the 2-4 weeks lifetime of GCs, the purpose of which is argued to be in the maintenance of the memory B cell pool (Heesters et al., 2016).

B cell fitness for Ag acquisition

For each B cell, we define the match length, ε, as the length of the longest common sub-string of its BCR and Ag sequences (Robert et al., 2018; Luo and Perelson, 2015), and assume it to represent the strength of BCR-Ag binding. Similarly, the match length of the complexed Ab in the IC with Ag is ω. The fitness, f_Ag, defined as the probability with which the B cell acquires Ag during a BCR-IC contact, depends on the relative magnitudes of ε and ω and can be derived from the free energy of spontaneous IC formation (Equation 1), spontaneous BCR-Ag complex formation (Equation 2) and competitive Ag acquisition by BCRs (Equation 3):

$$\mathrm{Ag}+\mathrm{Ab}\rightharpoondown \mathrm{Ag}-\mathrm{Ab}, ∆G_1=\kappa \omega$$ (Equation 1)

$$\mathrm{Ag}+\mathrm{BCR}\rightharpoondown \mathrm{Ag}-\mathrm{BCR}, ∆G_2=\kappa \epsilon$$ (Equation 2)

$$\mathrm{BCR}+\mathrm{Ag}-\mathrm{Ab}\rightharpoondown \mathrm{BCR}-\mathrm{Ag}+\mathrm{Ab}, ∆G=∆G_2-∆G_1$$ (Equation 3)

Here, κ is the constant, per-site free energy of binding of the Ab or BCR with the Ag. In previous models, steric factors, and relative positions of the interacting epitopes in three-dimensional space were either ignored (Luo and Perelson, 2015), or accounted for in an approximate manner (Wang et al., 2015a), and for simplicity, we follow the former. It follows that ΔG = κ(ε − ω). The relative fitness of a BCR is obtained by the normalization (f_Ag = ΔG − ΔG_min/ΔG_max − ΔG_min), where ΔG_min = − Lκ represents the scenario where the Ab in the IC has the highest possible affinity for the Ag and the BCR has no affinity, and ΔG_max = Lκ represents the opposite. Simplifying, we obtain

$$f_{Ag}=\frac{\epsilon -\omega +L}{2L}$$ (Equation 4)

We present a mechanistic derivation of this fitness function below (see subsection titled “Mechanistic derivation of B cell fitness for Ag acquisition”). Other functional forms of f_Ag such as exponential landscapes were considered (Figure S6), and did not qualitatively change the model behavior or predictions.

B cell fitness for T_fh cell help

B cells possessing relatively high amounts of internalized Ag, and therefore high pMHCII surface densities, compared to peers competitively elicit T_fh help (Victora and Nussenzweig, 2012). To decide whether a B cell succeeds, we let the amount of Ag acquired by the B cell be 9. (Note that this depends on f_Ag above.) Let θ_min and θ_max be the minimum and maximum amounts of Ag acquired across all B cells in the generation. We consider only B cells whose 9 is above a minimum Ag threshold, θ_c, as eligible for T_fh cell help. This follows from recent findings suggesting that BCR crosslinking by Ag leads to enhanced B cell signaling and T_fh cell help (Turner et al., 2018) and that BCR signaling and CD40 signaling from T_fh cells synergize to activate GC B cells (Luo et al., 2018). Further, if a B cell acquires Ag but does not receive T_fh help, it can revert to a naive state (Turner et al., 2017). Thus, although a B cell with a single successful Ag acquisition can receive T_fh when it arrives quickly, on average, for B cell activation to last until T_fh help is received, a minimum level of Ag acquisition may be required. We set θ_c = 3 for all the simulations and note that AM is not sensitive to changes in θ_c (Figures S5G-S5I). The probability of a B cell with θ > θ_c successfully eliciting help from T_fh cells is then written as

$$f_{T_{fh}}=\frac{\theta -{\theta }_{min}}{{\theta }_{max}-{\theta }_{min}}$$ (Equation 5)

This description ensures that relative and not absolute amounts of acquired Ag determine T_fh help (Victora et al., 2010; Victora and Nussenzweig, 2012), and the B cell internalizing maximum Ag always gets selected upon encountering a T_fh cell.

Termination

AM ends when the highest match length (ε = L) B cells are produced. Stochastic effects preclude B cells from all possessing BCRs with a perfect match length. Rather, an equilibrium distribution of B cells possessing BCRs with different match lengths is reached, representing a mutation-selection balance (Hartl and Clark, 2007). In some simulations, where the selection stringency is too high, or due to stochastic effects, no B cells survive. We thus end our simulations in one of two ways, whichever is earlier: (1) The B cell population recovers to nearly the initial value of 1000 cells following the initial dip and the composition of the GC B cell population equilibrates (the mean numbers of each cell type do not vary further to within a tolerance), as shown in Figures 2A and 2D–2F. For simulations with L = 3, this occurs within t_max = 84 GC cycles. (2) The GC B cell population is annihilated and the GC is extinguished.

Mechanistic Derivation of B Cell Fitness for Ag Acquisition

We present a mechanistic derivation of the fitness function f_Ag outlined in Equation 4. We consider the scenario where a BCR is bound to the IC forming a ternary complex of Ab, Ag and BCR (Figure S7). The ternary complex could dissociate in two ways: (1) The IC could dissociate, leaving the Ag-BCR complex intact. (2) The BCR could dissociate, leaving the IC intact. The former would amount to Ag acquisition by the BCR. We now compute the probability of this Ag acquisition. Although GC B cells are known to exert a force on the IC through the BCR (Batista and Neuberger, 2000; Natkanski et al., 2013; Kwak et al., 2018), Ag acquisition is still thought to depend on the intrinsic quality of the Ag-Ab and Ag-BCR interactions (Batista and Neuberger, 2000). Here, we therefore focus on these intrinsic interactions.

We let k₁ and k₂ be the dissociation rate constants of the Ag-Ab and BCR-Ab complexes, respectively. We assume that the dissociation events occur independently. The mean lifetimes of the complexes would thus be (1 /k ₁) and (1 /k₂), respectively. Assuming the dissociation events follow Poisson statistics, the waiting times for the dissociation events, t₁ and t₂, respectively, would follow exponential distributions:

$$g\left(t_1\right)=k_1 exp\left(-k_{1 }t\right) and g\left(t_2\right)=k_2 exp\left(-k_{2 }t\right)$$ (Equation 6)

where g(t₁) dt₁ is the probability that the IC would dissociate in time dt₁ near t₁ and g(t₂)dt₂ the probability that the BCR would dissociate in time dt₂ near t₂. For successful antigen capture by the BCR, t₂ must be smaller than t₁; i.e., the IC must dissociate earlier than the Ag-BCR complex. This probability of success is thus

$$P_S={\int }_{t_1=0}^{\infty }{\int }_{t_2=0}^{t_1}g\left(t_1\right)g\left(t_2\right)d{t}_{1}d{t}_2=\frac{k_2}{k_1+k_2}$$ (Equation 7)

where we have used Equation 6 for g(t₁) and g(t ₂). We recognize next that for antigen-antibody complexes, the on-rates are usually diffusion limited (Foote and Eisen, 1995) and are thus not expected to vary across different types of antibodies. The equilibrium association constants, K_a = (k_on /k_off), for different antibodies are thus largely determined by the off-rates. If we define K₁ and K₂ as the equilibrium association constants of the Ab-Ag and Ag-BCR complexes, respectively, then Equation 7 becomes

$$P_S=\frac{K_2}{K_1+K_2}$$ (Equation 8)

From equilibrium reaction thermodynamics, it follows that the Gibbs free energies of the reactions are related to the equilibrium association constants: ΔG₁ = − RT In K₁ and ΔG₂ = − RT In K₂, where R is the universal gas constant and T the absolute temperature. Using these relationships, Equation 8 becomes

$$P_S=\frac{exp\left({\displaystyle \frac{-∆G_2}{RT}}\right)}{exp\left({\displaystyle \frac{-∆G_1}{RT}}\right)+exp\left({\displaystyle \frac{-∆G_2}{RT}}\right)}=\frac{1}{exp\left({\displaystyle \frac{∆G_2-∆G_1}{RT}}\right)+1}$$ (Equation 9)

Measurements of the energetics of antigen-antibody interactions have shown that the free energies have a dominant contribution from the energy of the interaction and that the entropy plays a minor role (Eisen and Siskind, 1964). Here, we let the energy be determined by the match length, which for the Ag-Ab complex is defined as ω and for the Ag-BCR complex as ε. Equation 9 thus becomes

$$P_S=\frac{1}{exp\left(-\kappa \epsilon +\kappa \omega \right)+1}$$ (Equation 10)

where, −κ is the energy per unit match length. For Ag and Abs of lengths L, we recognize that the match lengths vary between 0 and L. Thus, P_S is maximum, P_max, when ε = L and ω = 0, and minimum, P_min, when ε = 0and ω = L. With these limits, we define a fitness landscape for B cells, where cells with the maximum P_S have fitness 1 and those with minimum P_S have fitness zero, and the fitness varies linearly with P_S. We thus obtain the fitness of a B cell with a given ε and ω as

$$f_{Ag}=\frac{P_S-P_{min}}{P_{max}-P_{min}}=\frac{\left(exp\left(\kappa L\right)-exp\left(-\kappa \epsilon +\kappa \omega \right)\right)\left(exp\left(-\kappa L\right)+1\right)}{\left(exp\left(\kappa L\right)-exp\left(-\kappa L\right)\right)\left(exp\left(-\kappa \epsilon +\kappa \omega \right)+1\right)}$$ (Equation 11)

We simplify the above expression in the limit where the energies are small, i.e., κL is small compared to unity, using terms up to the leading order in κ in the Taylor series expansions of the expressions. Thus, we obtain,$exp\left(\kappa L\right)-exp\left(-\kappa \epsilon +\kappa \omega \right)\approx 1+\kappa L-\left(1-\kappa \epsilon +\kappa \omega \right)=\kappa \left(\epsilon -\omega +L\right), exp\left(\kappa L\right)-exp\left(-\kappa L\right)\approx 2\kappa L, \mathrm{and} exp(-\kappa L)+1\mathit{\approx }exp\mathit{ }(-\kappa \epsilon \mathrm{+}\kappa \omega )\mathit{+}1\mathit{.}$ Simplifying Equation 11 yields the fitness function, f_Ag (Equation 4):

$$f_{Ag}=\frac{\epsilon -\omega +L}{2L}$$ (Equation 12)

Note that the above formalism would hold even when the Ag and BCR bind to different epitopes, provided the energy terms, ε and ω, apply to the corresponding epitope-based binding affinities.

Quantification and Statistical Analysis

For every scenario, we perform 5000 realizations of the GCR to obtain reliable statistics. We divide the 5000 realizations into n = 50 ensembles of 100 GCR realizations each, the latter representative of the number of GCs in a lymph node. For each ensemble we compute the means of several quantities mentioned below. From the n ensemble means, we obtain the overall mean (thick lines in all figures) and standard errors of the mean (shaded regions around the thick lines in all figures) of each of the quantities. We choose 100 GCs per lymph node, similar to a previous modeling study that considered the GCR in mice (Tam et al., 2016), and anatomical observations in rats (Hoshi et al., 1992). (The number of GCs per lymph node can go up to ~ 1000 in humans (Qatarneh et al., 2006).) We note that Abs from plasma cells produced in neighboring GCs could traffic to the GC of interest and vice versa and affect AM. Our focus here is on the influence of PI on AM. Following PI, the Abs administered are typically in large excess and would tend to dominate the Ab pool that enters GCs. The effects of endogenous Abs shared across GCs is thus likely to be limited. We therefore ignored the sharing of Abs across GCs, for simplicity, which allowed us to consider the 100 GCs in a lymph node as evolving independently. We use the following measures to quantify the GC dynamics and response.

Quality

The average instantaneous affinity of the GC B cells measures the quality of the GC response, and is defined as

$$\alpha \left(t\right)={\langle \frac{{\displaystyle \sum _{i=1}^{100}{n}^i\left(t\right)a^i\left(t\right)}}{{\displaystyle \sum _{i=1}^{100}{n}^i\left(t\right)}}\rangle }_{50}$$ (Equation 13)

where nⁱ(t) and aⁱ(t) are the population size and average affinity of the B cells in the i^th GC in an ensemble at GC cycle t, respectively. B cell affinity is defined in terms of the match length, ε. AM saturates when α(t) becomes time-invariant.

Quantity

The average instantaneous GC size is defined as

$$\mu \left(t\right)={\langle \frac{{\displaystyle \sum _{i=1}^{100}{n}^i\left(t\right)}}{x\left(t\right)}\rangle }_{50}$$ (Equation 14)

where x(t) is the number of surviving GCs in an ensemble at generation t. The quantity of the GC response is measured by the instantaneous output plasma cells per GC, ρ(t). We consider output plasma cells of ε≥2 because only affinity matured GC B cells with BCRs that bind sufficiently strongly to Ag have been shown to differentiate into plasma cells (Li et al., 2018). Therefore,

$$\rho \left(t\right)={\langle \frac{{\displaystyle \sum _{i=1}^{100}{\displaystyle \sum _{\epsilon =2}^L{p}_{\epsilon }^i\left(t\right)}}}{x\left(t\right)}\rangle }_{50}$$ (Equation 15)

where $p_{\epsilon }^i\left(t\right)$ is the number of plasma cells with BCRs of match length ε output from the i^th GC in an ensemble at GC cycle t. GC B cell apoptosis in a particular cycle (Figure 3B) is calculated as the percentage of the B cell population that failed T_fh-based selection in that cycle.

Quality and Quantity Combined

The effectiveness of the GC response is determined by a combination of serum Ab titers and their affinities for Ag. To estimate this effectiveness, we employ the following procedure. We define the instantaneous affinity-weighted plasma cell output of the GCs in a lymph node as

$$W\left(t\right)={\langle {\displaystyle \sum _{i=1}^{100}{\displaystyle \sum _{\epsilon =2}^L\frac{p_{\epsilon }^i\left(t\right)\epsilon }{L}}}\rangle }_{50}$$ (Equation 16)

The affinity-dependent weights, (ε /L), account for higher affinity plasma cells producing Abs that bind more efficiently to Ag and mount a stronger humoral response. Assuming that activated plasma cells die at the per capita rate δ_p (= 0.015 per generation (Kepler and Perelson, 1993; Tam et al., 2016)), the affinity weighted cumulative plasma cell output at the t^th generation is

$$P\left(t\right)=\sum _{\phi =1}^{t}W\left(\phi \right)e^{-{\delta }_p\left(t-\phi \right)}$$ (Equation 17)

If each plasma cell produces Abs at the rate β = 8.64 ×10⁷ Abs per generation, which corresponds to the estimated 2000 Ab molecules/plasma cell/second (Alberts et al., 2002), the instantaneous affinity weighted Ab output at the t^th generation would be

$$\psi \left(t\right)=\beta P\left(t\right)$$ (Equation 18)

Abs are cleared from circulation at the per capita rate δ_A(= 0.01165 per generation (Kepler and Perelson, 1993; Tam et al., 2016)). The cumulative size of the affinity weighted Ab pool at the t^th generation is therefore

$$\gamma \left(t\right)=\sum _{\phi =1}^t\psi \left(\phi \right)e^{-{\delta }_A\left(t-\phi \right)}$$ (Equation 19)

Thus, α(t) and ρ(t) are measures of the quality and quantity of the GC response, respectively, and γ(t) is a measure of the effectiveness of the response accounting for both quality and quantity. In the figures, ψ(t) and γ(t) are expressed in units of nmol Abs/generation/GC ensemble.

We used the MATLAB software (version 2018a) for all quantification and statistical analysis.

Supplementary Material

Supplemental Information can be found online at https://doi.org/10.1016/j.celrep.2019.11.030.

Highlights.

• An in silico model describes how passive immunization improves antibody responses

• A quality-quantity trade-off characterizes B cell selection in germinal centers

• Antigen availability and antibody affinity for antigen tune the trade-off

• The model synthesizes diverse observations and suggests optimal interventions