In situ structure determination by subtomogram averaging

Abstract

Cryo-tomography and subtomogram averaging are increasingly popular techniques for structural determination of macromolecular complexes in situ. They have the potential to achieve high-resolution views of native complexes, together with the details of their location relative to interacting molecules. The subtomogram averaging (StA) pipelines are well-established, with current developments aiming to optimise each step by reducing manual intervention and user decisions, following similar trends in single-particle approaches that have dramatically increased their popularity. Here, we review the main steps of typical StA workflows. We focus on considerations arising from the fact that the objects of study are embedded within unique crowded environments, and we emphasise those steps where careful decisions need to be made by the user.

Introduction

Cryo-electron tomography is the technique of choice for structural analysis of biological complexes in their native context. Through imaging in the electron microscope at a range of tilt angles, a 3D reconstruction is obtained of pleiomorphic and unique specimens. If many copies of a complex of interest are present within the tomographic reconstruction, subtomogram averaging (StA) can significantly increase its resolution, without detracting from the advantage that the reconstructed objects are embedded within their native biological context. StA is increasingly used for structural analysis of protein complexes in situ, whether it be in eukaryotic cells (e.g. Nuclear pore complexes [1•,2], ribosomes [3], proteasomes [4,5], coat protein complexes [6•,7] bacterial cells (e.g. secretion systems [8,9•,10], flagellar motors [11,12], S-layer [13], in purified organelles or viruses (e.g. viral glycoproteins [14,15], viral capsids [16••,17], mitochondrial complexes [18–20], translating ribosomes [21], or on reconstituted systems (e.g. membrane remodelling coat complexes [22••,23,24], cyto-skeletal motors [25].

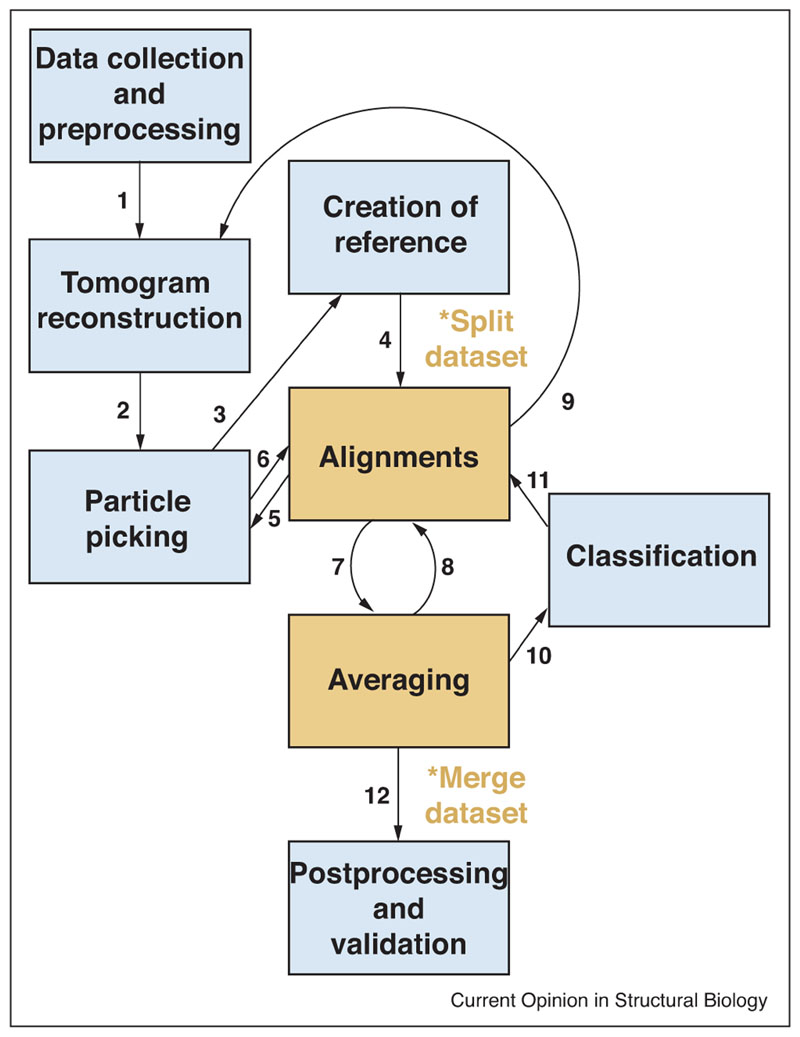
The typical workflow of StA is represented in Figure 1. It starts with collection of a tilt series, and tomogram reconstruction, and then it involves particle picking, subvolume extraction and generation of a starting reference, upon which iterations of alignment and averaging, and eventually classification are performed. The structures that are obtained are subjected to postprocessing and validation before being interpreted. At many stages through the process, the results can inform the previous steps, which can be repeated with refined parameters.

Figure 1.

Overview of the typical subtomogram averaging workflow. 1. Upon data collection, images are subjected to frame alignment, dose compensation, and - in some protocols - CTF correction, then back-projected to reconstruct the tomogram. 2. Coordinates for particle picking are defined and subvolumes extracted. 3. These can be averaged to obtain a starting reference. 4. The reference is then used to align subvolumes. At this stage the data set should be split in halves to follow gold-standard procedures. 5, 6. The first alignments can provide refined coordinates for subvolume extraction. 7, 8.Alignments and averaging cycles are iterated until convergence.9 In some protocols, subtomogram alignments can be used to refine the tilt geometry and obtain a more accurate tomogram reconstruction, from which higher resolution subtomograms can be extracted. 10, 11. During or after alignment, classification can be used to separate heterogeneous groups of particles. 12. The final averages are subjected to postprocessing (amplitude weighting and sharpening), and validation.

Processing cryo-tomographic data has necessitated development of ad hoc protocols to deal with tilted images and with anisotropic 3D volumes [26,27]. For instance, defocus-dependent modulation of image frequencies (as defined by the Contrast Transfer Function, CTF) varies across tilted images and within the height of the reconstructed volume, requiring dedicated CTF correction software. The limited angular range to which samples can be tilted (typically ±60°) leads to anisotropy in the reconstructed volumes (described as a missing-wedge in Fourier space), which must be compensated during subvolume alignments [26,27]. Moreover, while the complexity and diversity of the samples analysed are usually the reasons why StA is chosen over single particle analysis or other structural techniques, it also implies that data analysis protocols must be adapted to the object of interest. This is especially true during particle picking, initial orientation assessment, and in the validation and interpretation stages, as outlined below.

Here, we review the typical steps of the StA workflow (Figure 1), with an emphasis on those aspects that must be optimised depending on the particular context of the object analysed.

Preprocessing and tomogram reconstruction

When reconstructing cryo-tomograms for subtomogram averaging it is desirable to preserve high resolution information as much as possible. To this aim, pre-processing of tilt images includes steps that have been optimised for high-resolution single particle cryo-EM. Motion correction of frames within each tilt image improves on the degrading effects of beam induced sample motion and of drift. Drift tends to be worse at high tilts, making motion correction especially important in cryo-tomography. Exposure filtering to remove cumulative electron damage-derived noise [28] can be implemented on a tilt-by-tilt basis or within subframes of every tilt. Exposure filters work optimally when paired with dose-symmetric data collection schemes, where the high tilt images, in which high resolution information is corrupted by increased thickness and lower precision of CTF estimation, are effectively filtered in the dose-compensation procedure [29•].

To maximise high-resolutions in the averaged subtomograms, it is important that tilt images are aligned with the highest possible accuracy before back-projection. Tilt geometry must be optimised by iteratively minimising the residual differences between the actual positions of sample features and those predicted by the best geometrical tilt model [30,31]. When possible, this should be done using gold beads as fiducials. In certain samples (e.g. cell sections or lamellae), it is not possible to add gold beads and alignments must rely on image ‘patches’ to serve as fiducials [32,33]. Success in this case depends on the amount of signal available.

Currently, obtaining high-quality tilt series alignments suitable for high-resolution structure determination requires a manual procedure of fiducial optimisation, which significantly decreases the throughput. Recent developments use alignments of subtomograms to further refine the local geometry of the tilt series, improving high-resolution signal ([34], further discussed in the ‘Alignment and averaging’ section).

Accurate CTF estimation and correction are important aspects to consider when aiming to preserve high-resolution features. As discussed above, dose-symmetric tilt schemes ensure that the high resolution information is preserved in the lower tilts, where CTF estimation is more accurate due to higher SNR [29•]. Compared with single-particle reconstruction, cryo-tomography has the advantage that the relative defocus is known for each voxel in the reconstruction. This allows to calculate a 3D-CTF-corrected tomogram by back-projecting image pixels where signal has been restored using the appropriate z-height-adjusted defocus values [35,36•].

Tomogram content analysis

Current Single Particles Analysis studies handle the localisation of individual particles on micrographs as a straightforward task. In contrast, embarking on an StA project requires a decision on the specific strategy to determine the approximate locations of copies of the protein of interest inside each tomogram.

In the simplest scenario, particles can be selected as individual entities, both through manual inspection and interaction with the tomograms [37] or through some automated approach for pattern recognition. Such approaches range from exhaustive testing of the tomogram searching local maxima of similarity to a given template measured by cross-correlation [38], to more sophisticated applications of deep learning [39,40], a technique of artificial intelligence where the software is trained to mimic the performance of an expert human operator.

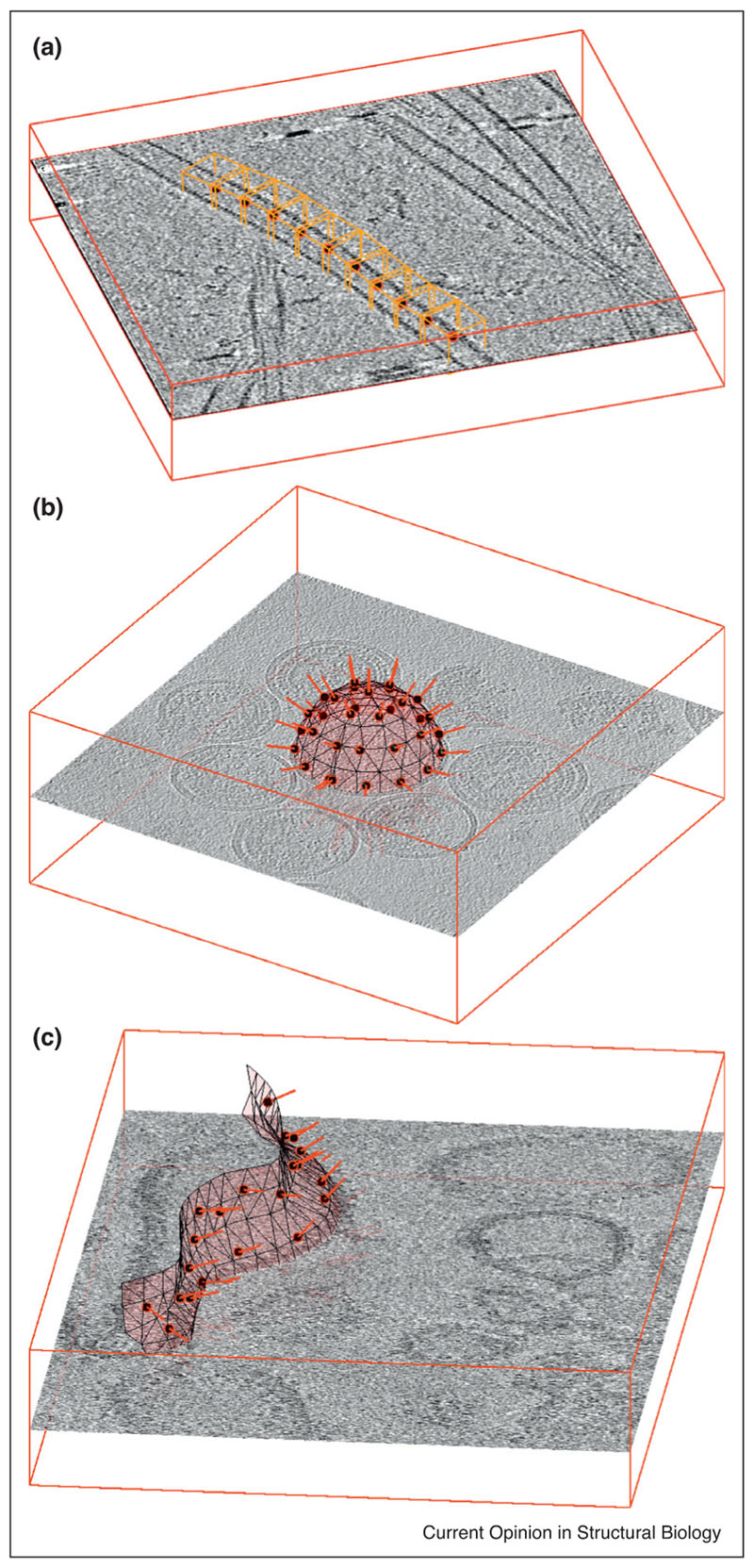
However, the signature ability of tomography is the exposition of the molecular context. Frequently the spatial location of the particles of interest in a tomogram is related to an approximately identifiable geometric distribution, induced by an organised structure in the cellular milieu. Particles maybe arranged as decorations, embedded insets, or building blocks of filamentous or membranous structures, with different levels of regularity. Particle identification in these cases can be articulated along the characterisation and modelling of the underlying shape (Figure 2). Parametrisation of - for example - a microtubule as a bent cylinder (Figure 2a), of a vesicle as an ellipsoid (Figure 2b) or of a mitochondrial membrane as a triangulated manifold (Figure 2c) allows to exploit the predicted spatial correlation of the particles in relation to such objects and extract them collectively. Hereby, the model is used to create a set of spatial locations, generated under the double constraint of being consistent with the support geometry and also within a physically meaningful distance among each other. For a sufficiently dense distribution of positions and a sufficiently large cropping side length, boxes extracted around these locations will probably contain actual parti-cles, although the position of the particle inside the subtomogram box will be random. The positions of particles inside the boxes can then be estimated through alignment of subtomograms, a procedure that can be aided by the approximate orientation that can be inferred for each particle from its relation to the model (typical examples are the normal to a membrane, or the direction of the axis of a filament) (Figure 3a,b [22••,23]).

Figure 2.

Examples of particle extraction for (a) filaments, (b) vesicles and (c) generically shaped membranes. In all three cases, the position of a subtomogram (red circle filled in black) is accompanied by an initial estimation of the orientation of the particle (red bar) given by the respective support geometry. In (a), orange boxes representing subtomograms are placed along the axis of a microtubule (data of microtubule-bound dynein-dynactin complexes from Grotjahn et al. [25]. The initial orientation of each subtomogram is given by the local orientation of the microtubule. In (b) the particles of interest are GAG proteins forming the capsid of HIV virus-like particles (VLPs) in solution (data from EMPIAR-10164). Their extraction is facilitated by using estimations of radius and centres to model the surface of the VLP as a sphere: locations of subtomograms are regularly distributed on it, while the local normals provide initial orientations. The tomogram in (c) shows membrane-assembled, in vitro reconstituted murine 5HT3 serotonins. The membrane of a non-spherical liposome is modelled as a triangulated surface, allowing the placement of a regular distribution of subtomogram centres and initial orientation assignations.

Figure 3.

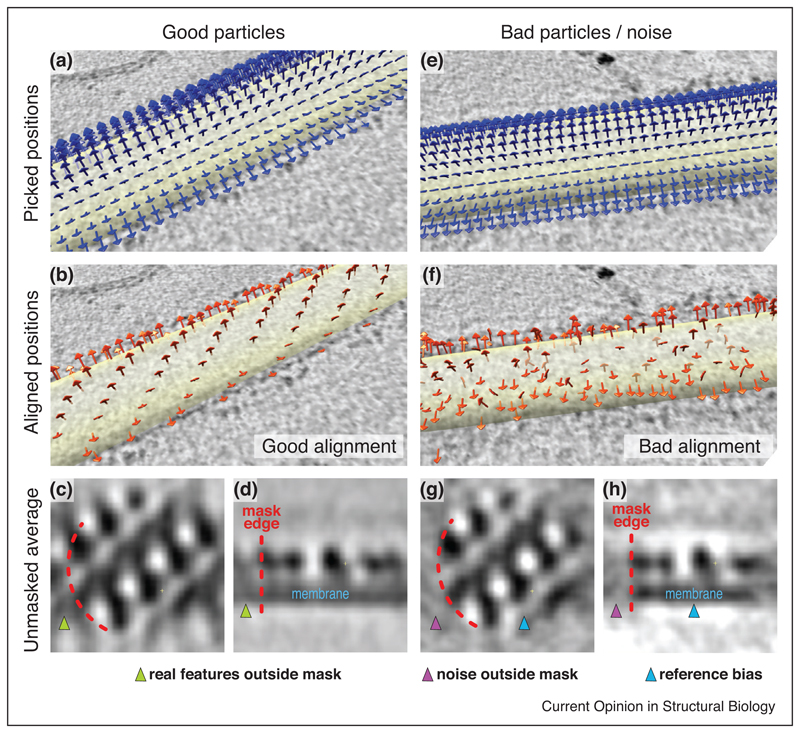
Example of validation in StA from COPII-coated tubules data [22••]. COPII forms a pseudo-helical lattice. (a) Arrows indicate the initial coordinates and orientations for particle picking on a coated tubule, where subvolume centres and sizes are chosen to oversample the tube surface, and rough orientations are assigned based on the underlying tubular geometry. (b) Coordinates after subtomogram alignment. The centres have shifted and form a clearly recognisable pseudo-helical pattern, validating the alignment. (c,d) Top and side cross-section of the average, respectively, obtained after alignments of subtomograms using a lattice-shaped starting reference and a mask (partially outlined in orange). The protein and membrane densities clearly continue outside the mask, validating the alignment. (e-h) As in (a-d), but on a tube where no ordered lattice was present. The pseudo-helical lattice is not apparent in (f), and in (g) and (h) the mask edge defines a sharp drop of the electron density, indicating that the average obtained mostly reflects reference bias.

As an organised structure might contain a large number of particles (ranging between tens and hundreds depending on the particular case), computer tools for efficient onscreen annotation of support geometries are a powerful resource [37]. Complementarily, the identification of support geometries can be facilitated through volumetric segmentation methods [41], ideally tailored to the characteristic of cryoET data — mainly low SNR and the presence of missing wedge [42,43]. In this insight, recent studies have explored the suitability of deep learning approaches for semiautomated identification of some of the structures in the cellular environment that are typically used as supporting geometries for subtomogram extraction [39].

Alignment and averaging

StA seeks to reconstitute the 3D shape of a macromolecular compound by integrating the signal of multiple noisy copies contained in the extracted set of subtomograms. Knowledge of the exact orientation and location of each particle inside its subtomogram box allows to align all the particles to a common reference, then to average them coherently. StA finds these parameters in an iterative fashion. A density map used as initial reference is compared to each particle in the data set, locating the combination of translation and rotation that maximises the similarity of that particle to the reference. The alignment parameters of the entire data set are then used to create an average that will be used as reference for a new iteration until convergence is attained. This generic procedure is known as refinement and its implementation entails several practical considerations:

• -The initial reference can be constructed by averaging a subset of the particles. In cases where the sample geometry allows to assign a rough initial orientation to particles (e.g. objects on a membrane or along filaments), the low-pass filtered reference created by averaging subtomograms will contain low-resolution features that correlate with those of each particle, greatly facilitating alignments. For example, the initial reference for particles extracted from the surface of a membrane might look like a smooth piece of membrane with relevant curvature.
• -Frequently, the particle of interest does not appear as an isolated entity inside the subtomogram, but embedded into a high intensity structure (as a membrane or filament), or closely surrounded by other inhabitants of the cytosol. This calls for a careful masking of the initial reference, that is, providing the algorithm with a mask file that expresses which pixels in the reference should contain the particle - and thus common signal in all subtomograms - and which ones can vary its content among the data set.
• -Similarity between reference and particle is measured through cross-correlation (refs), with appropriate adaption to account for the missing wedge of the tomogram and the mask imposed on the reference. Alternative approaches based on maximum likelihood use the similarity measured for each combination of translation of rotation to assign to it a probabilistic weight [44,45]. Either way, the best combination of translation and rotation parameters for a particle are determined by exhaustively testing on a set of shifts and Euler angles. Computationally, this calculation constitutes the most demanding task, and different approaches are available to reduce computing time: the set of scanned angles can be constrained to a neighbourhood of previously found alignment parameters; Fourier convolution allows to compute all translations simultaneously for a given orientation; similarly spherical harmonic transforms allow the simultaneous computation of all rotations for a given translation [46]; finally, the structure of the operation (which reuses the same data in a large number of computations) enables GPU implementations to yield impressive speedup factors [47].

Recent efforts explore the use of the alignment parameters computed on a set of subtomograms to realign the tilt series using the particles themselves as fiducials, refining the alignment generated by gold beads [34]. This potentially leads to more accurately aligned tilt series and correspondingly better tomograms and subtomograms, which, in turn, can be refined to produce a better alignment. This procedure can be iterated till convergence, and has been shown to produce considerable improvements for samples with large numbers of copies per tomogram.

Classification

Classification methods that have been reported to deal with heterogeneity can be separated into i) approaches aimed at characterising the heterogeneity of an aligned data set, and ii) algorithms performing classification and alignment simultaneously. In the former group, a frequent starting point is the exhaustive computation of the similarity of each pair of aligned subtomograms, giving rise to a covariance matrix. This matrix can be used to feed a Hierarchical Clustering method that locates groups of mutually similar particles [48], or as basis for a Principal Component Analysis [49], a widely used method for complexity reduction that captures the spatial features describing the largest sources of structural variance in the data set. Such features (eigen volumes) appear in order of relevance and can be used to express each particle as a reduced number of coefficients, which can then be clustered through k-means. Performance of these methods has been shown to improve significantly by a data-driven tuning of frequency band used to measure particle similarity [34].

The second family of methods is based on competitive alignment. The algorithm compares each particle with a set of different references, and assigns it to the reference that yields the highest score. As subsequent refinement iterations generate gradually better references, particle assignments can swap from one reference to other as the iterations progress. This procedure is similar to maximum-likelihood-based approaches which replace unique class assignments with probability weights [50].

In both families, masking constitutes a crucial decision, as it allows one to focus the analysis on the parts of the compound deemed to be flexible or conformationally different. While most methods allow to integrate this information as a prior if available, others are specifically designed to automatically analyse the regions of maximal variance to generate data-driven masks that update as the classification advances [51].

Validation

Once the classification and alignment procedures have reached convergence the final average is ready to be interpreted: subunits and domains are assigned and, where available, atomic models are fitted or built. Validation of the structure is crucial before any interpretation can be attempted. Many of the validation strategies in subtomogram averaging are shared with single particle reconstruction methods: for instance, the risk of creating an artefactual average through overfitting can be mitigated by the gold standard procedure [52]. This implies comparison between half datasets which were independently aligned against a band-pass filtered reference. Only information which is recovered beyond the high frequency limit of the reference filter can be considered for the next alignment iteration, and eventually defines the resolution to which the average can be interpreted.

Resolution is commonly assessed by Fourier Shell Correlation (FSC) [53]. The effects of using masks on the FSC have been described, and can be mitigated by phase randomisation methods [54]. Often, protein and lipid density within subtomograms continues beyond the actual particles to encompass associated macromolecules until the periphery of the box. The choice of mask will therefore significantly affect the average resolution, as non-correlating features are included in the FSC calculation. For this reason, and because of the inherent flexibility of all biological complexes, especially when resolved in situ, it is often desirable to measure the local resolution [55,56]. This might be combined with local filters to obtain a map where it is possible to interpret each feature at the appropriate level of detail. It remains important to calculate the gold-standard FSC as a diagnostic tool for overfitting or other typical artefacts [57••].

In cryo-tomography, the contextual information can be often used for validation of the alignments (as exemplified in Figure 3). For example, when subunits are arranged in a pattern with respect to each other, and particle picking was performed by oversampling the underlying geometrical model (Figures 2 and 3a,e) then the convergence of neighbouring subtomograms to form a recognisable pattern is a very good validation of the correctness of the alignments (compare Figure 3b and f). Moreover, for embedded objects typical of StA, a mask applied during alignments may cut across continuous density, such as that of a membrane. In this case, correct alignment of ‘real’ particles will produce an average where the membrane is visible beyond the mask (Figure 3c,d), while incorrect alignments, or alignments of noise will produce an average where the density drops off suddenly outside the mask (Figure 3g,h).

Summary

The complexity of the biological samples typically analysed in cryo-tomography defines this technique and constitutes its biggest potential. At the same time, the reasons that make StA an attractive approach for structural determination also define its current limitations, for example, in relation to the inefficiency in attaining high numbers of particles, or to the bias in the alignments imposed by contextual information outside the ‘particle’ and the difficulty in defining optimal masks.

StA is currently relatively low-throughput with respect to cryo-EM single particle approaches. Nevertheless, there is scope for improvements in automation of StA pipelines, especially in data collection, pre-processing and tomographic reconstruction. StA will greatly benefit from comprehensive software packages to optimise each processing step without the need for continuous conversion between formats and conventions [34,58,59]. Software which will facilitate the flexible combination of different approaches will also significantly improve usability and help expand the user community—simi-larly to what has been implemented in single particle analysis [52,60].

So far, only a few StA projects have achieved near-atomic resolutions [16••,22••,34], but it is important to note that novel and insightful biological information can be retrieved from lower resolution studies, as long as appropriate validation procedures are implemented. This is especially true for cryo-tomography and StA, since the macromolecular structure itself only constitutes one aspect of the result: the information about the spatial relationship of the complexes of interest between each other, and with other neighbouring cellular features can often provide much precious insight into their function.