Investigating the effect of changing parameters when building prediction models in post-stroke aphasia

Abstract

Neuroimaging has radically improved our understanding of how speech and language abilities map to the brain in normal and impaired participants, including the diverse, graded variations observed in post-stroke aphasia. A handful of studies have begun to explore the reverse inference: creating brain-to-behaviour prediction models. In this study, we explored the effect of three critical parameters on model performance: (1) brain partitions as predictive features; (2) combination of multimodal neuroimaging; and (3) type of machine learning algorithms. We explored the influence of these factors while predicting four principal dimensions of language and cognition variation in post-stroke aphasia. Across all four behavioural dimensions, we consistently found that prediction models derived from diffusion weighted data did not improve performance over and above models using structural measures extracted from T1 scans. Our results provide a set of principles to guide future work aiming to predict outcomes in neurological patients from brain imaging data.

Introduction

Stroke is a leading cause of severe disability¹ and approximately one third of chronic cases are left with speech and language impairments^2,3. Aphasia is not a singular, homogeneous symptom but rather refers to a broad range of diverse, contrastive language impairments. Both for advancing our theoretical understanding of the neurobiology of language and for a potential paradigm-shift in clinical prognosis, management and therapy pathways, it is critically important to predict these language and cognitive variations from brain imaging data. Recently, a handful of studies have embarked on using brain lesion information to predict performance on specific neuropsychological tests or aphasia types^4–10. The key aim of the current investigation was to take the next major step from these proof-of-principle studies towards understanding what effect three foundational parameters have on brain-to-behaviour prediction models: (1) how the brain is partitioned as features in the prediction models; (2) are there differences between different combinations of information derived from multimodal neuroimaging (e.g., does diffusion weighted imaging (DWI) improve prediction models over and above using typical clinical T1/T2 weighted images), and (3) are there differences between machine learning algorithms? Each of these foundational issues is discussed briefly below.

Before we discuss the three factors raised above, we note that there is a non-trivial issue regarding what measures or classifications should be predicted and how the predications should be evaluated. In the current study, we focussed on predicting cross-sectional aphasia symptomology. This can provide insights about the neurobiology of language and also be clinically useful in terms of diagnosing and potentially predicting deficits, and in turn, assist with selection of appropriate specialist treatment/rehabilitation pathways. In terms of aphasia symptomology, there is increasing agreement that binary aphasia classifications are limited. Instead of homogeneous, mutually-exclusive categories of aphasia type, there is considerable variability within and between groups, often leading to misdiagnosis or patients being classified as ‘mixed’^11–14. While it is possible to predict performance on individual neuropsychological tests, any assessment taps multiple underlying component abilities and hence performance across tests is often intercorrelated over patients. An alternative approach places patients as points in a continuous multidimensional space, where the axes represent primary neuro-computational processes^15–19. This approach also aligns with the fact that language activities (e.g., naming, comprehension, repeating, etc.) are not localised to different, single brain regions but instead reflect the interplay between primary systems^20–23. Rather than predicting inhomogeneous aphasia classifications or whole swathes of individual test results, targeting each patient’s position within the continuous multidimensional space offers a complete yet parsimonious behavioural description, summarised by the essential components. Regardless of the specific targets one would like to predict, there is an issue of how we validate prediction models generated within a research/clinical centre. The simplest approach is to use leave-one-out cross validation (LOOCV), where N-1 cases are used to fit a model and the single left out case is estimated (iterated so each case has been left out). This method does not guard against overfitting and k-fold (k=4-10) alternatives are preferred as the training sets have less overlap (resulting in less variance in the test error). These k-fold procedures require relatively larger samples than LOOCV as a larger proportion of the data is left out for testing.

Modern neuroimaging provides high dimensionality data (~10⁶ voxels) compared to the number of samples (~10²), which can lead to over-fitting problems when building prediction models. This large number of brain prediction features can be down-sampled in different ways: through the use of anatomical/functional atlases, methods to select a subset of features (i.e., recursive feature selection) or kernel methods to create similarity matrices. The most common procedure is to down-sample using anatomical atlases (e.g., the automated anatomical labelling [AAL] atlas) or functional atlases that have been derived by grouping voxels together based on their resting-state functional connectivity^24,25. One key alternative approach involves using areas identified as functionally relevant through activation or lesion mapping studies^4,26. For example, Halai et al.,⁴ used a functional model of language which contained three distinct neural clusters related to phonology (peri-Sylvian region), semantics (ventral temporal lobe) and speech output (precentral gyrus). The resultant functionally-partitioned lesions were able to predict the patients’ neuropsychological test scores as well as aphasia subtypes. Another option is to utilise knowledge about neurovascular anatomy, which heavily constrains the inherent ‘resolution’ of the brain sampling in a post-stroke population as well as the co-occurrence of voxel damage. Previous angiography studies demonstrated that the middle cerebral artery (MCA) branches typically supply a dozen cortical areas (orbitofrontal, prefrontal, precentral, central, anterior parietal, posterior parietal, angular, temporo-occipital, posterior temporal, middle, temporal, anterior and polar temporal area²⁷). Given that these seminal anatomical studies only provided hand-drawn renderings of the vascular regions, in a recent study we applied principal component analysis to extract the underlying, co-linear factors from the non-random lesioned tissue in post-stroke aphasia. This method resulted in 17 coherent clusters that closely reflected the pattern of cortical vascular supplies noted above²⁸.

The most common neuroimaging measure used in building prediction models is the amount of damage based on a T1 or T2 weighted image, either across the whole brain or for targeted structural/functional areas^4–10,29. Classical neurological studies proposed that certain features of aphasia might reflect white-matter disconnections as well as local grey matter damage³⁰. More recently, studies utilising direct electrical stimulation in neurosurgical patients have shown that different aspects of aphasia can be generated transiently through fascicular stimulation^31,32. This suggests that prediction models might be substantially improved by adding information about white-matter connectivity derived either from in vivo patient-specific diffusion-weighted imaging or with reference to population-level white-matter connectivity maps (though it is worth noting that the processing of DWI data is technically non-trivial and thus could be a financial and practical barrier for clinical adoption). The small handful of studies that have explored the addition of white matter information, have generated inconsistent findings. Studies that have incorporated patient specific structural connectivity data^9,33 have shown that lesion or connectome data can differentiate between pairs of aphasia type better than chance, yet the combination of information did not substantially or significantly improve the prediction accuracy and in some cases was actually lower than a model based simply on lesion size. Similarly, studies that have used some variant of the population level approach have also found inconsistences with respect to white matter connectivity data. Hope et al.,⁵ used white matter disconnections inferred by projection of the patients’ lesions to a white-matter population level atlas and found that information about white-matter disconnection did not improve aphasia prediction models over lesion features alone. Another recent sophisticated study used a multivariate learning approach (random forests) with a prediction stacking method to combine lesion, virtual tractography disconnections and resting-state fMRI to predict aphasia severity and WAB subscores⁸. Although the initially-reported correlations between predicted and observed WAB sub scores were encouragingly high (~0.8), when there was full separation between training and test data the prediction accuracy was reduced (0.66) and was little better than when using the best single predictor (r = 0.63 using a structural connectivity matrix). A recent study investigating disconnections and lesion load of white matter tracts³⁴ suggested that individual measures are to be preferred after reporting partially consistent results with previous studies using population level disconnection^35,36.

There are now a large number of learning algorithms for multivariate analyses, each associated with their own biases and assumptions^37–46. Yet it is not clear which algorithms should be used for any given problem, and to achieve the goals of this study, there is a need to handle multiple neuroimaging inputs as well as multiple partitions of the brain space. One approach that is designed to handle multiple data is multi kernel learning (MKL), which searches for meaningful groupings and combines their contribution⁴⁷. This methods creates a separate kernel for each modality/region and each are assigned weights⁴⁸. We note, however, that it is very difficult to determine why features have high weights and therefore interpretation of specific weights should be approached with caution^49,50. A modification of the MKL to allow for sparsity has been recently implemented in Pattern Recognition for Neuroimaging Toolbox (PRoNTo V2.1; http://www.mlnl.cs.ucl.ac.uk/pronto/)⁴⁶. This has additional benefits such as improved generalisability and the identification a smaller subset of features helps interpretability^51,52. In addition to the MKL method, the toolbox also implements three additional machines for regression: (a) kernel ridge regression (KRR), (b) gaussian process regression (GPR) and (c) relevance vector regression (RVR). Therefore, we opted to use this toolbox for its ease of use and integration with the Statistical Parametric Mapping software (Wellcome Trust Centre for Neuroimaging, http://www.fil.ion.ucl.ac.uk/spm/).

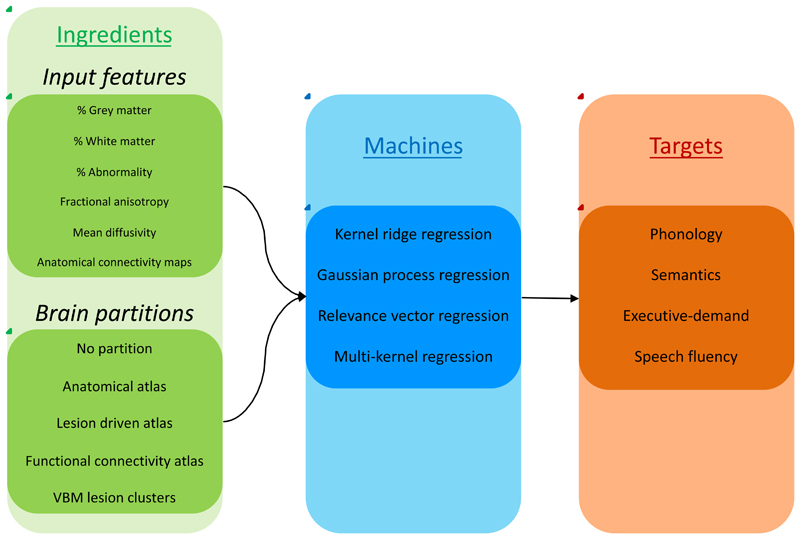
The current study was designed to undertake a systematic investigation of these foundational issues when building prediction models of the variation of aphasia presentation post stroke. Based on our previous research¹⁶, we focused on four orthogonal language and cognitive continuous dimensions as prediction targets (phonology, semantics, speech fluency and executive skill), and parametrically established the validity and reliability of this solution. For each prediction target we compared the accuracy of various model ‘recipes’ reflecting the different choices over brain parcellation (five methods), different measures of brain tissue and white matter integrity derived from multimodal imaging (six inputs), and different machine learning algorithms (four types). An overview of the model ‘recipe’ is shown in Figure 1 where all possible combinations of these varying ‘ingredients’ were tested. This allowed us to establish where there are differences in prediction model performance depending on the ‘recipe’ and whether this changed substantially depending on the prediction target.

Figure 1.

A schematic representation of the prediction model creations. For each model we used one or more inputs features and selected one brain partition (green box), which were entered into one of the machines (blue box) for training in order to predict a behavioural component (red box). We iterated the inputs using: a) each single input, b) all pair-wise combinations, c) T1 or diffusion related inputs, separately and d) all inputs together.

Results

Neuropsychological profile and lesion overlap

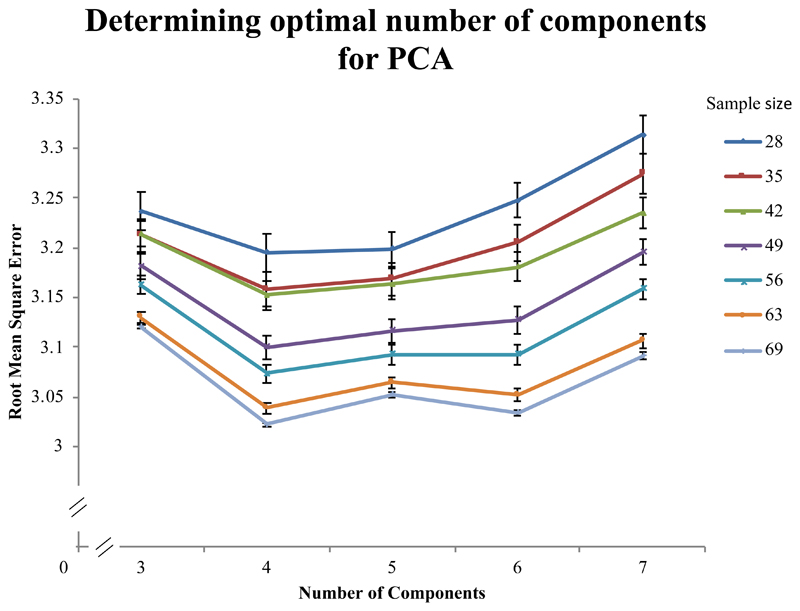
One subject was removed due to incomplete diffusion data during MRI acquisition. For the PCA of the extensive behavioural data, the Kaiser-Meyer-Olkin measure of sampling adequacy was 0.834 and Bartlett’s test of sphericity was significant (approx. Chi square = 1535.486, df = 210, p < 0.001). We implemented a 5-fold cross-validation approach to determine the optimal number of components within our data and found that a four factor solution was significantly better in all sample sizes except the lowest (N = 28), where it was numerically superior but not significantly different to a five factor solution (Figure 2). Therefore, data from 69 subjects were used in a PCA with varimax rotation to extract four factors (which were also the only factors with eigenvalue above one, accounting for 77.0% of the variance (F1 = 31.05%, F2 = 16.72%, F3 = 16.16% and F4 = 13.07%). The factor loading for each test variable is given in Supplementary Materials 1. The PCA model showed a high correlation between the predicted left out folds and observed data (r = 0.8128). The factors replicated findings from Halai et al.,¹⁶ which was based on a smaller subset (N=31) of this group. In brief, the first factor was termed phonology as repetition, naming and digit span loaded strongly; the second factor was termed semantics as picture matching and other comprehension tests were strongly related to this factor; the third factor was termed executive-demand as cognitively demanding tests that required problem solving loaded strongly; the fourth factor was termed speech quanta as it loaded with the amount of speech produced. Supplementary Material 2 displays demographic information for each participant.

Figure 2.

Cross validation approach to determine optimal number of components for principal components analysis (PCA). The graph shows the results for 3-7 factors in the PCA model, which were used to predict left out data (using 5-fold cross validation). The y-axis represents the root mean square error (RMSE), where lower values indicate better performance. The lines represent different sample sizes, where the total dataset contained data from 70 chronic stroke patients. In order to make sure the sub samples were not biased we randomly selected N cases 100 times and for each iteration we randomly shuffled the order of the cases 100 times (to avoid ordering bias for venetian blinds sampling). The RMSE was calculated on each shuffle using a PCA model based on 1: test variables-1 factors and averaged across the 100 shuffles. Standard error bars are displayed for each point.

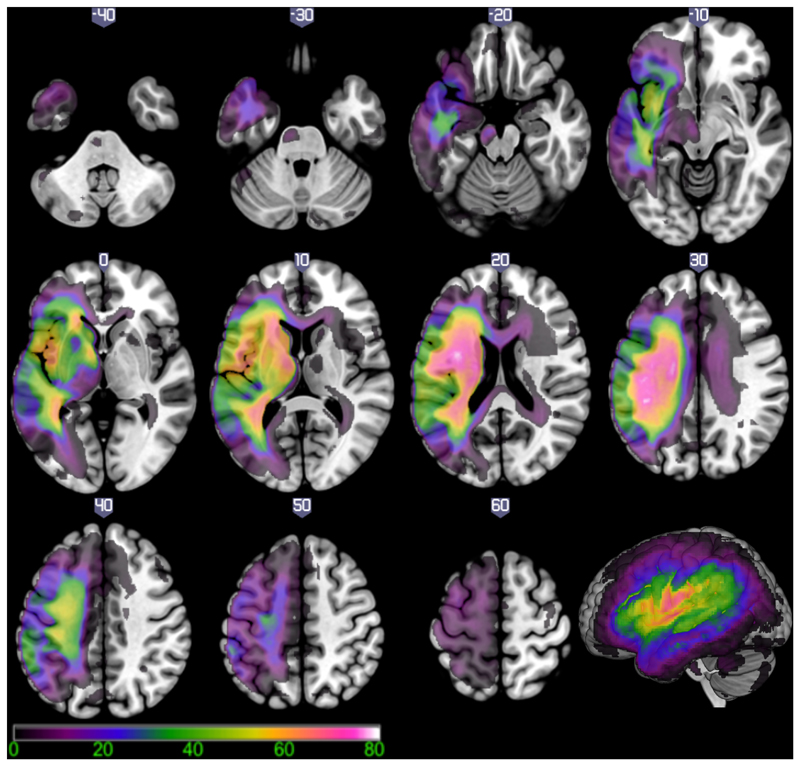
Figure 3 shows the lesion overlap map in the left hemisphere for the 69 subjects in this study converted into a percentage map. The voxel that was most frequently damaged (N=56 or 81.16%) was situated within the left superior longitudinal fasciculus/central operculum (MNI coordinate –38, -10, 24).

Figure 3.

Lesion overlap map for 69 patients with left hemisphere post stroke aphasia. Colour scale indicates the percentage of patients with damage to each brain region (scale 1-80%). The voxel that was most frequently damaged (81.16% of cases) was located in the superior longitudinal fasciculus/central operculum cortex (MNI coordinate -38, -10, 24).

Multivariate pattern recognition analyses

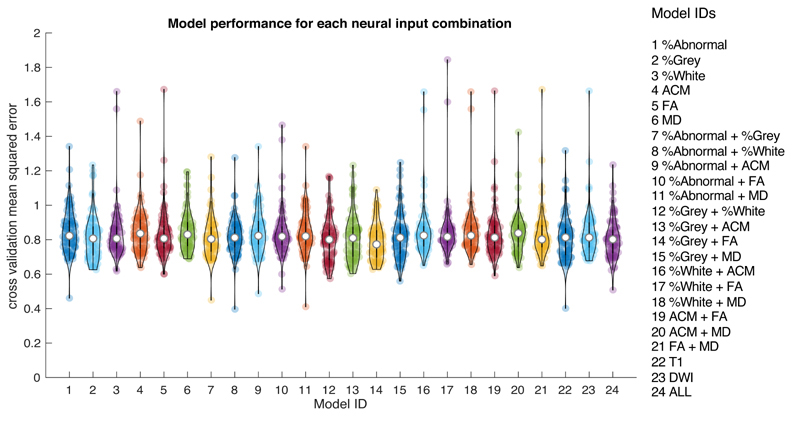
Due to the vast number of models, in the main body of the paper we present summaries of the results and specific details of the ‘winning’ models. Full details for all models are in Supplementary Materials 4. Each of the six imaging measures (% abnormality, % grey, % white, MD, FA and ACM) were tested as inputs (either alone or in combination) in separate models used to predict each behavioural factor (phonology, semantics, executive-demand and speech quanta). For each model, we determined the performance across four machines (KRR, GPR, RVR and MKR) and five brain partitions (no partition, anatomical atlas, function connectivity-based atlas, PCA derived functional clusters and PCA derived lesion clusters). First, we present summary violin plots showing the cross-validated mean squared error between predicted and observed scores for different model configurations. All reported mean squared error values indicate the median value of the overall set of models in a particular configuration. Model performance across different configurations were not normally distributed and therefore we used non-parametric tests with two tails. For all statistical comparisons, we provide an effect size (Cohen’s D) and Bayes factor (bf10 > 3 suggests evidence for difference between the pairs and bf10 < 0.3 suggests evidence for a null effect)⁵³. Figure 4, shows the results for all models based on the neural inputs, either as a single feature, pair-wise features, three features from T1 or diffusion and all inputs together – regardless of brain partition or machine. The results show relatively high consistency between different inputs, specifically the models with % Grey matter combined with FA produced the lowest error (MSE = 0.7729). The configuration with the next lowest error was % Grey matter combined with % White matter (MSE = 0.8005), which utilised two measures from the T1 image. A comparison between the two models showed no statistical difference (Wilcoxon test: Z = 1.765, p = 0.07756, effect size = 0.403, difference = 0.008 with 95% CI = 0.001 – 0.018) but the Bayes factor did not provide sufficient evidence of a null effect (bf10 = 0.541). Importantly, there were no further gains when adding extra neural inputs from either imaging modality (see Supplementary Materials 4 for details on all comparisons).

Figure 4.

Violin plots showing model performance (mean squared error between observed and predicted) for each neural input feature set used in this study (see Model IDs on the right for information) Each coloured dot represents the result of one model configuration and the white central dot represents the median.

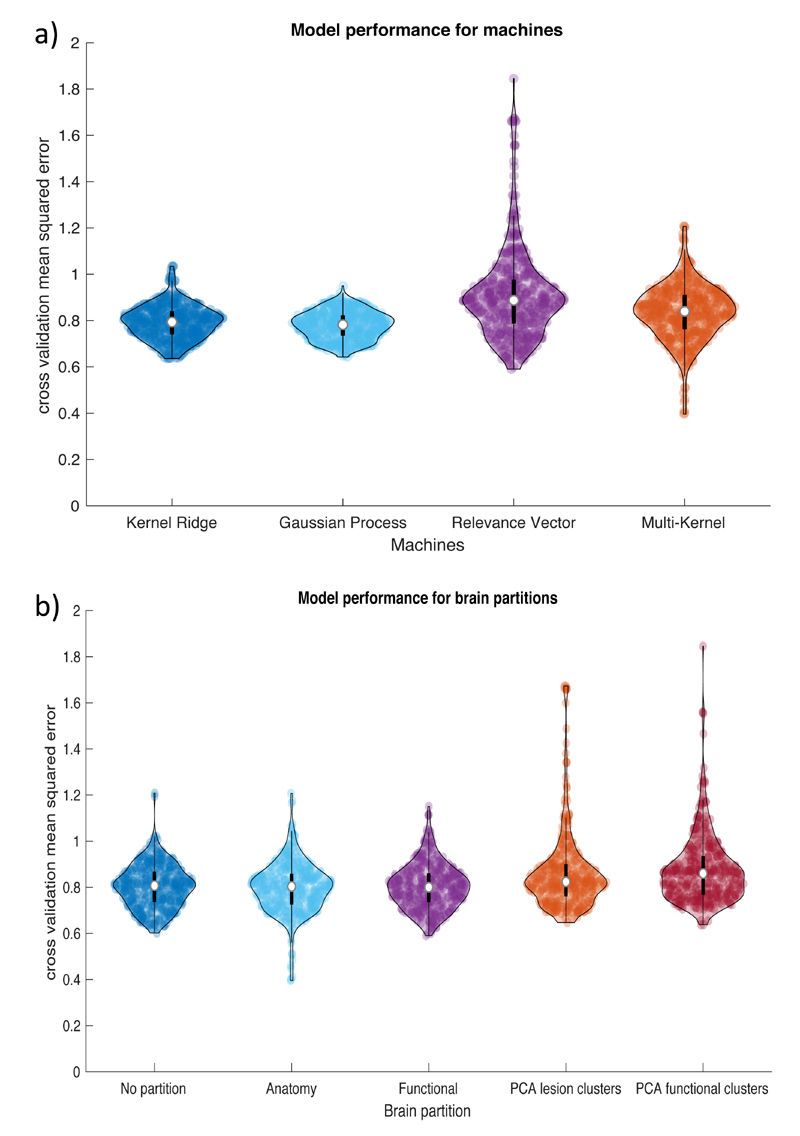
Figure 5, shows summary violin plots for the same data but now grouped by machines or brain partitions (Figure 5A and 5B, respectively). The statistical comparisons between the machines show that the error value for each machine was significantly different to each other. The Gaussian process models produced lower errors (MSE = 0.782) than the kernel ridge (MSE = 0.794, effect size = 0.715, difference = 0.012 with 95% CI = 0.009 – 0.016; bf10 = 6.90e⁹), multi-kernel (MSE = 0.840, effect size = 1.171, difference = 0.057 with 95% CI = 0.048 – 0.066, bf10 = 1.92e²²) and relevance vector models (MSE = 0.887, effect size = 1.948, difference = 0.104 with 95% CI = 0.092 – 0.117, bf10 = 6.80e³⁹). The results for the brain partition revealed that the functional atlas produced the lowest error (MSE = 0.800), but those models were not significantly lower than the anatomical atlas partition (MSE = 0.803, p = 0.066, effect size = 0.189, difference = 0.006 with 95% CI = 0 – 0.012, bf10 = 0.306) or using no partition (MSE = 0.807, p = 0.500, effect size = 0.069, difference = 0.002 with 95% CI = -0.004 – 0.008, bf10 = 0.072). These three were significantly lower than the PCA derived lesion clusters (MSE = 0.824 with p’s < 0.001, mean effect size = 0.282, mean difference = 0.03 with 95% CI = 0.019 - 0.043, bf10 > 2498) and VBCM derived functional clusters (MSE = 0.860 with p’s < 0.001, mean effect size = 0.391, mean difference = 0.057 with 95% CI = 0.042 – 0.072, bf10 > 1.13e⁹). There was no statistical difference between the latter two atlases but the Bayes factor proved insufficient (Wilcoxon test: Z = 2.332, p = 0.02, effect size = 0.119, difference = 0.013 with 95% CI = 0.002 – 0.024, bf10 = 0.835).

Figure 5.

Violin plots showing model performance (mean squared error between observed and predicted) for: A) four machine learning regression algorithms and B) five brain partitions. Each dot represents the result for one model configuration and the white circle represents the median. Abbreviations: principal component analysis (PCA).

Table 1 lists the best model configuration for each PCA factor score, when varying the input features, machines and brain partition. For Factor 1 (phonology), the model configuration with the lowest error consisted of using two neural inputs (ACM and MD) with the PCA derived lesion clusters and the KRR machine (r = 0.5093, MSE = 0.6376, p < 0.001). We compared this with the model with lowest error that utilised only T1 data (in any configuration) and found that the % grey matter input with the PCA derived functional clusters and the RVR machine (r = 0.4698, MSE = 0.7204, p < 0.001) did not significantly differ with the winning model (Wilcoxon test: Z = 0.1345, p = 0.893, effect size = 0.032, difference = -0.014 with 95% CI = -0.168 – 0.158, bf10 = 0.1334). The best model configuration for Factor 2 (semantics) was obtained using the MKR machine on the T1 triplet data based on the functional connectivity atlas partition (r = 0.5087, MSE = 0.6668, p < 0.001). The best model configuration for Factor 3 (executive-demand) was obtained using the MKR machine on a combination of % abnormality and % white matter data based on the combined anatomical atlas (r = 0.7333, MSE = 0.3963, p < 0.001). Finally, the best model for Factor 4 (speech fluency) was obtained using the RVR machine on a combination of % grey matter and FA data using no partition (r = 0.5228, MSE = 0.6274, p < 0.001). We compared this model with the lowest model that utilised only T1 data (in any configuration) and found that the % grey matter combined with % white matter inputs with the RVR machine and no brain partition (r = 0.5174, MSE = 0.6346, p < 0.001) did not significantly differ with the winning model (Wilcoxon test: Z = 1.085, p = 0.2778, effect size = 0.264, difference = -0.037 with 95% CI = -0.103 – 0.036, bf10 = 0.232).

Table 1.

Best overall models for each behavioural factor score. The first column indicates the factor and each corresponding row indicates the characteristics of the winning model (machine, modality, partition, mean square error (MSE) and correlation). Abbreviations: Anatomical connectivity map (ACM), mean diffusivity (MD), fractional anisotropy (FA), and principal component analysis (PCA).

	Winning model
Factor	Machine	Modality	Partition	MSE	Correlation
Phonology	Kernel Ridge	ACM and MD	PCA derived lesion clusters	0.6376	0.5093
Semantics	Multi-Kernel	Combined T1	Functional connectivity-based atlas	0.6668	0.5087
Executive-demand	Multi-Kernel	% Abnormality and % White matter	Anatomical atlas	0.3963	0.7333
Speech quanta	Relevance Vector	% Grey matter and FA	Whole brain – no partition	0.6274	0.5228

In summary, these results suggest that the T1 input features (in different combinations) produce sufficiently good models when compared to all other models that include diffusion measures (in isolation or combination with T1). The pattern of winning models suggest that the multi-kernel machine is preferred when the brain space is partitioned into a large number of regions. This outcome probably reflects the fact that the multi-kernel machine is designed to deal with multiple partitions, making it more sensitive to subtle effects at the local level which are then combined into the final model. In contrast, the kernel ridge or relevance vector machines work well for a small number or no partitions.

Discussion

Recent advances in multimodal neuroimaging and applied mathematics have provided the opportunity to build sophisticated brain-to-behaviour prediction models of cognitive, language, and mental health disorders. These are important for at least two reasons. First, prediction models provide formal and stringent tests of hypotheses about the neural bases of higher cognitive function. Rather than mapping variations in cognitive skill back to the brain, they test the reverse inference in which the importance of brain regions, connectivity or other brain imaging metrics in explaining behavioural variation are evaluated, thereby reflecting the causal relationship between variables. Secondly, from a clinical perspective, securing successful brain-to-behaviour prediction models could offer a step-change in clinical practice and research. This is especially true in disorders, such as post-stroke cognitive and language impairments, where the status of the damaged brain is clear long before the chronic behavioural profile emerges. Accordingly, accurate prediction models could be used to provide essential prognostic information to patients, carers and health professionals, as well as establish important new lines of clinical research including the use of predictions for guiding clinical management (i.e., what behaviours/neural features should be targeted), stratification to treatment pathways (i.e., which individuals will benefit from certain treatments based on their neurology), etc. Recently, a number of research groups have started to evaluate brain-to-behaviour prediction models for their ability to predict the diverse cognitive-language presentations found in post-stroke aphasia^4–10,33. The key aim of the current investigation was to take the next major step on from these proof-of-principle studies towards understanding three foundational issues that are critical in the next phase of brain-to-behaviour prediction models. We observed the impact on model performance when changing: (1) brain partition; (2) machine learning algorithms; and (3) combination of information derived from multimodal neuroimaging. The findings on each of these foundational issues are discussed briefly below alongside a consideration of why a change in how we conceptualise and describe symptoms may be needed.

Classically, variations in the type and severity of aphasia have been described with reference to formal clinical classification systems^54,55 Increasingly, contemporary aphasiological research and clinical practice has moved away from relying on these schemes. This is because, rather than forming homogeneous, mutually-exclusive categories, there are considerable variations within each aphasia type and overlapping symptoms between them. Accordingly, classification is difficult and often unreliable^11–14, limiting their utility for patient stratification, treatment pathways – and, importantly for the current study – their use as stable targets in brain-to-behaviour prediction models. Recent reconceptualisations have captured aphasiological variations in terms of graded differences along multiple, independent dimensions (with classical aphasia labels referring to approximate regions within this multidimensional space, much as colour labels indicate regions within the continuous hue space¹⁵). In order to use the dimensions from this aphasia space as prediction targets, it is important to test the space’s reliability and stability. This was confirmed by performing a 5-fold cross validation analysis to determine the optimal number of components. Furthermore, we demonstrated that this solution is stable when the sample size is reduced from N = 69 down to a minimum of N = 28. In addition, the nature and form of this four-factor solution has been observed with remarkable similarities across multiple independent studies with chronic^16–19 and acute⁵⁶ stroke aphasia.

In this investigation, we evaluated five different brain partitions (which provide the input feature data to the prediction models). We used whole brain atlases that were defined using anatomically- or functionally-coherent voxels to reduce the feature set to 133 and 268 partitions, respectively. Our results showed that these models typically outperformed those using a smaller number of parcellations (obtained using known functional partitions of language performance (3 features) or the lesion clusters that follow from an MCA stroke (17 features)). We suggest that there may be at least two reasons for this result: (1) the latter two partitions were confined to the left hemisphere only, whereas the former covered the whole brain. This suggests that areas outside of the lesion territory may contribute to the successful predictions, perhaps representing areas that are critical for successful recovery. (2) A simple second explanation is that a larger number of partitions allows for more subtle effects to be observed than when averaging into a smaller number of larger ROIs. It is not clear whether these particular anatomical/functional features are important per se or whether their superiority emerges purely from their higher resolution/greater number of partitions. Future work could determine if we would observe a similar set of results if there were a large number of features randomly partitioned (not adhering to functional or anatomical boundaries) across the whole brain.

In the last decade, there has been an explosion in tools for performing multivariate machine learning. Given the variety of options available, we compared the performance of four types of learning algorithms implemented in PRoNTo⁴⁶. These included kernel ridge regression (KRR), Gaussian process regression (GPR), relevance vector regression (RVR) and multi-kernel regression (MKR). Our results showed that MKR produced the best single models when used with a large number of ROIs features. This is probably unsurprising as MKR performs many SVR models within each ROI and then combines the information using a sparsity constraint. This is likely to capture subtle effects that are present at high resolutions which become diluted when using fewer ROIs or missing if parts of the brain space are not sampled. Recent work has documented the broader applicability of MKL methods in ECoG⁵¹, fMRI and structural T1⁵² data. Taking the results from the parcels and machines together, one can consider if model complexity might have played a role in our results (i.e., models that used a large number of partitions with the most sophisticated algorithm typically led to the best model performance). Calculating and controlling for model complexity are rendered non-trivial in multivariate models, hierarchical analysis steps and sparsity constraints. Future statistical and computational advances in quantifying model complexity will help to improve our ability to compare model performance more objectively.

Modern neuroimaging technology not only provides the opportunity for high resolution structural images but also multiple types of brain images. Such multimodal neuroimaging could improve the accuracy of prediction models through the combination of complementary brain measures. As noted in the Introduction, the handful of studies that have added direct or indirect measures of white-matter connectivity measures to prediction models based on standard T1/T2 data, have generated inconsistent results^5,8,9,33. Indeed, even studies with positive results have reported only modest gains in prediction accuracy. The evidence from the current investigation aligns with these observations: combinations of abnormal tissue, grey and white matter measures from the standard T1 scan are sufficient. Adding white matter integrity or connectivity measures (in the form of FA, MD or ACM) does not improve the mean squared error of the prediction models (observed using Bayes factor scores). This conclusion might seem at odds with classical and contemporary disconnection theories of language function^22,57–59 and demonstrations from cognitive neurosurgery that direct electrical stimulation to major fasciculi results in different aphasic features^31,32. Rather than being contradictory, it seems more likely that the result reflects the intrinsic nature of stroke, where infarction always involves a combination of grey and white matter damage⁶⁰. Accordingly, in stroke, there is a tight coupling between the area of damage and its disconnection from other regions, and this high collinearity makes white matter integrity measures redundant in brain-behaviour prediction models (even if the connection is neurocomputationally critical). Indeed, Hope et al.,⁵ observed a very high correlation between the first principal component of lesion and pseudo-disconnection data. In short, whilst disconnections are undoubtedly important in the nature of some impairments, in stroke this disconnection is caused by the local lesion and thus local measures are sufficient for building prediction models. Furthermore, although secondary connectivity changes (e.g., Wallerian degeneration or positive recovery-related improvements) might contribute to patients’ performance, again it is possible that, in stroke, they are triggered by the local lesion and thus, again, they share too much variance to improve prediction models significantly. We note here that this conclusion is very likely to be disease specific. Whilst the lesion is primary in stroke, in other diseases changes in brain volume are the end point of a cascade of brain changes. Thus, for example, in neurodegenerative diseases local pathology leads to cell loss, axonal thinning and ultimately regional atrophy. Accordingly, in these diseases it is not surprising that the additional of white-matter measures does improve brain-behaviour models⁶¹. While we do not believe the types of prediction models outlined in the current would generalise across diseases, the underlying question would be interesting to explore. For example, the international community researching Alzheimer’s disease have large multi-site data, which could be used in future studies.

Inevitably, every study has its limitations. Stability and reproducibility are critically important. In this study, we have taken important strides in this direction in terms of formal analyses of the stability of the PCA behavioural factors and the k-fold cross-validation not only of the prediction models but also of the data to be predicted. Future studies in our field could go even further by undertaking an additional, formal out-of-sample validation (e.g., on an independent behavioural and neuroimaging dataset) of the type that is becoming standard practice in related fields (e.g., the Alzheimer’s Disease Neuroimaging Initiative). This is not possible in the current study because comparable datasets (comprising the same ‘high resolution’ behavioural data and multimodal neuroimaging for every patient) does not exist. Whilst multiple research groups, including our own, have focussed their efforts to achieve a step-change in the number of participants included and the range of data collected, the ability to undertake these formal of out-of-sample evaluations will require a shared international community endeavour to agree an open access database containing an agreed behavioural and neuroimaging core dataset for all participants, and additional research on how to achieve this across different languages. Secondly, the models evaluated in the current study specifically target three language and one general executive behavioural component. It is unclear whether other domains affected post stroke (i.e. syntax, detailed executive abilities, mobility, mood/anxiety, etc/) would result in the same findings. Thirdly, in this systematic investigation we have examined a range of brain partitions, machine learning algorithms and neuroimaging measures. It will be important for future studies to explore additional options, including other learning algorithms (e.g., random forest, neural network models), alternative brain parcellations (both in resolution and basis) and different neuroimaging measures (e.g., positive structural changes compared to controls, the addition of functional MRI or indeed alternative ways to encode structural connectivity such as using graph theoretical measures). We believe that neuroimaging methods identifying the functional properties of remaining tissue may provide benefits over and above structural measures²⁶. Structural measures alone do not tell us whether the underlying tissue is functioning (either normally, at a reduced capacity or has been adapted), therefore novel decoding methods such as representational similarity analysis⁴² could reveal how brain processes have been affected post stroke which might be predictive of chronic deficits and/or recovery more generally. These studies will be able to determine which, if any, of these measures improve prediction accuracy, significantly and substantially, over and above lesion information alone. In the current study, we refrained from interpreting the neural weights as it is non-trivial (for example, see ^41,49). There are novel ways, however, which try to evaluate feature importance either as part of the modelling process (i.e. using sparse features) or post-hoc (i.e. using virtual lesioning approaches or weight transformations). Future studies should incorporate the methods to help provide theoretical insights into brain-behaviour relationships. We note explicitly that, although it is hard to compare model performance directly across different studies (as the input data and targets are different), our current results fair well relative to the existing investigations that utilised in vivo T1 and diffusion data. For example, a recent study used connections to predict various subtest scores from the Western Aphasia Battery⁹ and reported similar correlations between observed and predicted scores as those found in the current study using structural-only brain measures (in the range of 0.5 to 0.75 depending on the target language function). Despite the promising results, we acknowledge that there is substantial unexplained variance, which needs to be addressed in future studies and for generating accurate clinically-applicable tools.

In conclusion, this study suggests that using a large number of neural partitions (based on anatomical or functional similarity) in combination with a multi-kernel learning algorithm on neural features extracted from a T1 MRI lead to good model predictions of language and executive abilities in post-stroke behaviour. We did not find evidence that diffusion MRI measures improve model predictions. From a clinical implementation perspective, it suggests that the majority of the information needed for effective outcome prediction in stroke aphasia can be obtained using standard clinical MR scanning protocols, obviating the need for acquisition and processing of diffusion weighted data.

Methods

Participants

All participants gave written informed consent with ethical approval from the local ethics committee (North West Haydock MREC 01/8/94). Participation was on a voluntary basis and all travel expenses were reimbursed. Seventy chronic post-stroke patients were included (53 males, mean age ± standard deviation [SD] = 65.21 ± 11.70 years old, 12 months post onset median = 38 months, range = 12-278 months). All cases were diagnosed with aphasia (using the Boston Diagnostic Aphasia Examination [BDAE]), having difficulty with producing and/or understanding speech. Cases were recruited from local community clinics and from referrals from the local NHS. No restrictions were placed according to aphasia type or severity (therefore our sample included cases classed as global to anomic). Part or all of the cases were used in other published work from our group^{4,15,16,62–68}. Data from a healthy age and education matched control group (8 female, 11 male) was used in order to determine abnormal voxels using the automated lesion identification procedure⁶⁹. No statistical methods were used to pre-determine sample sizes as there is not a clear way to determine power when building multivariate prediction models. Data collection and analysis were not blind to the researchers; however, in the analysis for this study there was a separation between model training and test sets.

Neuropsychological assessment

As described in ⁴ all participants underwent an extensive and detailed neuropsychological battery of tests to assess a range of language and cognitive abilities^15,16. These included subtests from the Psycholinguistic Assessments of Language Processing in Aphasia (PALPA) battery⁷⁰: auditory discrimination using non-word (PALPA 1) and word (PALPA 2) minimal pairs; and immediate and delayed repetition of non-words (PALPA 8) and words (PALPA 9). Tests from the 64-item Cambridge Semantic Battery⁷¹ were included: spoken and written versions of the word-to-picture matching task; Camel and Cactus Test (pictures); and the picture naming test. To increase the sensitivity to mild naming and semantic deficits we used the Boston Naming Test⁷² and a written 96-trial synonym judgement test⁷³. The spoken sentence comprehension task from the Comprehensive Aphasia Test⁷⁴ was used to assess sentential receptive skills. Speech production deficits were assessed by coding responses to the ‘Cookie theft’ picture in the BDAE, which included tokens, mean length of utterance, type/token ratio and words-per-minute (see ¹⁶ for details). The additional cognitive tests included forward and backward digit span⁷⁵, the Brixton Spatial Rule Anticipation Task⁷⁶, and Raven’s Coloured Progressive Matrices⁷⁷. Assessments were conducted with participants over several testing sessions, with the pace and number determined by the participant. All scores were converted into percentage; if no maximum score was available for the test we used the maximum score in the dataset to scale the data.

Principal Component Analysis

There were two stages to the principal component analysis (PCA) used to generate the behavioural target dimensions: 1) determine the optimal number of components and the stability of the solution and 2) use that information to perform a varimax rotated PCA on the behavioural data. In the first stage we performed a 5-fold cross validation with venetian blind sampling using a freely available MATLAB toolbox⁷⁸. This toolbox builds a PCA model on the training set (z-score scaling to all variables) and is used to predict the variables in the hold out set⁷⁸. One variable is removed at a time and these held-out data are predicted using linear regression from the PCA model⁷⁹. The residuals of this reconstruction are calculated as root mean squared error in cross-validation and analysed as a function of the number of components (total N-1, where N = number of test variables). We repeated this step 100 times where, on each occasion, the order of the patients was shuffled to avoid biases in the venetian blinds sampling approach. We further repeated this process (100 times) using varying sample sizes in order to test the stability of the solution (i.e., we removed 10-60% of the data in 10% steps).

Having determined the optimal number of components, we performed a PCA with varimax rotation on each training fold (MATLAB R2018a). Following rotation, the loadings of each test allowed a clear behavioural interpretation of each factor. The PCA model coefficients were used to determine the factor scores expected for the test fold (by projecting the test fold data into the PCA model space); these scores were used as targets during modelling. An additional analysis was used to determine the predictability of the optimum PCA model, by comparing the similarity between the observed and predicted scores in each fold (by projecting the held-out cases into the component space using the coefficient matrix).

Acquisition of Neuroimaging Data

High resolution structural T1-weighted Magnetic Resonance Imaging (MRI) scans were acquired on a 3.0 Tesla Philips Achieva scanner (Philips Healthcare, Best, The Netherlands) using an 8-element SENSE head coil. A T1-weighted inversion recovery sequence with 3D acquisition was employed, with the following parameters: TR (repetition time) = 9.0 ms, TE (echo time) = 3.93 ms, flip angle = 8°, 150 contiguous slices, slice thickness = 1 mm, acquired voxel size 1.0 × 1.0 × 1.0 mm³, matrix size 256 × 256, FOV = 256 mm, TI (inversion time) = 1150 ms, SENSE acceleration factor 2.5, total scan acquisition time = 575 s.

The diffusion-weighted images were acquired with a pulsed gradient spin echo echo-planar sequence with TE=59 ms, TR ≈ 11884 ms (cardiac gated using a peripheral pulse monitor on the participant’s index finger), Gmax=62 mT/m, half scan factor=0.679, 112×112 image matrix reconstructed to 128×128 using zero padding, reconstructed in-plane voxel resolution 1.875×1.875 mm, slice thickness 2.1 mm, 60 contiguous slices, 43 non-collinear diffusion sensitization directions at b=1200 s/mm² (Δ=29 ms, δ=13.1 ms), 1 at b=0 and SENSE acceleration factor=2.5. The sequence was repeated twice with opposing phase encoding directions in the left-right plane. In order to correct susceptibility-related image distortions, a B0 image was collected at the beginning of each phase encoding sequence. Cardiac gating was implemented during diffusion data acquisition.

Neuroimaging pre-processing

T1-weighted MRI

The T1 images were pre-processed with Statistical Parametric Mapping software (SPM12: Wellcome Trust Centre for Neuroimaging, http://www.fil.ion.ucl.ac.uk/spm/). This involved transforming the images into standard Montreal Neurological Institute (MNI) space using a modified unified segmentation-normalisation procedure optimised for focal lesioned brains (⁶⁹ version 3). Data from all participants with stroke aphasia and all healthy controls were entered into the segmentation-normalisation. This procedure combines segmentation, bias correction and spatial normalisation through the inversion of a single unified model (see ⁸⁰ for details). In brief, the unified model combines tissue class (with an additional tissue class for abnormal voxels), intensity bias and non-linear warping into the same probabilistic models that are assumed to generate subject-specific images. The healthy matched control group was used in order to determine the extent of abnormality per voxel. This was achieved using a fuzzy clustering fixed prototypes approach, which measures the similarity between a voxel in the patient data with the mean of the same voxel in the control data. One can apply a threshold to the similarity values to determine membership to abnormal/normal voxel. We modified he default ‘U-threshold’ from 0.3 to 0.5 to create a binary lesion image after comparing the results obtained from a sample of patients to what would be nominated as lesioned tissue by an expert neurologist. All images generated for each patient were individually checked and modified (if needed) with respect to the original scan. The binary images were only used to create the lesion overlap map in Figure 3 (2mm³ MNI voxel size) and were not part of the main analyses. The continuous abnormal/normal images, was used in the main analyses as the values have in effect been normalised and represent a quantitative measure (termed % abnormality). This image only included hypo-trophic signal (i.e., lower T1-weighted signal than expected). In addition, the unified segmentation procedure outputs probability maps for the grey and white matter, which were also selected for use in the main analyses. The abnormality, grey and white probability maps were smoothed using an 8mm FWHM Gaussian kernel. We selected the Seghier et al.,⁶⁹ method as it is objective and efficient for a large sample of patients⁸¹, in comparison to a labour intensive hand-traced lesion mask. The method has been shown to have a DICE overlap >0.64 with manual segmentation of the lesion and >0.7 with a simulated ‘real’ lesion where real lesions are superimposed onto healthy brains⁶⁹. We should note here, explicitly, that although commonly referred to as an automated ‘lesion’ segmentation method, the technique detects areas of unexpected tissue class – and, thus, identifies missing grey and white matter but also areas of augmented CSF space.

Diffusion weighted imaging

The diffusion weighted images were pre-processed using tools from the FSL software (Oxford Centre for Functional MRI of the Brain; FMRIB v.5.0.9^82,83). Data were collected with reversed phase encode blips, resulting in pairs of images with distortions going in opposite directions. From these pairs the susceptibility-induced off-resonance field was estimated using a method similar to that described in Andersson, Skare & Ashburner⁸⁴ implemented in FSL and the two images were combined into a single corrected one (‘topup’ command). In the next step we used ‘eddy_openmp’ to correct for eddy current-induced distortions and subject movements⁸⁵. The ‘replace outliers’ option was used in order to identify outliers due to subject motion and replace the slices by using a non-parametric prediction based on Gaussian Process⁸⁶. Once the data had been pre-processed, we fitted a diffusion tensor model at each voxel (‘dtifit’ command) to obtain local mean diffusivity (MD) and fractional anisotropy (FA) values. An inclusive mask was created per subject using the MD map and thresholding 50% of the range of non-zero voxels. This had the effect of removing voxels in CSF and/or lesioned space where we would not expect to see sensible fibres/tracking (all masks were visually inspected). A probabilistic diffusion model using Bayesian Estimation of Diffusion Parameters Obtained using Sampling Techniques for crossing fibres (BEDPOSTX)^87,88 was applied to the inclusive voxels of the pre-processed data. All parameters for the estimation were set to default except the number of fibres = 3, burn in period = 3000 and model = 3 (‘zepplin’ axially symmetric tensor). Finally, we used ‘probtrackx2’ in order to obtain a whole brain anatomical connectivity map (ACM)⁸⁹. This was achieved by including all inclusive voxels as a seed and sending 50 streamlines per voxel. The output reflects how connected overall a voxel is to the rest of the brain. A B0 image in diffusion space was coregistered to the high resolution T1 image using ‘flirt’^90,91 (with mutual information and six degrees of freedom) to obtain a transformation matrix between diffusion and T1 space. The diffusion measures were then transformed into MNI space using the transformation matrix obtained from the normalisation produced above. These images were smoothed using an 8 mm FWHM Gaussian kernel to account for inter-subject variability.

Multivariate pattern recognition models

We used the pattern recognition of neuroimaging toolbox (PRoNTo V2.1) (http://www.mlnl.cs.ucl.ac.uk/pronto/)⁴⁶ to determine whether individual scores on principal components could be predicted based on multivariate analysis of the T1 and/or DWI data. In order to find an optimal solution we performed the regression analysis using three machine implementations in PRoNTo: 1) kernel ridge regression⁹², 2) relevance vector regression⁹³, 3) gaussian processes regression⁹⁴. In cases where we had multiple modalities and/or subdivided the brain mask into ROIs we used a fourth machine: multi-kernel regression (MKR)^95,96 as this method has been proposed to simultaneously learn and combine different models represented by different kernels. PRoNTo relies on kernel methods in order to overcome the high dimensionality problem in neuroimaging (approximately 2-5 × 10⁶ voxels per image versus 20-100 datasets). A pair-wise similarity matrix is built between all neuroimaging scans, summarised in a kernel matrix as NxN dimension, instead of Nxd. The default parameters were used for all machines. A ‘nested’ cross-validation was used in order to optimise the hyper-parameter, λ, controlling for regularisation in KRR and MKR (both using 10ⁱ with i=-2:5), while the GPR and RVR machines optimise hyperparameters automatically using a Bayesian framework. A 10-fold cross-validation scheme was used to assess the ability of the machines to learn associations between the predictors and targets. We applied some data operations to the training data kernels, the voxel-wise mean was subtracted from each data vector for all models and samples were normalised (vector norm = 1) for all models with multiple modalities and/or ROIs as recommended by the software. In the current report, we focus primarily on the mean squared error (MSE) and the significance of each machine was assessed by a permutation test of the observed scores (N=1000) with a p <0.05 alpha threshold. In order to determine the level of performance of different model ‘recipes’, we used Wilcoxon tests to compare the mean squared error after collating specific groups for each model parameter. For example, to examine the overall accuracy differences between different machines, we aggregated the MSE values for all models separately for KRR, GPR, RVR and MKR, and conducted pair-wise Wilcoxon tests (Bonferroni corrected for multiple comparisons). We also calculated Bayes factor for each comparison using a package developed in R⁹⁷, where evidence can be obtained in favour of a difference between pairs (>3), evidence for the null hypothesis (<0.3) or insufficient evidence (0.3-3) (based on criterion in ⁵³). In regards to model complexity, we believe this is not trivial when dealing with advanced machine learning pipelines. For example, it is unclear whether the number of parameters should include the number of voxels (as the raw inputs) or the similarity kernels, and how this is affected based on the number of partitions. In addition, the complexity of models that include sparsity constraints could be quantified using the full data or the final sparse solution (on which the model predictions are made). Given the difficulties in quantifying model complexity we did not correct this in our results. Finally, we report the effect size (Cohen’s D) for each nonparametric test by combining two equations (⁹⁸ and ⁹⁹), which converts a z-statistic to r to Cohen’s d.

Parcellations

We used five different masks to define the brain space. First, as a starting point we used a whole brain mask with no partitions in order to capture the overall status of the brain. We then used two anatomical based atlases: 1) we created a composite whole brain atlas that combined the Harvard Oxford cortical and subcortical atlases with the JHU white matter atlas. We binarised each voxel by assigning it to the maximum structural likelihood based on the probability values. For example, for each voxel we loaded the probability for 133 structures (48 bilateral cortical, 7 bilateral sub-cortical, 9 bilateral white matter tracts, bilateral lateral ventricles and brainstem) and assigned the voxel with a label that had the maximum likelihood. 2) We used a data driven method to identify lesion clusters for voxels with co-occurring damage in left hemisphere MCA stroke. The lesion clusters were obtained by applying a principal component analysis on the lesioned brain in order to extract the underlying structure of the damage. In effect the lesioned territory is split into partitions that reflect the neuro-vasculature while reducing the dimensions of the data, in this case 17 non-overlapping clusters²⁸. We also used two functional-based atlases: 1) whole brain atlas based on the functional connectivity similarity^24,100 and 2) a restricted-space, language model based on lesion correlates to three functional components of behaviour¹⁶.

The prediction models were developed in stages in order to determine the utility of each imaging modality. We had six neural inputs that represented data from T1 (% abnormality, % grey matter and % white matter) and diffusion imaging (FA, MD and ACM) scans. These were tested: 1) alone, 2) in 15 pair-wise combinations (i.e. % abnormality and % grey matter, % abnormality and % white matter, etc.), 3) as a triplet within each domain (T1 or diffusion), and 4) all together. There were four models created for each input modality, relating to the four principal behavioural factors. An overview of the model ‘recipe’ is shown in Figure 1.

Data availability

The conditions of our ethical approval do not permit public archiving of anonymised study data. Anonymised data necessary for reproducing the results in this article can be requested from the corresponding authors.

Code availability

The computer code that support the findings of this study are available from the corresponding author on reasonable request.