Electron cryomicroscopy with sub-Ångström specimen movement

Abstract

Most information loss in electron cryomicroscopy stems from particle movement during imaging, which remains poorly understood. We show this movement is caused by buckling and subsequent deformation of the suspended ice, with a threshold that depends directly on the shape of the frozen water layer set by the support foil. We describe a specimen support design that eliminates buckling and reduces electron beam-induced particle movement to less than an Ångström. The design allows precise foil tracking during imaging with high-speed detectors, lessening demands on cryostage precision and stability. It includes a maximal density of holes, increasing throughput in automated cryomicroscopy without degrading data quality. Movement-free imaging allows extrapolation to a three dimensional map of the specimen at zero electron exposure, before the onset of radiation damage.

Despite the current success of electron cryomicroscopy (cryoEM) in determining the structure of numerous macromolecular complexes that were previously intractable, several outstanding problems remain: Specimen movement at the beginning of electron beam irradiation degrades image quality and reduces information about the undamaged structure (1). Thus, all current cryoEM structures have varying degrees of radiation damage incorporated into the resulting atomic models. The throughput of modern synchrotron crystallography beam lines vastly exceeds that of current state-of the art electron microscopes, meaning high resolution structure determination by cryoEM is feasible but throughput is comparatively limited in practice (2). Rapid structure determination by cryoEM is further hampered by structural heterogeneity in many samples, and irreproducible and destructive interactions with surfaces during specimen preparation (3). Here we present a physical theory of the causes of movement of cryoEM specimens during imaging and use this work to design and implement a specimen support that eliminates movement and helps address some of these limitations.

Proteins, rapidly frozen for cryoEM in amorphous ice, are inherently low-contrast making them difficult to track and image. Previous work using virus particle tracking on amorphous carbon supports showed a “drum-like motion” which included deformation of the support foil and the ice layer, which together cause a rotation and vertical displacement of the particles of 150 to 250 Å (4, 5). More recent tracking methods yield similar types of trajectories for various smaller protein specimens (6, 7). Gold nanoparticles embedded in vitreous ice provide a high-contrast fiducial marker to measure the movement of the ice during a typical high-resolution, low-dose micrograph (Fig. 1A, Fig. S1). The types of movement that occur during cryoEM imaging, ordered by magnitude, are 1. stage drift, 2. bending of the support foil, 3. ice bending, 4. Brownian movement during irradiation, and 5. molecular vibrations (Supplementary Text). To isolate the movement of the ice layer, we eliminate the movement of the specimen support by using ultrastable gold foils which do not move during irradiation (8), and include the edge of the gold hole in the image for accurate (˂ 0.1 Å) stage drift correction. What remains is then the movement of the ice within the hole and the individual particles within the ice.

Fig. 1. Movement of gold nanoparticles in vitreous ice in a range of foil hole sizes.

(A)Typical drift-corrected electron micrograph used for tracking gold particles in vitreous water on all-gold supports; scale bar is 0.5 μm The inset (20 nm × 20 nm) shows an overlay of the positions of a gold nanoparticle at the beginning of irradiation and after a fluence of 60 e⁻/A² (B-C) The root mean squared displacements of 200 - 2000 particles from 10 - 50 movies of different diameter holes (UltrAuFoil R2/2 - 1.9 μm - yellow, UltrAuFoil R1.2/1.3 - 1.2 μm - green, UltrAuFoil R 0.6/1 - 0.8 μm - pink, and custom made grids with 0.3 um - purple, and 0.2 μm holes - blue) are plotted as a function of cumulative electron fluence for 0° (B) and 30° tilt (C). Error bars denote standard error in the mean. (D) Thin films of ice used in cryoEM buckle during vitrification if the compressive stress (N) exceeds a critical value (N ₀), determined by the aspect ratio $\left(\frac{2a}{h}\right)$ of the film. Electron irradiation causes the film to move in response to additional stresses in it, as is evident from the correlated particle movement at the beginning of irradiation. (E) The range of stable hole diameters can be determined for a given ice thickness (blue shaded region) The two critical aspect ratios (dashed lines) are calculated according to two theoretical models of buckling during vitrification (Supplementary Text). The black and red data points show the hole sizes and ice thicknesses for the gold particle and DPS datasets, respectively. Error bars denote standard deviations

From measurements of the movement of ~15 thousand particles from hundreds of holes in ultra-stable gold foils (8), with hole diameters from the typical 1-2 μm in standard specimen support foils down to 200 nanometers, a pattern of movement becomes clear (Fig. 1B-C, Fig. S2-S8). There is an abrupt, spatially correlated displacement of the particles at the onset of irradiation (during the first ~ 4 e⁻/Ų). This is followed by a less correlated movement that continues with reduced speed to the end of the exposure. The initial movement is particularly apparent in the tilted micrographs of the 2 μm holes, where the vertical (out of plane) displacement of the ice is 10 to 50 Å in a 30 e-/Ų exposure (Fig. S4). In contrast, the movement of the particles in 300 and 200 nm holes is isotropic (the same in the plane of the support and perpendicular to it), is spatially uncorrelated, and scales with the square root of the incident electron fluence, as would be the case for diffusional motion (Fig. S2, S9-S12).

To explain this movement we suggest a physical model, based on considering the stresses that are created in the specimen during vitrification, and the pseudo diffusion of the water molecules under electron irradiation (9) (Fig. 2, Supplementary Text). In typical cryoEM specimens, the ice deforms twice, once during freezing and again during irradiation with the electron beam. Vitreous water (low-density amorphous ice) has 6% lower density than liquid water at 4°C (10, 11). During cryoplunging, freezing occurs over a time interval of ≤ 10^–4 seconds (10). Within this time, the water density change is most rapid near the homogeneous nucleation temperature ≈ 235K (12, 13). As the water solidifies, the rapid cooling does not allow sufficient time for structural rearrangements of the water molecules and causes the buildup of compressive strain within the thin film (Fig. 2A). Once the compression exceeds a critical value, the film buckles, thus momentarily relieving the radial stress in the layer. Buckling only occurs if the stress exceeds a critical point, which is determined by the dimensions of the ice film, its elastic moduli, specific volume change relative to the support, and the constraints at the edge of the hole (Supplementary Text & Fig. S13-S15). As the vitreous film continues to cool to the temperature of the surrounding cryogen (typically liquid ethane at 90 - 93K), more stress builds up as a result of further relative density changes. This stress is stored in the film indefinitely at 77K (liquid nitrogen temperature).

Fig. 2. Model of the stress accumulation in thin films of amorphous ice during cryoplung-ing, and their response to electron irradiation.

The density of liquid and amorphous water is plotted (black markers) as a function of temperature, as reported in (12, 13), with a black line to guide the eye. During cryoplunging into liquid ethane, water is rapidly cooled, typically from 277K to 91K (black arrow). The largest specific volume change experienced by water below its homogeneous nucleation point (red) is ${\left(\frac{\Delta V}{V}\right)}_{\text{max}}\approx 6\%$. The thin film can only withstand compression of up to ${\left(\frac{\Delta V}{V}\right)}_{\text{crictical}}$ before it buckles (purple range corresponds to a 300 Å thick layer in a 1 μm hole). (B) The diffusivity of water molecules in liquid and amorphous ice is plotted (black crosses) as a function of temperature, as reported in (14). The black line is a fit to these values, as proposed in (14). The extrapolated diffusivity in amorphous ice at 84K is vanishingly low, ~ 10^–46 Ų/s. The blue shaded region indicates the range of diffusivity in amorphous ice at temperatures in the 0 -100K range, where it is stable indefinitely. During imaging with 300 keV electrons, water molecules move pseudo-diffusively by 1 Ų/(e⁻/ Ų) (9). At typical imaging fluxes of 0.1 - 10 e⁻/ Ų/s, this is equivalent to 0.1 - 10 Ų/s(orange) and corresponds to an instantaneous local temperature of 147K.

High energy electron irradiation increases the effective diffusivity of water molecules by 46 orders of magnitude (Fig. 2B) (14), causing the ice in the electron beam to behave as an ultraviscous fluid. This change in the mechanical properties of the film results in unbalanced bending moments in it; these cause a correlated and rapid displacement of the particles in the same direction as the pre-existing buckling (Fig. 1D), apparent in cryomicrographs. The movement is enabled and accompanied by random movement due to the continuous, pseudo diffusion of the surrounding water, and only occurs during electron irradiation. The predicted critical aspect ratio (diameter:thickness), above which the film is expected to buckle during freezing and become unstable during irradiation, is approximately 11:1 (Supplementary Text). When the aspect ratio of the vitreous ice film is below the critical value (i.e. 330 nm or 180 nm diameter holes for 300 Å thick ice in Figure 1B-C), the ice never builds up enough stress to buckle during freezing or deform under irradiation. Such films remain stable throughout irradiation, and only diffusive movement occurs (Fig. S16); this is limited to ˂ 1 Å RMS (root mean squared) in 30 e⁻/ Ų.

On the basis of the above theory, we propose a simple method for choosing the dimensions of a support foil to prevent buckling for a given specimen: The optimal foil thickness is set by the desired ice thickness, and the optimal foil hole diameter is ≤ 11× the ice thickness (Fig. S17). For example, for a 200 Å thick particle in 300 Å thick ice, the optimal hole diameter is below 330 nm. For 100 Å thick ice, potentially desirable for sub-100 kDa specimens, the optimal diameter is below 110 nm. In such small holes, the thickness of the suspended ice is largely controlled by the foil thickness; uniform and stable thin films of vitreous water can be formed. Unfortunately, for most single particle specimens, the desired foil hole size is less than the practical limit of conventional photolithography techniques currently used to make specimen supports, and evaporated foils of gold below about 400 Å thick are not stable because of their polycrystalline grain structure (15). We propose a specimen support design, “HexAuFoil” (Fig. 3) - which entirely eliminates the buckling of the suspended amorphous ice during irradiation - and provide a scaleable method for manufacturing these supports based on phase interference lithography (Talbot displacement (16,17)) and low temperature evaporation (Fig. S18-S19). The holes are arranged in a hexagonal pattern in a foil whose thickness (280 Å for the example in Fig. 3F) can be matched to the specimen, and still remain round (Fig. S19B). Interestingly, the nanoscale dimensions of the array imply that the foil has plasmon resonances in the visible range, which causes the foil to appear yellow on reflection with white light but blue on transmission (Fig. 3A-B, S18G), a property which might be used in the future for characterising the specimen before imaging with electrons. The foil is suspended across a 3 mm hexagonal mesh grid; together these hexagonal arrays increase the usable area tenfold over a standard cryoEM grid. More than 800 images can be acquired from a single stage position, accelerating the rate of automated data collection (18, 19), and more than 5000 individual holes can be imaged in a single 25 μm wide hexagon (Fig. 3C). Having the edge of the gold foil in each image (Fig. 3E-F, S20) has the additional benefit of allowing rapid and accurate drift tracking independent of the signal from the specimen within the holes, which reduces the demands on stage precision and stability.

Fig. 3. HexAuFoil is an all-gold specimen support designed for movement-free cryoEM imaging.

Optical micrographs, in (A) reflected and (B) transmitted unpolarized white illumination of the patterned gold foil (hexagonal array of 200 nm diameter holes with 600 nm pitch) on a 600-mesh thin-bar gold grid. The scale and the corresponding area are the same for (A) and (B). The blue color of the foil in transmitted light is due to a strong red absorption enhancement by the periodic hole pattern (Fig. S18G). (C) Transmission electron micrograph of a single hexagonal grid-opening on one of these grids. A 3 mm grid contains ~ 800 of these hexagons, each of which includes more than 5,000 holes in a regular pattern. The green circle encloses more than 800 holes, which can all be imaged at high magnification without moving the stage during high-speed data collection (Fig. S21). (D) Transmission electron micrograph of the holey gold foil. The arrows show the pitch of the regular hexagonal pattern. (E) Transmission electron micrograph of a single hole in the nanocrystalline foil. The roundness of the 200 nm hole is improved by reducing the gold grain size to 10 nm or less, which can be achieved by deposition onto a cooled template (Fig. S19). (F) Low-dose transmission electron micrograph, at 1.5 μm defocus, of the protein DPS (223 kDa) vitrified on a hexAuFoil grid with 260 nm holes

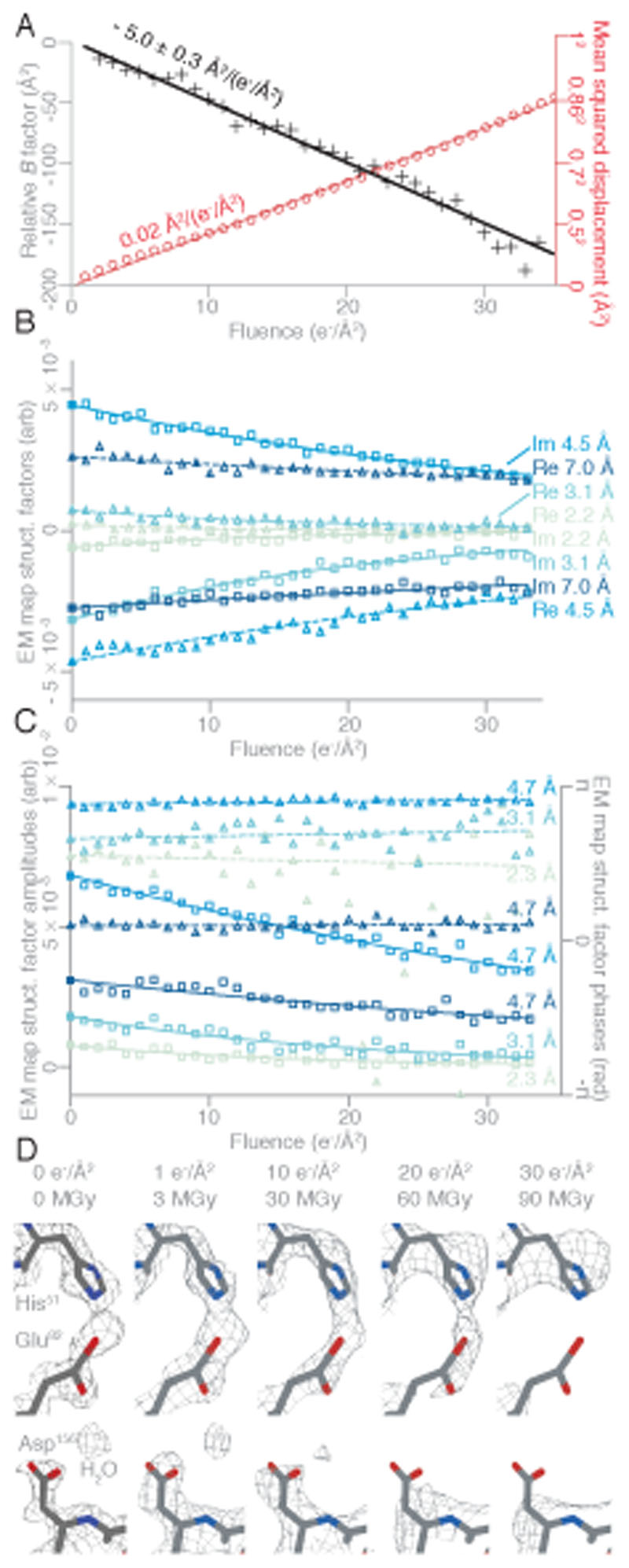
To demonstrate the use of movement-free specimen supports for high-resolution cryoEM, we determined the structure of the 223 kDa DNA protection during starvation protein (DPS) (20), plunge frozen on grids with 280 Å thick gold foil with 260 nm holes (Fig. 3F, S20-S22). The average resolution from an initial reconstruction from about 9 hours of automated data collection on a modern 300 keV microscope, easily reached ˂2 Å and the total particle displacement was 0.86 Å RMS in 35 e⁻/ Ų of irradiation (Fig. 4A, S23, Supplementary Text). The absence of buckling also ensured no tilting of the particles occured during imaging. In contrast to all previous sub-2 Å resolution single particle cryoEM datasets to date (Supplementary Text), maps reconstructed from each frame, show the first frame (1 e⁻/ Ų or 3 MGy) contains the most structural information (Fig. 4A) and the quality (B-factor) of sequential frames decays linearly with dose / fluence. A linear decay in B-factor with dose is expected from studies of radiation damage in X-ray and electron crystallography (21, 22) but had never been observed for single particle cryoEM due to movement of the specimen at the onset of irradiation.

Fig. 4. Structure of DPS determined at ˂2 Å resolution by extrapolation to zero dose with the use of a 260 nm hole support.

(A) Plot of the mean squared displacement during irradiation (red) for all DPS particles used in the reconstruction, and the relative B-factor for each frame with respect to the first (black) with linear fits to both. The displacement of the particles corresponds to diffusion with a constant of 0.02 Ų/(e⁻/ Ų) (red line). The B-factor decay which agrees with the expected slope from radiation damage alone (32). (B) The real (triangles) and imaginary (squares) parts of selected Fourier pixels are plotted as a function of fluence. (C) The phases (triangles) and amplitudes (squares) of selected Fourier pixels (at 2.3 Å, 3.1 Å, and two different pixels at 4.7 Å resolution) are plotted as a function of fluence. The real and imaginary parts (B), or phases and amplitudes (C) are extrapolated to their values before the onset of irradiation, corresponding to the undamaged structure (solid symbols at 0 fluence). The lines in (B) and (C) are exponential fits (to the real parts, imaginary parts, and amplitudes), or linear fits (to the phases). (D) Selected side chains and a water molecule from zero-dose extrapolated and per-frame DPS reconstructions show the progression of radiation damage. The residues from the refined model are colored by atom (C - gray, N - blue, O - red), and the contoured density map is shown as a mesh

Current cryoEM data processing and reconstruction algorithms derive the final reconstructed map by summing the information in each frame, down-weighted to account for movement and damage (23, 24). In contrast, decoupling specimen movement from radiation damage affords new approaches to reconstruction based on the physical theory of how the structure factors decay with exposure, due to mass loss and radiation damage only (Supplementary Text). First, a reconstruction can be calculated from a single frame corresponding to a total fluence of 1 e⁻/ Ų (Supplementary Text, Fig. S24), which is less than the typical dose limit used in X-ray crystallography (10 MGy (25)). Second, the complex structure factors at each pixel in Fourier space can be fit with exponential functions decaying with dose, which extrapolate back to an initial “undamaged” value at zero exposure (Fig. 4B-C). A similar method for amplitudes only was previously proposed, but not widely used in X-ray crystallography (26)). Maps produced by both of these methods show improved densities for radiation sensitive side chains, ordered water molecules and other complexed ions; high-resolution, ˂10 MGy reconstructions avoid potential problems in accurately modelling radiation sensitive parts of biological molecules, and make the per-atom B-factors directly interpretable as movement. Further, the progressive effects of radiation are directly evident in the sequential maps, and can be used to improve atomic modelling techniques and inform understanding of radiation damage (Fig. 4D). After fully removing movement, it is also possible to separate out the effects of other factors that reduce resolution such as particle heterogeneity, and deviation from symmetry (Fig. S22A). Elimination of beam-induced foil and ice movement provides an overall B-factor improvement of 54±10 Ų over motion corrected micrographs for this specimen in the sub-4 Å resolution range (Fig. S22B).

The specimen support described here reduces particle movement in a cryomicrograph to the limit set by pseudo-diffusion, which is on average less than the diameter of a hydrogen atom. This allows reconstruction of a complete map of an undamaged structure at 1.9 Å resolution. We note that interaction of the specimen with the air water interface remains a limitation for cryoEM specimen preparation (3), and can be the dominant factor determining the success of a project (Fig. S22D). Several approaches have been used to address this including adding a surface like functionalized graphene (27–30), and decreasing the time of interaction with surfaces before freezing (31). Both are compatible with the described support and current work is focused on integrating the hexAu-Foil design with other existing technologies and manufacturing the devices at scale. Movement-free imaging will also allow the investigation of lower temperature cryomicroscopy (closer to 0K) where the secondary effects of radiation damage may be further reduced from those at liquid nitrogen tem-peratures, thus affording more contrast per image. With these improvements, cryoEM will continue to rapidly expand our understanding of the structures and functions of biological molecules.

One sentence summary.

Eliminating specimen movement enables higher quality data in electron cryomicroscopy.

Data availability

The entire DPS dataset is publicly available in the Electron Microscopy Public Image Archive (EMPIAR-10445), the final reconstructed maps from each frame and the weighted sum are deposited in the Electron Microscopy Data Bank (EMD-11210), and the refined atomic model - in the Protein Data Bank (PDB-6ZGL). All code for zero dose data processing is freely available from the author’s website, http://www.mrc-lmb.cam.ac.uk/crusso/ and is deposited in Zenodo at https://dx.doi.org/10.5281/zenodo.3944689.