Multiscale modelling and homogenisation of fibre-reinforced hydrogels for tissue engineering

Abstract

Tissue engineering aims to grow artificial tissues in vitro to replace those in the body that have been damaged through age, trauma or disease. A recent approach to engineer artificial cartilage involves seeding cells within a scaffold consisting of an interconnected 3D-printed lattice of polymer fibres combined with a cast or printed hydrogel, and subjecting the construct (cell-seeded scaffold) to an applied load in a bioreactor. A key question is to understand how the applied load is distributed throughout the construct. To address this, we employ homogenisation theory to derive equations governing the effective macroscale material properties of a periodic, elastic–poroelastic composite. We treat the fibres as a linear elastic material and the hydrogel as a poroelastic material, and exploit the disparate length scales (small inter-fibre spacing compared with construct dimensions) to derive macroscale equations governing the response of the composite to an applied load. This homogenised description reflects the orthotropic nature of the composite. To validate the model, solutions from finite element simulations of the macroscale, homogenised equations are compared to experimental data describing the unconfined compression of the fibre-reinforced hydrogels. The model is used to derive the bulk mechanical properties of a cylindrical construct of the composite material for a range of fibre spacings and to determine the local mechanical environment experienced by cells embedded within the construct.

1. Introduction

Tissue engineering is a rapidly developing field where one of the main goals is to generate artificial biological tissues in vitro (e.g. cartilage, bone or blood vessels) [21]. These tissues may then be implanted to replace natural tissues that have degenerated, been damaged, or removed during surgery. A particularly active area of this field is the development of articular cartilage implants as mature cartilage tissue has limited intrinsic capacity to heal. Cartilage damage can occur through injury or diseases such as osteoarthritis, and in the United Kingdom a third of people aged 45 or older have sought treatment for osteoarthritis [1]. Implants must be biocompatible with native cartilage and also able to withstand the mechanically demanding environment of a loaded joint.

A promising direction in cartilage tissue engineering [25] involves seeding cells (mesenchymal stem cells and/or chondrocytes) on a scaffold consisting of an interconnected, 3D-printed lattice of polymer fibres combined with a cast or printed hydrogel; the seeded scaffold is then cultured in a bioreactor with biochemical and mechanical stimulation. Reinforced hydrogel composites are an ideal material for this purpose, since they are biocompatible with cartilage cells and the elastic fibres of the lattice endow the scaffold with greater structural integrity than a scaffold made only of hydrogel [42]. The principle challenge in this approach lies in developing practical strategies that generate artificial cartilage that mimics the form and function of the natural tissue. Mathematical modelling is a valuable tool for quickly and robustly assessing the efficacy of various combinations of cell-seeding strategies, biochemical and mechanical stimuli. The models can thereby guide experimental design; this is of value since these experiments are expensive, timeconsuming and cannot easily be sampled at multiple time points. An important modelling question is to predict the mechanical environment and stress distribution throughout the scaffold as a first step in developing appropriate strategies to seed the scaffold with mechanosensitive cells.

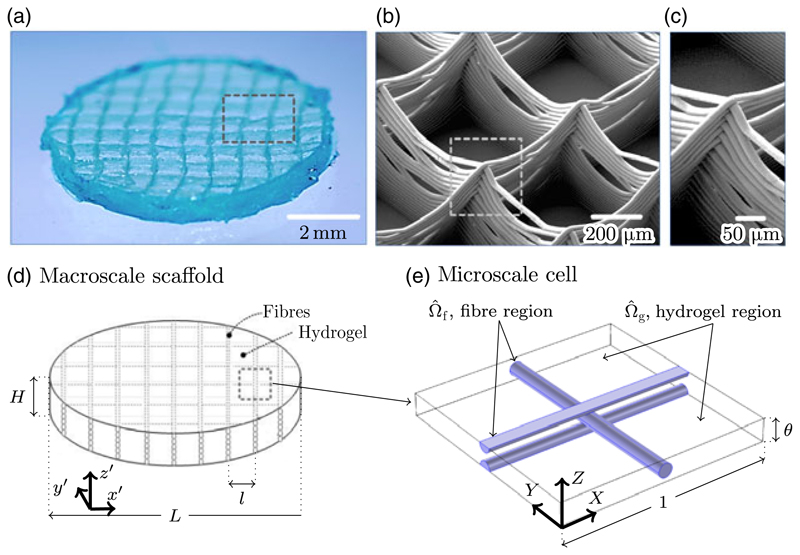
The scaffold of interest in this work comprises a soft gelatin methacrylate (GelMA) hydrogel cast around a 3D-printed, ε-polycapralactone (PCL) fibre lattice, for details see [11, 42]. The fibre lattice is created by melt electrospinning writing (MEW); a layer of parallel fibres at constant spacing is printed and then the next layer of parallel fibres at constant spacing is printed on top of the first layer, so that fibres in neighbouring layers meet at 90°, see Figure 1. The vertical distance between fibres is set by the extent to which each layer of fibres melts into the previous layer. When tested in unconfined compression, these fibre-reinforced scaffolds were shown to be up to 54 times stiffer (i.e. have a 54-fold increase in Young’s modulus) than the hydrogel alone [42]. The cells that are ultimately seeded within the construct are mechanosensitive and will therefore undergo phenotypic changes due to the local stress [28, 40]. Consequently, in order to understand the response of these cells to mechanical loading, it is first necessary to understand the stress induced within the fibre-reinforced hydrogel.

Figure 1.

(a) Optical microscope image of a fibre-reinforced hydrogel with a square fibre lattice of 800 μm. Note that the overall dimensions of the construct shown here are slightly different to those used in later experimental comparison. (b) Scanning electron microscopy (SEM) image of the fibre scaffold prior to it being cast in the hydrogel. (c) SEM image showing a detail of fibre buildup at the interconnection between printed vertical layers. (d) Schematic diagram of the idealised scaffold used in the homogenised model of this paper. (e) Schematic diagram of the microscale repeating cell, showing the microscale hydrogel region Ω̂_g, and the microscale fibre region Ω̂_f. The characteristic length scale at the microscale is the horizontal fibre spacing l, and the characteristic macroscale length is the overall diameter of the scaffold L. It is assumed that the scaffold diameter is much greater than the fibre spacing and that their ratio ε = l/L ≪ 1, which permits a separation of length scales as described in Section 2.3.

The fibre-reinforced hydrogel scaffold described above is an example of a composite material, combining constituent materials with known characteristics to create a new material with properties desirous for a certain application. Composite materials are prevalent in engineering and becoming more widespread in biological applications [16, 19, 43]. A natural approach to model composite materials is via mathematical homogenisation [24], which allows the macroscale response to mechanical loading of a composite material to be determined from the properties of its constituent materials and knowledge of the microstructure.

In the context of modelling the composite material of this paper, mathematical homogenisation involves writing down governing equations for the constituent materials and then exploiting the separation of length scales to decompose the full model into macroscale and periodic microscale components. This, in turn, allows the bulk effective material properties at the macroscale to be derived from the solution to a periodic microscale ‘cell’ problem. Having determined the effective macroscale properties of the material it is possible to predict, for instance, the response of the composite material to an applied mechanical load (which is the focus of this paper). A general introduction to homogenisation theory for composite materials can be found in [24], which systematically describes approaches for treating materials with periodic microstructure for one-, two- and three-dimensional problems. Formal asymptotic and volume averaging approaches to treating the cell problem are compared in [14].

Throughout this work we treat the GelMA hydrogel as a poroelastic material. Porous, fluidsaturated media of this type were originally modelled via a phenomenological description by Biot [7, 8], where deformations of the porous (typically elastic) material are coupled to the flow of the interstitial fluid. This formulation may also be derived rigorously via a formal asymptotic homogenisation procedure [3, 33, 29]. The main advantage of such an approach is that it accounts for interactions between the solid and fluid components at the microscale (for a known microstructure) and therefore obviates the need to fit the material parameters in the Biot model from experimental data. A focus of recent work on poroelasticity has been to improve the computational efficiency of both the upscaling procedure for specific microstructures and the numerical solution of the resulting macroscale equations [4, 10].

Homogenisation is a particularly useful tool in biological contexts, where small-scale structures and multiple spatial scales are ubiquitous. In such conditions it allows tissue-level models to be derived that include cell-level properties. For example, in [39] effective transport coefficients were determined for the delivery of drugs in tumours by homogenising the microscale flow in the small-scale blood vessels within the tumour. A similar approach was used to define criteria for the design of cartilage tissue engineering scaffolds in [38] by tuning the microscale properties of the scaffold to optimise the flow of nutrients. This is different to the homogenisation procedure of this paper since the goal here is to determine bulk effective mechanical properties of the scaffold.

A key aspect of describing natural or engineered tissues is to incorporate the effect of growth. Several recent approaches have addressed this question via homogenisation and poroelasticity. For example, the effective properties of a poroelastic medium with growth due to surface accretion of the solid phase were derived by [34] and lead to a new macroscale constitutive relationship describing this effect. A recent description of an active poroelastic medium [13] incorporated morphoelastic growth and derived effective governing equations under the assumption that growth occurs on a slower timescale than transport processes within the medium, as is typical in biological tissues. Also of interest are recent approaches that extend traditional homogenisation theory to incorporate the novel microstructure that arises in tissue engineering. For instance, one recent study derives an effective description of diffusion for porous media with spatially varying microstructure [9]; another details the homogenisation of reaction–diffusion processes in situations where the microstructure changes with time [35].

Homogenisation approaches have also been used to theoretically study the biomechanics and deformation of plant tissues. In one recent study [37] a macroscale description of the elastic properties and deformation of a plant cell wall was derived by considering the orientation of cellulose microfibrils (i.e. the microstructure) within individual plant cells. Another recent study [36] involves upscaling a coupled description of the microscale biochemical reaction–diffusion processes within plant cells and the mechanical properties of the cells, under the assumption that the elastic deformation of the cells and the dynamics of their internal biochemistry are interdependent.

An alternate approach to modelling fibre-reinforced hydrogels might involve adapting an existing multiphase model of cartilage; see [26] for a comprehensive review of such models. Fibre-reinforced hydrogels have similar mechanical properties to cartilage [42], so it might be argued that we should employ an existing multiphase model. However, the advantage of our homogenisation approach is that it explicitly incorporates the mechanical role of the printed fibres and directly relates the properties of the constituent materials to those of the composite material. This then facilitates the tunable design of scaffolds with the properties required via alterations in the number, spacing and properties of the fibres. Multiphase models have also previously been used to investigate the ways in which the local mechanical environment experienced by mechanosensitive cells in tissue engineering scaffolds influences their behaviour. Such issues were considered in a multiphase porous mixture model by [27] which focussed on various aspects of tissue growth. A key result of that study was to demonstrate that multiphase models can replicate experimentally observed cell aggregation. Another study extends this modelling approach to examine tissue construct growth in a perfusion bioreactor [32] and reveals that mechanotransduction effects induced during the culture period can indeed affect the composition of the resulting engineered tissue.

A recent study on reinforced hydrogel composites with application to cardiac tissue engineering demonstrated that MEW can reproducibly generate fibre lattices and that when cast in hydrogel the resulting scaffolds are biocompatible with cardiac progenitor cells [11]. Another recent study focused on the mechanical characterisation of fibre-reinforced hydrogel scaffolds, measuring the properties of both the overall scaffold and individual PCL fibres; this is of great interest since knowledge of both is required to parameterise the homogenised model of this paper. While finite element modelling of fibre-reinforced hydrogel scaffolds has previously been used to predict their overall mechanical properties [6], the homogenisation approach adopted here is more computationally efficient since it obviates the need to model each individual, repeating cell of the printed fibre lattice and the hydrogel contained within.

As stated above, we aim to understand how an applied load is distributed throughout a fibre-reinforced hydrogel construct to the embedded, mechanosensitive cells. We previously investigated the mechanics of the composite scaffold with a phenomenological model that described the stiffness of the composite [42]. This simple model considered the fibres as stretched, linearly elastic strings, and neglected any rate-dependent features of the material.

Here, we develop a more detailed model that yields greater understanding of the mechanical properties of the composite, including its time-dependent response to loading. By developing governing equations for the stress and deformation of the composite, we develop a framework that may be used to predict the stresses that cells embedded in the scaffold experience. In systematically deriving this macroscale description we incorporate detail of the microstructure (in particular the geometry and spacing of the printed fibres) and the properties of the constituent materials of the composite thus giving a mechanistic description of the effective behaviour of the composite, with a view to revealing properties of this material that would not be known prior to homogenisation. The resulting framework is sufficiently general that it could be adapted to predict the macroscale properties of periodic elastic–poroelastic composites in other applications.

1.1. Paper outline

We formulate a model for the composite material in Section 2, where the fibres are treated as a linear elastic material, and the hydrogel is treated as a poroelastic material. This permits a separation of length scales, since the size of the repeating fibre lattice is much smaller than the size of the overall scaffold. The associated microscale cell problem is described in Section 3. Homogenisation theory is employed in Section 4 to derive macroscale equations which feature effective material parameters determined from the solution to the microscale cell problem, thus determining the nature of the bulk material. This model is validated in Section 5, where numerical solutions of the homogenised equations are compared to unconfined compression tests on reinforced hydrogels. We discuss our results in Section 6, where we also suggest possible future directions to continue this work.

2. Scaffold description and model derivation

We aim to model the response of a fibre-reinforced hydrogel scaffold to an applied load or displacement, as discussed in Section 1, and shown schematically in Figure 1. These scaffolds are typically a few millimetres in height and a comparable dimension in width; our model will later be compared to experimental results where cylindrical scaffolds of height H ≈ 2 mm and diameter L ≈ 5.5 mm are held at a strain of 6%, for instance. Interest lies in the stress and displacement fields induced in this composite material when mechanically loaded.

The material properties of the fibre-reinforced hydrogel, and hence its response to an applied load, will depend on the material properties of the unreinforced hydrogel, as well as the diameter and spacing of the 3D-printed fibres. These diameters and spacings are typically much smaller than the size of the overall construct; for instance, in the experiments of [42] the fibres are of radius 20 μm and printed at fibre spacings between 200 μm and 1 mm. The vertical fibre spacing is difficult to determine since there is an unknown degree of melting between adjacent printed layers. In later simulations we estimate that melting results in significant overlap between the layers so that the gap between parallel fibres is 60% of the fibre radius.

The following section details a homogenisation procedure to derive effective macroscale material properties of the reinforced construct, allowing us to calculate the stress and displacement within this composite material due to an applied load. We begin by developing sub-models for the two constituents of the composite viewing the hydrogel as a poroelastic material, occupying a region denoted Ω_g, and the PCL fibres as linearly elastic, occupying a region denoted Ω_f. The difference between the overall size of the construct and the spacing between the fibres permits a separation of length-scales. We exploit this property together with the periodicity of the geometry of the fibre scaffold to homogenise over one ‘cell’ of the scaffold (see Figure 1) and obtain the desired description of this composite material.

2.1. Sub-models for the hydrogel and the elastic fibres

Following Detournay and Cheng [15], we describe the hydrogel as a poroelastic material comprised of incompressible fluid and elastic phases. In the hydrogel region Ω_g we have conservation of mass and assume that the flow of the fluid phase is governed by Darcy’s law. Thus, we write

$$\varphi \nabla \cdot v^{\prime }+\left(1-\varphi \right)\frac{\partial }{\partial t}\left(\nabla \cdot {\mathbf{\text{u}}}_{\text{g}}^{\prime }\right)=0,$$ (2.1)

$$\varphi \left(v^{\prime }-\frac{\partial {\mathbf{\text{u}}}_{\text{g}}^{\prime }}{\partial t^{\prime }}\right)=-\frac{k^{\prime }}{{\mu }^{\prime }}\nabla p^{\prime },$$ (2.2)

where ${\mathbf{\text{u}}}_{\text{g}}^{\prime }$ is the displacement of the solid phase, v′ is the velocity of the fluid phase and p′ is the fluid pressure. Equations (2.1) and (2.2) contain several (constant) parameters, namely the volume fraction of the fluid phase, ϕ (sometimes called the porosity), the intrinsic permeability of the solid phase, k′, and the viscosity of the fluid phase, μ′; the ratio of these last two parameters, k′/μ′, represents the effective permeability of the poroelastic material. Typical values for these parameters for the hydrogel of interest, GelMA, are given in Table 1 where these were obtained by fitting data from experimental relaxation tests on unreinforced GelMA to a model of a poroelastic material. A full description of this fitting procedure is given in Appendix A. We also require conservation of momentum in the hydrogel and introduce a constitutive relationship between the displacement and the stress. Following [24], these relationships are represented by

$$\nabla \cdot {\sigma }_{\text{g}}^{\prime }=0,$$ (2.3)

$${\sigma }_{\text{g}}^{\prime }=-p^{\prime }\mathbf{\text{I}}+{𝔻}^{\prime }:\nabla {\mathbf{\text{u}}}_{\text{g}}^{\prime },$$ (2.4)

$${𝔻}^{\prime }:\nabla {\mathbf{\text{u}}}_{\text{g}}^{\prime }={\mu }_{\text{g}}^{\prime }\left(\nabla {\mathbf{\text{u}}}_{\text{g}}^{\prime }+{\left(\nabla {\mathbf{\text{u}}}_{\text{g}}^{\prime }\right)}^T\right)+{\lambda }_{\text{g}}^{\prime }\left(\nabla \cdot {\mathbf{\text{u}}}_{\text{g}}^{\prime }\right)\mathbf{\text{I}},$$ (2.5)

where ${\mathbf{\sigma }}_{\text{g}}^{\prime }$ is the stress tensor (rank 2) in the hydrogel and 𝔻′ is the elasticity tensor (rank 4) for the solid phase of the hydrogel. Throughout this paper we follow the conventions for tensor products and derivatives given in [23, Chapter 1], which also defines these conventions in Einstein notation. In the constitutive relationship (2.4)–(2.5) we assume that the solid phase is linearly elastic, where ${\mu }_{\text{g}}^{\prime }$ and ${\lambda }_{\text{g}}^{\prime }$ are the bulk Lamé parameters of the poroelastic material (which are both assumed to be constant). The fitted values of these parameters for GelMA derived in Appendix A are given in Table 1; the corresponding values for the Young’s modulus $E_{\text{g}}^{\prime }$ and Poisson’s ratio ν _g of the elastic phase of the hydrogel, which relate to the Lamé parameters in the standard way, are also given in Appendix A.

Table 1.

Summary of dimensional parameters that appear in equations (2.1)–(2.11), along with the parameters used in the non-dimensionalisation procedure in Section 2.2

Quantity	Description	Representative value
ϕ	Porosity (GelMA)	(Later eliminated from model)
k′/μ′	Effective permeability (GelMA)	2.382 × 10–4 kPa–1 min–1 (Appendix A)
${\mu }_{\text{g}}^{\prime }$	Lamé’s first parameter (GelMA)	19.97 kPa (Appendix A)
${\lambda }_{\text{g}}^{\prime }$	Lamé’s second parameter (GelMA)	17.01 kPa (Appendix A)
${\mu }_{\text{f}}^{\prime }$	Lamé’s first parameter (PCL)	1.27 × 105kPa [12]
${\lambda }_{\text{f}}^{\prime }$	Lamé’s second parameter (PCL)	7.80 × 105kPa [12]
L	Overall diameter of scaffold	5.54–5.98 mm
H	Overall height of scaffold	1.80–2.04 mm
d	Fibre diameter	20 μm
l	Horizontal fibre spacing	300–800 μm
h	Vertical fibre spacing	32 μm
ϵ = l/L	Small parameter	5.0 × 10–2–1.4 × 10–1
T	Typical test time	1 min
P	Typical stress in hydrogel	1.67 × 104kPa

We model the PCL fibres as a linear elastic material. It is therefore straightforward to relate the stress and displacement in the fibre region Ω_f by requiring conservation of momentum and introducing an appropriate constitutive law. Following [24], for instance, we assume

$$\nabla \cdot {\sigma }_{\text{f}}^{\prime }=0,$$ (2.6)

$${\sigma }_{\text{f}}^{\prime }={ℂ}^{\prime }:\nabla {\mathbf{\text{u}}}_{\text{f}}^{\prime },$$ (2.7)

$${ℂ}^{\prime }:\nabla {\mathbf{\text{u}}}_{\text{f}}^{\prime }={\mu }_{\text{f}}^{\prime }\left(\nabla {\mathbf{\text{u}}}_{\text{f}}^{\prime }+{\left(\nabla {\mathbf{\text{u}}}_{\text{f}}^{\prime }\right)}^T\right)+{\lambda }_{\text{f}}^{\prime }\left(\nabla \cdot {\mathbf{\text{u}}}_{\text{f}}^{\prime }\right)\mathbf{\text{I}},$$ (2.8)

where ${\sigma }_{\text{f}}^{\prime }$ is the stress tensor (rank 2) in the fibres, ${\mathbf{\text{u}}}_{\text{f}}^{\prime }$ is the displacement in the fibre region and ℂ′ is the elasticity tensor (rank 4). In the constitutive relationship (2.7)–(2.8) ${\mu }_{\text{f}}^{\prime }$ and ${\lambda }_{\text{f}}^{\prime }$ are the (constant) Lamé parameters of this material. The values for PCL in Table 1 are taken from [12], and converted from the Young’s modulus $E_{\text{f}}^{\prime }$ = 363 MPa and Poisson’s ratio ν _f = 0.3 given in that study to Lamé parameters via equation (A1). As noted in Appendix A, published values for the Young’s modulus E _f vary between 53 and 363 MPa [5, 42, 41, 12] and published values of the Poisson’s ratio ν _f vary between 0.3 and 0.49 [17, 18, 12]. Thus, the values for the Lamé parameters of PCL given in Table 1 reflect the order of magnitude of these parameters; during later experimental comparison we will explore the parameter space defined by these published values.

We further assume that the fibres are perfectly bonded to the hydrogel, so that there are no voids between the fibre and gel regions. On the interface between the fibre and gel regions (denoted ∂Ω_f = ∂Ω_g) we impose continuity of stress and displacement, as well as a kinematic condition on the fluid velocity. These boundary conditions are

$${\sigma }_{\text{g}}^{\prime }\cdot \mathbf{\text{n}}={\sigma }_{\text{f}}^{\prime }\cdot \mathbf{\text{n}},$$ (2.9)

$${\mathbf{\text{u}}}_{\text{g}}^{\prime }={\mathbf{\text{u}}}_{\text{f}}^{\prime },$$ (2.10)

$$\left(v^{\prime }-\frac{\partial {\mathbf{\text{u}}}_{\text{g}}^{\prime }}{\partial t^{\prime }}\right)\cdot \mathbf{\text{n}}=0,$$ (2.11)

on ∂Ω_f = ∂Ω_g, where n is the outward pointing unit normal vector to Ω_f. Note that the kinematic condition (2.11) has the usual interpretation here, namely that at the interface between the poroelastic and elastic materials there is no fluid flow, relative to the gel, in the direction normal to this interface and, therefore, no fluid transport across this material boundary.

To summarise, the equations governing the constituent parts of this composite material consist of (2.1)–(2.5) to be solved in the poroelastic hydrogel region Ω_g, and (2.6)–(2.8) to be solved in the elastic PCL fibre region Ω_f, subject to the boundary conditions (2.9)–(2.11) on the interface between these regions ∂Ω_f = ∂Ω_g. We note that it is possible to reduce (2.1)–(2.5) to the more standard form of the Biot model for poroelastic media [8] by combining (2.1) and (2.2) to eliminate v, and substituting (2.4) into (2.3). The slightly longer form of the governing equations is retained here since it will (in Section 4) permit the explicit derivation of the effective macroscale fluid velocity and stress. Both of these quantities are of practical interest in tissue engineering to quantify the flow of nutrients through the scaffold and the local stress experienced by seeded cells.

2.2. Non-dimensionalisation

We define L to be the typical diameter of a sample of the fibre-reinforced composite and l to be the horizontal spacing between the printed fibres. In situations of practical interest the fibre spacing is small compared to the overall size of the composite and so we introduce the small parameter ε as

$$\epsilon =\frac{l}{L}\ll 1.$$ (2.12)

We non-dimensionalise equations (2.1)–(2.11), scaling lengths with the typical diameter of the fibre-reinforced scaffold, L, time with a typical timescale for mechanical testing the composite, T, and stresses with a typical pressure in the fluid phase of the hydrogel, P = μ′ L ²/(k′T). The dimensional variables (indicated by dashes) are replaced by dimensionless versions as follows:

$$\begin{array}{llll}{\mathbf{\text{u}}}_{\text{g}}^{\prime }=L{\mathbf{\text{u}}}_{\text{g}},\hfill & {\mathbf{\text{u}}}_{\text{f}}^{\prime }=L{\mathbf{\text{u}}}_{\text{f}},\hfill & p^{\prime }=Pp,\hfill & t^{\prime }=Tt,\hfill \\ {\sigma }_{\text{g}}^{\prime }=P{\sigma }_{\text{g}},\hfill & {\sigma }_{\text{f}}^{\prime }=P{\sigma }_{\text{f}},\hfill & x^{\prime }=L\mathbf{\text{x}},\hfill & v^{\prime }=\left(L/T\right)\mathbf{\text{v}},\hfill \end{array}$$ (2.13)

and the dimensional parameters are rescaled as follows:

$${𝔻}^{\prime }=P𝔻,{\mu }_{\text{g}}^{\prime }=P{\mu }_{\text{g}},{\lambda }_{\text{g}}^{\prime }=P{\lambda }_{\text{g}},$$ (2.14)

$${ℂ}^{\prime }=Pℂ,{\mu }_{\text{f}}^{\prime }=P{\mu }_{\text{f}},{\lambda }_{\text{f}}^{\prime }=P{\lambda }_{\text{f}}.$$ (2.15)

Under these scalings the dimensionless versions of equations (2.1)–(2.2), which represent conservation of mass and Darcy’s law in the hydrogel region Ω_g, are

$$\varphi \nabla \cdot \mathbf{\text{v}}+\left(1-\varphi \right)\frac{\partial }{\partial t}\left(\nabla \cdot {\mathbf{\text{u}}}_{\text{g}}\right)=0,$$ (2.16)

$$\varphi \left(\mathbf{\text{v}}-\frac{\partial {\mathbf{\text{u}}}_{\text{g}}}{\partial t}\right)=-\nabla p,$$ (2.17)

while equations (2.3)–(2.5), which govern conservation of momentum and the constitutive relationship, transform to give (2.18)–(2.20):

$$\nabla \cdot {\sigma }_{\text{g}}=0,$$ (2.18)

$${\sigma }_{\text{g}}=-p\mathbf{\text{I}}+𝔻:\nabla {\mathbf{\text{u}}}_{\text{g}},$$ (2.19)

$$𝔻:\nabla {\mathbf{\text{u}}}_{\text{g}}={\mu }_{\text{g}}\left(\nabla {\mathbf{\text{u}}}_{\text{g}}+{\left(\nabla {\mathbf{\text{u}}}_{\text{g}}\right)}^T\right)+{\lambda }_{\text{g}}\left(\nabla \cdot {\mathbf{\text{u}}}_{\text{g}}\right)\mathbf{\text{I}}.$$ (2.20)

In the elastic fibre region Ω_f the dimensionless versions of conservation of momentum and the constitutive relationship (2.6)–(2.8) are

$$\nabla \cdot {\sigma }_{\text{f}}=0,$$ (2.21)

$${\sigma }_{\text{f}}=ℂ:\nabla {\mathbf{\text{u}}}_{\text{f}},$$ (2.22)

$$ℂ:\nabla {\mathbf{\text{u}}}_{\text{f}}={\mu }_{\text{f}}\left(\nabla {\mathbf{\text{u}}}_{\text{f}}+{\left(\nabla {\mathbf{\text{u}}}_{\text{f}}\right)}^T\right)+{\lambda }_{\text{f}}\left(\nabla \cdot {\mathbf{\text{u}}}_{\text{f}}\right)\mathbf{\text{I}}.$$ (2.23)

Finally boundary conditions (2.9)–(2.11) transform to give

$${\sigma }_{\text{g}}\cdot \mathbf{\text{n}}={\sigma }_{\text{f}}\cdot \mathbf{\text{n}},$$ (2.24)

$${\mathbf{\text{u}}}_{\text{g}}={\mathbf{\text{u}}}_{\text{f}},$$ (2.25)

$$\left(\mathbf{\text{v}}-\frac{\partial {\mathbf{\text{u}}}_{\text{g}}}{\partial t}\right)\cdot \mathbf{\text{n}}=0,$$ (2.26)

on ∂Ω_f = ∂Ω_g.

2.3. Description of the microscale cell and separation of length scales

Having established the dimensionless governing equations and boundary conditions (2.16)– (2.26) we could, given sufficient computing resources, solve these equations numerically in the complex interpenetrating geometry defined by Ω_f and Ω_g. Instead we exploit the periodic geometry and the small size of the repeating ‘cell’ compared to that of the composite (i.e. 0 < ε ≪ 1). After non-dimensionalisation, typical lengths of the composite scaffold are x = 𝒪(1); we henceforth term this the macroscale variable. We introduce the microscale variable X = x/ε, so that X = 𝒪(1) is the length scale associated with the repeating cell. The presence of these disparate length scales suggests that it is appropriate to attempt an asymptotic separation of length scales.

The geometry of the microscale repeating cell is shown in Figure 1(e), with the orientation of the three components of X = (X, Y, Z) also indicated in this schematic diagram. The domain of a single cell is, in microscale variables, 0 ⩽ X ⩽ 1, 0 ⩽ Y ⩽ 1, 0 ⩽ Z ⩽ θ, where θ = h/l is the dimensionless microscale height of the cell. Within this cell there is a central cylinder of non-dimensional radius ρ, with its axis along (X = 0.5, Z = θ/2), representing a single printed PCL fibre. The fibres printed in the adjacent layers are perpendicular to this direction and, in order to maintain periodicity in the Z direction, are represented in the microscale cell as two half cylinders, each with non-dimensional radius ρ = d/(2l). The axis of one of the halfcylinders lies along the bottom of the cell at (Y = 0.5, Z = 0), while the axis of the other lies along the top of the cell at (Y = 0.5, Z = θ). The printed fibres overlap in the centre of the representative cell, where the adjacent layers have melted into each other and bonded. From the arrangement shown in Figure 1(e), it follows that θ/(4ρ) is a measure of the overlap between the fibres; this quantity is equal to 1 if adjacent fibre layers are just touching, and equal to 1/2 if they completely overlap. The union of the cylinder and the two overlapping half cylinders forms the microscale elastic fibre region Ω̂_f. The complement of Ω̂_f in this representative cell is the microscale hydrogel region Ω̂_g.

Following [34], we consider that all dependent variables are functions of x and X, so that e.g. u _f = u _f(x, X, t), and treat x and X as independent variables, in which case $\nabla \to {\nabla }_x+\frac{1}{\epsilon }{\nabla }_X$. We also introduce regular perturbation series expansions in ε for each dependent variable, so that ${\mathbf{\text{u}}}_{\text{f}}={\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}+\epsilon {\mathbf{\text{u}}}_{\text{f}}^{\left(1\right)}+\mathcal{O}\left({\epsilon }^2\right)$ and similarly for u _g and p. Substitution of these series expansions into (2.19) and (2.22) implies that the leading order term for the stresses must be at $\mathcal{O}\left(\frac{1}{\epsilon }\right)$, so that ${\mathbf{\sigma }}_{\text{f}}=\frac{1}{\epsilon }{\mathbf{\sigma }}_{\text{f}}^{\left(-1\right)}+{\mathbf{\sigma }}_{\text{f}}^{\left(0\right)}+\epsilon {\mathbf{\sigma }}_{\text{f}}^{\left(1\right)}+\mathcal{O}\left({\epsilon }^2\right)$ and similarly for σ _g Under these assumptions (2.18) and (2.21) supply at $\mathcal{O}\left(\frac{1}{{\epsilon }^2}\right)$ the following equations:

$${\nabla }_X\cdot {\sigma }_{\text{g}}^{(-1)}={\nabla }_X\cdot \left(𝔻:{\nabla }_X{\mathbf{\text{u}}}_{\text{g}}^{(0)}\right)=0,\text{in}{\Omega }_{\text{g}},$$ (2.27)

$${\nabla }_X\cdot {\sigma }_{\text{f}}^{(-1)}={\nabla }_X\cdot \left(ℂ:{\nabla }_X{\mathbf{\text{u}}}_{\text{f}}^{(0)}\right)=0,\text{in}{\Omega }_{\text{f}},$$ (2.28)

where we have substituted the $\mathcal{O}\left(\frac{1}{\epsilon }\right)$ components of stress from (2.19) and (2.22) into (2.27) and (2.28), respectively. On the interface ∂Ω_f the boundary conditions (2.24) at $\mathcal{O}\left(\frac{1}{\epsilon }\right)$ and (2.25) at 𝒪(1) supply

$$\left(𝔻:{\nabla }_X{\mathbf{\text{u}}}_{\text{g}}^{\left(0\right)}\right)\cdot \mathbf{\text{n}}=\left(\text{ℂ}:{\nabla }_X{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}\right)\cdot \mathbf{\text{n}},$$ (2.29)

$${\mathbf{\text{u}}}_{\text{g}}^{\left(0\right)}={\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)},$$ (2.30)

where we have used the expressions for the $\mathcal{O}\left(\frac{1}{\epsilon }\right)$ stresses in (2.29). We note that (2.27) and (2.28) define linear homogeneous problems for ${\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}\text{and}{\mathbf{\text{u}}}_{\text{g}}^{\left(0\right)}$ and that there is no external forcing from the boundary conditions (2.29)–(2.30). It follows that ${\nabla }_X{\mathbf{\text{u}}}_{\text{g}}^{\left(0\right)}={\nabla }_X{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}=0$ and so both ${\mathbf{\text{u}}}_{\text{g}}^{\left(0\right)}\text{and}{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}$ are independent of X, and therefore ${\mathbf{\sigma }}_{\text{g}}^{\left(-1\right)}={\mathbf{\sigma }}_{\text{f}}^{\left(-1\right)}=0$. Continuity of displacement on the cell-scale interface $\partial {\widehat{\Omega }}_{\text{f}}$ at leading order (2.30) implies that ${\mathbf{\text{u}}}_{\text{g}}^{\left(0\right)}\left(\mathbf{\text{x}},t\right)={\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}\left(\mathbf{\text{x}},t\right)$.

In the hydrogel region Ω_g, we see that (2.16)–(2.19) supply at $\mathcal{O}\left(\frac{1}{\epsilon }\right)$ the following equations:

$$\varphi \left({\nabla }_X\cdot {\mathbf{\text{v}}}^{\left(0\right)}\right)=0,$$ (2.31)

$${\nabla }_X{p}^{\left(0\right)}=0,\Rightarrow p^{\left(0\right)}\equiv p^{\left(0\right)}\left(\mathbf{\text{x}},t\right),$$ (2.32)

$${\nabla }_X\cdot {\sigma }_{\text{g}}^{\left(0\right)}=0,$$ (2.33)

where, as noted above, equation (2.32) implies that p ⁽⁰⁾ is independent of X. In the fibre region Ω_f, equation (2.21) at $\mathcal{O}\left(\frac{1}{\epsilon }\right)$ supplies

$${\nabla }_X\cdot {\sigma }_{\text{f}}^{\left(0\right)}=0,$$ (2.34)

while on ∂Ω_f boundary conditions (2.24) and (2.26) at 𝒪(1) supply

$${\sigma }_{\text{g}}^{\left(0\right)}\cdot \mathbf{\text{n}}={\sigma }_{\text{f}}^{\left(0\right)}\cdot \mathbf{\text{n}},$$ (2.35)

$$\left({\mathbf{\text{v}}}^{\left(0\right)}-\frac{\partial {\mathbf{\text{u}}}_{\text{g}}^{\left(0\right)}}{\partial t}\right)\cdot \mathbf{\text{n}}=0.$$ (2.36)

In the hydrogel region Ω_g, at 𝒪(1) equations (2.16) – (2.19) supply

$$\left(1-\varphi \right)\frac{\partial }{\partial t}\left({\nabla }_x\cdot {\mathbf{\text{u}}}_{\text{g}}^{\left(0\right)}\right)+\varphi {\nabla }_x\cdot {\mathbf{\text{v}}}^{\left(0\right)}=-\left(1-\varphi \right)\frac{\partial }{\partial t}\left({\nabla }_X\cdot {\mathbf{\text{u}}}_{\text{g}}^{\left(1\right)}\right)-\varphi {\nabla }_X\cdot {\mathbf{\text{v}}}^{\left(1\right)},$$ (2.37)

$$\varphi \left({\mathbf{\text{v}}}^{\left(0\right)}-\frac{\partial {\mathbf{\text{u}}}_{\text{g}}^{\left(0\right)}}{\partial t}\right)=-{\nabla }_x{p}^{\left(0\right)}-{\nabla }_X{p}^{\left(1\right)},$$ (2.38)

$${\nabla }_x\cdot {\sigma }_{\text{g}}^{\left(0\right)}+{\nabla }_X\cdot {\sigma }_{\text{g}}^{\left(1\right)}=0,$$ (2.39)

$${\sigma }_{\text{g}}^{\left(0\right)}=-p^{\left(0\right)}\mathbf{\text{I}}+𝔻:\left({\nabla }_x{\mathbf{\text{u}}}_{\text{g}}^{\left(0\right)}+{\nabla }_X{\mathbf{\text{u}}}_{\text{g}}^{\left(1\right)}\right).$$ (2.40)

In the fibre region Ω_f, at 𝒪(1) equation (2.22) supplies

$${\nabla }_x\cdot {\sigma }_{\text{f}}^{\left(0\right)}+{\nabla }_X\cdot {\sigma }_{\text{f}}^{\left(1\right)}=0,$$ (2.41)

$${\sigma }_{\text{f}}^{\left(0\right)}=ℂ:\left({\nabla }_x{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}+{\nabla }_X{\mathbf{\text{u}}}_{\text{f}}^{\left(1\right)}\right),$$ (2.42)

while on ∂Ω_f the boundary conditions (2.24)–(2.26) supply at 𝒪(ε)

$${\sigma }_{\text{g}}^{\left(1\right)}\cdot \mathbf{\text{n}}={\sigma }_{\text{f}}^{\left(1\right)}\cdot \mathbf{\text{n}},$$ (2.43)

$${\mathbf{\text{u}}}_{\text{g}}^{\left(1\right)}={\mathbf{\text{u}}}_{\text{f}}^{\left(1\right)},$$ (2.44)

$$\left({\mathbf{\text{v}}}^{\left(1\right)}-\frac{\partial {\mathbf{\text{u}}}_g^{\left(1\right)}}{\partial t}\right)\cdot \mathbf{\text{n}}=0.$$ (2.45)

3. Definition of cell problems

Having established that the leading order displacements ${\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}\text{and}{\mathbf{\text{u}}}_{\text{g}}^{\left(0\right)}$ are independent of the microscale, we now obtain the equations that govern the microscale variation at 𝒪(ε) in the displacements. Periodicity enables us to understand the microscale behaviour by considering a single repeating cell. We identify the restriction of Ω_f to the single repeating cell by ${\widehat{\Omega }}_{\text{f}}$ and likewise ${\widehat{\Omega }}_{\text{g}}$ is the restriction of Ω_g to the single repeating cell. To be clear, $\partial {\widehat{\Omega }}_{\text{f}}$ identifies the interface between Ω_f and Ω_g found within a single repeating cell. An example of this cell geometry is shown in Figure 1(d).

Substituting (2.40) into (2.33) and (2.42) into (2.34), and recalling that the leading order displacements and pressure are independent of X, we obtain

$$\begin{array}{cc}{\nabla }_X\cdot \left(𝔻:{\nabla }_X{\mathbf{\text{u}}}_{\text{g}}^{\left(1\right)}\right)=0,& \text{in}{\widehat{\Omega }}_{\text{g}}\end{array},$$ (3.1)

$$\begin{array}{cc}{\nabla }_X\cdot \left(ℂ:{\nabla }_X{\mathbf{\text{u}}}_{\text{f}}^{\left(1\right)}\right)=0,& \text{in}{\widehat{\Omega }}_{\text{f}},\end{array}$$ (3.2)

subject to the continuity of stress and displacement conditions given by equations (2.35) and (2.44) on the cell-scale interface ∂Ω̂_f

$$\left(ℂ:{\nabla }_X{\mathbf{\text{u}}}_{\text{f}}^{\left(1\right)}-𝔻:{\nabla }_X{\mathbf{\text{u}}}_{\text{g}}^{\left(1\right)}\right)\cdot \mathbf{\text{n}}=-p^{\left(0\right)}\mathbf{\text{n}}-\left(ℂ:{\nabla }_x{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}-𝔻:{\nabla }_x{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}\right)\cdot \mathbf{\text{n}},$$ (3.3)

$${\mathbf{\text{u}}}_{\text{f}}^{\left(1\right)}={\mathbf{\text{u}}}_{\text{g}}^{\left(1\right)}.$$ (3.4)

Boundary conditions on the surface of the repeating cell are provided by requiring ${\mathbf{\text{u}}}_{\text{f}}^{\left(1\right)}\text{and}{\mathbf{\text{u}}}_{\text{g}}^{\left(1\right)}$ to be periodic, with one additional boundary condition required to remove the translational freedom which is later set by requiring that various components of the microscale solution have zero mean on the microscale.

We note that equations (3.1) and (3.2) define linear homogeneous problems, subject only to linear forcing by the leading order displacement, ${\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}$, and the leading order pressure, p ⁽⁰⁾, via the Neumann boundary condition (3.3). Hence, their solutions are of the form

$${\mathbf{\text{u}}}_{\text{g}}^{\left(1\right)}=\mathbf{\text{r}}\left(\mathbf{\text{x}}\right)p^{\left(0\right)}+ℬ\left(\mathbf{\text{x}}\right):{\nabla }_x{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)},$$ (3.5)

$${\mathbf{\text{u}}}_{\text{f}}^{\left(1\right)}=\mathbf{\text{q}}\left(\mathbf{\text{x}}\right)p^{\left(0\right)}+\mathcal{A}\left(\mathbf{\text{x}}\right):{\nabla }_x{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)},$$ (3.6)

where r and q are vectors and 𝓑 and 𝒜 are rank 3 tensors. The solutions (3.5) and (3.6) are substituted into (3.1) and (3.2), respectively, and it follows from the linearity of (3.1) and (3.2) that

$$\begin{array}{cc}\left({\lambda }_{\text{g}}+{\mu }_{\text{g}}\right){\nabla }_X\left({\nabla }_X\cdot \mathbf{\text{r}}\right)+{\mu }_{\text{g}}{\nabla }^2\mathbf{\text{r}}=0,& \text{in}{\hat{\Omega }}_{\text{g}},\end{array}$$ (3.7)

$$\begin{array}{cc}\left({\lambda }_{\text{f}}+{\mu }_{\text{f}}\right){\nabla }_X\left({\nabla }_X\cdot \mathbf{\text{q}}\right)+{\mu }_{\text{f}}{\nabla }^2\mathbf{\text{q}}=0,& \text{in}{\hat{\Omega }}_{\text{f}},\end{array}$$ (3.8)

where we have exploited the constitutive (linearly elastic) assumptions for 𝔻 and ℂ, specified by equations (2.20) and (2.23), respectively. On the interface between the component materials equations (3.7)–(3.8) for r and q are subject to the boundary conditions

$$\begin{array}{cc}\left(ℂ:{\nabla }_X\mathbf{\text{q}}-𝔻:{\nabla }_X\mathbf{\text{r}}\right)\cdot \mathbf{\text{n}}=-\mathbf{\text{n}},& \text{on}\partial {\hat{\Omega }}_{\text{f}},\end{array}$$ (3.9)

$$\begin{array}{cc}\mathbf{\text{q}}=\mathbf{\text{r}},& \text{on}\partial {\hat{\Omega }}_{\text{f}}.\end{array}$$ (3.10)

We additionally require that r and q are periodic in X, and that

$${\displaystyle {\iiint }_{{\widehat{\Omega }}_g}\mathbf{\text{r}}\text{d}V}+{\displaystyle {\iiint }_{{\widehat{\Omega }}_{\text{f}}}\mathbf{\text{q}}}\text{d}V=0,$$ (3.11)

where dV is the volume element with respect to the microscale variables, so that the solution has zero mean on the microscale. We note that equations (3.7)–(3.11) for r and q define a linear elasticity problem on the repeating cell in which deformations in the gel region Ω̂_g and the fibre region Ω̂_f are coupled and caused by a jump in stress at the interface between Ω̂_g and Ω̂_f.

A similar procedure is applied to obtain governing equations for 𝓑 and 𝒜. We first rewrite the components of each rank 3 tensor in a vectorised form as

$${\mathbf{\text{b}}}^{\left(mn\right)}={ℬ}_{imn}{\mathbf{\text{e}}}_i,\text{and}{\mathbf{\text{a}}}^{\left(mn\right)}={\mathcal{A}}_{imn}{\mathbf{\text{e}}}_i,$$ (3.12)

where e _i are the Cartesian basis vectors, m, n = 1, 2, 3, and we sum over the repeated index i. Substituting these vectorised forms into (3.1) and (3.2), and exploiting the linearity of these problems, we obtain

$$\begin{array}{cc}\left({\lambda }_{\text{g}}+{\mu }_{\text{g}}\right){\nabla }_X\left({\nabla }_X\cdot {\mathbf{\text{b}}}^{\left(mn\right)}\right)+{\mu }_{\text{g}}{\nabla }^2{\mathbf{\text{b}}}^{\left(mn\right)}=0,& \text{in}{\hat{\Omega }}_{\text{g}},\end{array}$$ (3.13)

$$\begin{array}{cc}\left({\lambda }_{\text{f}}+{\mu }_{\text{f}}\right){\nabla }_X\left({\nabla }_X\cdot {\mathbf{\text{a}}}^{\left(mn\right)}\right)+{\mu }_{\text{f}}{\nabla }^2{\mathbf{\text{a}}}^{\left(mn\right)}=0,& \text{in}{\hat{\Omega }}_{\text{f}},\end{array}$$ (3.14)

where we have again made use of the constitutive assumptions (2.20) and (2.23). On the interface between the component materials, these problems for b ^(mn) and a ^(mn) are subject to the boundary conditions

$$\begin{array}{cc}\left(ℂ:{\nabla }_X{\mathbf{\text{a}}}^{\left(mn\right)}-𝔻:{\nabla }_X{\mathbf{\text{b}}}^{\left(mn\right)}\right)\cdot \mathbf{\text{n}}=-\left(ℂ:{\mathbf{\text{I}}}^{\left(mn\right)}-𝔻:{\mathbf{\text{I}}}^{\left(mn\right)}\right)\cdot \mathbf{\text{n}},& \text{on}\partial {\hat{\Omega }}_{\text{f}},\end{array}$$ (3.15)

$$\begin{array}{cc}{\mathbf{\text{b}}}^{\left(mn\right)}={\mathbf{\text{a}}}^{\left(mn\right)},& \text{on}\partial {\hat{\Omega }}_{\text{f}},\end{array}$$ (3.16)

where I ^(mn) is an indicator matrix whose (m, n)-th entry is 1, otherwise zero. We additionally require that b ^(mn) and a ^(mn) are periodic in X, and that

$${\displaystyle {\iiint }_{{\widehat{\Omega }}_g}{\mathbf{\text{b}}}^{\left(mn\right)}\text{d}V}+{\displaystyle {\iiint }_{{\widehat{\Omega }}_{\text{f}}}{\mathbf{\text{a}}}^{\left(mn\right)}\text{d}V}=0,$$ (3.17)

so that the microscale solution has zero mean. Thus, equations (3.13)–(3.17) represent a further nine linear elasticity problems on the repeating cell in which deformations in the gel region ${\widehat{\Omega }}_{\text{g}}$ and the fibre region ${\widehat{\Omega }}_{\text{f}}$ are coupled, and caused by a jump in stress at the interface between Ω̂_g and ${\widehat{\Omega }}_{\text{f}}$.

A similar procedure is applied to determine p ⁽¹⁾, the 𝒪(ε) pressure of the fluid phase in the hydrogel region. We note that as ${\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}={\mathbf{\text{u}}}_{\text{g}}^{\left(0\right)}$ is independent of X, equation (2.31) implies that the divergence of the fluid phase velocity in the poroelastic region is zero at leading order. We then take the divergence of (2.38) on the microscale to find that

$$\begin{array}{cc}{\nabla }_X^2{p}^{\left(1\right)}=0,& \text{in}{\hat{\Omega }}_{\text{g}}.\end{array}$$ (3.18)

Next we take the scalar product of (2.38) with n and, exploiting equations (2.44) and (2.45), obtain the following boundary condition for p ⁽¹⁾ on the hydrogel-fibre interface:

$$\begin{array}{cc}{\nabla }_X{p}^{\left(1\right)}\cdot \mathbf{\text{n}}=-{\nabla }_x{p}^{\left(0\right)}\cdot \mathbf{\text{n}},& \text{on}\partial {\hat{\Omega }}_{\text{f}}.\end{array}$$ (3.19)

Thus, equations (3.18)–(3.19) comprise a linear homogeneous cell problem for p ⁽¹⁾ subject to forcing by the leading order pressure p ⁽⁰⁾ via the Neumann boundary condition. As above, we formulate a solution to this problem as

$$p^{\left(1\right)}=f\cdot {\nabla }_x{p}^{\left(0\right)},$$ (3.20)

where f = f(X) is a vector. Upon substitution of (3.20) into (3.18) we obtain

$$\begin{array}{cc}{\nabla }_X^{2}f=0,& \text{in}{\hat{\Omega }}_{\text{g}}.\end{array}$$ (3.21)

Similarly, substitution of (3.20) into (3.19) provides the boundary condition

$$\begin{array}{cc}{\nabla }_{X}f\cdot \mathbf{\text{n}}=-\mathbf{\text{n}},& \text{on}\partial {\hat{\Omega }}_{\text{f}}.\end{array}$$ (3.22)

Finally, we require that f is periodic in x, and that

$${\displaystyle {\iiint }_{{\widehat{\Omega }}_g}f\text{d}V}=0,$$ (3.23)

so that the microscale solution has zero mean. Thus, equations (3.21)–(3.23) define linear, scalar problems for the three components of f.

4. Macroscale equations and effective parameters

To complete the homogenisation procedure we now average across the microscale solutions from Section 3 to obtain governing equations and effective material parameters for the composite material at the macroscale.

We integrate the 𝒪(1) continuity of mass equation (2.37) over the microscale repeating unit cell and divide by the cell volume. It follows from the divergence theorem, and application of the continuity of displacement condition (2.44) and the kinematic condition (2.45) that

$$\varphi {\nabla }_x\cdot {\mathbf{\text{v}}}^{\text{eff}}+\left(1-\varphi \right)\frac{\left|{\hat{\Omega }}_{\text{g}}\right|}{\left|\hat{\Omega }\right|}\frac{\partial }{\partial t}\left({\nabla }_x\cdot {\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}\right)=\frac{1}{\left|\hat{\Omega }\right|}\frac{\partial }{\partial t}{\displaystyle {\iiint }_{{\widehat{\Omega }}_{\text{f}}}{\nabla }_X\cdot {\mathbf{\text{u}}}_{\text{f}}^{\left(1\right)}\text{d}V},$$ (4.1)

where |Ω̂| is the volume of a microscale repeating unit cell, |Ω̂_g| is the volume within this cell occupied by the hydrogel, dV is the volume element with respect to the microscale variables and v ^eff is the effective velocity of the fluid phase of the hydrogel, namely

$${\mathbf{\text{v}}}^{\text{eff}}\left(\mathbf{\text{x}},t\right)=\frac{1}{\left|\hat{\Omega }\right|}{\displaystyle {\iiint }_{{\widehat{\Omega }}_g}{\mathbf{\text{v}}}^{\left(0\right)}\left(\mathbf{\text{x}},\mathbf{\text{x}},t\right)\text{d}V}.$$ (4.2)

We now substitute the solution for ${\mathbf{\text{u}}}_{\text{f}}^{\left(1\right)}$ given by (3.6) into the averaged continuity of mass equation (4.1) to obtain

$$\varphi {\nabla }_x\cdot {\mathbf{\text{v}}}^{\text{eff}}+\left(1-\varphi \right)\frac{\left|{\hat{\Omega }}_{\text{g}}\right|}{\left|\hat{\Omega }\right|}\frac{\partial }{\partial t}\left({\nabla }_x\cdot {\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}\right)=S^{\text{eff}}:\frac{\partial }{\partial t}{\nabla }_x{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}+{\text{Γ}}^{\text{eff}}\frac{\partial p^{\left(0\right)}}{\partial t},$$ (4.3)

where S ^eff is an effective compressibility tensor (rank 2) and Γ^eff is a parameter related to the compressibility of the composite material; this accounts for both the compressibility of the linear elastic materials in the composite (namely the PCL fibres and the solid phase of the hydrogel) and the effect associated with the flow of the incompressible fluid phase within the hydrogel due to the deformation of the solid phase (where water will be lost from the composite). These are defined as

$$S^{\text{eff}}=\frac{1}{\left|\hat{\Omega }\right|}{\displaystyle {\iiint }_{{\widehat{\Omega }}_{\text{f}}}{\nabla }_X\cdot \mathcal{A}\text{d}V},$$ (4.4)

$${\text{Γ}}^{\text{eff}}=\frac{1}{\left|\hat{\Omega }\right|}{\displaystyle {\iiint }_{{\widehat{\Omega }}_{\text{f}}}{\nabla }_X\cdot \mathbf{\text{q}}\text{d}V},$$ (4.5)

where dV is the volume element with respect to the microscale variables. To determine these effective parameters we first solve equations (3.7)–(3.11) and (3.13)–(3.17) to obtain 𝒜 and q for a particular geometry and then use these solutions in (4.4) and (4.5) above.

Continuing, we integrate the 𝒪(1) version of Darcy’s law (2.38) over the microscale repeating cell and divide by total cell volume to obtain

$$\varphi \left({\mathbf{\text{v}}}^{\text{eff}}-\frac{\left|{\hat{\Omega }}_{\text{g}}\right|}{\left|\hat{\Omega }\right|}\frac{\partial {\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}}{\partial t}\right)=-\frac{\left|{\hat{\Omega }}_{\text{g}}\right|}{\left|\hat{\Omega }\right|}{\nabla }_x{p}^{\left(0\right)}-\frac{1}{\left|\hat{\Omega }\right|}{\displaystyle {\iiint }_{{\widehat{\Omega }}_g}{\nabla }_X{p}^{\left(1\right)}\text{d}V}.$$ (4.6)

We then use equation (3.20) to substitute for p ⁽¹⁾ in equation (4.6). Rewriting the right-hand side of that equation in a more compact form, we obtain

$$\varphi \left({\mathbf{\text{v}}}^{\text{eff}}-\frac{\left|{\hat{\Omega }}_{\text{g}}\right|}{\left|\hat{\Omega }\right|}\frac{\partial {\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}}{\partial t}\right)=-K^{\text{eff}}{\nabla }_x{p}^{\left(0\right)},$$ (4.7)

where K ^eff is an effective permeability tensor (rank 2) for the composite material; this is defined as

$$K^{\text{eff}}=\frac{1}{\left|\widehat{\Omega }\right|}\left(\left|{\widehat{\Omega }}_{\text{g}}\right|\mathbf{\text{I}}+{\displaystyle {\iiint }_{{\widehat{\Omega }}_{\text{g}}}{\nabla }_X}f\text{d}V\right).$$ (4.8)

Thus, to determine the effective permeability K ^eff we first solve (3.21)–(3.23) to obtain f for a particular microscale geometry and then use that solution in (4.8). In later numerical simulations it is convenient to eliminate v ^eff by substituting (4.7) into (4.3) to give

$$-K^{\text{eff}}{\nabla }_x^2{p}^{\left(0\right)}+\frac{\left|{\hat{\Omega }}_{\text{g}}\right|}{\left|\hat{\Omega }\right|}\frac{\partial }{\partial t}\left({\nabla }_x\cdot {\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}\right)={\text{S}}^{\text{eff}}:\frac{\partial }{\partial t}{\nabla }_x{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}+{\text{Γ}}^{\text{eff}}\frac{\partial p^{\left(0\right)}}{\partial t}.$$ (4.9)

We remark that writing the equation in this form eliminates the porosity ϕ, obviating the need to know that quantity.

Finally, we integrate the 𝒪(1) conservation of momentum equations, (2.39) and (2.41), over the microscale repeating unit cell and divide by the total cell volume; we then apply continuity of stress at the hydrogel–fibre interface (2.43) to obtain a volume averaged conservation of momentum equation:

$${\nabla }_x\cdot {\sigma }^{\text{eff}}=\frac{1}{\left|\hat{\Omega }\right|}\left({\nabla }_x\cdot {\displaystyle \iiint {}_{\widehat{\Omega }\text{f}}{\sigma }_{\text{f}}^{\left(0\right)}\text{d}V}+{\nabla }_x\cdot {\displaystyle \iiint {}_{\widehat{\Omega }g}{\sigma }_{\text{g}}^{\left(0\right)}\text{d}V}\right)=0,$$ (4.10)

where σ^eff is an effective stress tensor (rank 2) representing the macroscale stress of the composite material. To develop an explicit expression for σ^eff we substitute the first order displacements, (3.5) and (3.6), into the definitions of leading-order stress, (2.40) and (2.42), to obtain

$${\sigma }_{\text{g}}^{\left(0\right)}=-p^{\left(0\right)}\mathbf{\text{I}}+𝔻:\left({\nabla }_x{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}+\left({\nabla }_X\mathbf{\text{r}}\right)p^{\left(0\right)}+\left({\nabla }_Xℬ\right):{\nabla }_x{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}\right),$$ (4.11)

$${\sigma }_{\text{f}}^{\left(0\right)}=ℂ:\left({\nabla }_x{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}+\left({\nabla }_X\mathbf{\text{q}}\right)p^{\left(0\right)}+\left({\nabla }_X\mathcal{A}\right):{\nabla }_x{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}\right).$$ (4.12)

On substituting these expressions into (4.10) we deduce that the appropriate form of the effective stress tensor is

$${\sigma }^{\text{eff}}={ℂ}^{\text{eff}}:{\nabla }_x{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}+G^{\text{eff}}{p}^{\left(0\right)},$$ (4.13)

where ℂ^eff is an effective elasticity tensor (rank 4), and G ^eff is a rank 2 tensor describing the hydrostatic component of the effective stress; these are defined as

$${ℂ}^{\text{eff}}=\frac{1}{\left|\hat{\Omega }\right|}\left(\left|{\hat{\Omega }}_{\text{f}}\right|ℂ+\left|{\hat{\Omega }}_{\text{g}}\right|𝔻+ℂ:{\displaystyle {\iiint }_{{\widehat{\Omega }}_{\text{f}}}{\nabla }_X\mathcal{A}\text{d}V}+𝔻:{\displaystyle {\iiint }_{{\widehat{\Omega }}_g}{\nabla }_Xℬ\text{d}V}\right),$$ (4.14)

$$G^{\text{eff}}=\frac{1}{\left|\hat{\Omega }\right|}\left(-\left|{\hat{\Omega }}_{\text{g}}\right|\mathbf{\text{I}}+ℂ:{\displaystyle {\iiint }_{{\widehat{\Omega }}_{\text{f}}}{\nabla }_X\mathbf{\text{q}}\text{d}V}+𝔻:{\displaystyle {\iiint }_{{\widehat{\Omega }}_{\text{g}}}{\nabla }_X\mathbf{\text{r}}\text{d}V}\right),$$ (4.15)

where |Ω̂_f| is the volume occupied by the fibres. Thus, to find the effective stress tensor σ^eff of the macroscale composite material for a particular (microscale) hydrogel–fibre geometry we first solve equations (3.7)–(3.11) and (3.13)–(3.17) to obtain the solution components of the microscale cell problem, namely r, q, 𝓑 and 𝒜, and then use these solutions in expressions (4.14) and (4.15) above.

To summarise, we have now derived a system of four macroscale equations for continuity of mass (4.3), Darcy’s law (4.7), conservation of momentum (4.10) and the effective stress tensor (4.13) which, subject to appropriate boundary and initial conditions, govern the macroscale variables for displacement ${\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}$, pressure in the hydrogel p ⁽⁰⁾ and the effective velocity of the fluid phase of the hydrogel v ^eff. Calculating these effective parameters involves evaluating 189 volume integrals; by exploiting the symmetry of the microscale cell geometry and the assumption that the fibres and the solid phase of the hydrogel are linear elastic only 39 of these integrals need to be evaluated, as described in detail in Appendix B.

5. Solution procedure and comparison with experiments

We now validate the model presented in Sections 3 and 4 against a series of experiments that were performed to establish how fibre spacing affects the mechanical properties of reinforced hydrogel scaffolds. These experiments involved scaffolds reinforced with PCL fibres 20 μm in diameter and 3D-printed at spacings of either 300 or 800 μm (with three replicates for each choice of fibre spacing). The fibre lattices are then cast in GelMA to produce cylindrical scaffolds with diameters between 5.54 and 5.98 mm and heights 1.80–1.98 mm. These composite samples were held in unconfined compression at a fixed strain between two parallel plates while the applied stress required to maintain this displacement was recorded; after an initial ramping phase the required stress decreases slowly due to the poroelastic relaxation of the composite.

Details of the numerical solution procedure for the microscale cell problem of Section 3 and the homogenised macroscale problem of Section 4 are given in Sections 5.1 and 5.2, respectively. The experimental relaxation tests are compared to our theoretical simulation results in Sections 5.3, with a focus on replicating the poroelastic relaxation phase of these experiments in the simulations.

5.1. Microscale solution procedure

The microscale cell problem requires the solution of the linear elasticity problems (3.7)–(3.11) and (3.13)–(3.17) to obtain r, q, b ^(mn) and a ^(mn), and the solution to Laplace’s equation (and boundary conditions) (3.21)–(3.23) to obtain f. These sub-problems are solved using the multiphysics package COMSOL, which can perform finite element simulations on the interpenetrating geometry of the fibres and hydrogel regions to a high degree of accuracy. The cell geometry was meshed with an internal routine that accounts for the shape of the two materials and generates a fine (non-adaptive) mesh with 12,990 vertices and 307,890 degrees of freedom. COMSOL implements period boundary conditions automatically and the solutions to these finite element simulations converge with a typical relative error of 𝒪(10^–11). These simulations are repeated to give values of the volume integrals in Section 4 for two cell geometries, described by the dimensionless parameter values given in Table 2, and for several values of the material parameters of PCL within the published range (as later described in Section 5.3).

Table 2.

Dimensionless parameters characterising the repeating cell for the two repeating cell geometries used in the simulations. The fibre radius is ρ, the dimen-sionless microscale height of the cell is θ = h/l and θ/4ρ is a measure of the vertical overlap between adjacent fibre layers, where a larger value indicates less overlap and θ/(4ρ) = 1 represents the case where the fibres are just touching.

Dimensional fibre spacing (μm)	ρ	θ	θ/4ρ
300	0.0333	0.1066	0.8
800	0.0125	0.04	0.8

For each of the cell geometries in Table 2 and each choice of the material parameters of PCL we use the COMSOL simulation results to calculate ℂ^eff, G, K ^eff, S ^eff and Γ^eff. As described in Section B, this requires the computation of only the volume integrals of the derivatives of the solution components given in Table B1. The form of the effective elasticity tensor Ceff in (4.14) reveals that the composite material can best be described as an orthotropic material in which two of the defined directions X and Y of the effective material properties of the composite are the same. This is not the same as a transversely isotropic material which has one distinguishable axis and is isotropic in any plane which lies perpendicular to that axis. In our material X and Y are interchangeable, but the two directions which are parallel to the directions of the fibres are both ‘special’ directions. This is intuitively simple to reconcile with the square grid pattern of the printed fibres. From these calculations we observe that ${ℂ}_{1111}^{\text{eff}}={ℂ}_{2222}^{\text{eff}}$ are an order of magnitude larger than ${ℂ}_{3333}^{\text{eff}}$, indicating that the composite material is much stronger along the fibre directions than perpendicular to the fibres. The other non-zero components of ℂ^eff are much smaller, which suggests that the composite material would be weaker in shearing.

5.2. Macroscale solution procedure

Having obtained the effective material parameters from the microscale problem, we proceed to solve the macroscale equations (4.3), (4.7), (4.10) and (4.13) with a finite element scheme. We aim to compare this with experiments on a cylindrical scaffold and the dimensions of the scaffolds from these experiments determine the choice of length scale L. For example, for the experiments with 300 μm fibre spacing we take this length scale to be L = 5.76 mm, the mean diameter of the three scaffolds, and the corresponding mean dimensionless scaffold height is η = H/L = 0.34. The solution domain is then

$$\begin{array}{cc}{x}^2+y^2⩽{(1/2)}^2,& 0⩽z⩽\eta .\end{array}$$ (5.1)

The scaffold is held between two plates, so no-slip conditions are appropriate at both the upper and lower surfaces of the cylinder. Additionally, we prescribe a time-dependent displacement in z on the upper surface as a means of implementing the loading strategy. The appropriate boundary conditions are then

$$\begin{array}{l}\begin{array}{cccc}{\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}=0,& & \frac{\partial p^{\left(0\right)}}{\partial z}=0,& \text{on}z=0,\end{array}\\ \end{array}$$ (5.2)

$$\begin{array}{l}\begin{array}{cccc}{u}_{\text{fl}}^{\left(0\right)}=u_{\text{f}2}^{\left(0\right)}=0,& u_{\text{f}3}^{\left(0\right)}=d\left(t\right),& \frac{\partial p^{\left(0\right)}}{\partial z}=0,& \text{on}z=\eta ,\end{array}\\ \end{array}$$ (5.3)

where $u_{\text{f1}}^{\left(0\right)},u_{\text{f2}}^{\left(0\right)}\text{and}{u}_{\text{f3}}^{\left(0\right)}$ are, respectively, the x, y and z components of ${\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}$. Different choices of the displacement function d(t) are required to simulate the relaxation tests, and these will be defined in the following section. We impose no stress boundary conditions on the curved surfaces of the cylinder:

$$p^{\left(0\right)}=0,{\sigma }^{\text{eff}}\cdot {\mathbf{\text{e}}}_R=0,\text{on}{x}^2+y^2={(1/2)}^2,$$ (5.4)

where e _R is the outward-pointing unit normal to the cylinder surface. In all simulations the initial conditions are

$${\mathbf{\text{u}}}_f^{\left(0\right)}\left(\mathbf{\text{x}},0\right)=0,$$ (5.5)

$$p\left(\mathbf{\text{x}},0\right)=0,$$ (5.6)

so that the scaffold is initially in an undeformed and unstressed reference state.

We use a finite element method to calculate numerical solutions of (4.9) and (4.10), subject to the boundary conditions (5.2)–(5.4) and the initial conditions (5.5) and (5.6). The effective stress σ^eff used in (4.10) and (5.4) is defined in terms of p ⁽⁰⁾ and ${\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}$ in (4.13). The domain x ² + y ² ⩽ (1/2)², 0 ⩽ z ⩽ η is partitioned into tetrahedral elements using the mesh generation package TetGen [22]. A finite element solution is then calculated, using an implicit approximation to all time derivatives, that uses a quadratic approximation to ${\mathbf{\text{u}}}_{\text{f}}^{\left(0\right)}$ on each element and a linear approximation to p ⁽⁰⁾ on each element. This finite element method has been shown to be stable for poroelasticity [31] and is therefore suitable here since the homogenised governing equations are of a similar form to those that describe small deformation poroelasticity.

5.3. Comparison with relaxation test experiments

The relaxation test involves applying a 6% strain at the top of the scaffold and recording the stress required to maintain this displacement over the course of 15 min, that is, for 0 ⩽ t ⩽ 15. In line with the experiments, the time-dependent displacement d(t) of the top-loading plate used in the simulations was chosen so that a strain of 6% was attained after an initial period of linear displacement over 0 ⩽ t < δ, where δ is a short initiation time. The form of the loading function for the relaxation test is then

$$d\left(t\right)=\xi \eta \left(\frac{1}{\delta }tH\left(\delta -t\right)+H\left(t-\delta \right)\right),$$ (5.7)

where ξ = 0.06 is the maximum applied strain, H(t) is the Heaviside step function, and δ takes a slightly different value for each choice of fibre spacing to match the initial transient strain applied in the experiments; these values are δ = 0.14 for the 300 μm fibre spacing and δ = 0.11 for the 800 μm fibre spacing.

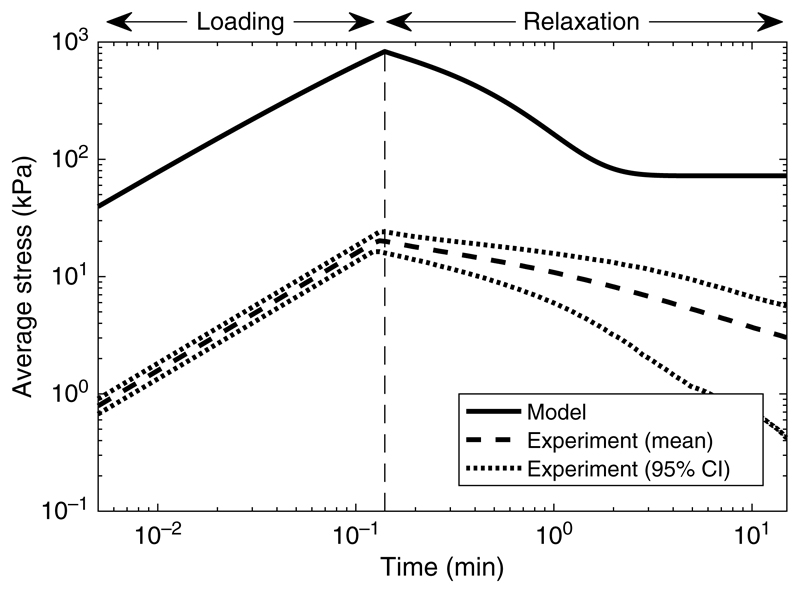
The results of the macroscale simulations of this relaxation test for 300 μm spacing are shown in Figure 2, along with experimental data based on three replicates of this test. The model exhibits qualitatively similar behaviour to the experiments, with an initial ramp-up phase followed by a relaxation phase. These results are all displayed in terms of ‘average stress’, defined as the total force applied at the top of the scaffold divided by the cross-sectional area. During the initial fast-loading phase the response of the scaffold is dominated by the fibres, and so the average stress is essentially linearly elastic. During the relaxation phase the scaffold exhibits poroelastic behaviour due to the flow induced in the fluid phase of the hydrogel.

Figure 2.

Numerical simulations of the relaxation text for 300 μm fibre spacing held at 6% strain (solid line), shown as the time-dependent stress response of the scaffold to the imposed displacement given in (5.7). Also shown is the mean time-dependent stress from three replicates of the experimental relaxation test (dashed line) and a 95% confidence interval on these data (dotted lines).

There are marked quantitative differences between the experiments and the simulations. The model overestimates the maximum stress attained after the initial loading by two orders of magnitude and displays a more rapid relaxation, reaching a steady state after approximately 2 min, whereas the measured experimental stress is still decreasing at 15 min.

As noted previously, the published values for the Young’s modulus $E_{\text{f}}^{\prime }$ of PCL fibres vary between 53 and 363 MPa [5, 12, 41, 42] and published values of the associated Poisson’s ratio ν _f vary between 0.3 and 0.49 [12, 17, 18]. In light of this we now embark on a sparse exploration of this parameter space, with a view to fitting appropriate material parameters for the batch of PCL used in these experiments.

Close inspection of the scaffolds used in the experiments suggests some possible explanations for these discrepancies. The printed fibre lattices do not exactly correspond to our idealised model, with the fibres in the uppermost layers sagging and adopting a curved shape, as shown in Figure 1(b) and (c). We hypothesise that when the scaffold is loaded these fibres do not come under tension as readily as the fibres in the lower layers. Additionally, as a result of casting the printed fibres in the hydrogel, there is a thin layer of pure (unreinforced) hydrogel at the top of the scaffold. We hypothesise that this thin layer will yield more readily to loading than the reinforced gel below it, and that the reinforced gel, therefore, experiences a lower strain than that applied to the scaffold as a whole. For instance, if the depth of the pure hydrogel layer is 5–10% of the height of the entire construct, then we estimate, based on the relative Young’s moduli of the PCL and the solid phase of the GelMA, that the strain applied to the reinforced hydrogel will be less than 1%. In this hypothetical situation the pure hydrogel layer would significantly deform during the initial loading. We propose this to account for both these effects by adjusting the applied strain in the model, via the parameter ξ in (5.7).

We now consider the effect of varying the three parameters described above, namely ξ, E _f and ν _f, on the time-dependent average stress predicted by the model. The role of changing the applied strain is shown in Figure 3(a), for four values of ξ ranging from the recorded value of 6% to a much smaller strain of 0.15%. The peak stress value at the end of the loading phase for the smallest of these applied strains is approximately two orders of magnitude smaller than the original 6% strain and of the same order of magnitude as the experimentally recorded stress. The shape of the relaxation profile is, however, uneffected by varying the strain; it still decays more rapidly than the experimentally observed profile.

Figure 3.

Examples of the sensitivity of the stress response to the key parameters of the model. (a) Varying the displacement ξ, with the fibre parameters fixed at E _f = 363.3 MPa and ν _f = 0.43. (b) Varying the Young’s modulus of the fibres E _f, with an applied strain of 6% and ν _f = 0.43. (c) Varying the Poisson’s ratio of the fibres ν _f, with an applied strain of 6% and E _f = 2.65 MPa.

The effect of lowering the Young’s modulus of the fibres E _f is shown in Figure 3(b) for three choices of this parameter, with the original 6% strain. To achieve a peak stress which is similar in magnitude to the experimentally observed value, E _f must be set to a value which is an order or magnitude smaller than the lowest published value of this parameter. At the lowest published value (of E _f = 53 MPa) the model overpredicts the peak value of stress, but the relaxation profile is similar to that seen experimentally. The effect of varying ν _f is shown in Figure 3(c); this has a relatively small effect on both the peak stress at the end of the loading phase and the rate at which the composite relaxes.

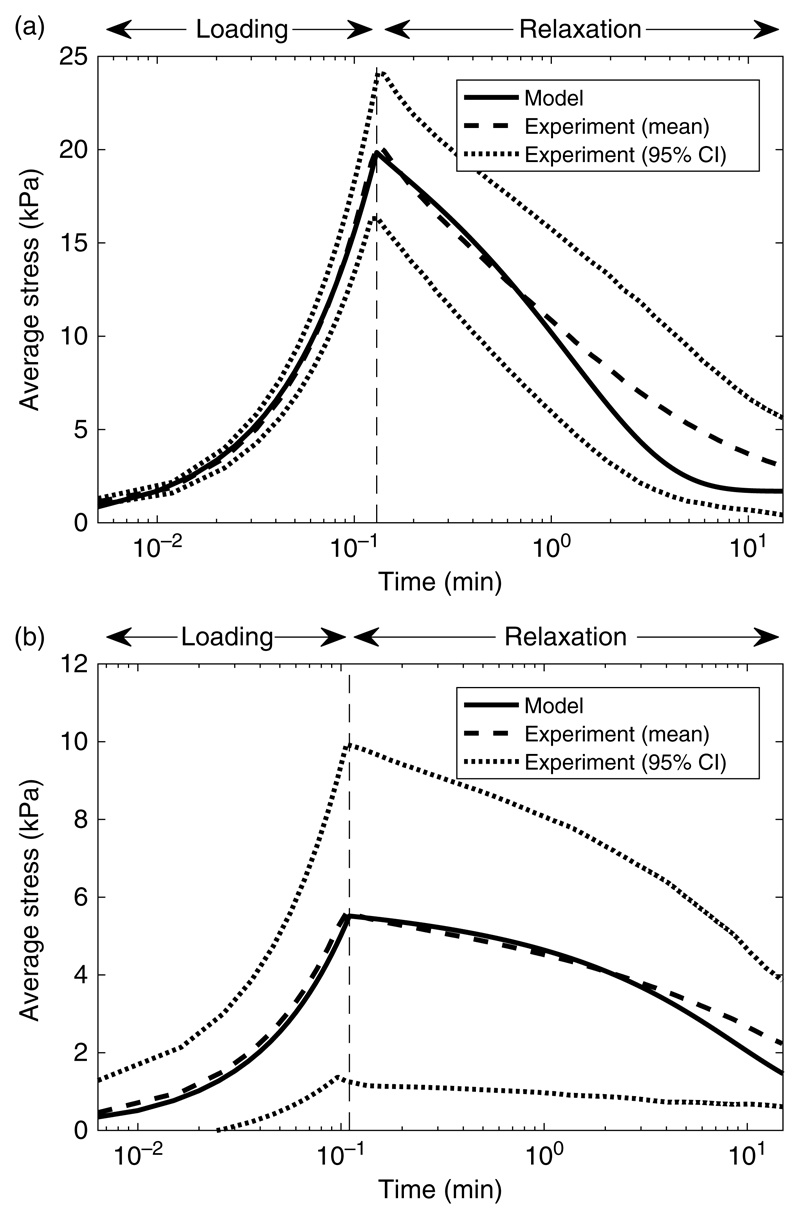
The sensitivity of the stress response to ξ and E _f shown in Figure 3(a) and (b) suggests that the model will come close to the observed stress if both parameters are lowered in combination. We have performed a sparse parameter sweep through these parameters to determine values which produce reasonable agreement with the observed data. The stress given by these parameters is shown in Figure 4(a). Here, the parameters ξ =0.45%, E _f = 90.8 MPa and ν _f = 0.49 produce a stress through the loading phase which closely follows the experiment and a relaxation phase which is in good agreement up to time of about t = 1, after which the model predicts a faster decay in stress.

Figure 4.

Numerical simulations of the relaxation text compared with the experimental data. (a) 300 μm fibre spacing with adjusted modelling parameters of ξ = 0.45%, E _f = 90.8 MPa and ν _f = 0.49 (solid line). (b) 800 μm fibre spacing with adjusted modelling parameters of ξ = 0.525%, E _f = 45.4 MPa and ν _f = 0.49 (solid line). Both (a) and (b) show the mean time-dependent stress from three replications of the experimental relaxation test (dashed line) and a 95% confidence interval on these data (dotted lines). Note that 300 μm fibre spacing data is the same as that shown in Figure 2 with a log scale on the vertical axis.

Further relaxation tests were performed for reinforced hydrogel scaffolds with fibres printed at a wider spacing of 800 μm, and data from three replicates of this experiment are compared to the homogenised model in Figure 4(b). Applying the model naively as in Figure 2 over-predicts the observed average stress by two orders of magnitude. The model solution shown in Figure 4(b) is for ξ =0.525%, E _f = 45.4 MPa and ν _f = 0.49; these parameters were obtained through a sparse parameter sweep, as described earlier. As before, the model follows the observations closely through the loading phase and remains in agreement with the stress in the relaxation phase for a longer time than in the 300 μm case. This agreement was obtained using a value of E _f which was half that of the 300 μm case, suggesting that the sagging of the fibres is more pronounced for this larger fibre spacing.

6. Discussion

We have used mathematical homogenisation theory to develop a new model to describe the deformation of a composite elastic–poroelastic material. This was motivated by a desire to determine the macroscale mechanical properties of fibre-reinforced hydrogels used in the tissue engineering of articular cartilage. Our model enables us to calculate the effective material properties of the composite given knowledge of the material parameters of the constituent materials (namely the GelMA hydrogel and the PCL fibres) and the geometrical arrangement of the fibres and hydrogel within a single repeating cell of the composite. By incorporating these details in a coherent, systematically derived description of the composite, we are able to gain mechanistic insight into its behaviour. Our initial application of the model, shown in Figure 2, predicted much stronger fibre-reinforced composites than those we tested experimentally, but exhibited good qualitative agreement with both the initial linear elastic loading phase and a poroelastic relaxation phase. Further numerical solutions, shown in Figure 3, demonstrate that the predicted stiffness of the composite is very sensitive to the Young’s modulus of the PCL fibres and the strain applied to the composite.

There are several possible explanations for why our model over-predicts the strength of the fibre-reinforced composites. In Section 5.3 we discussed two of these in detail, namely the sagging of the printed fibres, which effectively lowers the Young’s modulus of the fibres, and the presence of a layer of unreinforced hydrogel at the top of the scaffold, which means that an applied strain is not directly passed on to the reinforced composite material. Accounting for these effects, we obtained good agreement between the observed relaxation behaviour of the composite and our model, as shown in Figure 4. We postpone formally including these effects in the model for future work. Adding the extra thin layer of hydrogel would be a relatively straightforward extension of the current model. Accounting for the effect of sagging fibres would be more involved; in this case the cell geometry is no longer symmetric in z and therefore some of the computational advantages that this symmetry confers would be lost.

There are other possible sources of discrepancy between the model and the experiments. For instance, the vertical spacing between the fibres was estimated with knowledge of the total number of printed layers and the overall scaffold height. If the vertical overlap between the fibres in the definition of the cell geometry is further reduced, then the model predictions may be brought closer to the experimental data. Another possible source of the discrepancy is the boundary conditions imposed between the fibres and the hydrogel. We have assumed continuity of stress and displacement at the interface between the fibres and the hydrogel. In practice, a boundary condition that allows for some slip between the hydrogel and the fibres may be more appropriate and would probably lead to the model predicting a weaker fibre-reinforced composite. Modifying the homogenisation procedure to account for such effects is an interesting direction for future work.

Finally, the hydrogel may not be perfectly poroelastic. Some of the observed relaxation behaviour may be due to viscous relaxation, and incorporating these effects by using a different model for the hydrogel would require altering the homogenisation process. Such a model would introduce history dependence of the material and could potentially make it far less numerically efficient if a new set of cell problems had to be solved at each time step; see, for example, the discussion in [34].

The elastic material in our composite is much stronger than the poroelastic hydrogel; μ _f and λ _f are five orders of magnitude larger than μ _g and λ _g, which might suggest that it is possible to neglect entirely the contribution of the poroelastic region and model only the elastic fibre scaffold. This approach would not, however, capture the time-dependent response of the composite. Accounting for both the elastic and the dynamic poroelastic nature of these composites, as we do here, is important to understand their mechanical properties. An interesting direction for study might be to formally incorporate the difference in the material properties of the hydrogel and the fibres in the model by exploiting the small parameter associated with the ratio of the Young’s moduli of the elastic phase of the hydrogel and that of the fibres, and then repeating the homogenisation procedure.

Our model captures the key features of the fibre-reinforced hydrogel, in particular its orthotropic nature, and directly relates the material properties of the constituent hydrogel and fibres to those of the composite material. Modelling the mechanical properties of these scaffolds is an important step to inform tissue engineers about the stress experienced by cells when the scaffold is mechanically loaded, thus allowing future modelling work to consider the response of the cells to this stimulation. A key point of interest here is to understand how the scaffold is remodelled as the seeded cells deposit extracellular matrix components in response to loading, a process which eventually leads to implants which resemble natural articular cartilage. This might involve replacing the hydrogel phase with a cartilage-like phase that can explicitly describe the mechanical role of the extracellular matrix components; see [26] for a review of such models of cartilage. Candidate models for this replacement phase include the model of [30], which treats cartilage as a poroelastic material, or the detailed cartilage model of [2], which includes the mechanical effects of ions interacting with the extracellular matrix. Since the cells embedded in the scaffold are actively remodelling their surrounding mechanical environment, this approach should also account for the growth of the cartilage, and a natural framework to do this would be via the theory of morphoelasticity [20].

To conclude, this homogenised model successfully captures the orthotropic nature of the fibre-reinforced hydrogel scaffold, can (when suitably adjusted) predict the behaviour seen in experimental relaxation tests and provides a basis for future study of the mechanical stimulation of cell-loaded scaffolds.