Raman amplification in the ultra-small limit of Ag nanoparticles on SiO₂ and graphene: Size and inter-particle distance effects

Abstract

Size, shape and hot spots are crucial to optimize Raman amplification from metallic nanoparticle (NPs). The amplification from radius = 1.8 ± 0.4 nm ultra-small silver NPs was explored. Increasing NP density redshifts and widens their plasmon that, according to simulations for NPs arrays, is originated by the reduction of the interparticle distance, d, becoming remarkable for d ≤ R. Inter-particle interaction red-shifts (N130 nm) and widens (N90 nm) the standard plasmon of non-interacting spherical particles. Graphene partly delocalizes the carriers enhancing the NIR spectral weight. Raman amplification of graphene phonons is moderate and depends smoothly on d while that of Rhodamine 6G (R6G) varies almost exponentially due to their location at hotspots that depend strongly on d. The experimental correlation between amplification and plasmon position is well reproduced by simulations. The amplification originated by the ultra-small NPs is compared to that of larger particles, granular silver films with 7 < R < 15 nm grains, with similar extinction values. The amplification is found to be larger for the 1.8nm NPs due to the higher surface/volume ration that allows higher density of hot spots. It is demonstrated that Raman amplification can be efficiently increased by depositing low density layers of ultra-small NPs on top of granular films.

1. Introduction

The amplification of electromagnetic radiation due to localized surface plasmon resonances (LSPR) of metal nanoparticles (NPs) is highly efficient and commonly used to detect weak Raman signals of dilute analytes by the Surface Enhanced Raman Scattering technique (SERS). SERS has attracted scientists’ interest because of its high sensitivity, rapid response, unique spectroscopic fingerprint, and nondestructive data acquisition, in cases enabling the detection of individual molecules [1,2]. Some of the chemical species that this technique can detect are toxic or radioactive cations/anions, ionic nutrients [3], pesticides [4], drugs and pharmaceuticals, or explosive materials [5].

High Raman enhancement occurs when molecules are close to highly polarizable objects, as metallic NPs, due to the intense localized electric fields produced by the LSPR for resonant incident energies [6]. The optical properties of metal nanoparticles depend on size, shape and composition of the NPs, consequently, there is an intense activity on the optimization of these parameters [7–10]. Indeed, the aspect ratio of metal nanorods allows controlling the resonance wavelengths and reaching the infrared range which is useful for different therapies [11]. Besides, noble metal-based nanocomposites typically exhibit admirable optical and photoelectrochemical properties [12,13].

The SERS enhancement factor (EF)can be worked out by considering two multiplicative factors, one for the incident field and the other one for the emitted (Raman) field. This is why, in general, the enhancement is proportional to the fourth-power of the local electric field. In a first approximation, the electric field amplitude, E, due to the LSPR decays as a dipole field, E ~ d^-3, so, to benefit from the SERS mechanism, the molecule must be in close proximity to the NP (d) [4,14]. For individual gold NPs, in the range R = 20 to 50 nm, deposited on a mirror, the larger the NP size the higher the enhancement has been reported [15] while the optimum size for Ag NP colloids was found to be around R = 25nmwithin the 10–35nmstudied range [16], which is close to the optimum radius provided by Mie analytical calculations (around 20 nm) for non-interacting spheres [17]. From the experimental results the optimum size even for spherical NPs is still unclear. Amplification factors typically in the 10⁴ range, and in cases up to 10⁶, are reported for spherical colloidal silver NPs of 50–65 nmin diameter [16,18]. Moreover, considering a fixed total metal mass in solid SERS platforms, how Raman enhancement depends on NP size and on interparticle distance are still open questions. The EF depends strongly on the position of the molecule since the field is high at certain regions on the surface of the NP, depending on the incident light polarization and can be particularly high in gap regions between two NPs, also called hot-spots [19]. Chains of ultrasmall Rh NPs (~5 nm diameter) have recently been synthetized over DNA showing an increasing EF as the DNA concentration is reduced probably due to the increased creation of hot spots [20]. Some applications such as single molecule detection, rely on these hot-spots to obtain the needed EF ~ 10⁹, however, these experiments are not easily reproducible [21].

The most common SERS active platforms can be classified into three classes: (i) metal nanoparticles in suspension, usually made by the Lee and Meisel’s method [22,23], which is based on sodium citrate reduction of AgNO₃ under thermal condition and resultant Ag NPs with an average size of ~60 nm, or by laser ablation technique [24–27]; (ii) metal nanoparticles immobilized on solid substrates [28,29], like quartz [30], paper [5,31]; or alumina filters [27]; and (iii) nanostructures fabricated directly on solid substrates, for example by nanosphere lithography [32–34], that can be used to produce well-ordered 2D periodic arrays of nanoparticles. This work falls into the third category, since nanoparticles are deposited directly on solid substrates (fused silica or graphene/quartz) from the gas phase using the gas aggregation technique [35]. This is an advanced method to generate continuous flow of ultrafine particles with controlled size (from 1 to ~10 nm radius, i.e. up to 10⁶ atoms per particle) and narrow particle size distributions in a clean and controlled environment, as it can be operated in high vacuum or ultra-high vacuum, which avoids the presence of surfactants or any byproduct of the fabrication process.

In this work we were interested in evaluating the capability of ultrasmall monodisperse Ag NPs (R = 1.8 nm), which present a surface free of any chemicals, to amplify the Raman signal of graphene and of a reference molecule as the Rhodamine 6G (R6G). Even if these 1.8 nm NPs are close to the limit where the plasmon resonance almost vanishes due to enhanced surface damping, their size is still interesting enough as well as their high surface/volume ratio, much higher than those of the typically investigated (tens to hundred nm radii). Since the SERS effect is strongly dependent on the NP-analyte distance, the number of molecules that can fit on the NPs’ surface is relevant. In this sense, for a given metal mass, the available surface is inversely proportional to the NP radius. The relevance of the geometrical factors is evidenced by comparing the amplification originated in a graphene single layer and in the R6G molecules deposited either by spin or dip coating. To take advantage of the high resonance values of large NPs and of the high surface/volume ratio of the ultra-small NPs as well as to foster the presence of hot spots, nanostructured Ag thin films and ultra-small NPs were combined and tested. Near field plasmon simulations, which include the dependence on the size and average distance between NPs, are also discussed.

2. Materials and methods

Different sample series were fabricated: 1) Ag ultrasmall NPs deposited on fused silica (amorphous SiO₂) and on graphene transferred onto quartz (crystalline SiO₂) substrates, from “Graphenea” company, 2) Ag ultrathin films with nominal thickness from 1 to 5 nm deposited on fused silica and 3) combined Ag thin films and Ag-NPs also deposited on fused silica. In all cases, the fused silica substrates were cleaned with acetone and dried with N₂ gas.

Silver nanoparticle deposition was done at room temperature (RT) with the gas aggregation technique [36] a magnetron sputtering source (Nanogen50, from Mantis Ltd.) using an Ag target 99.95% purity. Ejection of atoms and nucleation of clusters are assisted by a mixture of Ar/He gas, carried along the aggregation chamber through an orifice and reaching the substrate. The base pressure was 5 × 10^-9 mbar and the work pressure were 2.5 × 10^-1 mbar inside the aggregation chamber and 2 × 10^-3 mbar inside the deposition chamber. The Ar/He ratio was 1:2.

These parameters give rise to spherical single crystalline nanoparticles with an average radius of R ~ 1.8 nm (Fig. 1, more TEM and HRTEM images are presented in Fig. S1 in the Supp. Info. file). The Ag NPs were simultaneously deposited on graphene/quartz and fused silica substrates. The procedure has been further described in a previous work [37]. An AFM image and two profiles of a dense film of Ag NPs deposited on fused silica for 900 s are shown in Fig. S2 in the Supp. Info-file.

Fig. 1.

TEM images of the Ag NPs (the red dashed line defines the NP profile) and size distribution extracted from the analysis of 94 NPs.

Silver thin films were deposited at RT by direct current magnetron sputtering of Ag target (99.95% purity) with an Ar pressure of 6 × 10^-3 mbar and a target power of 2 W. The deposition rate was calibrated to be 3.8 nm/min and the base pressure was ~1 × 10^-6 mbar. The combined Ag thin films and Ag NPs were fabricated as three-zone samples: in A and B zones an ultrathin Ag film was deposited and in B and C zones, Ag NPs were then deposited. Rhodamine 6G (R6G) solutions in methanol were spin-coated onto the different samples to evaluate their Raman amplification power. This procedure provides very homogeneous distribution of the Rhodamine. Alternatively, the samples were immersed in vertical position in the R6G solution. The homogeneity of the R6G concentration across the samples for both systems was checked by obtaining several absorption spectra from small regions (1mmdiameter) within the sample. In all cases at least 10 Raman spectra were acquired at different locations obtaining variations in the measured intensities below 20%. This variability within each sample is very small compared to changes observed from one sample to another.

The size and morphology of the Ag nanoparticles were analyzed using HRTEM and atomic force microscopy (AFM) in the tapping mode (equipment and software from Nanotec™). Commercial tips (Nanosensors PPP-NCH-w) with k = 34 N m^-1 and f₀ ≈ 270 kHz were used. The analysis of the images was carried out taking into account the convolution of the tip (typical radius 10 nm), which limits the lateral resolution of small objects. Nonetheless, the height resolution of this technique is in the Angstrom regime and provides reliable measurements in the z-direction. Several regions were probed to confirm the homogeneity of particle deposition. HRTEM images of Ag NPs deposited on carbon were obtained with a JEM2100HT microscope. Micro-Raman experiments were performed at room temperature using the 488 nm line of an Ar⁺ laser with an Olympus microscope (×100 and ×20 objectives), and a “super-notch-plus” filter from Kaiser. The scattered light was analyzed with a Horiba monochromator coupled to a Peltier cooled Synapse CCD. Optical absorption measurements were carried out in a UV–Vis Cary Spectrophotometer 4000, in the range between 200 and 800 nm. The substrate signal was removed.

Three-dimensional finite-difference time-domain (FDTD) simulations, were performed using Lumerical FDTD software [38], the simulations allowed us to calculate the electric field at any location as well as to calculate extinction spectra of NPs arrays. Calculations of electric fields and extinction spectra for a single NP (spheres and ellipsoids) were performed using Mie theory [17], these were used as the first step to test the results from the FDTD simulations.

3. Results and discussion

3.1. Plasmons of 1.8 nm Ag NPs: experiments and simulations

Ag 1.8 nm-NPs were deposited simultaneously on fused silica (FS) and on graphene single layers, previously transferred onto quartz (Gr/Q), for different times ranging from 300 s to 1200 s. The extinction spectra, obtained from optical transmittance measurements, reveal the variation in the plasmon intensity, position and width for the NPs deposited on both substrates (FS and Gr/Q) (Fig. 2a and b).

Fig. 2.

Extinction spectra (-log(T)) forAg NPs depositedon fused silica (FS) (a) and onGraphene on quartz (Gr/Q) (b) for different NPs deposition times. Comparison for NPs deposited on fused silica (lines) and graphene (symbols) for 900 s and 1200 s (c). The plasmon wavelength (d), FWHM (e), extinction intensity (f) and integrated area (j) are potted vs deposition time for the series deposited on Gr/Q and on FS.

The analysis of these curves is presented in Fig. 2d–g. Looking first at the NPs deposited on FS, we can see that the resonance wavelength of the plasmon is strongly red-shifted from 420 nm to above 460 nm with increasing deposition time (Fig. 2d). In addition, the plasmon significantly broadens as the NPs density (deposition time) increases (Fig. 2e). This occurs despite the fact that the NP radius (R = 1.8 nm) is invariable for series. The maximum values of the plasmon extinction (Fig. 2f) and the integrated plasmon intensity (Fig. 2g) scale with the deposition time.

We used Mie theory to calculate the extinction of non-interacting Ag spheres taking into account the change in the dielectric constant due to additional damping at the surface of the NP in the small size limit [6,39]. In Fig. 3a the plasmons normalized to the NP mass are shown. The plasmon resonance presents a small blue-shift of 8 nm from 20 to 2 nm NP radii (inset). For R N 20 nm significant red-shift and widening occur as well as a drastic decrease of the plasmon intensity. The most efficient plasmon for non-interaction Ag particles is indeed around R = 20 nm however, it is located in the UV (~365 nm) which is not convenient for practical use. Visible plasmons are preferred.

Fig. 3.

a) Mie calculationsof the extinction vs Ag NP radius normalized to theNP mass with corrected dielectric constant. Inset: plasmon resonancevs R(NP). b)Plasmon foraperiodic array of 2 nm NPs using FDTD simulations as a function of the inter-particle distance, d, normalized to theNP radius R, from d/R = 0.1 (blue) to 5 (yellow).c) Position and FWHM of the plasmon (of b) as a function of d/R. d) Fits to the 300 s and 1200 s AgNP plasmons (300/FS and 1200/FS) using the distributions of interparticle distances of the inset.

The resonance wavelengths (420–500 nm) and widths (FWHM ~ 100–200 nm) of the observed plasmons cannot be fitted by the Mie approach for 2 nm non-interacting Ag NPs (356 nm and 50 nm peak position and width, respectively). Moreover, the width of the measured plasmons bands cannot be due to a wide distribution of the NPs sizes since, in the present case, the radii distribution is extremely narrow (1.8 ± 0.8 nm, Fig. 1c). The relevant parameter here is related to the NPs density increase which is accompanied by a reduction of the interparticle-distance and the increasing probability to find connected particles forming clusters.

Three-dimensional finite-difference time-domain (FDTD) simulations were run to determine the dependence of the plasmon as a function of the inter-particle distance for NP pairs and 2D-NP-arrays with different NP sizes. We checked the results for different grid dimensions from the simulations against Mie exact analytical solution for large enough interparticle-distances. A key point is to evaluate the importance of a random distribution of the NPs, different interparticle distances around a mean value d, so we compared the results of the simulations for 2-NPs, periodic NPs arrays and scattered NPs (small number). However, large computational domains with fine details, such as randomly scattered NPs over the substrate presenting very different inter-particle distances, make such a simulation impractical, not only for obvious reasons related to the convergence of the simulations as a function of the grid, but also because of the fact that each simulation should be carried out with a particular electric (or magnetic) field polarization: the lack of local symmetry in the arrangement of the NPs would have required a large number of simulations. Averaging the extinction spectra for each polarization is later needed to compare the simulations with the experimental results. Similar problem related to the polarization occurs with NPs pair because of its axial in-plane symmetry. We have nevertheless run simulations on several random distributions of 15 NP. The conclusion was that the results from a periodic array of NPs with an interparticle distance d reproduce well the results obtained from randomly scattered NPs and has the enormous advantage that the symmetry of the periodic distribution allows for shorter simulation times.

Fig. 3b shows the simulated extinction spectra of a periodic array of R = 2 nm NPs with varying interparticle distance (d). Spectra are calculated over two orders of magnitude of the interparticle distance, d, and for different NP radii, R. When plotted against the interparticle distance normalized to the NP radius, d/R, the results are found to be very similar for radii up to 10 nm. In Fig. 3b and c, an important red shift of the plasmon resonance wavelength (up to N500 nm, so in good coincidence with the experimental spectra) is observed as the distance is reduced for d ≤ R as well as an increase of the plasmon width. A redshift has also been experimentally observed in the case of lithographically fabricated Au nanodisks pairs and simulated using the discrete dipole approximation (DDA) [40]. Also, the spectra become complex presenting more than one peak.

However, the shape of the measured spectra (Figs. 2 and 3d) cannot be fitted to a plasmon calculated for one particular interparticle distance. Convolutions of calculated spectra corresponding to interparticle-distance distributions, as those described by the functions presented in the inset of Fig. 3d for samples 300/FS and 1200/FS, are required. The distribution corresponding to the denser sample, Ag NPs deposited on fused silica for 1200 s (1200FS), is shifted to shorter inter-particle distances when compared to the sparser 300FS sample, as expected, with a significant weight of the very small distances and narrower width. Therefore, the reduction of the interparticle distances as the density increases is the origin of the shift of the plasmon to longer wavelengths and of its widening.

We have also evaluated the impact of a dielectric surface layer on the NP in the plasmon position and shape, resulting from the possible oxidation of the Ag NPs or the adsorption of airborne organic molecules. Contrary to the significant shift of the plasmon reported for large NPs covered by a SiO_x overlayer [41], here the impact is noticeable only for very high values of the refractive index of the dielectric layer. For instance, for a NP with an outer dielectric shell having a thickness 10% of the NP radius, and a refractive index of 2.1 the plasmon peak is red-shifted by 5% and some widening occurs at short (b1 nm) inter-particle distances (Fig.S3, SI). Here, Mie exact solution for layered spherical particles was also used as the initial check for the simulations, which were carried out for periodic arrays of dielectric-covered NPs. We can conclude that this factor plays no relevant role in the observed dependence of the plasmon with the deposition time.

Modifications of the plasmon profiles are detected when the Ag NPs are deposited on top of graphene, especially in the red and IR spectral regions (Fig. 2(b) and (c)). The most evident aspects are i) an increase of the extinction values, and also of the integrated extinction (Fig. 2f and g) ii) a substantial broadening (higher red and IR weight) and iii) a red-shift (Fig. 2e and d). The increased extinction values are most probably related to the more effective sticking of the NPs onto graphene during the deposition compared to that on fused silica. The higher IR spectral weight is due to the mediation of graphene in the NPs interaction providing a channel for electrical connection without, however, producing a total delocalization of the oscillating electrons. The simulations we run for the NPs on graphene failed to reproduce the IR tail due to the very small contact surface between the NPs and graphene that, however, may play an important role as physical connection between the NP and the conducting graphene layer certainly affects plasmon resonance characteristics. FDTD methods require the computational domain to be gridded and could be very time consuming if fine details in the geometrical layout play some important role. The one-point contact between NPs and graphene leads to non-reliable or meaningless results and the time required to run these simulations is rather impractical.

The effect of graphene is not identical to that of the dielectric constant of a material medium where NPs are embedded. A redshift has been found in DDA simulations of silver particles partially embedded in mica spheres [7], but an increase of the IR tail such as the one we observe for NPs on graphene has not been reported. All our simulations were run taking into account the presence of the substrate, the NPs are deposited on top of fused silica. In every case a very small red shift (2–3 nm) is obtained compared with isolated NPs, but the shape of the extinction spectra remains unchanged.

3.2. Raman amplification originated by 1.8 nm AgNPs

To evaluate the behavior of the Raman amplification for ultrasmall NPs, the square of the electric field, E², has been calculated for different particle radii, 1.2 b R b 10 nm, as a function of the interparticle distances for a periodic array of NPs. The behavior is similar in this radius range so the results are again given in R units (z/R). The square of the electric field, E², at the equatorial plane of the NPs is plotted for two distances, d = 1.6R and 0.3R, in Fig. 4. The incident wave is perpendicular to the substrate and the polarization is as indicated in Fig. 4a by the white arrow. Hot spots are formed at the surface of the NPs in the direction of the incident polarization and their intensity increases as the NPs become closer. Profiles of the electric field intensity along the line of maximum intensity (vertical black line in Fig. 4c) aswell as 10% inwards (blue line) and outwards (red line) the NP are shown in Fig. 4d. The hot spots are highly localized at certain points of the NPs surface but their extension increases significantly as the distance is reduced. The Raman amplification is therefore highly inhomogeneous over the surface of the NPs.

Fig. 4.

Images of E² for a periodic array of Ag NPs with d = 1.6R (a) and 0.3R (b) at the equatorial plane (z = 0) as indicated by the continuous line in the scheme of two NPs in c). d) Intensity profiles along the vertical lines indicated in c): the black line corresponds to the surface of the NP and the blue and red lines to positions shifted R/10 inwards and outwards, respectively. The substrate is at z/R = -1. Continuous and dash-dot lines correspond to d = 0.3R and d = 1.6R, respectively.

The Raman signals from the R6G molecules deposited on top of the NPs/Gr/Q samples by spin coating from 10^-3 M methanol solutions are shown for different NPs deposition times (from 300 s to 900 s) in Fig. 5a. Furthermore, different tests decreasing R6G concentration (Fig. 5b) revealed that Raman amplification due to Ag NPs (1200 s) is significant even for concentrations down to 10^-6 M. In these graphs, Raman intensity has been normalized to the absorbance of R6G of each sample since there is no Raman signal without NPs.

Fig. 5.

(a) Raman spectra of one monolayer R6G on AgNPs/graphene/quartz for different NPs deposition times, b) spectra for different R6G concentrations on 1200 s AgNPs/graphene/ quartz, c) graphene Raman signal for different AgNPs samples. d) Raman intensity of graphene (normalized to its value without NPs) and of R6G as a function of the NPs coverage.

Fig. 5d shows the dependence of the amplification of the Raman signal of the underlying graphene (calculated after normalizing to the intensity without NPs) and of the Raman signal the R6G molecules as a function of the Ag NPs plasmon extinction (related to the NPs coverage/deposition time as shown in Fig. 2). In this case, it is not possible to normalize the Raman intensity of the R6G to the signal without AgNPs since, the R6G density used was 1 molecule monolayer, as evaluated from its absorbance, and the Raman peaks are below the detection limit. Two important observations have to be discussed: i) the measured amplification for graphene phonons is much lower than for R6G molecules and ii) the amplification is not lineal with the plasmon intensity (closely related to the total mass) for the R6G vibrations while it is almost linear for graphene.

The very different dependence of the Raman enhancement for graphene and for R6G molecules is mainly originated by the different geometrical configurations: while graphene is a flat layer which contacts each NP only at one tangent point (blue line in Fig. 4c), the R6G molecules wrap the NPs (red circles in Fig. 4c). Fig. 6a shows the distribution of E² at the equatorial plane (z = 0), at the substrate position (z= -R), which also corresponds to graphene location, and at an inter-mediate plane (z = -R/2) for a periodic array of NPs with an interparticle distance of 1.6 R.

Fig. 6.

a) E² maps a) for a periodic array of NPs with d = 1.6 R atdifferent planes (z = 0, -R/2 and -R = substrate, the z origin isatthe equatorial plane of the NPs) and b) at the substrate (z = -R) for d = 1.6R and 0.3R. The circles indicate the particle size. Calculated Raman amplification for R = 2 nm vs d c) and vs the plasmon position d); e) experimental and calculated Raman intensity vs. plasmon position.

The electric field at z = -R, where graphene is located, presents the lowest values in the vicinity of the NP, explaining the much lower amplification observed in graphene Raman phonons than in R6G modes. Moreover, while the reduction of the interparticle distance has a huge effect on the electric field amplification in the vicinity of the regions where the NPs surfaces are closer (z = 0, Fig. 4), it has very weak effect at z =-R (Fig. 6b). At the graphene plane no hot spots are generated so the amplification is expected to be proportional to the NPs density as observed in Fig. 5d.

The calculated Raman amplification integrated over the whole surface of the spheres, where the R6G molecules are located, is presented in Fig. 6c as a function of the interparticle distance, d, for R = 2 nm Ag NPs for excitation wavelengths in the usual range for Raman spectroscopy (488 nm and 600 nm). This averaged amplification is strongly dependent on d and therefore on the plasmon position (Fig. 6d). The calculated trend and values fit very well the experimental Raman intensities (once multiplied by a normalization constant).

3.3. Rhodamine–Ag-NPs interaction

The interaction between the R6G molecules and the Ag NPs may be established probably involving charge transfer and configurational modifications of the molecules. It is well known that the absorption spectrum of molecules can vary not only depending on the solvent but also on their concentration since interactions between molecules and the formation of dimers modify their geometrical configuration and their electronic states.

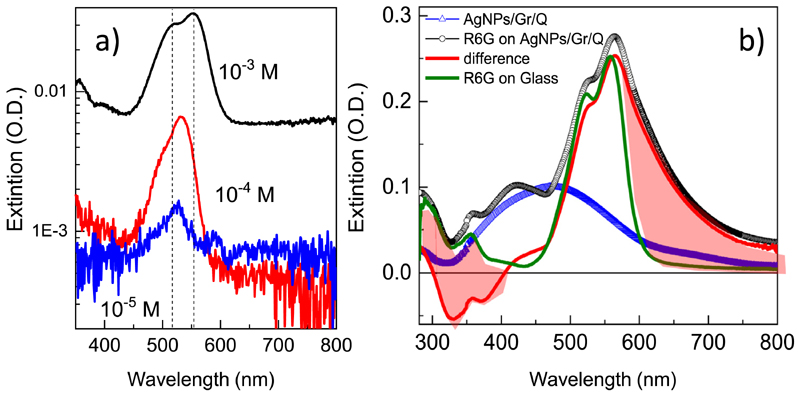
We have spin coated R6G films from solutions with concentrations from 10^-2 to 10^-5 M on glass to observe the modifications of the electronic structure around the HOMO-LUMO transitions observed by optical transmission (Fig. 7a). For films with OD values as low as 6 × 10^-3 (10^-4 M) the spectrum begins to be modified compared to that of 10^-5 M and, for OD = 0.03, the band at 524 nm clearly splits in two bands at 516 and 552 nm (for thicker films the spectrum shape remains almost unchanged). These changes are due to the inter-molecule interactions and to the formation of dimers or trimers [42,43]. However, different modifications occur when R6G molecules are deposited on the Ag NPs. Fig. 7b shows the spectrum for R6G deposited on the AgNPs 900/ Gr/Q sample (black circles) and that of the same sample (AgNPs 900/ Gr/Q) prior to the deposition of molecules (blue triangles) which shows the typical Ag plasmon. The green line plots the spectrum for a R6G film on glass with similar OD and the dashed red line is the difference between the spectra of the Ag NPs 900/Gr/Q sample with and without R6G. This difference spectrum differs significantly from that of R6G on glass (green line) evidencing the interaction between the R6G and the silver NPs.

Fig. 7.

a) Extinction measured for R6G films on glass spin coated form 10^-3 to 10^-5 M solutions. Note the logarithmic scale for O.D. b) Extinction for AgNPs deposited on graphene/quartz with R6G (black circles) and without R6G (blue triangles) and the red line is their difference. The green line is the extinction of R6G on glass. The red regions indicate the spectral weight transfer related to the deposition of R6G on AgNPs.

An important shift of spectral weight from the UV (b400 nm) to the red (N600 nm) occurs according to Fig. 7b (red areas). A shift of the Ag plasmon promoted by R6G molecules was previously reported for particular plasmon wavelengths [42], however, for the present plasmons no or small shift is expected. Moreover, the position of plasmons with and without R6G for low Rhodamine content (Fig. S4, SI) are almost identical. Simulations of the extinction spectrum corresponding to Ag NPs covered with R6G, as a layer with a refractive index different from that of air, do not account for the observed effect confirming the incidence of charge transfer processes.

3.4. Nanostructured Ag thin films vs. Ag ultrasmall NPs

A series of Ag thin films where deposited on fused silica with nominal thickness of 1, 2 and 4 nm (TF1, TF2 and TF4). In Fig. 8a an AFM topographic image and a characteristic profile of the 2 nm thick film, TF2, are shown. The films present a granular aspect with oblong grains and an aspect ratio that decreases between 10 (for TF1) and 3 (TF4) as the nominal thickness increases. The average in plane radii increase from ~7 (TF1) to 15 nm (TF4) (after deconvolution of the AFM tip size) as well as the average height from ~1.5 to 8 nm when nominal film thickness varies from 1 to 5 nm.

Fig. 8.

a) AFM image and profile of the Ag thin film TF2. b) Optical extinction of the films c) maximum extinction vs. the nominal film thickness and d) position vs. maximum extinction, e) Raman intensity of the 1653 cm^-1 R6G mode vs. extinction for the thin films and f) comparison of the Raman intensity of the 1.8 Ag NPs and Ag thin films.

The optical extinction curves of the films are plotted in Fig. 8b as and the Raman intensity of the R6G 1653 cm^-1 vibration versus the corresponding extinction value at the laser wavelength (488 nm) in shown in Fig. 8e. The increasing thickness of the films leads to i) a red-shift of the plasmon (Fig. 8d); ii) its broadening; and iii) an increase in its intensity (Fig. 8c).

The observed plasmon positions (450–550 nm) are extremely red-shifted compared to Mie predictions for the present sizes (360–365 nm). Moreover, the aspect ratio does not account for the observed trends in the plasmon features since it predicts the opposite trend: as the aspect ratio is reduced the plasmon blueshifts [7]. In this case also the interparticle distance is the most relevant parameter and explains the plasmon redshift as the nominal thickness increases. It is important to note that in the case of these larger oblong Ag NPs, the amplification of the R6G Raman signal is linear with extinction in O.D. (Fig. 8e), contrary to the exponential behavior observed for the 2 nm Ag NPs (Fig. 4c). An important observation is that the Raman amplification originated by ultra-small 1.8 nm NPs is higher than that due to 7–15 nm grains, which are close to the optimum size for non-interacting particles, for a given optical density. It can be concluded that the weight of the hot-spots in the amplification is important only for the extremely small NPs where the surface/volume ratio is high.

3.5. Combined nanostructured Ag films and 1.8 nm AgNPs

In order to evaluate the possibility to improve even more the amplification of the signal, more complex systems were fabricated combining thin films with R~10nm grains, to increase the Raman amplification related to a larger Agmass, and 1.8nm Ag NPs to promote the formation of hot spots. Each sample presents three regions: NPs (zone A), nanostructured thin film (TF) (zone B) and combined NPs and TF (zone C) deposited on fused silica substrates. In that way it is possible to reliably compare the plasmon characteristics of the different zones as well the Raman amplification of the R6G vibrational peaks of the molecules anchored afterwards by dip coating.

The nominal thickness of the nanostructured Ag film is either 3 or 5 nm (samples S3 and S5 respectively) and different Ag NPs densities were deposited for the different sample sets. Fig. 9a presents an AFM analysis of the three regions of the sample S3: zone A with only NPs (R ~ 2 nm obtained from the AFM height profiles), zone B corresponds to the 3 nm film TF with oblate spheroid grains and an aspect ratio around 5 and finally zone C where the average height is almost unchanged compared to zone B but the profiles reveal the presence of the Ag NPs. The scheme sketches the three situations within S3 sample with high AgNPs density (deposition time 600 s).

Fig. 9.

a) AFM topographic images and profiles and the schematized sections on the three regions of sample S3: A = NPs, B = TF and C = TF + NPs; b) extinction spectra of the three regions in samples with 3 nm (dots) and 5 nm (lines) thin films, in the inset a zoom of the NPs spectra is shown; c) Representative Raman spectra of R6G for sample 3 nm film in region B (red) and C (black). b shows the extinction spectra of samples S3 (dots) and S5 (lines) with low Ag NPs density (deposition time is 75 s). In black the regions without NPs (zone B) and in red with Ag NPs (zone C).

The plasmons correspondent to the Ag NPs (zone A), are extremely weak and present the resonance at 400 nm (see inset), while the TFs (zone B, red traces) are red shifted to 471 and 513 nm respectively for S3 and S5. The combination of NPs deposited on top of the films (zone C, black traces) leads to increased red-infrared spectral weight while the intensity at the maxima is slightly reduced. This is most probably due to some degree of delocalization of carriers from the grains promoted by the deposited NPs not reaching percolation since the sample is electrically insulating. For this very low NPs density (estimated to be around 9.7 × 10¹¹ cm^-2), the resonance at the laser excitation (488 nm) is reduced in the region TF + NPs and however, the R6G Raman signal increases a factor 3 by the deposition of the NPs in the case of S3 sample. However, for higher NPs density, the amplification only increases linearly with the OD. In this case the formation of hot spots is hindered by an increased delocalization of the carriers.

4. Conclusions

We have evaluated the amplification capability of ultra-small single crystalline silver NPs with ligand free surfaces of radius R ~ 1.8 nm and very narrow size distribution deposited on glass and on graphene. Increasing NPs density strongly red shifts the measured plasmon wavelength (from 400 to 500 nm) and increases its width irrespective of the substrate tested. Simulations of 2D Ag NPs arrays using three-dimensional finite-difference time-domain (FDTD) calculations showed that the reduction of the interparticle distance, d, leads to a redshift and widening of the plasmon. These effects are general for NPs with radii, R, upto 10n min terms of the normalized distance d/R and become important when d b R. The impact of a possible capping layer of the NPs (due to oxidation or adsorbed carbonaceous species)is calculated to be small. The measured plasmons are originated by distributions of interparticle distances that become narrower and shift to smaller distances as the density increases. The role of graphene as a substrate for NPs deposition is to partially delocalize the free carriers mediated by the conductive graphene single layer and favors the efficient sticking of the NPs on the substrate.

The amplification of Raman signals of graphene and of a spin coated Rhodamine 6G (R6G) film vary very differently on increasing the NPs density. In the case of graphene, the amplification increases linearly with the plasmon extinction at the excitation wavelength, while that for R6G it is almost exponential due to their different location relative to the NPs. The electric field at the substrate position (the position of graphene) presents a weak amplification and the reduction of the inter-particle distance does not modify significantly the electric field. On the contrary, the R6G molecules, which wrap the NPs, are affected by the very intense fields created at the smallest gaps in between the NPs as the distance decreases. The observed variation of the Raman intensity as a function of the plasmon resonance corresponds very well with the calculated amplification upon reducing the mean interparticle distance which is in turn associated to an increase of the plasmon resonance. The exponential behavior demonstrates the high efficiency of the hot spots formed at the interparticle gaps.

The amplification of these ultra-small NPs is also compared to that of larger grains (7 b R b 15 nm) of silver films. The red shift and widening of the plasmon observed as the film thickens is also mainly due to the reduction of the interparticle distance, however, the amplification of R6G is in this case only proportional to the plasmon extinction. Importantly, the amplification provided by the ultra-small NPs is higher than that of the larger grains from the films for the same extinction value, mainly due to the high electric fields at the ultra-small NPs gaps. From the applications view, it is relevant that it is possible to efficiently increase the amplification by depositing low density layers of ultrasmall NPs on top of granular thin films by creating extra hot spots. This work demonstrates that ultra-small NPs are more efficient for SERS than the commonly used larger NPs.

Supplementary Material

Supplementary data to this article can be found online at https://doi.org/10.1016/j.matdes.2020.108702.

Highlights.

• High amplification capability of silver ultra-small (radius R~1.8 nm) spherical nanoparticles with ligand-free surface.

• The reduction of inter-nanoparticle distance, d, red-shifts (N130 nm) and widens (N 90nm) the Ag plasmon.

• Raman signal amplification of Rhoda-mine and graphene vary very differently on d due to spatial electric field distribution.

• Amplification for 1.8 nm nanoparticles is higher than for larger grains due to higher available hot-spots density.

• Combining granular films with an extremely low-density layer of ultrasmall nanoparticles further enhances amplification.