Abstract
Diffusion MRI has the potential to provide important information about the connectivity and microstructure of the human brain during normal and abnormal development, noninvasively and in vivo. Recent developments in MRI hardware and reconstruction methods now permit the acquisition of large amounts of data within relatively short scan times. This makes it possible to acquire more informative multi-shell data, with diffusion sensitisation applied along many directions over multiple b-value shells. Such schemes are characterised by the number of shells acquired, and the specific b-value and number of directions sampled for each shell. However, there is currently no clear consensus as to how to optimise these parameters. In this work, we propose a means of optimising multi-shell acquisition schemes by estimating the information content of the diffusion MRI signal, and optimising the acquisition parameters for sensitivity to the observed effects, in a manner agnostic to any particular diffusion analysis method that might subsequently be applied to the data. This method was used to design the acquisition scheme for the neonatal diffusion MRI sequence used in the developing Human Connectome Project (dHCP), which aims to acquire high quality data and make it freely available to the research community. The final protocol selected by the algorithm, and currently in use within the dHCP, consists of 20 b=0 images and diffusion-weighted images at b = 400, 1000 and 2600 s/mm2 with 64, 88 and 128 directions per shell, respectively.
Keywords: diffusion MRI, HARDI, multi-shell, neonatal imaging
1. Introduction
Diffusion MRI (dMRI) has been the focus of intense research over the last 20 years, holding great promise for investigation of tissue microstructure due to the technique's unique sensitivity to the micron-scale diffusion of water. In recent years, there has been increasing interest in the use of so-called multi-shell dMRI, driven to a large extent by improvements in image acquisition and reconstruction methods, which can now provide the amount of data required within clinically feasible scan times. A number of promising methods have been proposed to model data of this nature (eg, Jensen et al1; Jeurissen et al2; and Kaden et al, among others3–6). Many of these approaches are based on the so-called standard model of diffusion,7 consisting of intra- and extra-axonal compartments convolved with a corresponding fibre orientation function, optionally with an additional isotropic cerebro-spinal fluid compartment.6,8–16
More recent work has also investigated the use of additional contrast mechanisms, such as spherical and planar tensor encoding,17–20 more complex Q-space trajectories,21 variable echo times22 and variable inversion times,23,24 among others. Many of these entail a considerable increase in scan time, and the use of custom sequences, limiting their widespread use in the immediate future. Furthermore, these methods are still under active research, and a consensus has yet to be reached regarding which of these should be deployed. We therefore decided to focus on optimisation of the multi-shell pulsed gradient spin echo (PGSE) sequence, as it is likely to remain the most widely used acquisition strategy for the foreseeable future, especially for large longitudinal and cross-sectional studies.
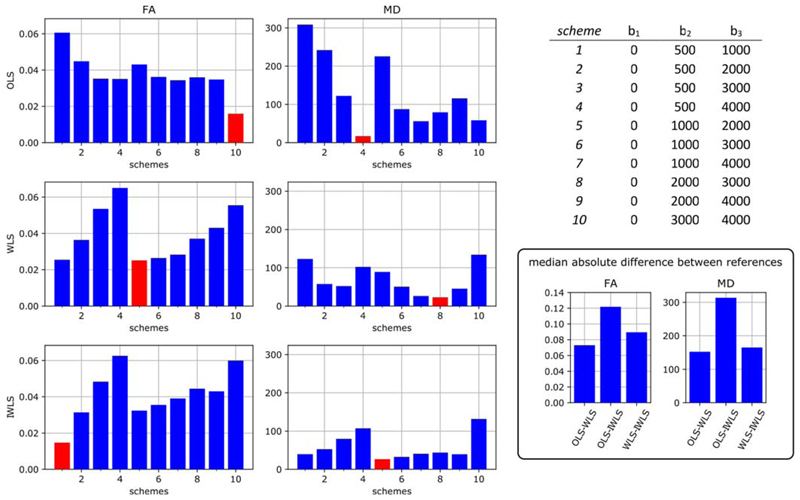
A common requirement for researchers when setting up a multi-shell dMRI protocol is the determination of optimal imaging parameters, particularly the number of b-value shells and the number of diffusion-weighting directions and the b-value per shell. However, there are many different reconstruction algorithms available, and no clear consensus as to which is best. The lack of ground truth is also problematic, motivating the use of hardware phantoms with known fibre configurations.25 This makes it very difficult to identify optimal imaging parameters, since any optimisation will typically aim to reduce errors in the estimated parameters of a given model; this obviously does not provide any guarantees that the data would be suitable for a different (possibly yet to be devised) reconstruction algorithm. To illustrate the difficulties with such an approach, Figure shows the median absolute deviation in DTI metrics computed using different subsets of an extended data acquisition to seek protocols that produce low errors. The approach is to calculate mean diffusivity (MD) and fractional anisotropy (FA) using a target analysis method of choice for all the available data (six shells, 50 directions on each, five subjects) to determine a “reference value” and then to do the same using only three of the shells to find feasible duration protocols that are reliable in the sense of producing the lowest median error (see the Appendix for full details). This was performed using three different commonly used tensor estimation strategies, namely, ordinary least-squares (OLS), weighted least-squares (WLS) and iteratively reweighted least-squares (IWLS),26–29 all implemented within MRtrix3. Depending on the analysis method used, different “optimal” protocols are identified (see the Figure 1 caption for details). It is striking that this is the case even although the same model of diffusion (the diffusion tensor) is assumed for all cases.
Figure 1.
Optimising sampling schemes for measuring fractional anisotropy (FA) and mean diffusivity (MD) using minimal discrepancy relative to a superset of all available data for three different DTI analysis methods (ordinary least squares [OLS], weighted least squares [WLS] and iteratively reweighted least squares [IWLS]). The optimal protocols, which are different in each case, are highlighted in red. The bar graphs show the median absolute difference in DTI metrics obtained using all the data compared with those obtained using different subsets of three of the available b-values. The results for MD are shown in units of μm2/s (FA is dimensionless). Differences were computed voxel-wise, and the median absolute difference was calculated over the whole brain for each of the five subjects included in the study, then averaged across subjects. Results are shown for FA (left) and MD (centre), computed using three commonly used estimators: OLS (top row), WLS (middle row) and IWLS (bottom row). The x-axis corresponds to the numbered schemes shown in the table on the top right, which specify the included shells. The schemes with the lowest discrepancy are highlighted in red. The bottom right panel shows the equivalent median absolute difference between the metrics obtained with the different fitting approaches using all the available data (ie, the difference between the references used for the other plots)
There is therefore a need for a means to determine acquisition parameters that provide the most eloquent, information-rich data in a manner agnostic to any particular reconstruction algorithm. This is particularly important for large-scale data collection projects that will provide a shared resource to be used by diverse academic groups for purposes that the users, rather than the data collectors, define.
This study was motivated by the need to optimise the dMRI acquisition scheme for the developing Human Connectome Project (dHCP), which aims to acquire structural, functional and diffusion MRI data from more than 1000 neonates and fetuses, among other clinical, behavioural and genetic measures (http://www.developingconnectome.org/). Since these data are to be made freely available to the wider neuroimaging community, it was important to acquire data suitable for the widest possible range of analysis methods. Moreover, the diffusion-weighted (DW) signal in the perinatal age range differs markedly from that in adults, in that it exhibits much higher apparent diffusion (suggesting increased extracellular and reduced intracellular content), and much lower anisotropy. Furthermore, these characteristics vary strongly as a function of both location and age, as the various structures in the brain mature at different rates. Much analysis work to date has used algorithms designed for adult studies, but there is clearly scope for optimising all aspects of the analysis/modelling pipeline and this could result in methods that are different from existing approaches.
Taken together, these factors provide strong motivation to develop a data-driven strategy that can be used to design data acquisitions for a desired target subject group, optimised for information content rather than to support a predefined processing method. To address this challenge, we propose to use an information-theoretic approach, similar in spirit to our previous work on optimising single-shell dMRI parameters.30
2. Methods
In this paper, we propose a framework to determine the optimal number of shells, along with the corresponding b-value and the number of directions sampled. To make this problem tractable, we separate the b-value dependence from the orientation dependence and treat each problem separately. For the b-value dependence, the central concept is then to identify a linear basis to represent the b-value dependence of the data (voxel values) as measured empirically, and to determine the number of coefficients of that basis that can realistically be measured in practice. Given this number, the task is then to identify a set of parameters (i.e., the number of shells, b-value per shell and the number of DW volumes per shell) that provide optimal sensitivity to these coefficients.
The angular dependence was itself the focus of previous work, applied to the adult case30; here, we simply deploy the same methodology to determine the per-shell sampling density required to capture the detectable number of spherical harmonics. Briefly, the approach expresses the dMRI signal for a single b-value shell using the spherical harmonics basis, and identifies the highest angular frequency term that can realistically be detected in the data. This analysis is performed only in voxels deemed to contain a single-fibre population, since these contain the highest angular frequency content, and also because this allows averaging across voxels (after realignment of the fibre direction to a common axis). For further details, the reader is referred to Tournier et al.30 This analysis provides an estimate of the angular frequency content at each b-value, which translates directly into the corresponding minimum number of directions required for nonlossy sampling (i.e., without aliasing in the angular domain). Once the optimal b-values have been identified, this analysis can be used to ensure that the sampling density within each shell is adequate.
To determine the sampling requirements across b-values, we focus on the b-value dependence of the orientationally averaged raw DW signal as a function of b-value. Assuming sufficiently dense and uniform sampling, the mean DW signal over a single b-value shell is rotationally invariant, and independent of the fibre arrangements.3,31,32 Near-uniform distribution of gradient directions can be obtained using electrostatic repulsion approaches,33,34 as used in this study, and sufficient sampling density can be verified using the approach described above.30
As an overview, this study consists of the following steps:
Acquire data that are sufficiently densely sampled in the b-value and angular domains to capture all the expected features of the DW signal.
Identify a suitable data-driven linear basis to represent the signal.
Estimate the effect size observed in the signal for each coefficient of that basis.
Identify the set of acquisition parameters that provide optimal sensitivity to these coefficients.
The optimisation of the acquisition parameters (the last step in the list above) was performed by:
For a given set of b-values and corresponding number of directions, define a measure of sensitivity to the coefficients of interest.
For a given set of b-values, optimise this sensitivity measure with respect to the number of directions per b-value shell.
Given a fixed number of b-value shells, optimise the sensitivity measure with respect to the value of these b-values (with the corresponding number of directions optimised as per the previous step).
Each of these steps is described in more detail in the following sections.
2.1. Data acquisition and preprocessing
Data were acquired from five neonates scanned at term-equivalent age (see Table 1 for details) on a Philips Achieva 3 T magnet at the Evelina Newborn Imaging Center at St. Thomas’ Hospital (London, UK). The study was approved by the National Research Ethics Committee and written informed parental consent was obtained prior to scanning. The system was equipped with a standard 32-channel head coil, using a DW pulsed gradient spin-echo EPI sequence (TE/TR = 70/2260 ms, 2 × 2 mm voxel size, 11 slices with 2 mm thickness with a 1 mm slice gap, 112 × 112 matrix, SENSE factor 2, single anterior–posterior phase-encode direction). Data were collected along 50 noncollinear directions optimised using electrostatic repulsion33 at b-values of 500, 1000, 2000, 3000 and 4000 s/mm2, along with five b=0 s/mm2 volumes. These directions were optimised using the MRtrix3 “dirgen” command, and the same set of 50 directions was used for each shell. We note that in adults, a spherical harmonic order of 8 (45 parameters) was shown to be sufficient to capture all realistically measurable components of the signal, even up to b = 5000 s/mm2.30 Therefore, the 50 directions used in the acquisition here are sufficient to satisfy this criterion, especially considering that neonatal data will exhibit lower anisotropy than observed in adults.35–37
Table 1.
Details of the subjects included in this study
| GA (weeks) | PMA (weeks) | Clinical features | Imaging findings |
|---|---|---|---|
| 39 + 2 | 45 + 4 | Smith-Lemli-Opitz syndrome | Cerebellar hypoplasia, small hypothalamic hamartoma |
| 38 + 0 | 40 + 1 | Fetal alcohol syndrome | Small but otherwise normal imaging appearance |
| 40 + 5 | 42 + 5 | Seizures, antenatal ventriculomegaly | Perisylvian polymicrogyria |
| 33 + 3 | 36 + 1 | Preterm | small germinal matrix haemorrhage |
| 39 + 6 | 40 + 5 | Meconium aspiration, mild hypoxia | Normal imaging appearance |
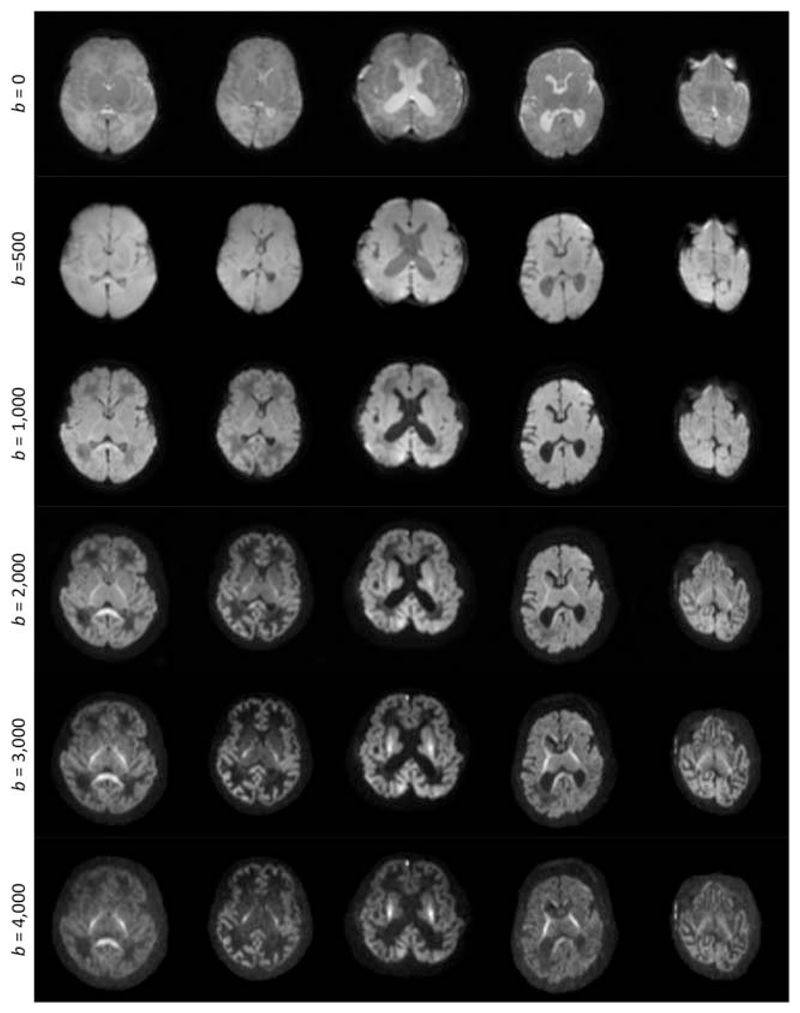
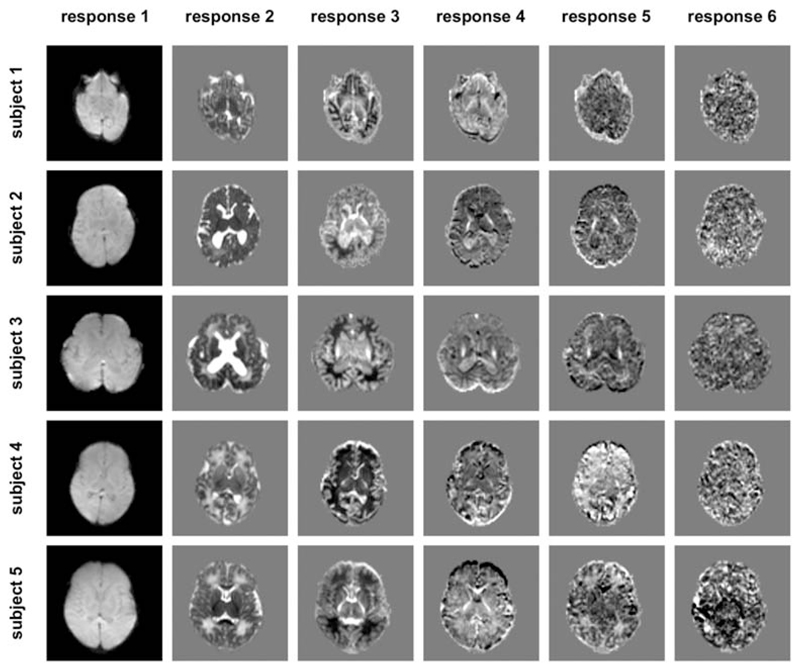
For each subject, the data were first corrected for motion- and eddy current-induced distortions using the FSL EDDY (version 5.0.8).38,39 The mean DW signal for each shell was then computed within a brain mask. Typical images of the resulting mean signal are shown in Figure 2.
Figure 2.
Images of the mean raw dMRI signal for all five subjects (columns), for each b-value (rows). These constitute the input for the optimisation algorithm. Note that the images are windowed independently for each b-value to allow visualisation of the contrast in the high b-value images
2.2. Identifying a suitable linear basis
In contrast to the angular domain, where spherical harmonics form a natural basis,30 there is no such natural basis to represent the b-value dependence of the signal. While some bases have been proposed,40–47 there is an inherent scale dependence that makes the analysis dependent on user-defined parameters (D).48 For this reason, we adopted a fully data-driven, model-free basis, derived using matrix decomposition approaches.
We use the compact singular value decomposition (SVD), which decomposes a general m × n matrix A (with m ≤ n) as USVT, where U is a m × m orthonormal matrix, S is a m × m diagonal matrix of singular values, and VT is a m × n orthonormal matrix. To make use of this decomposition, we form the compact SVD of the transpose of D:
| (1) |
More specifically, we consider a multi-shell protocol consisting of Ns b-values, with ns uniformly distributed DW directions for the shell index s. We form the Ns × Nv matrix D consisting of the mean DW signal for each brain voxel at each b-value, where Nv is the number of voxels in the subject-specific brain mask. We wish to decompose D into a Ns × Nv matrix W of per-voxel weights, and a Ns × Ns orthonormal basis matrix H, such that:
| (2) |
The weight and basis matrices can then be obtained as:
| (3) |
Furthermore, thanks to the properties of the SVD, the singular values (i.e., the diagonal of S) can be used to obtain an estimate of the typical component-wise effect sizes ϵ (this evaluates to the root-mean-square value of the weights across the rows of W):
| (4) |
2.3. Measure of sensitivity
The decomposition described above provides a linear breakdown of the effects observed in the data, and of their relative contributions. This can be used to predict the sensitivity to these various effects for a candidate acquisition with the same b-value shells, but different numbers of volumes per shell. Assuming independent and identically distributed Gaussian noise, the expected variance in the measured mean DW signal for each shell s is simply , with ns the number of volumes in shell s, and σ 2 the variance per measurement in the data. This rests on the observation that provided the sampling density is uniform and sufficiently dense (as per Tournier et al30), the variance in the mean DW signal for a given shell is inversely proportional to the number of DW volumes acquired at that b-value; the mean DW signal is orientationally invariant, and each volume contributes equally to its estimation.
The predicted variance in the mean per-shell signal can be used to predict the variance in the estimated basis coefficients using the law of propagation of errors.49 Based on Equation 1, if d = Hw is the vector of mean per-shell signals for a single voxel (where w is the corresponding vector of basis coefficients), the variance–covariance matrix Σw for the coefficients w is related to the corresponding variance–covariance matrix Σd for the mean per-shell signals d according to:
| (5) |
Since H is orthogonal by construction, H −1 = HT, yielding:
| (6) |
With repeated measurements per shell, (see above). Hence:
| (7) |
Finally, we compute the coefficient of variation (CV) for coefficient c as the ratio of its standard deviation (given by the square root of its variance Σw(c,c)) to its effect size ϵc (as provided in Equation 4):
| (8) |
Note that CVc is equivalent to the inverse of the contrast-to-noise ratio (CNR) of the coefficient of interest.
2.4. Optimising the number of directions per shell
The optimal acquisition should strive to minimise the combined CV of the Nc estimated coefficients. We therefore use the sum of squared coefficients of variation (SSCV) as a measure of optimality:
| (9) |
Note that if the effect size were the same for all coefficients, this is proportional to the sum of the variances, which is appropriate for independent measurements. However, when effect sizes differ, this measure is most strongly influenced by the coefficients with the highest CV, pushing the optimisation towards parameters that maximise the CNR of the noisiest components, without overly penalising high CNR components.
We now need to derive the number of directions per shell n = {ns} that maximise the sensitivity, and hence minimise the SSCV, within the constraint that the number of DW volumes, N total, is fixed by scan time limitations:
| (10) |
This can be solved using Lagrange multipliers:
| (11) |
The derivative with respect to the number of directions in shell s is:
| (12) |
Setting the derivative to zero yields:
| (13) |
This therefore provides the optimal number of DW volumes for shell s relative to the other shells. Since we assume that the total number of volumes is fixed by scan time constraints, the absolute numbers can trivially be obtained by normalising to N total:
| (14) |
where is the value obtained by setting λ in Equation 13 to an arbitrary constant. It is interesting to note that with this derivation, the fractions of measurements on each shell are independent of N total or σ: they depend purely on the intrinsic effects in the DW signal.
2.5. Optimising the b-values
So far, the derivation above holds for data acquired over a fixed number of shells with predetermined b-values. If a sufficiently large number of different combinations of shells and b-values were available, this could be used to identify the optimal set of parameters, by searching for the subset of b-values with minimum SSCV (Equation 9). It is, however, impractical to acquire data over a sufficient number of b-values to ensure the search is exhaustive, particularly in a neonatal cohort where scan times must be kept short.
We therefore used interpolation methods to resample the acquired data, allowing the generation of predicted data for any combination of b-values; this approximation is justified on the grounds that the diffusion signal varies smoothly as a function of b-value, so that interpolation errors are likely to be minimal. For this purpose, we use the Piecewise cubic Hermite Interpolating Polynomial (PCHIP) algorithm50 available in Matlab (MathWorks, Natick, MA, USA), which has the desirable property of explicitly preserving monotonic behaviour between sample points.
Given a fixed desired number of shells, the optimal b-values for each shell are determined using a simple nonlinear optimisation approach (the Nelder–Mead simplex algorithm,51 as implemented in Matlab’s fminsearch routine). For each iteration, the mean DW signals per voxel at the current b-values are obtained by PCHIP interpolation from the measured data. The SSCV of the parameters is then optimised with respect to the number of directions per shell as described earlier in Optimising the number of directions per shell (section 2.4). Finally, the optimised SSCV value is used as the cost function for the search over b-values.
2.6. Accounting for T 2 decay
So far, the derivation has ignored the effect of T 2 decay on the sensitivity of the acquisition. In practice, the shell with the highest b-value will dictate the echo time of the entire acquisition (assuming a constant echo time is desired, as is typically the case), and this will have a direct impact on the SNR of the data. To account for these effects, we include a b max-dependent T 2 decay term, assuming a standard PGSE sequence, similar to Alexander and Barker,52 with square diffusion-sensitising gradients and the following parameters:
A 5 ms delay between the 90° excitation pulse and the onset of the first DW gradient pulse.
A 5 ms pulse duration for the 180° refocusing pulse (including slice selection gradients and crushers, if any).
A 15 ms delay between the end of the second DW gradient pulse and echo time.
80 mT/m gradient strength.
The attenuation factor is then computed as exp(−TE/T 2), and is used to scale the effect sizes in Equation 4, inherently penalising parameters sets that include a high b-value shell. Results were generated assuming T 2 = 100, 150 and 200 ms, which are typical for neonatal brain,53 as well as ignoring T 2 relaxation.
2.7. Analysis within and across subjects
As described, the analysis requires input data in the form of a Ns × Nv matrix corresponding to the mean DW signal for each of the Ns = 6 b-value shells across all Nv brain voxels. The analysis was applied for each subject independently within a mask of the brain voxels (with Nv ranging from 14 894 to 23 481 voxels).
In addition, the analysis was also performed on a single dataset formed by concatenating the data for all subjects along the slice axis, for a combined total of Nv = 99 306 voxels. Unless otherwise stated, the results shown were produced with this combined analysis.
3. Results
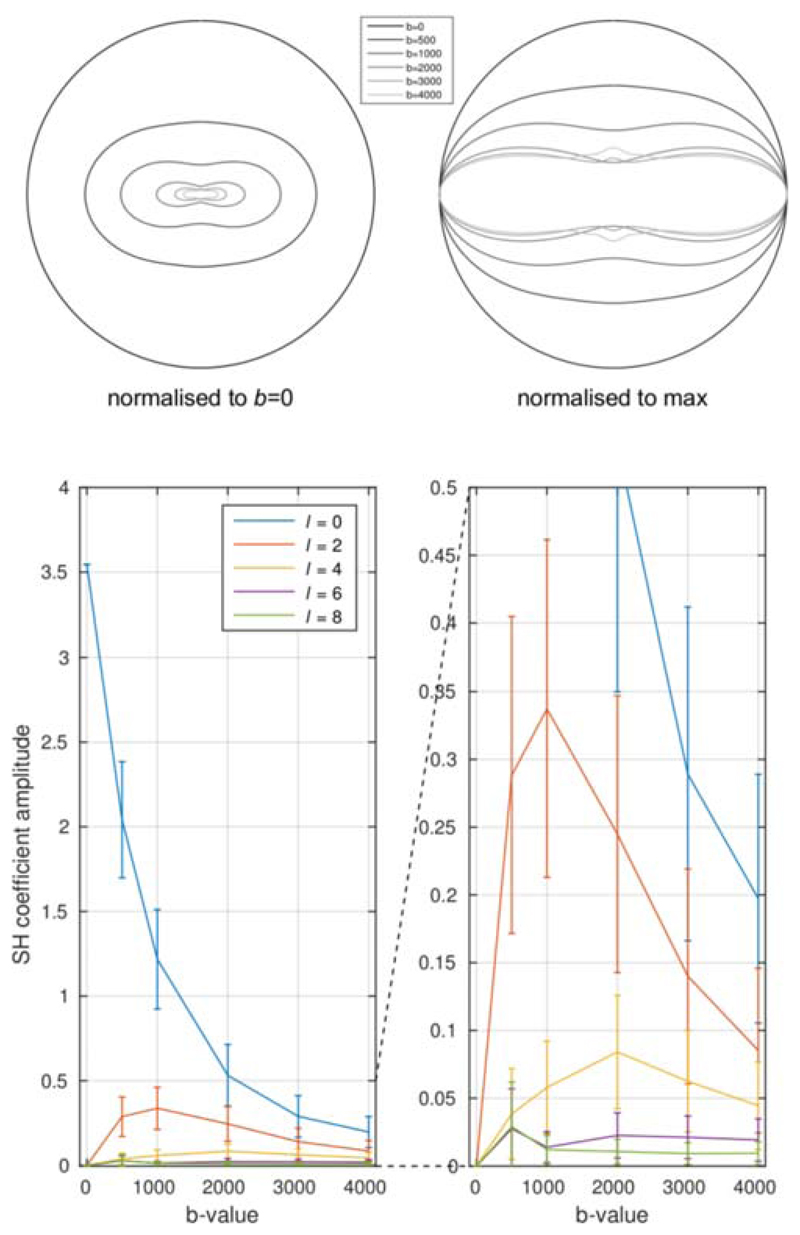
The angular domain analysis shows that the angular frequency content is much lower in neonates (Figure 3) than has been shown previously in adults,30 as expected. In our data, spherical harmonic terms of order 8 and above are indistinguishable from noise for any realistic SNR value (Figure S1). Note that this does not imply that these terms are strictly zero, but that they can, for all intents and purposes, be neglected for any reasonable voxel-wise analysis. Order 6 terms were also small but could be observed with b ≥ 2000 s/mm2, implying that a minimum of 28 directions are required at these b-values. At lower b-values, only spherical harmonic terms of order 2 or 4 could be detected, implying a minimum of 6 and 15 directions, respectively.
Figure 3.
Angular frequency content of dMRI signal in neonates, as a function of b-value (cf.30). Top: polar plot of the signal (fibre orientation is along the vertical axis), showing the rapid decrease in signal with increasing b-value, along with the expected increase in angular contrast. Bottom: a plot of the corresponding spherical harmonic coefficient amplitudes. Angular frequencies above l = 4 are already within the noise floor, although there is a suggestion that l = 6 might be detectable for b ≥ 2000 s/mm2. This implies that a minimum of 15 and 28 DW directions are required for b < 2000 s/mm2 and b ≥ 2000 s/mm2, respectively
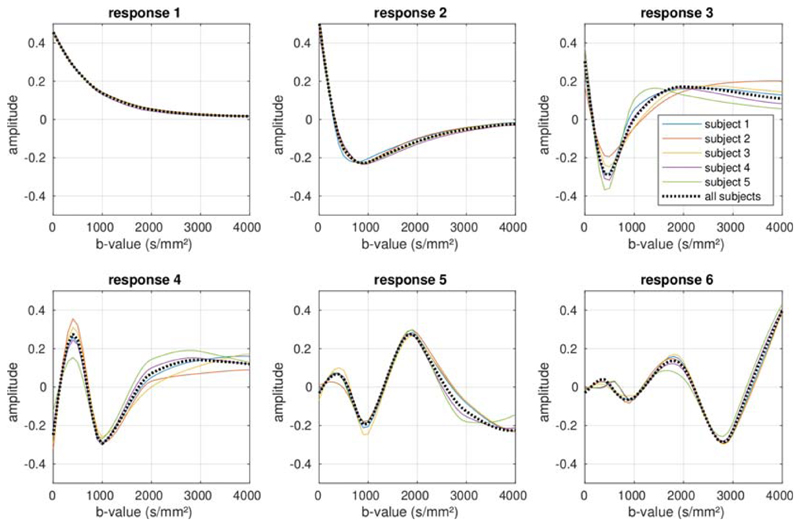
The basis functions H and weights maps W (cf. Equation 3) derived using SVD are shown in Figures 4 and 5, respectively, and are remarkably consistent across subjects. The first component corresponds to the mean DW signal over all voxels, with the higher-order components showing increasingly rapid oscillations with b-value. Clear structure can be observed in the corresponding weights maps for at least the first four components (although the fourth component may possibly contain some residual misregistration due to, for example, motion or eddy currents, as well as any actual biology-related structure). In our data, the fifth order lacks consistency across subjects, suggesting that the remaining spatial structure may be strongly related to artefacts in the data. The sixth and highest order that could be derived from the test data given the number of shells, lacks both consistency across subjects and anatomical coherence, suggesting that noise and artefacts have become completely dominant. The effect sizes for these components decrease rapidly for the higher-order coefficients, as shown in Table 2.
Figure 4.
The basis functions observed in the data, for all five subjects included in the study. The basis functions estimated from each subject when analysed independently are shown by the solid coloured lines, and show a high degree of consistency across subjects. The dotted black line shows the basis functions estimated from the combined data across all subjects. The basis functions can be seen to represent increasingly rapid oscillations in the b-value dependence, with the first component corresponding to the mean signal across the data. See Table 2 for the corresponding effect sizes
Figure 5.
Weights maps for each component in Figure 4, for all five subjects included in the study
Table 2.
Effect sizes for each observed component in the decomposition (as shown in Figure 4, across all subjects (arbitrary units)
| component | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| effect size | 1.000 | 0.134 | 0.038 | 0.018 | 0.009 | 0.004 |
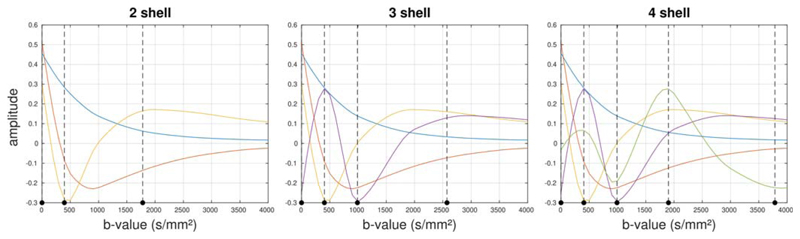
The optimal b-values selected by the algorithm are shown in Figure 6 for the case of 2-, 3- and 4-shells (not including the b=0 shell), assuming a T 2 value of 150 ms in neonatal brain tissue.53 Figure 7 shows the effect of different T 2 values for the 3-shell case. In all cases, a low b-value in the region of b = 400 s/mm2 is included, and can be seen to provide good separation between the first component and the other smaller components. In general, the algorithm seems to distribute b-values in a way that provides optimal separation between the different components, as desired. When more shells are included, the highest b-value selected increases, particularly when T 2 relaxation is ignored. When relaxation effects are included, the maximum b-value never exceeds b ≈ 2600 s/mm2.
Figure 6.
Optimal b-values selected by the algorithm, for 2-shell (left), 3-shell (middle) and 4-shell (right) cases, overlaid on the corresponding basis functions. The vertical dotted lines indicate the optimal b-values identified. Results obtained assuming a T 2 value of 150 ms
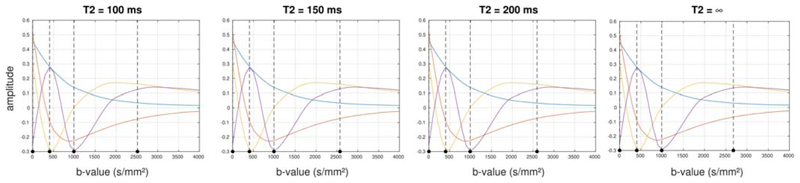
Figure 7.
Effect of T 2 on optimal b-values selected for the 3-shell case. The vertical dotted lines indicate the optimal b-values identified the T 2 value stated for each plot. While T 2 does have an influence, it is relatively minor, with lower T 2 leading primarily to a slightly reduced maximum b-value, with little to no impact on the other selected b-values
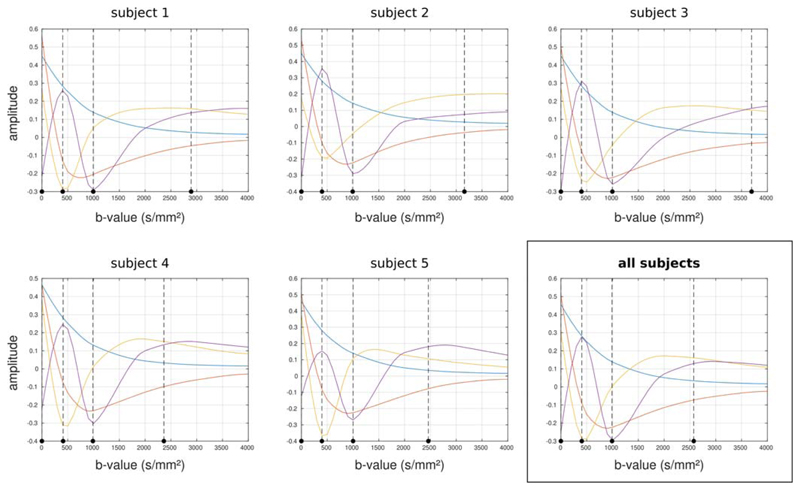
The b-values selected as optimal are stable across subjects, apart from the maximum b-value, as shown in Figure 8 for the 3-shell case. The maximum b-value varies in this case from b ≈ 2300 to 3500 s/mm2; this is likely related to the signal levelling out as a function of b-value in this range, leading to a broad optimum.
Figure 8.
Optimal b-values selected by the algorithm when applied to each subject individually for the 3-shell case and assuming T 2 = 150 ms. The vertical dotted lines indicate the optimal b-values identified in each case. While there is some variation in the maximum b-value, the other b-values remain very stable
Table 3 shows the optimal results for 2-, 3- and 4-shells assuming T 2 = 150 ms (suitable for neonates at 3T53). Along with the optimal b-values, the optimal number of directions per shell are also listed as a percentage of the total number of volumes acquired. For reference, the CNR for the coefficients themselves is shown in Table 4, assuming SNR = 30 and Ntotal = 100 imaging volumes. As expected, the CNR drops rapidly for the smaller coefficients, and is typically improved by using the smallest number of shells needed to characterise that coefficient (eg, b=0 + 2 shells to characterise the third coefficient). These CNR calculations can be generalised to arbitrary conditions by adjusting them based on the actual number of volumes and SNRb=0 values:
| (15) |
As expected, larger numbers of volumes are needed for the higher b-value shells. This is expected given the lower SNR available at these b-values, and also helps to ensure that the minimum orientation sampling density requirements (identified earlier using the angular frequency analysis) are satisfied.30
Table 3.
Optimal b-values (in s/mm2) for each shell and corresponding number of directions (Ntotal), expressed as a percentage of the total number of volumes acquired. Results are shown for the 2-shell, 3-shell and 4-shell cases, assuming a T 2 value of 150 ms
|
| ||||||
| 2 shells | b-value | 0 | 395 | 1781 | ||
| Ntotal | 12% | 29% | 59% | |||
|
| ||||||
| 3 shells | b-value | 0 | 404 | 990 | 2574 | |
| Ntotal | 6% | 19% | 28% | 47% | ||
|
| ||||||
| 4 shells | b-value | 0 | 405 | 990 | 1901 | 3784 |
| Ntotal | 3% | 9% | 16% | 29% | 43% | |
|
| ||||||
Table 4.
Contrast-to-noise ratios (CNR) for each component, as would be estimated using the corresponding parameters in Table 3. These values assume a T 2 value of 150 ms, a total of Ntotal = 100, and an SNR in the b=0 images of 30
| component | 1 | 2 | 3 | 4 | 5 |
| 2 shells | 152 | 18 | 6.0 | ||
| 3 shells | 125 | 16 | 4.5 | 2.7 | |
| 4 shells | 88 | 13 | 4.0 | 2.1 | 1.3 |
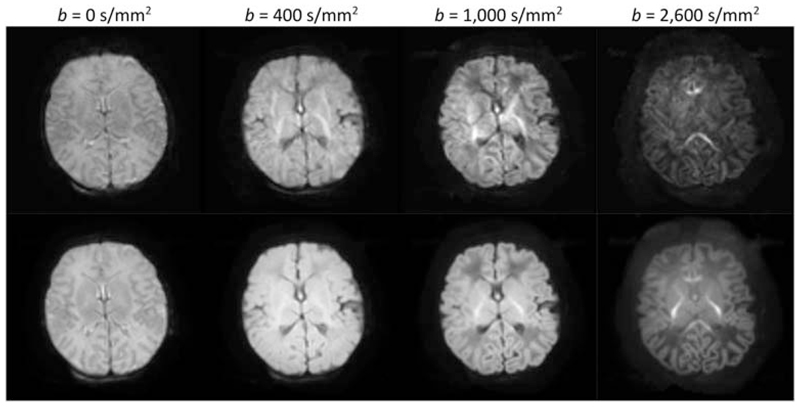
Based on this optimisation, a 3-shell protocol was adopted for the dHCP.54 The acquisition includes a total of 300 samples distributed in the proportions listed in Table 3. Figure 9 shows example images and shell average images acquired as part of the dHCP study (PGSE EPI acquisition with multiband factor 4, 64 slices, TE/TR = 90/3800 ms, 1.5 × 1.5 × 3 mm resolution, four phase-encoding directions, SENSE 1.2, Partial Fourier 0.855), after correction for EPI distortion, subject motion and outliers.38,39 While the individual images in the highest shell display the expected low SNR, the shell average reveals a highly coherent anatomical structure confirming its information richness, which can be well accessed by virtue of the large number of samples collected. All shells have angular sampling in excess of the requirements determined from the pilot data.
Figure 9.
Single diffusion-weighted images (top row) and mean diffusion-weighted image (bottom row) for each shell for a typical subject acquired using the final dHCP protocol
4. Discussion
This study provides a data-driven framework to identify the optimal parameters for multi-shell HARDI acquisitions, based on an information-theoretic approach. It is independent of any particular reconstruction/diffusion analysis algorithm, which is a significant advantage given that many of these approaches are under active development, have a number of different tuneable parameters, and are designed to provide different types of information. As illustrated in the Appendix, a protocol optimised for any one of these would therefore not be guaranteed optimal for any of the other methods (or indeed, any other parameters or outputs of the same method). The proposed design method allows protocols to be implemented now that will remain future-proof as novel analysis approaches are developed.
While a number of decompositions could be used for the b-value dependence, singular value decomposition is arguably the most appropriate for this study. The SVD provides a unique and complete signal representation with a clear interpretation as components of decreasing effect size. In contrast to other factorisations that deploy biophysical constraints, for example, to enforce nonnegativity in both weights and basis functions,55–57 the SVD deliberately avoids any such constraints. As such, we can ensure that the optimised multi-shell HARDI scheme is driven by the data itself, and not by implicit assumptions of a particular tissue model.
The optimisation suggests that the optimal number of directions per shell can be expressed as a fraction of the total number of volumes to be acquired. Furthermore, the CNR of the estimated coefficients will scale with the square root of the total number of measurements. These results can therefore easily be tailored to the particular circumstances under which the protocol is to be used, using the recommendations outlined below:
Identify the desired imaging parameters (eg, resolution, spatial coverage) that will determine the SNR and repetition time of the sequence. Divide the scan time allocated to this sequence by theTR to obtain an estimate of the total number of volumes to be acquired.
Based on the SNR and total number of volumes, compute the CNR for the various coefficients for the 2-, 3- and 4-shell scenarios, using Equation 15.
Decide on the number of shells that will be used by selecting that which predicts usable CNR for all estimated coefficients (ie, the CNR is above the noise floor for all coefficients).
Using our previous orientation-domain approach,30 verify that the number of directions for each b-value is sufficient to avoid aliasing, given the noise level in the images.
- If the number of directions per shell is not sufficient to avoid aliasing in the angular domain, the data acquisition will not provide optimal characterisation of the dMRI signal. There are several ways to address this issue:
- Increase the number of volumes in the acquisition, and hence the scan time, to meet the minimum sampling requirements.
- Select a lower number of shells, as this increases the number of directions for the remaining shells. This decision will depend on whether the error introduced by inadequate sampling of the b-value domain (i.e., having too few shells) is greater than that introduced by inadequate sampling of the angular domain (i.e., having too few directions).
- Redistribute directions between shells to ensure the minimum sampling requirements are met, striving to maintain the number of directions per shell as close to those identified as optimal. While this implies a departure from the optimal parameters for overall CNR, the actual impact is likely to remain acceptable for small adjustments, and can be evaluated using the approach outlined in this study.
It is interesting to note that the b-values identified as optimal are very robust across subjects (Figure 8): for the 3-shell case, b = 400 and 1000 s/mm2 are identified in all subjects with high reproducibility (the range is b = 397-411 and 988-1001 s/mm2, respectively). There is more variation for the highest b-value (ranging from b = 2360 to 3700 s/mm2), as can be seen from Figure 8. Moreover, these values are remarkably consistent when different numbers of shells are selected (b = 400 s/mm2 is present in all schemes, b = 1000 s/mm2 is present for the 3- and 4-shell schemes) (Figure 6). However, given the smoothness of the principal components, minor variations in the exact b-values used are unlikely to have a large impact on the optimality of the acquisition.
Perhaps surprisingly, these values are also remarkably insensitive to changes in T 2 (Figure 7). This can be explained by considering that to provide sensitivity to all Nc components, acquisition schemes will need to include a range of b-values, so that the highest b-value will necessarily be high relative to the others. This places a constraint on the minimum achievable echo time: any reduction in the echo time (and hence the maximum b-value) entails a greater reduction in sensitivity than the increase in SNR. Furthermore, this relative insensitivity is also likely to be a consequence of the long T 2 values observed in neonatal MRI at 3T, which typically range from more than 100 to 300 ms (see, for example, table 4 in Williams et al53). It is likely that the same analysis performed in adult data, where T 2 values are considerably shorter, would show a stronger effect of T 2.
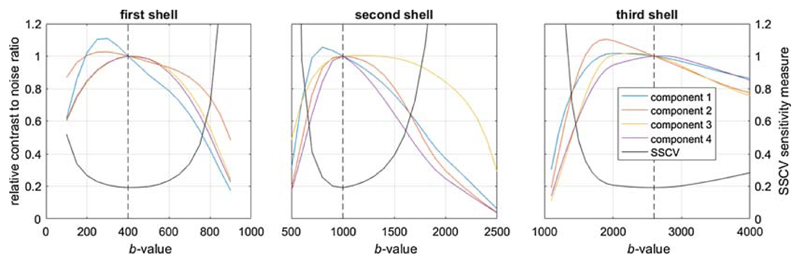
It is also interesting to look at the robustness of the acquisition to deviations in the parameters from the values identified as optimal. Figure 10 shows the effect of varying the b-value of each b≠0 shell in turn, in terms of its impact on the CNR of the individual components, and on the overall SSCV metric (the measure of sensitivity minimised in the present study). It is clear that higher sensitivity to individual components can be achieved, but this comes at the expense of sensitivity to other components. For example, lowering the first shell from b = 400 to b = 300 s/mm2 would increase sensitivity to the first component by ~10%, but would also reduce sensitivity to components 3 and 4 by ~10%. The SSCV measure shows a broad minimum, particularly for the highest shell, indicating that the acquisition would still perform well if the b-values differed somewhat from those identified.
Figure 10.
The impact of deviations from the optimal solution on the relative contrast-to-noise ratio (CNR) of each component (coloured lines) and on the sum of squared coefficients of variation (SSCV) measure (black line). Each plot shows the effect of changing the b-value of the corresponding shell away from the value identified as optimal (denoted by the dashed vertical line). The CNR for each component is shown as a fraction of its value at the overall optimum to allow all plots to coexist on the same scale. This suggests that the optimum is fairly broad, and performance is likely to be relatively tolerant of deviations in the b-values, particularly for the highest shell. In general, the acquisition is more sensitive to the largest component (component 1) with lower b-values, at the expense of sensitivity to the weakest components. This was produced assuming a scheme consisting of four b-value shells to estimate four components, and T 2 = 150 ms
Being entirely data-driven, the approach inherently provides parameters optimal for the particular cohort under investigation. In the present work, we focus on the neonatal age range, and the parameters identified should therefore only be considered optimal for this age range specifically. This approach could also be used to optimise protocols for ex vivo scanning, for instance. However, we note that the b-value optimisation procedure used here did not explicitly take the orientation information into account (beyond ensuring the minimum sampling density requirements are met); this approach may yield sub-optimal results if applied to the adult case where the angular dependence is much stronger. For instance, angular features in the signal have recently been shown to be critical to resolving degeneracies in the standard model7; since the approach taken here ignores these angular features, it cannot provide any guarantee of optimality for applications of this type. By contrast, the neonatal brain exhibits much lower anisotropy, and many of the most interesting features in this age range are likely to be better characterised by focusing on the b-value dependence of the mean DW signal (eg, Kaden et al3 and Reisert et al32), motivating in part the current approach. Joint optimisation of both angular and b-value dependences requires extended orthonormal q-space decompositions (D),48 and is the subject of ongoing work.
Due to its focus on the features of the raw signal, the optimisation performed here provides a solution that is generally suitable for any type of multi-shell dMRI analysis. However, it is likely that in certain applications, very specific aspects of the signal may be of interest, in which case a specially designed acquisition scheme may provide improved sensitivity for this particular purpose. We do, however, believe that such an acquisition would necessarily entail some loss of generality, with reduced sensitivity when used for other purposes.
As shown in Table 3, the lowest b-value selected by the algorithm, at b ≈ 400 s/mm2, is lower than has typically been used in previous multi-shell acquisitions (notably the Human Connectome Project), although it is in line with recommendations for diffusion kurtosis imaging (DKI)1,58 and neurite orientation density and dispersion imaging (NODDI).6 Furthermore, lower b-values are expected considering that mean diffusivity is higher in neonates than in the adult brain. On the other hand, the highest b-value selected is similar to those identified as optimal for fibre orientation estimation in adults30,52; the acquisition scheme should therefore be well suited to tractography applications. Finally, the number of DW directions per shell increases with higher b-value, most likely due to the stronger signal attenuation (coincidentally, increasing sampling density is also required to characterise the increasingly complex angular dependence of the signal at higher b-values).
A question that naturally arises from this work is whether and how the sampling directions should be optimised across shells. It has been suggested in previous work that the sampling directions should be chosen to provide uniform angular coverage across all shells.59 By contrast, in this study the directions were optimised for uniformity across each shell independently, with no attempt to introduce any interaction between shells. We motivate our approach using sampling theory, based on similar arguments to our previous work,30 as follows. We assume the diffusion signal is band-limited in the angular domain; that is, the diffusion signal varies smoothly as a function of orientation, and its angular frequency spectrum contains low harmonic terms only (depending on the b-value). By construction, our sampling scheme is sufficiently dense that all angular frequency components have been fully captured. When these conditions are met, there is no additional information to be gained by introducing inter-dependencies across shells, since the signal is already fully sampled. Furthermore, any attempt at introducing cross-shell dependencies can only push the sampling scheme away from per-shell uniformity, and hence compromise its overall quality. We therefore feel justified to optimise the directions on a purely per-shell basis (we do however note that optimisation across shells may be beneficial in the undersampled case, where each shell is not sufficiently sampled in isolation to capture all features of the signal; in this case, a suitable model of the signal may be able to make use of the complementary orientational information provided by the different shells).
Identifying the optimal number of shells to be included in the final protocol necessarily requires additional factors to be considered, most notably Ntotal, which is in turn dependent on details of the acquisition and the total feasible acquisition time. The minimum angular sampling requirement imposes an upper limit on the number of shells that can be acquired for a chosen Ntotal since increasing the number of shells necessarily reduces the number of directions per shell. However, these requirements are easily met for large Ntotal, as is the case for the dHCP. It is notable that adding higher shells can strongly suppress the number of samples available for lower shells as, at least in the neonatal case, almost 50% of the samples must be obtained using the maximum b-value. We used the per-voxel maps of weights for each component to help inform this balance, based on an expectation that meaningful components should exhibit anatomically plausible spatial patterns that are consistent across subjects. As shown in Figure 5, the maps for the fourth component do exhibit some anatomically plausible contrast (notably in the posterior limb of the internal capsule), whereas the fifth component is much less consistent across the test subjects, suggesting it was strongly impacted by noise and artefacts, probably related to residual misregistration. For this reason, and given the nonnegligible drop in CNR for all components when increasing the number of shells (Table 4), we decided to use a 3-shell (+ b=0) scheme for the final dHCP protocol, with 300 volumes acquired within 20 minutes using multiband factor 4.54
5. Conclusion
The approach presented in this study provides a means to design an optimal acquisition multi-shell HARDI protocol, based on maximising the information content of the data, independent of any particular reconstruction method. It is based on empirically measured data, with no reliance on any assumed model of microstructure. It focuses primarily on the mean DW signal per shell, with separately derived safeguards to ensure adequate angular sampling; this is appropriate for neonatal data given the low angular contrast in this age range. The analysis performed here suggests that a b=0 + 3 shells acquisition is suitable for neonatal imaging, consisting of b = 0, 400, 1000 and 2600 s/mm2 with numbers of DW directions per shell in proportions of 6:19:28:47; these were employed in the final diffusion MRI protocol for the dHCP project.
Supplementary Material
Highlights.
A data-driven method is presented to design multi-shell diffusion MRI acquisition schemes (b-values and no. of directions).
This method optimises the multi-shell scheme for maximum sensitivity to the information content in the signal.
When applied in neonates, the data suggest that a b=0 + 3 shell strategy is appropriate.
Acknowledgements
This work received funding from the ERC under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 319456, and was supported by the Wellcome EPSRC Centre for Medical Engineering at King’s College London (WT 203148/Z/16/Z), and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas' NHS Foundation Trust and King's College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.
Funding information
FP7 Ideas: European Research Council, Grant/Award Number: 319456; National Institute for Health Research; Wellcome Trust, Grant/Award Number: WT 203148/Z/16/Z
Abbreviations used
- CNR
contrast-to-noise ratio
- CV
coefficient of variation
- dHCP
developing Human Connectome Project
- dMRI
diffusion magnetic resonance imaging
- DTI
diffusion tensor imaging
- DKI
diffusion kurtosis imaging
- DW
diffusion-weighted
- EPI
echo planar imaging
- FA
fractional anisotropy
- HARDI
high angular resolution diffusion imaging
- IWLS
iteratively reweighted least-squares
- MD
mean diffusivity
- NODDI
neurite orientation density and dispersion imaging
- OLS
ordinary least-squares
- PGSE
pulsed gradient spin echo
- SENSE
sensitivity encoding
- SNR
signal-to-noise ratio
- SSCV
sum of squared coefficients of variation
- SVD
singular value decomposition
- TE
echo time
- TR
repetition time
- WLS
weighted least-squares
References
- 1.Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: The quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. 2005;53(6):1432–1440. doi: 10.1002/mrm.20508. [DOI] [PubMed] [Google Scholar]
- 2.Jeurissen B, Tournier JD, Dhollander T, Connelly A, Sijbers J. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. Neuroimage. 2014;103:411–426. doi: 10.1016/j.neuroimage.2014.07.061. [DOI] [PubMed] [Google Scholar]
- 3.Kaden E, Kruggel F, Alexander DC. Quantitative mapping of the per-axon diffusion coefficients in brain white matter. Magn Reson Med. 2015;75(4):1752–1763. doi: 10.1002/mrm.25734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sotiropoulos SN, Jbabdi S, Xu J, et al. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. Neuroimage. 2013;80:125–143. doi: 10.1016/j.neuroimage.2013.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.White NS, Leergaard TB, D’Arceuil H, Bjaalie JG, Dale AM. Probing tissue microstructure with restriction spectrum imaging: Histological and theoretical validation. Hum Brain Mapp. 2013;34(2):327–346. doi: 10.1002/hbm.21454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage. 2012;61(4):1000–1016. doi: 10.1016/j.neuroimage.2012.03.072. [DOI] [PubMed] [Google Scholar]
- 7.Novikov DS, Veraart J, Jelescu IO, Fieremans E. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. Neuroimage. 2018;174:518–538. doi: 10.1016/j.neuroimage.2018.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Assaf Y, Freidlin RZ, Rohde GK, Basser PJ. New modeling and experimental framework to characterize hindered and restricted water diffusion in brain white matter. Magn Reson Med. 2004;52(5):965–978. doi: 10.1002/mrm.20274. [DOI] [PubMed] [Google Scholar]
- 9.Ferizi U, Schneider T, Witzel T, et al. White matter compartment models for in vivo diffusion MRI at 300 mT/m. Neuroimage. 2015;118:468–483. doi: 10.1016/j.neuroimage.2015.06.027. [DOI] [PubMed] [Google Scholar]
- 10.Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging. Neuroimage. 2011;58(1):177–188. doi: 10.1016/j.neuroimage.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fieremans E, Novikov DS, Jensen JH, Helpern JA. Monte Carlo study of a two-compartment exchange model of diffusion. NMR Biomed. 2010;23(7):711–724. doi: 10.1002/nbm.1577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jelescu IO, Veraart J, Fieremans E, Novikov DS. Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue. NMR Biomed. 2016;29(1):33–47. doi: 10.1002/nbm.3450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jespersen SN, Bjarkam CR, Nyengaard JR, et al. Neurite density from magnetic resonance diffusion measurements at ultrahigh field: Comparison with light microscopy and electron microscopy. Neuroimage. 2010;49(1):205–216. doi: 10.1016/j.neuroimage.2009.08.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jespersen SN, Kroenke CD, Østergaard L, Ackerman JJH, Yablonskiy DA. Modeling dendrite density from magnetic resonance diffusion measurements. Neuroimage. 2007;34(4):1473–1486. doi: 10.1016/j.neuroimage.2006.10.037. [DOI] [PubMed] [Google Scholar]
- 15.Kroenke CD, Ackerman JJH, Yablonskiy DA. On the nature of the NAA diffusion attenuated MR signal in the central nervous system. Magn Reson Med. 2004;52(5):1052–1059. doi: 10.1002/mrm.20260. [DOI] [PubMed] [Google Scholar]
- 16.Sotiropoulos SN, Behrens TEJ, Jbabdi S. Ball and rackets: Inferring fiber fanning from diffusion-weighted MRI. Neuroimage. 2012;60(2):1412–1425. doi: 10.1016/j.neuroimage.2012.01.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Coelho S, Pozo JM, Jespersen SN, Jones DK, Frangi AF. Resolving degeneracy in diffusion MRI biophysical model parameter estimation using double diffusion encoding. Magn Reson Med. 2019;82(1):395–410. doi: 10.1002/mrm.27714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fieremans E, Veraart J, Ades-aron B, Szczepankiewicz F, Nilsson M, Novikov DS. Effect of combining linear with spherical tensor encoding on estimating brain microstructural parameters. Proc Intl Soc Mag Reson Med. 2018;26:254. [Google Scholar]
- 19.Reisert M, Kiselev VG, Dhital B. A unique analytical solution of the white matter standard model using linear and planar encodings. Magn Reson Med. 2019;81(6):3819–3825. doi: 10.1002/mrm.27685. [DOI] [PubMed] [Google Scholar]
- 20.Szczepankiewicz F, Lasič S, van Westen D, et al. Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: Applications in healthy volunteers and in brain tumors. Neuroimage. 2015;104:241–252. doi: 10.1016/j.neuroimage.2014.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Westin C-F, Knutsson H, Pasternak O, et al. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage. 2016;135:345–362. doi: 10.1016/j.neuroimage.2016.02.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Veraart J, Novikov DS, Fieremans E. TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental T2 relaxation times. Neuroimage. 2018;182:360–369. doi: 10.1016/j.neuroimage.2017.09.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.De Santis S, Barazany D, Jones DK, Assaf Y. Resolving relaxometry and diffusion properties within the same voxel in the presence of crossing fibres by combining inversion recovery and diffusion-weighted acquisitions. Magn Reson Med. 2016;75(1):372–380. doi: 10.1002/mrm.25644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hutter J, Slator PJ, Christiaens D, et al. Integrated and efficient diffusion-relaxometry using ZEBRA. Sci Rep. 2018;8(1):1–13. doi: 10.1038/s41598-018-33463-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ning L, Laun F, Gur Y, et al. Sparse reconstruction challenge for diffusion MRI: validation on a physical phantom to determine which acquisition scheme and analysis method to use? Med Image Anal. 2015;26(1):316–331. doi: 10.1016/j.media.2015.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Basser PJ. Inferring microstructural features and the physiological state of tissues from diffusion-weighted images. NMR Biomed. 1995;8(7):333–344. doi: 10.1002/nbm.1940080707. [DOI] [PubMed] [Google Scholar]
- 27.Koay CG, Chang L-C, Carew JD, Pierpaoli C, Basser PJ. A unifying theoretical and algorithmic framework for least squares methods of estimation in diffusion tensor imaging. J Magn Reson. 2006;182(1):115–125. doi: 10.1016/j.jmr.2006.06.020. [DOI] [PubMed] [Google Scholar]
- 28.Salvador R, Peña A, Menon DK, Carpenter TA, Pickard JD, Bullmore ET. Formal characterization and extension of the linearized diffusion tensor model. Hum Brain Mapp. 2005;24(2):144–155. doi: 10.1002/hbm.20076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Veraart J, Sijbers J, Sunaert S, Leemans A, Jeurissen B. Weighted linear least squares estimation of diffusion MRI parameters: Strengths, limitations, and pitfalls. Neuroimage. 2013;81:335–346. doi: 10.1016/j.neuroimage.2013.05.028. [DOI] [PubMed] [Google Scholar]
- 30.Tournier JD, Calamante F, Connelly A. Determination of the appropriate b value and number of gradient directions for high-angular-resolution diffusion-weighted imaging. NMR Biomed. 2013;26(12):1775–1786. doi: 10.1002/nbm.3017. [DOI] [PubMed] [Google Scholar]
- 31.Raffelt D, Tournier JD, Rose S, et al. Apparent fibre density: a novel measure for the analysis of diffusion-weighted magnetic resonance images. Neuroimage. 2012;59(4):3976–3994. doi: 10.1016/j.neuroimage.2011.10.045. [DOI] [PubMed] [Google Scholar]
- 32.Reisert M, Kellner E, Dhital B, Hennig J, Kiselev VG. Disentangling micro from mesostructure by diffusion MRI: A Bayesian approach. Neuroimage. 2017;147(Supplement C):964–975. doi: 10.1016/j.neuroimage.2016.09.058. [DOI] [PubMed] [Google Scholar]
- 33.Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med. 1999;42(3):515–525. [PubMed] [Google Scholar]
- 34.Papadakis NG, Murrills CD, Hall LD, Huang CL-H, Adrian Carpenter T. Minimal gradient encoding for robust estimation of diffusion anisotropy [small star, filled] Magn Reson Imaging. 2000;18(6):671–679. doi: 10.1016/s0730-725x(00)00151-x. [DOI] [PubMed] [Google Scholar]
- 35.Dubois J, Benders M, Cachia A, et al. Mapping the early cortical folding process in the preterm newborn brain. Cereb Cortex. 2008;18(6):1444–1454. doi: 10.1093/cercor/bhm180. [DOI] [PubMed] [Google Scholar]
- 36.Hüppi PS, Dubois J. Diffusion tensor imaging of brain development. Semin Fetal Neonat Med. 2006;11(6):489–497. doi: 10.1016/j.siny.2006.07.006. [DOI] [PubMed] [Google Scholar]
- 37.Yoshida S, Oishi K, Faria AV, Mori S. Diffusion tensor imaging of normal brain development. Pediatr Radiol. 2013;43(1):15–27. doi: 10.1007/s00247-012-2496-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Andersson JLR, Sotiropoulos SN. Non-parametric representation and prediction of single- and multi-shell diffusion-weighted MRI data using Gaussian processes. Neuroimage. 2015;122:166–176. doi: 10.1016/j.neuroimage.2015.07.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Andersson JLR, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage. 2016;125:1063–1078. doi: 10.1016/j.neuroimage.2015.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Assemlal H-E, Tschumperlé D, Brun L. Efficient and robust computation of PDF features from diffusion MR signal. Med Image Anal. 2009;13(5):715–729. doi: 10.1016/j.media.2009.06.004. [DOI] [PubMed] [Google Scholar]
- 41.Caruyer E, Deriche R. Diffusion MRI signal reconstruction with continuity constraint and optimal regularization. Med Image Anal. 2012;16(6):1113–1120. doi: 10.1016/j.media.2012.06.011. [DOI] [PubMed] [Google Scholar]
- 42.Descoteaux M, Deriche R, Le Bihan D, Mangin J-F, Poupon C. Multiple q-shell diffusion propagator imaging. Med Image Anal. 2011;15(4):603–621. doi: 10.1016/j.media.2010.07.001. [DOI] [PubMed] [Google Scholar]
- 43.Fick RHJ, Wassermann D, Caruyer E, Deriche R. MAPL: Tissue microstructure estimation using Laplacian-regularized MAP-MRI and its application to HCP data. Neuroimage. 2016;134(Supplement C):365–385. doi: 10.1016/j.neuroimage.2016.03.046. [DOI] [PubMed] [Google Scholar]
- 44.Hosseinbor AP, Chung MK, Wu Y-C, Alexander AL. Bessel Fourier Orientation Reconstruction (BFOR): An analytical diffusion propagator reconstruction for hybrid diffusion imaging and computation of q-space indices. Neuroimage. 2013;64(Supplement C):650–670. doi: 10.1016/j.neuroimage.2012.08.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Merlet SL, Deriche R. Continuous diffusion signal, EAP and ODF estimation via Compressive Sensing in diffusion MRI. Med Image Anal. 2013;17(5):556–572. doi: 10.1016/j.media.2013.02.010. [DOI] [PubMed] [Google Scholar]
- 46.Özarslan E, Koay CG, Shepherd TM, et al. Mean Apparent Propagator (MAP) MRI: A novel diffusion imaging method for mapping tissue microstructure. Neuroimage. 2013;78:16–32. doi: 10.1016/j.neuroimage.2013.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Rathi Y, Michailovich O, Laun F, Setsompop K, Grant PE, Westin C-F. Multi-shell diffusion signal recovery from sparse measurements. Med Image Anal. 2014;18(7):1143–1156. doi: 10.1016/j.media.2014.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Christiaens D, Cordero-Grande L, Hutter J, et al. Learning compact q-space representations for multi-shell diffusion-weighted MRI. IEEE Trans Med Imaging. 2019;38(3):834–843. doi: 10.1109/TMI.2018.2873736. [DOI] [PubMed] [Google Scholar]
- 49.Arras KO. An Introduction To Error Propagation: Derivation, Meaning and Examples of Equation Cy= Fx Cx FxT [Report] ETH Zurich; 1998. 1998. [DOI] [Google Scholar]
- 50.Higham DJ. Monotonic piecewise cubic interpolation, with applications to ODE plotting. J Comput Appl Math. 1992;39(3):287–294. [Google Scholar]
- 51.Nelder JA, Mead R. A simplex method for function minimization. Comput J. 1965;7(4):308–313. [Google Scholar]
- 52.Alexander DC, Barker GJ. Optimal imaging parameters for fiber-orientation estimation in diffusion MRI. Neuroimage. 2005;27(2):357–367. doi: 10.1016/j.neuroimage.2005.04.008. [DOI] [PubMed] [Google Scholar]
- 53.Williams L-A, Gelman N, Picot PA, et al. Neonatal brain: regional variability of in vivo MR imaging relaxation rates at 3.0 T—initial experience. Radiology. 2005;235(2):595–603. doi: 10.1148/radiol.2352031769. [DOI] [PubMed] [Google Scholar]
- 54.Hutter J, Tournier JD, Price AN, et al. Time-efficient and flexible design of optimized multishell HARDI diffusion. Magn Reson Med. 2018;79(3):1276–1292. doi: 10.1002/mrm.26765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Christiaens D, Sunaert S, Suetens P, Maes F. Convexity-constrained and nonnegativity-constrained spherical factorization in diffusion-weighted imaging. Neuroimage. 2017;146:507–517. doi: 10.1016/j.neuroimage.2016.10.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Jeurissen B, Tournier JD, Sijbers J. Tissue-type segmentation using non-negative matrix factorization of multi-shell diffusion-weighted MRI images. Proc Intl Soc Magn Resonan Med. 2015;23:349. [Google Scholar]
- 57.Reisert M, Skibbe H, Kiselev VG. The Diffusion Dictionary in the Human Brain Is Short: Rotation Invariant Learning of Basis Functions. In: Schultz T, Nedjati-Gilani G, Venkataraman A, O'Donnell L, Panagiotaki E, editors. Computational Diffusion MRI and Brain Connectivity. Cham: Springer International Publishing; 2014. pp. 47–55. [Google Scholar]
- 58.Poot DHJ, den Dekker AJ, Achten E, Verhoye M, Sijbers J. Optimal experimental design for diffusion kurtosis imaging. IEEE Trans Med Imaging. 2010;29(3):819–829. doi: 10.1109/TMI.2009.2037915. [DOI] [PubMed] [Google Scholar]
- 59.Caruyer E, Lenglet C, Sapiro G, Deriche R. Design of multishell sampling schemes with uniform coverage in diffusion MRI. Magn Reson Med. 2013;69(6):1534–1540. doi: 10.1002/mrm.24736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Howell BR, Styner MA, Gao W, et al. The UNC/UMN Baby Connectome Project (BCP): An overview of the study design and protocol development. Neuroimage. 2018;185:891–905. doi: 10.1016/j.neuroimage.2018.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Descoteaux M, Angelino E, Fitzgibbons S, Deriche R. Regularized, fast, and robust analytical Q-ball imaging. Magn Reson Med. 2007;58(3):497–510. doi: 10.1002/mrm.21277. [DOI] [PubMed] [Google Scholar]
- 62.Hess CP, Mukherjee P, Han ET, Xu D, Vigneron DB. Q-ball reconstruction of multimodal fiber orientations using the spherical harmonic basis. Magn Reson Med. 2006;56(1):104–117. doi: 10.1002/mrm.20931. [DOI] [PubMed] [Google Scholar]
- 63.Tuch DS. Q-ball imaging. Magn Reson Med. 2004;52(6):1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- 64.Behrens TEJ, Berg HJ, Jbabdi S, Rushworth MFS, Woolrich MW. Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? Neuroimage. 2007;34(1):144–155. doi: 10.1016/j.neuroimage.2006.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Tournier JD, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: Non-negativity constrained super-resolved spherical deconvolution. Neuroimage. 2007;35(4):1459–1472. doi: 10.1016/j.neuroimage.2007.02.016. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.