Agricultural land use and the sustainability of social-ecological systems

Abstract

Agricultural land expansion and intensification, driven by human consumption of agricultural goods, are among the major threats to environmental degradation and biodiversity conservation. Land degradation can ultimately hamper agricultural production through a decrease in ecosystem services. Thus, designing viable land use policies is a key sustainability challenge. We develop a model describing the coupled dynamics of human demography and landscape composition, while imposing a trade-off between agricultural expansion and in-tensification. We model land use strategies spanning from low-intensity agriculture and high land conversion rates per person to high-intensity agriculture and low land conversion rates per person; and explore their consequences on the long-term dynamics of the coupled human-land system. We seek to characterise the strategies’ viability in the long run; and understand the mechanisms that potentially lead to large-scale land degradation and population collapse due to resource scarcity. We show that the viability of land use strategies strongly depends on the land’s intrinsic recovery rate. We also find that socio-ecological collapses occur when agricultural intensification is not accompanied by a sufficient decrease in land conversion. Based on these findings we stress the dangers of uninformed land use planning and the importance of precautionary behaviour for land use management and land use policy design.

1. Introduction

Food production is the most basic and tangible example of humans’ dependence on nature. From Paleolithic hunter-gatherers, who relied on direct harvest from nature, to contemporary complex societies that rely on agriculture and livestock, human survival ultimately depends on what the land provides. An ever growing population and demand for food are putting unprecedented pressure on the environment (Tscharntke et al., 2012). Increased food consumption necessitates agriculture expansion; however, the last IPBES report (Bongaarts, 2019) highlights the role of agricultural land expansion as the main threat to biodiversity loss, mediated by the fragmentation and degradation of habitats (Corvalán et al., 2005; Jacobson et al., 2019; Nowosad and Stepinski, 2019). Degradation of the natural environment brings societal and economic consequences for human populations, as it can result in decreasing agricultural yields (Mitchell et al., 2014) and public health issues (Power, 2010). Conservation of biodiversity and natural spaces are often considered secondary objectives when compared to food security, but biodiversity and ecosystem services play an integral role in maintaining food supply. Agricultural productivity is strongly dependent on ecosystem services, such as pollination, nutrient cycling and pest control, that surrounding natural spaces provide (Mitchell et al., 2013). Therefore, conservation goals should not be seen as opposed to agricultural production or human well-being, as natural land is essential to provisioning services (Braat and de Groot, 2012; Cazalis et al., 2018). Allying natural and agricultural lands is the key to achieve sustainability and avoid a potential socio-ecological collapse.

The introduction of agriculture permitted the apparition of the first permanent human settlements. However, Neolithic settlements quickly became heavily reliant on the agricultural system and, as a result, when environmental disasters struck, the food supply and the population suffered (Downey et al., 2016). In some cases, as much as 60% of the population was lost due to failed crops. Over time technological developments made it possible for human societies to adopt more intense forms of agriculture, which increased resource production and food security. Agricultural production enabled the population to grow and allowed the development of complex societies via social differentiation and territorial expansion (Kuijt and Goring-Morris, 2002). This drive to increase agricultural production, however led to deforestation (DeFries et al., 2010), excessive freshwater use (Lilienfeld and Asmild, 2007), soil biodiversity loss (Tsiafouli et al., 2015), altered nutrient (Quinton et al., 2010) and water cycles (Davidson et al., 2012), decreased pollinator abundance, and increased vulnerability to environmental change, all of which can have deleterious effects on agricultural production. Agriculture is thus dependent on the natural environment, but it also heavily transforms this environment. The aim of future societies is to have agriculture improve social welfare, but how to achieve this, while limiting environmental degradation, is a major unknown.

Agriculture has been responsible for both the rise and fall of societies. Historical examples of societal collapse are geographically diverse and have occurred over various time scales(Cumming and Peterson, 2017). Several social, political and economical mechanisms have been proposed to explain such collapses (Tainter, 1988). However, for a number of them, the roots of societal decline can be traced back to ecological problems caused by resource over-exploitation and poor agricultural land management. The Mayan and the Anasazi collapses are two classic examples. In both cases, collapse is thought to have resulted from feedbacks between population growth and agricultural expansion and intensification, which led to greater environmental degradation and made the food production system unviable (Cumming and Peterson, 2017; Diamond, 2005; Roman et al., 2018). Food scarcity sows the seeds of economic trouble, social unease and political instability, which trap societies in positive feedback loop leading to collapse.

The current environmental crisis has reignited scientific interest in societal collapse. There is a general agreement that overpopulation and overconsumption are the main threats to environmental conservation and sustainability (Barrett et al., 2020). Thus, recent studies have addressed sustainability questions by explicitly considering human demography and consumption behaviour. In particular, modelling approaches have shown great potential to shed light on sustainability challenges, as they allow the exploration of different scenarios that would be impossible to reproduce experimentally. In a recent study, Motesharrei et al. (2014) used a dynamical model to show how social inequalities, in terms of resource consumption and contribution to labour, can undermine sustainability and cause societal collapses. This finding can be linked to other issues such as population growth (Kentor, 2001) and over-consumption (Ceballos et al., 2017), which contribute to environmental degradation and social instability. More recently, Henderson and Loreau (2018) and Henderson and Loreau (2019) proposed a general theoretical framework to explain human demography across history in relation to resource accessibility, which can be used to explain the population explosion in the last century and potential future scenarios. Broadening the spectrum of possible connections between nature and human populations, Cazalis et al. (2018) built a model to explore socio-ecological dynamics through the dependence of humans on several ecosystem services. Through an economic-ecological model (Lafuite et al., 2017; 2018; Lafuite and Loreau, 2017) investigated how time lags in the response of biodiversity to anthropic perturbations can feedback on the human population via shortages in food production and undermine the sus-tainability of the socioecological system. These studies provide the basis for our work, showing a link between humans and the environment through food consumption, which we represent by feedbacks between human population growth and agricultural land use.

Research on sustainable agricultural land use has led to the land sharing-sparing debate (Grau et al., 2013; Power, 2010). Whether it is better to protect larger areas of natural land and cultivate high-intensity fields on the remaining land; or protect smaller areas of natural land while practicing wild-life friendly, low-intensity agriculture, is a question that has not yet been fully answered. Different authors often arrive at different conclusions, some defending the sparing/intensification paradigm (Balmford et al., 2019; Phalan et al., 2011a; 2011b) and others the sharing or agroecological one (Perfecto and Vandermeer, 2010; Power, 2010). The sparing-sharing debate has been criticized for omitting the coupling between land use and human demography (Phalan, 2018). Furthermore, the discussion generally examines discrete, opposing strategies, yet there is an entire spectrum between these two extremes. The impact of agricultural intensification on sustainability is an important issue at present, as in the developing countries foreign demand is fueling the conversion of large areas of natural land into intensively cultivated monocultures (Fearnside, 2001; Pengue, 2005; Reboratti, 2010; Soares-Filho et al., 2006). The result is a uniform landscape that is highly vulnerable to environmental fluctuations, destruction of natural habitats, fragmentation, contamination of underground water sources and nutrient runoff. These practices are detrimental to the environment, but agriculture is necessary to feed the population. It is obvious that a balance needs to be achieved between food production and natural land conservation, as the actions taken today could jeopardize the population’s viability in the long run.

Here we build a model to explore the effects of different agricultural land use strategies on long-term human-environment dynamics. Through a simple and tractable model accounting for the interaction between human demography and land dynamics, we study the viability of agricultural socio-ecological systems under different land use strategies along an intensification-expansion spectrum. We introduce a trade-off between intensification and the land conversion effort and investigate for which land use strategies the population collapses due to land degradation. Our central premise is that increasing agricultural production can promote further population growth. Thus, agricultural intensification, via increasing agricultural yields, can have a positive feedback on human demography, initiating the need for larger production and therefore causing further natural land conversion to agriculture, which eventually leads to a more degraded landscape. We test the conditions under which increasing agricultural intensification fails to spare enough natural land and promotes unsustainable population growth, pushing the environment through a tipping point and ultimately leading the social-ecological system to collapse.

2. Model description

2.1. Bidirectional coupling between human demography and land dynamics

Our model considers the conversion of natural land to agricultural land in relation to the demand from the human population. As population dynamics are driven by the resources humans can access and consume, they ultimately depend on the landscape’s composition. Resource production depends on the landscape composition but also on agricultural intensity. We conceive agricultural land use along two dimensions: the conversion effort, which controls the spatial extension of agricultural land, and agricultural intensity. In the model, humans adopt a land use strategy ranging from low intensity and high land conversion rates, to high intensity and low land conversion rates. This negative relation between agricultural intensity and the land conversion effort is grounded in the land sparing-sharing debate. Highly expansive and intense agricultural land uses have been identified as unsustainable. Hence, the debate is whether the focus to achieve sustainability should be put on increasing intensification to reduce the converted areas or extensification to have a wildlife friendly agricultural landscape. We aim to reproduce these two strategic poles by imposing a trade-off between agricultural intensity and land conversion effort, hence reducing the two strategical dimensions to a single parameter. In this study, we do not consider the evolution of the strategy over time and assume it remains constant.

Agricultural land is exhausted and degraded, at different rates depending on the surrounding landscape, and ultimately becomes unproductive (Cramer et al., 2008; Henderson and Loreau, 2019). Natural land contributes to the recovery of surrounding land, acting, for example, as a species pool necessary for recolonization by native species (Baeten et al., 2010; Cramer et al., 2008). Hence, fragmentation of natural areas and degradation of natural patches surrounding degraded land can obstruct its spontaneous recovery. On the other hand, natural land can also become degraded. Indeed, a degraded state of land can propagate into a natural one, as is the case with a desertification front that propagates on semi-arid landscapes (Zelnik and Meron, 2018; Zelnik et al., 2017). The balance between the recovery and degradation processes depends not only on the extension of both natural and degraded land, but also on the borders between the two types of lands and on the level of degradation (Cramer et al., 2008).

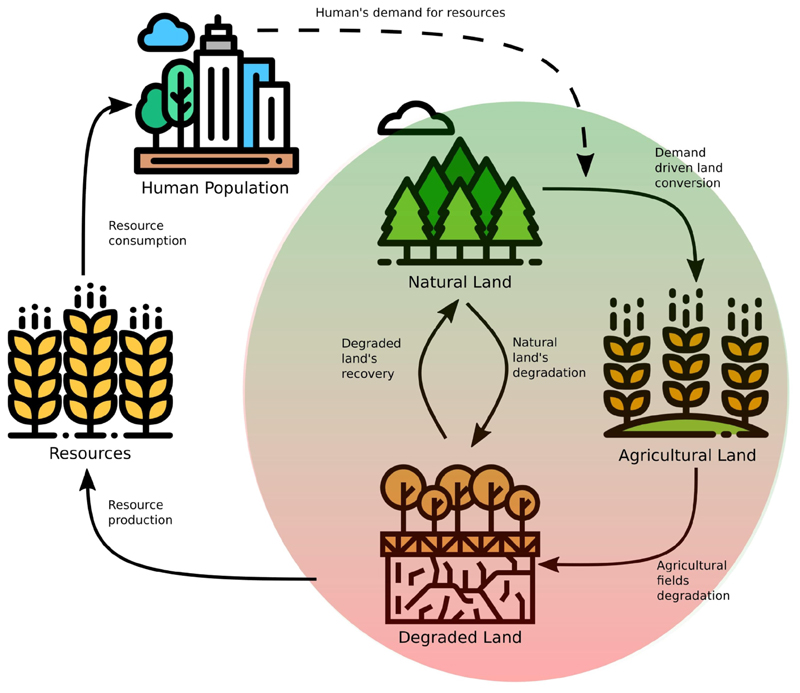
Fig. 1. Model’s graphical representation.

The right part of the diagram represents the landscape, composed of natural land, agricultural land and degraded land. The arrows between the three land types represent the possible land transformations we consider (conversion, recovery, degradation). Both the agricultural intensity and the landscape composition determine the number of resources that are produced and consumed by the human population. Human demography is entirely determined by resource access. Changes in the human population size modify the population’s demand for resources and feedback on the landscape’s composition by increasing or decreasing the conversion of natural land for agricultural purposes.

Table 1. Description of the model’s parameters.

Parameter name	Parameter description	Dimension	Nondimensional	Value
r 0	Population growth rate at low densities	time−1
y A	Maximum production per cultivated area	mass/area
C	Resources consumption per person	mass/person
K 0	Minimum land conversion rate per resources demand	mass−1 time−1	k 0	0.5
K	Maximum land conversion rate per resources demand	mass−1 time−1	k	4.5
E	Maximum agricultural fields degradation rate	time−1	e	1.0
Q	Ratio between area and border contribution	length−1	q	1.0
R	Recovery rate of degraded land per length of frontier with natural land	length−1 time−1	r	[0.1 – 3.5]
D	Maximum degradation rate of natural land per length of frontier with degraded land	length−1 time−1	d	[0.1 – 3.5]
β	Land use strategy parameter		β	[0 – 1]

2.2. Human demography

A number of studies have discussed the idea of a human carrying capacity and pointed to food supply as one of the main constraints to human population growth (Cohen, 1995; Fanta et al., 2018; Hopfenberg, 2003). In this study, we follow the same reasoning and assume human population size p follows logistic growth with a carrying capacity that evolves over time subject to changes in food supply.

The use of the logistic equation to describe the dynamics of human populations has been previously criticized (Board on Environmental Change and Society et al., 2014; Mote et al., 2020) and other studies have opted to explicitly model fertility and mortality processes by various functions related to consumption levels (Henderson and Loreau, 2019; Lafuite and Loreau, 2017; Motesharrei et al., 2014). Furthermore, Cohen (1995) has stressed the difficulties of estimating a human carrying capacity given that several bio-physical and social mechanisms that might constrain human population growth are dynamically evolving and possibly unidentified. However, historical population trends have been well recovered by logistic models using food-dependent carrying capacities (Fanta et al., 2018; Goldberg et al., 2016). Additionally, the unprecedented population increase of the 1960s to 2000s was also modelled using a logistic model, where Hopfenberg (2003) quantified the human carrying capacity using food production, showing good agreement with empirical data. More recently, Suweis et al. (2013) used the link between water availability and food production to calculate a human carrying capacity based on access to water resources, using population data from 1970 to 2011.

We assume the human carrying capacity to be the ratio between total resource production and per capita consumption K _p = Y/C, where Y is total resource production, depending on the landscape’s composition, and C is per capita resource consumption. As such, the carrying capacity endogenously changes over time as food production changes driven by the feedbacks between humans and the landscape. For a given consumption intensity, the maximum number of humans that can be sustained is then given by the ratio of production over per capita consumption:

$$\frac{dp}{d\tau }=r_{0}p\left(1-\frac{p}{K_p}\right)=r_{0}p\left(1-\frac{Cp}{Y}\right),$$ (1)

where r ₀ is the population’s growth rate at very low densities. We assume that r ₀ and C remain constant over time. This is a simplification, as it is known that technological developments and cultural evolution have driven changes in human fertility and consumption, as well as in agricultural productivity, which inevitably impact the human carrying capacity. However, in this study we do not consider the role of cultural and technological evolution, instead we focus on the land dynamics. Based on a previous model of socio-ecological interactions that included variations in food production efficiency (Cazalis et al., 2018), the inclusion of technology in the carrying capacity would likely shift the onset of collapse, vary the size of the collapse range and alter the viability range of parameters, but would not change the overall or long term trends.

2.3. Agricultural production

The number of resources produced (Y) depends on the area of agricultural land (a), but also on that of natural (n) and degraded (d) land, as well as on agricultural intensity, β. Noncultivated land, whether natural or degraded, provides ecosystem services that are crucial for agricultural production, such as pollination, nutrient cycling, pest control and water quality regulation (Mitchell et al., 2014). However, greater land degradation leads to fewer and lower-quality ecosystem services. Therefore, we do not consider natural and degraded land to contribute equally to agricultural production. Instead, we introduce an effective land function ϵ _l(n, d, β), which represents the effective area of non-cultivated land that provides ecosystem services to agricultural land:

$${ϵ}_l=n+\left(1-\beta \right)d.$$ (2)

The contribution of degraded land to effective land decreases with its level of deterioration, which in turn depends on the level of agricultural intensification (β). We assume that more intensive agriculture results in higher degrees of land degradation and as such intensive agriculture transitions to highly degraded land. For simplicity, the contribution of degraded land to effective land decreases linearly with agricultural intensity.

We model agricultural resource production Y as the sum of the contributions from the total cultivated area (area contribution) and from the border of agricultural land with non-cultivated land, both natural and degraded, represented by the effective land ϵ _l (border contribution). Therefore, the “area contribution” scales with agricultural land area and the “border contribution” with the square root of agricultural land area. Furthermore, we assume the relative weights of area, and border contributions in production depend on agricultural intensity (β). As agricultural intensification grows, production, Y, becomes less dependent on the ecosystem services provided by the surrounding non-agricultural land and more dependent on human inputs. Hence, increasing intensification diminishes the border contribution and increases the area contribution on production. Therefore, we assume the area contribution increases linearly with agricultural intensity, β, while the border contribution decreases linearly with β.

The amplitude of the area and border contributions is modulated by the functions Y _A(β) and Y _B(β). These two functions can be interpreted as the characteristic productivity of the area and border contributions, respectively. For a given agricultural intensity (β), Y _A(β) is the production per unit area of agricultural land and Y _B(β) is the production per unit area of effective land per unit length of the agricultural land’s border.

$$Y=\underset{\text{Area}\text{contribution}}{\underbrace{Y_A\left(\beta \right)\beta a}}+\stackrel{\text{Border}\text{contribution}}{\overbrace{Y_B\left(\beta \right)\left(1-\beta \right){ϵ}_l\sqrt{a}}}=y_A\beta \left(\beta a+Q{ϵ}_l\left(1-\beta \right)\sqrt{a}\right)$$ (3)

Agricultural intensity (β) ranges from 0 to 1, 0 being extreme low-intensity agriculture and 1 extreme high intensity. As intensification increases agricultural yields, we model the characteristic productivity of the area (Y _A) and border (Y _B) contributions as increasing functions of agricultural intensification. For simplicity, we assume a linear dependency, i.e., Y _A(β) = Y _A β and Y _B(β) = Y _B β. The parameters y _A and y _B are then the productivities per unit of intensification. We introduce the parameter Q = y _B/y _A, which represents the relative importance of the border and area contribution to resource production.

Fig. 2 shows the magnitude of agricultural resource production as a function of landscape composition. When β is close to 0, maximum production is obtained in a landscape where about a third of the land is agricultural. The food production is exclusively dependent on the services provided by the non-anthropogenic landscape. As we assume the services that non-cultivated land provides to agricultural land depend both on the area and quality of non-cultivated land and on the length of the border between them, at this extreme of the spectrum production scales with the square root of agricultural area. At the extreme, the fraction of natural land is not important because the degradation caused by the agricultural activity is extremely low, such that natural and degraded land contribute equally to effective land. As β grows, the fraction of natural land starts to have an impact, as degraded and natural land are not interchangeable anymore. When β approaches 1, production becomes exclusively dependent on agricultural land area. This is a scenario of extremely high agricultural intensity, where agricultural yields become independent of the services provided by the non-agricultural landscape, and rely exclusively on human inputs, such as fertilizers or pesticides. In the high intensity case, production is proportional to the area of agricultural land. Fig. 2 also shows that yields increase with intensification, as maximum attainable production (yellow areas in the figure) grows with β.

Fig. 2. Agricultural production as a function of landscape composition for different agricultural intensities.

The x and y axis correspond to the fraction of agricultural and natural land respectively. Each subplot corresponds to a different agricultural intensity (β). The production is normalised for each case, hence comparison of agricultural production’s magnitude between strategies is not possible. Instead, the figure shows the different effect that landscape composition has on each case. When agricultural intensity is very low (β = 10^–2), production strongly depends on the services provided by the non-agricultural landscape, hence it decreases when the fraction of agricultural becomes bigger than a certain threshold (A ≃ 0.4 in the plot). As intensification grows, natural land’s importance for production diminishes (β = 0.2, 0.4, 0.6, 0.8). On the high intensification extreme (β = 0.99), the production becomes exclusively dependent on human inputs, hence it grows monotonically with agricultural area.

2.4. Land dynamics: Agricultural land equation

Land conversion is driven by the human population’s demand for agricultural goods, which results on the conversion of natural land to agriculture. We assume that demand is equal to the total desired food consumption (Cp). Since we aim to investigate the impact of different land use strategies along the intensification-extensification spectrum on human-land dynamics, we impose a trade-off between agricultural intensity and land conversion rate. We model land conversion rate as a decreasing affine function of agricultural intensity (β). Nutrient runoff and soil erosion cause agricultural land degradation, which increases with intensity. Therefore, we model the degradation rate of agricultural land as a linear function of β, capturing the fact that high-intensity agriculture degrades the land faster than does low intensity agriculture. The dynamical equation for the agricultural land area is given by

$$\frac{da}{d\tau }=\underset{\text{Conversion}}{\underbrace{\left[K_0+\left(K-K_0\right)(1-\beta )\right]Cpn}}-\stackrel{\text{Degradation}}{\overbrace{E\beta a}}.$$ (4)

Parameters K ₀ and K are the minimum and maximum conversion rates per unit of demanded resources Cp, respectively. As the demand for resources is proportional to population density, K ₀ and K are also per capita rates of conversion. Therefore, in the following we will call them per capita conversion rates. In the extreme high intensity scenario (β = 1), the conversion rate per person is at its minimum K ₀. In the extreme low intensity scenario (β = 0), the conversion rate per person is at its maximum K.

2.5. Land dynamics: Natural land equation

Apart from being converted to agriculture, natural land area can either increase through the spontaneous recovery of degraded land or decrease by the propagation of the degraded state of land. The natural land at the edges of degraded land fosters its spontaneous recovery through both biotic and abiotic processes. It acts as a species pool, promoting native species recolonization, or as a source of good quality water or chemical compounds to restore soil chemistry (Baeten et al., 2010; Cramer et al., 2008). The size of the natural patches is also important as larger patches foster more species and are more resilient to abiotic fluctuations (Mitchell et al., 2013; 2015). Hence, the recovery process depends both on the area of natural patches and on the size of their border with degraded land. We propose a spontaneous recovery term that scales both with natural land area n and with degraded land’s border ∝ $\sqrt{d}$ (Mitchell et al., 2015). The propagation of degraded land’s occurs throguh a symmetric mechanism, where the potential for degradation grows with degraded land area and with the natural land’s border. Therefore, the equation for the change in natural land is

$$\frac{dn}{d\tau }=\underset{\text{Recovery}}{\underbrace{Rn\sqrt{d}}}-\stackrel{\text{Degradation}}{\overbrace{D\beta d\sqrt{n}}}-\underset{\text{Conversion}}{\underbrace{\left[K_0+\left(K-K_0\right)(1-\beta )\right]Cpn}}.$$ (5)

The parameters R and Dβ are the recovery and degradation rates, respectively. The degradation rate scales linearly with the agricultural intensification, such that more intensive agricultural land is more heavily degraded. Furthermore, heavily degraded land contributes to a greater extent to the degradation of natural land.

2.6. Nondimensionalization

We rescale the dynamical system by introducing the non-dimensional variables P, N, A and t, for population, natural land area, agricultural land area and time respectively:

$$\begin{array}{l}t=\frac{\tau }{T_0}=r_0\tau ,N=\frac{n}{A_0},\\ A=\frac{a}{A_0},P=\frac{p}{P_0}=p\frac{C}{y_A{A}_0}.\end{array}$$ (6)

Time is rescaled to the characteristic timescale of human demography T ₀ = 1/r ₀. Parameter A ₀ is the total amount of land, hence variables N and A represent the fraction of natural and agricultural land in the landscape, respectively. We normalize the population by P ₀ = y _A A ₀/C. P ₀ represents the population size that could be sustained if the whole landscape was cultivated with the highest intensity agriculture β = 1, given per capita consumption C. Indeed, when β = 1, if the whole landscape is cultivated, production is Y = β ² y _A A ₀ = y _A A ₀. The following dimensionless parameters emerge from the non-dimensionalisation: k ₀ – minimum land conversion rate, k – maximum land conversion rate, e – agricultural land degradation rate, r – spontaneous recovery rate of degraded land, d – degradation rate of natural land, and q – the relative importance of the border contribution to agricultural production.

$$\begin{array}{c}{k}_0=\frac{K_0{y}_A{A}_0}{r_0},k=\frac{K{y}_A{A}_0}{r_0},e=\frac{E}{r_0},\\ q=Q\sqrt{A_0}r=\frac{R\sqrt{A_0}}{r_0},d=\frac{D\sqrt{A_0}}{r_0}.\end{array}$$ (7)

The dynamical equations describing the non-dimensional system behaviour are

$$\{\begin{array}{l}\frac{dP}{dt}=P\left(1-\frac{P}{𝓎}\right)\\ \frac{dA}{dt}=\left[k_0+\left(k-k_0\right)\left(1-\beta \right)\right]PN-e\beta A\\ \frac{dN}{dt}=rN\sqrt{1-A-N}-d\beta \left(1-A-N\right)\sqrt{N}\\ -\left[k_0+\left(k-k_0\right)(1-\beta )\right]PN\\ 𝓎=\beta \left(\beta A+q\left(1-\beta \right)\left(N+\left(1-\beta \right)\left(1-A-N\right)\right)\sqrt{A}\right)\end{array}$$ (8)

3. Results

3.1. Exploitation of a pristine landscape: Sustainable vs. unsustainable land use strategies

We first look at the dynamics that follow the introduction of a small population in a pristine landscape. The time series are depicted in Fig. 3. No matter the land use strategy, the early transient dynamics are identical. The human population converts the natural land into agricultural fields, thus increasing resource production, which positively feeds back on the human population. The increased population, in turn, accelerates land conversion. This positive feedback loop causes a population explosion accompanied by a transformation of the landscape. Agricultural land expansion fuels an increase in degraded land. Both land conversion and increasing amounts of degraded land contribute to the decline of natural land. The decrease in natural land area ultimately causes a deceleration of agricultural expansion until no more land is converted. The human population peaks with the agricultural area.

Fig. 3. Temporal dynamics of the socio-ecological system for different agricultural land use strategies.

On the left: dynamics emerging from low intensity agriculture and a high land conversion effort. The socio-ecological system reaches a viable equilibrium. Center: dynamics emerging from intermediate agricultural intensity and conversion effort. The socio-ecological system collapses. On the right: dynamics emerging from high intensity agriculture and low land conversion effort. A viable equilibrium is reached again. Parameter values: r = 1.0, d = 1.0, k = 4.5, e = 1.0, k ₀ = 0.5, q = 1.0.

Degraded land cannot be converted back to agricultural land. This introduces a time delayed feedback as the stock of natural land is not instantaneously regenerated. The time delayed feedback causes the population to overshoot its carrying capacity. After the overshoot, the socio-ecological system can reach two different equilibria depending on the land use strategy β. We call viable equilibrium the one where the human population exists in the long term, and collapse equilibrium the one where the population goes extinct. In the viable equilibrium, the human population exists within a complex landscape, composed of a natural, agricultural and degraded land mosaic. In contrast, the landscape in the collapse equilibrium is fully degraded. Without agriculture, there is no resource production and the human population cannot be maintained.

The land use strategy spectrum can be divided into three regions according to the system’s asymptotic behaviour, as a function of the strategy β. The first region corresponds to values of β between 0 and the transition to the collapse equilibrium at the critical point β = β _c,1. We call this region the sharing side of the spectrum, as land use strategies in that range mimic land-sharing kinds of strategy (e.g. low intensity agriculture over large areas). The collapse range (referred to as Δβ later in the text) refers to the region of the spectrum where strategies lead to the collapse equilibrium. When land use strategies are inside the collapse range, the degraded land propagates into the whole landscape, leading to a population collapse. The region between the collapse range and the viable equilibrium is designated the sparing side of the spectrum, as the strategies in this region mimic land-sparing kind of strategies (e.g. high intensity agriculture over small areas).

3.2. On the path to socio-ecological collapse

The existence of the collapse range is due to changes in the stability of the viable equilibrium as a function of the agricultural land use strategy β. On the sharing side of the spectrum, the viable equilibrium is a stable focus-node. Hence, in the phase space, trajectories follow spirals before reaching the fixed point (Fig. 4 (a)), which translate into damped oscillations over time (column (a) of Fig. 5). As land use strategies come closer to the collapse range (β increases), the amplitude of the oscillations grow, which delays the system’s convergence to the viable equilibrium. When the land use strategy enters the collapse range, the viable equilibrium becomes a saddle-focus and loses stability (Fig. 4 (b)). The stability loss is caused by a subcritical Hopf bifurcation which leaves the collapse equilibrium as the sole stable attractor for the socio-ecological system.

Fig. 4. Phase representations of the socio-ecological system for strategies in the viable and collapse regions of the strategy spectrum.

The plots correspond to particular landscape planes of the three-dimensional phase space. The chosen planes are the ones containing the system’s viable equilibrium, hence determined by setting the population at its viable equilibrium value. The dotted grey lines are projections of the null planes for the population, the natural land and the agricultural land on the chosen landscape plane. The black solid lines are projections of simulated trajectories. The vector field depicted with blue arrows indicates the landscape’s direction of change for each landscape composition given a population at equilibrium. On the top: before (a) and after (b) the first transition to collapse. A subcritical Hopf bifurcation causes the stability loss of the viable equilibrium explaining the transition to collapse. On the bottom: emergence of a stable limit cycle (c) from a stable focus node (d) after a supercritical Hopf bifurcation. Parameter values: r = 1.0, d = 1.0, k = 4.5, e = 1.0, k ₀ = 0.5, q = 1.0. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 5. Temporal dynamics of the socio-ecological system at the edges of the collapse range.

Column (a): dynamics before the first transition to collapse. The equilibrium is reached after large amplitude damped oscillations. Column (b): dynamics after the first transition to collapse. Column (c): dynamics after the second transition to collapse. The growth of the oscillations’ amplitude pushes the system through a threshold and causes the collapse (bottom plot). Column (d): dynamics before the second transition to collapse. The collapse is avoided as the system oscillates around the equilibrium without reaching it. Parameter values: β _c,1 = 0.4106108, β _c,2 = 0.7272030, δβ = 10^–7, r = 1.0, d = 1.0, k = 4.5, e = 1.0, k ₀ = 0.5, q = 1.0.

On the sparing side of the spectrum, the transition to collapse has a different origin. As for the sharing side of the spectrum, the system converges to a viable equilibrium via damped oscillations (Fig. 4 (a)) which grow in amplitude as the collapse range is approached. However, in this case the system undergoes a supercritical Hopf transition when the critical point is reached. Hence, the stability loss of the viable equilibrium is accompanied by the birth of a stable limit cycle, which allows the socio-ecological system to potentially escape the collapse equilibrium (Fig. 4 (c)) and oscillate around the viable equilibrium. However, the amplitude of the oscillations grows as the land use strategy moves in the sharing direction (β decreases). Eventually, the oscillations become large enough to push the system through a tipping point provoking a socio-ecological collapse (bottom of column (c) in Fig. 5).

Analytically, we can determine a threshold landscape composition after which socio-ecological collapse is unavoidable. Analysis of the natural land’s dynamical equation gives the following condition

$$\frac{N}{D}\le {\left(\frac{d\beta }{r}\right)}^2,$$ (9)

where D = 1 – A – N is the fraction of degraded land. The threshold depends on the land recovery potential r, as well as on the degradation potential d β. The threshold represents the point at which the landscape is so deteriorated that the remaining fraction of natural land is not sufficient to recover the degraded land nor to maintain its natural state. Hence, degraded land starts propagating into the natural land, resulting in the complete degradation of the landscape and population extinction. Close to the second transition to collapse, oscillations approach the previous threshold (column (d) of Fig. 5). A small change in the land use strategy increases the oscillations’ amplitude and pushes the system through the tipping point, driving it to collapse (column (c) of Fig. 5).

3.3. Role of land recovery potential on the size of the collapse range

The size of the collapse range Δβ = β _c,2 – β _c,1 is highly dependent on the degraded land’s recovery potential (r), as Figs. 6 and 7 show. As the land recovery potential increases, the size of the collapse range decreases until it disappears. It is interesting to note that on the sharing side of the spectrum, when β < β _c,1, an increase in β leads to higher agricultural yields and larger populations. However, the decrease in the land conversion effort is not high enough to prevent the fraction of natural land to decrease. Indeed, agricultural intensification increases the natural land’s degradation rate βd, increasing the potential of degraded land to propagate into the rest of the landscape. When agricultural intensification is not accompanied by a sufficiently large reduction in the conversion effort, the system enters the path to collapse. At the critical point, the levels of degradation are sufficiently high to cause a socio-ecological collapse.

Fig. 6. Bifurcation diagrams for the land use strategy parameter β and for different values of natural land’s recovery capacity.

Socio-ecological steady states are plotted as a function of the land use strategy. The dotted lines correspond to the unstable equilibria and the solid ones to the stable ones. The size of the collapse region is Δβ. From the top to the bottom, the natural land’s recovery capacity increases. The values of the recovery capacity increase from top to bottom and were chosen to give a full picture of the steady state branches’ behaviour. Δβ decreases until disappearance as the recovery rate r increases. Parameter values for these simulation are r = 0.9, 0.97139, 1, 2, d = 1.0, k = 4.5, e = 1.0, k ₀ = 0.5 and q = 1.0.

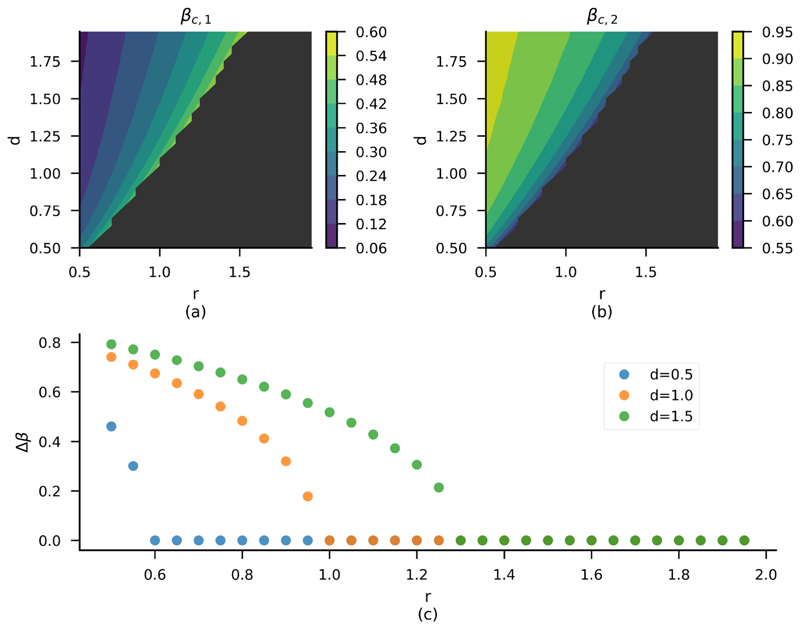
Fig. 7. Collapse range size Δβ in function of landscape’s intrinsic characteristics.

On the top: critical values β _c,1 (a) and β _c,2 (b) in function of the land’s recovery r and degradation d rates. The black colour depicts the region of the parameter space (r, d) where the human population is viable no matter the land use strategy. On the bottom: Size of the collapse range Δβ = β _c,1 – β _c,2 in function of the land’s recovery rate for different degradation rates. The amplitude of the collapse region sharply increases when r decreases. The parameter values are k = 4.5, e = 1.0, k ₀ = 0.5 and q = 1.0.

On the sparing side of the spectrum, when β > β _c,2, the decrease in the land conversion effort that accompanies the increase of intensification succeeds in sparing natural land and allows larger populations to exist in a landscape with a higher fraction of natural area. At the extreme of the sparing strategy spectrum, populations decrease when β rises. This is due to the decrease in the land conversion effort. Only a small fraction of land is converted to agriculture and as such a much lower population can be sustained with the same consumption level.

We investigated in more detail the relationship between the size of the critical region Δβ and the landscape intrinsic parameters r and d (Fig. 7). The controur plots of Fig. 7 show the variation of the critical values β _c,1 and β _c,2 as a function of r and d. For a given natural land degradation rate (d), increasing the recovery rate of degraded land (r) rises β _c,1 and diminishes β _c,2. When the difference between the two critical values reaches 0, the collapse range ceases to exist (black region in contour plots of Fig. 7). The non-linearity of the edge between the coloured (Δβ > 0) and black regions (Δβ = 0) of the contour plots shows that the collapse frontier is more sensitive to r than d, such that when an increase in degradation requires a smaller increase in r to off-set the increase in degradation.

3.4. The dangers of naive agricultural land use planning

As it is formulated, our model does not allow us to know how much the land conversion effort should diminish for a given increase in agricultural intensification, in order to avoid socio-ecological collapse. This is because we fixed a linear trade-off between the conversion effort and the intensity. In reality, the relationship between them can be highly nonlinear. In order to address the question, we release the linear trade-off assumption and let the land conversion effort to be independent of agricultural intensity. We then explore land use strategies along the two dimensions of intensification and extensification. In practice, this means we now have two parameters K (land conversion effort) and β (agricultural intensity) to describe a land use strategy instead of a single one. Hence, the equations for land become:

$$\{\begin{array}{l}\frac{dA}{dt}=KPN-e\beta A\\ \frac{dN}{dt}=rN\sqrt{1-A-N}-d\beta \left(1-A-N\right)\sqrt{N}-KPN\end{array}$$ (10)

In Fig. 8 we plot the regions of the land use strategy space, defined by the land conversion effort K and the agricultural intensity β where either the collapse equilibrium or the viable equilibrium are attained. The border between the two regions is concave rather than linear, which explains the existence of the collapse range Δβ we previously described. A linear decrease in the conversion effort in relation to agricultural intensity (solid black line in the graph) makes it unavoidable to cross the border between the viable and collapse equilibria. This result shows the non-triviality of designing sustainable land use strategies.

Fig. 8. Long-term system’s behaviour in the two-dimensional land use strategy space.

Land use strategy is defined by the couple intensification β and conversion effort K. The blue region corresponds to the set of strategies leading to a viable socio-ecological equilibrium, and the orange region corresponds with the ones leading to socio-ecological collapse. The solid black line depicts the linear trade-off between intensification and conversion effort that we were previously assuming. The border between the two regions is non-linear, which explains the existence of the collapse range Δβ. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

We investigated the impact of different land use strategies on the long-term sustainability of an agriculturally based human society. We considered agricultural land use planning along two strategical dimensions: expansion and intensification. Inspired by the land sparing-sharing debate we introduced in our model a land use strategy parameter (β) that controls the trade-off between agricultural intensity and land conversion effort, thus reducing the two dimensions of the strategy to a single parameter. We then studied the behaviour of the coupled socio-ecological system across a continuum of strategies ranging from low agricultural intensity and high conversion effort (β = 0) to high agricultural intensity and low conversion effort (β = 1). We find that agricultural intensification leads to irreversible land degradation and population collapse when not accompanied by a strong reduction of the land conversion effort. Furthermore, the relationship between agricultural intensification and conversion effort is not straightforward. Uninformed land use planning can drive the socio-ecological system to a critical transition that undermines sustainability and leads to irreversible collapse.

Our model predicts that the most suitable strategy to ally a large population and nature conservation is to practice extremely intense agriculture and minimise the conversion of natural land to agriculture. Alternatively, low agricultural intensification and high conversion efforts (i.e., extensive agriculture) lead to preserved landscapes, but with significantly lower population sizes. Therefore, for our current population the model seems to support the advocates of the sparing hypothesis. However, the existence of a collapse region in the middle of the strategy spectrum suggests that it is not simply a question of sparing.

Gradual increases in intensification eventually cause the adoption of land use strategies within the collapse region of our model. Therefore, if technological development in the agriculture sector stagnates, there is a greater risk of getting trapped in the collapse region. Furthermore, technology is not a panacea for all socio-ecological issues, as technology can lead to greater environmental degradation through what is known as ‘the Jevons paradox’ (Alcott et al., 2012). With reference to this paradox, increasing agricultural production efficiency has the potential to increase demand which ultimately degrades more land and drives the system towards collapse. Socio-ecological collapse can be avoided in the model by changing land use strategies quickly. Whether the levels of intensification required to overcome the collapse region are attainable or how to accurately measure intensity to know where we are on the spectrum are unclear.

It is evident that simultaneous increases in both agricultural expansion and intensification cannot be viable in the long term. However, current practices favour both intensification and expansion. The last century’s Green Revolution is a recent and striking example of how agricultural intensification can increase yields and food security. However, this was also the period of fastest population growth in history, which further increased demand and motivated agricultural intensification and expansion. The societal and economic benefits of agricultural intensification that ensure food security are undeniable. However, agricultural intensification and expansion have caused several environmental problems such as soil erosion, nutrient runoff, water pollution or habitat destruction and fragmentation. It has also caused profound societal transformations, in particular the disappearance of small agricultural producers, that fuel urbanisation and change consumption patterns.

Agricultural intensification is considered a plausible explanation of past societal collapses, such as in the Roman or Mayan examples (Diamond, 2005). Population collapse emerges from our model as a consequence of large-scale land degradation, which impairs agricultural production in two ways: first, the deterioration of the landscape critically depletes the stock of natural land, which is the primary source for conversion to agriculture; second, natural land depletion reduces the provision of ecosystem services to existing agricultural areas. Since land degradation can critically decrease agricultural production, it seems ironic that agricultural land use is nowadays considered to be among the major causes of land degradation. This dangerous feedback loop poses a serious threat to sustainability as agricultural expansion and/or intensification to cope with reduced production can further reduce production in the long term by accentuating land degradation. Thus, we stress the major importance that agricultural land use planning has on the sustainability of socio-ecological systems.

Furthermore, our results also highlight the importance of socio-ecologically informed agricultural land use policies to achieve sustainability. By removing the trade-off between land conversion and agricultural intensity in our model, we showed that sustainable land use strategies can be obtained for the entire spectrum of intensification we consider. However, the frontier between unsustainable and sustainable land use is far from trivial. The existence of unsustainable land use strategies comes from a bad evaluation of the needed reduction of land conversion for a given increase on intensification. As our model is a simplification of real population dynamics and land use planning, we do not claim that the frontier between sustainable and collapse paths is as we describe. However, we show that it is very likely for this frontier to be far from trivial, hence making it easy for uninformed land use planning to fail. Much the same way that science-based policies are considered crucial for climate change mitigation or human population sustainability (Motesharrei et al., 2016), our work stresses the need to incorporate informed agricultural land use planning into the policy agenda to achieve sustainability.

Globally, at an aggregated scale, it could be argued that we have not yet reached a critical point or planetary boundary (Steffen et al., 2015), however at a local scale this might not be true. Agricultural land use is not spatially homogeneous and agricultural production is often strongly localised: the Pampas in South America and the Great Plains in the United States are two examples. Moreover, these major agricultural regions are mostly expansive and intensive monocultures. Hence, at a regional scale there is neither sparing nor sharing, rather extensive exploitation, which makes the landscape highly susceptible to irreversible ecological degradation. In South American grasslands and forests, these practices have already caused major environmental degradation (Fearnside, 2001; Guerschman and Paruelo, 2005; Pengue, 2005), in addition to societal problems (Pengue, 2005). Agricultural expansion has already destroyed most of Brazil’s Atlantic Forest (Centre for Applied Biodiversity Science, 2003; Ribeiro et al., 2011), and now it is advancing over the Amazon Forest, one of the world’s biodiversity hotspots (Davidson et al., 2012; Lovejoy and Nobre, 2018; Nepstad et al., 2008; Soares-Filho et al., 2006). The variations in land management practices highlight the interest of considering a continuous range of both agricultural expansion and intensification rather than discrete levels of intensity (Roman et al., 2018) in modelling studies. The possibility of local collapses poses a threat to global sustainability, as it is unclear how these local collapses can propagate over the world, via environmental degradation but also via changes in trade or migration networks.

Our model is a simplified representation of agricultural practices, human demography and social structure, which allows us to explore a range of scenarios and understand the behaviours within the model, but it also omits details of our complex society. For example, it does not account for social and economic inequalities, which have been recognized as important drivers of socio-ecological dynamics (Motesharrei et al., 2016). Social and economic inequalities push the system away from a sustainable human-nature equilibrium (Cumming and von Cramon-Taubadel, 2018), thus would likely have a amplifying effect on the results. Additionally, the logistic model we use to describe human population dynamics is heuristic and does not reflect the actual mechanisms responsible for variations in human fertility and mortality (Mote et al., 2020). Lastly, we have assumed that humans cannot adapt to environmental degradation by changing land use strategies or fertility and consumption behaviours over time. This is a major limitation, as adaptive strategies could potentially prevent the predicted population collapse. However, these simplifications do not reduce the pertinence of our results, as the current trends have the potential to cause a collapse, if habits go unchanged. Moreover, if humans succeed, through changes in cultural patterns, to avoid a drastic population reduction, it is very likely that the changes will be dramatic and involve, for example, a complete socio-economical restructuring (Cumming and Peterson, 2017). Hence, our results highlight that our current socio-ecological system might be heading towards dramatic changes, even though it is hard to predict the form they will take.

5. Conclusions

By exploring a continuum of land use strategies, our work differentiates from previous models of coupled human-land dynamics and shows the importance of quantifying agricultural expansion and intensification levels to assess sustainable land use strategies. We modelled agricultural land use planning along two dimensions: expansion, given by the population’s conversion effort, and intensification. Expansion and intensification can act in synergy to increase landscape degradation, but there are also trade-offs between them. Agricultural expansion increases the stock of potential degraded land, while agricultural intensification can both speed and deepen agricultural land’s degradation.

Our results show how increasing agricultural intensification leads to socio-ecological collapse when there is an insufficient reduction of the land conversion effort. Agricultural intensification increases agricultural production, hence human population size, if consumption levels are kept equal. Population growth feeds back on the landscape’s composition by further accelerating land conversion. Eventually, land degradation reduces resource production and causes the population to overshoot its carrying capacity and ultimately decline.

It could be argued that technological development has the potential to stave off collapse, however the impact of new technologies on the environment is ambiguous. Technology has the potential to increase production efficiency, but could also further decouple food production from nature by replacing ecosystem services with synthetic inputs. The cure-all technology argument neglects feedbacks between technology and human behaviour, as well as its underlying dependence on the environment. Future work will put a greater focus on the links between changes in technology and behaviour and its impact on socio-ecological dynamics.

Our model illustrates a potential mechanism that may explain the decline of past societies but also a possible future collapse. As the global human population is projected to keep growing in the coming decades adapted agriculture management will become more important and reduce the potential risks of future socio-ecological collapse. Our model points to agriculture intensification as a possible solution, however it is imperative that this is not in combination with expansion. However, we also stress that determining the limits to agricultural expansion that are necessary to achieve sustainability is not a trivial task. Hence precautionary land use planning should be accompanied by changes in social norms, such as a reduction of consumption to increase the likelihood of a sustainable future.

By modelling the bi-directional feedbacks between human demography and land use, we have shown how misguided or uninformed agricultural land use planning can lead a socio-ecological system to collapse. This stresses the importance of informed land use planning to achieve sustainability. Through evidence based policy design, humans have the tools to modify precarious land use patterns and reduce the impact of agriculture on the environment, setting our socio-ecological system on a more sustainable path.

Code accesibility

All the open-source software to reproduce our analysis and the associated plots is available at https://doi.org/10.5281/zenodo.3988256.