Abstract
In positron emission tomography (PET) imaging, accurate clinical assessment is often affected by the partial volume effect (PVE) leading to overestimation (spill-in) or underestimation (spill-out) of activity in various small regions. The spill-in correction, in particular, can be very challenging when the target region is close to a hot background region. Therefore, this study evaluates and compares the performance of various recently developed spill-in correction techniques, namely: background correction (BC), local projection (LP), and hybrid kernelized (HKEM) methods. We used a simulated digital phantom and [18F]-NaF PET data of three patients with abdominal aortic aneurysms (AAA) acquired with Siemens Biograph mMR™ and mCT™ scanners respectively. Region of Interest (ROI) analysis was performed and the extracted SUV mean, SUV max and target-to-background ratio (TBR) scores were compared. Results showed substantial spill-in effects from hot regions to targeted regions, which are more prominent in small structures. The phantom experiment demonstrated the feasibility of spill-in correction with all methods. For the patient data, large differences in SUV mean, SUV max and TBR max scores were observed between the ROIs drawn over the entire aneurysm and ROIs excluding some regions close to the bone. Overall, BC yielded the best performance in spill-in correction in both phantom and patient studies.
Index Terms: PET, SPECT, PVE, spill-in effect, quantification
I. Introduction
POSITRON emission tomography (PET) is a useful imaging technique for disease diagnosis and treatment response evaluation. However, its quantification accuracy is often affected by the partial volume effect (PVE) resulting from the limited spatial resolution of the PET imaging system [1]–[3].
PVE could be in the form of spill-out effect, which leads to loss of activity from a target tissue to the surrounding regions, or spill-in effect, which results in excess activity moving from adjacent regions into a tissue [3]. The spill-in effect is particularly evident when a small region of interest (ROI) lies in close proximity to regions of very high tracer uptake [4]–[7].
Various techniques have been employed for spill-in correction, but none has proven effective when the ROI is located within 1-5 cm from a highly radioactive region such as the urinary bladder, myocardium or bone [5], [8]. Past studies have shown that in such situations the standardized uptake value (SUV) is often substantially overestimated and therefore invalid [4]. This effect can limit PET imaging in certain clinical investigations such as [18F]- NaF PET imaging of the abdominal aortic aneurysm (AAA) where extensive spill-in effect from the bone into the aneurysm can be observed [8]–[10]. Common image analysis techniques to mitigate the spill-in contamination include masking out the highly radioactive region in the image space, or simply excluding areas of spill in from regions of interest around the tissue of interest [8]–[10]. The challenge is the high dependence of the measurements on clinician expertise. In addition, a certain degree of potentially important physiological information might be lost from the excluded regions. There is therefore a clear need for more practical methods to correct for the spill-in effects.
Recently, a background correction (BC) technique was implemented which iteratively removes the entire background contribution from the reconstructed image [5], [7]–[11]. This method showed promising results for spill-in correction, but the BC technique to the best of our knowledge has been tested only in one clinical case, so far [8]. Also, its performance has not been compared with other correction techniques. Therefore, the aims of this study are: (1) to investigate the spill in effect in simulated phantom with known activity and patients with AAA lesions in close proximity to bone tissue; and also to see how this could potentially impact quantification in the regions of interest, (2) to evaluate the performance of the BC technique against two recently proposed PET correction techniques to compensate for spill-in effects in these cases. These two techniques were selected because they are new novel techniques which have been recently shown to mitigate errors due to partial volume effects, and because of their ease of implementation.
II. Theory
Spill-in correction of PET data was implemented using three approaches: (A) Background Correction (BC); (B) Local Projection (LP); and (C) Hybrid Kernel (HKEM) methods.
A. Background Correction (BC) Method
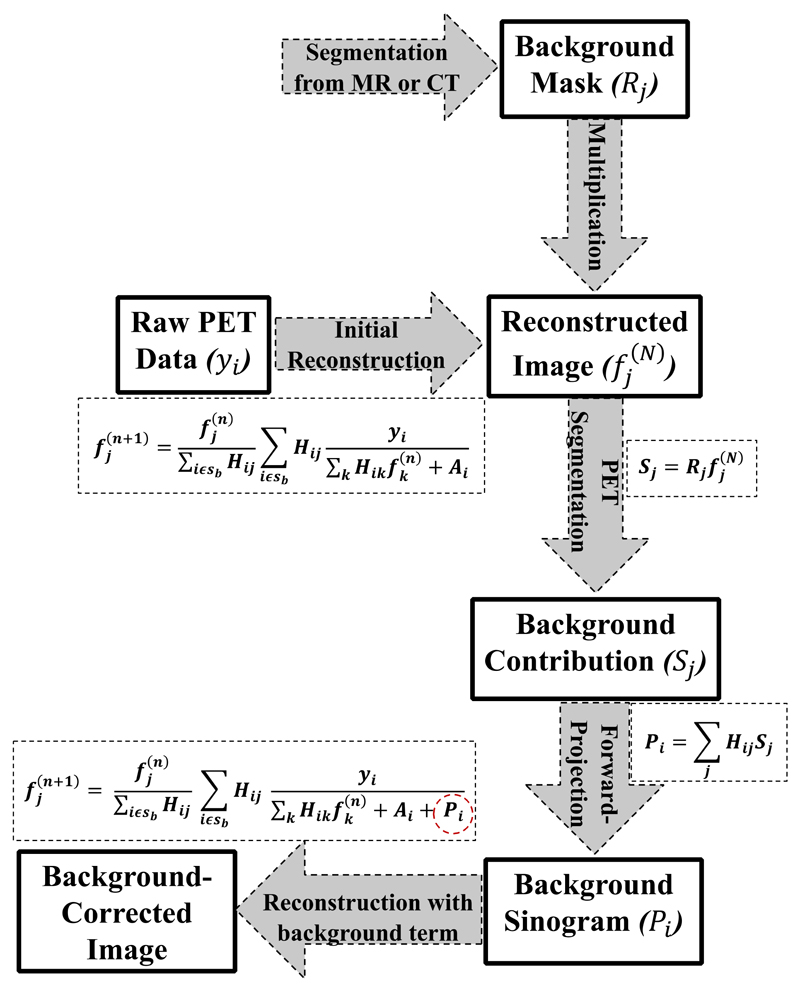
This method involves segmentation of the hot background region from a high-resolution anatomical image such as MR or CT. The region mask R j is multiplied by the reconstructed image at 3 iterations to obtain the background contribution S j = R j in the reconstructed image. This is forward-projected to obtain the sinogram (P i = Σj H ij S j), which is then combined with the original additive sinogram term A i of the OSEM reconstruction to obtain a corrected image. A flow chart of the algorithm is illustrated in Fig. 1 and defined by (1):
| (1) |
where y i is the recorded projection data for detector pair i, H ij is the system matrix defining the probability for an event located in image pixel j being detected by detector pair i, A i is the additive sinogram term (consisting of the randoms and scatter events), P i is the background sinogram contribution, added to the original additive sinograms A i of the standard OSEM reconstruction, and is the background-corrected activity in voxel j of the reconstructed image updated after the n th iteration.
Fig. 1.
Flowchart of the background correction (BC) method. For the current implementation, n is the number of iterations (i.e. n = 1,2,…,30) while N is the iteration at which the background contribution was estimated (i.e. N = 3).
It is worth noting that the BC reconstruction technique is the same as the standard OSEM reconstruction, where a uniform image is used as the initial estimate. The only difference is that in the BC technique, the additive sinogram term now consists of an extra component to account for the background contribution in addition to randoms and scatter. Also, the background region is not corrected for PVE, apart from the resolution modelling applied to the entire image. The BC technique was only used to correct for the extra spill in effect emanating from the hot background region into the ROIs.
The background contribution was estimated from PET images produced from an initial PET reconstruction with PSF modeling after three iterations which is a standard setting in most clinical PET protocols. More so, in our study, the estimated background regions were quite large, and hence, the background activity converged nearly after the 3rd iteration. This is demonstrated for the patient datasets in the supplementary Fig. S1.
B. Local Projection (LP) Method
A previously introduced local projection (LP) method [12], [13] was adapted for spill-in correction, where the image to be corrected is segmented into the target volumes of interest (VOIs) and a global background outside the target VOIs. In addition to the standard LP method, this study involved an additional hot region segmentation, which is responsible for the spill-in of activity into the target lesions. Therefore, in this study, the image to be corrected is segmented into a target VOI (consisting of the ROIs), and the global background outside the target VOI.
The measured emission projection counts, y i, can be modelled as the sum of the projection counts from the 2-tissue VOI, plus the counts originating from the global background outside the VOI, as shown in (2):
| (2) |
where y i are the expected counts per sinogram bin i, V j is the activity for each segmented tissue inside the VOI, C ij is the system matrix for each segmented tissue, and g out,i are the counts originating from the global background outside the target VOI.
Partial volume correction using the LP technique is performed as a post-reconstruction step. The system matrix values, C ij, for each segmented tissue and the global background, g out,i, are first computed. Then, the LP tissue-activities, V j, are obtained by maximizing the log-likelihood for the expected value y i as shown in (3).
| (3) |
where n i are the measured count per sinogram bin. This equation is solved iteratively where the values of y i, and V j and g out,i are updated after each iteration (k). The resulting tissue activities will then be substituted in place of the original activity in each voxel within the target VOI. The resulting image is forward-projected and the obtained sinogram is reconstructed with the STIR library. The forward projector used is based on Siddon’s matrix ray tracing algorithm with 10 tangential rays traced for each projection bin. A flow chart of the LP method is given in Fig. 2.
Fig. 2.
Flowchart of the LP method.
C. Hybrid Kernel Expectation Maximization (HKEM)
The recently proposed hybrid kernel expectation maximization (HKEM) method [14], [15], which uses information from both PET and an anatomical image in order to compensate for partial volume effects, was used in this study. The advantage of the kernel method is that it does not require segmentation and it achieves improved resolution for each individual voxel and also for the edges of a region [16], [17]. This technique, although it is not a dedicated partial volume correction technique, was used so as to explore the edge-preserving and noise-suppression performance in enhancing resolution recovery and reducing the spill-in effect from the hot background into the colder ROIs [18].
The kernel method re-parameterizes the expectation maximization (EM) algorithm in terms of spatial basis functions (kernel matrix K) and coefficients (α). Therefore, the image to be reconstructed, f j, can be expressed as:
| (4) |
where k mj is the mj th element of the kernel matrix, and α m is the coefficient vector to be estimated in the expectation maximization step as shown in (5):
| (5) |
Since the hybrid kernel method extracts information from both anatomical and PET images, the kernel matrix can then be expressed as:
| (6) |
where k a and k p are the kernel components from the attenuation and PET images respectively, calculated using the functions in (7) and (8):
| (7) |
| (8) |
where υ m and are the feature vectors calculated from the attenuation image and the n th iteration PET image, α, respectively, while σ a, σ p, σ da and σ dp are scaling parameters for the distances in (7) and (8). Further details and implementation of the HKEM technique can be found in [14] and [15].
In this work, we used a high-resolution MR attenuation correction (MRAC) image to extract the anatomical information needed for the algorithm. Moreover, for the aforementioned HKEM parameters, we used the values of σ a = σ p = 1, and σ da = σ dp = 3 yielding the best trade-off between image quality and noise according to a previous optimization study [15].
The advantage of the HKEM technique is the employment of the PET image to estimate one part of the hybrid kernel, thereby reducing the dependence on the anatomical image. Also, unlike BC and LP methods, there is no need for a preliminary reconstruction step.
III. Materials and Methods
Two datasets were used in this study: (i) a digital simulation using the XCAT2 phantom, and (ii) 3 clinical PET datasets from patients with abdominal aortic aneurysms (AAA) undergoing [18F]-NaF PET/CT imaging.
A. Simulation
For this study, the pelvic region was simulated using a digital anthropomorphic XCAT2 Phantom [19], [20] with a typical [18F]-FDG distribution. This simulated data include a fixed size bladder with SUV 55.5 (representing the hot source) and various-sized lesions with SUV 8 placed at different positions around the bladder (as shown in Fig. 3).
Fig. 3.
The simulated data from digital XCAT2 phantom: (a) is the emission image showing an active bladder surrounded with lesions of various diameters ranging from 6mm to 20 mm, while (b) is the attenuation image used for attenuation correction. The yellow ROIs in (a) are the selected background ROIs used to calculate the contrast.
Emission and attenuation images were generated, and these were blurred with the scanner specific PSF in order to simulate the partial volume effects from the scanner. The dedicated PSF kernel for the Siemens mMR scanner was modeled as a Gaussian filter with 4.1 mm axial and 4.0 mm transverse FWHM according to experimental point source PSF measurements with the Siemens mMR scanner [21]. The blurred images were then forward projected to obtain the sinograms using simulated Siemens mMR scanner. The forward projector used is based on Siddon’s ray tracing algorithm [22], tracing 10 tangential rays for each bin. Attenuation correction factors (ACF) were calculated from the attenuation image and this was used to attenuate the emission sinogram. Constant normalization and randoms sinograms were also generated, with the random counts making up to 20% of the total projection data. Scatter was estimated analytically using the single-scatter simulation (SSS) approach [23] as incorporated into STIR [24]. A scaling factor was applied to make the scatter count 35% of the total simulated events. The random and scatter sinograms were used to generate the additive term, while the attenuation and normalization sinograms were used as multiplicative terms.
Poisson noise was simulated for approximately 65M counts and 10 noise realizations were performed for statistical analysis. The noisy sinograms were reconstructed with STIR [25] using the iterative Ordered Subsets Expectation Maximization (OSEM) algorithm with 21 subsets and 10 full iterations. The images have 344 × 344 × 127 voxels of 2.086 mm × 2.086 mm × 2.031 mm. A scanner-specific point spread function (PSF) was incorporated into the reconstruction algorithm [26], [27] in order to perform a voxel-by-voxel resolution recovery as represented in (9).
| (9) |
where H kj represents the original system matrix, and is the system matrix convolved with the PET scanner-specific spatially invariant PSF in both forward and back projections.
PVE correction was performed with all the techniques highlighted in Section II. For the background correction (BC) method, the bladder was automatically segmented from the digital phantom and the bladder sinogram was included as an additive sinogram term in the OSEM reconstruction (details in section IIA). The LP method was implemented for the phantom using three regions, where the six lesions and the bladder are the target VOI, and the remaining background region form the global background.
ROI analysis was done by placing spherical ROIs with diameters equal to the lesion sizes on the exact position of the lesions. For each noise realization, the mean and maximum SUV values (SUVmean and SUVmax) in each ROI was estimated for quantification purpose. For each reconstruction technique, the Recovery Coefficient (RC), contrast (C) and coefficient of variation (CoV) of each lesion was estimated using (10) to (12). These were used as figures of merit to show the resolution recovery, image contrast as well as the noise properties of each correction technique.
| (10) |
| (11) |
| (12) |
where T j is the value of voxel j of the reconstructed image, j is one of the N T voxels of the target lesion, and k is one of the N B voxels of the background normal tissue. The background values were estimated as the average of the 3 yellow ROIs shown in Fig. 3a.
To estimate the spill in effect from the hot bladder into the surrounding lesions, we carried out another simulation with zero activity in the bladder. We then estimated the difference in the RC values using:
| (13) |
where RCSUV55.5 and RC SUV0 are the lesion RC values at bladder SUVs 55.5 and 0, respectively.
B. Patient Data
Three human patient datasets were selected from the archive of the SoFIA3 ([18F]-NaF uptake in abdominal aortic aneurysm) study [10] involving [18F]-NaF PET/CT imaging of AAA lesions. Each patient was injected with 125 MBq of [18F]-NaF and imaged on the Biograph mCT™ PET-CT scanner (Siemens Healthineers, Knoxville, TN, USA) [28]. A low-dose CT attenuation correction (CTAC) scan was performed (120 kV, 50 mAs, 5/3 mm) followed by a PET acquisition using 3 × 10 min bed positions to ensure coverage from the thoracic aorta to the aortic bifurcation. The data were reconstructed with OSEM using 21 subsets and 30 iterations. PSF modelling was incorporated into the reconstruction of all the spill-in correction methods as an isotropic 3D Gaussian kernel with 4.4 mm FWHM in both axial and transverse planes [21]. A sample patient scan showing the attenuation image, PET image and the segmented bone is shown in Fig. 4.
Fig. 4.
Sagittal view of an [18F]-NaF PET/CT scan of a patient with abdominal aortic aneurysm (AAA): (a) CT-based attenuation image where the AAA (circled with a blue dashed line) is in close proximity to a highly radioactive bone (shown with green arrow), (b) PET image, and (c) active bone segmented from the CTAC image, used for the background correction method.
For the patient data, a 3-tissue LP algorithm was implemented, where the image was segmented into a target VOI consisting of the aneurysm, and the hot bone (i.e. J = 2), and the global background outside the target VOI.
ROI analysis was performed by delineating the aneurysmal aorta to estimate the mean and maximum SUVs (SUVmean and SUVmax) in the aneurysm. Following the standard clinical quantification [10], [29], [30], we estimated the maximum target-to-background ratio (T BR max) using:
| (14) |
where SUV max (T) corresponds to the maximum SUV in the target (aneurysm), while SUV mean (Bp) is the mean SUV in the background (blood pool region in the inferior vena cava).
To demonstrate the magnitude of the spill-in effect from the bone to the aorta, we delineated two ROIs: ROI1, denoted as AAA, covers the entire aneurysm and ROI2, denoted as AAA-exc, excludes the AAA parts very close to the bone, as has been reported previously [8]. We then quantified the SUV at the aneurysm using these two regions. Information about these ROIs and the selection criteria are shown for all the 3 patient datasets in supplementary Fig. S2.
The performance of all the reconstruction algorithms was evaluated in terms of the contrast (C TB) of the aneurysm region against normal tissue and the coefficient of variation (COV) was used as the noise metrics for all algorithms, as given by (10-12).These metrics were computed at each iteration using AAA-exc in order to avoid the spill-in effects.
IV. Results
This section shows the ROI analysis obtained from the reconstructed images of both the phantom and patient datasets.
A. Simulation
Fig. 5 shows the RCmax and RCmean of all the lesions estimated at iteration 3 for all the reconstruction algorithms. OSEM and PSF show higher RCmax than other methods, especially for lesions L1 and L4. For lesion L1 which is closest to the bladder, there is a substantial RCmax overestimation of up to 40%. However, the correction methods: BC, LP and HKEM have almost steady RC values (close to 1) for all lesions except for lesion L2 which is greatly underestimated for all algorithms.
Fig. 5.
The mean RCmax and RCmean of lesions L1-L6 for all evaluated reconstruction algorithms at 3 iterations and bladder SUV 55.5. This shows the mean of the 10 noise realizations, and the error bar is given as the standard error of the mean. The dashed horizontal line denotes the expected lesion RC.
Fig. 6 shows the % Difference in RC for all lesions due to the activity in the bladder. This is estimated using (13). At 3 iteration, OSEM, OSEM+PSF and HKEM images show higher % change in RC values of up to 40% for lesions L1 and L2 which are close to the bladder. However, at iteration 10, the % change is within 20%. BC and LP images show a considerably lower % change in RC both at 3 and 10 iterations.
Fig. 6.
The % change in RCmax and RCmean of lesions L1-L6 for all evaluated reconstruction algorithms due to the activity in the bladder. This is estimated at 3 and 10 iterations (it) using (13). The error bar is given as the standard error of the mean.
To estimate the image contrast and noise properties of each method, the contrast and CoV were calculated for each lesion as iteration increases using (10) and (11), and this is shown in Fig. 7.
Fig. 7.
Contrast versus CoV against the iterations in each of the lesions for all reconstruction algorithms.
B. Patient Data
The convergence plots of all the reconstruction algorithms are shown in the supplementary Figure S4. The results showed that at lower iterations, OSEM images have higher quantitative values than PSF-based images, while PSF+LP images yielded the least quantitative values. However, as iteration increases, PSF-based images showed increased quantitative values than OSEM images. It could also be noted that there is lack of convergence in PSF-based images, except for PSF+LP images which showed good convergence. Fig. 8 shows the CT attenuation and PET reconstructed images of the three datasets under review. The PET images demonstrated a higher [18F]-NaF uptake in the aneurysm, compared to normal tissue. Also, we observed a high uptake in the adjacent bone, which might significantly influence quantification at the aneurysm. It could also be seen that for all the patients, PSF-based reconstructions attained a better contrast and more reduced noise than OSEM reconstruction, with the PSF+HKEM algorithm yielding the best performance. This was also shown for each reconstruction algorithm in terms of the contrast and COV in Fig. 9.
Fig. 8.
Sagittal views of the PET reconstructed images at 3 full iterations, shown for the 3 patients (top-to-bottom rows). All images are displayed with the same maximum SUV threshold value 6.
Fig. 9.
Contrast versus COV in the aneurysm as a function of iteration.
The spill-in activity from the bone into the aneurysm was estimated by drawing 2 ROIs on the aneurysm: ROI1 was drawn over the entire aneurysm region (AAA), while ROI2 was drawn such that it excluded regions close to the active bone (AAA-exc).
The difference in SUVs and TBR between AAA and AAA-exc as iteration increases was computed for all patients, and the result is displayed in Fig. 10. Substantial differences between AAA and AAA-exc were observed for SUVmean, SUVmax and TBRmax, with patient 3 exhibiting the largest difference. The difference decreased with iterations for all algorithms.
Fig. 10.
Quantification difference between AAA and AAA-exc for all metrics. This is shown for patients 1 – 3 (from top to bottom).
This discrepancy in SUV values between the two ROIs is partly due to the spill-in effect emanating from the adjacent active bone. PSF-based reconstructions performed well in reducing this spill-in activity for patient 1, but not for patients 2 and 3. For all 3 patients under review, PSF+BC exhibited the least differences between the two ROIs for all the quantitative metrics used, thereby suggesting the most robust spill-in correction performance.
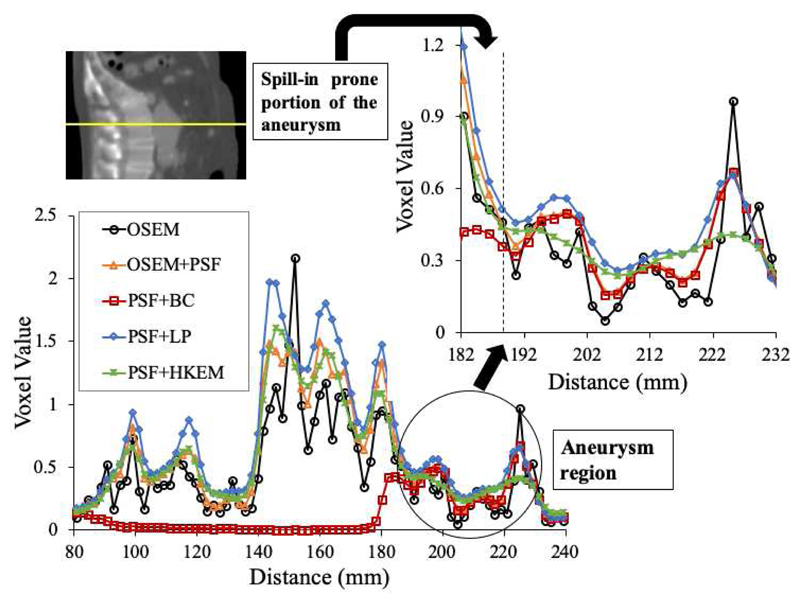
The spill-in effect from the bone into the aneurysm was also shown by drawing a line profile across the bone and the aneurysm as shown in Fig. 11. Indeed, the regions of the aneurysm in close proximity to the bone appeared to exhibit higher activity concentration, as they are expected to be more prone to the spill-in effects from the hot background signal in the bone tissues. This was true for all the reconstruction algorithms, except PSF+BC, where the bone contribution was successfully removed.
Fig. 11.
Profile across the bone and the aneurysm showing the portion of aneurysm in contact with bone as more prone to the spill-in effect.
V. Discussion
In this study, we have investigated the spill-in effects in target regions close to highly active background regions, especially as it applies to a characteristic set of clinical [18F]-NaF PET exams of abdominal aortic aneurysm. We have also comparatively evaluated the performance of recently proposed correction techniques, capable of compensating for the spill-in effects. These techniques were compared using simulated phantom with a Siemens Biograph mMR™ scanner template and AAA [18F]-NaF PET-CT data of three patients scanned with the Siemens Biograph mCT™ scanner.
For the simulation, the recovery coefficients increase with increasing lesion diameter, where lesion L2 with the smallest diameter of 6 mm has the smallest recovery coefficient as shown in Fig. 5. Although, one would expect the RC values for all lesions to improve with increasing iterations, this is only true for lesions L3, L4 and L6. Lesions L1, L2 and L5 have their RC reducing as iteration increases, until it converges at about 10 iterations (Supplementary Fig. S3). This behavior is attributed to the spill in effect in previous studies [7] as these lesions are closer to the bladder [4], [7]. This effect causes a substantial disparity in RC for all algorithms at lower iterations. Even though L1 and L3 have the same diameter (10 mm), the spill in effect resulted in the difference in RCmean and RCmax of up to 15% and 38% respectively between L1 and L3. The spill in effect also makes L5 (8 mm) to have higher RC than even L4 (20 mm). However, despite the spill in effect in L2 (6 mm), it still has lower RC than other lesions for all reconstruction algorithms. This is due to the fact that the spill in effect is probably offset by the spill out effect which is more prominent in small lesions. Comparing the reconstruction algorithms, OSEM and PSF images show a substantial overestimation in lesion SUVmax of up to 40% for lesions very close to the bladder, and small lesions are greatly underestimated. But BC, LP and HKEM methods have almost steady uptake recovery (close to 1) for all lesions except L2. BC also outperformed LP and HKEM in reducing the spill in effect in lesion L3.
The spill in effect due to the bladder activity is further validated in Fig. 6 where there is a large % difference in lesion RC values when the bladder SUV changes from SUV0 to SUV55.5. For proximal lesions (L1 and L2), this change is up to 40% for OSEM, PSF and HKEM images, but within 20% for BC and LP.
The performance of the reconstruction algorithms for the simulated phantom and patient PET images were evaluated in terms of convergence properties, contrast and COV as displayed in Figs. 6 and 9 and supplementary Figs. S3 and S4. For the simulation (Fig. S3), PSF has the highest RCmean for all the spheres, while LP has the lowest, except for lesion L2 where HKEM has the lowest RCmean. For all 3 patients (Fig. S4), OSEM yielded the highest SUVmean SUVmax and TBRmax at early iterations while the PSF+HKEM algorithm exhibited the lowest. However, at late iterations, PSF and PSF+BC methods attained the highest values. The high SUVs in OSEM reconstructed images might be due to the noise amplification of the algorithm, compared with PSF-reconstruction. This could be clearly seen in Figs. 8 and 9, where PSF-reconstructed images attained better noise reduction and higher contrast compared to the OSEM images. In addition to the considerable noise reduction, PSF+LP and PSF+HKEM images achieved higher contrast, with PSF+HKEM yielding the best performance. The substantial noise reduction attained with the PSF+HKEM method could be partly responsible for the considerably lower values obtained from the PSF+HKEM images. Although PSF+HKEM had higher contrast than PSF+LP (Fig. 8), the latter had a lower CoV (Fig. 9) because the activity in the aneurysm is more uniformly distributed in PSF+LP image than in PSF+HKEM image, thereby leading to a lower standard deviation, and hence lower CoV in PSF+LP image. It should also be noted, however, that PSF reconstructions exhibited a slow convergence, which has been a commonly reported issue in past PSF resolution modelling reconstruction studies [31], [32].
For the patient data, the spill-in effect from the active bone adjacent to the aneurysm resulted in major differences between the two ROIs (AAA and AAA-exc) for SUVmean, SUVmax and TBRmax (Fig. 10), especially for patient 3. This spill-in effect was further demonstrated by extracting a profile across the bone and the aneurysm as demonstrated in Fig. 11. It could be seen that regions of the aneurysm in close proximity to the bone were relatively more prone to the spill-in effect from the bone. This was true for all the reconstructions algorithms, except PSF+BC, where the bone contribution was successfully removed.
The differences in SUVs and TBR between AAA and AAA-exc decreased with a larger number of iterations for all algorithms, except PSF+BC which showed an almost zero difference in all cases. This suggests that the spill-in effect might have been reduced at later iterations, as previously reported [7]. This observation might be explained by the convergence of all algorithms with more iterations. However, a high noise amplification with little or no improvement in the image contrast was observed for higher number of iterations (Fig. 9).
It could also be noted that PSF+HKEM and PSF+LP images had considerably higher differences compared to the other techniques in all the quantification metrics used. Although PSF+LP performed slightly better than PSF+HKEM, it could not remove as much spill-in effects in the patient data as it did for the phantom data. This could be due to the assumption that the segmented tissue inside the VOI had a uniform activity concentration [12], [13]. Since this is not the case for the patient data, the LP method might have had the tendency to enforce a uniform uptake over the aneurysm and the bone tissues, thereby limiting the performance of the algorithm.
Also, the seemingly high spill-in effect in the PSF-based reconstructions could have been observed due to the commonly reported Gibbs artefacts, resulting in an overshoot around the hot region (i.e. bone) [31]–[33]. This might have led to the considerably higher values for AAA than AAA-exc, making it appear as though there is a higher spill-in effect with PSF reconstruction. However, the background correction (BC) technique corrected for this overestimation, and also improved the spill-in correction in the aneurysm.
The large difference between AAA and AAA-exc noticed for patient 3 might also have been observed due to inaccurate segmentation of the bone, and ROI-induced errors (where the aneurysm ROI partly covers the bone). This was also true for all the patient datasets where the performance of the LP method was dependent on segmentation (as earlier discussed). This suggests that these correction techniques were sensitive to segmentation errors (and potentially, misalignment of PET and CT images), which might have posed limitations to their performance. The effect of registration errors on the HKEM technique and the effect of segmentation errors on the BC reconstruction method have been separately studied in two previous investigations [7] [15]. Past studies have also shown that there is currently no firm consensus as to which correction approach is the best [34]–[36].
The performance of the BC techniques could have been further enhanced by further optimizing its implementation parameters. However, in this current work, the BC was implemented as a simple, yet effective, spill-in correction technique which could be easily adopted for routine use in the clinic. Thus, we estimated the background contribution at the 3rd iterations which is the most commonly employed iteration in clinical PET exams. More so, the estimated background regions were quite active and large, and hence, it was reasonably expected that the background activity would have nearly converged after the 3rd iteration, as demonstrated in the supplementary Fig. S1. However, for smaller background regions, a higher number of iterations might be required to ensure an adequate convergence. Or better still, we might need to update the background contribution at every iteration.
It is useful to note that the comparison between the correction algorithms might have been impacted by their varying degrees of contrast and convergence rates. Therefore, it would be helpful in future studies to carry out noise-matching in order to minimize the bias in evaluating the algorithms performances.
A major limitation in the simulation study is the crucial approximation of modelling an image-based system blurring and using the same analytical model to simulate and reconstruct the data. Although this is helpful for investigating the performance of the algorithms in correcting for the spill-in effect in each simulated lesion, it would have been preferable to utilize Monte Carlo simulators. Nevertheless, this limitation does not significantly impact the performance of the different algorithms because we also utilized acquired patient datasets which demonstrated similar trend in the performance of the algorithms for spill-in correction.
VI. Conclusion
We have investigated the impact of spill-in effects on PET quantification accuracy in regions of interest close to high background activity regions. For that purpose, we systematically evaluated the performance of three recently proposed promising spill-in correction techniques using both phantom PET/MR experimental data as well as abdominal aortic aneurysm PET/CT human patient data. The results showed that the BC method could be successfully used to correct for the spill-in effects in regions close to a hot background region. The BC method was also robust to ROI-selection variability thus enhancing the accurate PET signal quantification in large varieties of target regions of interest.
Supplementary Material
Acknowledgment
This work was undertaken on MARC1, part of the High-Performance Computing and Leeds Institute for Data Analytics (LIDA) facilities at the University of Leeds, UK. The authors would like to thank the people at the Biomedical Engineering and Imaging Institute at Mount Sinai (NY) for providing the phantom data acquired with the Siemens Bio-graph mMR™ scanner.
Mercy I. Akerele was supported by a PhD scholarship award from Schlumberger Foundation Faculty for the Future (Schlumberger Stitching Funds, The Netherlands). D. Deidda was supported by the University Research Scholarship, University of Leeds. Dr C. Tsoumpas is sponsored by a Royal Society Industry Fellowship (IF170011), the EPSRC Collaborative Computational Flagship Project (EP/P022200/1) and the EPSRC Collaborative Computational Project SyneRBI (EP/T026693/1).
Contributor Information
Mercy I. Akerele, Biomedical Imaging Science Department, Faculty of Medicine and Health, University of Leeds, UK; Department of Radiology, Weil Cornell Medical College of Cornell University, NY, USA.
Nicolas A. Karakatsanis, Department of Radiology, Weil Cornell Medical College of Cornell University, NY, USA; Biomedical Engineering and Imaging Institute, Icahn School of Medicine at Mount Sinai, NY.
Daniel Deidda, Biomedical Imaging Science Department, Faculty of Medicine and Health, University of Leeds, UK; Department of Statistics, University of Leeds, UK; Nuclear Medicine Imaging, Medical Radiation Physics, National Physical Laboratory, London, UK.
Jacobo Cal-Gonzalez, Medical University of Vienna, Vienna, Austria.
Robert G. Aykroyd, Department of Statistics, University of Leeds, UK
Steven Sourbron, Biomedical Imaging Science Department, Faculty of Medicine and Health, University of Leeds, UK.
Charalampos Tsoumpas, Biomedical Imaging Science Department, Faculty of Medicine and Health, University of Leeds, UK; Biomedical Engineering and Imaging Institute, Icahn School of Medicine at Mount Sinai, NY.
References
- [1].Erlandsson K, Buvat I, Pretorius PH, Thomas BA, Hutton BF. A review of partial volume correction techniques for emission tomography and their applications in neurology, cardiology and oncology. Phys Med Biol. 2012;57(21):R119–59. doi: 10.1088/0031-9155/57/21/R119. [DOI] [PubMed] [Google Scholar]
- [2].Zaidi H, Karakatsanis NA. Towards enhanced PET quantification in clinical oncology. Br J Radiol. 2018;91(1081) doi: 10.1259/bjr.20170508. 20170508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Rousset O, Rahmim A, Alavi A, Zaidi H. Partial volume correction strategies in PET. PET clinics. 2007;2(2):235–249. doi: 10.1016/j.cpet.2007.10.005. [DOI] [PubMed] [Google Scholar]
- [4].Liu Y. Invalidity of SUV measurements of lesions in close proximity to hot sources due to shine-through effect on FDG PET-CT interpretation. Radiol Res Pract. 2012 doi: 10.1155/2012/867218. 868218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Silva-Rodriguez J, Tsoumpas C, Dominguez-Prado I, Pardo-Montero J, Ruibal A, Aguiar P. Impact and correction of the bladder uptake on 18F-FCH PET quantification: a simulation study using the XCAT2 phantom. Phys Med Biol. 2016;61:758–773. doi: 10.1088/0031-9155/61/2/758. [DOI] [PubMed] [Google Scholar]
- [6].Akerele M, Wadhwa P, Vandenberghe S, Tsoumpas C. Comparison of partial volume correction techniques for lesions near high activity regions. 2017 IEEE Nucl Sci. Symp and Med Imag Conf (NSS/MIC); Atlanta, GA. 2017. pp. 1–7. [Google Scholar]
- [7].Akerele MI, Wadhwa P, Silva-Rodriguez J, Hallett W, Tsoumpas C. Validation of the physiological background correction method for the suppression of the spill-in effect near highly radioactive regions in positron emission tomography. EJNMMI Phys. 2018;5(1):34. doi: 10.1186/s40658-018-0233-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Akerele MI, Karakatsanis NA, Forsythe RO, Dweck MR, Syed M, Aykroyd RG, et al. Iterative reconstruction incorporating background correction improves quantification of [18F]-NaF PET/CT images of patients with abdominal aortic aneurysm. J Nucl Cardiol. 2019 doi: 10.1007/s12350-019-01940-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Bellinge JW, Schultz CJ. Optimising arterial 18F-sodium fluoride positron emission tomography analysis. J Nucl Cardiol. 2019 doi: 10.1007/s12350-019-01992-6. [DOI] [PubMed] [Google Scholar]
- [10].Forsythe RO, Dweck MR, McBride OMB, Vesey AT, Semple SI, Shah ASV, et al. 18F-Sodium Fluoride Uptake in Abdominal Aortic Aneurysms: The SoFIA3 Study. J Am Coll Cardiol. 2018;71(5):513–523. doi: 10.1016/j.jacc.2017.11.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Tsoumpas C, Thielemans K. Direct parametric reconstruction from dynamic projection data in emission tomography including prior estimation of the blood volume component. Nucl Med Commun. 2009;30(7):490–493. doi: 10.1097/mnm.0b013e32832cc1d7. [DOI] [PubMed] [Google Scholar]
- [12].Moore SC, Southekal S, Park M, Mcquaid SJ, Kijewski MF, Muller SP. Improved regional activity quantification in nuclear medicine using a new approach to correct for tissue partial volume and spillover effects. IEEE Trans Med Imaging. 2012;31(2):405–416. doi: 10.1109/TMI.2011.2169981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Cal-Gonzalez J, Li X, Heber D, Rausch I, Moore SC, Schafers K, et al. Partial volume correction for improved PET quantification in 18F-NaF imaging of atherosclerotic plaques. J Nucl Cardiol. 2017;25(5):1742–1756. doi: 10.1007/s12350-017-0778-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Deidda D, Karakatsanis NA, Robson PM, Efthimiou N, Fayad ZA, Aykroyd RG, Tsoumpas C. Effect of PET-MR Inconsistency in the Kernel Image Reconstruction Method. IEEE Trans Radiat Plasma Med Sci. 2019;3(4):400–409. doi: 10.1109/trpms.2018.2884176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Deidda D, Karakatsanis NA, Robson PM, Calcagno C, Senders ML, Mulder WJM, et al. Hybrid PET/MR kernelised expectation maximisation reconstruction for improved image-derived estimation of the input function from the aorta of rabbits. Cont Med Mol Imaging. 2019;2019:1–12. doi: 10.1155/2019/3438093. ID 3438093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Bland J, Mehranian A, Belzunce MA, et al. MR-guided kernel EM reconstruction for reduced dose PET imaging. IEEE Trans Radiat Plasma Med Sci. 2017;2(3):235–243. doi: 10.1109/TRPMS.2017.2771490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Bland J, Belzunce M, Ellis S, McGinnity C, Hammers A, Reader A. Spatially-compact MR-Guided kernel EM for PET image reconstruction. IEEE Trans Radiat Plasma Med Sci. 2018;2(5):470–482. doi: 10.1109/TRPMS.2018.2844559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Belzunce MA, Mehranian A, Reader AJ. Enhancement of partial volume correction in MR-guided PET image reconstruction by using MRI voxel sizes. IEEE Trans Radiat Plasma Med Sci. 2019;3(3):315–326. doi: 10.1109/TRPMS.2018.2881248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Segars W, Sturgeon G, Mendonca S, Grimes J, Tsui B. 4D XCAT phantom for multimodality imaging research. Med Phys. 2010;37(9):4902–4915. doi: 10.1118/1.3480985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Kainz W, Neufeld E, Bolch WE, Graff CG, Kim CH, Kuster N, et al. Advances in computational human phantoms and their applications in biomedical engineering - A topical review. IEEE Trans Radiat Plasma Med Sc. 2019;3(3):1–23. doi: 10.1109/TRPMS.2018.2883437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Karlberg AM, Saether O, Eikenes L, Goa PE. Quantitative comparison of PET performance-Siemens Biograph mCT and mMR. EJNMMI Phys. 2016;3(suppl 5) doi: 10.1186/s40658-016-0142-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Siddon RL. Fast calculation of the exact radiological path for a three-dimensional CT array. Med Phys. 1985;12:252–255. doi: 10.1118/1.595715. [DOI] [PubMed] [Google Scholar]
- [23].Watson CC, Newport D, Casey ME. A Single Scatter Simulation Technique for Scatter Correction in 3D PET. Three-Dimensional Image Recon. In: Grangeat P, Amans JL, editors. Radiol & Nucl Med Computational Imaging and Vision. Vol. 4. Springer; Dordrecht: 1996. pp. 255–268. [Google Scholar]
- [24].Tsoumpas C, Aguiar P, Nikita KS, Ros D, Thielemans K. Evaluation of the Single Scatter Simulation Algorithm Implemented in the STIR Library. 2004 IEEE Nucl Sci Symp Med Imag Conf; Rome, Italy. [Google Scholar]
- [25].Thielemans K, Tsoumpas C, Mustafovic S, Beisel T, Aguiar P, Dikaios N, Jacobson MW. STIR: Software for Tomographic Image Reconstruction Release 2. Phys Med Biol. 2012;57(4):867–883. doi: 10.1088/0031-9155/57/4/867. [DOI] [PubMed] [Google Scholar]
- [26].Rapisarda E, Bettinardi V, Thielemans K, Gilardi MC. Image-based point spread function implementation in a fully 3D OSEM reconstruction algorithm for PET. Phys Med Biol. 2010;55(14):4131–51. doi: 10.1088/0031-9155/55/14/012. [DOI] [PubMed] [Google Scholar]
- [27].Rogasch JM, Hofheinz F, Lougovski A, Furth C, Ruf J, Großer OS, et al. The influence of different signal-to-background ratios on spatial resolution and F18-FDG-PET quantification using point spread function and time-of-flight reconstruction. EJNMMI Phys. 2014;1(1):12. doi: 10.1186/2197-7364-1-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Irkle A, Vesey AT, Lewis DY. Identifying active vascular micro-calcification by 18F-sodium fluoride positron emission tomography. Nat Commun. 2015;6(7495):1–11. doi: 10.1038/ncomms8495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Vallabhaneni SR, Gilling-Smith GL, How TV, Carter SD, Brennan JA, Harris PL. Heterogeneity of tensile strength and matrix metalloproteinase activity in the wall of abdominal aortic aneurysms. J Endovasc Ther. 2004;11(4):494–502. doi: 10.1583/04-1239.1. [DOI] [PubMed] [Google Scholar]
- [30].Pawade TA, Cartlidge TRG, Jenkins WSA. Optimization and reproducibility of aortic valve 18F-fluoride positron emission tomography in patients with aortic stenosis. Circ Cardiovasc Imaging. 2016;9(10) doi: 10.1161/CIRCIMAGING.116.005131. pii: e005131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Rahmim A, Qi J, Sossi V. Resolution modeling in PET imaging: Theory, practice, benefits, and pitfalls. Med Phys. 2013;40(6) doi: 10.1118/1.4800806. 064301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Munk OL, Tolbod LP, Hansen SB, Bogsrud TV. Point-spread function reconstructed PET images of sub-centemeter lesions are not quantitative. EJNMMI Phys. 2017;4:5. doi: 10.1186/s40658-016-0169-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Nuyts J. Unconstrained image reconstruction with resolution modelling does not have a unique solution. EJNMMI Phys. 2014;1(1):98. doi: 10.1186/s40658-014-0098-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Soret MM, Bacharach SL, Buvat I. Partial-volume effect in PET tumor imaging. J Nucl Med. 2007;48(6):932–45. doi: 10.2967/jnumed.106.035774. [DOI] [PubMed] [Google Scholar]
- [35].Hutton BF, Thomas BA, Erlandsson K, Bousse A, Reilhac-Laborde A, Kazantsev D, et al. What approach to brain partial volume correction is best for PET/MRI? Nucl Instrum Meth Phys Res A. 2013;702:29–33. [Google Scholar]
- [36].Thomas BA, Cuplov V, Bousse A, Mendes A, Thielemans K, Hutton BF, Erlandsson K. PETPVC: a toolbox for performing partial volume correction techniques in positron emission tomography. Phys Med Biol. 2016;61(22):7975–7993. doi: 10.1088/0031-9155/61/22/7975. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.