Stress relaxation in epithelial monolayers is controlled by the actomyosin cortex

Abstract

Epithelial monolayers are one-cell thick tissue sheets that line most of the body surfaces, separating internal and external environments. As part of their function, they must withstand extrinsic mechanical stresses applied at high strain rates. However, little is known about how monolayers respond to mechanical deformations. Here, by subjecting suspended epithelial monolayers to stretch, we find that they dissipate stresses on a minute timescale and that relaxation can be described by a power law with an exponential cut-off at timescales larger than ~10 s. This process involves an increase in monolayer length, pointing to active remodelling of cellular biopolymers at the molecular scale during relaxation. Strikingly, monolayers consisting of tens of thousands of cells relax stress with similar dynamics to single rounded cells and both respond similarly to perturbations of the actomyosin cytoskeleton. By contrast, cell-cell junctional complexes and intermediate filaments do not relax tissue stress, but form stable connections between cells, allowing monolayers to behave rheologically as single cells. Taken together our data show that actomyosin dynamics governs the rheological properties of epithelial monolayers, dissipating applied stresses, and enabling changes in monolayer length.

Epithelial monolayers line most surfaces and internal cavities of the body, acting as physical barriers between the internal and the external environment. For this, epithelia must withstand substantial mechanical stresses^1–4. During development, strain in epithelia evolves slowly with rates of ~0.04%.s^{-1 5}; while in adult animals, strain rates of 10-100%.s^-1 occur during normal organ function^6–10. While in some organs, such as the lung, epithelia are subjected to deformations lasting only seconds, in others (skin, intestine, bladder), large deformations can be sustained for minutes^10–12. In addition, organisms need to withstand external mechanical insults. Thus, for optimal tissue resilience, the cells must be mechanically integrated to spread stresses across the whole tissue. Failure to do so can result in tissue fracture with consequences such as hemorrhage and septicemia^13–15. Indeed, tissue fragility appears as a symptom in patients carrying mutations in intermediate filaments and desmosomal proteins¹⁶, adherens junction proteins and actin cytoskeletal regulators^{17, 18}, and because of bacterial pathogens targeting intercellular adhesions¹⁶. The ability of living tissues to dissipate stresses decreases the risk of fracture¹⁹, protecting organisms against failure. Despite the importance of epithelial mechanics, little is known about how epithelia dissipate stresses in response to extension.

In isolated cells, many rheological behaviours operating at different timescales have been identified. At sub-second timescales, localised stress applied to the cell surface can be dissipated by redistribution of the fluid phase cytosol through the porous insoluble part of the cytoplasm²⁰. At longer timescales, a scale-free power law rheology is observed^{20, 21} and recent work has indicated the presence of a cut-off to this response imposed by the actomyosin cytoskeleton²². In multicellular aggregates, rheology may be influenced by the assembly of specialised intercellular junctions and junctional signaling^{23, 24}. Indeed, adherens junctions, which link the actin cytoskeletons of adjacent cells, exhibit viscoelastic properties²⁵. However, little is known about the stress response of cultured or embryonic epithelia to deformation - despite this being an important property for tissues. Nor is it known which molecular mechanisms participate in the process. In part, this derives from the difficulty of measuring stress in epithelia mechanically coupled to a relatively thick and rigid extracellular matrix (ECM).

Here, we study stress relaxation in epithelial monolayers devoid of ECM subjected to a physiologically relevant strain. Our analysis reveals that, at minute timescales, tissue rheology is dominated by the actomyosin cytoskeleton and that myosin contractility accelerates stress relaxation. By contrast, adherens junctions act as stable bridges connecting adjacent cells. As a consequence, the stress relaxation of an epithelial monolayer is similar to that of an isolated cell.

Stress relaxation is accompanied by a change in length

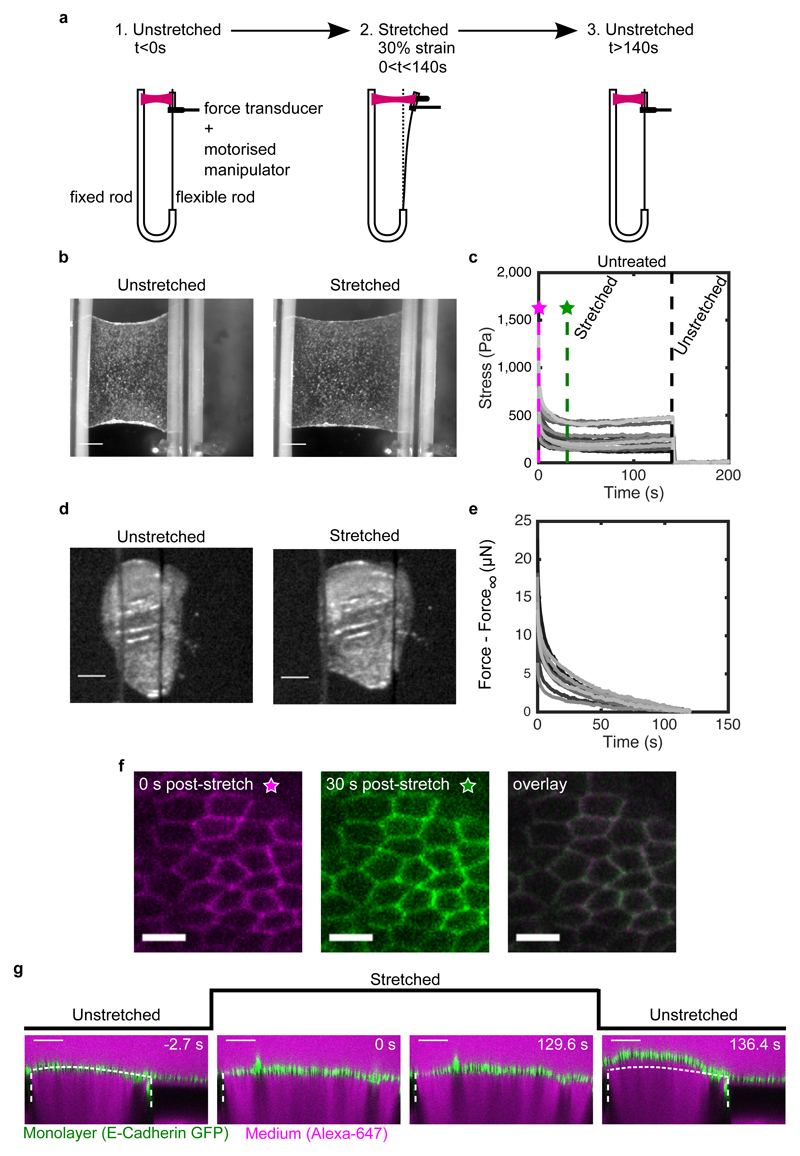
To investigate the response of epithelia to stress, we used monolayers of Madine-Darby Canine Kidney (MDCK II) cells devoid of a substrate and suspended between test rods^{13, 26}. Under these conditions, all stress in the system is borne by cells, simplifying interpretation and analysis (Fig S1). Suspended monolayers were subjected to a strain ε ₀ = 30% applied at a rate of 75%.s^-1, within the linear regime of the stress-strain response for monolayers¹³ and consistent with in vivo physiological conditions^{7, 10, 27}. Strain was then maintained for ~130-140 s (Fig 1a,b, Methods), while stress was monitored. Strikingly, ~70% of stress was dissipated within ~60 s (Fig 1c). Importantly, this behaviour was reproducible over several cycles. Moreover, cells maintained their characteristic apico-basal polarity and cytoskeletal organisation throughout^{13, 28}. In the body, epithelia are generally bound to ECM. Therefore, we confirmed the generality of the observed stress relaxation behaviour in a simple tissue comprising cells and ECM using Drosophila third larval instar wing imaginal discs (Fig 1d,e, SI). Wing discs displayed behaviours qualitatively similar to monolayers although the amplitude of stress relaxation was lower, likely because of the presence of ECM.

Figure 1. Stress relaxation in cell monolayers involves a change in length.

(a) Schematic diagram of the stress relaxation experiments. Monolayers were stretched to 30% strain at a 75%.s^-1 strain rate using a motorised micromanipulator and then kept at a fixed strain for ~130-140 s. The flexible rod was then returned to its initial position and the monolayers were left to recover. (b) Bright-field microscopy images of an epithelial monolayer before and during stretch. (Scale bar: 0.5 mm) (c) Stress relaxation curves of cell monolayers (n=17). The magenta and green dashed lines show 0 s and 30 s after application of stretch. Stresses go to zero upon return of the flexible rod to its initial position (t=140 s, black dashed line). (d) Bright-field microscopy images of Drosophila larval wing discs before and during stretch. (Scale bar: 100 μm) (e) Stress relaxation curves of Drosophila larval wing discs (n=12). (f) Confocal microscopy images of monolayers expressing E-Cadherin GFP for 0 s (left) and 30 s (middle) after stretch. Both images were overlayed to detect potential cell shape change during relaxation (right). (Scale bar: 10 μm) (g) Cross section of a monolayer expressing E-Cadherin GFP before application of stretch (−2.7 s), during stretch (0 s and 129.6 s) and upon release (136.4 s). The length of the monolayer upon release is different from its length before application of stretch. The monolayer appears in green, the surrounding medium appears in magenta due to inclusion of Alexa-647, and the glass substrate appears dark due to dye exclusion. The white dashed lines indicate the positions of the glass substrates. The part of monolayer situated between the two dashed lines is suspended. The dotted white line indicates the shape of the monolayer before application of stretch. (Scale bar: 100 μm). This experiment is representative of n=22 monolayers.

In living tissues, stress relaxation can arise from molecular or cellular processes. In our experiments, cellular processes, such as oriented cell division or neighbour exchange^{1, 19, 29}, are unlikely to contribute, since they necessitate tens of minutes (Fig 1c,f). During stress relaxation, we could not observe any changes in organisation or cell morphology (Fig S2c,d, SI). Nevertheless, when the test rod is returned to its initial position at the end of an experiment, the monolayer buckles (Fig 1g, Video S1). Thus, stress relaxation involves an increase in monolayer length as the result of remodelling at the subcellular scale.

Monolayer stress relaxation is biphasic

Stress relaxation started immediately after extension and was biphasic, with a large amplitude fast relaxation occurring within the first ~6 s, followed by a smaller amplitude slow relaxation, which reached a plateau after ~60 s, as previously observed¹³ (Fig 1c, 2a). This plateau indicates that the material behaves like a solid at minute timescales. Examination of the relaxation curves in log-log and log-linear scales revealed that stress decays as a power law in the first phase and as an exponential in the second (Fig S3). We confirmed the power law nature of the first phase by performing stress relaxation experiments for a range of deformations (Fig S4c-f, SI). Based on these observations, the relaxation can be described by $A{t}^{-\alpha }{e}^{-\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$\tau $}\right.}+B$ (Methods), with the first phase characterised by the exponent α and the second phase by the time constant τ (α = 0.3 ± 0.03, τ = 14.9 ± 5.8 s, n = 17 monolayers). B/ε ₀ is equivalent to an elasticity, and A sets the amplitude of relaxation. Interestingly, the power law exponent α ~ 0.30 was consistent with reports for cell aggregates subjected to compression³⁰. Relaxation in Drosophila wing discs displayed similar characteristics, although the parameters differed (Fig S5c-h, Table 2, SI). Thus, larval and cultured epithelia display fluid-like properties at second timescales and solid-like properties at minute timescales.

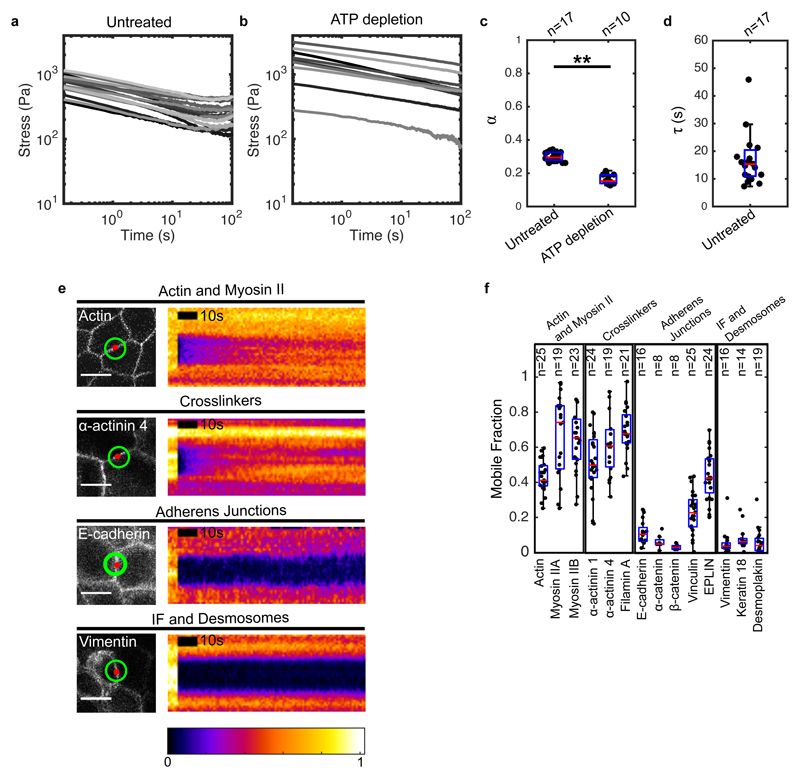
Figure 2. Significant cytoskeletal remodelling occurs over the timescale of stress relaxation.

(a,b) Stress relaxation curves of untreated (a, n=17) and ATP depleted (b, n=10) monolayers plotted on a logarithmic scale. (c) Boxplots comparing the power law exponent α of untreated and ATP-depleted monolayers. (** p < 0.01) (d) Boxplot of the exponential time constant τ for untreated monolayers. (e) Confocal microscopy images and kymographs of FRAP experiments. Left panels: the image shows localisation of the protein of interest, the red circle shows the bleached region, and the green circle shows the region imaged for fluorescence recovery. Right panels: each kymograph shows the normalised fluorescence intensity across the junction within the green circle. Intensities are normalised to the maximum intensity in each kymograph. (Scale bar: 10 μm) (f) Mobile fractions obtained from the FRAP curves for the cytoskeletal, adhesive, and junctional proteins examined. In all boxplots, the number of cells or monolayers examined is indicated above the graph.

To explore the robustness of this biphasic behaviour, we subjected cultured monolayers to a 30% strain applied at different strain rates and to different strains at a fixed 75%.s^-1 strain rate. In both cases, the data was well described by our empirical fit function (Fig S6, S8, SI). Taking loading into account, we confirmed that our initial experimental conditions (30% strain applied at 75%.s^-1) are close to a pure step strain for monolayers, validating our fitting approach (Fig S6-7, SI). Interestingly, τ increased with strain with a slope significantly larger than zero (Fig S8g, slope = 70.1 ± 57.1 s, p < 0.05). The dependence of τ on strain is surprising and may arise because the rate of processes dissipating stress does not depend on strain.

The transition between the two relaxation phases occurs for t ~ 6 (Fig S3c). This short timescale suggests that passive, ATP-independent processes govern the power law behaviour, while active ATP-dependent processes participate in the second phase. When we examined stress relaxation curves from ATP-depleted tissues in log-log scale, we noticed that they did not display the plateau at long timescales characteristic of exponential relaxation (Fig 2a-c, S4a, SI), indicating that the second phase was indeed ATP-dependent.

Monolayer stress relaxation depends on actomyosin

As stress relaxation is accompanied by an increase in monolayer length, we hypothesised that it may involve dynamic turnover of cytoskeletal and adhesive structures. We focused on subcellular structures known to play a role in cell and tissue mechanics^{31, 32} such as the actin cytoskeleton^{13, 33–35}, intermediate filaments^{36, 37}, and the intercellular junctions connecting these structures (adherens junctions^{13, 38, 39} and desmosomes¹⁵).

To identify key components of these structures in MDCK monolayers, we used mRNA sequencing (SI) and selected proteins amongst the most abundant in each candidate structure for further examination (Fig S9a).

We reasoned that only proteins that display significant turnover over the timescale of our experiments could significantly contribute to stress relaxation. To characterise turnover, we used Fluorescence Recovery After Photobleaching (FRAP) and estimated the extent of recovery after 100 s (mobile fraction, SI, Fig 2e,f, S9b,c, Table 1). Actin, myosin and crosslinkers were the most dynamic, with mobile fractions larger than 0.4, consistent with a potential role in stress relaxation (Fig 2f, Table 1). In contrast, proteins of the cadherin-catenin complex, intermediate filaments and desmosomes appeared stable, with mobile fractions smaller than 0.1. Proteins involved in mechanotransduction exhibited intermediate mobility (EPLIN and vinculin).

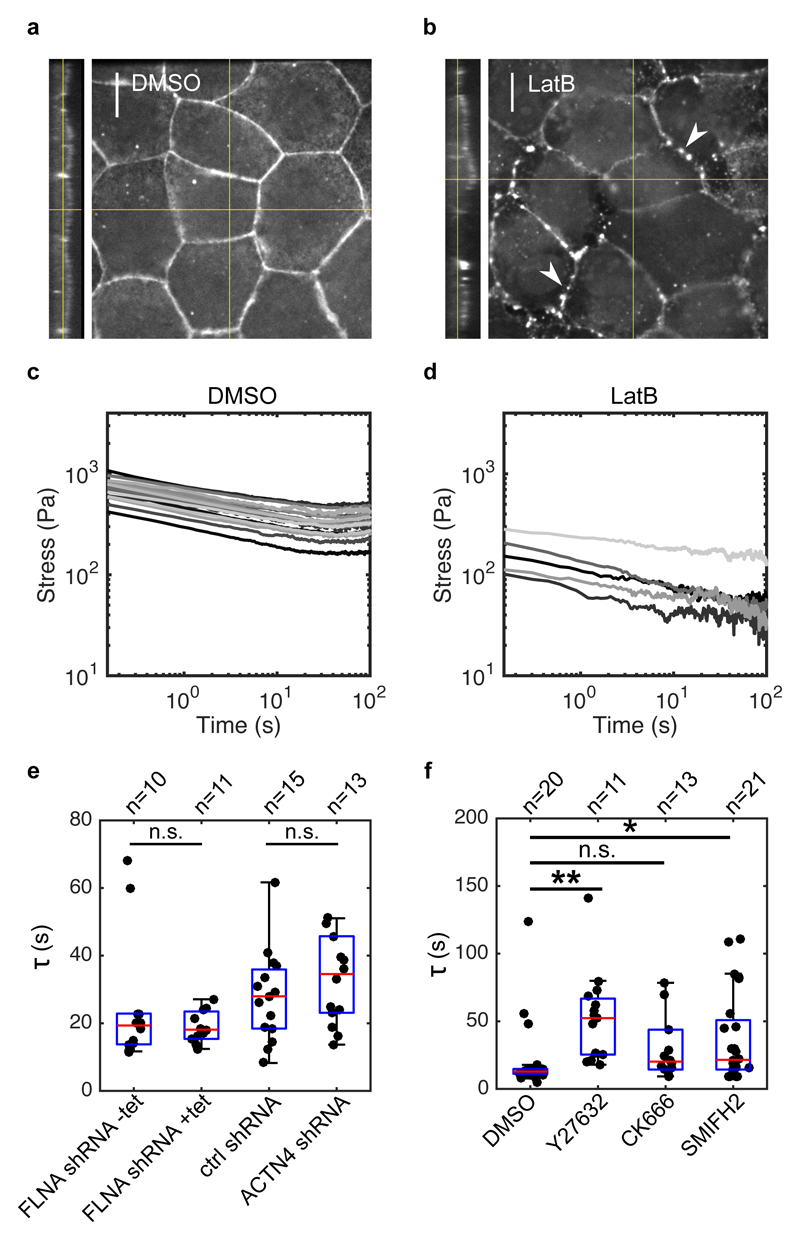
To test for a role for actomyosin, we depolymerised F-actin using latrunculin B (Fig 3a,b). This led to a remarkable softening of the monolayer, suggesting that intermediate filaments bear little stress at this range of strain (Fig 3c,d). Furthermore, relaxation curves appeared linear in the logarithmic scale, pointing to a delay in the second phase or its abrogation (Fig 3d). Thus, the actin cytoskeleton governs the second phase of relaxation. As actin-related proteins with fast turnover localised to both intercellular junctions and the submembranous cortex (Fig S10), this suggested that either of these actomyosin-rich structures may contribute to relaxation in the second phase.

Figure 3. Monolayer stress relaxation is slowed by perturbations to actomyosin.

(a,b) Confocal microscopy images showing F-actin distribution in monolayers treated with DMSO and latrunculin B for 1 h. Junctional actin localisation was perturbed following latrunculin treatment, leaving puncta of actin at the junctions (white arrows). (Scale bar: 10 μm). The monolayer yz-profile is shown on the left hand side of the xy panel. (c,d) Stress relaxation curves of monolayers treated with DMSO and latrunculin B for 1 h displayed in a logarithmic scale. (e) Boxplots comparing the exponential time constant τ in monolayers depleted for actin crosslinkers Filamin A and α-actinin 4 (p = 0.34 for FLNA shRNA +tet and p = 0.40 for ACTN4 shRNA, compared to their respective controls). (f) Boxplots comparing the exponential time constant τ following treatments with DMSO, Y27632, CK666 and SMIFH2 (** p < 0.01 for Y27632, n.s. p < 0.05 with 75% statistical power for CK666, and * p < 0.05 for SMIFH2, all compared to DMSO). In all boxplots, the number of monolayers examined is indicated above the graph.

Perturbing actomyosin slows relaxation

Actin’s function is multi-faceted: it is the building block for generating filamentous actin, F-actin serves as a scaffold for myosin contractility, and crosslinkers can modulate the network’s mechanics.

Previous work has identified specific roles for actin networks generated through distinct nucleation pathways via the Arp2/3 complex and formins in epithelial tissues^{40, 41}. To determine their respective role in monolayer stress relaxation, we inhibited actin nucleation through Arp2/3 using CK666, and through formins using SMIFH2 (SI). Formin inhibition led to a weakly significant increase in the relaxation time τ (Fig 3f). However, Arp2/3 inhibition had no significant effect.

To investigate the role of myosin contractility, we treated monolayers with Y27632, an inhibitor of Rho-kinase. Y27632 significantly reduced the elasticity B/ε ₀ (Fig S12f) and increased the relaxation time τ (Fig 3f, S12a), leading to curves that appeared more linear in logarithmic scale and implying that myosin activity accelerates the return to mechanical equilibrium.

Finally, we explored whether crosslinkers influence the dynamics of relaxation by generating friction in the actomyosin network, as in single cells^{22, 42}. We found that depletion of the dominant actin crosslinkers in the system (filamin A and α-actinin 4, Fig S9a) had no impact on stress relaxation (Fig 3e, S11).

Together, these results indicate that F-actin remodelling functions together with myosin contractility to ensure rapid relaxation of stress.

Monolayer relaxation is similar to relaxation of isolated cells

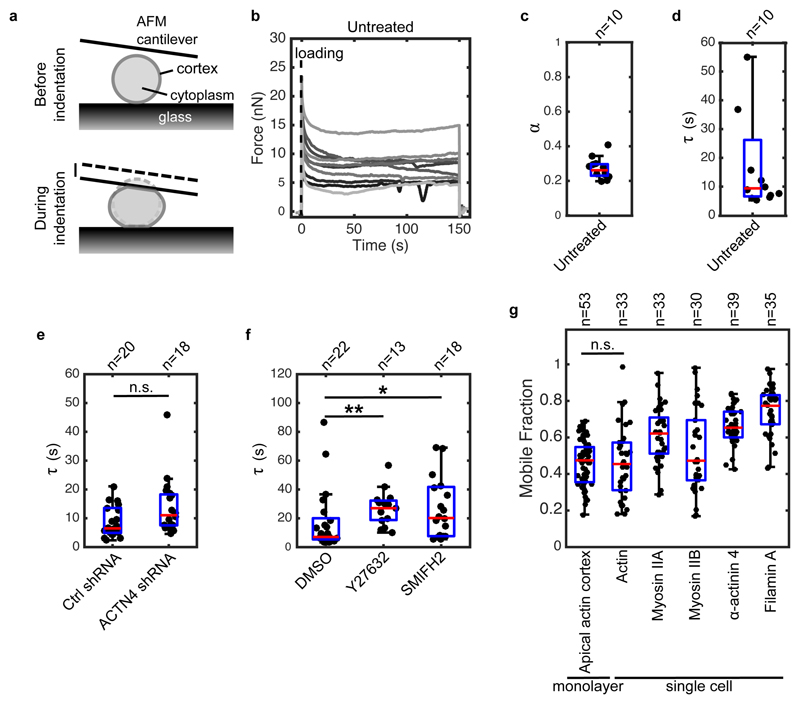
Interestingly, stress relaxation in monolayers appeared similar to reports examining single cells^{22, 43}. To investigate this, we characterised the relaxation of isolated MDCK cells by compressing single rounded cells with a tipless Atomic Force Microscope (AFM) cantilever to stretch the cortex in the free surfaces of the cell (Fig 4a)²². The transitory phase of force relaxation lasts ~20 s and reports on dissipation mechanisms, while the plateau reports on cellular cortical tension^{22, 44} (Fig 4b). Similar to monolayers, single cells relaxed following a power law at second timescales and an exponential at minute timescales, consistent with previous work²² (Fig 4b, S13a). Fitting these curves with our empirical function yielded a time constant τ = 13.4 ± 15.0 s, similar to monolayers (p = 0.18), and an exponent α = 0.25 ± 0.05, weakly but significantly smaller than in monolayers (p < 0.05, Fig 4c,d).

Figure 4. The dynamics of stress relaxation and the extent of actomyosin turnover are similar in single cells and monolayers.

(a) Diagram representing the experimental setup. At time t = 0 s, a single rounded cell is compressed between the glass surface and a tipless AFM cantilever. Cell compression leads to stretching of the cortex at the cell free boundaries. The evolution of force over time is measured by monitoring changes in cantilever deflection with an optical lever. (b) Temporal evolution of force in single rounded cells. A step deformation representing ~30% of cell height was applied at t = 0 s and maintained constant for 150 s. Each individual trace corresponds to a different cell. (c-d) Boxplots reporting the power law exponent α and exponential time constant τ for untreated rounded cells. (e) Boxplots comparing the characteristic relaxation times for cells expressing non-silencing shRNA (Ctrl shRNA) and shRNA targeting α-actinin 4 (ACTN4 shRNA) (n.s. p < 0.05 with 51% statistical power). (f) Boxplots comparing the characteristic relaxation times for cells treated with DMSO, Y27632, and SMIFH2 (** p < 0.01 for Y27632 and * p < 0.05 for SMIFH2, both compared to DMSO). (g) Boxplots comparing the mobile fraction of actomyosin proteins in the cortex of rounded cells after 100 s recovery after photobleaching as well as actin turnover in the apical cortex of cells within monolayers. In all boxplots, the number of cells examined is indicated above the graph.

Next, we investigated if the second phase of stress relaxation in single cells was sensitive to the same perturbations as monolayers. Depletion of α-actinin 4 had no effect (Fig 4e, S13). Treatments with Y27632 and SMIFH2 both increased τ, as in monolayers (Fig 4f), and decreased cellular cortical restoration force C (Fig S14).

Furthermore, we characterised actomyosin localisation and turnover in single rounded cells. Actin, myosins, and crosslinkers localised to the cortex of rounded cells (Fig S15c). Their turnover dynamics were similar to those measured in monolayers (Fig 4g, Fig S15a-b, Table 3). Therefore, single cells display similar stress relaxation to monolayers, are sensitive to similar perturbations, and have similar actomyosin turnover. This suggests that stress relaxation may originate in the actin cortex, the only actin- and myosin-rich structure common to isolated cells and monolayers. Consistent with this, the mobile fraction of actin in the apical cortex of cells within monolayers was not significantly different from that in single rounded cells (0.46 ± 0.13, p = 0.6, Fig 4g).

A phenomenological model for monolayer stress relaxation

To investigate the mechanical origins of the ATP-dependent regime and the dynamics of length change, we fitted the second phase of relaxation with rheological models representing the monolayer as an integrated mechanical system, in light of the similarities in the relaxation of single cells and monolayers. Based on our data, we reasoned that ATP-dependent monolayer mechanics should consist of an elastic branch, describing the response at minute-long timescales using a spring κ, placed in parallel with a viscous branch, that describes the transitory regime (Fig 5a, S16a).

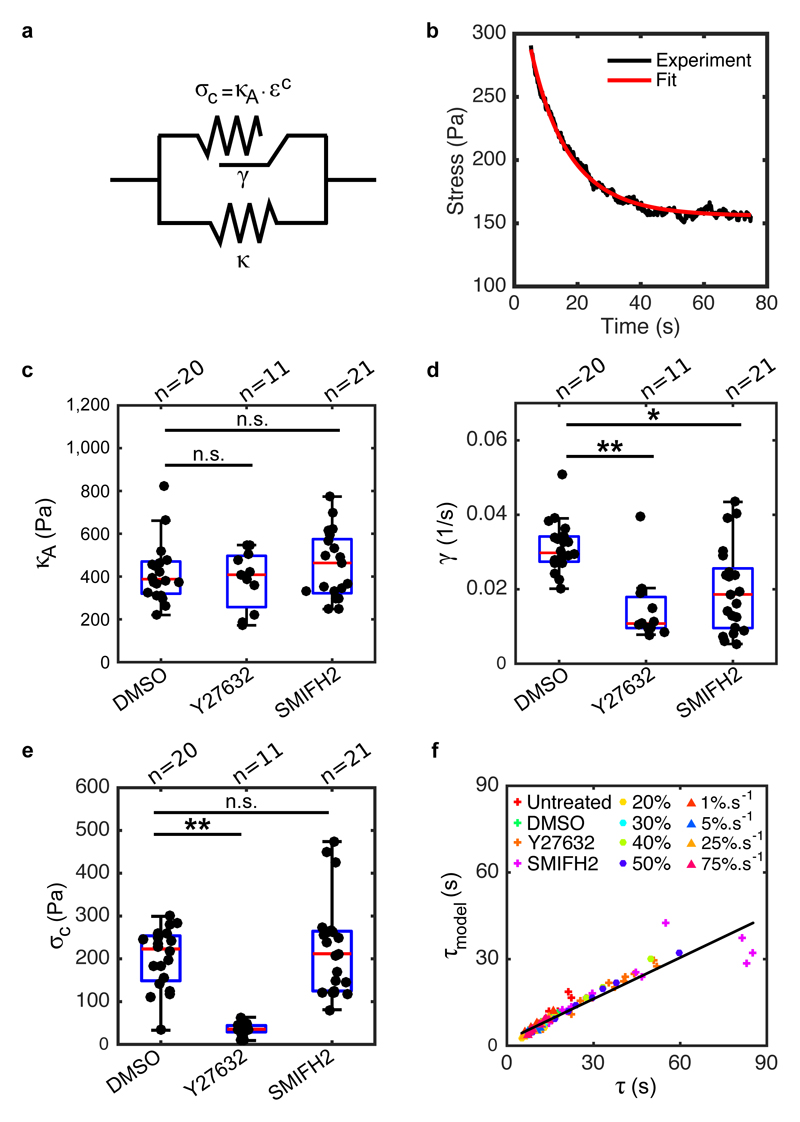
Figure 5. Formin-mediated actin polymerisation and myosin contractility contribute to rheological properties during stress relaxation.

(a) Diagram of the rheological model consisting of an active branch (top) and an elastic branch (bottom). The elastic branch consists of a spring with stiffness κ and this gives the steady-state behaviour of the monolayer. The active branch describes the transitory regime in response to mechanical perturbation and it comprises an active contractile element that consists of a spring κ_A subjected to a pre-strain ε^c. This active spring can change its resting length L(t) at a rate γ. (b) The second phase of a representative relaxation curve (black) is fitted with the rheological model shown in a (red). (c,d,e) Boxplots comparing the elastic modulus κ_A, the length-change rate γ and the pre-stress σ_c for monolayers treated with DMSO, Y27632 or SMIFH2. (κ_A: p = 0.95 for Y27632 and p = 0.58 for SMIFH2; γ: ** p < 0.01 for Y27632 and * p < 0.05 for SMIFH2; σ_c:** p < 0.01 for Y27632 and p = 0.80 for SMIFH2; all compared to DMSO) (f) Time constant τ _model calculated from the rheological model using equation (9) as a function of the time constant τ determined from fitting with the empirical function (equation (1)) for the different loading regimes and the different perturbations. In all boxplots, the number of monolayers examined is indicated above the graph.

Although a viscous branch consisting of a spring κ_M in series with a dashpot with viscosity η reproduces the experimental stress evolution (Fig S16, Methods) and provides the evolution of monolayer length (SI), its characteristic time is fixed by material parameters ${\tau }_M=\raisebox{1ex}{$\eta $}\!\left/ \!\raisebox{-1ex}{${\kappa }_M$}\right.$ independently of strain, in contradiction with our observations (Fig S8g). As an alternative, we used a model that considers length as an explicit variable⁴⁵ because epithelia often change length during development^{46, 47}. Because of the role of myosin and changes in length during relaxation, we modelled the viscous behaviour using an active contractile element consisting of a spring κ_A subjected to a constant pre-strain ε^c (Fig 5a). In response to an applied strain ε ₀, this spring changes its resting length L(t) as:

$$\dot{L}/L=\gamma \left({\epsilon }^e(t)-{\epsilon }^c\right)/|{\epsilon }^e(\text{t}=0\text{s})-{\epsilon }^c|$$

with γ a length-change rate. ε^e(t) is the effective strain defined as:

$${\epsilon }^e(t)=(l_m-L(t))/L(t)$$

with l_m the actual length of the monolayer imposed by deformation. Over time, the change in resting length L(t) dissipates stress with an exponential decay (equation (6)), similar to a Maxwell material (supplementary equation (14)), converging towards the pre-stress σ_c = κ_A.ε^c. After relaxation, stress in the monolayer reaches a plateau σ _∞ = κε ₀ + κ_Aε^c with a characteristic time that increases with strain as τ _model = ε ₀/[γ(1 + ε ₀)], as observed in experiments (Fig S8g). The resting length of the active branch and the elastic branch may be different because they originate from different cytoskeletal structures.

In monolayers, we measured a pre-stress σ_c ~ 141 Pa (Fig S17a,c, SI), consistent with an active element. Following relaxation, the stress in the elastic branch (σ _∞ − σ_c) appears to scale linearly with strain (Fig S17b), pointing to a spring-like behaviour with κ ~ 1006 Pa (Fig S17b). We fitted the second phase of stress relaxation using equation (7) to determine κ_A and γ, using our measurements of σ_c and κ, together with the relationship σ_c = κ_A.ε^c (Fig 5b, S17c-g, κ_A ~ 601 Pa, ε^c = 0.26 and γ ~ 0.03 s^-1, Methods). We then confirmed our model’s robustness to variations in strain and strain rate (SI). The characteristic times τ _model obtained from the model correlated well with those determined from empirical fitting for all conditions (Fig 5f). In experiments, τ increased with applied strain (Fig S8d,g), a scaling that could be explicitly derived from our rheological model with no change in material parameters (Fig S19e, Methods). Furthermore, for small applied strain, τ _model becomes linearly proportional to ε ₀:τ _model ~ ε ₀/γ. Using this approximation, linear fits of our observations (Fig S8g) suggest that τ(ε ₀) intercepts with the y-axis close to 0 s (intercept = −5.5 ± 11.4 s, p = 0.31 compared to zero), consistent with our model. The slopes of these fits predict γ ~ 0.03 ± 0.02 s^-1, similar to the values obtained by fitting relaxation curves for 30% strain (Fig S17e, p = 0.28). This suggests that γ stems from constitutive strain-independent biochemical reactions.

Myosins and formins accelerate length change

To link mechanical behaviour to biological mechanisms, we analysed perturbation experiments using our rheological model. The effect of F-actin depolymerisation suggested that both branches of our model are actin-rich structures (Fig 3a-d). Next, we measured changes to κ and σ_c from experiments and obtained κ_A and γ from curve fitting with the condition σ_c = κ_A.ε^c. Both treatment with Y27632 and SMIFH2 decreased the length-change rate γ, but had no effect on the stiffness κ_A (Fig 5c,d). Therefore, both formins and myosin contractility contribute to stress relaxation by ensuring rapid length change. Interestingly, Rho-kinase inhibition also decreased the pre-stress σ_c and stiffness κ, while formin inhibition affected neither (Fig 5e, S20a, SI). Thus, myosin contributes to both the active and the elastic parts of the system, perhaps through its different functions (contractility and crosslinking) or because each branch represents a distinct actomyosin structure.

Discussion

Here, we characterise stress relaxation and the molecular turnover of stress-bearing biological structures in isolated cells and epithelial monolayers. Our data paint a picture in which intercellular junctions form stable interconnections between cells allowing the monolayer to behave as a single cell with its rheology controlled by cortical actomyosin. Together F-actin remodelling and myosin contractility endow the monolayer with solid-like mechanical properties at minute timescales, act as driving forces to reach a new mechanical steady-state following extension, and regulate monolayer length.

Monolayer rheology is controlled by cellular rheology

Stress relaxation in monolayers displayed many similarities to stress relaxation in single cells. This is surprising since the cytoskeletal organisation of single rounded cells and cells within epithelia differ markedly.

Yet, when subjected to a step deformation, both single cells and monolayers displayed an initial phase of relaxation following a power law followed by an exponential decay reaching a plateau at minute-long timescales, consistent with previous reports^{22, 43}. The plateau indicates that both single cells and monolayers switch from a liquid-like behaviour at second timescales to a solid-like behaviour on minute-long timescales.

In the second phase of relaxation, stress in monolayers and single cells decayed with a time constant τ that was identical (~14 s). In both situations, τ depended strongly on myosin contractility and formin activity. These similarities imply that the rheology of single cells and monolayers is governed by actomyosin structures common to both.

Molecular mechanisms controlling monolayer rheology

In line with the role of actomyosin in stress relaxation, we observed that cortical proteins turn over significantly over the timescale of mechanical relaxation in single cells and monolayers. In contrast, the adhesive structures present in monolayers remodel far less. Therefore, adherens junctions form stable interconnections between cells allowing the monolayer to behave as a single cell with its rheology controlled by actomyosin. As the submembranous cortex is the only actomyosin-rich structure common to both single rounded cells and cells within epithelial monolayers (Fig S10, S15) and as it turns over to a similar extent in both configurations (Fig 4g), this suggests that cortical actomyosin controls stress relaxation. This further implies that rheology at the tissue-scale may be controlled by emergent properties of actomyosin gels at the molecular-scale⁴⁸.

Interestingly, the relaxation time τ increased with applied strain (Fig S8g) but why remodelling of the cortex should take longer for larger strain is unclear. Cortical remodelling requires nucleation of new actin filaments and depolymerisation⁴⁹. When monolayers are stretched, their apical and basal areas increase¹³ potentially leading to a decrease in the concentration of actin nucleators at the membrane. As cortex thickness is regulated^{50, 51}, the lower nucleator concentration may lead to a longer remodelling time.

Monolayer length changes in response to application of stress

Previous theoretical and experimental studies have suggested that changes in the resting length of cells and tissues may underlie stress relaxation^{45, 46}. In line with this, we showed that monolayer length increases in response to sustained stretch (Fig 1g). This length change stems for a change in the length of the active branch of our model and depends on formin-mediated polymerisation and myosin contractility (Fig 5). Although length increase in the active branch dissipates part of the stress, our model and experiments indicate that the elastic branch does not change length at minute timescales. Further work will be necessary to determine which actomyosin structure underlies this elastic-like behaviour. The realisation that some monolayer structures can change resting length over minute timescales in response to stress may have important consequences for our understanding of developmental morphogenesis, which often involves large tissue deformations in response to stress generated elsewhere in the embryo. Our results show that, in addition to cellular level processes which necessitate tens of minutes, molecular turnover can change cellular cortical area to dissipate stresses in minutes.

Methods

Cell culture and generation of cell lines

MDCK II cells were cultured at 37C in an atmosphere of 5% CO₂ in air in high glucose DMEM (ThermoFisher) supplemented with 10% FBS (Sigma) and 1% penicillin-streptomycin (ThermoFisher). Mechanical experiments and imaging were performed in Leibovitz’s L15 without phenol red (ThermoFisher) supplemented with 10% FBS.

In order to visualise the junctional and cytoskeletal structures, as well as to determine the turnover kinetics of various proteins, stable lines of MDCK II cells expressing the following proteins were used: E-Cadherin GFP, actin GFP, Lifeact-GFP, α-catenin GFP, β-catenin GFP, vinculin GFP, EPLIN GFP, α-actinin 1 GFP, α-actinin 4 GFP, filamin A GFP, vimentin GFP, keratin 18 GFP, desmoplakin GFP, NMHCIIA GFP and NMHCIIB GFP. Cell lines expressing E-Cadherin GFP, Lifeact-GFP and keratin 18 GFP were described in Harris et al.¹³. Other cell lines were generated by linearisation of plasmids encoding the FP tagged protein of interest with the appropriate restriction enzyme. The following plasmids were used: α-catenin GFP (a kind gift of Dr E Sahai, the Francis Crick Institute, UK), β-catenin GFP (a kind gift of Dr Beric Henderson, University of Sydney, Australia), vinculin GFP (a kind gift of Prof Susan Craig, Johns Hopkins University, USA), EPLIN GFP (a kind gift of Prof Elizabeth Luna, University of Massachusetts, USA, Addgene plasmid 40947), α-actinin 1 GFP⁵², α-actinin 4 GFP (a kind gift of Prof Doug Robinson, Johns Hopkins University, USA), filamin A GFP (a kind gift of Dr Paul Shore, University of Manchester, UK), vimentin GFP (a kind gift of Prof Robert Goldman, Northwestern University, USA), desmoplakin GFP (a kind gift of Prof Kathleen Green, Northwestern University, USA, Addgene plasmid 32227), NMHCIIA GFP and NMHCIIB GFP (both kind gifts of Dr Robert Adelstein, National Heart, Lung and Blood Institute, USA, Addgene plasmids 11347 and 11348). The cell line expressing actin GFP was generated by inserting actin-GFP into a retroviral vector (pLPCX, Takara Clontech), generating retrovirus as described in Harris et al.¹³, and transducing it into MDCK cells. To create all other stable cell lines, the plasmid of interest was first linearised with the appropriate restriction enzyme and then transfected into wild type MDCK II cells using electroporation (Lonza CLB). ~10⁶ cells were transfected with 10 μg (NMHCIIA-GFP, NMHCIIB-GFP) or 2 μg (all other plasmids) of cDNA according to manufacturer’s instructions and then selected with antibiotics for 2 weeks. In order to achieve a homogenous level of fluorescence expression, cells were sorted using flow cytometry. Cells expressing E-Cadherin GFP were cultured in presence of 250 ng.ml^-1 puromycin. Cells expressing actin GFP were selected in presence of 1 μg.ml^-1 puromycin. All other cell lines were selected in presence of 1 mg.ml^-1 G418.

To study the role of crosslinkers, cell lines stably expressing shRNA targeting filamin A and α-actinin 4 were used. Filamin A shRNA was expressed in a tetracycline-inducible manner⁵³. These cells were cultured in presence of 5 μg.ml^-1 blasticidin and 800 μg.ml^-1 G418. To induce expression of shRNA, cells were incubated in presence of 2 μg.ml^-1 doxycycline for 72 h prior to the experiments. Plasmids encoding non-silencing shRNA and shRNA targeting α-actinin 4 were a kind gift from Prof Bill Brieher (University of Illinois Urbana-Champaign, USA). Following linearisation of the plasmids, stable cell lines expressing control shRNA and α-actinin 4 shRNA were generated by transfecting the plasmids into wild type cells using electroporation (Lonza CLB) as described above. Control and α-actinin shRNA lines were amplified and selected in presence of 4 μg.ml^-1 puromycin. Protein depletion was ascertained using Western blotting.

Generating suspended cell monolayers

Suspended cell monolayers were generated as described by Harris et al.^{13, 26}. Further information is provided in SI.

Mechanical testing procedure

The mechanical testing setup was assembled on top of an inverted microscope (Olympus IX-71) (Fig S1a). First, the petri dish containing the stress measurement device was secured on the microscope stage with 4 pieces of plasticine. The force transducer (SI-KG7A, World Precision Instruments) with a tweezer-shaped mounting hook (SI-TM5-KG7A-97902, World Precision Instruments) was mounted on a 3D motorised micromanipulator (Physik Instrumente) with a custom-made adaptor. The fixed rod of the device was held with the arm of a 3D manual micromanipulator (Fig S1a), while the top Tygon section of the flexible rod was held with the tip of the force transducer (Fig S1c). Both motorised and manual micromanipulators were equipped with a magnetic plate that secured them to the custom-made metal stage of the microscope.

Using the motorised micromanipulator, the monolayers could be extended to different strains with controlled strain rates. Extended monolayers exerted restoring forces on the flexible rod, causing the transducer tip to bend. The extent of bending was translated into a voltage value that was converted into a digital signal using a data acquisition system (USB-1608G, Measurement Computing) and recorded onto a computer. Both the data acquisition system and the motorised micromanipulator were controlled with a custom-written code in Labview. The monolayer and the transducer tip were imaged every 0.5 s using a 2× objective (2× PLN, Olympus).

The mechanical testing procedure consisted of several steps:

• - Initial approach: The tip of the force transducer was initially brought into contact with the Tygon tubing and then positioned such that the left tweezer arm was out of contact but within 50 μm distance from the Tygon tubing. This enabled identification of the contact point of the transducer tip with the device during the mechanical testing procedure (Fig S1c).
• - Preconditioning: The monolayers were subjected to 8 cycles of loading to a 30% target strain at a 1%.s^-1 strain rate. This ensured breakage of any residual collagen attached to the monolayer (especially close to the rods), as well as causing the samples to evolve into a “preconditioned” state, where the slope of the stress-strain curve did not change in successive cycles. Hence, several experiments could be conducted on the same sample with a high degree of reproducibility.
• - Stress relaxation experiments: The monolayers were extended to 30% strain at a 75%.s^-1 strain rate and then kept at a fixed 30% strain for ~130-140 s. The micromanipulator was then returned to the position it occupied before stretch (Fig 1a). This released the monolayers and they were left unstretched for ~130-140 s to recover before performing another stress relaxation experiment. This stress relaxation experiment was repeated 3 times on each monolayer.
• - Loading until failure: The monolayers were extended until failure at 1%.s^-1 strain rate. After rupturing the monolayer, the flexible rod was returned to its initial position.
• - Calibration of the device: To allow conversion from voltages to force, the device was calibrated. For this, the wire was extended at the same rate and to the same extent as in the cycling experiments. This was repeated 5 times. The length of the wire L_w was measured using a Canon FD macro-lens (Canon, Surrey, UK) interfaced to a Hamamatsu EMCCD camera (Hamamatsu Orca ER, Hamamatsu UK, Hertfordshire, UK) (Fig S1b). Together with the mechanical properties of the wire, knowledge of L_w enable determination of the bending stiffness of the wire and hence the force applied for a given deflection.

A detailed description of the procedure for conversion of voltages to forces is given in SI.

Drosophila wing disc mechanical testing

The stress measurement devices and the mechanical testing procedure used for the Drosophila wing discs were similar to those for monolayers with a few modifications (see SI).

Single rounded cell mechanical testing procedure

Prior to experiments, MDCK cells were trypsinised and plated sparsely in a glass bottomed Petri dish (35 mm diameter, WPI) and left to settle for 10-30 minutes. The experiments were conducted while the cells remained rounded and before they started to spread.

Force relaxation measurements were conducted using a CellHesion 200 Atomic Force Microscope (JPK Instruments, Berlin, Germany) mounted on a scanning laser confocal microscope (Olympus IX81 with a FV1000 confocal head) and tipless silicon SPM-Sensor cantilevers (ARROW-TL1Au-50, Nano World) with nominal spring constant of 0.03 N.m^-1. The sensitivity of each cantilever was measured from the slope of a force-displacement curve acquired on a glass coverslip, and the spring constant was calibrated using the thermal noise fluctuation method. The spring constants estimated for each experiment ranged between 0.055-0.06 N.m^-1.

Before conducting force relaxation experiments, force-displacement curves were acquired on the cell and a glass region close to it. Using these two curves, we estimated the cell height as the difference between the cantilever contact with the cell and glass. Next, we estimated the target force required to indent the cell by ~30%. Finally, force relaxation curves were acquired by indenting the cell to the target force of 5-40 nN at a rate of 75%.s^-1 and maintaining the cantilever at a constant height for 150 s while the force was recorded.

Analysis of the relaxation curves

To analyse the response of monolayers to a step deformation, the first 75 s of the stress relaxation curves were fitted with a function consisting of a power law with an exponential cut-off:

$$\sigma (t)=A{t}^{-\alpha }{e}^{-\frac{t}{\tau }}+B$$ (1)

The fitting procedure was as follows. First, the initial conditions for the fitting were determined. B was the residual stress after the curves plateaued and was defined as the average of stress between 70 s < t < 75 s. A + B was defined as the initial stress at the second timepoint (t = 0.150 s) after the step deformation (Fig S3a). The first timepoint after application of the step deformation was ignored to allow the calculations to be performed on a logarithmic scale. To estimate α, the first 5 s of the curves were used. In practice, σ(t < 5 s) − B was plotted as a function of time on a logarithmic scale and fitted with a line, with α being the slope of this line (Fig S3b). To estimate τ, τ(5 < t < 20 s) − B was plotted in a semi-logarithmic scale and fitted with a line, with μ being the slope of this line (Fig S3c). Each experimental relaxation curve was fitted using equation (1), with the free parameters A, α, and τ. B was also allowed to vary by 15% to optimise the fits (Fig S3d). The trust-region-reflective least squares algorithm, a built-in Matlab fitting procedure, was used for the fitting. The fitting was performed for the three individual repeats of the stress relaxation experiments on each monolayer. The fitted values obtained from the three repeats were then averaged to obtain a single value for each parameter.

For ATP depletion experiments, we followed the same general procedure except that we fitted experimental curves with a function of the form At ^−α.

The same procedures were also followed to fit the relaxation curves of single rounded cells and larval wing discs. For single cell relaxation curves, since the residual force reports on cortical restoration force, we have denoted it a different parameter C, which was estimated and fitted similar to B for monolayers. Due to the slower relaxation of the larval wing discs, we fitted the first 120 s of the relaxation curves and B was defined as the average of stress between 115 < t < 120 s.

The goodness of fit was determined using the coefficient of determination r ² and curves with r ² < 0.80 were excluded from further analysis. This represented less than 3% of experimental curves acquired. We also ensured that there was no systematic bias in the fit residuals. Outliers were determined as described in the statistical analysis section and the curves for which either of the two parameters α and τ were outliers were not included for statistical analysis. On average, less than 13% of the data was excluded from analysis.

Analysis of the relaxation curves taking loading into account

The relaxation modulus G(t) describes the behaviour of a viscoelastic material and is obtained from the response of the material to a step in strain. This ideal loading condition cannot be achieved experimentally. In practice, strain is applied with a constant strain rate $\dot{\epsilon }$ until reaching the target strain ε ₀, after which strain is kept constant. Thus, the temporal evolution of stress σ(t) in the material is given by the convolution between the relaxation modulus and the derivative of the strain:

$$\sigma (t)={\displaystyle {\int }_0^{t}G(t-t^{\prime })}\frac{d\epsilon (t^{\prime })}{d{t}^{\prime }}d{t}^{\prime }$$ (2)

where the relaxation modulus is of the form $G(t)=A^{\prime }{t}^{-\alpha }{e}^{-\frac{t}{\tau }}+B^{\prime }$ and A′ and B′ are related to A and B in equation (1) as follows: A = ε ₀ A′ and B = ε ₀ B′.

We fitted the relaxation responses of monolayers loaded at a 75%.s^-1 strain rate, using equation (2). Due to the singularity of G(t) at t = 0 s, we fitted the relaxation curves in the range [Δt, t_max], with Δt being 0.150 s (our experimental timestep). The response of the material predicted using the average parameters extracted from fitting with equation (2) (Fig S7a, black line) are in good agreement with those obtained approximating our experimental conditions to an ideal step strain (Fig S7a, red line). Statistical comparisons indicate that the parameters obtained through both methods are not significantly different (Table S2). Thus, the relaxation responses obtained for strain rates of 75%.s^-1 can be approximated by an ideal step strain.

Chemical treatments

Chemical treatments are described in detail in SI.

Fitting the second phase of the relaxation with the Standard Linear Solid (SLS) model

The second phase of the relaxation curves (defined for t > 6 s) was fitted with the SLS model, which consists of an elastic branch with stiffness κ in parallel with a Maxwell branch (Fig S16a). The Maxwell branch consists of a spring of stiffness κ_M in series with a dashpot of viscosity η.

Following application of a step strain ε ₀ at t = 0 s, the stress in the Maxwell branch will relax as follows:

$${\sigma }_M(t)={\epsilon }_0{\kappa }_M{e}^{-\frac{{\kappa }_M}{\eta }t}$$ (3)

The characteristic time τ _M for this relaxation is:

$${\tau }_{\text{M}}=\frac{\eta }{{\kappa }_M}$$ (4)

Experimental data σ_raw(t) was fitted as follows: first the residual stress B was subtracted from the raw stress because it represents the stress in the elastic branch and stays constant over time. Next, the stress in the Maxwell branch (i.e. σ_M(t) = σ_raw(t) − B) was fitted with the stress relaxation function (3), allowing κ_M and η to vary. 88% of the fitted curves had a coefficient of determination r ² > 0.8.

Fitting the second phase of the relaxation with the rheological model

The second phase of the relaxation curves (defined for t > 6 s) was fitted with the rheological model shown in Fig 5a, which consists of an elastic branch with stiffness κ and an active branch. The active branch consists of a spring of stiffness κ_A subjected to a pre-strain ε^c that can adapt its resting length L(t) to return to ε^c after extension. Thus, in response to an applied strain ε ₀ that changes the monolayer actual length l_m from l ₀ to l ₁, the monolayer stress is $\sigma (t)=\kappa {\epsilon }_0+{\kappa }_A{\epsilon }^e(t)\text{with}{\epsilon }^e(t)=\frac{l_m-L(t)}{L(t)}\text{and}{l}_m=l_1$ the actual length of the monolayer imposed by deformation.

In our modelling, we used the following evolution law for the resting length L(t) of the active branch:

$$\frac{\dot{L}}{L}=\gamma \frac{({\epsilon }^e(t)-{\epsilon }^c)}{|{\epsilon }^e(0)-{\epsilon }^c|}$$ (5)

where γ is the rate of change in resting length. In choosing our empirical evolution function, we reasoned that the material parameters describing the response of the active element γ, ε^c, and κ_A should not change when we fit experimental curves for different applied strain because the initial state of the monolayer is the same (Fig S8, S19).

Following application of a step strain at t = 0 s that changes the actual length from l_m = l ₀ to l_m = l ₁, the monolayer resting length L(t) will adapt. Since the monolayers are pre-stressed and contractile, the value of the resting length before application of the deformation is given by L(0⁻) = l ₀/(1 + ε^c). This provides the initial pre-strain: ε^c = [l ₀ − L(0⁻)]/L(0⁻). Using equation (5), the evolution of the resting length is calculated as:

$$L(t)=\frac{l_0}{1+{\epsilon }^c}[(1+{\epsilon }_0)-{\epsilon }_0{e}^{-\frac{\gamma }{{\epsilon }_0}t}]$$ (6)

Knowing that σ = κ_Aε^e, this will lead to stress relaxation in the active branch after application of deformation of the form:

$${\sigma }_A(t)={\kappa }_A\left(\frac{(1+{\epsilon }_0)(1+{\epsilon }^c)}{(1+{\epsilon }_0)-{\epsilon }_0{e}^{-\frac{\gamma }{{\epsilon }_0}t}}-1\right)$$ (7)

where ε ₀ is the applied strain defined as ${\epsilon }_0=\frac{l_1-l_0}{l_0}.$

The characteristic time τ _model for this relaxation can be calculated as:

$${\tau }_{\text{model}}={\left(\frac{d\sigma }{dt}{|}_{t=0}\right)}^{-1}(\sigma (\infty )-\sigma (0))$$ (8)

$${\tau }_{\text{model}}=\frac{{\epsilon }_0}{\gamma (1+{\epsilon }_0)}$$ (9)

Experimental data σ_raw(t) was fitted as follows: first the residual stress B was subtracted from the raw stress because it represents the stress in the elastic branch and stays constant over time. The pre-stress σ_c was determined in separate measurements because it cannot be determined during stress relaxation experiments (SI, Fig S17a,c). This pre-stress was then added to the stress in the active branch to yield σ_A(t) = σ_raw(t) − B + σ_c. Knowing that the measured pre-stress σ_c is equal to κ_A.ε^c, we substituted ε^c with σ_c/κ_A in equation (7) and σ_A(t) was fitted with the stress relaxation function (7), allowing κ_A and γ to vary. The obtained analytical curves fitted the experimental data well (r ² > 0.8 for 88% of the relaxation curves) without any systematic bias in the residuals.

Statistical analysis

All data analysis and curve fitting were conducted using custom-written code in Matlab. For each dataset, outliers were defined as the values that fell outside the range [q ₁ − w × (q ₃ − q ₁),q ₃ + w × (q ₃ − q ₁)], where q ₁ and q ₃ were the 25th and 75th percentiles of the data and w was 1.5. Outliers were excluded from statistical analysis. The normality of the data was tested using both Lilliefors and Shapiro-Wilk tests in R, which confirmed non-normality of some datasets. Statistical analysis was performed in Matlab, using a two-sided Wilcoxon rank sum test that does not assume normality of the data. To determine whether a single dataset was significantly different from zero, Wilcoxon signed rank test in Matlab was used. Datasets with p < 0.01 were deemed to be highly significantly different and are denoted by a double asterisk (**). Datasets with p < 0.05 were deemed to be significantly different and are denoted by a single asterisk (*). Changes with p > 0.05 or where statistical power was less than 0.8 were considered non-significant. For all boxplots, the edges of the box represent the 25th and 75th percentiles of the data, the red line marks the median and the whiskers extend to include the most extreme data points that are not considered to be outliers. Points on each boxplot represent individual monolayers or cells. Each dataset is pooled across experiments performed on at least 3 individual days.