Activation and disruption of a neural mechanism for novel choice in monkeys

Abstract

The neural mechanisms mediating the ability to make value-guided decisions have received substantial attention in both humans and animal models. Experiments in animals typically involve long training periods. By contrast, real-world decisions often need to be made spontaneously between novel options. It is therefore possible that neural mechanisms targeted in animal studies differ from those required for novel decisions typically revealed in human imaging studies. Here we show that primate medial frontal cortex (MFC) has a causal role in novel inferential choices when options have not previously been experienced. Macaques spontaneously inferred values of new options via similarities with component parts of previously encountered options. Functional magnetic resonance imaging (fMRI) suggested this ability was mediated by MFC, an area rarely investigated in monkeys; MFC activity reflected a different process of comparison for novel versus familiar options. A second fMRI experiment found that multidimensional option representations in MFC employed a grid-cell-like coding scheme, well known in the context of spatial navigation, to integrate dimensions in this nonphysical space when making novel choices. By contrast, orbitofrontal cortex held specific object-based value representations. In a third experiment, minimally invasive ultrasonic disruption of MFC, but not adjacent tissue, altered estimation of novel choice values.

The neural mechanisms enabling us to learn the values of choice options are increasingly well understood^1,2. It is known that neurons in macaque orbitofrontal cortex (OFC) encode the values of choice options learned incrementally through repeated exposure to stimuli and the outcomes they predict^1,2. OFC neurons are active when values are compared to decide between two options³. The value comparison processes central to decision-making has a signature that can be captured in fMRI recordings taken from the same macaque brain areas⁴. However, while similar processes may occur in humans, decision-making-related neural activity is most prominent in a different brain region: medial frontal cortex (MFC)^5,6. This might be because value representations are established in a very different way in investigations of human decision-making: the values of component parts of options are typically defined in advance and then during the experiment, human participants infer the value of novel options instantly from their component parts^7–9.

For example, participants might learn that one stimulus feature indicates the magnitude of reward at stake, while another indicates the probability of reward delivery. If a new option composed of the same features is encountered, its value can be estimated even before it is chosen for the first time. This captures an important characteristic of human decision-making: we make first-time decisions based on inferences from previously encountered options.

Novel inferential choices in macaques

The present study was designed to investigate whether macaques could perform novel inferential decisions and to examine the underlying neural mechanisms. In macaques it is possible to control precisely the choice exposure history, and, by combining neuroimaging and focal disruption techniques, to both record from neural circuits and to examine their causal role in behaviour^4,10. A series of three experiments (Fig.1) allowed us to identify a neural circuit for novel decisions, reveal a grid structure in its representation of option values, and determine the impact of its disruption with a recently established minimally invasive ultrasonic procedure^11–15.

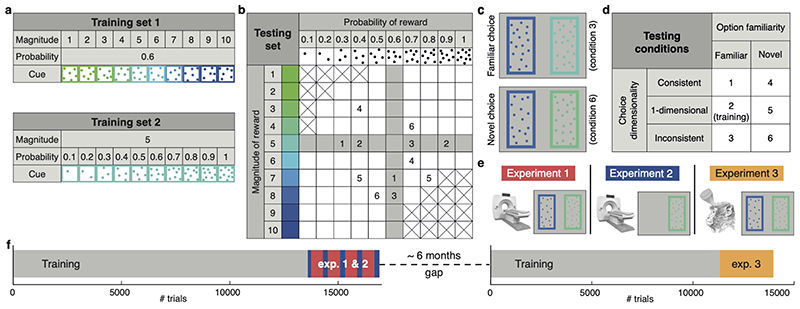
Fig. 1. Experimental design.

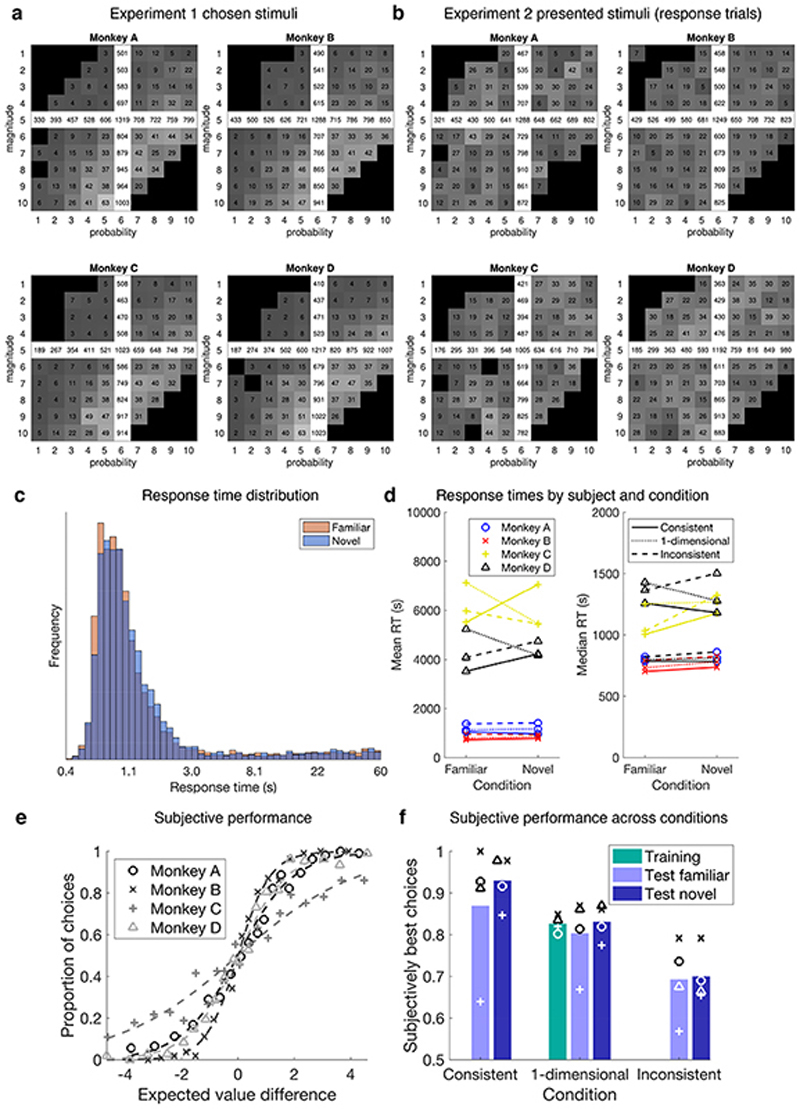
(a) Training set 1: stimuli varied in reward magnitude (drops of juice), cued by colour. Training set 2: stimuli varied in reward probability, cued by dot numerosity. (b) Testing set: stimuli varied in both magnitude and probability. Grey: familiar options; white: novel options. Crossed squares were not tested. Pairs of numbers exemplify choices in different conditions. (c) Stimulus appearance in two example trials. (d) Diagram of the 2 (familiarity) by 3 (dimensionality) design. (e) Illustration of the experiments’ features. 1: fMRI and decision task; 2: fMRI and single option (no decision) task; 3: TUS and decision task. (f) Timeline. Grey: training with sets 1 and 2 on alternating days. Red: experiment 1. Blue: experiment 2. Yellow: experiment 3.

Four macaques learned about two stimulus sets (Fig.1a). In set 1 colour indicated the magnitude of juice at stake (1-10 drops) with a fixed 0.6 probability. In set 2, dot number indicated the probability (0.1-1) of receiving a 5-drop reward. Animals encountered these two stimulus sets for 12800-13800 trials over a three-month period. These sets (Fig.1b, shaded area) spanned a notional two-dimensional “value space” much of which remained unexplored during training. Then experiment 1 began and fMRI data were collected while subjects chose either between two familiar options or between two previously unencountered options (Fig. 1b, white area). Although visually similar (Fig.1c), familiar and novel options had a very different reinforcement history (Extended Data Fig.1a,b).

During testing, the dimensionality and difficulty of the familiar and novel decisions were matched. Difficulty refers to expected value difference; dimensionality refers to whether both magnitude and probability favoured the same option (consistent condition), options only differed in one attribute (one-dimensional condition), or magnitude favoured one option and probability the other (inconsistent condition; Fig.1b,d).

Subjects’ accuracy was close to ceiling throughout the training (Fig.2b). Importantly, during testing monkeys chose accurately under both familiar and novel conditions (Fig.2c,d), with comparable response times (Extended Data Fig.1c,d).

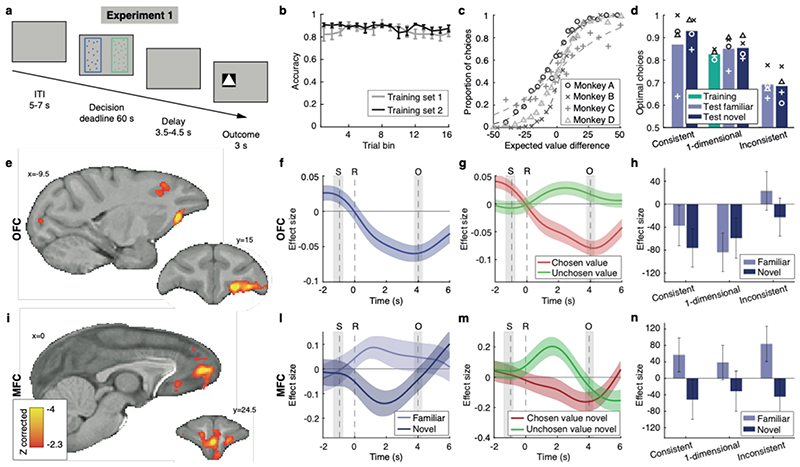
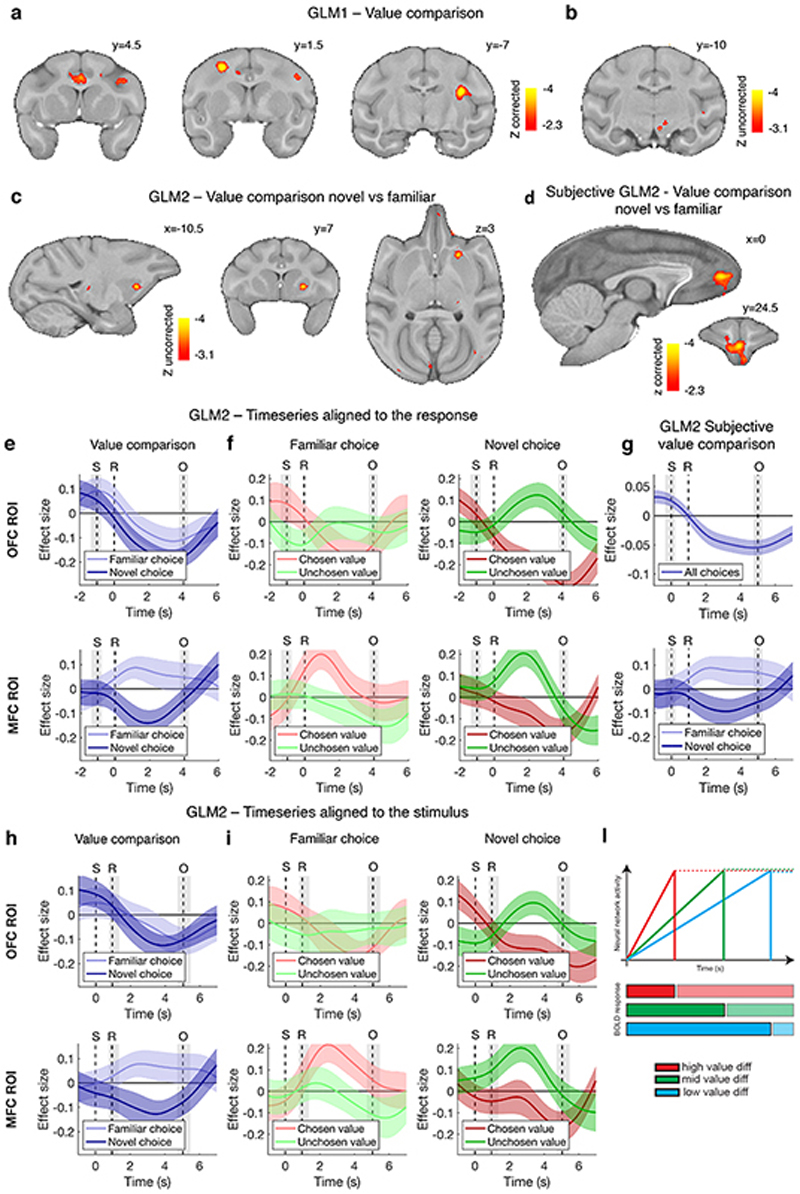
Fig. 2. Experiment 1, neural correlates of familiar and novel decisions.

(a) Trial timeline. (b) Proportion of correct responses during training. Error bars represent standard error of the mean (SEM). (c) Test performance (probability of choosing right as a function of right minus left expected value). (d) Comparison of performance across training and testing conditions. Optimal choices maximise expected value. Bars represent mean of four subjects. (e) Value comparison signal, i.e. chosen value minus unchosen value, across all trials, whole-brain cluster-corrected. (f) Time-course of the parametric modulation of the BOLD signal in OFC for all trials, time-locked to response. S: stimulus, R: response, O: outcome. Coloured line: mean of all sessions; coloured shade: SEM across sessions. Grey shades: interquartile ranges of stimulus and outcome time distributions. Same conventions apply in panels g,l,m. (g) Value comparison signal in OFC split into its components. (h) Value comparison signal in OFC split by condition. Error bars represent SEM. (i) Comparison signal difference between novel and familiar conditions, whole-brain cluster-corrected. Scale bar applies to both panels e and i. (l) Parametric modulation of the BOLD signal in MFC for novel and familiar choices separately. (m) Chosen value and unchosen value contributions to the comparison signal in MFC for novel trials only. (n) Value comparison signal in MFC split by condition. Same conventions as panel h. In all panels n=4 monkeys x n=12 sessions.

A value comparison signal in OFC

A signature of value comparison during choice has been repeatedly observed in fMRI experiments across species: activity in key decision areas reflects both the chosen and the rejected option values, but with opposite signs^4,7,8. This “value comparison” signal (chosen minus unchosen value) is a parametric effect occurring on top of average trial-induced activity; unlike in humans where it takes a positive sign, it consistently takes a negative sign in macaques^4,14. It reflects the key decision variable determining behaviour in computational models of decision-making^16,17 (Extended Data Fig.2l, Supplementary Information) and is dissociable from other indices of difficulty such as response time [Methods, general linear model (GLM) 1, Extended Data Fig.3a]. We observed such a value comparison signal in OFC ([-9.5 15 4.5], cluster-corrected at Z > 2.3, P = 0.017, max Z = 4.53, Fig.2e,f,g, Extended Data Table 1) regardless of whether familiar or novel option decisions were taken (Extended Data Fig.2e); trials not requiring dimension integration contributed more to the overall signal (Fig.2h). Extended Data Fig.2a,b illustrates additional effects in lateral frontal and cingulate cortex, insula, and midbrain.

A novelty effect for choices in MFC

We subsequently compared the parametric effects of value difference in novel and familiar choice trials (Methods, GLM2, Extended Data Fig.3b). A prominent difference was observed in anterior MFC [0 24.5 7.5], between the rostral and the anterior cingulate sulci in area 32, extending into areas 14m and 10¹⁸ (cluster-corrected at Z > 2.3, P = 10^-6, max Z = 4.14; Fig.2i,l,m; Extended Data Table 1; Extended Data Fig.2c illustrates an additional result in striatum). This region is similar to the human brain region active during decision-making, both in terms of cytoarchitecture and functional interactions^18,19. Although MFC remains relatively unexplored in macaque, major differences in anatomical connections suggest major differences in function between MFC and OFC²⁰.

An independent (“leave-one-out”) ROI analysis revealed that both the positive familiar and the negative novel effects were significantly different from zero (t ₄₇ = 2.09, Cohen’s d = 0.30, P = 0.042; t ₄₇ = -2.10, Cohen’s d = -0.30, P = 0.041) and neither were affected by dimensionality (familiar: F _2,141 = 0.29, P = 0.75; novel: F _2,141 = 0.05, P = 0.95) (Fig.2n). We show results based on objective, assumption-free definitions of value, but they remained qualitatively the same when using subjective value estimates (Methods eq.1, Extended Data Fig.2d,g, Extended Data Table 1).

Further inspection of the OFC general value comparison signal and the MFC novel value comparison signal revealed that they could both be decomposed into components reflecting the values of the taken and rejected options (Methods, Fig.2g,m). This reflects the competition of the two option representations during decision-making, and the facilitation of this competition when the chosen option is higher and the alternative option is lower in value^3,21.

Option identity representation in aOFC

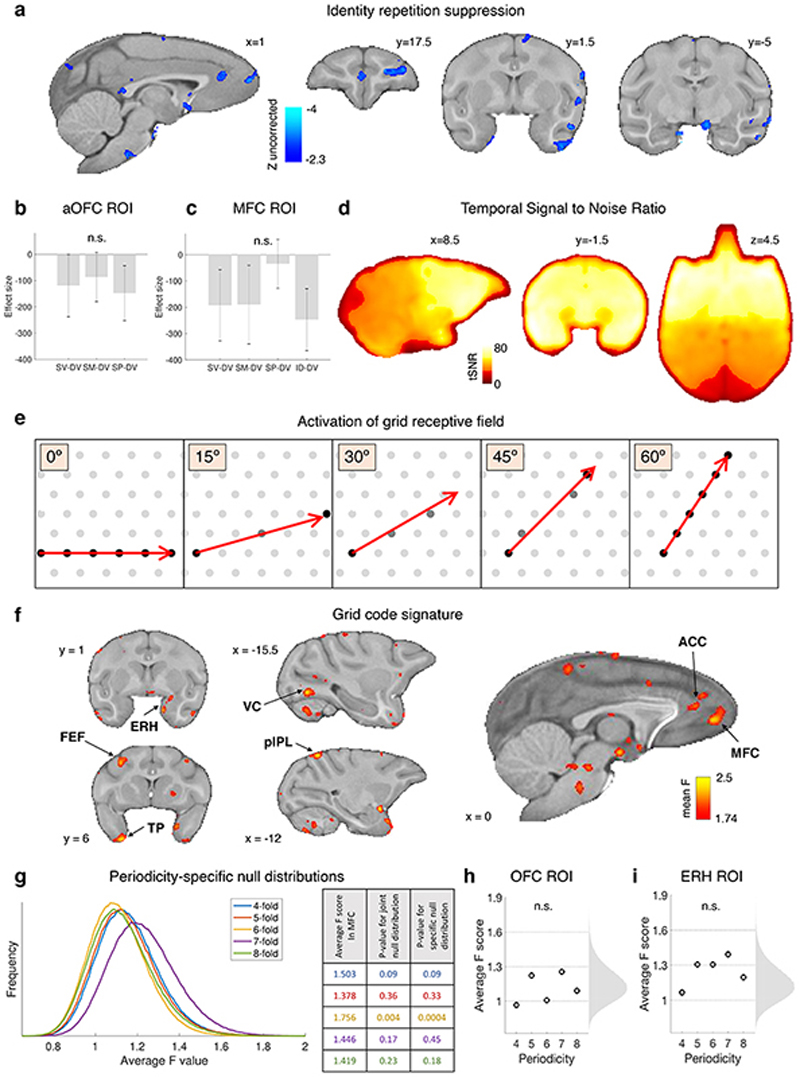
To understand how decisions between novel options were possible, a second fMRI experiment investigated the nature of the individual option representations that drive the comparison process and how they differed in MFC and OFC; specifically, we asked what mechanisms allow inference of novel option values. To investigate representations more directly, macaques did not have to make decisions in experiment 2; instead, trials displayed a single option and the relationship between options on successive trials was manipulated (Fig.3a). Data were collected on days interleaved with experiment 1 (Fig.1f). We exploited the fMRI activity suppression occurring when the same neural representation is activated repeatedly²² (Fig.3b). We measured the “repetition suppression” effect when a given option was identical to the preceding option as opposed to when it was different in value, on both dimensions, to the previous option (Methods, GLM3, Extended Data Fig.3c). Greater suppression seen in anterior OFC ([-7.5 27 9] near frontal pole) in the experiment’s later stages suggested the presence of representations linked to specific option identities building up with experience (cluster-corrected within frontal cortex at Z > 2.3, P = 0.028, peak Z = 3.67, Fig.3e, Extended Data Table 1). The representation was not of value per se, because successive options with the same integrated value, but different probability and magnitude components, did not cause suppression in this area, nor did the repetition of just magnitude or just probability without the other dimension (Extended Data Fig.4b). Extended Data Fig.4a shows that similar activity patterns were also found in the temporal lobe. Such option-specific value representations resemble those previously investigated in macaque and human mOFC^1,19,22 and perirhinal cortex²³.

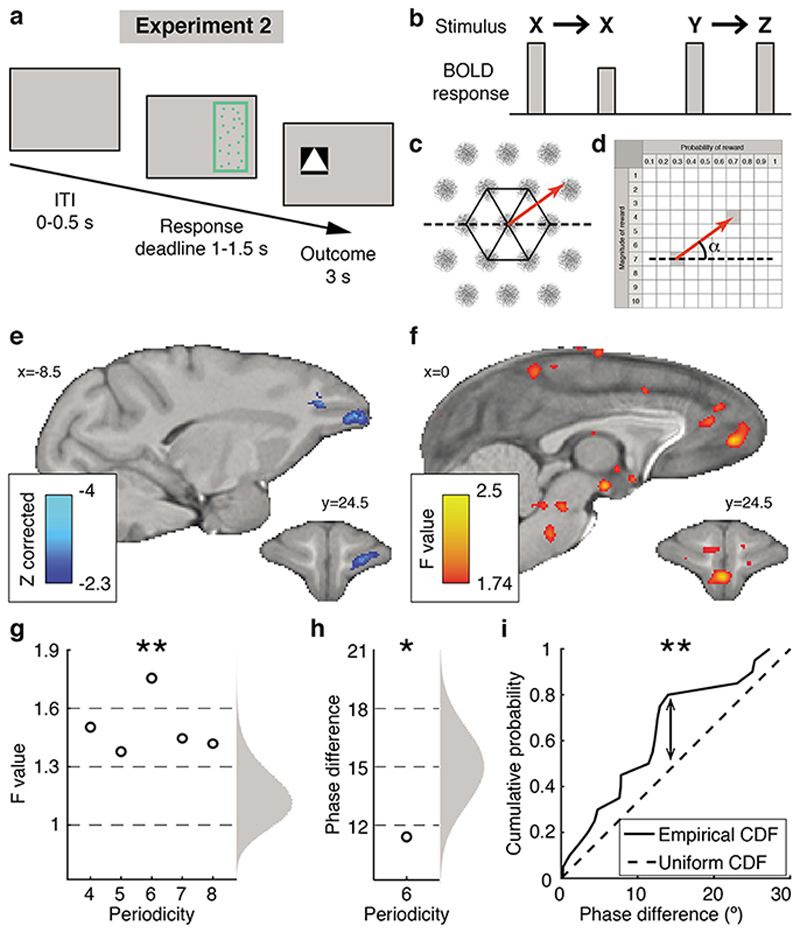
Fig. 3. Experiment 2, stimulus and value space neural representations.

(a) Trial timeline. (b) Illustration of repetition suppression effect. (c) Hexagonal symmetry (in black) of the receptive field of an ideal grid-cell (in grey) and a trajectory (in red) between two locations. (d) Illustration of the angle of the trajectory (in red) in value space from one option to the next. The angle is relative to a fixed orientation (dotted line). (e) Repetition suppression effect for option identity, cluster-corrected within frontal cortex. Test based on sessions 3 to 5. (f) Quadrature test for a hexagonal symmetry: average F values, P < 0.001 uncorrected (group level F-statistic cluster-correction is not possible²⁶). (g) Nonparametric test of the average F values for periodicities from four- to eight-fold; randomized null distribution on the right; a Bonferroni correction with factor 5 is applied; Results did not change with periodicity-specific null distributions (Extended Data Fig.4g). Data in panels g-h-i are from the MFC ROI defined independently in experiment 1. (h) Average phase difference between grid orientation estimates from two interleaved trial subsets from each session. Right: a priori null distribution. (i) Illustration of Kolmogorov-Smirnov test: empirical and a priori cumulative distribution functions (CDF) of phase differences across sessions. * P < 0.05, ** P < 0.01. In all panels (except e) n=4 monkeys x n=5 sessions.

An MFC grid-code represents value space

Having established MFC’s role in novel multidimensional decisions in experiment 1, we next used the single options in experiment 2 to investigate whether novel value representations might be constructed by grid-like encoding of the non-physical space spanned by the two dimensions of value. Position in physical space is encoded by cells in entorhinal cortex with a distinctive hexagonal pattern of receptive fields²⁴ (Fig.3c); encoding of conceptual spaces, including the value space we investigate here, might happen in an analogous manner^25–27. Previous fMRI experiments have demonstrated grid-cell-like patterns in human entorhinal cortex^26,28 by measuring activity variations dependent on whether navigation through space aligns with grid axes. Such fMRI studies have focused on entorhinal cortex, but typically the most prominent effect measured is in MFC near area 32^26,28. If the choice space that macaques navigate in our study (Fig.1b) is an abstract analogue of physical space and is encoded by a grid-cell-like pattern, then a rapid succession of options (corresponding to navigation in value space) may activate this neural representation. We hypothesised that even step-like transitions between options may modulate the fMRI signal, as previously seen for continuous physical movements²⁸ or saccadic eye movements²⁹, depending on their alignment with the hexagonal grid. We ran a quadrature test to seek activity periodically increasing and decreasing every 60° according to the angle of the trajectory from one option to the next (Fig.3c,d, Extended Data Fig.4e; Methods, GLM4, Extended Data Fig.3d).

We found such activity within the same MFC area identified for novel decisions (Fig.3f): a non-parametric F-test revealed a significant six-fold symmetry (adjusted P = 0.004) but no modulation for other periodicities between four- and eight-fold (Fig.3g). Notably no such activity patterns were found in OFC (Extended Data Fig.4h) and, conversely, the objectspecific activity patterns seen in OFC were not found in MFC (Extended Data Fig.4c). At the whole brain level, we observed some limited hexagonal modulation (P < 0.001 uncorrected) in entorhinal cortex and other locations outside our a priori ROIs (Extended Data Fig.4f).

However, the non-parametric F-test in the entorhinal ROI was not significant (Extended Data Fig.4i), possibly because of slightly lower tSNR (Extended Data Fig.4d). MFC grid orientation estimates obtained from interleaved halves of each session were consistent (mean phase difference 11.4°, Fig.3h; one-sample one-sided Kolmogorov-Smirnov test: KS stat = 0.33, P = 0.009, Fig.3i), although estimates across sessions were not consistent (KS stat = 0.2, P = 0.18), suggesting grid remapping.

MFC sonication affects value integration

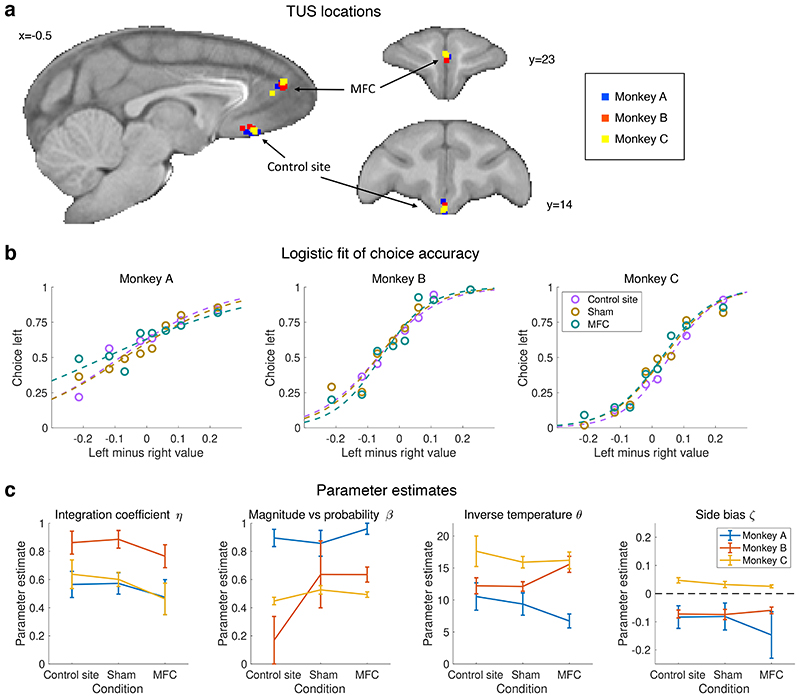
In the third experiment, we causally validated an implication of experiments 1 and 2. If the MFC grid representation supports a two-dimensional representation of option value, and this integrated representation of magnitude and probability allows extrapolation to new options, then disruption of this map in MFC should particularly affect the ability to make novel choices on the basis of integrated option values (Fig.4). It would still be possible to choose based on each dimension independently, but the ability to account for the interaction between magnitude and probability may be impaired (Fig.4b). In experiment 3, we therefore examined the impact of focal disruption of the previously identified MFC region on choice behaviour, using transcranial ultrasound stimulation (TUS) (Fig.4a). We employed an “offline” procedure altering activity in a circumscribed brain region for approximately an hour after a 40 s stimulation; such a procedure has been successfully and selectively applied before to adjacent frontal areas^11,12,14 and its offline nature avoids potential auditory confounds³⁰. We compared TUS to the centre of the MFC activation to both a non-stimulation control condition (sham) and an active control condition: stimulation of a more posterior medial frontal region at the periphery of the MFC activation (Fig.2i, Fig.4d, Extended Data Fig.5a). To specifically test MFC’s role in integrating information across dimensions we adapted the behavioural task to include only “inconsistent” decision trials (conditions 3 and 6 in Fig. 1b,d), in which whenever reward probability was higher for one option, magnitude was higher for the other option. We focused on these trials because they require dimension integration and cannot be solved by focusing on a single dimension; we report specifically results for novel choices.

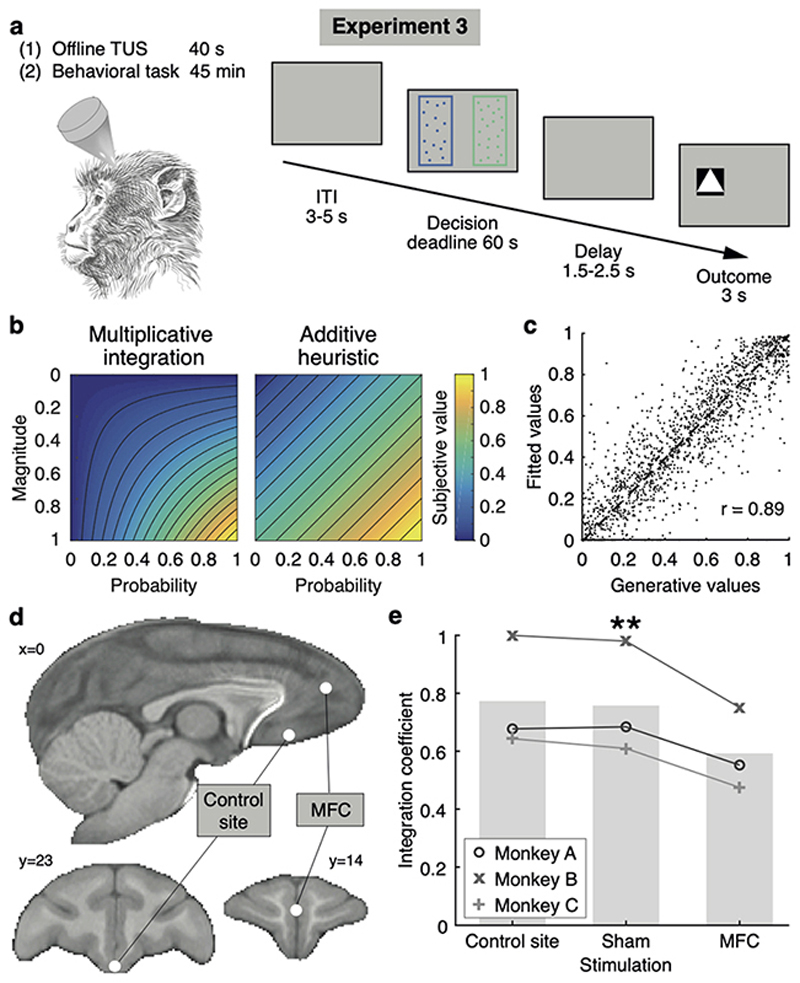
Fig. 4. Experiment 3, behavioural impact of neurostimulation.

(a) Trial timeline in the task following transcranial ultrasound stimulation (TUS). All trials were inconsistent trials. (b) Illustration of the difference in subjective value when using an optimal multiplicative approach (diml x dim2) or a simpler additive approach (dim1+dim2)/2. (c) Recovery of the integration coefficient (ratio of the two approaches) in a simulation with novel trials. (d) Stimulation sites in MFC (ROI identified in experiment 1) and a control site in more posterior frontal cortex. (e) Integration coefficient fits after sham TUS, control site TUS, and MFC TUS; n=3 monkeys x n=4 sessions per condition; ** P < 0.01.

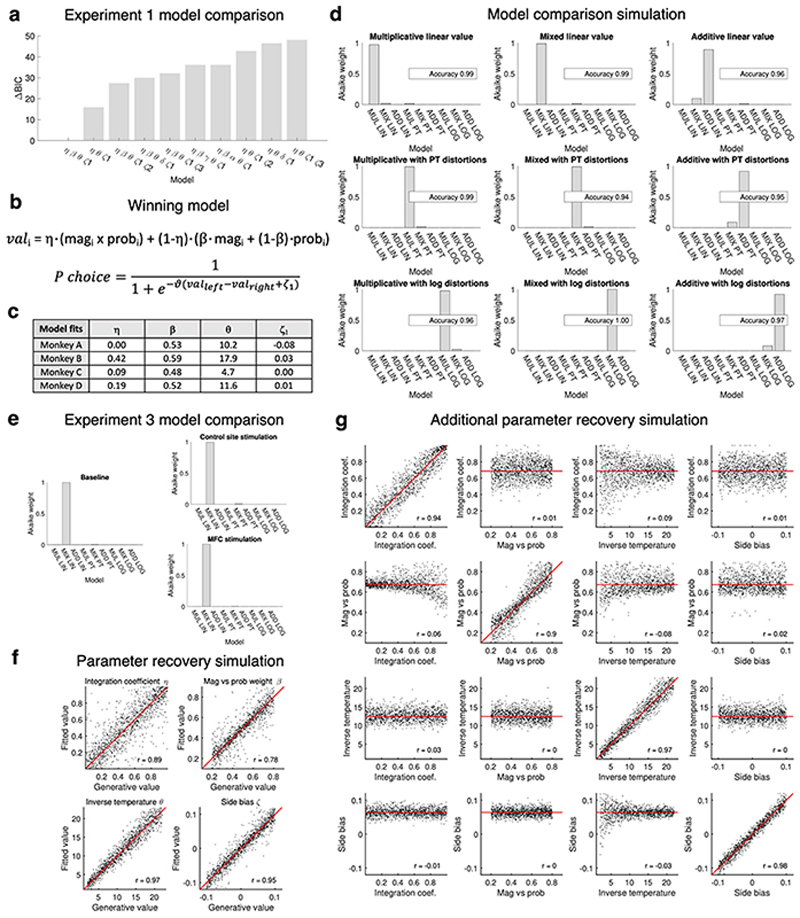
Three monkeys were tested, and we used a computational model selected as the best fit in both experiments 1 and 3 (Methods, Extended Data Fig.6a,b,e) to characterize the internal representation of value driving their behaviour. We reasoned that subjects’ choices may be driven by multiplicative value (magnitude times probability), maximizing long-term reward, or by additive value (magnitude plus probability), a simpler heuristic still providing good outcomes on average despite containing no information about the interaction between dimensions (Fig.4b), or they might use a mixture of both³¹. The model containing a mixture of additive and multiplicative approaches was better than alternative ones based on just one type of attribute combination or models including saturating basis functions (Extended Data Fig.6a,e). A parsimonious interpretation of these modelling results is that when choosing multiplicatively, subjects acted as if they first inferred a single integrated value per option, and then compared options; this could be mediated by the two-dimensional grid-like representation of option values. Conversely, when choosing additively, subjects may have compared the option magnitudes and, separately, compared the probabilities, without constructing integrated representations of each option.

One model parameter (the “integration coefficient”) represented how much of the behaviour could be explained by the multiplicative rather than the additive approach. We ran multiple simulations to demonstrate the reliability of the model selection and the parameter recovery (Methods, Extended Data Fig.6d,f,g). In particular, the estimate of the integration coefficient was accurate in novel trials (Fig.4c, Extended Data Fig.6f) and not confounded by choice stochasticity (Extended Data Fig.6g) or non-linear functions over value dimensions (Extended Data Fig.6d). To further confirm the model validity, we showed that integration coefficient estimates within subjects were more similar to each other than estimates across subjects in both experiment 1 (F _3,20 = 3.43, P = 0.037) and 3 (F _2,9 = 7.34, P = 0.013) (Methods). Finally, we report human behavioural data illustrating a cross-species match in the way multidimensional value-based decisions are taken (Methods, Extended Data Fig.7).

In comparison to both the sham and active control conditions, MFC TUS led to a specific and significant reduction in the integration coefficient but not the stochasticity or any other parameter (F _2,4 = 24.2, adjusted P = 0.024, Fig.4e; Extended Data Fig.5b,c; MFC vs sham Cohen’s d = -5.8) in novel choices. This suggest the monkeys’ apparent ability to base decisions on the integrated representation of each option’s value was compromised after MFC stimulation, and choices increasingly relied on the simpler heuristic of considering the attributes separately.

Conclusion

Multiple mechanisms underlie decision-making in primates. Monkeys and people learn specific option identities and their reward associations in a neural network spanning anterior temporal lobe, perirhinal cortex, and OFC^1,23 (Fig.2e, 3e). While numerous studies have probed this circuit in macaques, we show here that another neural circuit may mediate the primate ability to choose between new options based on no or little previous experience (Fig.2i, Fig.3f). It constructs valuations from past experiences of other options sharing features via a grid-like representation of reward and probability in MFC (a region interconnected with the medial temporal lobe²⁰). It is becoming clear that the principles underlying physical space representation in medial temporal structures also apply in areas of high-level cognition such as interactive decision-making³² and behavioural organization³³. Not only is MFC active during novel choices, but MFC disruption impairs making such choices on the basis of an appropriately integrated representation of the options’ component features (Fig.4).

Methods

Ethical compliance

All procedures were conducted under a UK Home Office license according to the Animal (Scientific Procedures) Act 1986 and the European Union guidelines (EU Directive 2010/63/EU).

Behavioural training

Four male Rhesus macaques, here referred to as A, B, C and D, aged between 4-7 years and weighing between 11-13 kg at the time of the experiments, were trained to perform binary choices in a computer-based task. Monkeys lived on a 12-hour light-dark cycle, were fed once per day after testing, and had ad-lib water access for an average of 15 hours a day (and a minimum of 3).

MRI-compatible cranial implants (Rogue Research) were surgically implanted to prevent head movements. During training and testing, monkeys sat in the sphinx position in a purpose-built MRI-safe chair (Rogue Research) with the head fixed. The monkeys responded by touching either of two custom-built infrared sensors aligned with the stimuli. Training was performed in a wooden custom-made mock scanner.

Stimuli and feedback were controlled by Presentation software (Neurobehavioral Systems Inc.) and shown on a screen at a distance of 30 cm. A grey background throughout the task ensured constant luminosity. The juice was 25% blackcurrant Ribena, 75% water, and for monkeys C and D half a banana per litre was blended in. Juice was delivered through a spout in 0.5 ml drops. Pre-recorded MRI noise (~100 dB) was played throughout training sessions.

Monkeys were extensively trained with familiar stimuli only, for 65 (± 10) sessions, corresponding to 13300 (± 500) trials and 12000 (± 1200) responses, before commencing testing in the MRI scanner. Training sessions were either fixed-probability or fixed-magnitude, interleaved; each session included both single-option and binary one-dimensional choice trials. Subjects were trained to the different task timings of experiments 1, 2 and 3.

MRI scanning and data processing

Structural and functional magnetic resonance images (MRIs) were acquired using procedures described before³⁴. This meant that fMRI data were collected during task performance with a gradient-echo T2* echo planar imaging (EPI) sequence on a 86 x 86 x 36 grid, with a voxel resolution of 1.5 mm isotropic; interleaved slice acquisition, parallel imaging acceleration factor 2, TR = 2.28 s, TE = 30 ms and flip angle = 90°.

MR images were preprocessed and analysed using tools from the FMRIB Software Library (FSL)³⁵ and the Magnetic Resonance Comparative Anatomy Toolbox (MrCat) (https://github.com/neuroecology/MrCat https://www.neuroecologylab.org). The T1-weighted images were processed in an iterative fashion cycling through a macaque-optimised implementation of FSL’s brain-extraction tool (BET)³⁶, RF bias-field correction, and linear and non-linear registration (FLIRT and FNIRT)^37,38 to the Macaca mulatta McLaren template in F99³⁹ as implemented in MrCat. The GRE image was used to aid the offline T2* EPI image reconstruction based on SENSE (Windmiller Kolster Scientific)⁴⁰.

A T1w group template specific to the set of subjects was constructed using two iterations of 1) registration to an initial template in F99 space³⁹, 2) group averaging, 3) registration to the new group template. This was accomplished using tools from Advanced Normalisation Tools (ANTs) as implemented in MrCat whereby at each step the group template was registered to the source template, thus avoiding drift and retaining registration to F99 space. All coordinates reported (in millimetres) refer to F99 space and results are shown on the group template.

While the monkeys were head-fixed, their limb and body movements during task performance distort the main (B0) magnetic field in a time-varying manner, causing non-linear motion-related artefacts in the phase-encoding direction varying on a slice by slice basis. To correct for these artefacts, using a processing pipeline implemented in MrCat, each slice was registered, first linearly, then non-linearly, to a robust reference based on EPI volumes from the same timeseries with least distortion. To avoid overfitting, the degrees of freedom were constrained in several ways: only distortions along the phase-encoding direction were considered; registration was initialized using priors from temporally neighbouring slices; low-order solutions were preferred over high-order registration (rigid > affine > non-linear); nonlinear degrees of freedom were regularized using b-splines.

Finally, the slice-registered average functional image was non-linearly registered to the high-resolution structural reference of each subject, and this was registered to the groupspecific template using ANTs. Brain-extraction of EPI timeseries was based on masks obtained in the high-resolution structural space. Next, EPI images were spatially smoothed (3 mm FWHM) and temporally high-pass filtered (cut-off 100 s). First-level whole-brain analyses (see below) were performed on the low-resolution images in the original acquisition space.

Experiment 1: design

Experiment 1 included 12 fMRI sessions of 180 binary choice trials per subject; no-response trials were repeated at the end of each session. Trials were divided into six conditions with 30 trials each. Factors were:

• familiarity of the options:

  • ○
    familiar (both options were familiar)
  • ○
    novel (both options were novel)
• dimensionality of the pair:

  • ○
    consistent (one option was associated with both higher reward magnitude and higher reward probability than the other option)
  • ○
    one-dimensional (the two options had one identical attribute, but differed in the other attribute)
  • ○
    inconsistent (one option had higher magnitude and the other option had higher probability)

The expected value range of the stimuli (i.e. magnitude times probability) during training was 0.5 to 6 drops; this was preserved during testing. Combinations with an expected value outside the familiar range were excluded (crosses in Fig.1b).

Average expected value sum (left value plus right value) was matched across all conditions (6 ± 0.02 drops). Value difference was necessarily different across dimensionality conditions; but was matched across familiarity conditions, both in terms of mean and variance (within ranges of 0.02 drops and 0.035 squared drops, respectively). Finally, the correlation between the best value and the worst value offered across trials was lower than r = 0.33 when merging all familiar conditions and when merging all novel conditions. Trials were presented in pseudo-random order. This stimulus schedule was designed to allow the dissociation of neural signals related to the comparison signal from the value sum.

For each trial, stimuli were presented for up to 60 s until response (median RT = 952 ms). The action-outcome delay lasted 3.5–4.5 s (uniform distribution). A visual cue indicated either positive (upward triangle) or negative (downward triangle) outcome; if positive, juice was simultaneously delivered through a spout. The outcome cue lasted 3 s whether positive or negative. The inter-trial interval (ITI) had a duration between 5-7 s (uniform distribution) (Fig.2a).

These delays made it possible to decorrelate the blood-oxygen-level dependent (BOLD) signal related to decision-making and response from the BOLD signal related to subsequent feedback processing and juice consumption. The hemodynamic response function (HRF) in the macaque is faster than in humans⁴¹, peaking in approximately 3 s. Motor response-related activity was accounted for by confound regressors in the GLM analysis as described below.

Monkey C failed to complete the planned stimulus sequences in some sessions, but the trials performed were used for analysis. Incomplete trials were 73 and 45 in two choice sessions (but still below 40%) and few in three further sessions (below 5%). In sum monkey C performed 94% and all other monkeys performed over 99.9% of the programmed trials in experiment 1.

When monkeys stopped working, if they restarted within 15 min the fMRI acquisition was continued, otherwise it was stopped, and the cognitive task restarted from the beginning after a break. No separate runs were merged for data analysis. Experiment 1 scans had an average duration of 43 min (σ = 2 min) for monkeys A and B, and 88 min (σ= 15 min) for monkeys C and D.

Decision fMRI analysis

A univariate general linear model (GLM) approach was taken for the statistical analysis of the whole-brain functional data using FEAT (FMRI Expert Analysis Tool) Version 6.00, part of FSL⁴².

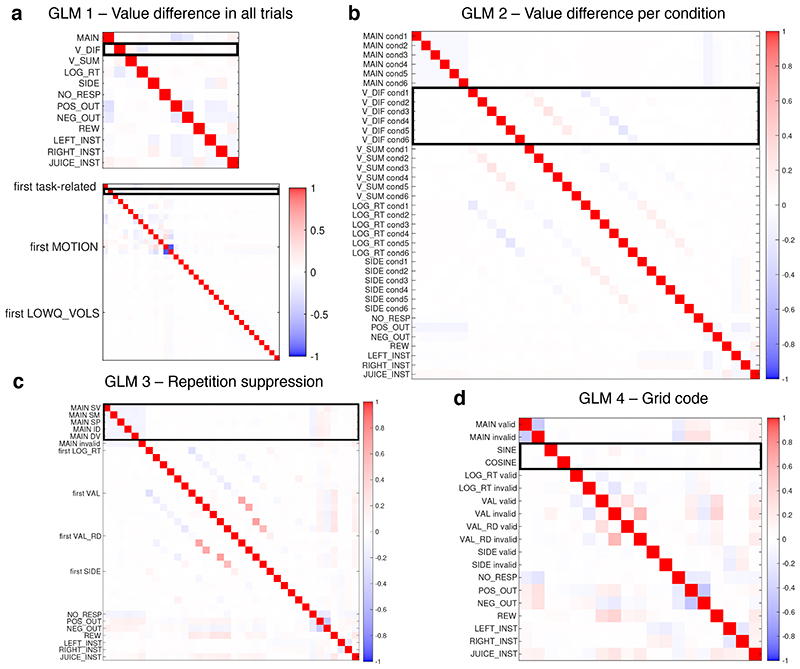
GLM 1:	BOLD = β1 MAIN + β2 V_DIF + β3 V_SUM + β4 LOG_RT + p5 SIDE + β6
	NO_RESP + β7 POS_OUT + β8 NEG_OUT + β9 REW + β10 LEFT_INST + β11
	RIGHT_INST + β12 JUICE_INST + β13…25 MOTION + β26…n LOWQ_VOLS

MAIN	Regressor representing the main effect of decision (boxcar with onset 1000 ms before response and duration 500 ms).
V_DIF	Parametric regressor representing the value difference (chosen minus unchosen option value). This is a positive number if the subject makes an optimal choice and negative otherwise.
V_SUM	Value sum.
LOG_RT	Logarithm of response time.
SIDE	Response side, left or right.

The V_DIF, V_SUM, LOG_RT and SIDE were temporally aligned to MAIN. Regressors onset was on average aligned to the stimulus onset (median familiar response time 931 ms, interquartile range 751-1314 ms, median novel response time 969 ms, interquartile range 7751394 ms). This allowed us to capture decision-related activity even though we allowed a RT up to 60 s; in practice 10% of trials had a RT above 3 s and 5% of trials above 15 s. Had we aligned the regressors to the stimulus onset, we would not have captured the decision-related neural activity in these slow RT trials. Excluding those trials would have unbalanced the task design, because slow RT was correlated with task parameters such as value sum and value difference (Bayesian ANCOVA: Bayes factor of model including both value sum and value difference covariates = 10.4, posterior likelihood = 0.78). Importantly, a Bayesian ANOVA indicated no effect of familiarity on logRT (Bayes factor of the null model = 10.1, posterior likelihood = 0.91).

While the absence of an effect of condition on response times reassure us that our BOLD analysis strategy will not be compromised by differential timeseries alignment in the familiar and novel conditions, this test may not be ideal for revealing small differences in decision time that might be associated with the additional cognitive processes needed in the novel condition. Effects associated with such cognitive processes might be measurable if the decision time had been dissociated from the motor response time that is subject to a number of sources of variation.

NO_RESP	Trials where no response was given (boxcar of 500 ms from stimulus onset).
POS_OUT	Regressor aligned to the outcome for rewarded trials, duration of 500 ms.
NEG_OUT	Outcome of unrewarded trials (but where a response was recorded)
REW	Parametric regressor denoting reward amount in rewarded trials (1–10 drops), temporally aligned to POS_OUT.

All binary and parametric regressors were normalized. All regressors were HRF-convolved with a gamma function (mean lag 4 s, standard deviation 2 s) peaking at 3 s.

LEFT_INST	Regressor aligned to the onset of the volume in which a left-hand movement was recorded, with a duration of 1 TR = 2.28 s.
RIGHT_INST	Analogous regressor for right-hand movements.
JUICE_INST	Regressor with onset and duration corresponding to juice delivery but fixed amplitude.

The latter three regressors modelled instant signal distortions not due to neural activity bt to changes in the main magnetic field caused by movement. These regressors were not HRF-convolved.

MOTION	13 noise regressors indexing the time-varying signal distortions, including the mean signal intensity timecourse and 12 remaining principal components describing the volume-by-volume magnetic field distortions induced by limb and body movements as estimated during preprocessing.
LOWQ_VOLS	Regressors flagging low-quality EPI volumes, suffering from strong artefacts, to be excluded from the analysis.

Volume quality was assessed based on 1) slice-registration cost (the normalized correlation between the current volume and the robust average after optimal registration), 2) linear scaling along the phase-encoding direction (directly related to signal intensity loss due to motion distortion), 3) non-linear deformation (penalizing volumes that require highly non-linear deformations). On average 90 volumes per session were excluded (5.8% of the total). Each LOWQ_VOLS regressor was equal to one for one volume and zero otherwise.

Extended Data Fig.3a illustrates the average correlations among regressors across sessions; correlations varied slightly across sessions depending on stimuli and animals’ behaviour. No two task-related regressors had a correlation larger than 0.3 when averaging sessions. Additionally, looking at each session separately, the regressor of interest (V_DIF) did not correlate with any other regressor except LOG_RT with absolute values larger than 0.3. It correlated with LOG_RT with values between -0.3 and -0.46 in ten sessions. Some confound regressors had higher correlations with each other in individual sessions, but this may not prevent a correct estimation of the regressor of interest.

To test the difference in neural response between familiar and novel trials, a second GLM was created, in which each of the first five (decision-related) regressors modelling decision, value difference, value sum, log response time and response side were split into 6 copies, one per condition.

GLM 2:

BOLD = β1,c MAINc + β2,c V_DIFC + β3,c V_SUMC + β4,c LOG_RT + β5,c SIDE + β6 NO_RESP + β7 POS_OUT + β8 NEG_OUT + β9 REW + β10 LEFT_INST + β11 RIGHT_INST + β12 JUICE_INST + β13…25 MOTION + β26…n LOWQ_VOLS                                        [for conditions c=1…6]

Averaging sessions, no two task-related regressors had a correlation stronger than 0.3 (Extended Data Fig.3b). Looking at individual sessions and specifically at the six V_DIF_c regressors of interest, 19% of them had a correlation between 0.3 and 0.56 (i.e. they shared between 9% and 31% of variance) with the V_SUM_c regressor in the same condition. 23% had a correlation between 0.3 and 0.5 (9% and 25% shared variance), and 5% a correlation between 0.5 and 0.68 (25% and 41% shared variance) with the LOG_RT_c regressors in the same condition. 7% of them had a correlation between 0.3 and 0.45 with the SIDE_c regressors in the same condition.

The value difference effects in the novel conditions were then contrasted with those in the familiar conditions (β_2,4 + β_2,5 +β_2,6 - β_2,1 - β_2,2 - β_2,3 where the β_2,c coefficients belong to the V_DIF_c regressors).

Sessions were analysed at the first-level using the FEAT tool in FSL, which computed contrasts of parameter estimates, as well as variance estimates, for each contrast. These were then transformed into standard space using ANTs and fed into FEAT for a higher-level mixed effects analysis with FLAME 1+2 [FMRIB’s Local Analysis of Mixed Effects, stage 1 and 2^43,44].

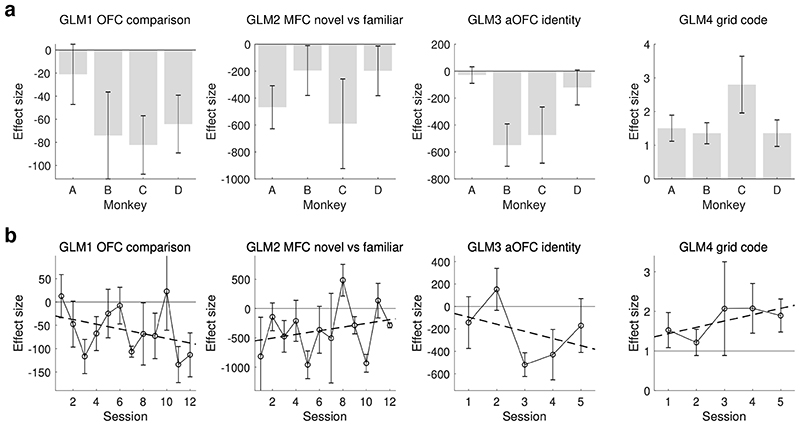
In the higher-level analysis all 48 sessions were equally weighted. We treated sessions rather than subjects as a random variable because in order to reliably estimate the variance, a random variable should have at least 10 levels⁴⁵; at the same time, we confirmed that the variation in the regressors of interest between sessions from the same individual was the same as the variation between individuals (Bayesian ANOVA, posterior probability in GLM1 = 0.89; in GLM2 > 0.999; in GLM3 = 0.99; in GLM4 = 0.98). Results are reported as Z (Gaussianised T) statistical images, and clusters were determined using a voxel threshold of Z = 2.3 (P = 0.01) and a cluster significance threshold of P = 0.05. We also report the average effect size in each subject separately (Extended Data Fig.8a). All results were consistent across subjects.

Analyses based on GLMs 1 and 2 were repeated modifying the regressors V_DIF and V_SUM according to a subject-specific definition of subjective value, as estimated by the subjective value model described below; all results were qualitatively the same (Extended Data Fig.2g).

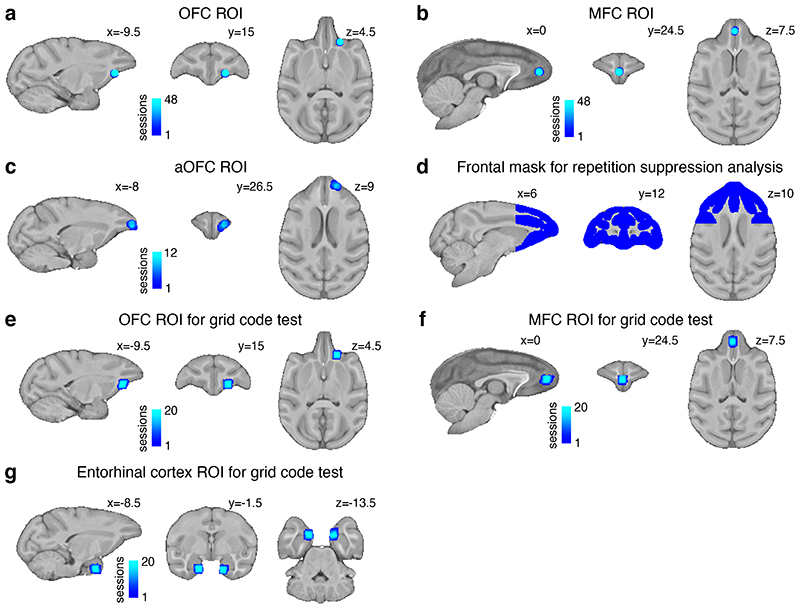
Regions of interest (ROIs) were defined as 5 mm diameter spheres in standard space, centred at the peak of the group-level activation for a given contrast built on the objective definition of value (Extended Data Fig.9a,b). A leave-one-out procedure ensured that the specific ROI for each given session was located at the peak of the group-level effect including all other sessions except the session itself. The peak was defined as the voxel with maximum Z value of the cluster-corrected statistical map after 1.5 mm kernel filtering.

To examine the timecourse of effects in the MFC and OFC ROIs (main Fig.2f,g,l,m), filtered BOLD timeseries were averaged across voxels, then temporally up-sampled (spline interpolation) by a factor of 10. MOTION and LOWQ_VOLS confounds were regressed out of the timeseries and the residuals were aligned to the response time and normalized; a GLM was fit at each timestep independently using ordinary least squares (OLS). An alternative version of the same plots shows the timeseries aligned to the stimulus (Extended Data Fig.2h,i). Note that the hemodynamic response to any event is expected to peak with a lag of 2-4 s. For all timecourses, GLMs 1 and 2 were reduced to include decision-related regressors only and excluding outcome-related regressors. To create the timecourses in Fig.2g,m and Extended Data Fig.2f,i we replaced V_DIF_c and V_SUM_c with regressors representing their components: the value of the chosen option (V_CHOSEN_c) and the value of the unchosen option (V_UNCHOSEN_c).

Subjective value modelling

A normative approach to the present task prescribes to select the option with highest expected value:

$$\begin{array}{l}{\text{val}}_{\text{i}}={\text{mag}}_{\text{i}}\cdot {\text{prob}}_{\text{i}}\hfill \\ {\text{p}}_{\text{left}}=({\text{val}}_{\text{left}}>{\text{val}}_{\text{right}})\hfill \end{array}$$

where mag_i is the magnitude of reward for option i, prob_i is the probability of reward for option i, val_i is the value attributed to option i and p_i is the probability of choosing option i.

However, the animals’ subjective representation of the options’ value can diverge from this normative approach. To best capture these representations, we designed alternative decision models, differing in nine respects, each represented by a free parameter, and tested which model best explained the observed choices. We subsequently used the winning subjective model of value to replace the objective definition.

Instead of estimating the expected value, subjects might simplify the problem by estimating the additive value^46,47 (Fig.4b), defined as:

$${\text{val}}_{\text{i}}=\beta {\text{mag}}_{\text{i}}+(1-\beta ){\text{prob}}_{\text{i}}$$

where β is the magnitude/probability weighting ratio. Subjects may not be able to fully compute the optimal form of value, but still be partially able to do so, and their behaviour may be described as if it was driven by a mixture of the two definitions of value:

$${\text{val}}_{\text{i}}=({\eta \text{mag}}_{\text{i}}\cdot {\text{prob}}_{\text{i}})+(1-\eta )({\beta \text{mag}}_{\text{i}}+(1-\beta ){\text{prob}}_{\text{i}})$$

where η is the integration coefficient determining the relative contribution of multiplicative and additive value. A widely used framework in behavioural economics is prospect theory⁴⁸:

$$\begin{array}{l}{\text{W}}_{-}{\text{mag}}_{\text{i}}={{\text{mag}}_{\text{i}}}^{\alpha }\hfill \\ W_{-}{\mathit{\text{prob}}}_i=e^{-{(-\log ({\mathit{\text{prob}}}_i))}^{\gamma }}\hfill \end{array}$$

where W_mag_i is the weighted magnitude of option i, and W_prob_i is the weighted probability of option i [we use the formula from Prelec⁴⁹]; α and γ are the magnitude and probability distortion parameters respectively. We considered the common assumption that subjects’ choice may not be deterministic, but modelled by a softmax function:

$$p_{\mathit{\text{left}}}=\frac{1}{1+e^{-\vartheta ({\mathit{\text{val}}}_{\mathit{\text{left}}}-{\mathit{\text{val}}}_{\mathit{\text{right}}})}}$$

where θ is the inverse temperature parameter. It is also possible to assume a differen noise, independent from the value difference between options⁵⁰:

$$p_{\mathit{\text{left}}}=(1-\delta )\frac{1}{1+e^{-\vartheta ({\mathit{\text{val}}}_{\mathit{\text{left}}}-{\mathit{\text{val}}}_{\mathit{\text{right}}})}}+\delta \frac{1}{2}$$

where δ is the random noise parameter. Finally, three types of spatial biases were tested. Stable side bias assumes that the subject is a priori more likely to choose options on one side of the screen. Repetition side bias assumes that the subject is more likely to keep choosing the side chosen in the previous trial. Win-stay-lose-shift (WSLS) side bias assumes that the subject is more likely to choose one side if the same side was rewarded in the previous trial or if the opposite side was unrewarded:

$$p_{\mathit{\text{left}}}=(1-\delta )\frac{1}{1+e^{-\vartheta (va{l}_{left}-va{l}_{right}+{\zeta }_1+prev{\zeta }_2+wsls{\zeta }_3)}}+\delta \frac{1}{1+e^{{\zeta }_1+prev{\zeta }_2+wsls{\zeta }_3}}$$

where ζ₁ is the stable side bias parameter, ζ₂ is the repetition side bias parameter, multiplied by the factor prev that is either +1 or -1 depending on the previous choice, and ζ₃ is the win-stay-lose-shift side bias parameter, multiplied by the factor wsls that is either +1 or -1 depending on the previous choice and reward.

In summary, we ran a nested model comparison, treating each subject independently. The most complex model tested was defined as follows:

$$\begin{array}{c}{W}_{ma{g}_i}=ma{g}_i^{\alpha }\\ W_{{\mathit{\text{prob}}}_i}=e^{-{(-\log ({\mathit{\text{prob}}}_i))}^{\gamma }}\\ va{l}_i=(\eta W_{ma{g}_i}\cdot W_{{\mathit{\text{prob}}}_i})+(1-\eta )(\beta W_{ma{g}_i}+(1-\beta )W_{{\mathit{\text{prob}}}_i})\\ p_{\mathit{\text{left}}}=(1-\delta )\frac{1}{1+e^{-\vartheta (va{l}_{\mathit{\text{left}}}-va{l}_{\mathit{\text{right}}}+{\zeta }_1+\mathit{\text{prev}}{\zeta }_2+wsls{\zeta }_3)}}+\delta \frac{1}{1+e^{{\zeta }_1+prev{\zeta }_2+wsls{\zeta }_3}}\end{array}$$

All 2⁹ possible models can be obtained from the same system of equations by fixing one or more parameters to their default values of η=1, β=0.5, α=1, γ=1, θ=∞, δ=0, ζ₁=0, ζ₂=0, ζ₃=0 respectively. Fixing a parameter to its default value is equivalent to removing the bias or noise that it represents from the model. The normative model is the one with all parameters fixed to their default value. Note that not only η, β and δ but also α and γ from prospect theory, were bound between 0 and 1. θ was bound to a maximum of 50 and the side bias parameters were bounded between ±1 to avoid extreme errors.

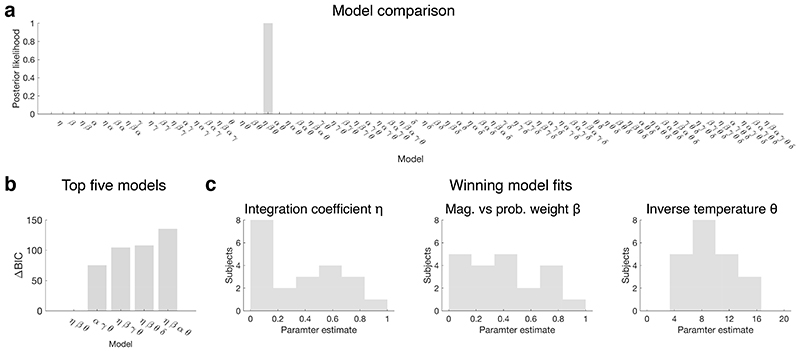
The winning model had a difference of 21.5 in BIC score with respect to the second best model (Schwarz weight > 0.999). It included 4 parameters: η (integration coefficient), β (magnitude / probability weighting ratio), θ (choice inverse temperature), ζ₁ (fixed side bias). It did not include α (magnitude distortion), γ (probability distortion), δ (random noise), nor ζ₂ and ζ₃ (repetition side bias and win-stay-lose-shift side bias). This means that the winning model (eq.1, Extended Data Fig.6b) was a softmax choice driven by left minus right value difference but biased by side, and value was defined as a mix of magnitude multiplied by probability and magnitude summed with probability. The numerical values of the coefficients are reported in Extended Data Fig.6c.

$$\begin{array}{l}{\text{val}}_{\text{i}}=({\eta \text{mag}}_{\text{i}}\cdot {\text{prob}}_{\text{i}})+(1-\eta )({\beta \text{mag}}_{\text{i}}+(1-\beta ){\text{prob}}_{\text{i}})\hfill \\ p_{\mathit{\text{left}}}=\frac{1}{1+e^{-\vartheta ({\mathit{\text{val}}}_{\mathit{\text{left}}}-va{l}_{\mathit{\text{right}}}+\zeta 1})}\hfill \end{array}$$ (eq.1)

We ran simulations using the winning model, to test whether it was possible to recover the generative parameters of artificial datasets for which the ground truth was known. We created 10,000 artificial agents, using random combinations of the four free parameters in the following ranges: 0≤η≤1, 0.2≤β≤0.8, 2≤θ≤22, -0.1≤ζ₁≤0.1. Artificial agents produced stochastic choices based on the real stimulus schedules and coefficients were recovered from the choices alone. The correlations (Pearson’s r) between the generative and fitted parameters were: η = 0.91; β = 0.93; θ = 0.99; ζ₁ = 0.85. The β recovery was only assessed for agents whose η was smaller than 0.8, because for a perfectly multiplicative agent, β does not influence behaviour.

Experiment 2: design

In experiment 2 setup and stimuli were identical to experiment 1, but only one stimulus was presented per trial (randomizing side at each trial) and all stimuli were novel. The timing was as follows: ITI jittered 0-500 ms, stimulus shown for a fixed duration, no outcome delay, outcome time 3 s. The exact stimulus duration was adjusted based on training performance and was 1.1, 1, 1.5 and 1.4 s for monkeys A, B, C and D respectively. Trials with late or no response were repeated at the end of the session. Outcome time started at the end of the fixed stimulus time, regardless of RT. This temporal structure was designed to minimize the interval between successive stimuli (4.5 ± 0.25 s) and ensure that stimulus presentation length was constant. As in experiment 1, outcome time also had a fixed duration independent of reward (Fig.3a).

Experiment 2 consisted of five sessions run on interleaved days with Experiment 1. More precisely, the session order was:

2 1 1 1 2 1 1 1 2 1 1 1 2 1 1 1 2 (numbers referring to each experiment)

The planned stimulus schedules of Experiment 2 consisted of either 156 or 234 trials. First sessions for each subject were shorter (156 trials) to minimise the exposure to novel stimuli before experiment 1. Because of the fast response deadlines, subjects sometimes failed to respond in time. If any trial t was missed, both pairs to which it belonged ([t-1,t] and [t,t+1]) had to be repeated. Even though missed trials were repeated whenever possible at the end of the same session, not all planned pairs could be acquired within the maximum scan time. Sessions 1 and 2 of monkey C contained too few trials (66 and 70, respectively) to be analysed and were therefore discarded. This was compensated by acquiring two extra sessions at the end of the experiment. On average, 235 trials (σ=76) were acquired per session, from which 194 trials (σ=53) were retained in the repetition suppression analysis and 148 (σ=33) in the grid code analysis, as reported in Supplementary Table 1. To compensate the fast pace, we added 30 s breaks every 26 trials for monkeys A, C and D.

Repetition suppression analysis

One use of the sequential single-option data was to test the neural representation of stimuli depending on their identity, value and value components, through BOLD adaptation^22,51. The key comparison was between the stimulus on any given trial and the stimulus on the preceding trial. We distinguished five conditions:

ID	Identical, if the present stimulus is identical to the previous stimulus.
SM	Same magnitude, if it has the same magnitude, but not the same probability, as the previous stimulus.
SP	Same probability, if it has the same probability, but not the same magnitude, as the previous stimulus.
SV	Similar value, if both the magnitude and the probability differ from the previous stimulus but the expected value (their product) is close to the previous one (difference <0.31 drops and =0.2 on average).
DV	Different value, if both dimensions differ from the previous stimulus and the expected value is not close (>0.31 drops and =1.5 on average).

Side did not influence condition. Pairs were concatenated in such a way that a given stimulus would count both as the second element of a pair and as the first element of the next pair. Only pairs in which responses were recorded for both trials within the deadline were analysed. Sequences never contained more than three identical stimuli in a row, and at most nine of such triplets.

The repetition of missed pairs of trials meant that sometimes new pairs of successive stimuli were introduced. The full set of successful trials for each session was therefore resampled post hoc, discarding some trials, in order to make use of most of the new unplanned pairs while maintaining the balance of the design. In particular we kept the average stimulus value in each conditions within a range of 0.1 drops of one another; moreover, the average relative value difference between pairs of stimuli was also below 0.1 drops in each condition (while the absolute value change was by definition 0 for ID, small for SV and large for DV). In this way, we selected an average of 38 trials (σ=12) per condition per session for analysis (Supplementary Table 1).

GLM 3:

BOLD = β1,c MAINc + β2,c LOG_RTc + β3,c VALc + β4,c VAL_RDc + β5,c SIDEc + β6 NO_RESP + β7 POS_OUT + β8 NEG_OUT + β9 REW + β10 LEFT_INST + β11 RIGHT_INST + β12 JUICE_INST + β13…25 MOTION + β26…n LOWQ_VOLS                                        [for c = conditions 1-6]

Five conditions are described above (ID, SM, SP, SV, DV), the last condition comprises invalid trials. The first trial of a session, trials following a missed deadline and trials following a planned 30 s break are counted as invalid because they cannot be meaningfully compared with the preceding trial. As described above, additional trials were discarded to balance the design. Regressors are defined as in GLM2, except:

VAL	Parametric regressor representing the expected value of the single option available.
VAL_RD	Parametric regressor representing the (signed) value change relative to the previous option.

Regressors associated with the decision are modelled as boxcars aligned to stimulus onset with duration of 500 ms. Regressors associated with the outcome and instantaneous regressors were modelled as in GLM1. As above, all parametric regressors were normalized and all regressors excluding the instantaneous ones were HRF-convolved.

The regressors of interest, namely the five constant regressors representing the five types of valid pairs, had a correlation of r < 0.17 with any other regressor on average, and an r < 0.31 in any given session (Extended Data Fig.3c).

For each session, four contrasts of interest were calculated based on the five MAINc regressors: identity minus different value (ID-DV), same magnitude minus different value (SM-DV), same probability minus different value (SP-DV) and similar value minus different value (SV-DV).

At the group level, two strategies were considered to combine sessions: a simple average or a linear trend across sessions. The underlying assumption behind the latter approach is that neural representations of stimulus identity, value and its components may not be present when a subject has no experience with the novel stimuli, but that such representations may potentially be constructed with practice across the duration of the experiment. To test this, we could have set a linear contrast for the five sessions for each subject (-2, -1, 0, 1, 2). However, as reported above, monkey C did not complete sessions 1 and 2. As an alternative, we excluded sessions 1 and 2 for each subject, and averaged the remaining sessions (weights 0 0 1 1 1).

As in experiment 1, results are reported as Z (Gaussianised T) statistical images, and clusters were determined with a threshold of Z > 2.3 and cluster-corrected significance threshold of P = 0.05. Given the limited number of sessions and trials per condition, we performed a search limited to the anterior part of the frontal cortex. The mask was defined using areas identified as grey matter during segmentation performed by an implementation of FAST⁵² optimized for macaque MRI as part of MrCat. The mask was cut posteriorly at y = 4.5 mm and corrected manually, excluding subcortical structures and the temporal poles and then it was expanded by one voxel in all directions (Extended Data Fig.9d).

The ID-DV contrast revealed two significant clusters within the frontal mask. In the main text we report the strongest one in anterior OFC; another cluster was observed in the left principal sulcus (Extended Data Fig.4a). The LOO procedure used to select the regions for further testing (Extended Data Fig.9c, Extended Data Fig.4b) was restricted to the lateral orbital surface and defined a 5 mm spherical ROI as above.

Grid code analysis

A second approach was taken to analyse experiment 2 data, to search for a grid-like encoding of the two-dimensional value space defined by reward magnitude and probability (Fig.1b, 3d and Extended Data Fig.4e). A fast succession of stimuli may be conceived as movements between locations (options) in this space. We defined valid trials as described above for the repetition suppression analysis; additionally, ID trials were considered invalid, because no movement through the value space occurs. In this way, 148 trials (σ=33) were analysed per session (Supplementary Table 1). Valid trials were associated with the angle of the trajectory between the locations of the preceding stimulus and the current stimulus. We expected a systematic modulation of the BOLD signal for trajectories with angles that are aligned versus misaligned with the orientation of the grid, which is assumed to be fixed. If all possible directions are tested, a pattern of signal increase and decrease every 60 degrees is predicted. As a consequence, the signal is expected to be a sinusoidal function of the trajectory angle with a periodicity of six; this is because within a full 360° cycle there are six ways of aligning to the grid (Fig.3c,d, Extended Data Fig.4e).

As the grid orientation is unknown, we assumed an arbitrary standard orientation parallel to the probability axis (Fig.3d) and created two regressors for the fMRI analysis: the sine and the cosine of six times the trajectory angle a. If one or both of these regressors correctly predict BOLD signal variations, this indicates that neural activity follows a six-fold pattern regardless of the angle. We therefore ran an F-test over both the sine and the cosine regressor beta estimates; the same test was then repeated for all periodicities between four-fold and eight-fold.

GLM 4:

BOLD = β1,c MAINc + β2 SIN +β3 COS + β4,c LOG_RTC + β5,c VALC + β6,c VAL_RDc + β7,c SIDEc + β8 NO_RESP + β9 POS_OUT + β10 NEG_OUT + β11 REW + β12 LEFT_INST + β13 RIGHT_INST + β14 JUICE_INST + β15…27 MOTION + β28…n LOWQ_VOLS                                        [for c = conditions 1-2]

The GLM included two regressors for the main effects of valid and invalid trials; as in GLM3, they were aligned to the stimulus onset, with a duration of 500 ms. The regressors of interest were SIN and COS, defined as sine(n x α) and cosine(n x α), where n is the periodicity, ranging between four and eight in separate instances of the analysis, and a is the trajectory angle. These regressors were only present for valid trials, with onset and duration matched to MAIN_valid. All other confound regressors were identical to those in GLM3. The correlation of the sine and cosine regressors was r < 0.11 with any other regressor on average, and r < 0.27 in any given session (Extended Data Fig.3d). The grid-code was tested in an objectively defined space, but the predictions were not distinguishable from those stemming from a subjective definition, because our subjective value model did not include distortions within each single dimension, and the magnitude-probability weighting ratio fit was close to 0.5 for all animals (similar weight for the two dimensions).

If at the session level we ran an F-test of SIN and COS, a second level parametric test could not be run across sessions with standard tools because the skewness of the F-distribution may increase the false-positive rate²⁶. Therefore, we took a non-parametric approach to estimate the likelihood of obtaining by chance a result such as the one observed.

The statistical values were averaged within 3 x 3 x 3 voxel ROIs in acquisition space (Extended Data Fig9e,f,g), then averaged across sessions and subjects. We performed the nonparametric group-level analysis to test whether neural activity was modulated by a hexagonal pattern. To avoid double-dipping, we only tested the two ROIs obtained from experiment 1 in OFC and MFC and a third ROI in entorhinal cortex defined a priori based on previously published results^26,28. A direct comparison of the intensity of the grid code signal and the value comparison signal was not possible because different experimental designs were required to measure them.

To create the null distribution, we tested all possible 3 x 3 x 3 voxel ROIs across the brain in acquisition space, for all sessions and periodicities. These F-values formed a first-order distribution. Then averages of 20 random samples from this distribution formed a second-order distribution representing the likelihood of obtaining a given average F-value from a random brain location and random periodicity. Twenty is the number of subjects (four) times the sessions (five). Such a second-order distribution is illustrated in main Fig.3g, Extended Data Fig.4h,i and was used to test the significance of the hexagonal patterns in the regions of interest. As a control, we created separate null distributions for each periodicity. Using these distributions to test each periodicity separately did not change the results reported in the paper (all control periodicities: adjusted P > 0.05, 60° periodicity: adjusted P = 0.0004; Extended Data Fig.4g).

To confirm the validity of the grid-like signal with a further test, we ran two more GLMs. They were in all respects identical to GLM4, except that valid trials were split into two interleaved subsets: odd and even trials. In one GLM, the regressors of interest (sine and cosine of 6 times the trajectory angle) were only defined for the even subset of trials; odd trials were included in the “invalid” group. Vice-versa, in the other GLM the regressors of interest were only defined based on odd trials and the rest went to the “invalid” group. From both GLMs and each session, the grid orientation was estimated as:

$$\arctan \left(\frac{{\beta }_{\sin }}{{\beta }_{\cos }}\right)/6$$

where β_sin is the beta coefficient for the sin(6α) regressor estimated through the GLM and β_cos for the cos(6α) regressor; α is the angle of the trajectory from the previous trial option to the present trial option, relative to a standard baseline. For each subject and each session, we measured the phase difference between the independent estimates from the two GLMs; note that this difference can never exceed 30° because of the 60° periodicity of the grid (for example, the phase difference between 1° and 58° is 3°, because 1° is the same as 61°).

We then ran a one-sample one-sided Kolmogorov-Smirnov test to assess if these values were smaller than values sampled from a uniform distribution from 0° to 30°, which is what would be expected by chance. Moreover, in order to test consistency across sessions we measured the phase difference between estimates from pairs of successive sessions (2 vs 1, 3 vs 2, 4 vs 3, 5 vs 4) for each subject.

Experiment 3: design

Three of the same Rhesus macaques, monkeys A, B and C, participated in experiment 3. After a break of 140 days (± 30), in which they participated in a different experiment involving an independent cognitive task, the monkeys again underwent extensive training on the familiar one-dimensional trials (condition 2). They performed 11,000 familiar trials (± 750) in 52 sessions (± 6). In total, there was an interval of 230 days (± 35) between experiment 2 and experiment 3. In experiment 3, both training and testing were performed in a custom-built wooden mock-scanner; pre-recorded MRI scanner noise was played at a moderate intensity (82 dB). The task was analogous to the task of experiment 1. Sessions included 220 binary choice trials, they were half familiar and half novel but all inconsistent trials (conditions 3 and 6).

Experiment 3 consisted of 12 sessions per subject, in three conditions: transcranial ultrasound stimulation (TUS) applied to the MFC target, TUS applied to a posterior and ventral control target in MFC (Fig.4d, Extended Data Fig.5a), and a sham TUS procedure. Overall, four sessions per condition per subject were acquired.

Each stimulus schedule was experienced three times by each subject, once in each condition (MFC, control site, sham procedure). Therefore, each subject in each of the three conditions responded to the same four stimulus schedules. Trials with no response within 60 s were repeated at the end of the session. All subjects completed all the pre-planned trials. Stimulation conditions were interleaved in pseudo-random order, the stimulus schedules were also balanced in the same way, and no two consecutive sessions were assigned to the same condition or schedule.

To avoid the possibility of after-effects of stimulation persisting into a subsequent session, we ran the sessions on alternate days, leaving 48 hours between consecutive sessions. Because of external circumstances, monkey C experienced a nine-day gap between the first six sessions and the following six. Overall, subjects completed experiment 3 in 28 days (± 4).

TUS procedure

TUS was applied using an “offline” stimulation protocol reported previously^11,12,14,34. Target sites were anterior medial frontal cortex [-0.5 23 11.5] and posterior medial frontal cortex [0 14 -1.5], as shown in Fig.4d and Extended Data Fig.5a. Following stimulation, the monkeys were moved to a different room for behavioural testing. The TUS procedure including setup lasted on average 20 minutes; subsequent behavioural testing lasted on average 47 minutes (σ=9).

TUS analysis

To confirm that the subjective model was not misled by a pattern of decisions reflecting saturating basis functions distorting each dimension, we ran a simulation. Three artificial agents performed 440 choices each as in the baseline condition of experiment 3. We compared nine models including three types of basis functions:

• linear

• non-linear as in prospect theory

• logarithmic

and three types of dimension combinations:

• purely multiplicative

• mixed

• purely additive

Each model included an inverse temperature and a side bias parameter; the mixed models included an integration parameter; the additive and mixed models included a magnitude vs probability parameter; the prospect theory models included two more free parameters (α and γ). We generated 300 artificial choice sets for each of the nine models. The generative parameters not explicitly tested were taken from the real data fits of the three monkeys in experiment 3 (magnitude vs probability β = 0.86/0.64/0.53, inverse temperature θ = 9.4/12.1/15.9, side bias ζ = -0.08/-0.07/0.03 respectively). The other generative parameters were set a priori; the prospect theory weights were α = 0.8 and γ = 0.6 as commonly encountered in humans, and the integration coefficient was η = 0.5. The logarithmic weights had no free parameter but were rescaled between 0 and 1 with the formulas:

• log(10 mag)/log(10)

• log(10 prob)/log(10)

The model comparison showed that for each of the nine models, the AIC score was lowest for the true generative model (Extended Data Fig.6d).

We ran the same model comparison using the real values from the baseline condition of experiment 3 (all sessions for each subject merged). The winning model was the one with linear basis functions and mixed multiplicative and additive attribute combination, matching the result of experiment 1. The difference in AIC score with the second-best model was 11.3 (conditional probability = 0.996). Finally, we ran the same model comparison fitting the choices in the control stimulation and the MFC stimulation conditions, and the same model (linear, mixed) was selected, with a delta AIC of 9.7 and 12 respectively (Extended Data Fig.6e).

A simulation was run to assess the ability of the selected model to correctly recover the integration coefficient. It was the same as described in experiment 1 (10,000 agents with real parameters drawn from the same predefined ranges) but here agents made choices based on experiment 3 schedules (440 familiar and 440 novel choices). Because trials were all inconsistent, a negative correlation between magnitude difference and probability difference was present, and stronger for familiar trials. Nevertheless, our model was able to correctly recover the generative parameters of the artificial novel choices. The correlation between the simulated and recovered integration coefficient h was 0.89 (Pearson’s r) for novel trials (Fig.4c, Extended Data Fig.6f) and 0.51 for familiar trials. Additive and multiplicative values were necessarily more similar to each other in familiar trials, given the nature of the choice space, causing the noisy recovery of the familiar coefficients. Therefore, we only report testing for the effect of stimulation in novel trials.

To show the absence of interference between parameters, we ran four additional separate simulations: in each case three ground-truth parameters were fixed to the average values estimated from the monkeys (η=0.69, β=0.83, θ=11.3, ζ₁=0.06) and the fourth parameter varied. Extended Data Fig.6g shows that variation in irrelevant parameters did not bias the recovery of any given parameter (all r < 0.1). A repeated-measures ANOVA with three within-subject conditions: MFC site, control site and sham stimulation, was used to test for differences in the model parameters across conditions. This showed a significant effect of integration coefficient but no other parameters. The results reported in the main text come from the fit of each session separately (110 novel trials) but equivalent results are obtained from the fits after merging all sessions within each condition (440 novel trials).

As a final check, to empirically test the ability of our model to capture a real cognitive variable, rather than noise, we hypothesised that the integration coefficients estimated from separate choice subsets of the same subject should be more similar to each other than the integration coefficients estimated from different subjects. Pairs of sessions in experiment 1 were merged and each of the six pairs per subject was fitted separately. Each of the four sessions per subject in experiment 3 was also fitted separately. We ran a one-way ANOVA for each experiment and found a significant effect of subject in both experiment 1 (F _3,20 = 3.43, P = 0.037) and experiment 3 (F _2,9 = 7.34, P = 0.013). These tests were performed on coefficients estimated from small datasets, but our simulation revealed sufficient recovery rates. Experiment 1: η recovery r = 0.70; Experiment 3: η recovery r = 0.73.

Human dataset

To compare human and macaque decision-making strategies, we re-analysed a dataset collected in human participants from Chau et al. 2014⁷. Detailed methods can be found in the original publication. In brief, 21 healthy human participants chose repeatedly between stimuli associated with different reward magnitudes (in Pounds) and probabilities. They were presented with a total of 300 binary choice trials. Half the trials, randomly interleaved, included a third distractor option that could not be chosen, but these distractor options are not taken into account in our re-analysis of the data. In sum, this binary value-based decision-making task was highly similar to ours.

We repeated the model comparison described above on these data to determine the bestfitting model of subjective value for human participants. We did not consider potential side bias parameters because Chau et al. presented the options in any of four quadrants of the screen, so side biases would require twice as many parameters to be modelled.

The winning model for the human choice data was identical to the one identified in our experiments 1 and 3. It included integration η, magnitude vs probability weight β and inverse temperature θ, and no other parameter, with a ΔBIC = 75 relative to the second-best model, and a Schwarz weight > 0.999 (Extended Data Fig.7).

Extended Data

Extended Data Fig. 1. Experiment 1 behaviour.

(a-b) Number of times each stimulus was chosen within experiments 1 (a) and 2 (b). White: familiar options; grey: novel options (shading corresponds to relative frequency). Note that the same training trials were added to the familiar test trials in both panels a and b. (c) Response time (RT) distribution. Mean familiar and novel RT = 3.082 and 3.060 s respectively; median familiar and novel RTs = 0.931 s and 0.969 s respectively. (d) RTs by subject and condition. We found no difference between familiar and novel RTs (paired t-test for mean: t ₁₁ = 0.1, P = 0.92 and median: t ₁₁ = 1.4, P = 0.19). Each dot in the graphs represents one subject and one level of dimensionality. A Bayesian ANOVA over all trials (n=8511) with subject as mixed effect and familiarity as fixed effect supported the null hypothesis - no difference between familiar and novel RTs - with a posterior likelihood of 0.91. (e) Logistic fit of the probability of choosing the right-hand option as a function of right minus left subjective value, as in main Fig.2c for objective performance. (f) Subjective performance across conditions, as in Fig.2d. Performance is expressed as the proportion of choices in favour of the option with highest subjective value, as estimated by our model. Bars represent the mean of four subjects.

Extended Data Fig. 2. Additional fMRI results of experiment 1.

(a) The parametric modulation of BOLD signal by the difference in value between the unchosen and chosen options, estimated with GLM1, activated other clusters beyond the OFC depicted in Fig.2e. One cluster encompassed numerous areas including ACC, dlPFC, insula (corrected at Z > 2.3, P = 10^-5, peak Z = 4.66 [11.5 2.5 17.5]); others were located in the visual cortex (not illustrated). (b) We also report an observation highlighting an area likely involved in our task in the midbrain in the vicinity of the ventral tegmental area, (P < 0.001, uncorrected). A similar observation has been made in a task resembling our familiar task in analyses of individual neuron firing rates in the ventral tegmental area (M Matsumoto, personal communication). (c) The contrast of BOLD modulation by the value comparison signal (chosen minus unchosen value) in novel versus familiar trials, estimated with GLM2, which activated MFC as depicted in Fig.2i, is also visible in the ventral striatum (P < 0.001, uncorrected). A similar observation has been made in a task resembling our familiar task in analyses of individual neuron firing rates in the ventral striatum⁵³. (d) fMRI effect of value comparison as in main Fig.2i, but using a subjective estimate of value (whole-brain FWE cluster-corrected at Z > 2.3, P = 0.002, peak Z = 3.87 [0 24.5 7.5]). (e) Average timecourse of the value comparison signal from GLM2 in OFC (top) in familiar and novel trials separately, in analogy with what reported for MFC in Fig.2l, replicated here (bottom). (f) Timecourses of the component effects (value of chosen option; value of unchosen option) as in Fig.2g,m but separately for familiar, novel, MFC and OFC. Top row: orbitofrontal ROI; bottom row: medial frontal ROI. (g) Timecourse analysis of the value comparison signal, as in Fig.2l, but using a subjective definition of value. (h-i) Timecourses of the parametric modulation of the BOLD signal for the same contrasts as in panels e,f and ROIs defined in the same way, but time-locked to the stimulus presentation. (l) Relationship between network dynamic and BOLD response. This shows that in a driftdiffusion or an attractor model, if activity falls immediately after the threshold is reached (thick lines in the top panel and bright colours in the bottom panel), the BOLD response will be negatively correlated with value difference, as in macaques; but if the activity is maintained for longer (dotted lines in the top panel and shaded colours in the bottom panel), the BOLD response will be positively correlated with value difference, as in humans (Supplementary Information). Illustration reproduced with permission⁴.

Extended Data Fig. 3. FMRI design matrices.

Correlations among task-related regressors (averaged across sessions) in all GLMs. Additionally, for GLM1 (a, bottom) the thirteen motion regressors and the first ten low-quality volume regressors are also illustrated. For all other GLMs, these regressors are not illustrated. Black line: regressors of interest. (a) GLM1: experiment 1 decision task, value comparison analysis, all trials. (b) GLM2: experiment 1 decision task, value comparison analysis, trials divided by condition depending on familiarity and dimensionality. There are six copies of each decision-related regressor. (c) GLM3: experiment 2 single-option task, repetition suppression analysis. There are six copies of each decision-related regressor, one per condition depending on the preceding stimulus. (d) GLM4: experiment 2 single-option task, grid-code analysis. There are two copies of each decision-related regressor: valid and invalid trials. Correlations here shown for 6-fold modulations of the BOLD signal; they were similar for other periodicities (4 to 8 fold), as well as for the two halves of the phase consistency design.

Extended Data Fig. 4. Additional fMRI results of experiment 2.

(a) Using whole-brain FWE cluster correction, no significant repetition suppression effects were found elsewhere in the brain. However, for the sake of completeness, we illustrate here the distribution of uncorrected effects throughout the brain indicating the locations of potential representations of specific identities of stimuli; contrast of BOLD activity elicited by stimuli preceded by identical stimuli vs stimuli preceded by different stimuli (ID-DV, GLM3). Outside the prefrontal mask (Extended Data Fig.9d), repetition suppression effects analogous with those reported in the main text for anterior OFC (Fig.3e), were observed in the anterior temporal lobe / perirhinal cortex, in entorhinal cortex and the perigenual ACC, in the principal sulcus and in medial frontal pole (Z > 2.3, uncorrected). (b) After Bonferroni correction (all t ₁₁ < 1.42, all adjusted P > 0.28) there were no significant repetition suppression effects in aOFC when successive stimuli had the same value but different probability and magnitude components (SV) compared to successive stimuli with different values (DV), nor when successive stimuli sharing just the same magnitude component (SM) or the same probability component (SP) were compared to DV stimuli. Error bars represent standard error of the mean (SEM) in this panel and the next. As in main Fig.3e, this test is restricted to sessions 3-5 of experiment 2. (c) No significant effect of repetition suppression was observed in MFC (ROI identified in experiment 1) after Bonferroni correction (all t ₁₁ < 2.1, all adjusted P > 0.09) for the same contrasts as shown in panel b, plus the effect of identical stimuli versus different stimuli (ID-DV). (d) Temporal signal to noise ratio; the tSNR was very good in the anterior part of brain, but slightly lower at the edges, which may potentially explain the weak grid effect in entorhinal cortex. (e) Illustration of the relationship between trajectory angle and response of grid cells. In grey, schema of the receptive field of an ideal grid cell (multiple neighbouring cells tend to align with each other). In red, trajectory from one location to the next one in a two-dimensional space. The amount of activation of the cell’s receptive field varies continuously with the trajectory angle and repeats itself every 60°. In this example, it is maximum at 0° and 60° and minimum at 30°, but in the general case the orientation of the grid is not known a priori. (f) Additional sections of the whole-brain distribution of quadrature test scores for a hexagonal grid code, also reported in main Fig.3f, averaged across 20 sessions and thresholded at F > 1.74 (P < 0.001 uncorrected). Consistent with previous results in humans, we observed a six-fold modulation of the BOLD signal in entorhinal cortex (ERH), visual cortex (VC), anterior cingulate cortex (ACC), frontal eye field (FEF), temporal pole (TP), and posterior intraparietal lobule pIPL. These results are presented without cluster correction (because of the non-normal distribution of the F statistics, standard cluster correction could not be performed). (g) Separate null distributions for each periodicity. Each distribution is based on all sessions and locations within the brain, for a given GLM. Non-parametric tests of each periodicity based on these distributions gave the same results as those based on the joint distribution. P-values are reported in the table. (h-i) Statistical results from the grid code test at different periodicities. No significant effect after Bonferroni correction in OFC (h), nor entorhinal cortex (ERH) (i). The results reported in panel i refer to right ERH; they were qualitatively the same as those from left ERH. The shuffled null distribution is shown to the right and the F values indexing grid effects for each periodicity are shown to the left in each panel. None of the periodicities reached significance in either region, even if some voxels in entorhinal cortex exceeded the P < 0.001 threshold for the 6-fold symmetry, as reported in panel f.

Extended Data Fig. 5. Additional data related to experiment 3.

(a) TUS locations recorded at end of each session. (b) Logistic fits of choices in experiment 3, divided by subject and condition. Each circle represents 55 choices. There was no effect of neurostimulation on the slope of the psychometric curve (repeated-measures ANOVA: F _2,4 = 0.05, P = 0.95). (c) Parameter estimates of all the subjective model parameters. Error bars represent SEM across the four sessions per subject per condition, fitted separately. A systematic effect of stimulation is present for the integration coefficient after Bonferroni correction (F _2,4 = 24.2, uncorrected P = 0.006, corrected P = 0.024), but no effects of magnitude vs probability (F _2,4 = 1.5, uncorrected P = 0.32); inverse temperature (F _2,4 = 0.2, uncorrected P = 0.83) or side bias (F _2,4 = 0.9, uncorrected P = 0.48). Post-hoc one-tailed paired t-tests on the integration coefficient confirmed a significant effect of ultrasound stimulation in novel trials specific to the MFC condition. MFC vs sham, t ₂ = 5.17, Cohen’s d = -5.8, P = 0.018; MFC vs control site t ₂ = 4.97, Cohen’s d = -2.6, P = 0.019. Note that the large error margins in the “magnitude vs probability” parameter β fits in monkey B are due to the fact that this parameter only affects behaviour when the integration coefficient β is lower than 1.

Extended Data Fig. 6. Subjective value modelling.

(a) Results of the full model comparison based on experiment 1 data (Methods). 512 models were tested, each one including or excluding 9 possible parameters corresponding to decision biases. The winning model includes 4 parameters: integration coefficient η, magnitude vs probability weight β, inverse temperature θ, fixed side bias ζ₁, with a BIC difference of 15.9 relative to the second-best model, corresponding to a Schwarz weight = 0.999. (b) Equation defining the winning model (Methods, eq.1). (c) Parameter estimates for the four parameters of the winning subjective value model in experiment 1. (d) Simulation of a reduced model comparison, created to test whether the way individual dimensions (magnitude, probability) are represented by linear or non-linear functions can be dissociated from the way the dimensions are combined together. Nine models were used to generate artificial decisions and then they were compared to assess whether recovery was reliable. “MUL”: multiplicative dimension integration; “MIX”: mixed multiplicative and additive combination; “ADD”: additive dimension combination. “LIN”: linear basis functions; “PT”: non-linear distortions defined as in Prospect Theory; “LOG”: logarithmic basis functions. Each panel represents a separate model comparison based on artificial choices generated according to the model described in the panel title. 100 repetitions (with 3 simulated agents performing 440 decisions each) were run; in all cases the total Akaike weight indicated a strong conditional probability in favour of the true model; the accuracy values in the onsets refer to the proportion of repetitions in which the true model won the model comparison. (e) Results of the model comparison based on the real data from experiment 3, in which the same 9 models from the previous analysis (panel d) were compared. In the baseline condition and also in the ultrasound stimulation conditions, choices were best represented by a linear model (no saturating basis functions) with mixed multiplicative and additive dimension combination, which is consistent with the winning model in experiment 1 (panels a,b). (f) Results of a simulation using the winning model. This shows good recovery of all model parameters and most importantly the integration coefficient h: correlation between true and fitted value r = 0.89. Recovery based on 440 artificially generated choices; the red lines indicate ground-truth values (an equivalent result was obtained based on experiment 1 stimulus schedules). (g) Parameter recovery from a further simulation of experiment 3 with the same model: three parameters were fixed at realistic values and only one was varied at any time. Recovery based on 440 artificially generated choices; the red lines indicate ground-truth values. On-diagonal panels show recovery of each parameter as a function of itself (high accuracy), off-diagonal panels show recovery of each parameter as a function of the irrelevant ones (no cross-correlations).

Extended Data Fig. 7. Human decision-making data.

Both humans and macaques perform binary value-based decision-making in a similar manner. These human data were first reported by Chau and colleagues⁷, but here they have been re-analysed (with permission) using the same approach as the one applied to the data obtained from macaques in experiment 1. (a) 21 subjects performed 300 choices each; a model comparison identified the same subjective value model (ηβθ) described above as the one best explaining their behaviour, with a Schwarz weight > 0.999. Side bias ζ was not tested. (b) The BIC score difference with the second-best model was 75. (c) The human subjects displayed a range of different behaviours, as revealed by the histograms of the integration, magnitude versus probability, and inverse temperature parameter fits. In particular, we noted how some subjects were fully additive (η=0) but others were very good at integrating the two dimensions of value (with η approaching 1).

Extended Data Fig. 8. fMRI effects split by subject and session.

(a) Effect sizes for key analyses are shown separately for each subject and GLM. Error bars represent SEM. (b) Key effects plotted session by session. The continuous horizontal line represents the absence of an effect. The dotted line is a linear fit. Error bars represent SEM. No trend was statistically significant (GLM1: t ₁₀ = -1.30, P = 0.22; GLM2: t ₁₀ = 0.63, P = 0.54; GLM4: t ₃ = 1.57, P = 0.21). Note that the selection of the aOFC ROI for GLM3 (third graph in panel b) was biased towards finding a temporal trend, because it was based on the effect of the last three sessions of each subject. It was merely included here for completeness.

Extended Data Fig. 9. Masks and ROIs.

(a) Spherical (5 mm diameter) OFC ROI used for timecourse analysis of experiment 1 (Fig.2f,g,h, Extended Data Fig.2e,f,g,h,i top row), centred on the peak of the activation for GLM1, reported in Fig.2e, with a leave-one-out procedure. (b) Spherical (5 mm diameter) MFC ROI used for experiment 1 timecourse analysis and repetition suppression analysis (Fig.2l,m,n, Extended Data Fig.2e,f,g,h,i bottom row, Extended Data Fig.4c), centred on the peak of the activation for GLM2, reported in Fig.2i, with a leave-one-out procedure. (c) Spherical (5 mm diameter) aOFC ROI used for further repetition suppression analyses (Extended Data Fig.4b), centred on the peak of the activation for GLM3, reported in Fig.3e, with a leave-one-out procedure. (d) Frontal cortex mask used in the repetition suppression analysis (Fig.3e) defined as cortical gray matter anterior to y=4.5 and expanded by one voxel. (e) 3x3x3 voxel OFC ROI defined in acquisition space for the grid-code signature analysis (Extended Data Fig.4h), centred on the peak of the activation for GLM1. (f) 3x3x3 voxel MFC ROI defined in acquisition space for the grid-code signature analysis (Fig.3g,h,i), centred on the peak of the activation for GLM2. The locations in panels e-f are the same as in panels a-b and are therefore independent with respect to experiment 2. The only difference is that the ROIs in panels e-f are defined in acquisition space. (g) 3x3x3 voxel entorhinal cortex ROI used for grid-code signature analysis (Extended Data Fig.4i) defined a priori.

Extended Data Table 1. Loci of fMRI activations.

Centres of ROIs reported in the main text may differ slightly from the coordinates above because ROIs were based on Z peaks after smoothing. Clusters for GLM3 were restricted to the frontal mask. Separate results using an objective and a subjective definition of value.

Value difference (GLM1)
area	x	y	z	max Z	P value
V2	-26.5	-33	1.5	4.54	3*10-6
dlPFC	11.5	2.5	17.5	4.66	3*10-6
V2	-6	-43.5	3	3.78	0.0004
OFC (13)	-9	14.5	4.5	4.53	0.0169
V2	25	-32.5	9.5	4.58	0.0222

Value difference novel vs familiar (GLM2)
area	x	y	z	max Z	P value
MFC	-0.5	25	8	4.14	3*10-7

Repetition suppression for identical stimuli (GLM3)
area	x	y	z	max Z	P value
OFC (11)	1.5	29	9.5	3.67	0.0277
dlPFC	-8.5	17	13	3.46	0.0417

Subjective value difference (GLM1 subj)
area	x	y	z	max Z	P value
dlPFC	12	2	17.5	5.16	1*10-13
V2	-26.5	-32.5	2	4.38	5*10-6
V2	25	-32.5	9.5	4.51	3*10-5
V2	-6.5	-43.5	3.5	3.67	0.0012
OFC (13)	-9	14.5	4	4.79	0.0113

Subjective value difference novel vs familiar (GLM2 subj)
area	x	y	z	max Z	P value
MFC	0	24.5	7.5	3.88	0.0028

Data availability

The behavioural data supporting this study (experiments 1 and 3) are available in the OSF repository, https://osf.io/kzhaq/. The raw fMRI data supporting this study are available from the corresponding author upon reasonable request. The unthresholded statistical fMRI maps associated with this study are available in the NeuroVault repository, https://neurovault.org/collections/8491/. The source data underlying the plots in the figures are provided as a Source Data file.

Code availability

The MATLAB custom code supporting the behavioural results of this study is available in the same OSF repository, https://osf.io/kzhaq/. Any remaining code that supports the findings of this study is available from the corresponding author upon reasonable request.