Abstract
This study numerically investigated the thermal effect of human body on the time-dependent dispersion of cough droplets with evaporation process. The thermal flow of human body was imitated using a 3D thermal manikin with real body features, while a recent developed multi-component Eulerian-Lagrangian approach was used to address the effects of inhomogeneous temperature and humidity fields on droplet evaporation. By comparing the results yielded without and with the human body heat, the outcomes demonstrated strong impact of human body heat on the droplets mass fraction and local air velocity distributions. Inspirable droplets could potentially drop into respirable droplets by evaporation, although the evaporation rate was not significantly affected by body heat. The thermal effect of human body revealed its vital impacts on the time-dependent droplets dispersion. Due to the buoyancy driven thermal flow, both the vertical velocity and displacement of small droplets (≤20 μm) were completely reversed from descending to ascending, while the deposition time of large droplets (≥50 μm) were significantly delayed. With the reduced droplet size by evaporation and droplets lifted into breathing zone by human thermal effect, the inhalability and infection risks of cough droplets would be much higher in real occupied indoor spaces.
Keywords: Cough droplets, CFD, Evaporation, Time-dependent droplet size, Thermal plume, Vapour plume
Highlights
-
•
Inspirable droplets could drop into respirable droplets through evaporation process.
-
•
Human body heat strongly affects the local droplets mass fraction.
-
•
Evaporation rate is not sensitive to human body heat but to the RH and droplet size.
-
•
Cough droplets could be lifted to breathing zone by buoyancy driven thermal flow.
-
•
Human thermal effect promotes evaporation process by delaying droplets deposition.
1. Introduction
Infectious respiratory diseases, such as tuberculosis (TB), influenza and Middle East respiratory syndrome coronavirus (MERS-CoV), have been as much a big concern to the public as the damages to individuals. One of the most common clinical symptoms of the infectious respiratory diseases is cough [1,2]. After being emitted through this airway defensive behaviour, coughing droplets (e.g. saliva and mucus) containing infectious pathogens can be directly transmitted and quickly further spread in the air. Epidemiology studies of influenza infections have found that coughing is even more efficient than sneezing, breathing or talking in relation to the transmission of infection [2,3]. To better assess the occupant health in associated with infection risks in public space, it is vital to obtain deep understandings of the coughing process and accurate transmit characteristics of the exhaled droplets in occupied indoor spaces.
The dispersion of respiratory droplets is jointly controlled by the droplet size and their interactions with the ambient airflow. When individual coughs, the size of the expelled droplets could be diversely ranged from 0.1 μm to 1000 μm [[4], [5], [6]], which is wide enough to cause both viral and bacterial infections [5]. Also, such a wide size range implies that the transport and dispersion of the droplets could be completely different [7] after expelling through the same cough. Unlike the large droplets that would quickly deposit to the floor due to high inertia and mass, small droplets would be easily carried by the local airflow and tend to suspend in the air for longer time. With potentially longer travel time and distance, the inhalable chance of smaller droplets is greatly increased. Because of this, 10 μm is used as the cut off diameter to distinguish between the respirable droplets (<10 μm) that would easily penetrate deeper into the respiratory system, and the inspirable droplets (10–100 μm) that would have more impacts onto the surfaces of the upper airways [5,8]. Thus, it is of the great importance to include the full-size range of the coughing droplets when assessing the potential health risks brought by coughing. Experimental measurements from real person cough proved that the real size distribution of cough droplets was not consistent or uniform after being expelled [6,9] and the droplet diameters would be generally reduced [10,11]. Chao et al. [6] concluded that the high velocity induced by the expulsion of the air jet during coughing could promote more productions of smaller droplets (4–16 μm) comparing to other behaviours such as speaking. Therefore, the size distribution characterisation of the expelled droplets needs to be carefully underpinned when modelling coughing in prior to the assessment of infection risks of individuals.
With the importance of precisely depicting the time-dependent droplet size was raised, the evaporation process of the droplets in associate with the relative humidity (RH) of the environment was confirmed as the main cause of droplet size reduction [6,10]. When droplets consisting of water and small number of non-volatile compounds [12,13] were expelled, the water in the droplets started gradually evaporating until the solid droplet nuclei with smaller equilibrium diameters are formed by the remaining non-volatile components. Mathematical models were developed to realise the size-time relations under different temperature and humidity conditions [12,14,15]. Due to the complexity of integrating the evaporation process and the dispersion process, most existing studies applied simplified mathematical models to simulate the evaporation process. The inhomogeneous humidity field induced by the evaporating droplets was either ignored or simulated with over-simplified transportable scalar models [12,14,15]. Since the inhomogeneous vapour concentration would significantly affect the droplet trajectories by changing the function of time and droplets size, it is important to fully address the inhomogeneous water vapour concentration on droplet evaporation. With that in need, a multi-component Eulerian-Lagrangian approach that explicitly solves the continuity equation of the water vapour was proposed in the previous study [16] to enhance the mathematical models for modelling evaporation process of coughing.
Although mathematical models of modelling the droplets evaporation were reported in the literature, existing studies on cough droplet dispersion in indoor spaces were mostly conducted without considering the droplet evaporation and the varying dominant mechanism of droplets movement induced by the size change. Most studies used particles with equilibrium droplet nuclei diameters to represent the droplet size after the size reduction due to evaporation [17,18], since the evaporation process took place very quickly for respirable droplets (less than 10 μm) under ideal condition (0% RH) [12,14]. However, the droplet evaporation process is inhomogeneous. The same process could take more than 100s for droplets with initial diameter of 100 μm under an opposite ideal condition of 100% RH [14]. To further test the impact of droplet size and RH change on evaporation process, our previous research [16] conducted several case studies with combinations of various ambient RH (10%–90%), exhaled humidity and droplets amount. The outcomes demonstrated that the dynamic behaviours of droplets were significantly affected by evaporation and RH, including the change of droplet dispersion, promote increase of pathogen mass carried by find and ultrafine droplets. The evaporation process could take from 1 s to as long as 10 s for larger droplets ranged from 10 μm to 100 μm, under a more realistic ambient condition of 50% RH. With such long-time span, the size distribution pattern of the droplets would be completely reformed. Also, the inhomogeneous vapour concentration would significantly affect the droplet trajectories by changing the function of time and droplets size. Therefore, it is essential to consider the simultaneous droplets size reduction by the evaporation process and to fully address the inhomogeneous water vapour concentration on droplet evaporation when assessing the trajectory and concentration-based infection risks of respiratory droplets in indoor spaces.
In modern built environments, the thermal plume induced by human body heat is the principle thermal flow due to the prevalence of displacement HVAC system and the energy-saving appliances [19,20]. However, this essential factor: the thermal flow in indoor environment from human body heat, was generally overlooked when integrating the droplets evaporation into indoor environment. Since investigating the cough droplets evaporation process would inevitably increase the computational cost, the computational domains were very restricted in most existing studies [12,14,16]. Cough was generally released through a narrow surface imitating the mouth only, whereas human model was either completely removed or overly simplified (i.e. cylinders and blocks). Clearly, the corresponding thermal plume induced by the human metabolic body heat could not be captured properly by these approaches. However, the thermal plume was reported as a very important factor on local airflow and contaminant fields from several indoor micro-environment studies [21,22]. With seating posture, the metallic body heat would generate two major ascending thermal plumes (on top of the head and in front of the main torso, respectively), while realistic computational thermal manikin (CTM) is required to capture these features [20,23]. With coughing behaviour, these thermal plumes, especially the one in front of the main torso, would consistently interact with the coughing jet flow both during the coughing and after it. This interaction would not only change the local airflow distribution in the vicinity of the human body, but certainly affect the local evaporation factors (air pressure, temperature and etc.). It was proved by the previous studies that even small changes of the local airflow would cause very different transport trajectories of the particles and droplets [7,20]. Most importantly, since the ascending thermal plume was capable of carrying contaminants from the near-floor level into the breathing zone [22], the inhalability and infection risks could be significantly enlarged after considering the human body thermal effect.
Therefore, this study investigated this overlooked factor of human thermal effect and how it affected the droplets evaporation and dispersion characteristics. A realistic seating CTM with full body features was employed to capture the accurate thermal plume pattern in the vicinity of the manikin body, while the CTM was reasonably simplified using a quantifiable approach developed in the authors’ previous study [20] to reduce the computational cost without over sacrificing the accuracy. The evaporation process of coughing was modelled using the multi-component Eulerian-Lagrangian approach. The outcomes of this study demonstrated the significant impacts of human thermal effect on the local flow development, the transport trajectories of the droplets, as well as the other droplets transport characteristics (distance, directions, velocity, etc.).
2. Method
2.1. Mathematic models for droplet evaporation
The multi-component Eulerian-Lagrangian model was employed to realise the mechanistic modelling of droplet evaporation process. The surrounding air was considered as an ideal mixture by dry air and water vapour (i.e. humid air), in which the thermal dynamic properties of the mixture were calculated by:
| (1) |
where, φ represents the material properties (), while and are the mass fractions of dry air and water vapour (), respectively.
As the dry air and water vapour molecules were assumed to be ideally mixed, they would share the same local velocity, pressure and temperature and thereby the momentum and energy equations were solved based on the air mixture:
| (2) |
| (3) |
where, is the interfacial forces acting on the droplet surfaces, is the pressure gradient and is the momentum source due to buoyancy. and are the enthalpy and temperature of mixed air, respectively. is the interphase heat transfer rate across the droplet interfaces.
The continuity equations of the dry air and the water vapour were solved separately to capture the transport characteristics of each phase:
| (4) |
| (5) |
where, is the mass-averaged mixture velocity, is the kinematic diffusivity of water vapour in the air mixture and is the mass source of water vapour due to droplets evaporation.
The droplets transport and trajectories were tracked using the Lagrangian framework. Dominating forces (i.e. drag force ) and the buoyance force ) were considered and expressed in Equation (6) – (8):
| (6) |
| (7) |
| (8) |
where, , and are droplets velocity, diameter and density, respectively.
The composition of saliva droplets was assumed as 98.2% water and 1.8% non-volatile solid compounds based on the existing literature [13,16]. The evaporation process of the heavily weighed water component was controlled by the equilibrium vapour pressure relative to the ambient pressure at the surface of droplets. When droplets suspended in the air after coughing, the evaporation was predominated by the diffusion mechanism and the mass transfer rate:
| (9) |
where, is the dynamic diffusivity of water vapour in the continuum and is the Sherwood number [24]. Molecular weights of the vapour and the mixed air were represented by and , respectively. is the equilibrium mole fraction of water vapour at the droplet surface, while is the equilibrium mole fraction of water vapour in the air mixture. is the ambient pressure, and are the partial pressures of water vapour, at the droplet surface and in the air mixture, respectively.
The temperature decrease of the droplet by the latent heat of phase change was calculated by:
| (10) |
where, is the interfacial heat transfer rate and is the latent heat. The temperature gradient inside a droplet was not considered.
2.2. Model validation
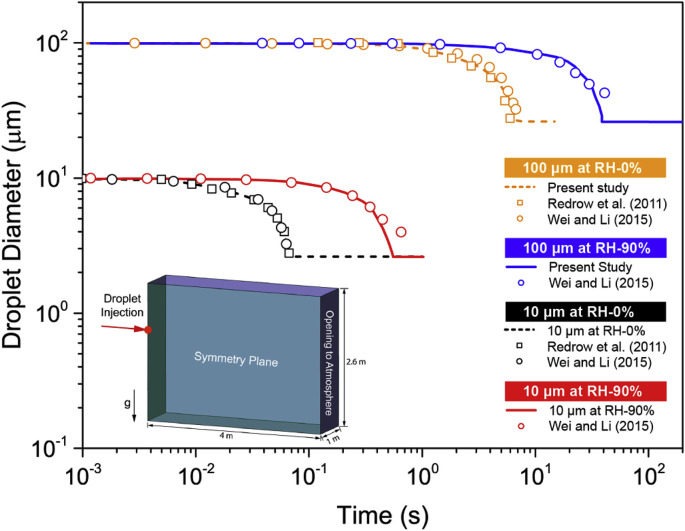
As aforementioned, the evaporation process would have critical impacts on the droplet size reduction as well as the rate of the size change, while the size would directly decide the transport fate of the droplets and the corresponding distributions. Therefore, the mathematical model for droplets evaporation was firstly pretested in an enclosed chamber to compare the results with existing studies in the literature [12,25] before applying the detailed CTM and considering the corresponding thermal effect of the human body. It was assumed that free falling droplets evaporate in quiescent air and the dispersion of humidity is driven by the mechanism of molecular dispersion only, while the effects of the ventilation parameters are not considered.
The computational domain and the conditions of the validation case were set accordingly to the existing study by Wei and Li [25]. As illustrated in Fig. 1 , droplets were released from an injection nozzle with diameter of 2 cm locating at 2 m height from the ground. To increase the efficiency, only half of the chamber with dimensions of 4 m × 1 m × 3 m was created due to the symmetric distribution characteristics of the airflow field. The ambient conditions including air temperature and humidity were considered by setting an opening at the opposite end of the chamber to the droplet injection plane. Two representative droplet sizes (i.e. 10 μm and 1000 μm) were simulated under the relative humidity of 0% and 90%, respectively. The predicted time-dependent droplets diameter reduction was compared to the theoretical calculations by Redrow et al. [12] and Wei and Li [25]. It can be seen from Fig. 1, the numerical predictions from this study yielded very good agreement to the reported data in the existing literature. The dramatic differences on the evaporation rate were accurately captured using the proposed multi-component Eulerian-Lagrangian model, while the impacts of the RH change on the evaporation process were also successfully predicted. Although 0% and 90% RHs were not realistic room humidity condition, successful prediction of evaporation process at both high and low ends of RH proved the robustness of the proposed model.
Fig. 1.
Evaporation model validation.
3. Computational models and boundary conditions
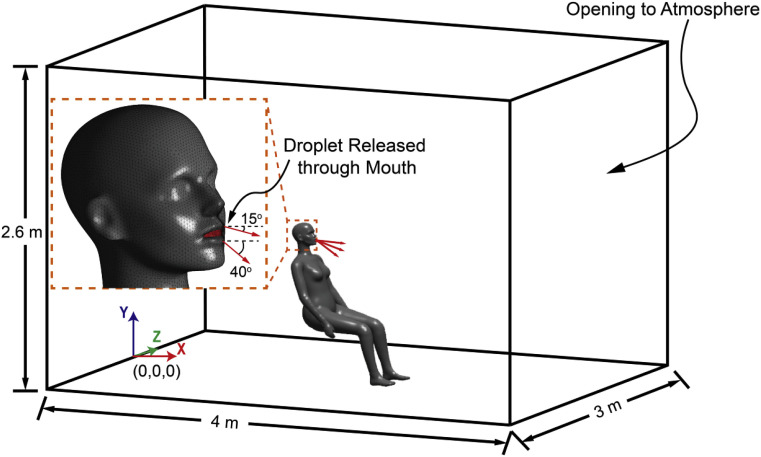
A full-size enclosed chamber with dimensions of 4 m-length × 3 m-width × 2.6 m-height was then employed along with a 3D seating manikin model to investigate the effects of human body heat on the coughing evaporation in an indoor environment (Fig. 2 ). The 3D scanned manikin (downloaded from http://www.ie.dtu.dk/manikin [26]) was firstly simplified using surface decimating approach [20] to reduce the computational cost without over-sacrificing the accuracy. The front, back and side walls of the computational domain were set as free-flow opening with zero-gauge pressure to allow the air flowing in and out depending on the interior conditions. This would allow sufficient interactions between the local coughing flow and the ambient airflow. Computations were conducted under a quiescent condition to allow the evaporation of droplets fall freely, while the constant air temperature of 25 °C was set at RH of 50%.
Fig. 2.
Computational domain with seating CTM.
The computational domain was discretised using the unstructured tetrahedron mesh in ICEM 17.2 [27]. To capture the detailed gradient change of the thermal buoyancy flow in the vicinity of CTM surface, 10 prism layers with total height of 15 mm were generated adjacent to the CTM surface. The mesh independency test was conducted using the grid convergence index (GCI) [28] and the y + values at CTM surfaces [27]. It was achieved at 2.3 million with the 90% mesh quality above 0.8 and the maximum y + values below 3 at the CTM surfaces. Further refining the mesh did not contribute considerable differences of air velocity profiles, droplets mass fraction or droplets diameter reduction. The airflow field was solved using the incompressible Navier-Stokes equations along with the Boussinesq approximation for the thermal buoyance flows. High-resolution advection scheme was applied to achieve better robustness and accuracy of the advection terms, while the RNG k-ε model was applied for the air turbulence due to its reliable performance in predicting indoor airflows [29,30]. The independence of the droplet trajectory numbers was also tested and achieved at 25,000. Transient simulation was conducted with adaptive time steps to match the simultaneous gradient change of airflow and droplet fields. Very small initial time-steps of 0.01 s were used at the beginning of the cough with maximum increase ratio of 1.1. The total droplet tracking time was 40 s, which took 60 h to finish each simulation using a workstation with 40 CPU cores (2.8G Hz Intel Xeon) and 128 GB RAM.
To generate the realistic amount of thermal buoyancy flow, the overall heat load and proper distributions of the heat load around the CTM surface were strong required. Previous studies found that the total heat load of a human body was around 90 W [31,32], while the convective heat load occupied approximately 40% of the total heat load [31,33]. Since the radiation was not considered in this study, a convective heat load of 36 W was applied to the seating CTM in the chamber. The detailed heat load distribution at each segment of the CTM was given in Table 1 . An equivalent heat flux of 22.83 W/m2 was applied on the CTM surface, which was very similar to the published experimental measurements [31,32] and numerical results [33,34], as compared in Table 2 .
Table 1.
Heat load distributions of CTM.
| Head | Neck | Upper Torso | Arm (Left) | Arm (Right) | Leg (Left) | Leg (Right) | Total Area | |
|---|---|---|---|---|---|---|---|---|
| Area (m2) | 0.100 | 0.021 | 0.445 | 0.157 | 0.158 | 0.348 | 0.347 | 1.577 |
| Weighting Factor (%) | 6.3 | 1.4 | 28.2 | 10.0 | 10.0 | 22.1 | 22.0 | 100 |
| Heat Load (W) | 2.27 | 0.50 | 10.15 | 3.60 | 3.60 | 7.96 | 7.92 | 36 |
| Heat Flux (W/m2) | 22.83 | 22.83 | 22.83 | 22.83 | 22.83 | 22.83 | 22.83 | 22.83 |
Table 2.
Comparisons of heat load conditions on human bodies.
| Convective heat load (W) | Convective heat flux (W/m2) | Tskin-Tatm (oC) | Convective heat transfer coeff. (W/m2 oC) | |
|---|---|---|---|---|
| Present Study | 36 | 22.83 | 5.81 | 3.69 |
| deDear et al.[31] (Exp.) | 33.98 | 23.1 | 7 | 3.3 |
| Licina et al.[32] (Exp.) | 35.6 | 22.39 | 6 | 3.78 |
| Topp et al.[33] (Sim.) | 38 | 23.60 | 5.1 | 5.0 |
| Li et al.[34] (Sim.) | 35.6 | 22.39 | 5.39 | 3.63 |
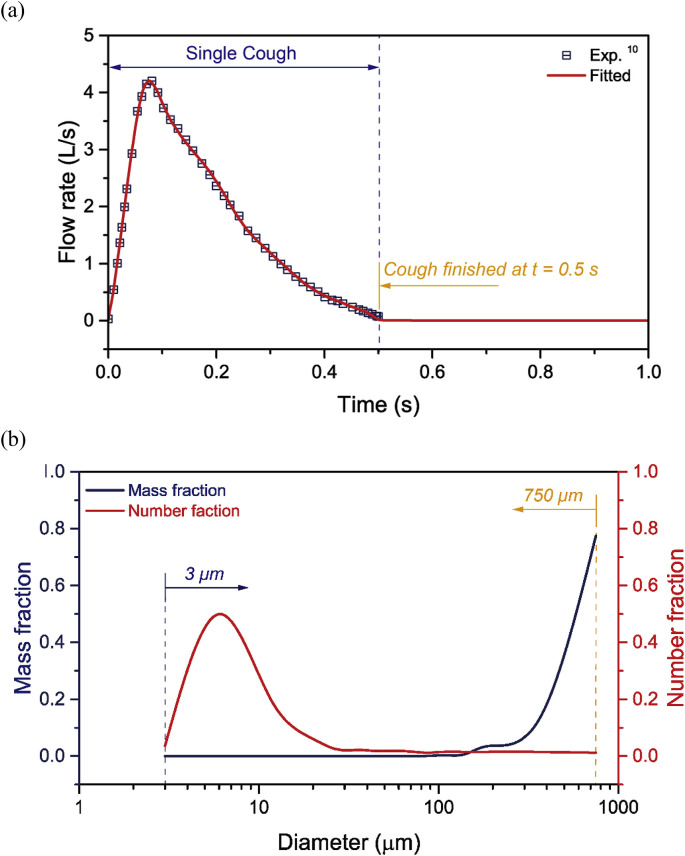
Coughing flow and droplets were expelled through the mouth of the seating CTM, as demonstrated in Fig. 2. To match the real cough condition, the downward cough angles were set as 15° near the upper lip and 40° near the lower lip, based on the experimental measurements of real human coughs by Gupta et al. [9]. A single cough behaviour was simulated by applying one pulse air jet with duration of 0.5 s, in which the time-dependent cough flow rate was also set accordingly to the experimental coughing measurements [9], as demonstrated in Fig. 3 a. Considering the size of droplets disperses widely through human coughing, droplets with initial diameters from 3 μm to 750 μm were employed in this study. Detailed droplets release conditions at the mouth were carefully set using the number and mass probability density distributions of the expelled cough droplets, which were experimental measured at 10 mm distance from the mouth by Chao et al. [6] (Fig. 3b).
Fig. 3.
Cough flow rate and Droplets inject conditions at the CTM mouth; (a) Air flow rate of a single cough 9 and (b) Size and mass distribution of cough-expelled droplets 6.
4. Results and discussion
4.1. Effects of human body heat on cough flow
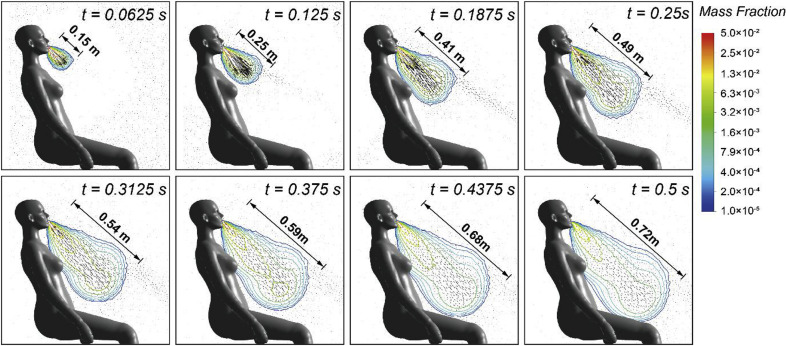
Expelled coughing flow adjacent to the seating CTM was firstly analysed to understand its transient development characteristics. The time-dependent velocity vectors and the droplets mass fraction contours of the cough flow within the coughing period was demonstrated in Fig. 4 . Since the cough flow rate was generally high at the first half of the coughing period (0 s–0.25 s), the coughing velocity was also expected to be significant during the same period, in which the maximum velocity of the cough flow reached 21.7 m/s. Existing experiment measurements in the literature also verified that the maximum cough velocity could be as high as 22 m/s [9,17]. Due to such strong cough jet, the cough flow quickly travelled to nearly 0.5 m away from the mough within 0.25 s, followed by a much slower development to 0.72 m at the end of the cough. The maximum cough velocity was then significantly reduced to 1.2 m/s (only about one-twenties of the peak value) at the end of the cough.
Fig. 4.
Air velocity vectors and droplets mass fraction contours during the coughing period.
Since the evaporation-induced humidity was considered, the cough flow containing 5% mass of water could significantly affect the local humidity in the vicinity of the CTM body. It can be noticed from the droplets mass fraction contours in Fig. 4 that the humidity of the surround airflow in the vicinity of the CTM was clearly elevated after the cough was expelled. This elevated air humidity became larger with the development of the cough flow and formed a strong vapour plume, in which the droplets mass fraction inside the vapour plume was much higher than the bulk air region.
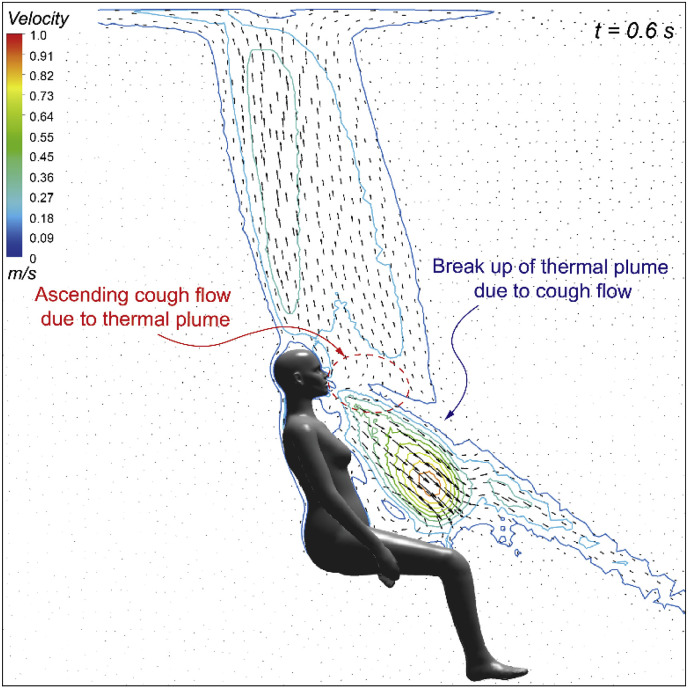
Whilst the cough flow revealed a dramatic and simultaneous velocity change before and after coughing, the buoyancy driven thermal flow induced by human body heat, on the other hand, was more steady and consistent at around 0.2 m/s to 0.25 m/s [21,35] above the manikin head and in front the main torso for seating posture (Fig. 5 ). It seems that the ascending thermal flow had very limited impacts on the cough jet flow near the beginning of the cough when the jet velocity was nearly 22 m/s. However, the interactions between these two flows, especially the impact of the thermal flow could become more obvious and dominating once the cough flow was weakened at the end and after the cough, as shown in Fig. 5. Therefore, detailed comparisons with and without considering the manikin body heat were focused after the cough (t > 0.5 s) when the cough jet flow became weaker and further dispersed into the surrounding air. The corresponding results on the airflow field and the droplets mass fraction in the vicinity of the manikin body was given in Fig. 6 .
Fig. 5.
Interactions between cough flow and thermal plume.
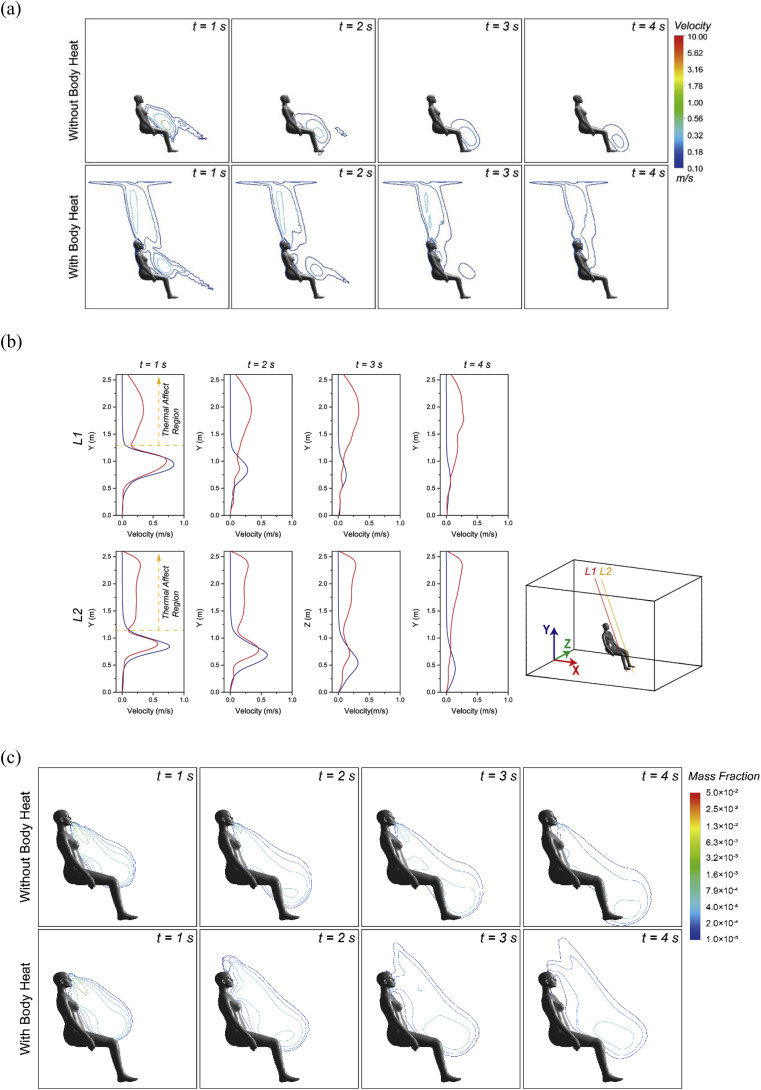
Fig. 6.
Comparisons of prediction results with and without the body heat after cough (1 s - 4 s); (a) Predicted velocity contours, (b) Velocity profiles at two selected lines in front of the CTM and (c) Mass fraction.
The thermal flow induced by human body heat can be clearly noticed from the velocity contour predictions, as shown in Fig. 6a. This ascending thermal flow formed obvious thermal plumes on top of and in front of the manikin, which quick attached and interacted with the descending cough jet flow. Since the cough flow still remained relatively high momentum just after the cough (t = 1s), the cough flow pattern did not show significant differences with and without considering the human thermal effect. However, with the time went on, the thermal plume became more dominating. The cough flow was clearly brought up by the ascending thermal plume and eventually became part of the long-lasting thermal plume when considering the human body heat, whereas the cough flow continued to travel downward and gradually dispersed in the case without body heat. To further quantify the differences caused by the thermal plume, velocity profiles were compared at two selected lines adjacent to the manikin with same incline angle, as provided in Fig. 6b. Velocity deviations can be clearly noticed at heights above 1 m, in which the two ascending thermal plume started merging and thereby the effect of the thermal plume were maximised. As a result, after considering the body heat, the vertical component of the air velocity was considerably increased and led to a higher overall velocity profiles in the thermal affect region.
With the local cough flow being different after adding the human body heat, the humidity change at the surrounding air was also expected to be affected. A further comparison of the droplets mass fraction in the vicinity of the manikin with and without considering the body heat was studied Fig. 6c. The outcomes proved the hypothesis with the high droplets mass fraction area being significantly changed. The prediction yielded higher humidity of the local air near the breathing zone and above the CTM after considering the human body heat.
4.2. Effects of human body heat on droplets transport
The droplets size reduction induced by the evaporation process was then investigated in prior to assessing the thermal effect of human body on droplet dispersion and transport. The results illustrated in Fig. 7 demonstrated very clear and quick size reductions of small droplets (e.g. from 3.5 μm to approximately 0.75 μm within 0.1 s), while the evaporation process time was gradually longer with the increase of droplet size. For very large droplets (>100 μm), the evaporation process did not finish or even start due to the early deposition of these large droplets. The reduced droplet nuclei sizes were approximately 26% of their initial size, which were vital when investigating the droplet dispersion and transport characteristics. Consequently, some inspirable droplets (10 μm - 100 μm) turned into respirable droplets (<10 μm) and thereby the inhabitability and infectivity of these droplets would be different after considering the evaporation process. In terms of the thermal effect, although the local temperature in the vicinity of the body was increased by the body heat, it had very limited boost on the size reduction of the droplets. The evaporation process was not significantly affected by the local temperature change. However, the thermal effect of human body did not just increase the local temperature, it also created the ascending thermal flow around. This ascending thermal flow was expected to significantly affect the droplets transport and dispersion due to its solid impacts on the local airflow field as aforementioned.
Fig. 7.
Effects of the human body heat on the time-dependent sizes of droplets.
The droplets transport trajectories were compared and discussed to visualise the qualitative differences caused by the thermal effect of human body. Fig. 8 a compared the droplets trajectories yielded by the cases without and with the human body heat at three moments when cough was just finished (t = 0.5 s), slightly after cough (t = 2 s) and relatively longer time after (t = 8 s). At t = 0.5 s, as the cough was just finished, the droplets were mainly carried out by the relatively strong jet cough flow and thereby and difference was not obvious. However, with the time went on and the jet flow became weaker, the droplets started to be driven partially by the ascending thermal flow, while some droplets began to travel upward in the case with body heat. Eventually, the buoyancy driven thermal plume mainly dominated the droplets transport at t = 8 s and the amount of droplets travelling upward became considerable.
Fig. 8.
Effects of the human body heat on droplet trajectories; (a) Droplets trajectories at various time (0.5 s, 2 s and 8 s) and (b) Droplets trajectories of three size groups (<10 μm, 10–100 μm and >100 μm) at t = 10 s.
To distinguish the impact of the human thermal effect at different size range of droplets. The droplets trajectories at t = 10 s were further compared under three size groups as demonstrated in Fig. 8b. The outcomes showed obvious trajectory differences of the droplets less than 10 μm when including the human body heat. Suspensions of droplets could be clearly noticed in the breathing zone of the seating manikin. As a results, the risks of inhaling these droplets would be greatly increased. Despite these suspended droplets in the breathing zone of the source occupant, the rest of the droplets travelled further away due to the strong jet flow of coughing. Under densely occupied environment, these further travelled droplets could easily enter the micro-environment of other occupants. These occupants would thereby encounter very high chance of inhaling these droplets induced by their own thermal plumes.
Similar findings were also observed when the droplets size was between 10 μm and 100 μm, although some of the droplets were still dominated by the inertial and gravity and settled to the ground. On the other hand, the trajectories were almost identical for large droplets (>100 μm) and the effects of thermal flow was minimised due to their high inertia and mass. More detailed size groups were used in the following discussions to investigate the body heat impacts on various sizes of droplets and their corresponding transport characteristics.
Representative droplets size classifications were created and listed in Table 3 , based on the experimentally measured classifications by Chao et al. [15]. Since the above findings revealed that the trajectories of droplets larger than 100 μm were almost identical with and without the human body heat, the extreme large droplets (larger than 200 μm) were not included in the follow discussions. It is worth noting that the collision of droplets could lead to a different droplets size distribution. To better match the classifications with the experimental data, the droplets were assumed not colliding with each other in this study. For future model improvement, experimental observations of droplet collisions using high-resolution images are in great demand. With small droplets that could be potentially lifted by the ascending thermal flow, the instantaneous droplets velocity was compared between the cases without and with the human body heat, as shown in Fig. 9 . It was obvious that the time-dependent vertical velocity profiles were completely different for the droplets between 3.5 μm and 20 μm. Almost all these droplets obtained an upward velocity against the gravity after the cough with human body heat. The opposite vertical velocity of droplets reflected very different transport characteristics of the droplets before and after considering the human thermal effect. For relatively large droplets (35 μm and 50 μm), the instantaneous velocities of droplets were not significantly changed after considering the thermal flow. However, the active droplets travelling time of these droplets were clearly different with and without considering the thermal effect. The 50 μm droplets quickly deposited to the ground within 10 s before considering the human body heat, whilst the same group droplets took another 8 s longer to deposit after considering the human body heat. That it to say, the droplets (50 μm) travelled in the room nearly twice longer due to the ascending thermal plume adjacent to the manikin. The impacts of the body heat was more critical on droplets of 35 μm. These droplets were fully deposited approximately 12 s after cough without human body heat, whilst the same group of droplets suspended in the air rather than depositing to the ground due to the dominant effect of the ascending thermal flow. Consequently, the time of these droplets in the air was tremendously increased. Therefore, the human body heat significantly affected the one of the most crucial droplet dispersion parameter: the droplets travelling time. This impact would be vital when assessing droplets trajectory-based health risks in indoor spaces.
Table 3.
Size classifications of droplets.
| Representative size classifications (μm) |
||||||||
|---|---|---|---|---|---|---|---|---|
| 3.5 | 6 | 12 | 20 | 35 | 50 | 112 | 175 | |
| Size range (μm) | 3–4 | 4–8 | 8–16 | 16–24 | 30–40 | 40–60 | 100–125 | 150–200 |
Fig. 9.
Time-dependent droplet vertical velocity at various droplet size classifications.
As the droplet instantaneous velocity were found very different after considering the human thermal effect, the droplet travel displacements were further investigated and compared. Fig. 10 demonstrated the droplets travel displacement along the vertical direction where the buoyancy driven thermal plume mainly developed. The median displacement of each droplet classification was added to quantify the profile. The median curves yielded from droplets sizes of both 3.5 μm and 12 μm showed significantly different travel displacements of droplets without and with considering the human thermal effect. Although the travel displacements were almost identical during the coughing period, the plotted curves immediately departure away after the cough between the compared cases. The transport directions of these small droplets were completely changed after including the buoyancy driven thermal flow. Instead of gradually going downward, most of these droplets travelled upward above their initial release position and was eventually brought up into the breathing zone (±0.2 m from the mouth) of the occupant. For 50 μm droplets, the ascending thermal flow also significantly increased travelling time and delayed deposition. With later deposition, the travel distance of 50 μm, especially along the horizontal direction could be increased and the droplets would be able to travel further away from the source.
Fig. 10.
Time dependent droplets vertical travel displacement at (a) 3.5 μm, (b) 12 μm and (c) 50 μm.
As the impact of human body heat on the droplets travel displacements was found significant, the actual droplets travel displacements of the entire droplet classifications (3.5 μm - 175 μm) after considering human body heat were summarised in Fig. 11 . The predicted outcomes revealed that the small droplets up to 20 μm were easily brought up by the buoyancy driven thermal plume. As a result, these droplets travelled further upward and would have very high chance to entry the breathing zone of the occupant. Although the thermal plume might not be strong enough to lift the larger droplets (≥50 μm) into the breathing zone, it significantly delayed the deposition time of these large droplets as found in Fig. 10 and thereby the travel distance would be significantly increase. With further travel distance and longer travel time, the cough droplets would potentially cause higher health risks, especially under densely occupied environment where the thermal effect of occupants would be dramatically enlarged. Consequently, the risks of inhaling these droplets would be significantly increased and the inhalable size range of droplets could also be widened in real situations. Therefore, it is essential to include the thermal effect of human body into consideration when assessing the infection risks and air quality in indoor spaces.
Fig. 11.
Time dependent droplets vertical travel displacements at various size classifications (with body heat).
5. Conclusion
The cough flow and droplets transport characteristics were investigated in this study using the multi-component Eulerian-Lagrangian approach. The effects of human body heat were focused and its impacts on the critical parameters (local airflow field, the droplets size distribution, transport characteristics, etc.) were carefully evaluated.
The outcomes from this study revealed a strong impact of human body heat on the mass fraction predictions of expelled droplets, as well as the local velocity distribution in the vicinity of human body. Most importantly, it significantly changed the time-dependent transport characteristics of the expelled droplets. For droplets classified from 3.5 μm to 20 μm, the ascending thermal flow was dominating the droplets transport and could lift these droplets upward into the occupant's breathing zone. The inhalable chance of small droplets classified from 3.5 μm to 20 μm was dramatically increased. On the other hand, larger droplets (≥50 μm) were too heavy to be brought up into the breathing zone by the thermal flow in the single occupant case. However, it was expected that wider range of droplets would able to be lifted into the breathing zone when multi occupants were involved in a densely occupied environment where the effects of the human body heat were significantly enlarged.
In terms of the cough droplet evaporation, the presented results found that the increment of local temperature induced by the human body heat was not the key parameter to cause significant rate change of the evaporation process at room RH of 50%. However, the inclusion of human body significantly affected the other key parameter of droplets transport: the deposition time. With consideration of the buoyancy driven flow, the deposition time of droplets classified at 50 μm was nearly twice longer, while droplet of 35 μm suspended in the air without depositing. With significantly delayed deposition time, the travel distance of these droplets would be dramatically increased and could cause further spread of the cough droplets.
Acknowledgement
The financial supports provided by the Natural Science Foundation of China (Grant No. 91643102) and Australian Research Council (Project ID: DP160101953) are gratefully acknowledged.
References
- 1.Tyrrell C.S.B., Allen J.L.Y., Carson G. Influenza and other emerging respiratory viruses. Medicine. 2017;45(12):781–787. doi: 10.1016/j.mpmed.2017.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lee C.S., Lee J.H. Dynamics of clinical symptoms in patients with pandemic influenza A (H1N1) Clin. Microbiol. Infect. 2010;16(4):389–390. doi: 10.1111/j.1469-0691.2010.03117.x. [DOI] [PubMed] [Google Scholar]
- 3.Monto A.S., Gravenstein S., Elliott M., Colopy M., Schweinle J. Clinical signs and symptoms predicting influenza infection. Arch. Intern. Med. 2000;160(21):3243–3247. doi: 10.1001/archinte.160.21.3243. [DOI] [PubMed] [Google Scholar]
- 4.Yang S., Lee G.W.M., Chen C.M., Wu C.C., Yu K.P. The size and concentration of droplets generated by coughing in human subjects. J. Aerosol Med. 2007;20(4):484–494. doi: 10.1089/jam.2007.0610. [DOI] [PubMed] [Google Scholar]
- 5.Gralton J., Tovey E., McLaws M.L., Rawlinson W.D. The role of particle size in aerosolised pathogen transmission: a review. J. Infect. 2011;62(1):1–13. doi: 10.1016/j.jinf.2010.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chao C.Y.H., Wan M.P., Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M., Mengersen K., Corbett S., Li Y., Xie X., Katoshevski D. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. J. Aerosol Sci. 2009;40(2):122–133. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Li X., Inthavong K., Ge Q., Tu J. Numerical investigation of particle transport and inhalation using standing thermal manikins. Build. Environ. 2013;60:116–125. [Google Scholar]
- 8.Stilianakis N.I., Drossinos Y. Dynamics of infectious disease transmission by inhalable respiratory droplets. J. R. Soc. Interface. 2010;7(50):1355–1366. doi: 10.1098/rsif.2010.0026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gupta J.K., Lin C.H., Chen Q. Flow dynamics and characterization of a cough. Indoor Air. 2009;19(6):517–525. doi: 10.1111/j.1600-0668.2009.00619.x. [DOI] [PubMed] [Google Scholar]
- 10.Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M., Mengersen K., Corbett S., Chao C.Y.H., Li Y., Katoshevski D. Size distribution and sites of origin of droplets expelled from the human respiratory tract during expiratory activities. J. Aerosol Sci. 2009;40(3):256–269. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Xie X., Li Y., Sun H., Liu L. Exhaled droplets due to talking and coughing. J. R. Soc. Interface. 2009;6(Suppl 6):S703–S714. doi: 10.1098/rsif.2009.0388.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Redrow J., Mao S., Celik I., Posada J.A., Feng Z.-g. Modeling the evaporation and dispersion of airborne sputum droplets expelled from a human cough. Build. Environ. 2011;46(10):2042–2051. [Google Scholar]
- 13.Nicas M., Nazaroff W.W., Hubbard A. Toward understanding the risk of secondary airborne infection: emission of respirable pathogens. J. Occup. Environ. Hyg. 2005;2(3):143–154. doi: 10.1080/15459620590918466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liu L., Wei J., Li Y., Ooi A. Evaporation and dispersion of respiratory droplets from coughing. Indoor Air. 2017;27(1):179–190. doi: 10.1111/ina.12297. [DOI] [PubMed] [Google Scholar]
- 15.Chao C.Y., Wan M.P. A study of the dispersion of expiratory aerosols in unidirectional downward and ceiling-return type airflows using a multiphase approach. Indoor Air. 2006;16(4):296–312. doi: 10.1111/j.1600-0668.2006.00426.x. [DOI] [PubMed] [Google Scholar]
- 16.Li X., Shang Y., Yan Y., Yang L., Tu J. Modelling of evaporation of cough droplets in inhomogeneous humidity fields using the multi-component Eulerian-Lagrangian approach. Build. Environ. 2018;128:68–76. doi: 10.1016/j.buildenv.2017.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhu S., Kato S., Yang J.-H. Study on transport characteristics of saliva droplets produced by coughing in a calm indoor environment. Build. Environ. 2006;41(12):1691–1702. [Google Scholar]
- 18.Ge Q., Li X., Inthavong K., Tu J. Numerical study of the effects of human body heat on particle transport and inhalation in indoor environment. Build. Environ. 2013;59:1–9. [Google Scholar]
- 19.Melikov A., Kaczmarczyk J. Measurement and prediction of indoor air quality using a breathing thermal manikin. Indoor Air. 2007;17(1):50–59. doi: 10.1111/j.1600-0668.2006.00451.x. [DOI] [PubMed] [Google Scholar]
- 20.Yan Y., Li X., Yang L., Tu J. Evaluation of manikin simplification methods for CFD simulations in occupied indoor environments. Energy Build. 2016;127:611–626. [Google Scholar]
- 21.Salmanzadeh M., Zahedi G., Ahmadi G., Marr D.R., Glauser M. Computational modeling of effects of thermal plume adjacent to the body on the indoor airflow and particle transport. J. Aerosol Sci. 2012;53:29–39. [Google Scholar]
- 22.Rim D., Novoselec A., Morrison G. The influence of chemical interactions at the human surface on breathing zone levels of reactants and products. Indoor Air. 2009;19(4):324–334. doi: 10.1111/j.1600-0668.2009.00595.x. [DOI] [PubMed] [Google Scholar]
- 23.Voelker C., Maempel S., Kornadt O. Measuring the human body's microclimate using a thermal manikin. Indoor Air. 2014;24(6):567–579. doi: 10.1111/ina.12112. [DOI] [PubMed] [Google Scholar]
- 24.Ranz W.E., Marshall W.R. Evaporation from droplets, parts I & II. Chem. Eng. Prog. 1952;48(4):173–180. [Google Scholar]
- 25.Wei J., Li Y. Enhanced spread of expiratory droplets by turbulence in a cough jet. Build. Environ. 2015;93:86–96. [Google Scholar]
- 26.Nilsson H., Brohus H., Nielsen P. Aalborg University Denmark & Gavle University Sweden; 2007. Benchmark Test for a Computer Simulated Person-manikin Heat Loss for Thermal Comfort Evaluation: Version of February 2007. [Google Scholar]
- 27.ANSYS® . ANSYS, Inc.; 2017. Academic Research Release 17.2, Help System, Coupled Field Analysis Guide. [Google Scholar]
- 28.Roache R.J. Perspective a method for uniform reporting of grid refinement studies. J. Fluid Eng. 1994;116:405–413. [Google Scholar]
- 29.Chen Q. Comparison of different k-ε models for indoor air flow computations. Numer Heat Tr B-Fund. 1995;28(3):353–369. [Google Scholar]
- 30.Chen F., Yu S.C.M., Lai A.C.K. Modeling particle distribution and deposition in indoor environments with a new drift–flux model. Atmos. Environ. 2006;40(2):357–367. [Google Scholar]
- 31.deDear R.J., Arens E., Hui Z., Oguro M. Convective and radiative heat transfer coefficients for individual human body segments. Int. J. Biometeorol. 1997;40(3):141–156. doi: 10.1007/s004840050035. [DOI] [PubMed] [Google Scholar]
- 32.Licina D., Melikov A., Sekhar C., Tham K.W. Human convective boundary layer and its interaction with room ventilation flow. Indoor Air. 2015;25(1):21–35. doi: 10.1111/ina.12120. [DOI] [PubMed] [Google Scholar]
- 33.Topp C., Nielsen P.V., Sorensen D.N. Application of computer simulated persons in indoor environmental modeling. Build. Eng. 2002;108(2):1084–1089. [Google Scholar]
- 34.Li X., Yan Y., Tu J. The simplification of computer simulated persons (CSPs) in CFD models of occupied indoor spaces. Build. Environ. 2015;93:155–164. [Google Scholar]
- 35.Yan Y., Li X., Tu J. Effects of manikin model simplification on CFD predictions of thermal flow field around human bodies. Indoor Built Environ. 2016;27(5):606–621. [Google Scholar]