The impact of infectious diseases on hotel occupancy rate based on independent component analysis

Abstract

The recent global outbreak of Influenza A (H1N1), or the more commonly known as swine flu, has negatively affected the tourism and hospitality industries in many countries. This article reports a study that applied independent component analysis, a novel statistical technique, to separate the dominant factors which determine the levels of hotel occupancy rates in Hong Kong. Empirical findings would provide useful insights on how the dynamic lodging demand reacts to epidemics based on the severity and duration of the events.

1. Background

The rapid growth of the tourism and hospitality industries serves as the major driving force for academic researchers to investigate the accurate forecasting of lodging demand in tourist destinations. For instance, Tsai et al. (2006) studied the relationship between hotel room demand/supply functions and room rate using a simultaneous equations model for determinants of room demand/supply in Las Vegas. In terms of optimal hotel rates, Pan (2007) proposed an optimal room rate model to set pricing strategies at peak or low seasons. Recently, Slattery (2009) suggested employing the Otus theory to study the relationships between economic structure and demand/supply of hotel rooms.

In this paper, a novel time series model is presented which models multivariate time series data. The advantage of this model is that the discovered factors are mutually independent and a univariate time series model can be applied to these factors without considering the factors’ interdependence. The next section introduces the methodologies of independent component analysis. On the basis of this model, empirical studies on Hong Kong hotel occupancy rates are analyzed. The most dominant factor of infectious diseases is subsequently detected. At last, managerial implications and concluding remarks are provided.

2. The modeling process

Independent component analysis (ICA) is a statistical technique that aims to capture observed data in terms of a linear combination of underlying latent variables. These latent variables are assumed to be non-Gaussian and mutually independent. A typical ICA model for an N-dimensional multivariate time series {x ₁=(x _it, …, x _Nt)′}: t  = 1, …, T) is

$$x_t=A{s}_t$$

where s _t is a vector of statistically independent latent variables called independent components (ICs). A is an unknown constant mixing matrix, and T is the number of observations of the time series. The task of ICA is to identify both the ICs and the matrix A. Various algorithms for parameter estimation have been developed for ICA. Among them, a widely used one is the FastICA algorithm, which was proposed by Hyvärinen et al. (2001).

Since traditional ICA algorithms lack the ranking of ICs, Wu et al. (2006) proposed an ordering algorithm for independent components based on the minimizing mean squared errors (MSE) criterion. Based on this ordering method, ICs are sorted in a way such that modeling errors are minimized and dominant ICs are identified. Modifying the approach of Wu et al. (2006), the major steps of modeling hotel occupancy rate using ICA are presented as follows:

• 1.Import the multivariate dataset (X) with number of N time series, each time series has T observations.
• 2.Use the FastICA algorithm to find the independent components (S) and the mixing matrix (A).
• 3.Use the independent component (IC) ordering method to order the ICs to find 1st IC, 2nd IC, 3rd IC, and so on.
• 4.Set the number of dominant ICs to keep for further analysis.
• 5.Use time series models (e.g., Moving Average) to analyze the dominant ICs concerned and suggest for managerial applications accordingly.

3. Empirical results

The previously mentioned ICA modelling procedure was applied to model hotel occupancy rates. The dataset used in this study was the monthly hotel occupancy rates grouped by geographical districts of Hong Kong from January 1996 to Feb 2009 (http://partnernet.hktb.com/pnweb/jsp/comm/index.jsp), representing the available data during the research.

The hotel occupancy rates series were collected from six geographical districts which are labelled from X1 to X6. This classification of Hong Kong hotels by districts was to follow the official system used by the Hong Kong Tourism Board (HKTB). The historical hotel occupancy rates of these districts are plotted in Fig. 1 .

Fig. 1.

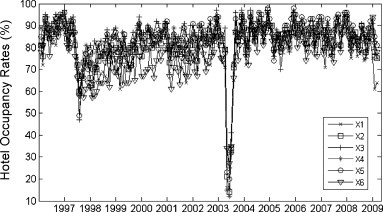
Historical hotel occupancy rates by districts in Hong Kong.

The time series in Fig. 1 have clear seasonal fluctuations. Moreover, these time series exhibit similar trends and have some overlaps. The pair-wise correlation coefficients among these time series ranging from 0.75 to 0.96, suggesting that the hotel occupancy rates in different districts show a high degree of consistent directional tendency. However, modelling multivariate time series with high correlation is more difficult than univariate cases and may cause the problem of collinearity. As such, the FastICA algorithms were used to decompose multivariate time series into mutually independent time series, and subsequently employed the IC ordering method to rank the ICs based on their importance in prediction. After that, univariate time series models were used on each independent series.

The order of computed ICs and the sum of variance of corresponding IC are shown in Table 1 . The sum of variance refers to the summation of variance in the original time series which can be explained by a particular IC. A larger value of sum of variance relates to a stronger overall prediction power of the IC. According to Table 1, the 1st IC is clearly the dominant IC that needs to be further examined.

Table 1.

Sum of variance of ICs and its ranking.

Overall IC order	1st IC	2nd IC	3rd IC	4th IC	5th IC	6th IC
Original IC number	IC1	IC5	IC6	IC3	IC4	IC2
Sum of variance	480.35	89.79	68.03	36.19	11.93	7.48

The key statistics of the 1st IC are presented in Table 2 .

Table 2.

The modelling results of the 1st IC.

Original occupancy rates time series by district	Variance explained by the 1st IC	Weighting of the 1st IC	Historical average occupancy rates (January 1996–February 2009)
X1	67.2%	0.091	78.4%
X2	79.5%	0.094	81.6%
X3	67.5%	0.082	84.8%
X4	91.2%	0.102	83.1%
X5	73.1%	0.094	84.6%
X6	39.5%	0.070	77.1%

Table 2 reveals that IC1 is the common 1st IC of the original time series concerned. It explains the largest proportion of variance in the data, meaning that the 1st IC has very strong prediction power on hotel occupancy rates. The practical meaning of the 1st IC was further analyzed.

Since hotel occupancy rates were monthly data, it is necessary to remove the seasonal effects and smooth the trends of the influencing factor. A moving average model with window size of 12-month MA(12) was applied to the 1st IC and results were plotted in Fig. 2 . The x-axis represents the time horizon from 1996 to 2009 and the y-axis denotes the level of the time series.

Fig. 2.

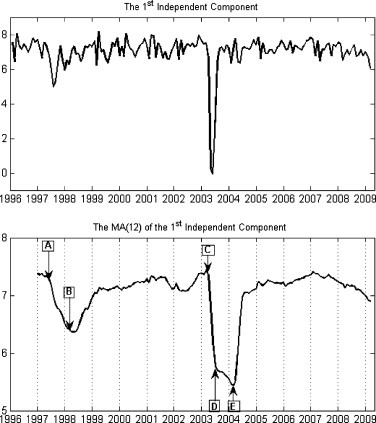
The strong influencing factor discovered by the 1st IC.

As indicated in Fig. 2, the curve is fairly stable in most years with the exception of two significant concaves in periods 1997–1998 and 2003–2004. The weightings of the mixing matrix for the 1st IC (influencing factor) are all positive (see Table 2). This implies that when the curve goes down, hotel occupancy rates will decrease. The very sharp decrease of the 1st influencing factor in 2003 clearly indicates the damage to the hotel industry in Hong Kong. Having reviewed records of important events in the years where drops were noticed, outbreaks of serious infectious diseases were found in Hong Kong. The following events were the epidemics in Hong Kong which are characterized by the time series in the lower panel of Fig. 2 (HKTA, 1999, HKTB, 2005).

• • Events A and B: Starting from mid-1997 till January 1998, the H5N1 bird influenza (avian flu) had sustained.
• • Event C: In March 2003, the first outbreak of SARS (Severe Acute Respiratory Syndrome) was reported in Hong Kong.
• • Event D: In June 2003, the last case of SARS was reported in Hong Kong.
• • Event E: In January 2004, the Individual Visit Scheme (IVS) was introduced that allows residents in some cities in Mainland China to freely visit Hong Kong. The hotel and tourism industries in Hong Kong had experienced a very quick recovery since then.

The timetables of the occurrences of infectious diseases actually match the 1st IC. In other words, the practical meaning of the 1st influencing factor is the impact of infectious diseases on hotel occupancy rates.

4. Managerial implications

It is well-known that health and safety are major concerns when people travel (Kozak et al., 2007). Using the case of SARS, Chien and Law (2003) have advocated that hotel managers should be well prepared for unexpected epidemics. By mastering the influencing factor of infectious diseases, the impact on hotel occupancy rate and its lasting time can be accessed for the potential occurrence of future epidemics. The recent outbreak of Influenza A has already had a very negative impact on the hotel industry in Hong Kong and many other regions. By analyzing the existing and expected infectious cases as well as the fatality rate, one can quantitatively estimate the extent of influence of the disease on hotel occupancy rates and the induced financial loss by comparing the previous outbreaks such as avian flu and SARS.

The proposed ICA model suggests that an unexpected outbreak of infectious disease/s will greatly lower hotel occupancy rate due to the sharp downturn of tourist arrivals. Therefore, at an operational level, hotel managers should take actions to minimize operation costs during a crisis. Some feasible choices could be shutting down unnecessary equipment, reducing consumption of electricity and water, as well as stop using some high-cost but under-utilized facilities. With the temporally decrease of tourists due to the threat of diseases, hotels could consider flexibly changing their marketing strategies by attracting local residents for dining and lodging to raise both hotel revenues and occupancy rates. Lastly, the model has an influence on decision-making of hotel development projects as a popular district will have a higher risk of experiencing larger drops in occupancy rates during an outbreak of influential diseases. This should be taken into account during hotel development.

5. Conclusions

In this paper, a factor modelling approach based on independent component analysis techniques was presented to extract the dominant driving-forces of hotel occupancy rates. With the time series data of Hong Kong hotel occupancy rates, an infectious disease influencing factor was identified that can capture the acute influence of bird influenza and SARS on hotel occupancy rates. With the availability of additional data, the model can be extended to access the likely impact of other infectious diseases on a region's hotel industry. To summarize, the successful implementation of the model would be beneficial to hotel managers on planning for potential crises.