Abstract
Several case clusters occurred in high-rise residential buildings in Hong Kong in the 2003 SARS (the severe acute respiratory syndrome) epidemic, which motivated a series of engineering investigations into the possible airborne transport routes. It is suspected that, driven by buoyancy force, the polluted air that exits the window of the lower floor may re-enter the immediate upper floor through the window on the same side. This cascade effect has been quantified and reported in a previous paper, and it is found that, by tracer gas concentration analysis, the room in the adjacent upstairs may contain up to 7% of the air directly from the downstairs room. In this study, after validation against the experimental data from literatures, Eulerian and Lagrangian approaches are both adopted to numerically investigate the dispersion of expiratory aerosols between two vertically adjacent flats. It is found that the particle concentration in the upper floor is two to three orders of magnitude lower than in the source floor. 1.0 μm particles disperse like gaseous pollutants. For coarse particles larger than 20.0 μm, strong deposition on solid surfaces and gravitational settling effect greatly limit their upward transport.
Keywords: Particles, Lagrangian method, Eulerian method, Transport, Deposition
Nomenclatures
- C
particle concentration (g/m3)
- C0
initial indoor particle concentration (g/m3)
- CC
cunningham correction factor
- CD
drag coefficient
- Cj
particle concentration in the jth cell (g/m3)
- Ct
indoor particle concentration at time t (g/m3)
- dp
particle diameter (μm)
- Dp
Brownian diffusivity (m2/s)
- dt(i, j)
the ith particle residence time in the jth cell (s)
correction factor for turbulent kinetic energy
other additional force per unit mass (N/kg)
drag force per unit mass (N/kg)
gravity force per unit mass (N/kg)
gravitational acceleration (m/s2)
- k
turbulent kinetic energy (m2/s2)
- Le
eddy length scale (mm)
- M
flow rate of each trajectory (g/s)
- SC
particle source term (g/sm3)
- Sϕ
pollutant source term (g/sm3)
- t
time (t)
- tcross
eddy crossing time (s)
- teddy
eddy lifetime (s)
- tL
Lagrangian time scale (s)
velocity vector (m/s)
fluctuation part of instantaneous velocity in i direction (m/s)
particle velocity (m/s)
fluctuation part of instantaneous velocity normal to the wall (m/s)
- uτ
wall shear velocity (m/s)
- Vj
the volume of the jth cell (m3)
gravitational settling velocity calculated from Stokes's law (m/s)
- Vmet
meteorological wind speed (m/s)
- Vy
wind speed at the height of y (m/s)
- y
height above the ground in the calculation of wind speed (m)
- ycell
the distance between the wall and the first cell center (m)
- y+
non-dimensional wall distance ()
Greek letters
- α
air change rate (h−1)
- ε
viscous dissipation rate (m2/s3)
- εp
particle eddy diffusivity (m2/s)
- κ
particle loss-rate coefficient caused by deposition (h−1)
- λ
molecular mean free length (μm)
- μ
molecular viscosity of the air (g/ms)
- μeff
turbulent effective viscosity (g/ms)
turbulent viscosity (m2/s)
- ςi
a random number with Gaussian distribution
- ρ
air density (kg/m3)
- ρp
particle material density (kg/m3)
- σc
non-dimensional number 1.0
- τp
particle response time (s)
1. Introduction
The SARS outbreak in 2003 stimulated a series of engineering investigations into the airborne infectious diseases transmission mechanisms in the built environment. A few studies attempted to combine epidemiologic investigations with airflow analysis, but the airflow analysis remained to be preliminary [1], [2]. In the investigation of the outbreak in a high-rise residential estate in Hong Kong, the CFD simulation did indicate that the transmission pattern between adjacent high-rise blocks qualitatively agrees with the wind direction. In the related study aiming to reveal the vertical transmission pattern in one building, multi-zone modeling technique was employed, which had inadequacies in modeling airflow through large window openings [3]. Niu and Tung [4] used on-site tracer gas measurement to experimentally investigate the re-entry possibility of exhaust air from the lower floor into the immediate upper floor for high-rise residential buildings with single-sided natural ventilation conditions (Fig. 1 ). It was revealed that the upstairs room may contain 7% of the exhaust air from the lower floor, which can help explain the presence of SARS-CoV RNA found on the window sill deposits in the upstairs of an index patient. Gao et al.'s [5] CFD study on the dispersion of one tracer gas agrees with the on-site measurement. With the help of the Wells–Riley infection risk model, Gao et al. [5] estimated the vertical cross-household infection risk in the upper floor using the data of tuberculosis. It was found that a significant infection risk up to 6% for the upstairs residents can be resulted in, when merely assuming an 8 h continuous stay at home.
Fig. 1.
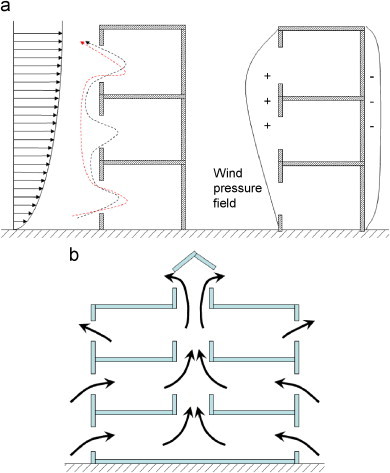
Schematic view of pollutant transport by the cascade effect in natural ventilation.
On the other hand, recent systematic reviews [6], [7] concluded that person to person respiratory virus transmission could occur in three possible modes: airborne transmission, droplet transmission, and direct contact with secretions (or fomites). Currently, by droplets transmission it is meant short-distance (usually less than 1 m) transmission via large droplets (⩾5 μm diameter) generated during coughing, sneezing, or talking, and by airborne transmission it is meant long-distance transmission via the dissemination of virus-laden droplet nuclei (particles less than 5 μm that result from the evaporation of large droplets). But whether the three transmission modes are mutually exclusive and which mode is the most significant transmission route for a particular disease are debatable. In general, it is believed that respiratory droplets movements in the room air play a key role for airborne transmitted diseases. Arguably, airborne transmission does not necessarily cause long range infections since a wide range of other confounding factors are also playing important roles, and these include the shedding rate, viability and infectiousness of the pathogen and the wind, temperature and humidity conditions. In general, aerosol dynamics differs from gaseous pollutants due to the effects of gravity, inertia and deposition at solid surfaces. Therefore, as a companion paper of Gao et al. [5], which studied the airflow and gaseous pollutants between vertically adjacent floors, this study simulates the transport possibilities of droplet residuals by using both Lagrangian and Eulerian methods. The aim is to explore whether the virus-laden aerosols could be carried upward by inter-flat airflows between floors in high-rise residential buildings when the gravity and surface deposition effects are considered.
2. Numerical approaches
2.1. Airflow field
Prior to modeling particle movements, the airflow field is simulated by using a commercial code, Fluent [8], which solves the mass, momentum, and energy equations in a finite-volume procedure with a staggered grid system. The convection terms are discretized by second order upwind scheme and the diffusion term by central difference also with second-order accuracy. The variables at the near-wall cells and the corresponding quantities on the wall are bridged by the standard logarithmic law wall function. The turbulent effect is modeled by the RNG k–ε model [9]. Although large eddy simulation (LES) has been adopted to investigate wind field and indoor–outdoor airflows due to its capacity of handling the unsteadiness and intermittency of the flow as well as providing detailed information on the turbulence structure, the RANS models are extensively used in industrial and engineering practice because they generally use about one order of magnitude less CPU time than LES while keeping an acceptable accuracy.
2.2. Assumptions for particle modeling
When particle loadings, denoted by volume fraction, are higher than 10−6, particles significantly affect the turbulent flow and two-way coupling between the phases has to be taken into account. If particle loadings are even higher than 10−3, particle–particle interaction becomes important [10]. Since indoor particulate levels normally vary from several to hundreds of μg/m3 (about 105–107 particles/m3) the two-phase flow can be deemed as dilute systems and one-way coupling is rational. A single-phase turbulence model can be used to represent the mixture.
In both numerical approaches, all particles are assumed to be spherical. Particle coagulation, reflection at walls, re-suspension, and phase-change such as evaporation, which may actually occur in indoor environments, are ignored. According to Hinds [11], coagulation rate is proportional to the square of the number concentration. Supposing a diameter of 1.0 μm and a concentration of 107 particles per m3, 1% decrement of particle number concentration needs about 500 days. This time scale is much larger than the indoor airflow time scale in that the indoor air can be renewed several times per hour. Particles’ bounce back from a solid surface is influenced by particle size, surface material, orientation, initial momentum and even electrostatic forces. Fine particles have a strong probability to stick on the solid surfaces, especially on those made of synthetic fibers [12]. Morawska [13] demonstrated that pure water droplets may completely evaporate within 0.003 and 0.3 s for 1 and 10 μm droplets respectively, at a condition of 80% relative humidity (RH). These periods are much shorter than their settling time, the indoor airflow time scale, and even shorter than the sneezing and coughing processes (around 0.5 s). Nicas et al. [14] suggested that evaporation from respiratory particles with an initial diameter less than 20 μm be treated as an instantaneous process. The droplets produced from sneezing and coughing could have a significant amount of pathogens-carrying residues. The equilibrium diameter of the desiccated particles is generally estimated to be around one-half of its initial diameter [14]. Small pathogens-carrying particles (diameter less than 10 μm) can reach the alveolar region with a different efficiency, posing an infection risk for a susceptible person [11]. Based on this information, in this study we simulated the movements of particles with diameter of 1, 10, and 20 μm.
2.3. Lagrangian method—discrete random walk model
Mathematical treatments of indoor particle movements include: the Euler–Lagrange method and the Euler–Euler method. Each method has its own pros and cons [15], [16].
The Lagrangian approach considers the fluid phase as a continuum and predicts the trajectory of each discrete phase particle by integrating the force balance on the particle. The particle momentum equation can be expressed as:
| (1) |
and can be written as and , respectively, where the Cunningham correction to Stokes’ drag law is computed from . The third term in Eq. (1) represents the additional forces exerted on the particles. In the current study, Brownian force, and Saffman's Lift force are taken into account in that they may be significant for fine particles. Thermophoretic force is included as well to reflect the non-isothermal condition. As the density ratio between particles and air is in the order of O(103), other forces, such as Basset force, pressure gradient force, virtual mass force, are neglected because their fraction in is infinitesimal [17]. Detailed descriptions of these forces are available in the Fluent manual [8]. The effect of turbulence on particle dispersion is modeled by using a stochastic method, i.e. the discrete random walk (DRW) model to simulate the fluctuating velocity. Stochastic realizations of turbulence have been successfully applied in many works [18], [19]. The DRW model assumes turbulence is isotropic and the random velocity fluctuations follow a Gaussian probability distribution:
| (2) |
The fluctuating velocities remain constant over a time interval that is the minimum between two time scales: the characteristic lifetime of the eddy and the time required by the particle to move across the eddy. This time interval is also called interaction time between the particle and eddies. The eddy life time is defined as:
| (3) |
The crossing time is calculated by
| (4) |
| (5) |
In a new interaction time, the particle is at a new location, and the calculation of the particle velocity and trajectory is continued using the new local instantaneous air velocities.
The ordinary differential Eq. (1) is integrated with the fifth-order Runge–Kutta method. The particle motion is advanced with a time step which is one order of magnitude smaller than the crossing time. For the treatment of particle deposition at solid surfaces in Lagrangian method, particles reaching a wall surface are assumed to be trapped, meaning the calculation of trajectories is terminated.
However, in DRW model isotropic turbulence assumption is not applicable at near-wall regions. In the boundary layer, velocity fluctuations in the direction normal to the wall are substantially smaller than in the spanwise and streamwise directions. Thus, isotropic decomposition of kinetic energy over-predicts the deposition rate of small particles [20], [21]. In this scenario, Reynolds stress model or LES are much more preferable [22]. If the flow field is simulated in the framework of two-equation models, to settle this problem Wang and James [23] developed the following equations to modify the turbulent kinetic energy for the first cells close to the wall:
| (6) |
| (7) |
With the help of Eqs. (6), (7), the near-wall kinetic energy is artificially reduced, prior to tracking the particles’ trajectories. Its improvement on the prediction of deposition rate will be examined in the validation section.
2.4. Eulerian method—the drift-flux model
In the Eulerian approach, both the fluid phase and the particulate phase are treated as interpenetrating continua. In order to save computational load, a simplified Eulerian method, i.e. the drift-flux method, is used. In this model, a drift velocity consisting of gravitational setting and diffusion is taken into account between particles and bulk air. The governing equation for particle transport in turbulent flow is written as:
| (8) |
The gravitational settling velocity of particles () is calculated by Stokes equation [11]. In view of that in the present study, the Reynolds number for particles is usually less than 1.0, equals . For particles with very small relaxation time, particle eddy diffusivity approximates the carried fluid turbulent diffusivity [24]. Generally speaking, for particles larger than 1.0 μm, Bownian diffusion is much weaker than the turbulent diffusion and gravitational settling effect is significant. Therefore, in the implementation of Eq. (8), we replace by μ eff. Eq. (8) is discretized directly into an algebraic equation by the finite volume method, which is unlike the other numerical treatment where the settling term is moved into the source term. For the boundary condition at walls, a semi-empirical deposition model by Lai and Nazaroff [25] is adopted, which is able to link the local airflow condition with the deposition process, by expressing the deposition velocity as a function of particle density, size, and friction velocity.
3. Validations
Lu et al. [26] measured particles decay in a two-room chamber with a size of width×depth×height=5 m×3 m×2.4 m (Fig. 2 ). The chamber is divided into two rooms by a partition in the middle. There is a large opening with height×width=0.95 m×0.70 m between the rooms. The clean air is supplied into one room through the inlet (1.0 m×0.5 m) and exhausted from the other room through the outlet (1.0 m×0.5 m) at the low level. The air change rate equals 9.216 h−1. In the experiments, the oil–smoke particles with a material density of 865.0 kg/m3 are equally divided into five size groups (1, 2, 3, 4, and 5 μm). Once the released particles are uniformly distributed in room 1 without initial motion, dampers at both inlet and outlet diffusers are opened and the supply fan is switched on. The particle mass concentrations at the centers of the two rooms are measured to represent the average concentrations in each room.
Fig. 2.
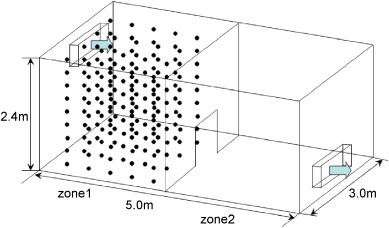
Geometry of the two rooms connected by an internal door.
To numerically simulate this case, each zone is divided into 84,000 cells and 8000 sample particles (1600 particles in each size group) are tracked. The particle mass carried by each sample particle is the ratio of the total particle mass injected into room 1 in the experiment to the samples (8000 particles). By counting the suspended particles, the numerical mass concentration in each room can be determined. The temporal evolutions of particle concentrations from measurements, the DRW model, the DRW model plus near-wall modification, and the drift-flux model are illustrated in Fig. 3 . For comparison, the decay process of tracer gas (CO2) is simulated as well. It is observed that the simulation results from tracer gas and the drift-flux model are in agreement with the experiments although the mean concentration in room 2 is slightly under-predicted. Particle loss in rooms is caused by the combined effect of ventilation and deposition. Using a well-mixed model, the mass concentration in room 1 can be calculated by the following equation:
| (9) |
Fig. 3.
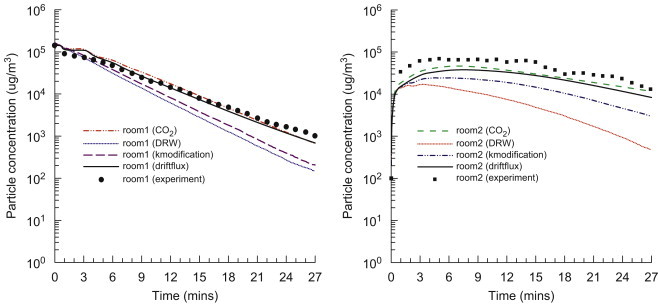
Temporal evolutions of particle concentrations in rooms 1 and 2.
Because the deposition rate of particles ranging from 1 to 5 μm is much lower than the current air change rate, the particle mass concentration decrement should be similar with the decay of CO2. The DRW model greatly under-predicts the concentrations in both rooms by over-predicting the deposition rates. Near-wall modification can improve the prediction, but a large discrepancy with measured data still appears. We believe that this amplified deposition is mainly caused by the anisotropic turbulence in the boundary layer, rather than by the “all trap” assumption at walls.
Chen et al. [27] experimentally investigated the concentration distributions of mono-dispersed 10 μm particles with a material density of 1400 kg/m3 in a simple model room using a phase Doppler anemometry system (Fig. 4 ). Particles are mixed into the supply air with a stable particle flow rate by a solid particle disperser. Particle concentration is normalized by the inlet concentration, which is considered to be uniform. Air inlet and outlet (0.04 m×0.04 m) are symmetrical with the central plane y=0.2 m. The supply velocity is 0.225 m/s.
Fig. 4.
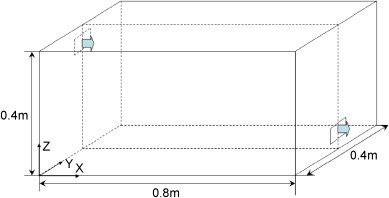
Geometry of the scaled chamber.
Fig. 5 compares the simulated and measured concentration profiles at the center plane. Because the DRW model does not directly provide the particle concentration, the scheme of particle source in-cell (PSI-C) is adopted to correlate the concentration with the trajectories:
| (10) |
Fig. 5.
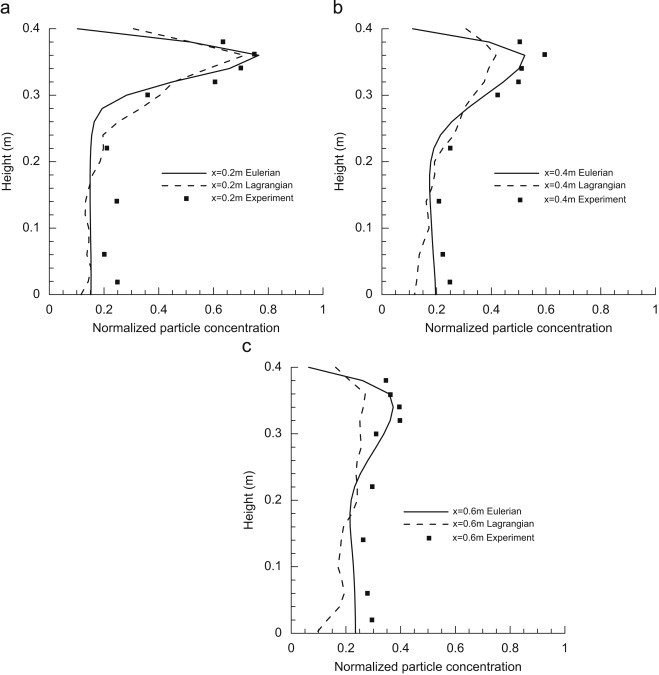
Comparison of the measured and simulated particle concentrations at the center plane.
Statistically stable concentration requires sufficient particle trajectories. These required trajectories also depend on the number of computational cells. In the present computational domain of 16,000 cells, 40,000 particle tracks are found to be stable. Compared with 20,000 particles, the difference of the proportion of particles with each kind of fate (deposited onto a certain wall or exhausted) to the total released numbers is less than 0.5%. Fig. 5 indicates again that the drift-flux model performs better than the DRW model, and that the DRW model under-predicts the concentration, especially in the region close to the floor. Fig. 6 shows the concentrations in the plane y=0.2 m after near-wall kinetic energy modification. In the right part under the ceiling, an unreasonably high concentration appears. It implies that the modification does not improve the simulation in this case. Inherently, the DRW model will show a tendency for fine particles to concentrate in low-turbulence regions of the flow, and it may give non-physical results in strongly non-homogeneous diffusion-dominated flows.
Fig. 6.

Normalized particle concentration distributions from Lagrangian simulation with near-wall modification of kinetic energy.
Based on our experiences and a small-scale literature review, the performances of Lagrangian and Eulerian approaches are summarized in Table 1 . In the following simulations, we use the drift-flux model to evaluate the concentration distributions in the adjacent flats and only use the DRW model to visualize the movement of individual particles.
Table 1.
Comparison of Lagrangian and Eulerian approaches in modeling particle dispersion and deposition
| Method number | Primary phase |
Second phase |
Performance |
References | |||
|---|---|---|---|---|---|---|---|
| Turbulence model | Near wall treatment | Particle modeling | Boundary condition at walls | Dispersion | Deposition | ||
| 1 | k–ε models | Wall functions | DRW model | Particles trapped at walls | Acceptable | Greatly over-predicted | [20], [28] |
| 2 | k–ε models | Wall functions and kinetic energy modification | DRW model | Particles trapped at walls | a | Over-predicted | [20], [29], [30] |
| 3 | k–ε models | Wall functions | Drift-flux model | Particle concentration at wall=0 or flux=0 | Acceptable | b | [31], [32] |
| 4 | k–ε models | Wall functions | Drift-flux model | Empirical deposition models | Acceptable | Depending on deposition models | [27], [33] |
| 5 | Reynolds stress model | Wall functions | DRW model | Particles trapped at walls | Acceptable | Slightly over-predicted | [20] |
| 6 | Large eddy simulation | Wall functions | Lagrangian method | Particles trapped at walls | Good | Good | [28], [34], [35] |
No information.
Particle deposition is under-predicted if the concentration gradient is assumed to be zero, and over-predicted if the concentration is assumed to be zero.
4. Case set-up
A four-storey building is placed in a large computational domain (Fig. 7 ). Windows are opened on the windward side on the second and third floor. The room dimensions are height (Y)×length (X)×width (Z)=2.7 m×3.1 m×2.4 m and the window height (Y)×width (Z)=1.2 m×0.75 m. The bottom of the window is 0.8 m above the room floor. The domain boundary at x–y plane is defined as symmetry. It means the building and its surroundings are extended in the negative and positive z-direction. This treatment is based on the fact that in many high residential blocks in Hong Kong, the shape of the whole building is like a vertical slab.
Fig. 7.
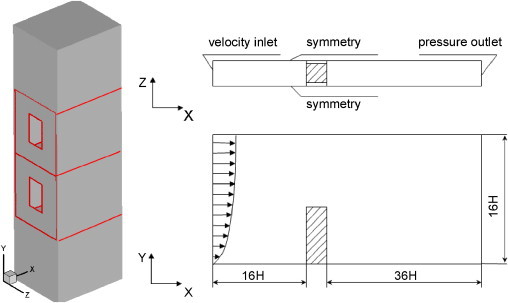
Description of the building model and the computational domain.
Heat is released only from the internal walls on the second and third floors. The atmospheric air temperature is 20 °C and the indoor wall surface temperature is 25 °C. In the simulation of a windless case, a uniform velocity profile (0.1 m/s) is set at the domain inlet. However, in a normal urban environment, even in a windless day in meteorology, the wind speeds are usually higher than 0.1 m/s. Therefore, a small meteorological wind speed, V met (wind speed usually taken at 10 m above the ground level), at 1.0 and 4.0 m/s is considered. The wind profile in an urban environment is calculated by
| (11) |
The turbulence on the inlet boundary is characterized by turbulence intensity and length scale, which are 8% and 1 m (for a wind speed of 1.0 m/s, the kinetic energy is 9.6×10−3 m2/s2, and dissipation rate 1.55×10−4 m2/s3). Given the low-speed conditions, 8% is acceptable since a general estimation of it in the wind field is 10% [36]. The length scale is taken to be around 20% of the height of the two flats. Particles of 1.0, 10.0, and 20.0 μm, without an initial speed, are generated at a rate of 8 mg/s in the middle of the second floor at the height of 1.6 m. The material density of the particles is 1000 kg/m3.
5. Results and discussions
The airflow fields indoors and outdoors, the air change rates (ACHs) of the lower and upper floor, and the ratio of the gaseous pollutant concentrations between the floors have been discussed in an earlier publication [5]. In the pure-buoyancy driven case, the ACHs through the windows are highest for both floors. A gentle approaching wind of 1.0 m/s normal to the window has very little influence on the ACH. However, 4.0 m/s wind could lower the ACH by 30–50% by suppressing the buoyancy force. In the windless situation, 7.5% of the air leaving from the window of the lower floor can re-enter into the upper floor. 1.0 m/s wind deflates the plume emitted from the lower window into the upper window, resulting in a higher re-entry ratio (10.9%). But 4.0 m/s wind confines the convection of air and thus reduces the ratio to 3.5%.
The particle concentrations are calculated based on the airflow conditions in Gao et al. [5]. Fig. 8 compares the particle concentrations and shows the concentration ratios of the upper floor to the lower floor. It is observed that the concentrations and their ratio for 1.0 μm particles are close to the values of CO2. The results of 10.0 and 20.0 μm particles differ from the 1.0 μm particle remarkably. Different from gaseous pollutants, two factors constrain the cascade effect of coarse particles: the particle’ gravity which counteracts with the upward buoyancy force and the deposition at solid surfaces. The latter one is a self-cleaning mechanism of particles which contributes to the decreased suspended concentrations in the lower floor and the reduced outlet concentrations. For an approximate estimation of particle’ settling effect, the ratio of two time scales is indicative: the time required by the particle to settle down across the room height and the time needed to refresh the total volume of room air once [31]. For the current air change rate of 7.2–10.1 h−1, the ratio of the falling time of 2.7 m (room height) for particles larger than 15 μm to the air change time is comparable.
Fig. 8.

Mean mass fractions (kg/kg) of particles in the lower and upper floors and their ratios (in the legend, “Lag ratio” is the ratio of numbers of particles deposited onto the inner surfaces of the upper floor to the total 8000 particles produced in the middle of the lower floor).
As wind speed increases from 0.1 to 4.0 m/s, the windward airflow field simulated by the k–ε model becomes more diffusion-dominated. The ratio of particle concentration in the upper floor to that in the lower floor decreases. In case of 4.0 m/s, the ratio is 0.3% for 20.0 μm particles. It implies that in the design of ventilation and air distribution systems, the indoor air speed level is essential to determine the suspension of particles in the room air. Air at higher speeds could entrain larger particles, and even makes deposited particles re-suspended. Although, according to the deposition model by Lai and Nazaroff [25], high friction velocity in the boundary layer will also increase the deposition velocity, this effect is negligible for particles larger than 2.5 μm because deposition onto the upward facing surfaces caused by gravitational force constitutes most of the overall deposition.
The ratios predicted from the DRW model are much less than those predicted from the drift-flux model. In spite of the different definitions of the “ratio” in the two approaches, excluding the factor that some particles may enter into the upper floor and then move out of the same floor through the window, the particulate mass in the upper floor predicted by the DRW model is still lower than that by the drift-flux model. Fig. 8 shows that the discrepancy becomes large for fine particles, and small for coarse particles. For a close view of the results from the DRW model, Table 2 gives the numbers of deposited particles in both flats. Even for 1.0 μm particles, more than 70% of the particles have been predicted to be absorbed by the inner surfaces of the lower flat. This result is obviously irrational. Therefore in current settings, the application of the DRW model may falsely give us an overoptimistic result with regard to the upward transport of viruses by natural ventilation airflows. In the best case when wind velocity is 4.0 m/s, three out of 8000 particles of 20.0 μm can get into the upper floor. In terms of infection risk, this may still be indicative, given that one infected person may sneeze several times and one sneeze produces more than one million particles [37].
Table 2.
Particles deposition onto the inner surfaces of the lower and upper floors in the simulations using DRW model (totally 8000 particles are released)
| Cases | dp=1.0 μm | dp=10.0 μm | dp=20.0 μm | |
|---|---|---|---|---|
| 0.1 m/s | Lower floor | 5828 | 6223 | 7252 |
| Upper floor | 226 | 187 | 76 | |
| 1.0 m/s | Lower floor | 5437 | 5876 | 7247 |
| Upper floor | 110 | 95 | 77 | |
| 4.0 m/s | Lower floor | 7232 | 7426 | 7819 |
| Upper floor | 22 | 14 | 3 |
In principle, the Lagrangian method has an advantage to track the trajectory of each particle. Fig. 9 shows the locations of 500 representative particles at various times after their generations. In less than 3 min, particles could enter the space of the upper floor. This may well explain the epidemiologic findings that the SARS virus was found within the deposits on the window-sill above the room whose host was infected during the SARS outbreak in Hong Kong.
Fig. 9.
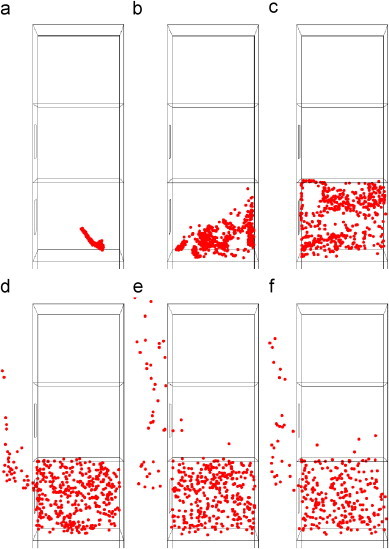
Spatial distributions of 1.0 μm particles from Lagrangian simulations in which 500 particles are generated at t=0 s in the center of the lower floor: (a) t=30 s, (b) t=70 s, (c) t=100 s, (d) t=130 s, (e) t=160 s, and (f) t=200 s.
In this study, the particle dispersion characteristics between two adjacent flats is studied. According to Duguid [37], in a cough more than 4900 particles are generated, and in a sneeze more than one million. Particles smaller than 24 μm make up about 90% of the total aerosol numbers, while particles greater than 24 μm contain more than 90% of the total aerosol mass. It remains unclear how many pathogens of some airborne diseases such as SARS are carried in each of the particle size bin. In any event, fine pathogen-containing particles can pose a higher infection risk via airborne inhalation of airborne residues and coarse pathogen-containing particles increase the risk via direct contact after rapid deposition.
Finally, the effect of particle source location in the lower floor and initial particle velocities are not considered here. Occupants may move frequently in their rooms. If the infected one coughs or sneezes at the window, a more serious situation than in this simulation may be envisaged. Sneezed or coughed particles usually have very high initial momentums. This makes the initial direction assumption an important factor in analyzing the movements of particles. Careful analysis of these considerations will be of the interest in the future studies.
6. Conclusions
In this paper, the cascade effect of particles with diameters of 1.0–20.0 μm is numerically investigated using both Eulerian and Lagrangian approaches. The following conclusions could be drawn:
-
•
In the Lagrangian frame, tracking particles based on the time-averaged airflow field simulated by k–ε models and wall functions over-predicts the deposition rate. This over-prediction is more substantial for fine particles. Modification of the near-wall kinetic energy may alleviate this problem. However, sometimes the modification could lead to unreasonable spatial distributions of particles.
-
•
Both simulation approaches revealed that the cascade effect exists for particulate pollutants. The particle concentration in the upper floor is two to three orders of magnitude lower than that in the lower floor, depending on the particle sizes. 1.0 μm particles disperse like gases. Strong deposition at solid surfaces and gravitational settling of particles larger than 20.0 μm greatly limit the upward transport of them.
-
•
Current simulation deals with single-sided natural ventilation where buoyancy is the major driving force. The effect of wind is more complicated. A high wind velocity could suppress the buoyancy force, and limit the dispersion of particles between flats.
In this study, the airflow field is obtained by steady-state simulation using the k–ε model. But it should be noted that the buoyancy-driven naturally ventilated flows are inherently unsteady. The effect of the instantaneously fluctuating velocities on the air exchange between indoor and outdoor spaces and on the movements of particles is unable to be captured by the Reynolds-averaged Navier–Stokes modeling. Here LES can potentially provide more accurate predictions, which will be explored in our future studies.
Acknowledgments
The project was funded by the Central Earmarked Research Grant from Research Grant Committee of Hong Kong SAR government under the project no. PolyU 5125/04E and the Research Fund for Infectious Disease Control (RFIDC) under project no. 03040642.
References
- 1.Yu I.T.S., Li Y.G., Wong T.W., Tam W., Chan A., Lee J.H.W. Evidence of airborne transmission of the severe respiratory syndrome virus. New England Journal of Medicine. 2004;350(17):1731–1739. doi: 10.1056/NEJMoa032867. [DOI] [PubMed] [Google Scholar]
- 2.Li Y., Huang X., Yu I.T.S., Wong T.W., Qian H. Role of air distribution in SARS transmission during the largest nosocomical outbreak in Hong Kong. Indoor Air. 2005;15(2):83–95. doi: 10.1111/j.1600-0668.2004.00317.x. [DOI] [PubMed] [Google Scholar]
- 3.Li Y., Duan S., Yu I.T.S., Wong T.W. Multi-zone modeling of probable SARS virus transmission by airflow between flats in Block E, Amoy Gardens. Indoor Air. 2005;15(2):96–111. doi: 10.1111/j.1600-0668.2004.00318.x. [DOI] [PubMed] [Google Scholar]
- 4.Niu J.L., Tung C.W. On-site quantification of re-entry ratio of ventilation exhausts in multi-family residential buildings and implications. Indoor Air. 2008;18(1):12–26. doi: 10.1111/j.1600-0668.2007.00500.x. [DOI] [PubMed] [Google Scholar]
- 5.Gao NP, Niu JL, Perino M, Heiselberg P. The airborne transmission of infection between flats in high-rise residential buildings-tracer gas simulation. Building and Environment 2007. doi:10.1016/j.buildenv.2007.10.023. [DOI] [PMC free article] [PubMed]
- 6.Brankston G., Gitterman L., Hirji Z., Lemieux C., Gardam M. Transmission of influenza A in human beings. Lancet Infectious Diseases. 2007;7(4):257–265. doi: 10.1016/S1473-3099(07)70029-4. [DOI] [PubMed] [Google Scholar]
- 7.Tellier R. Review of aerosol transmission of influenza A virus. Emerging Infectious Diseases. 2006;12(11):1657–1662. doi: 10.3201/eid1211.060426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fluent. Fluent 6.2 user's guide. Lebanon NH: Fluent Inc.; 2005.
- 9.Yakhot V., Orszag S. Renormalization group analysis of turbulence: I. Basic theory. Journal of Scientific Computing. 1986;1(1):1–51. doi: 10.1103/PhysRevLett.57.1722. [DOI] [PubMed] [Google Scholar]
- 10.Elghobashi E. On predicting particle-laden turbulent flows. Applied Scientific Research. 1994;52(4):309–329. [Google Scholar]
- 11.Hinds W.C. Wiley, Inc; 1999. Aerosol technology: properties, behavior, and measurement of airborne particles. [Google Scholar]
- 12.Abadie M., Limam K., Allard F. Indoor particle pollution: effect of wall textures on particle deposition. Building and Environment. 2001;36(7):821–827. [Google Scholar]
- 13.Morawska L. Droplet fate in indoor environments, or can we prevent the spread of infection? Indoor Air. 2006;16(5):335–347. doi: 10.1111/j.1600-0668.2006.00432.x. [DOI] [PubMed] [Google Scholar]
- 14.Nicas M., Nazaroff W.W., Hubbard A. Toward understanding the risk of secondary airborne infection: emission of respirable pathogens. Journal of Occupational and Environmental Hygiene. 2005;2(3):143–154. doi: 10.1080/15459620590918466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Loth E. Numerical approaches for motion of dispersed particles, droplets and bubbles. Progress in Energy and Combustion Science. 2000;26(3):161–223. [Google Scholar]
- 16.Zhang Z., Chen Q. Comparison of the Eulerian and Lagrangian methods for predicting particle transport in enclosed spaces. Atmospheric Environment. 2007;41(25):5236–5248. [Google Scholar]
- 17.Zhao B., Yang C., Yang X., Liu S. Particle dispersion and deposition in ventilated rooms: testing and evaluation of different Eulerian and Lagrangian models. Building and Environment. 2008;43(4):388–397. [Google Scholar]
- 18.Chao C.Y.H., Wan M.P. A study of the dispersion of expiratory aerosols in unidirectional downward and ceiling-return type airflows using a multiphase approach. Indoor Air. 2006;16(4):296–312. doi: 10.1111/j.1600-0668.2006.00426.x. [DOI] [PubMed] [Google Scholar]
- 19.Gao Z., Mashayek F. Stochastic modeling of evaporating droplets poly-dispersed in turbulent flows. International Journal of Heat and Mass Transfer. 2004;47(19–20):4339–4348. [Google Scholar]
- 20.Tian L., Ahmadi G. Particle deposition in turbulent duct flows-comparison of different model predictions. Journal of Aerosol Science. 2007;38(4):377–397. [Google Scholar]
- 21.Zhang Z., Chen Q. Experimental measurement and numerical simulation of particle transport and deposition in the ventilated rooms. Atmospheric Environment. 2006;40(18):3396–3408. [Google Scholar]
- 22.Wang Q., Squires K.D. Large eddy simulation of particle deposition in a vertical turbulent channel flow. International Journal of Multiphase Flow. 1996;22(4):667–683. [Google Scholar]
- 23.Wang Y., James P.W. On the effect of anisotropy on the turbulent dispersion and deposition of small particles. International Journal of Multiphase Flow. 1999;25(3):551–558. [Google Scholar]
- 24.Hinze J.O. McGraw-Hill; New York: 1975. Turbulence. [Google Scholar]
- 25.Lai A.C.K., Nazaroff W.W. Modeling indoor particle deposition from turbulent flow onto smooth surfaces. Journal of Aerosol Science. 2000;31(4):463–476. [Google Scholar]
- 26.Lu W.Z., Howarth A.T., Adam N., Riffat S.B. Modelling and measurement of airflow and aerosol particle distribution in a ventilated two-zone chamber. Building and Environment. 1996;31(5):417–423. [Google Scholar]
- 27.Chen F.Z., Yu S.C.M., Lai A.C.K. Modeling particle distribution and deposition in indoor environments with a new drift-flux model. Atmospheric Environment. 2006;40(2):357–367. [Google Scholar]
- 28.Liu Y., Matida E.A., Gu J., Johnson M.R. Numerical simulation of aerosol deposition in a 3-D human nasal cavity using RANS, RANS/EIM, and LES. Journal of Aerosol Science. 2007;38(7):683–700. [Google Scholar]
- 29.Matida E.A., Finlay W.H., Lange C.F., Grgic B. Improved numerical simulation of aerosol deposition in an idealized mouth-throat. Journal of Aerosol Science. 2004;35(7):1–19. [Google Scholar]
- 30.Lai A.C.K., Chen F. Modeling of particle deposition and distribution in a chamber with a two-equation Reynolds-averaged Navier–Stokes model. Journal of Aerosol Science. 2006;37(12):1770–1780. [Google Scholar]
- 31.Murakami S., Kato S., Nagano S., Tanaka Y. Diffusion characteristics of airborne particles with gravitational settling in a convection-dominant indoor flow field. ASHRAE Transactions. 1992;98(1):82–97. [Google Scholar]
- 32.Zhao B., Guan P. Modeling particle dispersion in personalized ventilated room. Building and Environment. 2007;42(3):1099–1109. [Google Scholar]
- 33.Gao N.P., Niu J.L. Modeling particle dispersion and deposition in indoor environments. Atmospheric Environment. 2007;41(18):3862–3876. doi: 10.1016/j.atmosenv.2007.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Uijttewaal W.S.J., Oliemans R.V.A. Particle dispersion and deposition in direct numerical and large eddy simulations of vertical flows. Physics of Fluids. 1996;8(10):2590–2604. [Google Scholar]
- 35.Béghein C., Jiang Y., Chen Q. Using large eddy simulation to study particle motions in a room. Indoor Air. 2005;15(4):281–290. doi: 10.1111/j.1600-0668.2005.00373.x. [DOI] [PubMed] [Google Scholar]
- 36.Li X.X., Liu C.H., Leung D.Y.C., Lam K.M. Recent progress in CFD modelling of wind field and pollutant transport in street canyons. Atmospheric Environment. 2006;40(29):5640–5658. [Google Scholar]
- 37.Duguid J.P. The size and duration of air-carriage of respiratory droplets and droplet-nuclei. Journal of Hygiene. 1946;44(6):471–479. doi: 10.1017/s0022172400019288. [DOI] [PMC free article] [PubMed] [Google Scholar]


