Abstract
The outbreak of atypical pneumonia, referred to as severe acute respiratory syndrome (SARS), has spread to many countries in the world. SARS may infect human bodies by the tiny droplets or particles carrying various virus and bacteria, which are generated by the respiratory system of infected patients. This paper presents the numerical analysis of the influence of generating ways of the droplets or particles on the transport and distribution of the droplets or particles indoors. The drift flux model, which considers the settling of particles or droplets under the effect of gravitational sedimentation, is adopted to simulate the droplets transport and distribution indoors during respiration and sneezing or coughing process, while the simplified model for solving the continuous fluid flow is combined. Two different cases considering the normal respiration and coughing or sneezing are studied, respectively, and two different outlet velocities from the mouth for the sneezing or coughing process are considered. The results show that droplets or particles generated by normal breathing process transport a relatively short distance, while droplets or particles generated during coughing or sneezing may travel much longer distances, which may pose adverse effect on human bodies for defending the SARS or other infectious diseases.
1. Introduction
Severe acute respiratory syndrome (SARS) is a recently described illness of human with a high case-fatality rate that has spread widely since November 2002. By late April 2003, over 4300 SARS cases and 250 SARS-related deaths from over 25 countries around the world were reported by the World Health Organization (WHO). Most of these cases occurred after exposure to SARS patients in household or healthcare settings [1].
As a kind of epidemic disease, SARS may infect human bodies by the tiny droplets or particles carrying various virus and bacteria, which are generated by the respiratory system of infected individuals. Some other infectious diseases such as flue, measles and mumps are also transmitted from person to person by inhaled airborne particles [2]. People staying indoors may be infected easily by the virus carried through the droplets or particles since there are limited air exchange rates indoors.
Normal respiration, sneezing or coughing generates the tiny droplets composed of water and air or fine particles. These generating ways have different generating rates and duration, resulting in different effects on indoor environment and human bodies. The main purpose of this paper is to study the transport of droplets or particles generated by the respiratory system indoors during different generating processes. Because it is difficult to examine the transport and diffusion of droplets or particles from respiratory system by experiments, a three-dimensional and time-dependent numerical method is adopted in this study. For simplification, “particles” or “droplets” is termed uniformly as “particle” in this paper, which is a general rule in aerosol science [3].
2. Mathematical model
To calculate the three-dimensional and non-isothermal airflow inside ventilated rooms, a well validated simplified methodology combined with N-point air supply opening model [4], a zero equation turbulence model [5] is applied. For indoor environment, the settling under the effect of gravitational sedimentation may play an important role on the particles diffusion. To take the gravitational sedimentation into account, the drift flux model, which has been applied and validated successfully for indoor particles simulation [6], [7], is adopted.
2.1. Governing equations
The governing equations for airflow and particles diffusion in vector form are as follows:
| (1) |
| (2) |
| (3) |
| (4) |
where , V and P are the air density (kg/m3), velocity vector (m/s) and pressure (Pa), respectively. V s is the settling velocity of particles (m/s). C is the mass concentration of particle. Here, relative concentration is used with an assumed unit concentration (1.0) from the mouth. The effective viscosity is the sum of molecular and turbulent viscosity (kg/m s). Turbulence is modeled by the zero equation turbulence model developed by Chen and Xu [5]. is the scalar quantity of air. The non-dimensional numbers and represent the turbulent diffusivity of and C, respectively. Here the values are set as 1.0. f is the body force due to air density (temperature) difference, which is modeled by using the Boussinesq approximation (Pa). S C is the droplets generated rate indoors (μg/s).
The main assumptions used for the simulation of particle transport include:
-
(1)
The airflow is isothermal.
-
(2)
The effect of particles on turbulence is not considered, as it is believed that the low particle loadings and comparatively small particle settling velocities have a very small effect compared to the high inflow turbulence levels [8].
-
(3)
The particle size distribution will not be altered by coagulation due to low particle loadings.
-
(4)
The evaporation of particles is neglected for simplification.
Strictly speaking, assumption (4) above only applies to solid particles. Many droplets in the 0.5–1.0 μm range can evaporate quickly in rooms with normal relative humidity levels. Evaporation could lead to loss of particle momentum and increase of particle buoyancy. In this research, evaporation is neglected because only short-term behavior (in the order of seconds or less) of particles is considered. For longer time domain, the droplet evaporation could be a major factor that deserves more research.
The settling velocity of a particle derived by equaling the fluid drag force on the particle with the gravitational force can be expressed as
| (5) |
where C D is the drag coefficient, d p is the diameter of the particle (μm), and are the density of the particle and the ambient air (kg/m3), respectively, and g is the gravitational acceleration (m/s2). The settling velocity always has the same direction as gravitation, namely, perpendicularly downward.
The drag coefficient is either derived by Stokes equation (Re<1) or a revised equation (1<Re<1000) [3]:
| (6) |
Re is the Reynolds number according to the relative velocity of particle and air.
The settling velocity is a velocity relative to air under steady condition. When Re<1, the settling velocity equals the product of the acceleration due to gravity and the relaxation time of the particle [3]. And when Re>1, the settling velocity is derived by iterating the drag balance equation based on Eq. (6).
2.2. Boundary conditions
The supply inlet is described by the N-point supply opening model to consider the complex geometry of actual diffusers [4]. And all variables are defined at the supply inlet. Outlet boundary conditions are set as the Neumann boundary condition, that is, mass flow boundaries are specified to ensure that the mass flow rate out of the domain is the same as the mass flow rate into the flow domain. For the zero equation turbulence model, wall functions are not needed for the region near the walls, where the algebraic equations of turbulent viscosity are applied directly [5].
The wall boundary condition of particle is simplified as zero normal gradients. That is, , where n is the direction normal to the wall. As the number of deposited particles is usually much smaller than that of exhausted particles by ventilation [9], the deposition process cannot exert a strong influence on the flow field in indoor environment.
2.3. Numerical methods
The equations above are discretized into algebraic equations by finite volume method and the coupling between velocity and pressure is solved by the SIMPLE algorithm [10]. In the course of discretization, the power law scheme and the second-order central difference are, respectively, implemented for the convection and diffusion terms. The resulting set of discretized equations for each variable are solved by a line-by-line procedure, combining the tri-diagonal matrix algorithm (TDMA) and the linear under-relaxation iteration. Non-uniform staggered grid system is employed with denser grids clustering near the bounded walls so as to resolve the boundary layer properly.
A well-validated CFD program developed by the authors, STACH-3 [4], which utilized the simplified methodology mentioned above, is used as the simulation tool.
3. Cases studied
To study the different transport and distribution characteristics of particles from human respiratory system indoors, a full-scale room is selected. The geometry of the room is X×Y×Z=5 m×3 m×3 m. The room is ventilated by one grille on a side wall and the grille size is 0.5 m(Z)×0.125 m(Y) and an exhaust of the same size is located at the bottom of the same wall. Both the inlet and outlet are symmetrical about the middle line in the XY plane (). One person is assumed to stay at the opposite side of the inlet and outlet. Fig. 1 shows the schematic of the ventilated room and the person.
Fig. 1.
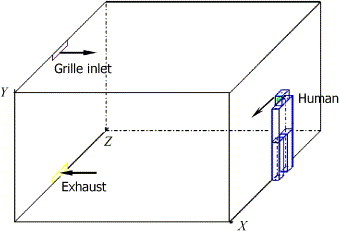
Schematic of the ventilated room and the person.
Two different cases considering the normal respiration and coughing/sneezing process are studied, respectively. The outlet velocity of normal respiration process is periodic [11] and that of coughing or sneezing process is pulse [2]. The assumed velocity as boundary conditions in simulation is depicted in Fig. 2 . For respiration process, we assume breathing from the nose and the direction of inhaling/exhaling is 30° downward (Fig. 2(a)). Two different outlet velocities from mouth for sneezing or coughing process are considered (V em=20 and 100 m/s, Fig. 2(b)). It should be noted that many people sneeze more than once in a cycle of sneezing. However, we only consider sneezing or coughing once for simplification. In fact, the results in the following will show that sneezing or coughing only once may cause long transport distance and high concentration of particles, which implies that sneezing or coughing more than once may cause higher concentration. The outlet particle concentration by respiration, sneezing or coughing is assumed as 1.0, which may be used as a relative value. Table 1 presents the air supply parameters and other boundary conditions.
Fig. 2.
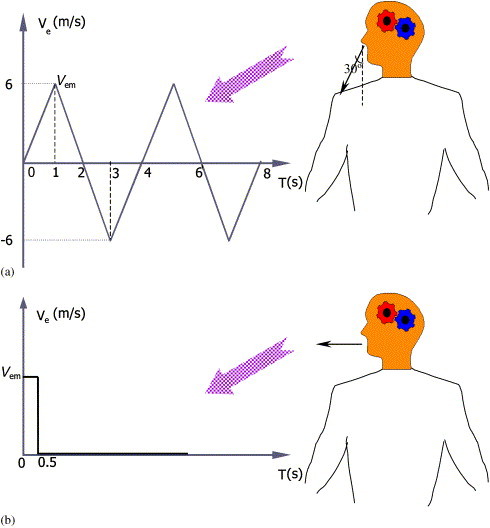
The outlet velocity of the generating ways of the particles from respiratory system. (a) Normal respiration process, (b) sneezing or coughing process ( or 100 m/s).
Table 1.
Supply parameters and other boundary conditions
| Cases | Ventilating air exchange rate (ACH) | Supply air velocity (m/s) | Supply particle concentration | Exhale velocity | Exhale flow volume (l/min) | Outlet particle concentration |
|---|---|---|---|---|---|---|
| Respiration with nose | 0.5 | 0.1 | 0.0 | Vem=6 m/s [11]Fig. 2(a) | 4.5 [11] | 1.0 |
| Coughing or sneezing (1) | 5.0 | 1.0 | 0.0 | Vem=20 m/s [2]Fig. 2(b) | 50.0 | 1.0 |
| Coughing or sneezing (2) | 5.0 | 1.0 | 0.0 | Vem=100 m/s [2]Fig. 2(b) | 250.0 | 1.0 |
As larger particles (d p>1 μm) generated from humans can only be transported within 1.0–1.5 m and these larger particles constitute less than 5% of all the particles or droplets of one human [12], only fine particles are considered in the present study. Two different sizes of particles, 1.0 and 0.5 μm, are considered. Because results for the two sizes have little difference, only the results of 1.0 μm are presented next. The particle density is assumed as 600 kg/m3, which is the approximate density of ash particles or droplets of mixture composed of water and air. In fact, because the particles are fine ones, the density of particles does not remarkably influence the transport and distribution of the particles.
4. Results and discussion
4.1. Respiration process
The airflow and particle transport are calculated in two respiratory periods (8 s) since the respiratory process begins in the ventilated room. Fig. 3 shows the streamline at the symmetrical plane (Z=1.5 m) during the first respiration period (see Fig. 2(a)). Because of the relatively smaller air flow volume when breathing, the inhaling and exhaling processes have little influence on the room air flow pattern. Fig. 4 gives the particle concentration at different times when the human is exhaling or inhaling. It is seen that the particle concentration reduces to below 0.001% of the outlet particle concentration within 1.0 m away from the human. The air exchange rate per hour (ACH) for this case is 0.5. Thus, we can imagine that a larger air exchange rate may cause better indoor environment with lower particle concentration and shorter spreading distance of particles. This implies that the transport distance of particles or droplets generated by normal respiration of patients is limited.
Fig. 3.
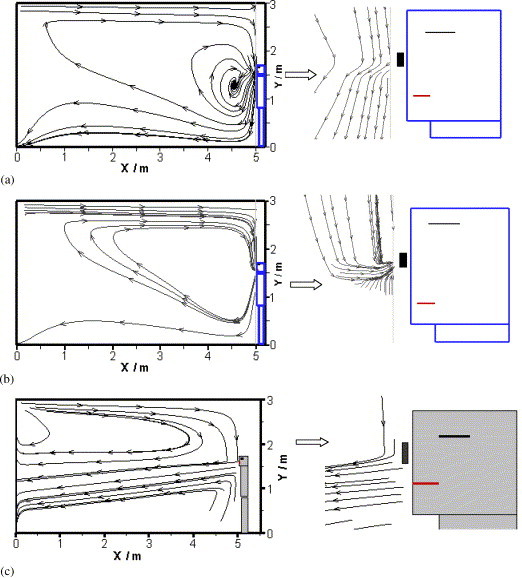
The streamline at the symmetrical plane (Z=1.5 m) at different times. (a) Exhaling (normal respiration, t=1.0 s), (b) inhaling (normal respiration, t=3.0 s), (c) sneezing or coughing (Vm=100.0 m/s) (t=0.5 s).
Fig. 4.
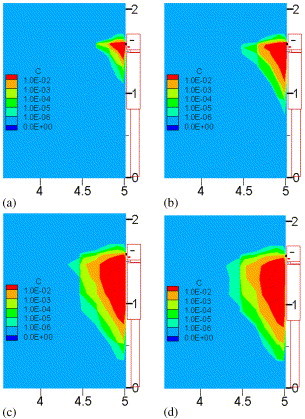
Particle concentration at different times during normal exhaling or inhaling: (a) t=0.5 s, (b) t=1 s, (c) t=2.5 s, (d) t=3.0 s.
4.2. Sneezing or coughing process
Unlike normal respiration, sneezing or coughing may produce a large amount of particles of droplets, with a diameter of about 10–100 μm. However, they will split into smaller particles of 1–4 μm in a very short time [2]. Therefore, 1.0 μm is again adopted as the particle diameter in the simulation. Fig. 3(c) shows the streamline at the symmetrical plane (Z=1.5 m) for an initial velocity V em=100.0 m/s (see Fig. 2(b)). It is seen that the large outlet velocity will maintain a much longer distance of particle transport due to the large momentum. Fig. 5 compares the simulated flow pattern with the measured one by [2]. The results seem reasonable. Fig. 6 further gives the particle concentration distribution at different times since the sneezing or coughing begins, which indicates that sneezing or coughing may cause long transport distance of particles, although the ventilation air exchange rate is rather large (5 ACH). Comparison of the two different outlet velocities of the sneezing or coughing case indicates that larger sneezing or coughing velocity will cause further transport and higher concentration of the exhaled particles or droplets. Fig. 7 shows the three-dimensional view of the particle concentration distribution at several different times. The contour zone stands for the particle concentration where the value is larger than 1% of the outlet concentration. If we define “affecting range” as the distance from the patient to where the concentration reduces to the “safe threshold”, and define “safe threshold” as the percentage of outlet concentration that will not cause adverse effect on people, Fig. 7 depicts the “affecting range” of the sneezing or coughing if we consider 1% as the “safe threshold” (in fact, the exact threshold needs careful study). The figure also proves that particles generated during coughing or sneezing may travel a long distance, which may pose adverse effect on human bodies for defending the SARS or other infectious diseases. From the results, good personal habits, that is, covering the nose and mouth when sneezing or coughing, is very important for preventing the transmission of the diseases from human to human.
Fig. 5.

Comparison of the simulated flow pattern with the measured one when sneezing or coughing. (a) Simulated, (b) measured [2].
Fig. 6.
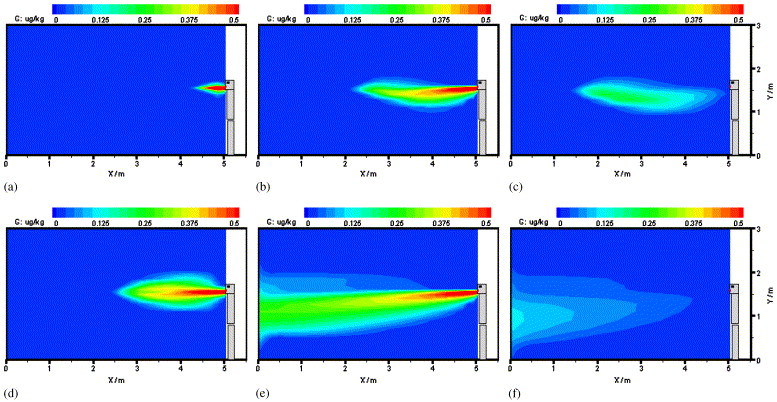
Particle concentration at different times when sneezing or coughing (a–c: Vem=20 m/s, d–f: Vem =100 m/s): (a) t=0.05 s, (b) t=0.5 s, (c) t=0.8 s, (d) t=0.05 s, (e) t=0.5 s, (f) t=0.8 s.
Fig. 7.
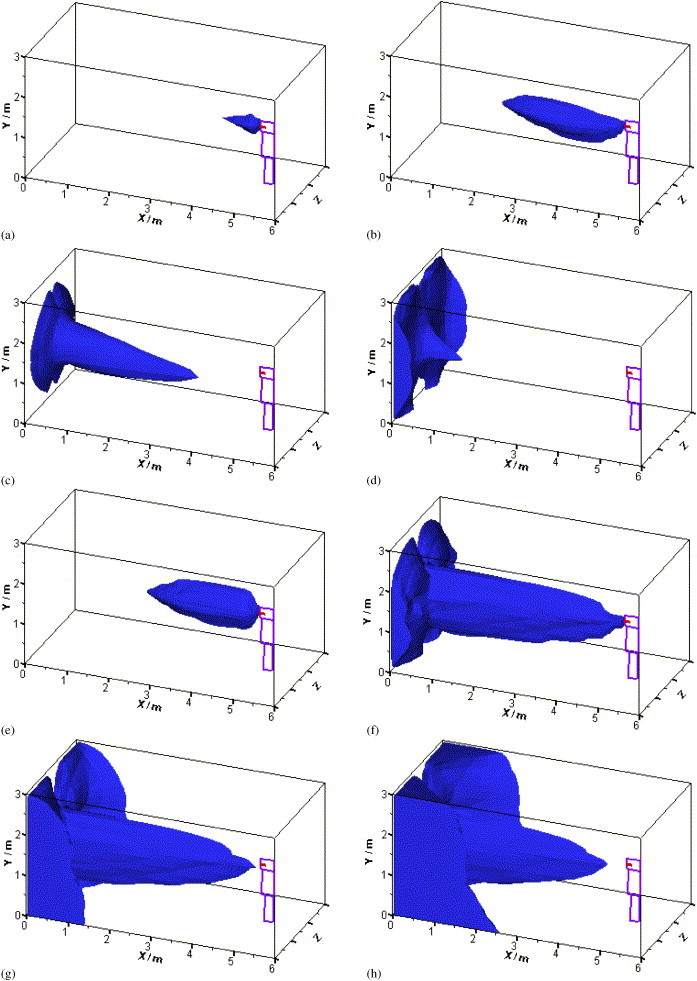
3-D view of the particle concentration at different times when sneezing or coughing (a–d: Vem=20 m/s, e–h: Vem=100 m/s): (a) t=0.05 s, (b) t=0.5 s, (c) t=5 s, (d) t=10 s, (e) t=0.05 s, (f) t=0.5 s, (g) t=0.6 s, (h) t=1 s.
It should be noted that the above results are based on oversimplified and ideal scenarios without considering many influencing factors such as the evaporation of the droplets, supply and return air system orientation, blockage of air and particle movement, etc. Thus, the results should be used with caution. This study, however, may be considered as a direction in understanding the complex phenomena of particle transport indoors and ultimately, preventing the transmission of infectious diseases such as SARS.
5. Conclusions
Numerical studies on the transport and distribution of particles or droplets generated by normal respiration and sneezing or coughing indoors result in the following conclusions:
Normal respiration process produces fewer particles or droplets, which have small influence on indoor environment. And the particles or droplets may only transport a short distance by normal respiration.
Sneezing or coughing may produce more particles or droplets, which will transport a long distance. A normal sneezing or coughing with outlet velocity of 20 m/s will cause the particles or droplets to transport a distance longer than 3 m, and larger outlet velocity will have even longer distance in shorter time. For the purpose of defending humans against the diseases, good personal habits are very important to prevent the virus spreading via sneezing or coughing.
Acknowledgements
This study is financially supported by the National Nature Science Foundation of China under Grant 50346007.
References
- 1.Rota PA, Oberste MS, Monroe SS, Nix WA, Campagnoli R, Icenogle JP, Penaranda S, Bankamp B, Maher K, Chen M, Tong Su, Tamin A, Lowe L, Frace M, DeRisi J, Chen Q, Wang D, Derdman D, Peret TCT, Burns C, Ksiazek TG, Rollin PE, Sanchez A, Liffick S, Holloway B, Limor J, McCaustland K, Olsen-Rassmussen O, Fouchier R, Gunther S, Osterhaus ADME, Drosten C, Pallansch MA, Anderson LJ,Bellini WJ. Characterization of a novel coronavirus associated with severe acute respiratory syndrome. Science Express, 2003.10.1126/Science, 1085952, 2003. [DOI] [PubMed]
- 2.Deacon J. The Microbial World—Airborne microorganisms. http://helios.bto.ed.ac.uk/bto/microbes/microbes.htm. Institute of Cell and Molecular Biology, and Biology Teaching Organisation, University of Edinburgh, 2001.
- 3.Hinds W.C. Wiley; New York: 1982. Aerosol technology: properties, behavior, and measurement of airborne particles. [Google Scholar]
- 4.Zhao B., Li X., Yan Q. A simplified system for indoor airflow simulation. Building and Environment. 2003;38(4):543–552. [Google Scholar]
- 5.Chen Q., Xu W. A zero-equation turbulence model for indoor air flow simulation. Energy and Buildings. 1998;28(2):137–144. [Google Scholar]
- 6.Murakami S., Kato S., Nagano S., Tanaka Y. Diffusion characteristics of airborne particles with gravitational settling in a convection-dominant indoor flow field. ASHRAE Transactions. 1992;98(1):82–97. [Google Scholar]
- 7.Holmberg S., Li Y. Modelling of the indoor environment-particle dispersion an depositoin. Indoor air. 1998;8:113–122. [Google Scholar]
- 8.Elghobashi S. On predicting particle-laden turbulent flows. Applied Scientific Research. 1994;52:309–329. [Google Scholar]
- 9.Nazaroff W.W., Cass G.R. Mathematical modelling of indoor aerosol dynamics. Environmental Science and Technology. 1989;23(2):157–165. [Google Scholar]
- 10.Patankar S.V. Hemisphere; Washington, DC: 1980. Numerical heat transfer and fluid flow. [Google Scholar]
- 11.Brown B.H., Smallwood R.H., Barber D.C., Lawford P.V., Hose D.R. Institue of Physics publishing; Bristol and Philadelphia: 1999. Medical physics and biomedical engineering. [Google Scholar]
- 12.Badeau A, Afshari A, Goldsmith T, Frazer D. Preliminary prediction of flow and particulate concentration produced from normal human cough dispersion. Proceedings of the second joint EMBS/BMES conference. Houston, TX USA. October, 23–26, 2002, p. 246–247.


