Abstract
Decision-making problems in emergency response are usually risky and uncertain due to the limited decision data and possible evolvement of emergency scenarios. This paper focuses on a risk decision-making problem in emergency response with several distinct characteristics including dynamic evolvement process of emergency, multiple scenarios, and impact of response actions on the emergency scenarios. A method based on Fault Tree Analysis (FTA) is proposed to solve the problem. By analyzing the evolvement process of emergency, the Fault Tree (FT) is constructed to describe the logical relations among conditions and factors resulting in the evolvement of emergency. Given different feasible response actions, the probabilities of emergency scenarios are estimated by FTA. Furthermore, the overall ranking value of each action is calculated, and a ranking of feasible response actions is determined. Finally, a case study on H1N1 infectious diseases is given to illustrate the feasibility and validity of the proposed method.
Keywords: Emergency response, Fault tree analysis (FTA), Scenario probability estimation, Ranking
1. Introduction
Emergencies, i.e., natural disasters, industrial incidents, infectious diseases and terrorist attacks etc., often cause losses of life or injury, property damages, social and economic disruptions or environmental degradations. For example, the Severe Acute Respiratory Syndrome (SARS) broken out in east Asia early 2003 resulted in the death of hundreds of people, the global panic and the inestimable economic loss. When an emergency occurs, the relevant management personnel or decision-makers (DMs) need to decide what actions to take instantly so as to mitigate or minimize the negative effects. Usually, the decision-making problems in emergency response are complicated due to the limited decision data and possible evolvement of emergency scenarios [1], [2]. Therefore, how to select an effective response action in the earlier stage of emergency is an important research topic of emergency management.
Some studies have been conducted to deal with the decision-making problem in emergency response [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11]. For example, Hämäläinen et al. [1] proposed a multi-attribute risk analysis method to select a strategy for protecting the population in a simulated nuclear accident. Shim et al. [2] developed a decision support system (DSS) for controlling river basin flood. Körte [3] proposed a method named ‘contingent risk and decision analysis’ to solve the decision-making problems under variable environment. Levy [4] developed a DSS for flood risk management by integrating the multi-criteria decision-making (MCDM) method, the remote sensing, GIS, the hydrologic models, and the real-time flood information systems. Based on [4], Levy and Taji [5] proposed a group analytic network process (GANP) approach to provide a support to hazard planning and emergency management under incomplete information. Fu [6] proposed a fuzzy optimization method for selecting the most desirable action to control the flood of reservoir. Geldermann et al. [7] proposed a MCDM-based evaluation method for nuclear remediation management. Lim and Lee [8] proposed a spatial multi-criteria decision analysis approach for evaluating flood damage reduction actions. Yu and Lai [9] proposed a distance-based group decision-making (GDM) method to solve unconventional multi-person multi-criteria emergency decision-making problems. Peng et al. [10] proposed an incident information management framework based on data integration, data mining and multi-criteria decision making. Ergu et al. [11] proposed a simple consistency test process to make ANP more suitable to solve decision-making problems in emergency cases.
The existing studies have made significant contributions to decision analysis in emergency response. In existing studies, various decision-making methods are proposed according to the characteristics of different actual emergency events, such as nuclear accident [1], [7], flood disaster [2], [4], [6], [8] and so on. In some actual emergency situations, like infectious diseases and fire hazards etc., the decision-making problems have dynamic and risky characteristics. This needs to consider a special risk decision-making problem with several distinct characteristics including dynamic evolvement process of emergency, multiple scenarios, and impact of response actions on the emergency scenarios. However, the existing decision analysis methods seldom consider to solve the decision-making problems with the above characteristics. Therefore, it is necessary to further investigate the risk decision-making problem considering the characteristics of dynamic evolvement and multiple scenarios in emergency response.
The Fault Tree Analysis (FTA) is one of the most powerful tools for predicting reliability of a complex system by depicting the logical relations among components or sub-systems in the system. By FTA, the occurrence frequency or probability of the system hazardous events can be estimated [12], [13], [14], [15], [16], [17], and the root causes of system hazardous events can be found. In this paper, we incorporate FTA into the analysis of risk decision-making problem with the characteristics of dynamic evolvement and multiple scenarios in emergency response. An emergency with multiple scenarios is regarded as a ‘system’, the undesirable scenarios of the emergency are regarded as ‘system hazardous events’, and the conditions and factors resulting in the evolvement of emergency are denoted as middle events and basic events. Accordingly, a fault tree (FT) for the emergency is constructed to describe the logical relations among scenarios, conditions and factors. Based on the constructed FT, the probabilities of emergency scenarios can be estimated with respect to each feasible response action. Furthermore, based on obtained probabilities of emergency scenarios, classical risk decision-making method can be employed to calculate the overall ranking value of each action.
The rest of this paper is organized as follows. Section 2 formulates the risk decision-making problem in emergency response based on the analysis of the practical background of SARS diseases. In Section 3, the FT for an emergency is constructed to describe the logical relations among the conditions and factors resulting in the evolvement of emergency scenarios. In Section 4, the probabilities of emergency scenarios are calculated with respect to each feasible response action. Section 5 provides an approach to ranking feasible response actions by calculating overall ranking values of actions. Section 6 demonstrates a case study on the H1N1 infectious diseases. Finally, Section 7 summarizes and highlights the main features of this paper.
2. The risk decision-making problem in emergency response
In this section, we first analyze the practical background of SARS diseases, and then describe the risk decision-making problem in emergency response.
2.1. SARS diseases
SARS is a contagious respiratory disease caused by the SARS corona virus. The first case of SARS was found in Guangdong province in China on November 16, 2002. Since there was no precedent of SARS, an inefficient control action was implemented, which leaded to a rapidly spreading of SARS. In early 2003, more infected cases were successively found in different provinces in China, including, 6 cases in Guangxi province on January 4, 3 cases in Sichuan province on February 10, and 1 case in Hunan province on February 14, etc. SARS continuously spread to other countries and regions by traveling passengers. On February 15, 2003, a doctor from Guangdong province, who had been infected by SARS, arrived at Hongkong, and infected 15 hotel visitors. The infected visitors then traveled to Canada, Singapore, Taiwan and Vietnam, and caused further widely spreading of SARS. According to the report of the World Health Organization (WHO), the SARS disease in 2003 resulted in 8096 known infected cases, 774 confirmed human deaths, the global panic and the inestimable economical loss.
Comparing with the explosive spreading of SARS in 2003, the recurrence of SARS in 2004 was rarely known by public. Two infected cases were respectively found in Beijing and Hefei in April 2004 [18]. The first infected case was a researcher working in a lab of SARS corona virus. Based on the experience obtained in 2003, an effective action was taken to control the spreading of SARS in no time. It restricted the disease to only 9 infected cases finally.
It can be seen from the above practical background of SARS diseases in 2003 and 2004 that emergency response is a risk decision-making problem. Take the spreading of SARS as an example, the emergency response problem usually has the following distinct characteristics: (1) the spreading of SARS disease is dynamic; (2) the spreading of SARS has multiple possible scenarios, and the probability of each scenario is variational; (3) each action of emergency response would change the probabilities of scenarios. Therefore, in order to find the most desirable control action, it is necessary to estimate the probabilities of scenarios by analyzing the conditions and factors that could impact the evolvement of emergency.
2.2. Problem description
Based on the above analysis of practical background of an emergency situation, SARS, we depict a new risk decision-making problem in emergency response in this paper. The following notations are used to describe the problem.
-
•
: the set of feasible response actions (alternatives), where denotes the th response action, .
-
•
: the vector of costs, where denotes the cost of action , . Usually, the cost of action consists of several parts, such as the cost of human resource, the cost of relief goods and so on. For the convenience of analysis, let denote the total cost of composed of all parts, , and it is in monetary form.
-
•
: the scenario vector, where denotes the current scenario of the emergency; denotes the th potential scenario in the evolvement process of the emergency, . In this paper, we further define the damage result under scenario is more serious than that under , if , . In addition, we assume that scenarios are sequential, and in other words, could occur only if has already occurred, if. Usually, vector can be determined by consulting experts, collecting related statistical data or conducting study on cases.
-
•
: the set of criteria for describing the damage result of emergency, where denotes the th criterion for describing the damage result, .
-
•
: the damage result vector under scenario , where is the damage result concerning criterion and under scenario , , .
-
•
: the weight of cost, .
-
•
: the vector of criterion weights, where is the weight of criterion , , . Here, we consider . Usually, and can be obtained either directly from the assignment of the DM or indirectly using existing procedures such as AHP [19], [20].
-
•
: the probability matrix, where denotes the probability of scenario if response action is taken, , . Usually, is unknown in the earlier stage of emergency, which is needed to be estimated by an appropriate approach.
The problem mainly addressed in this paper is how to estimate and to select the most desirable response action(s) among set based on , , , and the obtained .
As we mentioned before, the problem is a risk decision-making problem. We describe it as a decision tree in Fig. 1. It can be seen from Fig. 1 that there are two possible results of scenario if response action is implemented, i.e., either the emergency will evolve into scenario with probability or end () with probability . Furthermore, if the emergency evolves into scenario , there are also two possible results, i.e., either the emergency will evolve into scenario with probability or end () with probability . Similarly, if the emergency evolves into scenario , there are also two possible results, i.e., either the emergency will evolve into scenario with probability or end () with probability . If the emergency ends after the occurrence of scenario , then damage result vector is .
Remark 1
It is necessary to point out that is the probability of scenario given that response action is implemented, rather than the conditional probabilities of scenario given that scenario has occurred, , .
Fig. 1.
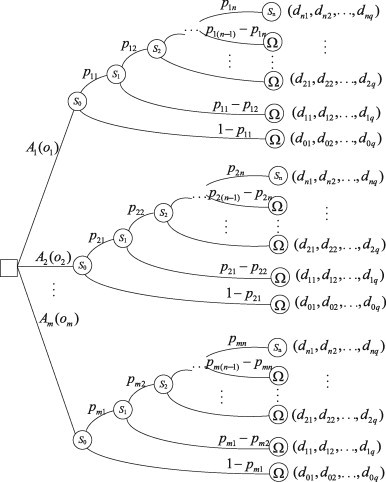
The risk decision-making problem in emergency response.
To solve the risk decision-making problem described above, a FTA-based method is proposed. First, a FT is constructed to depict the logical relations among conditions and factors resulting in the evolvement of emergency. Then, based on the constructed FT, the probabilities of different scenarios are calculated given different response actions. Furthermore, based on the obtained probabilities, the overall ranking value of each action is calculated to determine a ranking of the feasible response actions. In the next section, we will construct the FT for an emergency.
3. Constructing the FT for an emergency
FTA is a powerful diagnosis technique and widely used for demonstrating the root causes of undesirable event in system failure, as well as depicting the logical relations among components, manufacturing processes, and sub-systems [12], [13], [14], [15], [16], [17]. It was originally developed by Bell Laboratories for the US Air Force in 1962 and was later adopted and extensively applied by the Boeing Company. Now, FTA is wildly used in many fields, such as chemical industries [16], liquefied natural gas terminal emergency shutdown system [17] and so on. In this paper, the principle of FTA is employed to estimate the probabilities of emergency scenarios. Thus, constructing a FT beforehand is necessary in order to depict the logical relations among the conditions and factors driving the evolvement of emergency scenarios. In the following, we first introduce the basic components of FT, and then give the steps for constructing the FT for an emergency.
3.1. Basic components of FT
Usually, a FT is composed of a series of events and logic gates. The main events include:
-
•
Top event: is the most undesirable system failure event and the object of the analysis, denoted as □.
-
•
Middle event: is the sub-system or component failure event and the cause of the top event, denoted as □.
-
•
Basic event: is the primary failure event and the cause of the top event or middle events, denoted as ○.
-
•
The main logic gates include:
-
•
Logic gate ‘OR’: indicates that output event occurs if at least one of the input events occurs, denoted as
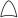 .
. -
•
Logic gate ‘AND’: indicates that output event occurs only if all of the input events occur, denoted as
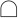 .
.
There may be many other types of events and logic gates involved in complex system reliability analysis, but, for the sake of concisions, we only list the most commonly used ones here. For other types of events and logic gates, please refer to [14], [15].
3.2. Steps for constructing the FT for an emergency
The construction of the FT for an emergency is a deductive procedure. The core idea is to identify the conditions and factors that emergency can evolve into scenario from scenario , . The FT should be developed level by level, and each level should be completed before any consideration is given to the next level. To successfully construct the FT for an emergency, the following steps are suggested:
Step 1. The most undesirable scenario is defined as top event.
Step 2. Define boundary conditions for the analysis. The boundary conditions include: (1) physical boundaries: define what factors, status and emergency scenarios will be included in the FT as events; (2) boundary conditions concerning environmental stresses: define what external stresses (e.g., virus variation) should be included in the FT as events; (3) level of resolution: determine how far down we should identify the potential reasons for an event in detail.
Step 3. Classify all events into middle events and basic events. If an event represents a primary factor that may result in the evolvement of emergency, it is classified as a basic event; if an event represents a secondary factor that may result in the evolvement of emergency, it is classified as a middle event that requires a further investigation to identify the prime causes.
Step 4. Complete the gates. If the upper level event will occur given that a single lower event occurs, then the events should be linked with ‘OR’ gate; if the upper level event will occur only if two or more lower events occur simultaneously, then the events should be linked with ‘AND’ gate.
Using the above steps, the FT for an emergency can be constructed. In addition, computer-aided FT construction methods have also been proposed in literatures [21], [22], [23], [24], [25], which can also be used to construct the FT for an emergency.
4. Calculating the probabilities of scenarios
Based on the constructed FT, a logical expression of each scenario can be formulated. Then, by estimating the probabilities of basic events, the probabilities of scenarios can be calculated given different response actions. In the following, the procedure for calculating the probabilities is briefly described.
Suppose there are basic events in the FT for an emergency, denoted as , respectively. According to the constructed FT, a logical expression of scenario is first formulated as
| (1) |
In the logical expression, the basic events or middle events are linked by logic operation symbol ‘’ if they are linked by ‘OR’ gate (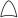 ) in the constructed FT; the basic events or middle events are linked by logic operation symbol ‘’ if they are linked by ‘AND’ gate (
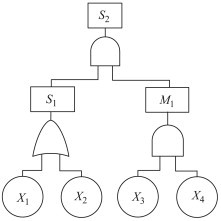
) in the constructed FT; the basic events or middle events are linked by logic operation symbol ‘’ if they are linked by ‘AND’ gate (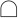 ) in the constructed FT.
) in the constructed FT.
Next, in order to estimate the probabilities of basic events, several experts should be invited to participate in the decision analysis. In fact, it is not easy for the experts to determine or define the probabilities of basic events directly since many factors need to be considered. In this situation, the indirect elicitation technique [26], [27], Delphi method [28] or Nominal Group Technique [29] can be used to determine the probabilities of basic events. In the indirect elicitation technique, a series of data on historical similar events are provided to the experts. Then, the experts are asked to compare the probabilities of basic events with those of historical similar events, which will be helpful to determine the experts' personal judgment on the probabilities of basic events. Further, based on the experts' personal judgment, Delphi method [28] and Nominal Group Technique [29] are employed to determine a consistency collective judgment on the probabilities of basic events. Therefore, a probability matrix of basic events can be obtained, which is represented by
In , denotes the probability of basic event if response action is implemented, , .
Furthermore, according to and , the probability of scenario given response action can be calculated by
| (2) |
where is the function corresponding to . In , the logic operation in is replaced by probability operation ; the logic operation in is replaced by . Therefore, according to , , , the probability matrix of scenarios is constructed, i.e.,
where denotes the probability of scenario if action is implemented, , .
To illustrate the above computation procedure more clearly, a simple numerical example is given below.
Example 1
Fig. 2 shows an illustrative example of the FT for an emergency.
Fig. 2.
An illustrative example of FT.
In Fig. 2, is the most undesirable scenario of emergency (top event); is an undesirable scenario in the lower level of , and is the middle events; , , and are four basic events. , and are linked by 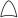 . It denotes that occurs if at least one of and occurs. , and are linked by
. It denotes that occurs if at least one of and occurs. , and are linked by 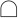 . It denotes that occurs only if all of and occur simultaneously. Similarly, occurs only if all of and occur simultaneously.
. It denotes that occurs only if all of and occur simultaneously. Similarly, occurs only if all of and occur simultaneously.
According to Fig. 2, the logical expressions of and can be respectively formulated, i.e.,
| (3) |
| (4) |
where and denote the logic operations of ‘OR’ and ‘AND’.
Suppose two feasible response actions (or alternatives) and are considered to be implemented in emergency response. The probability matrix of basic events determined by indirect elicitation technique and Delphi method is
Then, according to Eq. (3) and matrix , the probability of can be calculated given action or , i.e.,
| (5) |
| (6) |
Similarly, according to Eq. (4) and matrix , the probability of can be calculated given action or , i.e.,
| (7) |
| (8) |
Therefore, we can construct the probability matrix of scenarios, i.e.,
5. Determining the ranking of feasible response actions
Based on , the overall ranking values of different response actions can be calculated to determine a ranking of actions. In the following, we briefly described the computation procedure of overall ranking values.
First, to make different criteria have the same range of measurement, the costs and criterion values are normalized into the numbers from 0 to 1 respectively. Let be the vector of normalized costs, where is the normalized cost of response action , . Let be the vector of normalized criterion values, where is the normalized criterion value concerning with respect to scenario , , . The calculation formulas of and can be respectively expressed by
| (9) |
| (10) |
where and ; and . By Eqs. (9) and (10), the costs and criterion values are all unified into benefit type [30], [31], i.e., the greater is, the better action will be; similarly, the greater is, the better damage result concerning with respect to scenario will be.
It can be seen from Fig. 1 that there are possible damage results, i.e., the emergency ends after the occurrence of scenario , , , , or . The probabilities of the damage results are , , , and if response action is implemented. Let denote the expected criterion value of action concerning , , . According to and , can be represented by
| (11) |
Furthermore, let denote the overall ranking value of response action , which can be represented by
| (12) |
In Eq. (12), is the weight of cost, is the weight of criterion , .
It can be seen that the greater is, the better response action will be. Therefore, according to overall ranking values , we can determine a ranking of all feasible response actions.
In summary, the steps of the FTA-based method for risk decision-making in emergency response are given below.
Step 1. Construct the FT for an emergency using the steps proposed in Section 3.2.
Step 2. Determine logical expression according to Eq. (1), .
Step 3. Determine matrix using indirect elicitation technique and Delphi method.
Step 4. Calculate using Eq. (2), , .
Step 6. Calculate using Eq. (11), , .
Step 7. Calculate using Eq. (12), .
Step 8. Determine a ranking of all feasible response actions according to .
6. Case study
In this section, to illustrate the feasibility and validity of the FTA-based method, we investigate a case on H1N1 infectious disease in University B, one of the most famous universities in China. First, the introduction of the case is given. Then, the FTA-based method is used to choose a desirable response action for controlling the spreading of H1N1 in the university. In addition, a sensitivity analysis is conducted to show the impact of parameters on the ranking of feasible response actions.
6.1. Introduction of the case
H1N1 virus is a subtype of influenza A virus and was the most common cause of human influenza in 2009. In September, an infected person of H1N1 was diagnosed in University B, which has 30,000 students and staff living on campus. After persuading the infected person to take quarantine measures, the university needs to take further action to control the spreading of H1N1 by selecting one from six feasible emergency response actions. The six feasible response actions are given as below.
-
•
: Taking no additional countermeasures. The cost of is 0 million RMB, ;
-
•
• : Persuading all close contacts of the infected person to take quarantine measures. The cost of is 0.1 million RMB, ;
-
•
: Adopting and furthermore, providing antisepsis equipments to dormitories and classrooms of the infected person, and measuring the temperatures of relevant students and staff every 12 h. The cost of is 0.2 million RMB, ;
-
•
: Adopting and furthermore, suspending the classes in the institute of the infected person, and control the flow of people between the institute and other institutes. The cost of is 0.5 million RMB, ;
-
•
: Adopting and furthermore, providing antisepsis equipments to all dormitories and classrooms, and measuring the temperatures of all students and staff of the university every 12 h. The cost of is 0.8 million RMB, ;
-
•
: Adopting and furthermore, suspending all classes in the university. The cost of is 2 million RMB, .
To select a desirable response action, the university invited five experts of epidemiology and three experts of emergency management to participate in the decision-making process. By consulting the experts, four potential scenarios in the evolvement process of infectious disease are determined as below.
-
•
: New infected persons are detected in the infected person's close contacts.
-
•
: New infected persons are detected in the same institute or dormitories of the infected person and his/her close contacts.
-
•
: Multiple new infected persons are detected in other institutes and dormitories.
-
•
: The pandemic of H1N1 in University B.
When make a decision, the following criteria are considered:
-
•
: the number of infected persons;
-
•
: the panic degree of students and staff;
-
•
: the negative effect on the reputation of the university.
The DM provides the weight of cost and weight vector of criteria, i.e., and . The values concerning criterion are estimated by experts; the values concerning and are evaluated by experts in the scale of scores of 0–100 (0: no panic or negative effect; 100: serious panic or negative effect). The criterion values with respect to different scenarios are shown in Table 1.
Table 1.
The criterion values with respect to different scenarios.
| 0 | 0 | 0 | |
| 10 | 20 | 10 | |
| 40 | 50 | 40 | |
| 100 | 80 | 70 | |
| 200 | 100 | 100 |
6.2. Choosing a desirable response action using the FTA-based method
To select a desirable action, the FTA-based method proposed in this paper is used and the procedure is summarized as follows.
6.2.1. Constructing the FT for H1N1 infectious disease in the university
The most undesirable scenario is defined as the top event. Then, according to the analysis of historical similar infectious diseases, the conditions or factors that could result in scenario are identified, i.e., “Multiple new infected persons are detected in other institutes and dormitories ()” and “The infection routes are unclear ()”. Additionally, , and are linked by ‘AND’ gate ( ) since will occur only if and occur simultaneously.
) since will occur only if and occur simultaneously.
Similarly, the causes of are identified, i.e., “New infected persons are detected in the same institute or dormitories of the infected person and his/her close contacts ()” and “New infected persons have contacted persons in other institutes and dormitories ()”. Additionally, , and are also linked by ‘AND’ gate ( ). The causes of are regarded as “Healthy persons are infected by intermediary, such as tableware, classroom, etc ()” or “Healthy persons are infected by undetected infected ones ()”. , and are linked by ‘OR’ gate (
). The causes of are regarded as “Healthy persons are infected by intermediary, such as tableware, classroom, etc ()” or “Healthy persons are infected by undetected infected ones ()”. , and are linked by ‘OR’ gate ( ) since will occur if one of and occurs.
) since will occur if one of and occurs.
The above deductive procedure are repeated until the root causes of scenario are analyzed clearly. Thereby, the FT for H1N1 infectious disease in University B is constructed, which is shown in Fig. 3. The meanings of the symbols in Fig. 3 are given in Table 2.
Fig. 3.
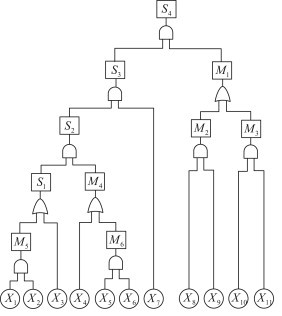
The FT for H1N1 infectious disease in University B.
Table 2.
The meanings of symbols in Fig. 3.
| Symbols | Meanings of symbols |
|---|---|
| New infected persons are detected in the infected person's close contacts | |
| New infected persons are detected in the same institute or dormitories of the infected person and his/her close contacts | |
| Multiple new infected persons are detected in other institutes and dormitories | |
| The pandemic of H1N1 in University B | |
| The infection routes are unclear | |
| Healthy persons are infected by intermediary, such as tableware, classroom, etc | |
| Healthy persons are infected by undetected infected ones | |
| The ineffective monitoring measures on infection routes | |
| Healthy persons are infected by the close contacts | |
| New infected ones infect healthy persons in the same institute | |
| The close contacts are not taken quarantine measures | |
| The close contacts have been infected | |
| Several persons in the same dormitory have been infected | |
| The classrooms in the institute of the infected ones have not been disinfected timely | |
| The infected ones in the institute are not detected timely | |
| The infected ones contact with others in group activities of the institute | |
| New infected persons have contacted with persons in other institutes and dormitories | |
| The classrooms in other institutes have not been disinfected timely | |
| The infected ones enter the classroom in other institutes | |
| The infected ones in other institutes are not detected timely | |
| The infected ones contact with others in group activities of the university |
6.2.2. Calculating the probabilities of scenarios
According to Fig. 3, the logical expressions of , , and can be respectively formulated, i.e.,
| (13) |
| (14) |
| (15) |
| (16) |
Then, indirect elicitation technique [26], [27] and Delphi method [28] are used to help the experts determine a consistency collective judgment on probabilities of basic events. The probability matrix of basic events is shown in Table 3.
Table 3.
The probability matrix of basic events.
| 1 | 0.8 | 0.6 | 0.8 | 0.9 | 0.8 | 0.7 | 0.8 | 0.9 | 0.9 | 0.8 | |
| 0 | 0.8 | 0.6 | 0.8 | 0.9 | 0.8 | 0.7 | 0.8 | 0.9 | 0.9 | 0.8 | |
| 0 | 0.8 | 0.6 | 0.4 | 0.4 | 0.7 | 0.6 | 0.8 | 0.9 | 0.9 | 0.8 | |
| 0 | 0.8 | 0.6 | 0.4 | 0.4 | 0.2 | 0.1 | 0.8 | 0.2 | 0.9 | 0.8 | |
| 0 | 0.8 | 0.6 | 0.4 | 0.4 | 0.2 | 0.1 | 0.4 | 0.2 | 0.4 | 0.8 | |
| 0 | 0.8 | 0.6 | 0.4 | 0.4 | 0.2 | 0.1 | 0.4 | 0.2 | 0.4 | 0.1 |
Furthermore, according to Eqs. (2) and (13), (14), (15), (16), the formulas for calculating probabilities of scenarios , , and are constructed with respect to action , i.e.,
| (17) |
| (18) |
| (19) |
| (20) |
According to Table 3 and Eqs. (17)–(20), the probabilities of scenarios given different response actions can be obtained, and shown in Table 4.
Table 4.
The probabilities of scenarios given different response actions.
| 0.92 | 0.8685 | 0.6079 | 0.5603 | |
| 0.6 | 0.5664 | 0.3965 | 0. 3654 | |
| 0.6 | 0.3408 | 0.2045 | 0.1884 | |
| 0.6 | 0.2688 | 0.0269 | 0.0206 | |
| 0.6 | 0.2688 | 0.0269 | 0.0101 | |
| 0.6 | 0.2688 | 0.0269 | 0.0031 |
6.2.3. Determining the ranking of actions
Using Eq. (9), the vector of normalized costs is determined, i.e., ; using Eq. (10), the normalized criterion values are obtained, and shown in Table 5. Then, using Eq. (11), the expected criterion values of different actions are determined, and shown in Table 6. Using Eq. (12), the overall ranking value of each action is determined, i.e.,
Table 5.
The normalized criterion values.
| 1 | 1 | 1 | |
| 0.95 | 0.8 | 0.9 | |
| 0.8 | 0.5 | 0.6 | |
| 0.5 | 0.2 | 0.3 | |
| 0 | 0 | 0 |
Table 6.
The expected criterion values of different actions.
| 0.3612 | 0.2610 | 0.2970 | |
| 0.5834 | 0.5181 | 0.5415 | |
| 0.7633 | 0.6787 | 0.7199 | |
| 0.9113 | 0.7872 | 0.8451 | |
| 0.9166 | 0.7893 | 0.8483 | |
| 0.9200 | 0.7907 | 0.8504 |
, , , , , .
Finally, according to the overall ranking values, a ranking of all feasible response actions is determined, i.e., .
6.3. Sensitivity analysis
In the following, a sensitivity analysis is conducted to show the impact of parameters on the ranking of feasible response actions. The sensitivity analysis includes two parts. One is to analyze the impact of the weight of cost on ranking of actions. The other is to analyze the impact of probabilities of basic events on ranking of actions.
6.3.1. The impact of the weight of cost on ranking of actions
The weight of cost implies the relative importance degree of cost comparing with the damage results. Analyzing the influence of weight of cost on ranking of actions would provide more valuable data for decision analysis in emergency response.
Consider the weight of cost is changed to , . It can be seen that if . Let be the vector of criterion weights corresponding to . Then, we have
| (21) |
obviously, .
In the above case study, we have and . If is changed into , then according to Eq. (21), we have . Furthermore, according to Eq. (12), the overall ranking value of each response action can be determined, i.e., , , , , , . Thus, a new ranking result of feasible response actions can be obtained, i.e., .
The overall ranking values of the six feasible response actions with regard to different are plotted in Fig. 4. It can be seen from Fig. 4 that action , or should be selected if is greater. Conversely, action , or should be selected if is smaller.
Fig. 4.
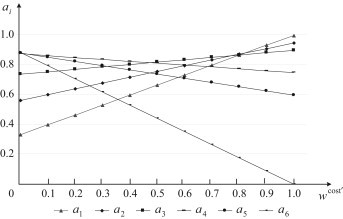
Curves of overall ranking values of the six feasible response actions with regard to different .
6.3.2. The impact of probabilities of basic events on ranking of actions
There are two types of basic events in the FT for an emergency case. The first type includes the events used to describe the current scenario of emergency, whose probabilities will not change with different response actions, such as and in Fig. 3. The second type includes the events used to describe conditions and factors resulting in the evolvement of emergency, whose probabilities will change with different response actions, such as , . In the following, the sensitivity analysis will be respectively conducted with respect to the probabilities of each type of events.
It can be seen from Fig. 3, Table 2, Table 3 that and belong to the first type of basic events. If the first infected person has not been detected timely, then the probabilities of and would be greater. Conversely, probabilities of and would be smaller. In addition, it can be seen from the practical meanings of and that there is inter-dependence between the probabilities of and . In other words, if the probability of is greater, then the probability of is also greater. Consider the probabilities of and are changed to and , respectively. Here, for the convince of analysis, we suppose . The overall ranking values of the six feasible response actions with regard to different values of are plotted in Fig. 5.
Fig. 5.
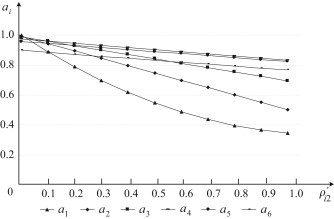
Curves of overall ranking values of the six feasible response actions with regard to different .
It can be seen from Fig. 5 that all of the overall ranking values of actions decrease with the increase of . Action is the best one only if approaches 0.
It can be seen from Fig. 3, Table 2, Table 3 that , belong to the second type of basic events. Here, we take and as two examples. Consider the probabilities of and are respectively changed to and . The overall ranking values of the six feasible response actions with regard to different and are plotted in Fig. 6, Fig. 7, respectively.
Fig. 6.
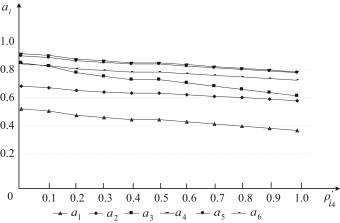
Curves of overall ranking values of the six feasible response actions with regard to different .
Fig. 7.
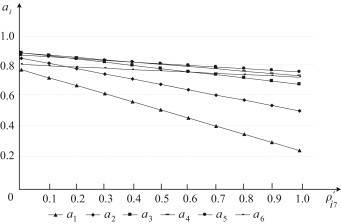
Curves of overall ranking values of the six feasible response actions with regard to different .
Fig. 6, Fig. 7 show that the overall ranking values are more sensitive to than . Thus, preventing the occurrence of will more effectively mitigate/reduce the expected damage results of emergency.
7. Conclusions
This paper presents a novel FTA-based method for risk decision-making in emergency response. By constructing the FT, the logical relations among the conditions and factors driving the evolvement of emergency are described. Then, based on the constructed FT, the probabilities of emergency scenarios are estimated given each feasible action. Furthermore, according to the obtained probabilities, the ranking of actions is determined by calculating the overall ranking values of feasible actions. The major contributions of this paper are discussed as follows.
First, this paper discovers and formulates a new risk decision-making problem in emergency response with distinct characteristics including the dynamic evolvement of emergency, multiple scenarios and their probabilities, and influence of response actions on probabilities of the scenarios. It is a new idea for describing the decision-making problem in emergency response and lays a good foundation for further conducting studies on risk decision analysis in emergency response.
Second, the key of the proposed method is to estimate the probabilities of scenarios given each feasible response action. For this, the principle of FTA is introduced, and the steps for constructing the FT for an emergency are given. The attempt to introduce FTA into decision analysis makes it possible to capture the dynamic evolvement process of emergency and estimate the probabilities of emergency scenarios before the response actions are implemented. It is valuable and important for developing and enriching theories and methods of decision analysis in emergency response.
Third, using the proposed method, not only the ranking of feasible response actions can be derived, but also the sensitivity analysis can be conducted conveniently. The data obtained by sensitivity analysis provide supplement and inducement to DMs, which is important to support the decision-making of DMs in the process of emergency response.
It is important to highlight that, since the proposed method is new and different from the existing methods, it can give experts or decision analysts one more choice for identifying the appropriate method to solve the problem of emergency response.
In terms of future research, two directions are worthy of pursuing. One is to extend the proposed method to the situation that probabilities or possibility of basic events are in the form of uncertain or fuzzy data, such as interval numbers, linguistic terms or institution fuzzy numbers. The other is to develop the dynamic risk decision-making methods in emergency response on the basis of the method proposed in this paper.
Acknowledgment
This work was partly supported by the National Science Fund for Excellent Innovation Research Group of China (Project no. 71021061), the National Science Foundation of China (Project nos. 90924016, 71001020, 71071029, 71101020 and 71101021), the Fundamental Research Funds for the Central Universities, NEU, China (Project nos. N100406012 and N110706001) and Doctoral Scientific Research Foundation of Liaoning Science and Technology Committee (Project no. 201120013).
References
- 1.Hämäläinen R.P., Lindstedt M.R.K., Sinkko K. Multiattribute risk analysis in nuclear emergency management. Risk Analysis. 2000;20(4):455–467. doi: 10.1111/0272-4332.204044. [DOI] [PubMed] [Google Scholar]
- 2.Shim K.C., Fontane D.G., Labadie J.W. Spatial decision support system for integrated river basin flood control. Journal of Water Resources Planning and Management. 2002;128(3):190–201. [Google Scholar]
- 3.Körte J. Risk-based emergency decision support. Reliability Engineering and System Safety. 2003;82(3):235–246. [Google Scholar]
- 4.Levy J.K. Multiple criteria decision making and decision support systems for flood risk management. Stochastic Environmental Research and Risk Assessment. 2005;19(6):438–447. [Google Scholar]
- 5.Levy J.K., Taji K. Group decision support for hazards planning and emergency management: a group analytic network process (GANP) approach. Mathematical and Computer Modeling. 2007;46(7–8):906–917. [Google Scholar]
- 6.Fu G.T. A fuzzy optimization method for multicriteria decision making: an application to reservoir flood control operation. Expert Systems with Applications. 2008;34(1):145–149. [Google Scholar]
- 7.Geldermann J., Bertsch V., Treitz M., French S., Papamichail K.N., Hämäläinen R.P. Multi-criteria decision support and evaluation of strategies for nuclear remediation management. Omega. 2009;37(1):238–251. [Google Scholar]
- 8.Lim K.S., Lee D.R. The spatial MCDA approach for evaluating flood damage reduction alternatives. KSCE Journal of Civil Engineering. 2009;13(5):359–369. [Google Scholar]
- 9.Yu L., Lai K.K. A distance-based group decision-making methodology for multi-person multi-criteria emergency decision support. Decision Support Systems. 2011;51(2):307–315. [Google Scholar]
- 10.Peng Y., Zhang Y., Tang Y., Li S.M. An incident information management framework based on data integration, data mining, and multi-criteria decision making. Decision Support Systems. 2011;51(2):316–327. [Google Scholar]
- 11.Ergu D, Kou G, Shi Y, Shi Y. Analytic network process in risk assessment and decision analysis. Computers and Operations Research, in press. 〈 10.1016/j.cor.2011.03.005〉. [DOI]
- 12.Lee W.S., Grosh D.L., Tillman F.A., Lie C.H. Fault tree analysis, methods, and applications: a review. IEEE Transactions on Reliability. 1985;34(3):194–203. [Google Scholar]
- 13.Kim C.E., Ju Y.J., Gens M. Multilevel fault tree analysis using fuzzy numbers. Computers & Operations Research. 1996;23(7):695–703. [Google Scholar]
- 14.Bertsche B. Springer-Verlag; Berlin Heidelberg: 2008. Reliability in automotive and mechanical engineering. [Google Scholar]
- 15.Liu D.X., Amari S.V. Fault tree analysis. In: Misra K.B., editor. Handbook of Performability Engineering. Springer-Verlag; London limited: 2008. [Google Scholar]
- 16.Lin M.S., Chang M.S., Chen D.J., Ku K.L. The distributed program reliability analysis on ring-type topologies. Computers & Operations Research. 2001;28(7):625–635. [Google Scholar]
- 17.Cheng S.R., Lin B.S., Hsu B.M., Shu M.H. Fault-tree analysis for liquefied natural gas terminal emergency shutdown system. Expert Systems with Application. 2009;36(9):11918–11924. [Google Scholar]
- 18.Gao X., Shan G.L., Liu H.L., Xie X.Q., Lu H.Y., Zeng G. Analysis on characteristics of transmission and diagnosis of SARS in Beijing in 2004. Chinese Journal of Public Health (in Chinese) 2005;21(5):522–523. [Google Scholar]
- 19.Saaty T.L. McGraw-Hill; Toronto: 1980. The analytical hierarchy process. [Google Scholar]
- 20.Peng Y., Kou G., Wang G.X., Wu W.S. Ensemble of software defect predictors: an AHP-based evaluation method. International Journal of Information Technology & Decision Making. 2011;10(1):187–206. [Google Scholar]
- 21.Lapp S.A., Powers G.J. Computer-aided synthesis of fault-trees. IEEE Transactions on Reliability. 1977;24(1):2–13. [Google Scholar]
- 22.Bossche A. Computer-aided fault tree synthesis I: system modeling and causal trees. Reliability Engineering & System Safety. 1991;32(3):217–241. [Google Scholar]
- 23.Bossche A. Computer-aided fault tree synthesis II: fault tree construction. Reliability Engineering & System Safety. 1991;33(1):1–21. [Google Scholar]
- 24.Khan F.I., Abbasi S.A. Analytical simulation and PROFAT II: a new methodology and a computer automated tool for fault tree analysis in chemical process industries. Journal of Hazardous Materials. 2000;75:1–27. doi: 10.1016/s0304-3894(00)00169-2. [DOI] [PubMed] [Google Scholar]
- 25.Wang Y., Teague T., West H., Mannan S. A new algorithm for computer-aided fault tree synthesis. Journal of Loss Prevention in the Process Industries. 2002;15(4):265–277. [Google Scholar]
- 26.Figueira J., Mousseau V., Roy B. ELECTRE methods. In: Figueira J., Greco S., Ehrgott M., editors. Multiple Criteria Decision Analysis: State of the Art Surveys. Springer; 2005. chapter 4. [Google Scholar]
- 27.Nowak M. Aspiration level approach in stochastic MCDM problems. European Journal of Operational Research. 2007;177:1626–1640. [Google Scholar]
- 28.Linstone H., Turloff M. The Delphi method: techniques and applications. Addison-Wesley; London, UK: 1975. [Google Scholar]
- 29.Clemen R.T., Winkler R.L. Combing probability distribution from experts in risk analysis. Risk Analysis. 1999;19(2):187–203. [Google Scholar]
- 30.Peng Y., Kou G., Wang G.X., Shi Y. FAMCDM: A fusion approach of MCDM methods to rank multiclass classification algorithms. Omega. 2011;39:677–689. [Google Scholar]
- 31.Kou G., Lu Y.Q., Peng Y., Shi Y. Evaluation of classification algorithms using MCDM and rank correlation. International Journal of Information Technology & Decision Making. 2012;11(1):197–225. [Google Scholar]


