Abstract
We propose that the recently defined persistent homology dimensions are a practical tool for fractal dimension estimation of point samples. We implement an algorithm to estimate the persistent homology dimension, and compare its performance to classical methods to compute the correlation and box-counting dimensions in examples of self-similar fractals, chaotic attractors, and an empirical dataset. The performance of the 0-dimensional persistent homology dimension is comparable to that of the correlation dimension, and better than box-counting.
Keywords: Persistent homology, fractal dimension, chaotic attractors, topological data analysis
1. Introduction
Loosely speaking, fractal dimension measures how local properties of a set depend on the scale at which they are measured. The Hausdorff dimension was perhaps the first precisely defined notion of fractal dimension [23, 41]. It is difficult to estimate in practice, but several other more computationally practicable definitions have been proposed, including the box-counting [10] and correlation [34] dimensions. These notions are in-equivalent in general.
Popularized by Mandelbrot [57, 58], fractal dimension has applications in a variety of fields including materials science [17, 44, 92], biology [6, 52, 66], soil morphology [68], and the analysis of large data sets [7, 86]. It is also important in pure mathematics and mathematical physics, in disciplines ranging from dynamics [81] to probability [8]. In some applications, it is necessary to estimate the dimension of a set from a point sample. These include earthquake hypocenters and epicenters [39, 47], rain droplets [28, 54], galaxy locations [37], and chaotic attractors [34, 81].
We propose that the recently defined persistent homology dimensions [1, 77] (Definition 1 below) are a practical tool for dimension estimation of point samples. Persistent homology [20] quantifies the shape of a geometric object in terms of how its topology changes as it is thickened; roughly speaking, i-dimensional persistent homology (PHi) tracks i-dimensional holes that form and disappear in this process. Recently, it has found many applications in fields ranging from materials science [43, 73] to biology [31, 89]. There are further applications of persistent homology in machine learning, for which different methods of vectorizing persistent homology have been defined [2, 11]. In most applications, larger geometric features represented by persistent homology are of greatest interest. However, in the current context it is the smaller features — the “noise” — from which the dimension may be recovered.
For a finite subset of a metric space {x1, …, xn} and a positive real number α define the α weight to be the sum of the lengths of the (finite) PHi intervals to the α power:
If μ is a measure on bounded metric space, are i.i.d. samples from μ, and i is a natural number the PHi-dimension measures how scales as n → ∞. In particular, if , then . See below for a precise definition.
We estimate the persistent homology dimension of several examples, and compare its performance to classical methods to estimate the correlation and box-counting dimensions. We study the convergence of estimates as the sample size increases, and the variability of the estimate between different samples. The examples we consider are from three broad classes: self-similar fractals, chaotic attractors, and empirical data. The sets in the former class (shown in Figure 1(a)–1(c)) have known dimensions, and are regular in a sense that implies that the various notions of fractal dimension agree for them. That is, they have a single well-defined “fractal dimension.” This makes it easy to compare the performance of the different dimension estimation techniques. In those cases, our previous theoretical results [77] imply that at least the zero-dimensional version of persistent homology dimension will converge to the true dimension. The second class of fractals we study are strange attractors arising from chaotic dynamical systems, see e.g. Figure 1(d)–1(f). Generically, these sets are not known to be regular, and the various definitions of fractal dimension may disagree for them. Finally, we apply the dimension estimation techniques to the Hauksson–Shearer Southern California earthquake catalog [40].
Figure 1.
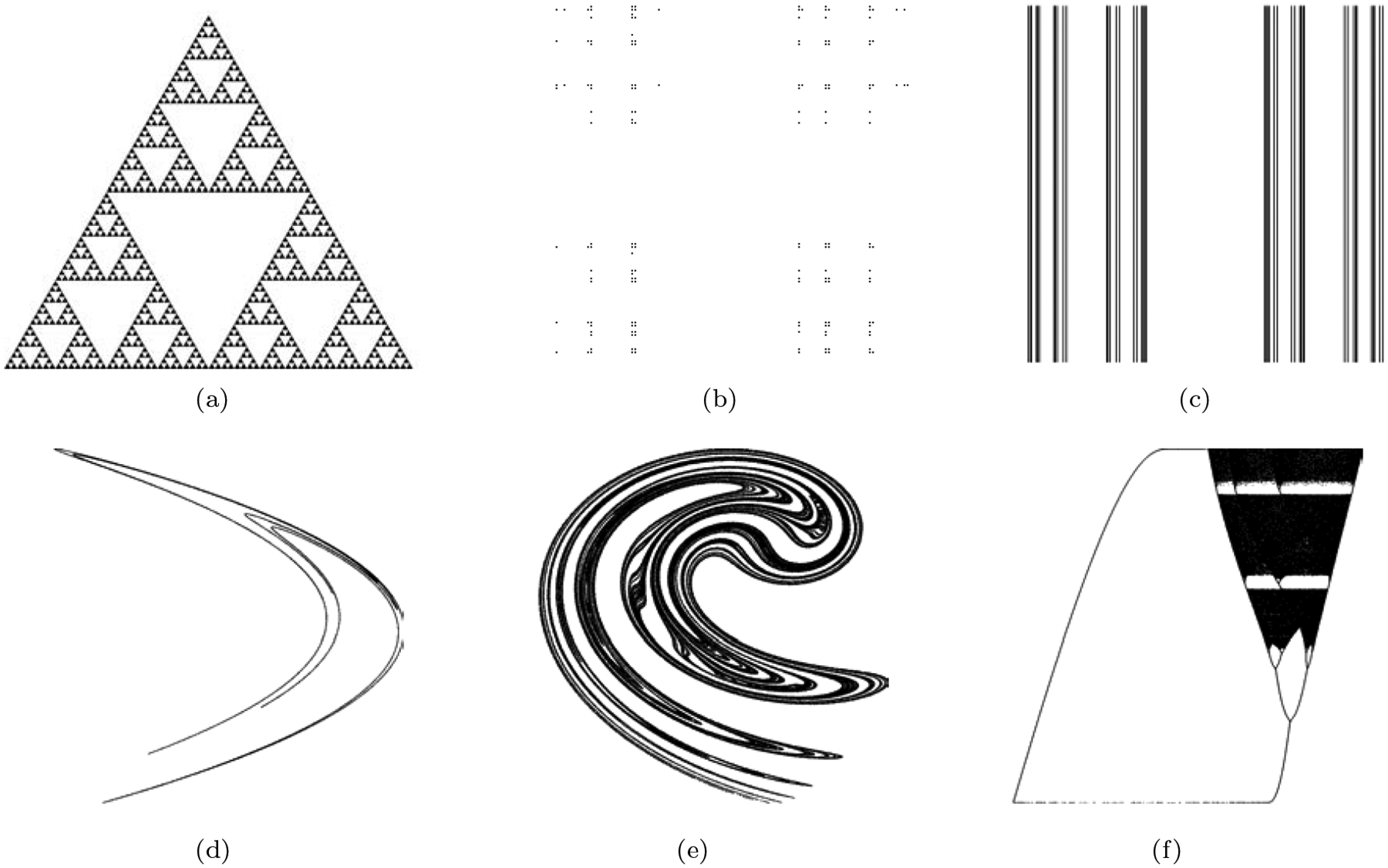
Three self-similar fractals: (a) the Sierpinski Triangle, (b) the Cantor dust, and (c) the Cantor set cross an interval; and three chaotic attractors arising from the: (d) Hénon map (e) Ikeda map and (f) Rulkov map.
We also propose that a notion of persistent homology complexity due to MacPherson and Schweinhart [56] may be a good indicator of how difficult it is to estimate the correlation dimension or persistent homology dimension of a shape.
In summary, we conclude the following.
Effectiveness. Based on our experiments, the PH0 and correlation dimensions perform comparably well. In cases where the true dimension is known, they approach it at about the same rate. In most cases, the box-counting, PH1, and PH2 dimensions perform worse.
Efficiency. Computation of the PH0 dimension is fast and comparable with the correlation and box-counting dimensions. The PH1 dimension is reasonably fast subsets of , but the PH1 and PH2 dimensions are quite slow for point clouds in , and computations for sets with higher ambient dimension are impractical.
Equivalence. For a large class of regular fractals the PH dimension coincides with various classical definitions of fractal dimension. However, there are fractal sets for which these definitions do not agree, with sometimes surprisingly large differences (e.g. the Rulkov and Mackey-Glass attractors). Within the class of PHi dimensions, there is variation between dimension estimates coming from different choices of the homological dimension or scaling weight. All this said, it can be difficult to determine whether dimensions truly disagree, or if the convergence is very slow.
Error Error estimates, whether they are the “statistical test error” of the correlation dimension or the empirical standard deviation of estimates between trials, do not contain meaningful information about the difference between the dimension estimate and the true dimension. In general, it is difficult to tell whether a dimension estimate has approached its limiting value.
Ease-of-use We found one simple rule for fitting a power law to estimate the PH0 which worked well for all examples, in contrast to the correlation dimension and (especially) the box-counting dimension.
In the following, we briefly survey previous work comparing different methods for the estimation of fractal dimension (Section 1.1), outline the different methods considered here (Section 2), and discuss the results for each example (Sections 3, 4, and 5).
1.1. Background and Previous Work.
Many previous studies have compared different methods for fractal dimension estimation. These include surveys focusing on applications to chaotic attractors [83], medical image analysis [52], networks [70], and time series and spatial data [32]. Fractal dimension estimation techniques have also been applied for intrinsic dimension analysis in applications where an integer-valued dimension is assumed [13, 63].
Several previous studies have observed a relationship between fractal dimension and persistent homology. Estimators based on 0-dimensional persistent homology (minimum spanning trees) were proposed by Weygart et al. [87] and Martinez et al. [61]; we explain their relationship to the current work after Definition 1 below. The PhD thesis of Robins [69], arguably the first publication in the field of topological data analysis, studied persistent Betti numbers of fractals and proved results for the 0-dimensional homology of totally disconnected sets. In 2012, MacPherson and Schweinhart introduced an alternate definition of PH dimension, which we refer to here as “PHi complexity” to avoid confusion (Section 2.1.3). The two previous notions measure the complexity of a shape rather than a classical dimension; they are trivial for , for example. A 2019 paper of Adams et al. [1], proposed a PH dimension that is a special case of the one we consider here, and performed computational experiments on self-similar fractals. However, they do not compare the estimates with those of other fractal dimension estimation techniques. In 2018, Schweinhart [78] proved a relationship between the upper box-counting dimension and the extremal properties of the persistent homology of a metric space, which was a stepping stone to the paper where the current definition was introduced [77]. The latter paper did not undertake a computational study of the persistent homology dimension; we mention relevant theoretical results in Section 2.1.1.
The second class of fractals we study arise in dynamical systems. A dynamical system describes the motion of trajectories x(t) within a phase space, with a rule for describing how x(t) changes as time t increases, and are referred to as either discrete or continuous depending on whether or . An attractor A is an invariant set (that is, if x(t) ∈ A, then x(s) ∈ A for all s > t) in the phase space such that if x(t) is close to A, then its distance to A will decrease to zero asymptotically as t → ∞. Some attractors are simple, consisting of a collection of points or smooth periodic orbits, but some are complicated, such as those shown in Figure 1 (d–f). In dissipative systems strange attractors — attractors with a fractional dimension — can occur.
For self-similar fractals, dimension is easy to compute exactly and approximate computationally. The situation for strange attractors is quite different; in general, the fractal dimension of an attractor cannot be computed analytically. The measures on these sets may not be regular, and the different notions of dimension appear to disagree in many cases. Note that when estimates for different notions of fractal dimension disagree, it is difficult to tell whether this is because (1) one method converges much faster than the other (2) there is a significant systematic error in the estimates, or (3) the two definitions are genuinely different.
To offer a further cautionary tale, in [46] the authors study a family of quasi-periodically forced 1D maps with an attracting invariant curve. As a parameter changes, the curve becomes less stable and it becomes increasingly wrinkled; for any resolution, parameters exist for which the curve will appear to be a strange non-chaotic attractor [35]. However, until the invariant curve completely loses stability, the attractor remains a smooth 1-dimensional curve. Hence, no matter how fine a resolution we use to compute our dimension estimate, we can never be sure that our estimate is close to its convergent value.
The Lyapunov exponents of a dynamical system describe its exponential rates of expansion and contraction, and can be used to define the Lyapunov dimension of the attractor [91]. The Kaplan-Yorke conjecture claims that the Lyapunov dimension of a generic dynamical system will equal the information dimension of its attractor [27, 48]. For a class of strange attractors arising from 2D maps, Young showed this to be the case, and moreover that the Lyapunov, Hausdorff, box-counting, and Rényi dimensions all coincide [90]. Other attractors appear to exhibit multifractal properties in the sense that different notions of fractal dimension disagree. The multifractal properties of such an attractor can be studied with a one-parameter family of dimensions such as the generalized Hausdorff [33] or Rényi dimensions [5, 67]. We can also examine this with the PHi dimensions by varying the weight parameter α — see Figure 12.
Figure 12.

Attractor PHi dimension estimates for various choices of α.
The Takens embedding theorem also illustrates the importance of fractal dimension to the study of attractors. In an experimental setting, it is often impossible to record all of the relevant dynamic variables. However, one can reconstruct the entire attractor from the time series of a single observed quantity using a time delay embedding [81]. Namely, for a choice of time delay τ and embedding dimension m, a 1-dimensional time series may be used to construct a m-dimensional time series consisting of points . If m is at least twice the box-counting dimension of the attractor, then generically this reconstruction will be diffeomorphic to the original attractor [75]. These techniques have been widely applied and we briefly mention some references which use this in the context of topological data analysis [29, 62, 64].
2. Dimension Estimation Methods
2.1. Persistent Homology Dimension.
We give a brief, informal introduction to persistent homology for the special case of a subset of Euclidean space. For a more in depth survey, see [14, 21, 22, 30].
Note that the definition of the PH dimension also makes sense for subsets of an arbitrary metric space.
Persistent homology [20] quantifies the shape of a geometric object in terms of how the topology of the set changes as it is thickened. To be precise, if X is a subset of , define the family of ϵ-neighborhoods by
Figure 2 shows ϵ-neighborhoods of the Sierpinski triangle S and a sample of 100 points from that set. The Sierpinski triangle S contains infinitely many holes which disappear as we thicken it. The first homology group of Sϵ is an algebraic invariance which essentially counts the number of holes in Sϵ. The last hole to disappear is in the center of the triangle; it vanishes when we have thickened the triangle by . Persistent homology represents this largest hole by the single interval . The next three largest holes disappear at and correspond to three intervals . The following nine holes are represented by nine intervals , and so on. These are the first dimensional persistent homology intervals of the Sierpinski triangle, which we denote by PH1 (S).
Figure 2.

ϵ-neighborhoods for the Sierpinski triangle (above) and a sample of 100 points from that set (below).
The zero-dimensional persistent homology of a metric space tracks the connected components that merge together as the geometric object is thickened. The Sierpinski triangle is already connected at ϵ = 0, so PH0 (S) is trivial. However, the finite point sample x shown in Figure 2 has 100 components. As we thicken x by an amount ϵ the first component disappears when ϵ equals δ/2, where δ is the smallest pairwise distance between the points. This corresponds to the interval (0, δ/2) in PH0 (x). One can find all PH0 intervals of x by increasing ϵ and forming an interval whenever there are two points x1, x2 ∈ x so that d(x1, x2) < ϵ and x1 and x2 are in different components of for all ϵ0 < ϵ. This is essentially the same as Kruskal’s algorithm for computing the minimum spanning tree on x, which leads to a proof that there is a bijection between the edges of that tree and the intervals of PH0(x) where an interval corresponds to an edge of twice its length.
Roughly speaking, the higher dimensional homology groups Hi(Xϵ) count the number of higher dimensional “holes” in Xϵ. The higher dimensional persistent homology is defined in terms of how these groups Hi(Xϵ) change as ϵ increases. The structure of the persistent homology is captured by a unique set of intervals that track the birth and death of homology generators as ϵ changes [12, 14]. We denote this set of intervals by PHi (X).
Traditionally, the information contained in persistent homology is plotted in a persistence diagram showing the scatter plot (birth, death) for each interval. The persistence diagrams of the Sierpinski triangle, and point samples from it with 100 and 1000 points are shown in Figure 3. Note that the 1-dimensional persistent homology of the point sample with 1000 roughly approximates that of the Sierpinski triangle, with 1 interval that dies around , three that die around , and 9 that die around . This is a consequence of the “bottleneck stability” of persistent homology [15].
Figure 3.
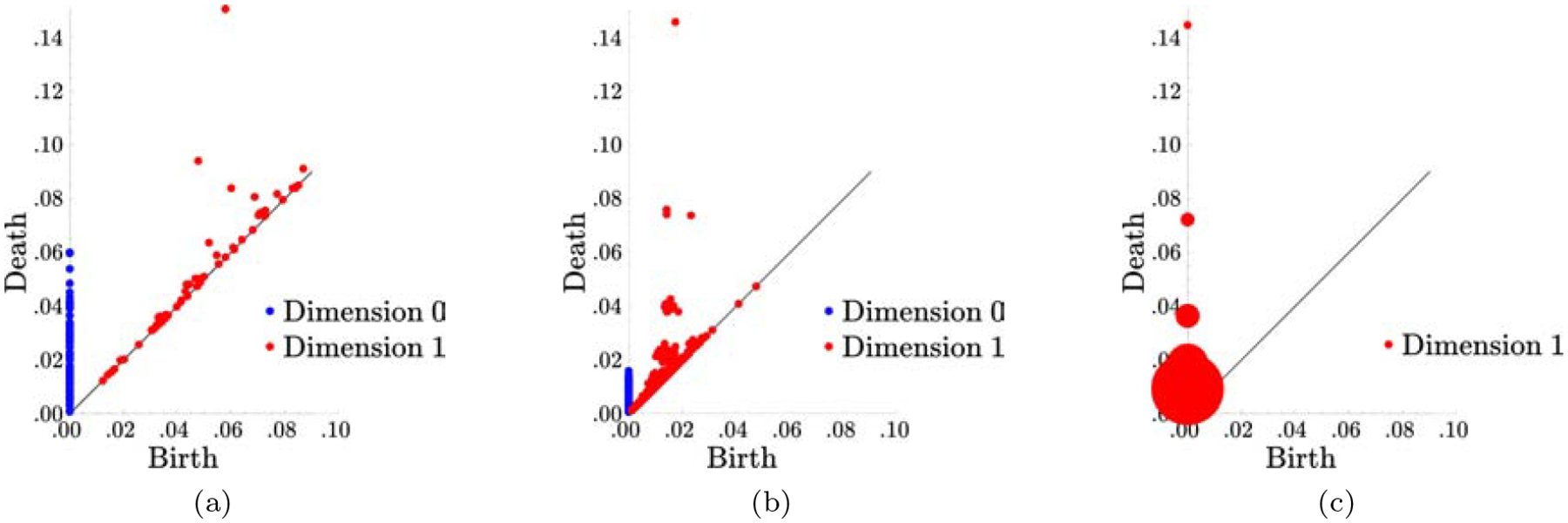
Persistence diagrams for (a) 100 point sample from the Sierpinski triangle, (b) 1000 points from the Sierpinski triangle and (c) the Sierpinski triangle itself (where the area of a dot is proportional to the number of persistent homology intervals with corresponding birth and death time).
It is a remarkable fact that if x is a finite subset of Euclidean space, then the intervals PHi (x) can be computed exactly and efficiently. This is done by replacing the infinite family of ϵ-neighborhoods with a finite sequence of finite simplicial complexes, called the Alpha complex of x; these complexes are subcomplexes of the Delaunay triangulation on x [20].
Note that there is more than one way to define the persistent homology of a metric space. Here, we use the persistent homology of the Čech complex persistent homology of X. If X is a subset of Euclidean space, this is equivalent to the persistent homology of the ϵ-neighborhood filtration of X described above (as well as the persistent homology of the Alpha complex, if X is finite). Another common (in-equivalent) notion is the persistent homology of the Vietoris–Rips Complex on X [18, 88]. We use the Čech complex because there are efficient algorithms to compute its persistent homology for finite subsets of and , as discussed below. A persistent homology dimension defined in terms of the Vietoris—Rips complex also has nice properties [77], and may work better in examples without an embedding into a small-dimensional Euclidean space.
2.1.1. Definition of the PH dimension.
Consider a sample {x1, …, xn} of independent points from the natural measure on the Sierpinski triangle. As n increases, the persistence diagram of the point sample will converge (in the bottleneck distance) to the persistence diagram of the Sierpinski triangle itself. As such, it might seem strange that we can recover the dimension of that set from the 0-dimensional persistent homology of the samples (PH0(S) is trivial). However, one may notice in Figure 3 that there is a large cluster of points, both 0- and 1-dimensional, along the plotted diagonal line. These points are generally considered to be “noise” and do not significantly contribute to the larger features of interest in other applications of persistent homology. However, the rate at which this “noise” decays is linked to the dimension of the underlying object.
To track the growth of this “noise”, we define the power-weighted sum for α > 0 by:
where the sum is taken over all finite intervals and |I| denotes the length of an interval. The scaling properties of random variables of the form as n → ∞ has been studied extensively in probabilistic combinatorics [3, 49, 80, 93], and the case i > 0 has recently been of interest [19, 77]. Motivated by a theorem of Steele [80] and the computational work of Adams et al. [1], Schweinhart [77] introduced the following definition of the persistent homology dimension.
Definition 1. Let X be a bounded subset of a metric space and μ a measure defined on X. For each and α > 0 we define the persistent homology dimension:
where
We write this as the dimension, and sometimes omit the i or α when making general statements.
That is, if scales as . Larger values of α give relatively more weight to large intervals than to small ones. The case α = 1 is closely related to the dimension studied by Adams et al. [1], and agrees with it if defined. Weygaert et al. [87] defined a family of minimum spanning tree dimensions that are equivalent to the PH0 dimensions, and used heuristic arguments to claim that they coincide with the generalized Hausdorff dimensions for chaotic attractors. Martinez et al. [61] asserted that the α → 0 of the PH0 dimension gives the Hausdorff dimension for point samples from chaotic attractors.
It is a corollary of Steele [80] that if μ is a non-singular measure on , and 0 < α < m then . Schweinhart [77] proved that if μ satisfies a fractal regularity hypothesis called Ahlfors regularity, then equals the Hausdorff dimension of the support of μ (which coincides with the box-counting dimension under the regularity hypothesis). He also proved that if d equals the upper box-counting dimension of the support of μ and α < d then , as well as weaker results about the cases where i > 0.
Note that if μ is supported on a k-dimensional subspace of , then Hi (X) is trivial for i ≥ k. It follows that . As such, even if μ is regular, its PHi dimension may not equal its Hausdorff dimension unless the Hausdorff dimension is sufficiently large. In particular, if μ is a d-Ahlfors regular measure supported on a 2-dimensional subspace of , d > 1.5, and α < d then –dimension of μ equals d. [77]
Schweinhart’s results show that the and dimensions of the natural measures on the Sierpinski triangle, Cantor set cross an interval, and Cantor dust equal the Hausdorff dimensions of those sets when α is less than the true dimension.
2.1.2. Computation of the PH dimension.
We use different methods to compute persistent homology for the cases i = 0 and i > 0. In the 0-dimensional case, we use minimum spanning tree-based algorithms that work much more quickly, and are fast even for point samples with high ambient dimension. We use the implementation of the dual–tree Boruvka Euclidean minimum spanning tree algorithm [59] included in the mlpack library [16] to compute the edges of the minimum spanning tree on a point sample. This algorithm was sufficiently fast for point clouds with 106 points in . See [59] for a brief survey of other algorithms to compute minimum spanning trees for point sets in Euclidean space and abstract metric spaces.
For i > 0, we use GUDHI to compute the persistent homology of the Alpha complex of the point sample. [60, 71] Both this computation and the previous one could be optimized by re-writing the data structures to support insertion of vertices.
Given a sample of n points x1, …, xn, we compute the α-weighted sum for 100 logarithmically spaced values of ci between 1, 000 and n. Then, we use linear regression to fit a power law to the data . After some trial-and-error, we found that fitting the power law between x = cn and x = c⌊n⌋/2 provided a reasonable estimate for all examples tested. Using a smaller range sometimes produced better convergence when i > 0, but also introduced more oscillations in the estimate. Alternate non-linear regression methods did not seem to result in better performance. Figure 4(a) shows the power law fits this method produces for a sample from the Lorenz attractor.
Figure 4.

Dimension estimation for a sample of 106 points from the Lorenz attractor, using the methods described in Section 2. Power laws were fitted in the ranges denoted by the arrows.
2.1.3. PH complexity.
In some instances, the dimension of a metric space can be computed in terms of the persistent homology of the metric space itself. For example, as shown in Figure 3(c), the 1-dimensional persistent homology of the Sierpinski triangle contains intervals that scale as its dimension. This is captured by an alternate notion of PH dimension defined by MacPherson and Schweinhart [56], which measures the complexity of the connectivity of the shape rather than the classical dimension. Here, we refer to it as the “PH complexity” of a shape to differentiate it from notions of dimension. As we will see below, this quantity may be an indicator of when the dimension is hard to estimate using any of the methods presented here.
If X is a subset of a metric space, define the cumulative PHi curve Fi by
Then the PHi complexity of X is
Note that for any i. Also, if S is the Sierpinski triangle in Figure 2, our computation of the persistence diagram of S shows that and .
We can estimate Fi(X, ϵ) from samples; as the Hausdorff distance between {x1, …, xn} and X converges to zero, bottleneck stability implies that Fi(X, ϵ) will converge for values of ϵ large relative to the Hausdorff distance. In Figure 10 below we compute of the Ikeda attractor.
Figure 10.

To estimate of the Ikeda attractor, we fit a power law in the range marked by the arrows. Note that PH1 exhibits two regimes: noise from the point sample and persistent features of the attractor itself. PH0 is only noise, as the Ikeda attractor is connected.
2.2. The Correlation Dimension.
The correlation dimension [34] is commonly used in applications because it is easy to implement and provides reasonable answers even for relatively small sample sizes. A probability measure μ on a metric space X induces a probability measure ν on the distance set of X. Define the correlation integral of X as the cumulative density function of ν:
The correlation dimension equals the limit
if it exists. There is an extensive literature on the estimation and properties of the correlation dimension; see for example [9, 24, 65, 79, 84].
2.3. Computation of the Correlation Dimension.
For a finite point sample x1, …, xn one can estimate the correlation dimension as
where
if n is taken to ∞ appropriately as ∈ → 0. That is, C(n, ∈) measures the number of distances less than ∈ in proportion to the number of all inter-point distances.
As with other dimension estimates, this limiting expression converges logarithmically slowly. To accelerate the convergence, we can essentially apply l’Hôpital’s rule to find the limit by computing a slope. To do so, we fix a collection of logarithmically spaced values ∈1 < … < ∈m, and compute a linear regression through the data (log ∈i, log C(n, ∈i)). Our estimate for the correlation dimension is then given by the slope of the line of best fit. For a fixed point sample, the values of ∈1 and ∈m are often chosen by hand to avoid outliers and edge effects.
While computing the inter-point distances is prohibative for very large n, such a calculation is not needed, as many of these distances are large and do not factor into the dimension calculation [83]. Using a kd-tree, one can quickly compute the shortest distances with effort. After some trial-and-error, we settled upon the heuristic for choosing ∈1 and ∈m as below:
See Figure 4(b). This heuristic provides a way to choose values of ∈1 and ∈m consistently amongst different fractals and different sample sizes. It appears to give near-optimal convergence rates to the true dimension for self-similar fractals, and estimates that agree with the values in the literature for the Hénon, Ikeda, and Lorenz attractors [34, 79, 83].
As has been previously reported [83], the “statistical test error” from the linear regression calculation does not have much predictive value about the limiting dimension — see Figure 5. Also, it is much smaller than the empirical standard deviation of the dimension estimate between trials in some cases.
Figure 5.

Correlation dimension estimates for (a) the Cantor dust and (b) the Lorrenz attractor. The evenly dashed red are above/below the dimension estimate by the amount of the statistical test error. The unevenly dashed blue lines are one standard deviation above/below the estimate, where the standard deviation is taken across 50 trials.
2.4. The Box-counting Dimension.
The box-counting dimension [10] of a bounded subset of X of is defined in terms of the number of cubes of width δ needed to cover X. Let be the cubes in the standard tiling of by cubes of width δ, and let Nδ (X) be the number of cubes in that intersect X. Define the upper and lower box-counting dimensions by
respectively. If the upper and lower box-counting dimensions coincide, the shared value is called the box-counting dimension of X and is denoted dimbox (X). There are many equivalent definitions; see Falconer [25] for details.
Many studies have investigated the properties and estimation of the box-counting dimension, including [50, 74, 82].
2.4.1. Computation of the Box-counting Dimension.
We found it difficult to find a general method to compute the box-counting dimension that worked well for different examples and different numbers of samples. For example, computing box-counts of the form and fitting a power law between 2−i and 2−j resulted in estimates that were sensitive to i, j, and the number of samples. In some cases, it was easy to cherry-pick a specific choice just because it seemed to have the best convergence to the true dimension, though other choices resulted in power law fits that looked just as good. See Figure 6 for an example, which plots the error in the dimension estimate for many possible power law fits. Only very specific choices have errors as small as estimates of the correlation and PH0 dimensions for the same sample.
Figure 6.

(a) Box-counts for a sample of 106 points from the Sierpinski triangle. (b) Error in the dimension estimate obtained by fitting a power law to the box counts between widths of the form 2−i/2 and 2−j/2. Compare to the error of correlation dimension and dimension estimates in Figure 7(b), which are smaller than .002 for all samples of sizes between 2 105 and 106 points. Only dark squares would yield comparably good estimates for the box-counting dimension.
We settled on the following method, which produced reasonably good results for planar examples. It is based on the observation that if are samples from and δ > 0 then the box count Nδ (x1, …, xm) should converge to Nδ (X) as n → ∞. For a sample {x1, …, xm}, we estimate the box-counting dimension from the smallest boxes for which Nδ (x1, …, xm) appears to have stabilized.
For a a family of point samples xm in (where the sizes of xm are logarithmically spaced as before) we rescale and translate the point samples so they are contained in a unit cube. Then, we compute box-counts of the form Ni/10000 (xm) for 1 ≤ i ≤ 1000. We fit a power law to the data (i/10000, Ni/10000(xm)) in the range (⌈j/2⌉, j), where j is the smallest index so that
We used linear regression to fit the power law; non-linear regression did not produce substantially different results. See Figure 4(c).
We tried several variations. For example fitting the power law in the range (⌈.9j⌉, j) produced estimates that converged faster with n for some examples but exhibited large oscillations in others.
3. Results for Self-similar Fractals
We compare the performance of the fractal dimension estimation procedures for four different self-similar fractals: the Sierpinski triangle (S), the Cantor dust (C × C), the Cantor set cross an interval (C × I), and the Menger sponge (M). The first three are subsets of , and M is contained in . We chose these sets to illustrate the observed relationship between and the performance of dimension estimation techniques; see Table 1. Definitions of the sets and sampling methods are contained in Appendix A.
Table 1.
Data for the four self-similar fractals studied here. As discussed in Section 3.2, lower values of α appear to yield better dimension estimates when .
| Example | True Dim. | |||
|---|---|---|---|---|
| S | 0 | − | ||
| C × I | 0 | − | ||
| C × C | − | |||
| M | 0 |
For each set, we sample 50 trials of 106 points from the corresponding natural measure. We compute 100 dimension estimates for each trial, at logarithmically spaced numbers of points between 103 and 106. To show the convergence of the dimension estimate to the true value, we plot number of points against the dimension estimate averaged across the trials, with thinner dotted lines one standard deviation above and below the estimate.
Dimension estimates for the four examples are plotted in Figure 7. In all examples, the PH0 dimension and the correlation dimension perform better than the PH1 or box-counting dimensions. The relatively poor performance of the PH1 dimension can be ascribed to the fact that the weighted sums are smaller and noisier than the corresponding sums (see Figure 4(a)). As mentioned previously, it was difficult to find an effective general method to produce box-counting estimates. This is illustrated for the Sierpinski triangle in Figure 6. While the plot of box width vs. box count looks linear for a large range on the log–log plot, only very specific choices of bounds will produce dimension estimates with errors on the same order as the PH0 and correlation dimensions. These bounds vary unpredictably with the sample size and example.
Figure 7.

Dimension estimates for self-similar fractals. Note that (b) is a close-up of (a). We omitted the box-counting dimension in (e) because the automated procedure described in Section 2.4.1 did not result in stable estimates until n was larger than 105.
The convergence of the PH0 and correlation dimensions to the true dimension is very similar in all four examples. The correlation dimension estimates exhibit oscillations as the sample size increases, a phenomenon often ascribed to the fractal’s lacunarity [83]. The PH0 dimension estimate appears less sensitive to oscillations, but this is likely due to how the power law fit is performed in the computations (as described in Section 2.1.2); choosing a narrower range over which to fit a power law results in a more oscillatory estimate. That said, for sizable samples, it is impractical to compute the correlation integral over a large range. The PH0 dimension provides a computationally practicable way to use information from multiple lengthscales. It also has the advantage of having the parameter α which can be tuned to give a better estimate — see Section 3.2 for a discussion on the choice of α. The variance of the correlation dimension estimate is slightly lower, but this doesn’t mean much when oscillations are present.
3.1. Percentage Error.
An interesting pattern emerges when we compare the percentage error of the dimension estimates across the three planar examples, as in Figure 8. Both PH0 and correlation dimensions perform best for the Sierpinski triangle , second best for the Cantor set cross an interval , and worst for the Cantor dust . That is, dimension estimation appears to be more difficult when the connectivity of the underlying set is more complex. Note that can be computed (see [56]), and could be used as an indicator of whether additional caution is warranted when discussing dimension estimation results.
Figure 8.

Percentage error for the correlation , and dimensions for three self-similar fractals.
For the PH1 dimension, the situation is different and the difficulty of dimension estimation appears to (unsurprisingly) be related to rather than . The rate of convergence was fastest for the Cantor set cross an interval , but slower for the Cantor dust and Sierpinski triangle .
We exclude the Menger sponge from these figures, as the ambient dimension likely influences the difficulty of dimension estimation.
3.2. Dependence on α.
Estimates of the and dimensions for various choices of α are shown in Figures 9. In the cases where , there are only small differences between dimension estimates for different choices of α, with perhaps a slight advantage for higher values of α (Figures 9(a) and 9(d)). However, when , dimension estimates for different values of α are substantially different. Lower values of α yield better estimates when for planar examples, and middle values of α (i.e. equal to about half the true dimension) seem to provide the best convergence for i = 1, 2 (but convergence is slow, especially for i = 2.)
Figure 9.

PHi dimension estimates for various choices of α. (g) and (h) show the standard deviation of the dimension estimate between trials.
Lower values of α appear to give dimension estimates that have a higher variance between samples — see Figures 9(g) and 9(g) for the Sierpinski triangle, which is representative.
4. Results for Attractors
For each chaotic attractor we sample 50 randomly selected initial conditions, and generate a time series of 106 points after discarding an initial transient trajectory (except the Mackey-Glass attractor, where we sample 25 initial conditions). For each time series, we compute 100 dimension estimates for each trial, at logarithmically spaced numbers of points between 103 and 106. The various dynamical systems we studied are described in Appendix B and the dimension estimates we obtained for N = 106 are summarized in Table 3 and Figure 11.
Table 3.
Dimension estimates for chaotic attractors, averaged over 10 trials of 106 samples.
| Correlation | Box-counting | |||||
|---|---|---|---|---|---|---|
| Hénon | 1.21 | 1.22 | 1.28 | 1.28 | 1.52 | 1.36 |
| Ikeda | 1.68 | 1.72 | 1.71 | 1.72 | 1.71 | 1.72 |
| Rulkov | 1.01 | 1.52 | 1.62 | 1.87 | 2.02 | < 2.13 |
| Lorenz | 2.04 | > 1.90 | 2.06 | 2.05 | < 2.14 | < 2.12 |
| MG | 3.04 | > 2.45 | 3.59 | 3.70 | − | − |
Figure 11.
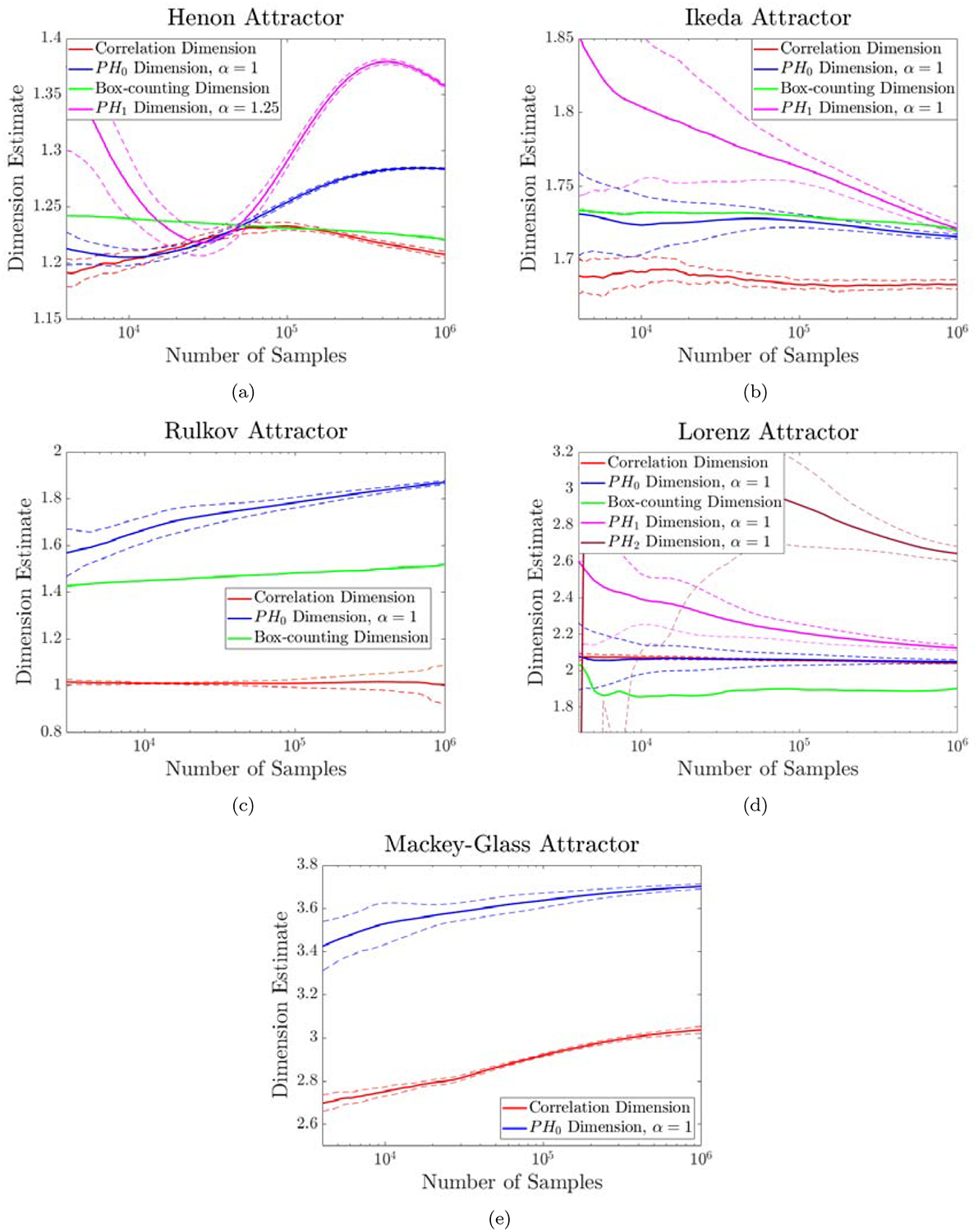
Average dimension estimates for various attractors, with dashed lines denoting ±1 sample standard deviation. Note the different scales.
In all cases, we are skeptical that the box-counting dimension has approached a limiting value. The upper box dimension is known to be an upper bound for the [77] and correlation dimensions, but most of our estimates of these dimensions tend to be higher than our estimates of the box-counting dimension. This comports with previous observations that box-counting estimates do not seem to converge well for strange attractors [36].
Of the two-dimensional maps we studied, the Ikeda map appears to be most well-behaved. The box-counting, PH0, and even the PH1 dimension all seem to converge to a common value of 1.71, with a correlation dimension of 1.68 not that far off. The Ikeda attractor I was the only chaotic attractor we studied with non-trivial persistent homology at multiple lengthscales (rather than the persistent homology “noise” of point samples). Here, we compute its PH1 complexity, . Figure 10 shows the cumulative interval count function defined in 2.1.3, for a sample of 106 points from the Ikeda attractor. The PH0 curve only shows very small intervals, which come from the noise of point samples. This is as expected, because the Ikeda attractor is connected. However, the PH1 curve shows two different regimes, one that corresponds to noise and one that appears to be picking up on the elongated holes visible in Figure 1(e). The cumulative length plot appears to follow a power law in the range ∈ = .0005 to ∈ = .005 Fitting a power law to this range gives an estimate of . This is lower than the dimension estimates for the Ikeda attractor, indicating that the elongated holes in that set scale at a different rate than its other properties.
For the Hénon attractor, both PH0 and PH1 dimension estimates had large oscillations which make it hard to say whether they will converge to values different from either the box-counting or correlation dimensions. The correlation dimension exhibited smaller oscillations, which comports with previous observations by Theiler [85], who also warns of the danger of estimating the dimension of attractors with long-period oscillations. Previous studies [4] have claimed that the Hénon attractor is multifractal for the parameters chosen here, but we are not confident enough in our dimension estimates to make such an assertion.
The Rulkov attractor is non-homogeneous, as easily evidenced by Figure 1(f), and not surprisingly our fractal dimension estimates differed from each other, ranging from 1.00 (correlation dimension) to 2.13 ( dimension). The estimates began above 2 for small samples sizes and decreased toward 2 as the number of samples increased. For various values of α, the dimension estimates ranged from 1.38 for α = 1 to 1.88 for α = 1.25 (see Figure 12). As one may see in Figure 11(c), the variance of the correlation dimension estimate increases with sample size, suggesting the heuristic we chose for fitting the correlation integral requires further fine-tuning for this example. The Rulkov map is noninvertible, so it does not belong to the class of 2D maps considered in [90] where many of the fractal dimensions are known to coincide. While it is difficult to determine if numerical dimension estimates have converged, our results certainly suggest that the various fractal dimension definitions may not agree for the Rulkov attractor.
For the Lorenz attractor, the PH0 and the correlation dimensions performed well and both appear to converge toward 2.05. However, neither the PH1 nor the PH2 dimensions perform well. In fact, nearly 105 are needed before the PH2 dimension estimate less than 3, the ambient dimension in which the points reside! As in other cases, this is likely due to the fact that higher dimensional persistent homology contains less information — see Figure 4. The sum of the lengths of the PH1 and PH2 intervals of a point sample of 106 points are 10 and 400 times smaller than the sum of the lengths of the PH0 intervals, respectively. Also, the plot of n versus is much noisier for PH2 than PH0.
Lastly we consider the Mackey-Glass equation, a delay differential equation for which it is still an open conjecture whether there exist parameters for which the system exhibits mathematically provable chaos. The phase space for this system is infinite dimensional, and we use a projection into for our fractal dimension calculations. In [26] Farmer reports the attractor’s Lyapunov dimension to be 3.58, and we obtain a dimension estimate close to this value. However, the spectrum of dimension for various α had the largest spread of any of the fractals we studied, except the Rulkov attractor, ranging between 3.59 for α = .5 and 4.06 for α = 3.5 (see Figure 12). While none of our dimension estimates appear to oscillate, all appear to converge slowly. The box-counting dimension estimation method described in Section 2.4.1 performed particularly poorly for this example, perhaps due to the high dimension and co-dimension. The estimate in Table 3 was computed by fitting a power law by hand. We did not attempt to compute either the PHi dimensions for 1 ≤ i ≤ 7, because the algorithm we use is impractical if the ambient dimension is greater than 3.
5. Earthquake Data
We estimate the dimension of the Hauksson–Shearer Waveform Relocated Southern California earthquake catalog [40, 51]. The hypocenter of an earthquake is the location beneath the earth’s surface where the earthquake originates. One can use the dimension estimate to study the geometry of earthquakes, i.e. by comparison to dimension estimates for fractures in rock surfaces or dislocations in crystals (see Section 6 of [47]). Previously, Harte [39] estimated the correlation dimension of earthquake hypocenters in New Zealand and Japan, and Kagan [47] studied the correlation dimension of earthquakes in southern California and developed extensive heuristics to correct for errors in that computation.
We downloaded the coordinates of the hypocenters of the earthquakes in the catalogue from the Southern California Earthquake Data Center Website [76], and selected the waveform-relocated earthquakes of magnitude greater than 2.0. This gave a data set of 74,929 earthquakes. The deepest earthquake in the data set is 33 kilometers below sea level and the depth distribution has a single peak, so we did not split the data set into multiple samples as Harte did. The data set had small relocation errors, with the error in distance between nearby hypocenters estimated to be less than .1 kilometer for 90% of such distances [40].
The presence of location errors means that a different methodology is required to estimate the correlation dimension than from the previously considered examples, where estimates at shorter lengthscales produce better results. To estimate the correlation dimension we plotted the correlation integral (Figure 13(a)) and determined that the best range to fit a power law was between 2 and 8.5 kilometers. This yields a correlation estimate of about 1.66. This can be compared to Kagan’s estimate of 1.5 for earthquakes from an earlier version of the same earthquake catalog that was processed with different methodology (Figure 8 of [47]), and to Harte’s estimates of 1.8 and 1.5 for shallow earthquakes in Kanto, Japan and Wellington, New Zealand, respectively.
Figure 13.

Dimension estimation for the earthquake hypocenter data set. Power laws were fitted in the ranges marked by the arrows.
Figure 13(b) shows the plot of n versus used to estimate the PH0 dimension. We estimated that the dimension is approximately 1.76 when α = 1. Similar computations for α = .5 and α = 1.5 yielded dimension estimates of 1.75 and 1.83, respectively. From this, and the comparison with the correlation dimension, we have evidence that the earthquake probability distribution is not regular. Also, note that the dimension plot (Figure 13(b)) appears to follow a power law in a large range, and the dimension can be estimated without fiddling with example-specific parameters. This precludes difficulties that arose in Harte’s analysis where the correlation dimension estimate was very sensitive to the scale at which it was measured(Figure 20 in [39]). Of course, the correlation dimension has an advantage of interpretability at different lengthscales — the x-axis in Figure 13(a) is kilometers, while it is number of samples in Figure 13(b).
The box-counting, PH1, and PH2 dimensions did not produce good results. In the former case, it is unclear whether the plot of box width versus box count (Figure 13(c)) follows a power law at any range, but certainly no range shorter than 5 kilometers. Fitting between 5 and 10 kilometers yielded an estimate of .91, which is very different than the estimates computed with other methods. Fitting at larger length scales, between 20 and 50 kilometers produced an estimate of 1.22. It is not surprising that the PH1 and PH2 dimensions produced poor results, given the small sample size.
We also estimated that likely equals zero for the earthquake data, for i = 0, 1, 2.
6. Conclusion
Overall the performance of our PH0 dimension calculations is comparable to the correlation dimension, and gives dimension estimates that are often greater for non-regular sets. Both the PH0 and correlation dimensions were more reliable than either the box-counting, PH1, or PH2 dimensions. The correlation dimension and the PH0 dimension are easy to implement and quick to compute. The PH0 dimension may be more user-friendly in the sense that a single choice of power law range worked well for all examples. Of these two, we do not view one dimension estimation technique as “better” than the other. Rather, they are complementary methods that — if the underlying set is not regular — can provide complementary information.
In many applications of persistent homology, small intervals are often ignored in favor of larger features and discarded as “noise”. However, as we have demonstrated here, there is sometimes signal in that noise. Adding the PH dimension to the current suite of PH-based techniques used in applications such as machine learning will offer an orthogonal data descriptor.
Table 2.
Dimension estimates for self-similar fractals, averaged over 10 trials of 106 samples.
| True | Correl. | Box | |||||||
|---|---|---|---|---|---|---|---|---|---|
| S | ≈ 1.585 | 1.585 | 1.586 | 1.585 | 1.585 | 1.587 | 1.620 | − | − |
| C × I | ≈ 1.631 | 1.633 | 1.618 | 1.629 | 1.623 | 1.634 | 1.642 | − | − |
| C × C | ≈ 1.262 | 1.263 | 1.267 | 1.263 | 1.289 | 1.268 | 1.303 | − | − |
| M | ≈ 2.727 | 2.716 | 2.703 | 2.705 | 2.706 | 2.878 | 2.773 | 2.945 | 2.881 |
Highlights.
We propose that the recently defined persistent homology (PHi) dimensions are a practical tool for dimension estimation.
We implement an algorithm to compute the PHi dimensions and apply it to a variety of examples, including self-similar fractals, chaotic attractors, and earthquake hypocenters.
The accuracy and speed of the PH0 dimension estimation algorithm is comparable to that of the correlation dimension, and better than the box-counting dimension.
Acknowledgments
Research of the first author was supported in part by NIH T32 NS007292 and NSF DMS-1440140 while the author was in residence at the Mathematical Sciences Research Institute in Berkeley, California, during the Fall 2018 semester.
Research of the second author was supported in part by a NSF Mathematical Sciences Postdoctoral Research Fellowship under award number DMS-1606259.
Appendix A. Self-Similar Fractals
A.1. The Sierpinski Triangle.
The Sierpinski triangle (Figure 1(a)) is defined by iteratively removing equilateral triangles from a larger equilateral triangle. Begin by sub-dividing the equilateral triangle formed by (0, 0),(1, 0), and into four congruent triangles, and removing the center triangle. Repeat this process on the remaining three triangles, and continue ad infinitum. The Sierpinski triangle equals three copies of itself rescaled by the factor 1/2 so the dimension of the resulting set is (for a self-similar set equal to m copies of itself rescaled by a factor r, the self-similarity dimension equals .
We sampled points from the natural measure on the Sierpinski Triangle by sampling random integers {a1, a2, …} ∈ {0, 1, 2} and computing
In practice, we end this procedure at i = 64.
A.2. The Cantor Dust.
The standard middle-thirds Cantor set C is the set formed by removing the interval (1/3, 2/3) from the closed interval [0, 1], and iteratively removing the middle third of the remaining intervals. The dimension of C is . The Cantor dust (Figure 1(b)) is the product C × C; its dimension is .
We sampled points from the natural measure on C by sampling random integers {a1, a2, …} ∈ {0, 1} and computing
In practice, we truncated the summation at i = 64. A point (x1, x2) from the natural measure on the Cantor dust can then be sampled by independently sampling x1 and x2 as above.
A.3. The Cantor Set Cross an Interval.
Consider the set C × [0, 1], where C is the Cantor set defined in the previous section. The dimension of this set is , one greater than the dimension of the Cantor set.
We sampled points (x, y) from the natural measure on the Cantor set cross an interval by sampling a random point x on the Cantor set by the procedure described in the previous section, and a random real number y from the uniform distribution on [0, 1].
A.4. The Menger Sponge.
The Menger sponge is defined by iteratively removing cubes from a larger cube. Begin by sub-dividing the unit cube in into nine smaller sub-cubes, and remove nine of them: one from the center of the original cube one from the center of each of the eight faces. Repeat this process on each of the 20 remaining sub-cubes and continue ad infinitum. The resulting structure is equal to 20 copies of itself rescaled by a factor 1/3 so the dimension of the resulting set is .
For j ∈ ⋉ we sample a uniform three-tuple of integers (xi, yi, zi) ∈ {0, 1, 2} throwing out and resampling any three-tuple for which two or more of the coordinates equals one. To sample a point from the natural measure on the Menger sponge, we form the sum
In practice, we end this procedure at i = 64.
Appendix B. Chaotic Attractors
B.1. Hénon Map.
The Hénon map [42] is given by (xn, yn) ↦ (xn+1, yn+1) where:
We used the parameters of a = 1.4 and b = 0.3. We generated 50 time series using randomly chosen initial conditions, computing a trajectory of length 1.1 · 107 and discarding the initial 106 points in the series.
B.2. Ikeda Map.
The complex Ikeda map [38] is given by zn ↦ zn+1 where:
We used the parameters:
We generated 50 time series using randomly chosen initial conditions, computing a trajectory of length 1.1 · 106 and discarding the initial 105 points in the series.
B.3. Rulkov Map.
The chaotic Rulkov map [45, 72] is given by (xn, yn) ↦ (xn+1, yn+1) where:
We use the parameters
We generated 50 time series using randomly chosen initial conditions, computing a trajectory of length 1.1 · 106 and discarding the initial 105 points in the series.
B.4. Lorenz System.
The Lorenz system [53] given by the system of ordinary differential equations below:
We use the parameters:
We generated 50 time series using randomly chosen initial conditions, integrating forward for 1.01×105 units of time, and discarding the initial 103 units of time. We used MATLAB’s ode45 integrator with a relative error tolerance of 10−9 and an absolute error tolerance of 10−9. We sampled our trajectories at a rate of 10Hz, producing time series with 106 points each.
B.5. Mackey-Glass.
The Mackey-Glass equation [55] is given by the scalar delay differential equation below:
| (1) |
We take parameters:
A natural phase space for this dynamical system is the Banach space of continuous functions . For our dimension calculations we discretize this space using a projection map (for m = 8) which evaluates a function y ∈ C at m maximally spaced points on the interval [−τ, 0].
We generated 25 time series using randomly chosen initial conditions and integrating forward for units of time. We used MATLAB’s dde23 integrator with the default error tolerances for the first 5,000 units of time, and the remainders of each trajectory were computed using a relative error tolerance of 10−5 and an absolute error tolerance of 10−9. The initial transient periods of 104 units of time were discarded, and the remainders were sampled at a rate of , producing time series with 106 points each.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
JONATHAN JAQUETTE, Department of Mathematics, Brandeis University Waltham, MA 02453.
BENJAMIN SCHWEINHART, Department of Mathematics, Ohio State University Columbus, OH 43210.
References
- [1].Adams Henry, Aminian Manuchehr, Farnell Elin, Kirby Michael, Mirth Joshua, Neville Rachel, Peterson Chris, Shipman Patrick, and Shonkwiler Clayton. A fractal dimension for measures via persistent homology. Abel Symposia, 2019. [Google Scholar]
- [2].Adams Henry, Chepushtanova Sofya, Emerson Tegan, Hanson Eric, Kirby Michael, Motta Francis, Neville Rachel, Peterson Chris, Shipman Patrick, and Ziegelmeier Lori. Persistence images: A stable vector representation of persistent homology. Journal of Machine Learning Research, 2017. [Google Scholar]
- [3].Aldous David and Steele J. Michael. Asymptotics for Euclidean minimal spanning trees on random points. Probability Theory and Related Fields, 1992. [Google Scholar]
- [4].Arneodo A, Grasseau G, and Kostelich E. Fractal dimensions and f(α) spectrum of the Hénon attractor. Physics Letters A, 1987. [Google Scholar]
- [5].Badii R and Politi A. Renyi dimensions from local expansion rates. Physical Review A, 1987. [DOI] [PubMed] [Google Scholar]
- [6].Baish James W. and Jain Rakesh K.. Fractals and cancer. Perspectives in Cancer Research, 2000. [PubMed] [Google Scholar]
- [7].Barbara Daniel and Chen Ping. Using the fractal dimension to cluster datasets. In KDD ‘00 Proceedings of the sixth ACM SIGKDD international conference on Knowledge discovery and data mining, 2000. [Google Scholar]
- [8].Beffara Vincent. The dimension of the SLE curves. Annals of Probability, 2008. [Google Scholar]
- [9].Borovkova S, Burton R, and Dehling H. Consistency of the Takens estimator for the correlation dimension. Annals of Applied Probability, 1996. [Google Scholar]
- [10].Bouligand MG. Ensembles impropres et nombre dimensionnel. Bulletin des Sciences Mathematiques, 1928. [Google Scholar]
- [11].Bubenik Peter. Statistical topological data analysis using persistence landscapes. Journal of Machine Learning Research, 2015. [Google Scholar]
- [12].Cagliaria Francesca and Landibc Claudia. Finiteness of rank invariants of multidimensional persistent homology groups. Applied Mathematics Letters, 2011. [Google Scholar]
- [13].Camastra Francesco and Staiano Antonino. Intrinsic dimension estimation: advances and open problems. Information Sciences, 2015. [Google Scholar]
- [14].Chazal F, de Silva V, Glisse M, and Oudot S. The Structure and Stability of Persistence Modules. Springer, 2016. [Google Scholar]
- [15].Cohen-Steiner David, Edelsbrunner Herbert, and Harer John. Stability of persistence diagrams. Discrete & Computational Geometry, 37(1), 2007. [Google Scholar]
- [16].Curtin RR, Edel M, Lozhnikov M, Mentekidis Y, Ghaisas S, and Zhang S. mlpack 3: a fast, flexible machine learning library. Journal of Open Source Software, 2018. [Google Scholar]
- [17].Davies S and Hall P. Fractal analysis of surface roughness by using spatial data. Journal of the Royal Statistical Society Series B, 1999. [Google Scholar]
- [18].De Silva Vin and Ghrist Robert. Coverage in sensor networks via persistent homology. Algebraic and Geometric Topology, 2007. [Google Scholar]
- [19].Divol Vincent and Polonik Wolfgang. On the choice of weight functions for linear representations of persistence diagrams. arXiv:1807.03678, July 2018. [Google Scholar]
- [20].Edelsbrunner H, Letscher D, and Zomorodian A. Topological persistence and simplificitaion. Discrete and Computational Geometry, 2002. [Google Scholar]
- [21].Edelsbrunner Herbert and Harer John. Persistent homology — a survey. Contemporary Mathematics, 2008. [Google Scholar]
- [22].Edeslbrunner Herbert and Morozov Dmitriy. Persistent homology: Theory and practice. Technical Report LBNL6037E, Lawrence Berkeley National Laboratory, 2013. [Google Scholar]
- [23].Edgar Gerald A.. Classics on Fractals Studies in Nonlinearity. Westview Press, 2003. [Google Scholar]
- [24].Takens F Dynamical Systems and Bifurcations, chapter On the numerical determination of the dimension of an attractor. Springer, 1985. [Google Scholar]
- [25].Falconer Kenneth. Fractal Geometry: Mathematical Foundations and Applications. Wiley, 2014. [Google Scholar]
- [26].Farmer J Doyne. Chaotic attractors of an infinite-dimensional dynamical system. Physica D: Nonlinear Phenomena, 4(3):366–393, 1982. [Google Scholar]
- [27].Frederickson Paul, Kaplan James L, Yorke Ellen D, and Yorke James A. The Liapunov dimension of strange attractors. Journal of differential equations, 49(2):185–207, 1983. [Google Scholar]
- [28].Gabella Marco, Pavone Sabastiano, and Giovanni Perona. Errors in the estimate of the fractal correlation dimension of raindrop spatial distribution. Journal of Applied Meteorology, 2000. [Google Scholar]
- [29].Garland Joshua, Bradley Elizabeth, and Meiss James D. Exploring the topology of dynamical reconstructions. Physica D: Nonlinear Phenomena, 334:49–59, 2016. [Google Scholar]
- [30].Ghrist Robert. Barcodes: the persistent homology of data. Bulletin of the American Mathematical Society, 2008. [Google Scholar]
- [31].Giusti Chad, Pastalkova Eva, Curto Carina, and Itskov Vladimir. Clique topology reveals intrinsic geometric structure in neural correlations. Proceedings of the National Academy of Sciences, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Gneiting Tilmann, Sevcikova Hana, and Percival Donald. Estimators of fractal dimension: Assessing the roughness of time series and spatial data. Statistical Science, 2012. [Google Scholar]
- [33].Grassberger Peter. Generalizations of the Hausdorff dimension of fractal measures. Physics Letters A, 1984. [Google Scholar]
- [34].Grassberger Peter and Procaccia Itamar. Measuring the strangeness of strange attractors. Physica D: Nonlinear Phenomena, 1983. [Google Scholar]
- [35].Grebogi Celso, Ott Edward, Pelikan Steven, and Yorke James A. Strange attractors that are not chaotic. Physica D: Nonlinear Phenomena, 13(1–2):261–268, 1984. [Google Scholar]
- [36].Greenside HS, Wolf A, Swift J, and Pignataro T. Impracticality of a box-counting algorithm for calculating the dimensionality of strange attractors. Physical Review A, 1982. [Google Scholar]
- [37].Guzzo Luigi, Iovino Angela, Chincarini Guido, Giovanelli Riccardo, and Haynes Martha P.. Scale-invariant clustering in the large-scale distribution of galaxies. Astrophysical Journal, Part 2 - Letters, 1991. [Google Scholar]
- [38].Hammel SM, Jones CKRT, and Moloney Jerome V. Global dynamical behavior of the optical field in a ring cavity. JOSA B, 2(4):552–564, 1985. [Google Scholar]
- [39].Harte D. Dimension estimates of earthquake epicentres and hypocentres. Journal of Nonlinear Science, 1998. [Google Scholar]
- [40].Hauksson Egill, Yang Wenzheng, and Sheare Peter M.. Waveform relocated earthquake catalog for southern California (1981 to june 2011)r. Bulletin of the Seismological Society of America, 2012. [Google Scholar]
- [41].Hausdorff Felix. Dimension und außeres maß. Mathematische Annalen, 1918. [Google Scholar]
- [42].Hénon Michel. A two-dimensional mapping with a strange attractor In The Theory of Chaotic Attractors, pages 94–102. Springer, 1976. [Google Scholar]
- [43].Hiraoka Yasuaki, Nakamura Takenobu, Hirata Akihiko, Escolar Emerson G, Matsue Kaname, and Nishiura Yasumasa. Hierarchical structures of amorphous solids characterized by persistent homology. Proceedings of the National Academy of Sciences, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Hu Song, Sun Xuexing, Xiang Jun, Li Min, Li Peisheng, and Zhang Liqi. Correlation characteristics and simulations of the fractal structure of coal char. Communications in Nonlinear Science and Numerical Simulation, 2003. [Google Scholar]
- [45].Ibarz Borja, Casado José Manuel, and Sanjuán Miguel AF. Map-based models in neuronal dynamics. Physics reports, 501(1–2):1–74, 2011. [Google Scholar]
- [46].Jorba Angel and Tatjer Joan Carles. A mechanism for the fractalization of invariant curves in quasi-periodically` forced 1-d maps. Discrete & Continuous Dynamical Systems-B, 10:537–567, 2008. [Google Scholar]
- [47].Kagan Yan Y.. Earthquake spatial distribution: the correlation dimension. Geophysical Journal International, 2007. [Google Scholar]
- [48].Kaplan James L and Yorke James A. Chaotic behavior of multidimensional difference equations In Functional differential equations and approximation of fixed points, pages 204–227. Springer, 1979. [Google Scholar]
- [49].Kesten Harry and Lee Sungchul. The central limit theorem for weighted minimal spanning trees on random points. Annals of Applied Probability, 1996. [Google Scholar]
- [50].Liebovitch Larry S. and Toth Tibor. A fast algorithm to determine fractal dimensions by box counting. Physics Letters A, 1989. [Google Scholar]
- [51].Lin G, Shearer PM, and Hauksson E. Applying a three-dimensional velocity model, waveform cross correlation, and cluster analysis to locate southern California seismicity from 1981 to 2005. Journal of Geophysical Research: Solid Earth, 2007. [Google Scholar]
- [52].Lopes R and Betrouni N. Fractal and multifractal analysis: A review. Medical Image Analysis, 2009. [DOI] [PubMed] [Google Scholar]
- [53].Lorenz Edward N. Deterministic nonperiodic flow. Journal of the atmospheric sciences, 20(2):130–141, 1963. [Google Scholar]
- [54].Lovejoy Shaun and Schertzer Daniel. Fractals, raindrops and resolution dependence of rain measurements. Journal of Applied Meteorology, 1990. [Google Scholar]
- [55].Mackey Michael C and Glass Leon. Oscillation and chaos in physiological control systems. Science, 197(4300):287–289, 1977. [DOI] [PubMed] [Google Scholar]
- [56].MacPherson RD and Schweinhart B. Measuring shape with topology. Journal of Mathematical Physics, 53(7), 2012. [Google Scholar]
- [57].Mandelbrot Benoît. Fractals: Form, Chance and Dimension. W.H.Freeman & Company, 1977. [Google Scholar]
- [58].Mandelbrot Benoît. The Fractal Geometry of Nature. W. H. Freeman and Co., 1982. [Google Scholar]
- [59].March William B., Ram Parikshit, and Gray Alexander G.. Fast Euclidean minimum spanning tree: Algorithm, analysis, and applications. KDD ‘10 Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining, 2010. [Google Scholar]
- [60].Maria Clément. Persistent cohomology In GUDHI User and Reference Manual. GUDHI Editorial Board, 2015. [Google Scholar]
- [61].Martinez Vicent J., Dominguez-Tenreiro R, and Roy LJ. Hausdorff dimension from the minimal spanning tree. Physical Review E, 1992. [DOI] [PubMed] [Google Scholar]
- [62].Mischaikow Konstantin, Mrozek Marian, Reiss J, and Szymczak Andrzej. Construction of symbolic dynamics from experimental time series. Physical Review Letters, 82(6):1144, 1999. [Google Scholar]
- [63].Mo Dengyao and Huang Samuel H.. Fractal-based intrinsic dimension estimation and its application in dimensionality reduction. IEEE Transactions on Knowledge and Data Engineering, 2012. [Google Scholar]
- [64].Myers Audun, Munch Elizabeth, and Khasawneh Firas A. Persistent homology of complex networks for dynamic state detection. arXiv preprint arXiv:1904.07403, 2019. [DOI] [PubMed] [Google Scholar]
- [65].Nerenberg MAH and Essex Christopher. Correlation dimension and systematic geometric effects. Physical Review A, 1990. [DOI] [PubMed] [Google Scholar]
- [66].Peng Xin, Qi Wei, Wang Mengfan, Su Rongxin, and He Zhimin. Backbone fractal dimension and fractal hybrid orbital of protein structure. Communications in Nonlinear Science and Numerical Simulation, 2013. [Google Scholar]
- [67].Renyi Alfred. Probability Theory. North Holland Publishing Company, 1970. [Google Scholar]
- [68].Rieu Michel and Sposito Garrison. Fractal fragmentation, soil porosity, and soil water properties: I. theory. Soil Science Society of America Journal, 1991. [Google Scholar]
- [69].Robins Vanessa. Computational topology at multiple resolutions: foundations and applications to fractals and dynamics. PhD thesis, University of Colorado at Boulder, 2000. [Google Scholar]
- [70].Rosenberg Eric. A Survey of Fractal Dimensions of Networks. Springer, 2018. [Google Scholar]
- [71].Rouvreau Vincent. Alpha complex In GUDHI User and Reference Manual. GUDHI Editorial Board, 2015. [Google Scholar]
- [72].Rulkov Nikolai F. Regularization of synchronized chaotic bursts. Physical Review Letters, 86(1):183, 2001. [DOI] [PubMed] [Google Scholar]
- [73].Saadatfar Mohammad, Takeuchi Hiroshi, Robins Vanessa, Francois Nicolas, and Hiraoka Yasuaki. Pore configuration landscape of granular crystallization. Nature Communications, 8, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Sarkar N and Chaudhuri BB. An efficient differential box-counting approach to compute fractal dimension of image. IEEE Transactions on Systems, Man, and Cybernetics, 1994. [Google Scholar]
- [75].Sauer Tim, Yorke James A, and Casdagli Martin. Embedology. Journal of statistical Physics, 65(3–4):579–616, 1991. [Google Scholar]
- [76].SCEDC. Southern california earthquake center, 2013. Caltech.Dataset.
- [77].Schweinhart B. The persistent homology of random geometric complexes on fractals. arXiv:1808.02196 [Google Scholar]
- [78].Schweinhart Benjamin. Persistent homology and the upper box dimension. arXiv:1802.00533, 2018. [Google Scholar]
- [79].Julien Clinton Sprott and George Rowlands. Improved correlation dimension calculation. International Journal of Bifurcation and Chaos, 11(07):1865–1880, 2001. [Google Scholar]
- [80].Michael Steele J. Growth rates of Euclidean minimal spanning trees with power weighted edges. Annals of Probability, 1988. [Google Scholar]
- [81].Takens Floris. Dynamical Systems and Turbulence, chapter Detecting Strange Attractors in Turbulence, pages 366–381. Springer, 1980. [Google Scholar]
- [82].Taylor Charles C. and Taylor James. Estimating the dimension of a fractal. Journal of the Royal Statistical Society. Series B (Methodological), 1991. [Google Scholar]
- [83].Theiler James. Estimating fractal dimension. Journal of the Optical Society of America A, 1990. [Google Scholar]
- [84].Theiler James. Statistical precision of dimension estimators. Physical Review A, 1990. [DOI] [PubMed] [Google Scholar]
- [85].Theiler James Patrick. Quantifying Chaos: Practical Estimation of the Correlation Dimension. PhD thesis, California Institute of Technology, 1988. [Google Scholar]
- [86].Traina Caetano, Traina Agma, Wu Leejay, and Faloutsos Christos. Fast feature selection using fractal dimension. Journal of Information and Data Management, 2010. [Google Scholar]
- [87].van de Weygaert Rien, Jones Bernard J.T., and Martinez Vincent J.. The minimal spanning tree as an estimator for generalized dimensions. Physics Letters A, 1992. [Google Scholar]
- [88].Vietoris Leopold. Uber den höheren zusammenhang kompakter räume und eine klasse von zusammenhangstreuen¨ abbildungen. Mathematische Annalen, 1927. [Google Scholar]
- [89].Xia Kelin and Wei Guo-Wei. Persistent homology analysis of protein structure, flexibility, and folding. International journal for numerical methods in biomedical engineering, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [90].Young Lai-Sang. Dimension, entropy and Lyapunov exponents. Ergodic theory and dynamical systems, 2(1):109–124, 1982. [Google Scholar]
- [91].Young Lai-Sang. Mathematical theory of Lyapunov exponents. Journal of Physics A: Mathematical and Theoretical, 46(25):254001, 2013. [Google Scholar]
- [92].Yu Boming. Analysis of flow in fractal porous media. Applied Mechanics Reviews, 2008. [Google Scholar]
- [93].Yukich JE. Asymptotics for weighted minimal spanning trees on random points. Stochastic Processes and their Applications, 2000. [Google Scholar]


