Activity Dependent and Independent Determinants of Synaptic Size Diversity

The extraordinary diversity of excitatory synapse sizes is commonly attributed to activity-dependent processes that drive synaptic growth and diminution. Recent studies also point to activity-independent size fluctuations, possibly driven by innate synaptic molecule dynamics, as important generators of size diversity.

Abstract

The extraordinary diversity of excitatory synapse sizes is commonly attributed to activity-dependent processes that drive synaptic growth and diminution. Recent studies also point to activity-independent size fluctuations, possibly driven by innate synaptic molecule dynamics, as important generators of size diversity. To examine the contributions of activity-dependent and independent processes to excitatory synapse size diversity, we studied glutamatergic synapse size dynamics and diversification in cultured rat cortical neurons (both sexes), silenced from plating. We found that in networks with no history of activity whatsoever, synaptic size diversity was no less extensive than that observed in spontaneously active networks. Synapses in silenced networks were larger, size distributions were broader, yet these were rightward-skewed and similar in shape when scaled by mean synaptic size. Silencing reduced the magnitude of size fluctuations and weakened constraints on size distributions, yet these were sufficient to explain synaptic size diversity in silenced networks. Model-based exploration followed by experimental testing indicated that silencing-associated changes in innate molecular dynamics and fluctuation characteristics might negatively impact synaptic persistence, resulting in reduced synaptic numbers. This, in turn, would increase synaptic molecule availability, promote synaptic enlargement, and ultimately alter fluctuation characteristics. These findings suggest that activity-independent size fluctuations are sufficient to fully diversify glutamatergic synaptic sizes, with activity-dependent processes primarily setting the scale rather than the shape of size distributions. Moreover, they point to reciprocal relationships between synaptic size fluctuations, size distributions, and synaptic numbers mediated by the innate dynamics of synaptic molecules as they move in, out, and between synapses.

SIGNIFICANCE STATEMENT Sizes of glutamatergic synapses vary tremendously, even when formed on the same neuron. This diversity is commonly thought to reflect the outcome of activity-dependent forms of synaptic plasticity, yet activity-independent processes might also play some part. Here we show that in neurons with no history of activity whatsoever, synaptic sizes are no less diverse. We show that this diversity is the product of activity-independent size fluctuations, which are sufficient to generate a full repertoire of synaptic sizes at correct proportions. By combining modeling and experimentation we expose reciprocal relationships between size fluctuations, synaptic sizes and synaptic counts, and show how these phenomena might be connected through the dynamics of synaptic molecules as they move in, out, and between synapses.

Introduction

Properties of mammalian glutamatergic synapses can be extremely diverse. This diversity is manifested in the broad distributions of many functional and morphological properties, such as postsynaptic current amplitude, dendritic spine volume and postsynaptic density (PSD) area. Such distributions are not only broad but also rightward skewed and heavy-tailed, and are often described as log-normal (Murthy et al., 1997; Harms and Craig, 2005; Harms et al., 2005; Song et al., 2005; Arellano et al., 2007; Lefort et al., 2009; Minerbi et al., 2009; Loewenstein et al., 2011; Ikegaya et al., 2013; Keck et al., 2013; Statman et al., 2014; Cossell et al., 2015; Zhang et al., 2015; Hobbiss et al., 2018; Ishii et al., 2018; Masch et al., 2018; Sakamoto et al., 2018; Sammons et al., 2018; Wegner et al., 2018; Santuy et al., 2018; for review, see Barbour et al., 2007; Buzsáki and Mizuseki, 2014; Scheler, 2017). Such distributions, reflecting of a majority of weak/small synapses and a diminishing tail of increasingly stronger/larger synapses, were suggested to optimize storage capacity, neuronal firing rates and long-distance information transfer and thus impart important properties to neuronal networks (Song et al., 2005; Barbour et al., 2007; Lefort et al., 2009; Ikegaya et al., 2013; Buzsáki and Mizuseki, 2014; Scheler, 2017; Humble et al., 2019).

The diversity of synaptic sizes reflected in these distributions is commonly assumed to result from activity-dependent synaptic plasticity that drives the growth of some synapses and the downsizing of others. Moreover, the skewed shape of these distributions is assumed to reflect the cumulative outcome of such processes (van Rossum et al., 2000; Song et al., 2005; Lefort et al., 2009; Gilson and Fukai, 2011; Zheng et al., 2013; Buzsáki and Mizuseki, 2014; Effenberger et al., 2015; Scheler, 2017; Uzan et al., 2018). Somewhat unexpectedly, however, synaptic size diversity does not seem to be markedly reduced in animals that develop in the complete absence of synaptic transmission (Lu et al., 2013; Sando et al., 2017; Sigler et al., 2017), echoing findings of earlier cell\organotypic-culture studies (Harms and Craig, 2005; Harms et al., 2005; Yasumatsu et al., 2008).

Longitudinal in vitro and in vivo imaging reveals that sizes of individual glutamatergic synapses fluctuate considerably over time scales of hours and days (Yasumatsu et al., 2008; Minerbi et al., 2009; Loewenstein et al., 2011; Kaufman et al., 2012; Fisher-Lavie and Ziv, 2013; Cane et al., 2014; Ishii et al., 2018; for review, see Ziv and Brenner, 2018). Importantly, such fluctuations persist following abrupt suppressions of network activity or synaptic transmission (Yasumatsu et al., 2008; Minerbi et al., 2009; Dvorkin and Ziv, 2016). These intrinsic fluctuations, probably driven by the innate dynamics of synaptic molecules—binding, unbinding, and turnover (Kasai et al., 2010; Ziv and Fisher-Lavie, 2014; Shomar et al., 2017; Triesch et al., 2018)—were suggested to drive synaptic size diversification and determine the shape and scale of size distributions (Yasumatsu et al., 2008; Minerbi et al., 2009; Kasai et al., 2010, Loewenstein et al., 2011; Kaufman et al., 2012; Statman et al., 2014; Shomar et al., 2017; Ishii et al., 2018; Ziv and Brenner, 2018; Humble et al., 2019). It remains unclear, however, whether intrinsic size fluctuations are indeed sufficient to give rise to a full repertoire of synaptic sizes and at the right proportions.

Given the significance attributed to synaptic “weights”, understanding the fundamental forces that drive synaptic size diversification and define proportions of differently sized synapses would seem to be important. We therefore set out to examine the contributions of activity-dependent and -independent processes to synaptic size diversification. We first asked whether intrinsic, activity-independent size fluctuations are sufficient to give rise to a full repertoire of synaptic sizes. We then examined how innate processes that drive intrinsic fluctuations might set the shape and scale of synaptic size distributions and define the sizes of synaptic populations. Finally, we studied interrelationships between these processes and how these are affected by network activity.

Materials and Methods

Experimental design and statistical analyses.

Because of the long duration of each experiment (∼1 week), data could not be collected as age-matched pairs from the same cell-culture preparations. Thus, individual experiments typically came from separate cell-culture preparations, resulting in extensive sampling of preparations, reducing sensitivity to this source of variability. Comparisons between treatments were typically based on tens (neurons) or thousands (synapses) of data points except for biochemical and proteomic studies (see Fig. 8), which were based on 2(7) and 2(4) separate experiments (replicates), respectively.

Figure 8.

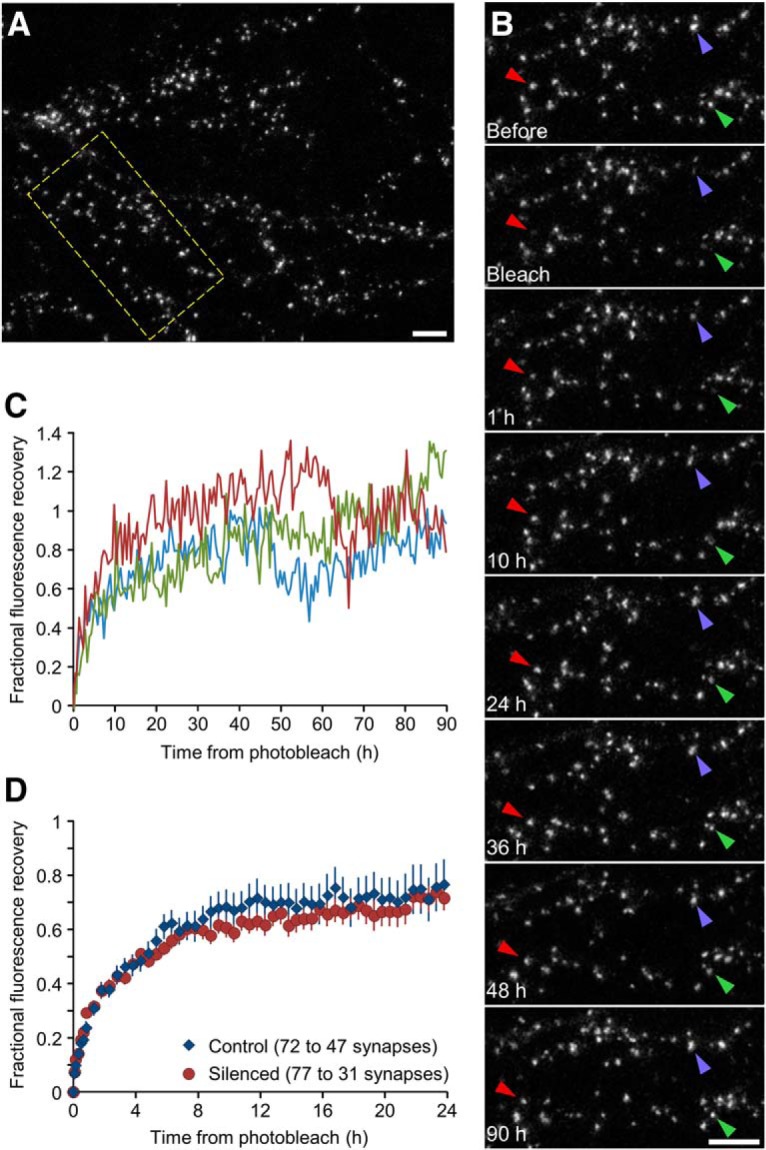
Fluorescence recovery after photobleaching recovery curves. A, A neuron in a silenced network expressing PSD-95:EGFP. Scale bar, 10 μm. B, FRAP of three synapses (arrowheads) in region enclosed in rectangle in A. After photobleaching, the synapses were followed for 90 h. Scale bar, 10 μm. C, Recovery curves for the three synapses shown in B. D, Mean (±SEM) recovery curves in silenced and control networks (77 synapses from 6 experiments and 72 synapses from 7 experiments, respectively). Note that the duration over which photobleached synapses could be tracked varied, resulting in lower numbers of tracked synapses at longer time points.

Statistical tests used were based on minimal assumptions. Specific tests used and significance values are provided in the main text and figure legends. Error bars are either SD or SEM as indicated in legends.

All software used for simulations of Figures 5 and 6 (Visual Basic for Applications), and Figures 7, 9, and 10 (C code) was posted on line (see the section “Code accessibly”); data used to create all plots and the full proteomic dataset are available upon request.

Figure 5.

Simulating synaptic size dynamics as a stochastic Kesten process. A, Sizes of 1922 synapses were initialized using the experimental data of Figure 4F (t = 24) and evolved as stochastic Kesten processes for 320 steps using values of <ϵ> (and <η>) obtained in control networks (4J). Simulation parameters are indicated at bottom. Synaptic sizes at the last simulation step were plotted against their sizes 24 steps beforehand. Dashed line is a linear regression fit, whose parameters and coefficient of determination (R²) are indicated (top). B, Same data as in A, plotted as size change in last 24 steps as a function of synaptic size 24 h beforehand. Dashed line is a linear regression fit. C, Synaptic size distributions along the simulation. Dashed line is the experimentally measured distribution of normalized PSD-95 fluorescence of 1922 tracked synapses. Note the stability of this distribution over the duration of the simulation. D–F, Same as A–C but for 2032 synapses in chronically silenced networks using the experimentally derived values of <ϵ> (and <η>) obtained in silenced networks (Fig. 4J). G–I, Magnitude of synaptic size fluctuations in the simulated data using <ϵ> and <η> values derived from silenced and control networks. Averages of SDs, coefficients of variation and range/mean values calculated for all synapses over the last 24 simulation steps. Indicated p values are for t tests assuming unequal variances. J, Rates of synaptic elimination during simulations, that is, synapses whose sizes momentarily reached a value of zero and were thereafter removed. K, Convergence rates to stable (limiting) distributions. Four thousand synapses were initialized to a uniform value of 0.1 and evolved for 480 steps using values of <ε> (and <η>) obtained in control networks. L, Same as K using <ε> (and <η>) values obtained in chronically silenced networks. Note the slower convergence to the limiting distribution compared with K. M, Synaptic elimination during the simulations of K and L.

Figure 6.

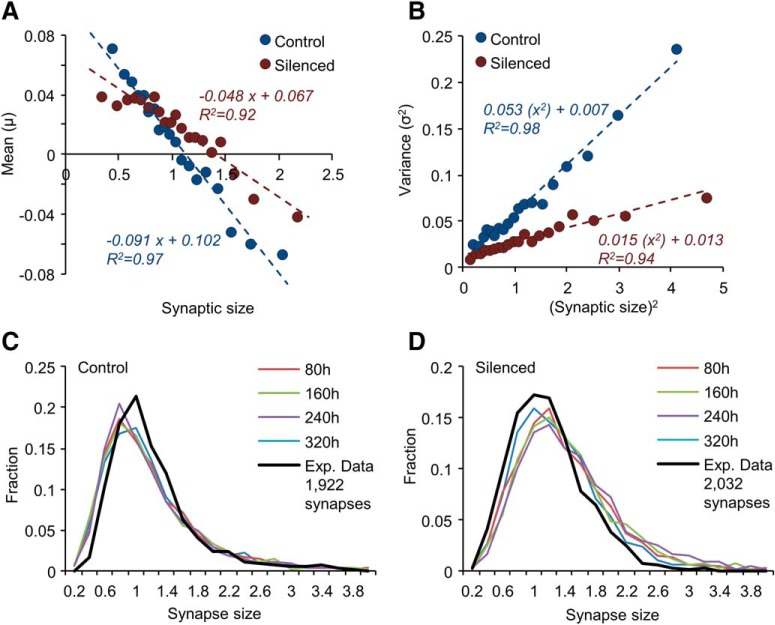
Simulating synaptic size dynamics as a nonlinear Langevin process. A, B, Statistics of synaptic size change. Means (μ; A), and variances (σ²; B) of size changes as functions of initial synaptic size (normalized). Data obtained from synapses tracked for 24 h. Each data point represents the average (A) or the variance (B) of size changes in a group of changes measured at 8 h intervals, binned by initial size (20 groups, 1764 and 1852 size change measurements in each group, control and silenced networks, respectively). The horizontal position of each dot represents the average initial size (A) or the square of this value (B) within the group. Dashed lines are linear regression fits to the data points; fit parameters are shown near each regression line. C, D, Evolution of synaptic sizes. Sizes of 1922 synapses (C; Control) and 2032 (D; Silenced) synapses were initialized using the experimental data of Figure 4F (t = 24) and evolved as a discrete nonlinear Langevin process as described in the main text and in Materials and Methods, using the parameters derived from A and B. Size distributions at 80 h intervals (10 simulation steps) are shown as color coded plots. Black lines are experimentally measured distributions. The small differences from experimentally measured distributions mainly result from the slight mismatch between estimates of <ϵ −1> and <η>, that should be identical in stationary distributions. This might reflect estimation errors or indicate that distributions were not yet fully stationary (as predicted by Fig. 5K,L, in particular for silenced networks).

Figure 7.

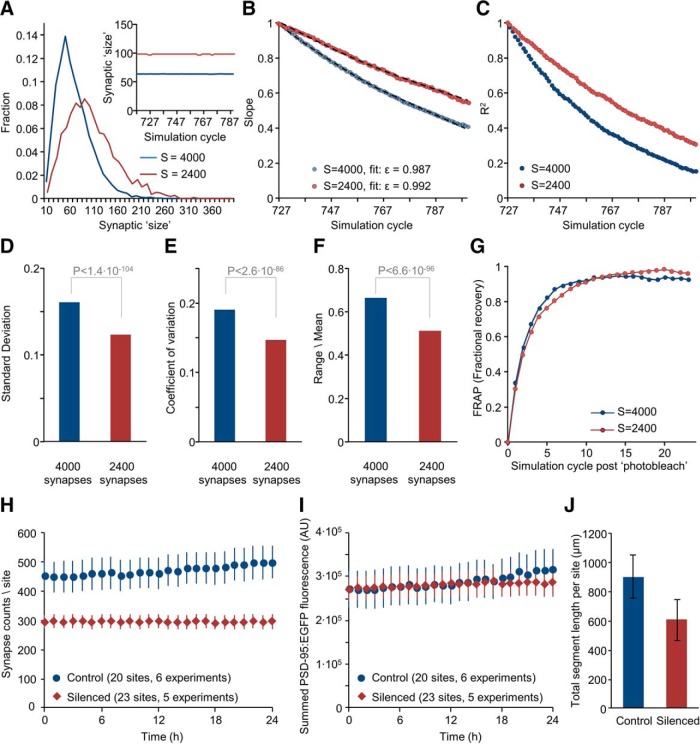
Relationships between innate synaptic molecule dynamics and synaptic size dynamics and distributions. A, Illustration of the mesoscopic model used here to explore the aforementioned relationships. The model includes 4000 simulated synapses, each of which consists of a postsynaptic membrane - a 50 × 50 matrix of potential binding sites (slots) and synaptic scaffold molecules that bind to and unbind from these slots with indicated probabilities (see text for further details). The dark gray area indicates the immediate 3 × 3 neighborhood that influences the binding and unbinding probabilities, in this case of the light blue molecule. At any given moment, scaffold molecules can be either bound (bright blue) or free (light blue). Free molecules are part of a global pool shared by all synapses. B, Limiting distributions of synaptic sizes (4000 synapses) at the last simulation step (cycle 799) for two values of unbinding constants indicated at bottom right. C, Mean synaptic size during last 72 simulation steps. D, Synaptic sizes at last stimulation step plotted against their sizes 24 steps beforehand for the same two unbinding constant values. Linear regression fits to the two datasets and their respective parameters are shown. E, Slopes of linear regression lines as in D for the 72 last simulation steps for the two unbinding constants; apparent <ϵ> values derived from these data are indicated. Fits using these values of <ϵ> are shown as black dashed lines. F, Coefficients of determination (R²) of linear regression fits as in D for the 72 last simulation steps and two unbinding constants. G, Size changes for the two unbinding constants after 24 simulation steps (cycles 776–799) plotted as a function of initial size (cycle 776). Lines are linear regression fits. Fit parameters are indicated accordingly. H–J, Magnitudes of synaptic size fluctuations in data simulated for the two unbinding constants. Averages of SDs, coefficients of variation, and range/mean values calculated for all synapses over the last 24 simulation steps. Indicated p values are for t tests assuming unequal variances. K, Simulated FRAP curves for the two unbinding constants (200 synapses, 24 simulation time steps).

Figure 9.

Effects of increased PSD-95 abundance on innate synaptic molecule dynamics, synaptic size dynamics and size distributions. A, Simulated limiting distributions of synaptic sizes (4000 synapses, last step of simulations) for two levels of global PSD-95 abundance (N_total) as indicated at bottom right. Inset, Mean synaptic size during last 72 simulation steps. B, Slopes of linear regression lines as in Figure 7D for the last 72 simulation steps for the two values of N_total; apparent <ϵ> values derived from these data are indicated. Fits using these values of <ϵ> are shown as black dashed lines. C, Coefficients of determination (R²) of linear regression fits as in Figure 7D for the last 72 simulation steps for two N_total values. D–F, Magnitude of synaptic size fluctuations in the simulated data for the two values of N_total. Averages of SDs, coefficient of variations and range/mean values calculated for all synapses over the last 24 simulation steps. Indicated p values are for t tests assuming unequal variances. G, Simulated FRAP curves for the two N_total values (200 synapses, 24 simulation time steps). H, Western blots of total PSD-95 levels in chronically silenced and control networks. Four networks in each condition. I, Average (±SEM) of normalized density of PSD-95 bands in Western blots from silenced and control networks (7 replicates from 2 experiments). Difference was not statistically significant (p = 0.62; t test assuming unequal variances). J, SILAC-based comparisons of synaptic protein abundance in silenced and control preparations. Mean ± SD of estimates from four replicates (or 3 where indicated; numbers in bars, top row). Numbers in bars (bottom row) indicate total number of peptides used to obtain H–M estimates. Legend, Gene name followed by common name.

Figure 10.

Effects of silencing on synaptic counts and innate synaptic molecule dynamics. A, Simulated limiting distributions of synaptic sizes (4000 and 2400 synapses, last simulation step) using the same value of N_total (= 640,000). Inset, Mean synaptic size during last 72 simulation steps. B, Slopes of linear regression lines as in Figure 7D for the last 72 simulation steps for 4000 and 2400 simulated synapses; apparent <ϵ> values derived from these data are indicated. Fits using these values of <ϵ> are shown as black dashed lines. C, Coefficients of determination (R²) of linear regression fits as in Figure 7D for the last 72 simulation steps. D–F, Magnitude of synaptic size fluctuations in the simulated data for 4000 and 2400 simulated synapses. Averages of SDs, coefficients of variation and range/mean values calculated for all synapses over the last 24 simulation steps. Indicated p values are for t tests assuming unequal variances. G, Simulated FRAP curves for simulations of 4000 and 2400 synapses (200 photobleached synapses, 24 simulation time steps). H, Average (±SEM) PSD-95:EGFP puncta counts per field-of-view (site) measured in silenced and control networks over 24 h periods (same dataset as in Fig. 2). I, Average (±SEM) of summed PSD-95:EGFP puncta fluorescence in each field-of-view in silenced and control networks. J, Total dendritic segment length per field-of-view (μm, average ± SD) in silenced and control networks (20 and 20 fields-of-view, respectively).

Cell culture.

Primary cultures of rat cortical neurons were prepared as described previously (Minerbi et al., 2009) using a protocol approved by the Technion committee for the supervision of animal experiments (IL-116-08-71). Briefly, cortices of newborn (1 d-old) Wistar rats (either sex; Charles River Laboratories) were dissected, dissociated by trypsin treatment followed by trituration using a siliconized Pasteur pipette. A total of 1–1.5 × 10⁶ cells were then plated on thin-glass multielectrode array (MEA) dishes (Multi Channel Systems MCS), precoated with polyethylenimine (Sigma-Aldrich) to facilitate cell adherence. The preparations were then transferred to a humidified tissue culture incubator and maintained at 37°C in a gas mixture of 5% CO₂, 95% air, and grown in medium containing minimal essential medium (MEM; Sigma-Aldrich), 25 mg/L insulin (Sigma-Aldrich), 20 mm glucose (Sigma-Aldrich), 2 mm l-glutamine (Sigma-Aldrich), 5 mg/ml gentamycin sulfate (Sigma-Aldrich), and 10% NuSerum (Becton Dickinson Labware). Seven days after plating, one-half of the culture medium was replaced with feeding medium similar to the medium described, but devoid of NuSerum, containing a lower l-glutamine concentration (0.5 mm) and 2% B-27 supplement (Invitrogen). Approximately one-half of the medium was then replaced three to four times per week.

DNA constructs, lentivirus production, and transduction.

A third generation lentiviral expression system was used to introduce exogenous DNA into rat cortical neurons. The vector used here [FU(PSD-95:EGFP)W] was described in detail by Minerbi et al. (2009). Lentiviral particles were produced using a mixture of the expression vector and the packaging vector mix of the ViraPower plasmid lentiviral expression system (Invitrogen). HEK293T cells were cotransfected with a mixture of FU(PSD-95:EGFP)W and the three packaging plasmids: pLP1, pLP2, and pLP\VSVG. Transfection was performed in T75 flasks when the cells had reached 80% confluence, using 3 μg of the vector, 9 μg of the packaging mixture, and 36 μl of Lipofectamine 2000 (Invitrogen). Supernatant was collected after 48 and 72 h, filtered through 0.45 μm filters, aliquoted, and stored at −80°C. Transduction of cortical cultures was performed on Day 4–5 in vitro by adding 20 μl of the filtered supernatant to each MEA dish.

Pharmacological manipulations.

To chronically silence network activity, a mixture of three pharmacological agents was used: tetrodotoxin (TTX; Alomone Labs), (2R)-amino-5 phosphono pentanoate (APV; Sigma-Aldrich) and 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX; Sigma-Aldrich). The agents were first applied on Day 1 in vitro, and additionally applied to feeding media every 3 consecutive days to maintain the same concentration in media. Final concentrations in the MEA dish were 1 μm (TTX), 10 μm (CNQX), and 50 μm (APV). These agents were also added to the perfusion media during long-term imaging sessions.

Electrophysiological recordings.

Network activity was recorded continuously from MEA electrodes (59 electrodes, 30 μm diameter, arranged in an 8 × 8 array, spaced 200 μm apart). A submerged platinum wire loop connected to a custom designed cap covering the MEA dish was used as a common reference (ground). Recordings from MEA dishes were performed using a commercial 60-channel headstage (inverted MEA-1060-BC, MCS) with a gain of 53× and frequency limits of 0.02–8500 Hz. This signal was further filtered with frequency limits of 150–3000 Hz and amplified (20×) using a filter/amplifier (FA60S-BC, MCS). The 60 channels of amplified and filtered data were connected to 60 of the 64 analog to digital input channels of a data acquisition board (PD2-MF-64-3M/12; United Electronic Industries) using a home built connection box. Data acquisition was performed using custom software [Closed Loop Experiment Manager (CLEM); Hazan and Ziv, 2017]. Data were collected at 16 kSamples/s. Action potentials were identified as negative threshold-crossing events, with the threshold calculated as 5× root-mean-square of traces recorded at the beginning of each experiment. Data were imported, converted and analyzed using custom scripts in MATLAB (MathWorks).

Long-term imaging.

All fluorescence and bright-field images were obtained from neurons growing on thin glass MEA dishes, as described in the section “Cell culture”. These particular dishes are fabricated of very thin glass (180 μm), which allows for the use of high numerical aperture, oil-immersion objectives and are thus ideally suited for high-resolution imaging. Images were acquired using a custom-built confocal laser scanning (inverted) microscope based on a Zeiss Axio Observer Z1 using a 40×, 1.3 NA Plan-Fluar objective. The system was controlled by custom software and includes provisions for automated, multisite time-lapse microscopy. MEA dishes were mounted on the headstage/amplifier, which was attached to the microscope's motorized stage. The dish was covered with a custom-designed cap containing inlet and outlet ports for perfusion and air as well as a reference ground electrode as mentioned above. Continuous perfusion with fresh feeding medium (described in the section “Cell culture”) was performed at a rate of 4 ml/d using an ultra-low-flow peristaltic pump (Instech Laboratories), and a pair of silicon tubes. The tubes were connected to the dish through the appropriate ports in the custom-designed cap. A mixture of 95% air and 5% CO₂ was continuously streamed into the dish at very low rates through a third port, with flow rates regulated by a high-precision flow meter (Gilmont Instruments). The base of the headstage/amplifier and the objective were heated to 37°C and 36°C, respectively, using resistive elements, separate temperature sensors, and controllers, resulting in temperatures of ∼37°C in the culture medium. Images of PSD-95:EGFP were obtained by excitation at 488 nm using a solid-state continuous wave laser (Coherent) and emissions were read simultaneously through a 500–550 nm bandpass filter (Semrock) and >570 nm (Chroma) after splitting the emission between two detectors using a 555 nm long-pass filter (Chroma). Time-lapse recordings were usually performed by averaging 5 frames at 10 focal planes spaced 0.8 μm apart. All data were collected at a resolution of 640 × 480 pixels, at 12 bits/pixel. Data were collected sequentially from multiple sites using a motorized stage to cycle automatically through these sites at 60 min intervals. Focal drift was corrected automatically by using the confocal microscope autofocus system.

Fluorescence recovery after photobleaching.

Photobleaching was performed by defining 16 × 16 pixel (∼3.2 × 3.2 μm) regions-of-interest and scanning them repeatedly at 488 nm at high illumination intensity using the imaging systems' acousto-optical tunable filter to limit illumination to the defined regions. Photobleaching was controlled through the confocal microscope's ActiveX interface from scripts written in Visual Basic for Applications executed in Microsoft Excel. Fluorescence of each photobleached synapse was normalized (Ft, norm) according to:

Where F_t is the fluorescence at time t, F_min is fluorescence at the end of the photobleaching procedure, and F₀ is the fluorescence just before the photobleaching procedure.

Image analysis.

All image analysis was performed using custom written software (“OpenView”), which allows for automated or manual tracking of individual fluorescent puncta and measuring their fluorescence intensities over time (Kaufman et al., 2012). 9 × 9 pixel (∼1.8 × 1.8 μm) areas were centered on fluorescent puncta and mean pixel intensities within these areas were obtained from maximal intensity projections of Z section stacks. For measuring distributions of puncta intensities, areas were placed programmatically on fluorescent puncta at each time step using identical parameters. For tracking identified puncta, areas were placed initially over all puncta and then a smaller subset (typically 200 per site) was tracked thereafter. As the reliability of automatic tracking was not absolute, all tracking was verified and, whenever necessary, corrected manually. Puncta for which tracking was ambiguous were excluded.

To correct for some neuron to neuron variability in PSD-95:EGFP expression levels, raw puncta fluorescence measurements were normalized to mean PSD-95:EGFP puncta fluorescence of each neuron at the first time point (determined by placing areas programmatically on fluorescent puncta in the field-of-view), allowing us to pool data from different neurons and experiments.

Images for figures were processed by uniform contrast enhancement and low-pass filtering using Adobe Photoshop and prepared for presentation using Microsoft PowerPoint.

Western blots.

Cortical cell preparations were grown in 12-well plates whose surface had been pretreated with polyethylenimine (Sigma-Aldrich) to facilitate cell adherence. Cells were washed using Tyrode's solution (in mm:119 NaCl, 2.5 KCl, 2 CaCl₂, 25 HEPES, 30 glucose, buffered to pH 7.4) and lysed in RIPA buffer, 8M urea, 100 mm Tris-HCl. Protein concentrations were measured by the Bradford assay, using BSA as the standard. Equal protein amounts (25 μg) were separated by SDS gel electrophoresis and transferred to nitrocellulose membranes. Membranes were blocked by nonfat milk, and then staining was performed using anti PSD-95 (Clone 108E10, Synaptic Systems; 1:1000) and anti-Actin (Merck; 1:10,000) as primary antibodies. As a secondary antibody, peroxidase-conjugated, anti-mouse (ImmunoResearch Laboratories; 1:10,000) was used. Before exposure, ECL (Enhanced Chemiluminescence, Pierce) was used for immunodetection.

Multiplexed SILAC and mass spectrometry.

For multiplexed SILAC experiments, cells were prepared, raised in, and fed with lysine and arginine-free MEM (Biological Industries) to which “heavy” (H) variants (Lys8, [¹³C₆, ¹⁵N₂]; Arg10, [¹³C₆, ¹⁵N₄]) or “medium” (M) variants (Lys6, [¹³C₆]; Arg6, [¹³C₆]), were added to match nominal lysine and arginine concentrations in standard cell culture media (0.4 and 0.6 mm, respectively). Cells were harvested after 21–22 d in culture by scraping in lysis buffer containing 10% SDS, mixed together (as pairs of silenced and control sets) and run on preparative gels as follows: 20% of protein mixtures with additional concentrated Laemmli buffer were sonicated, boiled and separated on 4–15% SDS-PAGE. Each lane was sliced into 5 sections (1 being the stacking gel section), which were analyzed separately. Proteins in each slice were reduced with 3 mm DTT (60°C for 30 min), modified with 10 mm iodoacetamide in 100 mm ammonium bicarbonate (in the dark, room temperature for 30 min) and digested in 10% acetonitrile and 10 mm ammonium bicarbonate with modified trypsin (Promega) at a 1:10 enzyme-to-substrate ratio, overnight at 37°C. An additional second trypsinization was done for 4 h. The resulting tryptic peptides were desalted using C18 tips (Harvard) dried and resuspended in 0.1% Formic acid. Peptides were analyzed by LC-MS/MS using a Q Exactive HF mass spectrometer (ThermoFisher) fitted with a capillary HPLC (Easy nLC 1000, ThermoFisher). The peptides were loaded onto a homemade capillary column (25 cm, 75 μm ID) packed with Reprosil C18-Aqua (Dr. Maisch GmbH, Germany) in solvent A (0.1% formic acid in water). Peptide mixtures were resolved with a 5–28% linear gradient of solvent B (95% acetonitrile with 0.1% formic acid) for 105 min followed by gradient of 15 min gradient of 28–95% and 15 min at 95% acetonitrile with 0.1% formic acid in water at flow rates of 0.15 μl/min. MS was performed in positive mode (m/z 300–1800, resolution 120,000) using repetitive full MS scans followed by collision-induced dissociation (HCD, at 27 normalized collision energy) of the 20 most dominant ions (>1 charges) selected from the first MS scan. A dynamic exclusion list was enabled with exclusion duration of 20 s.

MS data were analyzed using MaxQuant 1.5.2.8. (http://www.maxquant.org) searching against the rat Uniprot database with mass tolerance of 20 ppm for the precursor masses and 20 ppm for the fragment ions and 4.5 ppm after calibration. Oxidation on methionine, phosphorylation on STY, gly-gly on K, and protein N-terminus acetylation were accepted as variable modifications and carbamidomethyl on cysteine was accepted as static modifications. Minimal peptide length was set to 6 aa and a maximum of two miscleavages was allowed. Peptide- and protein-level false discovery rates were filtered to 1% using the target-decoy strategy. Protein tables were filtered to eliminate identifications from the reverse database, common contaminants and single peptide identifications. SILAC analysis was performed using the same software. H/M ratios for all peptides belonging to a particular protein species were pooled by the software, providing an average ratio for each protein. Data used in subsequent analyses were filtered according to the following criteria: (1) H/M ratios were quantified for at least 2 peptides in 3 of 4 experiments, and (2) no less than 8 peptides were quantified in total. For the set of 226 synaptic proteins, total peptide numbers per protein were ∼38 ± 25 and ∼32 (average ± SD and median, respectively). All ratios were normalized to median H/M ratios in each sample (2630 stringent proteins only). A median H/M ratio of 1.06 was obtained for 85 ribosomal proteins after this normalization, indicating that normalization was acceptable.

Simulation of synaptic dynamics as Kesten processes.

Simulation of synapse size dynamics as stochastic Kesten processes was done as described by Statman et al., 2014. At the beginning of each simulation, simulated synapses were set to initial values (see next paragraph). Their sizes were then evolved as follows: at each step and for each synapse, random values for ϵ and η were obtained from Gaussian distributions with means of <ϵ> and <η> and SDs as indicated in Figure 5A, D, K, and L. The random ϵ and η values were then used to calculate the new synapse size x_t+1 from the prior size x_t such that x_t+1 = ϵ_tx_t + η_t. Synapses whose “sizes” fell below zero were eliminated (set to 0) and not evolved further. Distributions of synaptic sizes were calculated only for synapses with non-zero sizes.

For each condition (silenced, control), <ϵ> was obtained from experimental data using multilinear regression fits to scatter plots such as those shown in Figure 4D–I (for a detailed explanation of this fitting process, see Statman et al., 2014). For stationary size distributions and for normalized fluorescence data, the value of <η> is 1 − <ϵ> (Statman et al., 2014) and thus <η> was set to 1 − <ϵ>. For the plots in Figure 5A–J, initial synapse sizes were taken from the t = 24 h time point of the ∼2000 synapses tracked in each condition, and these were evolved for 320 time steps. For the plots in Figure 5K–M, 4000 synapses were initialized to an identical value of 0.1 and thereafter evolved for 480 time steps.

Figure 4.

Synaptic size dynamics in chronically silenced networks. A, Magnitude of synaptic size fluctuations in silenced and control networks. The SD of normalized fluorescence was calculated for each synapse over 24 h periods. Each data point is the average of these values for one field-of-view (∼100 synapses, typically belonging to 1 neuron). Twenty-three and 20 fields-of-view for each condition from 5 and 6 separate experiments, respectively. Indicated p values are for t tests assuming unequal variances. B, Same as A but for coefficients of variation calculated for each synapse. C, Same as A but for range/mean values [= (max − min)/mean] calculated for each synapse. D–F, Normalized PSD-95:EGFP fluorescence values of individual synapses in control networks plotted at three time points (2, 12, and 24 h) against their fluorescence at t = 1. Dashed lines are linear regression fits, whose parameters and coefficients of determination (R²) are indicated. Synapses (1922) from six separate experiments. G–I, Same as D–F for chronically silenced networks. Synapses (2032) from five experiments. J, Slopes of linear regression fits in plots such as those of D–I at increasing time points. Filled circles, Synapses tracked for 24 h (same data as in D–I); open circles, a smaller dataset in which synapses were tracked for 48 h (959 and 957 synapses, Control and Silenced networks, respectively). Lines are fits based on <ϵ> values derived from multilinear regression analysis of synapses tracked for 48 h. For further details on this analytical approach, see Statman et al., 2014. K, Coefficients of determination (R²) in plots such as those of D–I at increasing time points. Filled and open circles as in J. L, Changes in normalized PSD-95:EGFP fluorescence after 24 h (fluorescence _{t = 24} − fluorescence _{t = 1}) plotted as a function of fluorescence at t = 1. Lines are linear regression fits to the data. Same data as in F and I. Note the significantly shallower slope of the linear regression fit in silenced networks. Also note that as all data are provided in normalized fluorescence (that is, normalized to mean fluorescence levels of each neuron) the greater absolute PSD-95:EGFP fluorescence in silenced networks is not apparent in these plots.

Simulations were performed using Visual Basic for Applications within Microsoft Excel.

Simulation of synaptic dynamics as a Langevin process.

During the review of this paper, it was pointed out by one of the reviewers that the aforementioned Kesten process can be also formulated as a nonlinear Langevin process, if the noise terms of ϵ and η are assumed to be normally distributed random variables. Specifically, given that the Kesten process is expressed as follows:

then

(note that in this discrete mapping, the actual values of ϵ and η depend on the time interval Δt. For simplicity, we assume Δt = 1 and that ϵ and η values are for this specific time interval).

Assuming that (ϵ−1)_t and η_t are normally distributed random variables then:

where N₁ and N₂ are the random variables with means and variances of a,b (for N₁) and c,d (for N₂), respectively, such that a = <ϵ − 1> (the mean of ϵ − 1), b = σ_ϵ−1² (the variance of ϵ − 1), c = <η> (the mean of η), and d = σ_η² (the variance of η).

Because ϵ and η are assumed to be independent (but see below):

Thus, the Kesten process can be expressed as a nonlinear Langevin process:

After substituting a–d with the equivalent Kesten process terms we arrive at the following:

which is a form of a nonlinear Langevin process.

Although fluctuations in momentary values of ϵ and η are assumed to occur independently (as this is the simplest assumption), the validity of this assumption is unknown. The formulation of the process as a nonlinear Langevin process sidesteps this matter by using a single noise term, which is assumed to be a normally distributed random variable. Note, however, that in the most general case, the Kesten process makes no assumptions on the independence of ϵ and η or the shape of their distributions.

Using this formulation, values for < ϵ − 1 > , < η > ,σ_ϵ−1,σ_η for Δt = 8 h were obtained from linear regression fits to binned synaptic size changes as shown in Figure 6, A and B (Control: −0.0913, 0.1024, 0.2294, 0.0828; Silenced −0.0481, 0.0675, 0.1220, 0.1138, respectively). Then, starting with the experimentally observed distributions in control and silenced networks, we evolved the size of each synapse iteratively for 40, 8 h steps using the Langevin process described, specifically:

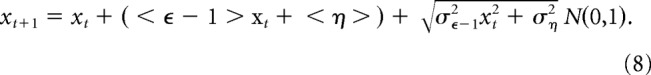Here too, synapses whose sizes fell below zero were eliminated and not evolved further. Distributions of synaptic sizes were calculated only for synapses with non-zero sizes. Simulations were performed using Visual Basic for Applications within Microsoft Excel.

Mesoscopic model of size dynamics.

The mesoscopic model used to explore relationships between binding and unbinding kinetics of synaptic molecules, size fluctuations and distributions was based on the model described by Shomar et al., 2017. Here, each synapse was modeled as a 50 × 50 square matrix of sites/slots to which scaffold molecules can bind. Scaffold molecules could bind nonspecifically directly to the matrix with a low but non-zero probability α and to scaffold molecules in adjacent slots (see Fig. 7A) such that the probability of binding to a particular slot increased linearly with the number of occupied neighboring slots. At each time step and for each unoccupied slot, the fraction of occupied neighboring slots χ, was determined. Then, the probability P_on for a free scaffold molecule to bind to that slot was determined according to (1) λ_on, the maximal binding probability (a constant); (2) χ, the fraction of neighboring occupied slots, and (3) N_free, the amount of free (unbound) scaffold molecules, as well as α, such that:

A random number was then sampled from a uniform distribution between 0 and 1. Binding “occurred” if this number was smaller than P_on, in which case, N_free was decremented.

Similarly, for each step and each occupied site, the chances of unbinding were calculated according to χ, the fraction of occupied neighboring sites and λ_off, the maximal unbinding probability (a constant) such that:

Here too, a random number between 0 and 1 was sampled from a uniform distribution and unbinding occurred if this number was <P_off, in which case, N_free was incremented.

At the beginning of each simulation, all scaffold molecules were placed in the free pool, and matrices were set to be empty. Synaptic size at any time step was defined as the momentary number of molecules bound to its matrix. The procedure described was run for 800 steps for 4000 synapses (matrices), all of which shared (and competed over) a common pool of scaffold molecules. All presented data were taken from the last 72 simulation steps (steps 727–799).

FRAP was simulated by marking the bound molecules of 200 synapses as “bleached” at simulation step 600, and then following their exchange with “unbleached” molecules from the pool of free molecules over the subsequent 200 steps. As typical FRAP data in experiments were obtained from medium to large-sized synapses, FRAP curves in simulations were prepared only from synapses whose average size in the 24 time steps preceding the simulated bleach procedure was equal to or exceeded average synaptic size during this period.

Unless stated otherwise, the following parameters were used: λ_on = 1.25 × 10⁻⁶; λ_off = 0.5; α = 1 × 10⁻⁹; Total scaffold molecules = 640,000.

To attain good performance, simulations were written in C, using the fast cryptographic random number generator ISAAC (indirection, shift, accumulate, add, and count; http://burtleburtle.net/bob/rand/isaacafa.html) to generate streams of pseudorandom numbers. Size trajectories and FRAP data were saved as text files and thereafter imported into Excel for further analysis and presentation.

Code accessibility.

Code for simulations of synaptic size fluctuations, distributions, and loss modeled as Kesten and nonlinear Langevin processes (see Figs. 5, 6; Visual Basic for Applications within Microsoft Excel) can be found on Model DB (http://modeldb.yale.edu/262059).

Code for mesoscopic simulations of synaptic size fluctuations and distributions (see Figs. 7, 9, 10; C code) can be found on Model DB (http://modeldb.yale.edu/262060).

Results

Distributions of synaptic sizes in chronically silenced networks are broad and rightward skewed

As described in the Introduction, much of synaptic size diversity is attributed to myriad synaptic plasticity processes, which depend, in turn, on network activity. It thus might be expected that in neurons with no history of network activity or synaptic transmission, size diversity would be less extensive, and this difference would be manifested in distributions of synaptic sizes. To examine this expectation, we raised networks of cultured rat cortical neurons from Day 1 in culture in TTX (1 μm), CNQX (10 μm), and APV (50 μm), potent inhibitors of voltage gated sodium channels, AMPA-type and NMDA-type glutamate receptors, respectively. No overt effects on cell viability were observed, in agreement with many early studies (van Huizen et al., 1985, Ramakers et al., 1993; Craig et al., 1994; Verderio et al., 1994; Benson and Cohen, 1996; Murthy et al., 2001) as well as more recent ones (Wrosch et al., 2017; Hobbiss et al., 2018).

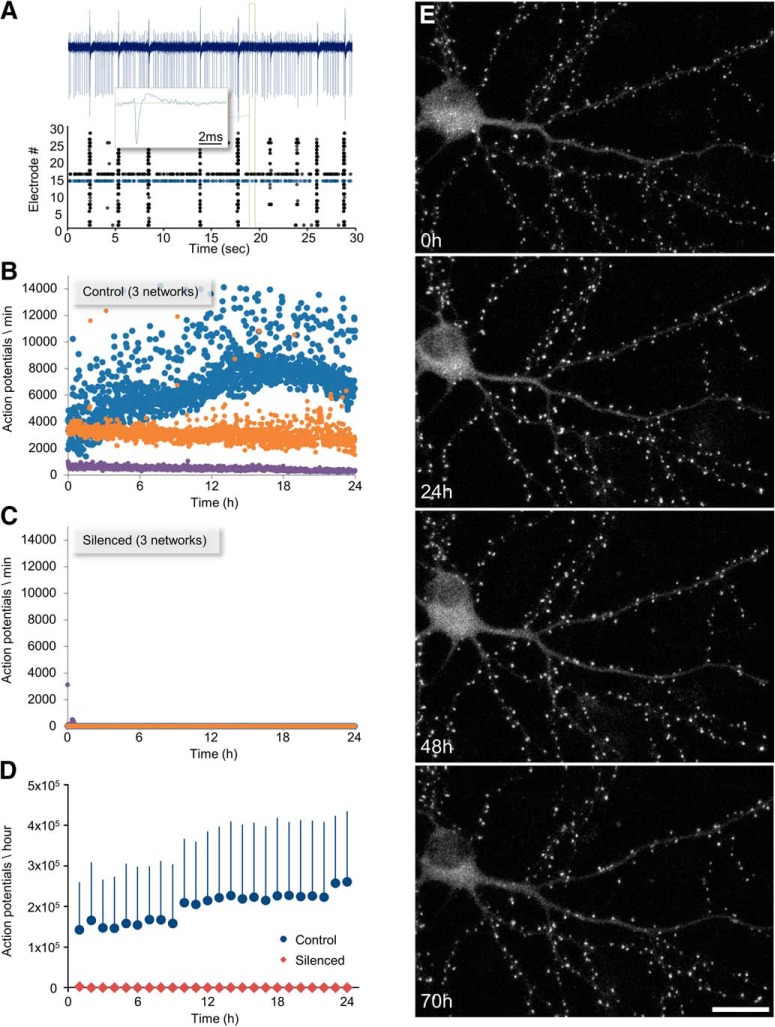
To verify the elimination of all spiking activity, the networks were grown on thin-glass MEA dishes, which allow for chronic, noninvasive recordings of network activity from 59 electrodes (Fig. 1A). As shown in Figure 1B–D, these pharmacological agents fully suppressed the vigorous spontaneous activity typical of such networks.

Figure 1.

Long-term recordings of synaptic remodeling and network activity in chronically silenced networks. A, Extracellular recordings of network activity. A 30 s recording from a control (non-silenced) network of cortical neurons growing on an MEA substrate. Activity in these preparations typically appears in form of network-wide bursts separated by periods of quiescence or sparse activity. Action potentials recorded from 30 of the 59 electrodes are shown as raster plots (bottom). Two neurons in this network fired tonically, the activity of one (blue dots) is shown in full (blue trace, top). Inset, The waveform of one action potential (green rectangle). B, Network activity recorded over 24 h from three control networks (color coded). Each dot represents the total number of action potentials recorded from all 59 electrodes in a 1 min window. Activity levels varied from one network to another. Examples of networks with high (blue), intermediate (orange), and low (purple) activity levels are shown here. Time t = 0 represents the beginning of the imaging session. C, Networks chronically treated with TTX, CNQX, and AP5 are entirely silent (3 different networks). D, Average (±SD) activity levels (1 h averages) in control and silenced networks. E, A cortical neuron expressing PSD-95:EGFP in a chronically silenced network, followed at 1 h intervals for 70 h. Time t = 0 represents the beginning of the imaging session (20 d in culture). Maximal intensity projection of 10 sections. Scale bar, 20 μm.

The effects of chronic silencing on excitatory synapse sizes were determined by expressing an EGFP-tagged variant of the PSD protein PSD-95 (PSD-95:EGFP) in a small number of neurons (Fig. 1E). PSD-95 is a major postsynaptic scaffold protein that regulates the number of AMPA and NMDA receptors at the postsynaptic membrane (Won et al., 2017). PSD-95:EGFP fluorescence is correlated with PSD area (Cane et al., 2014) and thus represents a good proxy of synaptic size. Expression was performed using lentiviral vectors, resulting in very low PSD-95:EGFP overexpression (Minerbi et al., 2009).

Experiments were performed on networks raised in culture for ∼3 weeks. At this stage, the developmental phases of rapid dendritic growth, axonal arborization and synapse formation are over for the most part, and neuronal structure becomes relatively stable, allowing individual synapses to be followed reliably for 24–48 h and beyond. Silenced (or control) networks growing on MEA dishes were mounted at Day 19–21 in culture on a combined MEA recording/imaging system used in prior studies from our laboratory (Minerbi et al., 2009; Kaufman et al., 2012, Rubinski and Ziv, 2015; Dvorkin et al., 2016). The MEA dishes were maintained at 37°C in an atmospheric environment of 5% CO₂/95% air and perfused at very slow rates (2 volumes/d) with fresh cell culture media containing (or free of) the aforementioned pharmacological agents. After 24 h adjustment periods, automated multisite confocal microscopy was initiated, during which images of 4–10 fields-of-view (portions of dendritic arbors of different neurons expressing PSD-95:EGFP) were obtained at 60 min intervals at 10 focal planes, using the microscopes “autofocus” system to correct for focal drift.

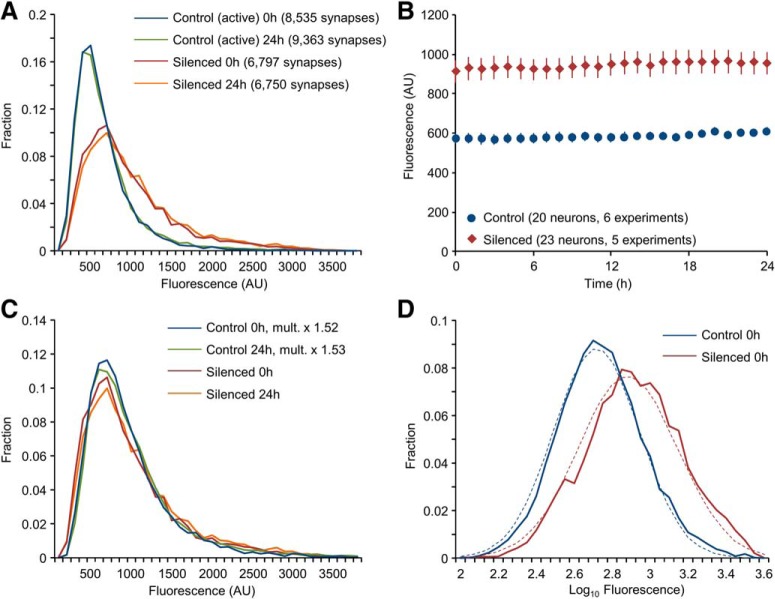
Following the experiments, PSD-95:EGFP puncta were identified anew at each time point (programmatically, using a puncta detection algorithm as described in Materials and Methods) and intensities and numbers of all puncta were determined (Silenced networks: 23 neurons, from 5 separate experiments, ∼6800 synapses; Control networks: 20 neurons from 6 separate experiments, ∼9000 synapses). As shown in Figure 2A, distributions of synaptic PSD-95:EGFP fluorescence in chronically silenced networks were broad and rightward skewed (skewness ≈ +1.4 and +2.2, silenced and control networks, respectively; note that skewness = 0 for normal distributions). In fact, distributions in the silenced networks were much broader than those observed in active networks, with mean PSD-95:EGFP fluorescence being ∼1.5 times greater than mean fluorescence measured in active networks (Fig. 2B; p = 4.6 × 10⁻⁶ by neuron; p = 0.019 by experiment; t test, assuming unequal variances; in agreement with Kim et al., 2007; Noritake et al., 2009; Sun and Turrigiano, 2011; Shin et al., 2012) suggesting that chronic silencing was associated with significant synaptic growth (Murthy et al., 2001; Sando et al., 2017; but see Harms et al., 2005; Yasumatsu et al., 2008). Distributions at early and late time points (1 and 24 h, respectively) were very similar (Fig. 2A). Mean synaptic PSD-95:EGFP fluorescence was also stable (Fig. 2B). Plotting distributions of PSD-95:EGFP fluorescence in control networks in scaled units (i.e., multiplying the fluorescence of each synapse by ∼1.5), suggested that shapes of synaptic size distributions in chronically silenced and active networks were similar (Fig. 2C), in excellent agreement with prior findings in acutely silenced networks in vitro (Turrigiano et al., 1998; Hobbiss et al., 2018) and in vivo (Keck et al., 2013). Finally, distributions of synaptic sizes in both silenced and active networks were well approximated by log-normal distributions (Fig. 2D).

Figure 2.

Distributions of synaptic sizes in chronically silenced networks are broad, rightward skewed and stable. A, Distributions of PSD-95:EGFP puncta fluorescence in chronically silenced and control networks at two time points, 24 h apart. Silenced networks: 23 neurons from 5 separate experiments, ∼6800 synapses; Control networks: 20 neurons from 6 separate experiments, ∼9000 synapses. B, Mean PSD-95:EGFP puncta fluorescence in silenced and control networks. Error bars are SEM (23 and 20 neurons, respectively). C, Scaled size distributions. PSD-95:EGFP fluorescence values of all puncta in the control dataset were multiplied by the silenced/control PSD-95:EGFP fluorescence ratios at t = 0 (1.519) and t = 24 (1.532). Distributions were then prepared from the scaled data, and plotted alongside distributions obtained in silenced networks (same data as in A). D, Fits to log-normal distributions. Distributions of log₁₀ values of PSD-95:EGFP puncta fluorescence for chronically silenced and control networks (same data as in A). Dashed lines are fits to log-normal distributions.

These findings thus confirm prior reports that extensive synaptic size diversification can occur in the absence of activity-dependent synaptic plasticity processes (Van Huizen et al., 1985; Harms and Craig, 2005; Harms et al., 2005; Yasumatsu et al., 2008; Sando et al., 2017; Sigler et al., 2017). Moreover, they reveal that the emergence of broad, rightward skewed and stable size distributions, remarkably similar to those observed in active networks, can arise de novo rather than through the scaling of distributions initially established in active networks. Thus, activity-independent processes can play decisive roles in synaptic size diversification and in establishing appropriate proportions of differently sized synapses.

Intrinsic size fluctuations are sufficient to produce differently sized synapses at appropriate proportions

As mentioned in the Introduction, prior studies suggest that synaptic sizes are affected by intrinsic size fluctuations, as are the shape and scale of synaptic size distributions (Yasumatsu et al., 2008; Loewenstein et al., 2011; Kaufman et al., 2012; Statman et al., 2014; Rubinski and Ziv, 2015; Ishii et al., 2018; Ziv and Brenner, 2018; Humble et al., 2019). Yet, as characteristics of intrinsic size fluctuations in neurons with no prior history of network activity were not measured to date, it remained unknown whether such intrinsic fluctuations are sufficient to produce the extensive diversity and broad, skewed distributions of synaptic sizes observed in chronically silenced networks.

To examine this possibility, we followed individual synapses in chronically silenced (and active) networks for 24–48 h, measuring PSD-95:EGFP fluorescence of each synapse at each time point as illustrated in Figure 3A (Minerbi et al., 2009; Fisher-Lavie and Ziv, 2013; Rubinski and Ziv, 2015; Dvorkin et al., 2016). Fluorescence measurements were made from maximal intensity projections of all Z-sections to minimize the effects of focal positioning errors. Only synapses that could be tracked reliably were included in these analyses, excluding PSD-95:EGFP puncta that disappeared, split, or merged during the experiments. To correct for some variability in PSD-95:EGFP expression levels and to allow for data pooling, the fluorescence of each synapse was normalized to the mean puncta fluorescence of its respective neuron, measured at the first time point. Additionally, to minimize the influence of measurement noise, all data were smoothed using a three time-point low-pass filter (see Statman et al., 2014). As illustrated for 16 synapses in Figure 3A, synaptic sizes changed considerably over time scales of many hours, even in chronically silenced networks (3B). Comparing the initial synaptic “configuration” (the set of inputs to this dendrite in terms of synaptic sizes) to synaptic configurations at later time points suggests that size fluctuations are associated with a gradual “erosion” of synaptic configurations (Fig. 3C,D).

Figure 3.

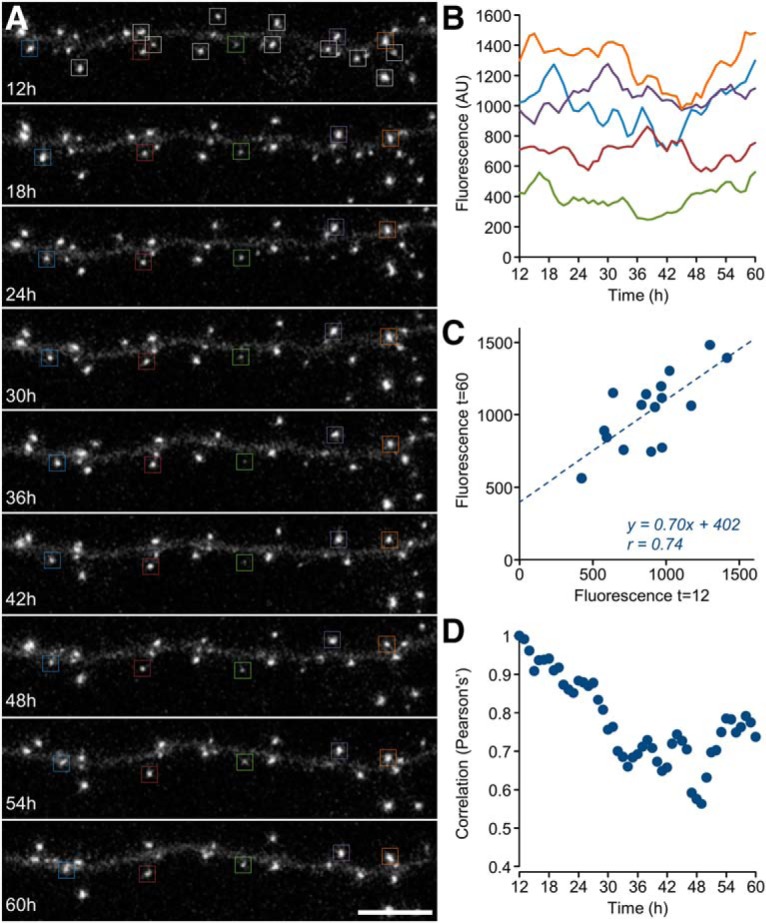
Synaptic size fluctuations in chronically silenced networks. A, A dendritic segment of a neuron in a chronically silenced network (20 d in culture) expressing PSD-95:EGFP followed for 60 h at 1 h intervals (only a subset of images is shown). Sixtenn synapses (top, rectangles) were tracked for 48 h and their fluorescence measured. Synapses not enclosed in rectangles are synapses whose tracking was ambiguous and were therefore excluded. A subset of tracked synapses is marked with color coded rectangles in all eight panels. Time t = 0 represents the beginning of the imaging session. Scale bar, 10 μm. B, Forty-eight hour trajectories of the fluorescence of the color-coded synapses in A. C, A comparison of fluorescence values for the 16 synapses shown in A at t = 12 and t = 60. The dashed line is a linear regression fit. Fit parameters and Pearson's correlation coefficient are indicated. D, Pearson's correlation coefficients in plots such as C for all 48 time points.

Magnitudes of temporal fluctuations in synaptic sizes were quantified for 2032 and 1922 synapses (23 and 20 neurons, 5 and 6 separate experiments, silenced and control networks, respectively) by calculating the SD, coefficient of variation, and the range/mean (Fisher-Lavie et al., 2011; Zeidan and Ziv, 2012; Ziv, 2013) of the normalized fluorescence of each synapse over 24 h periods. As shown in Figure 4A–C, all three measures suggested that magnitudes of size fluctuations were reduced in silenced networks relative to control (active) networks, but only by 20–34%.

To determine whether these somewhat subdued fluctuations could give rise to the broad and skewed size distributions observed in chronically silenced networks, we analyzed these within the context of a statistical framework we previously developed (Statman et al., 2014). The basic premise of this framework is that synaptic size dynamics are driven by continuous, noisy multiplicative downscaling, which is continuously offset by noisy additive growth, resulting in size fluctuations that have noisy multiplicative and additive components. This statistical process, known as a Kesten process, faithfully reproduces many experimental observations concerning synaptic size fluctuations, size distributions, their stability, and their scaling (Statman et al., 2014; Rubinski and Ziv, 2015; Ziv and Brenner, 2018). Importantly, this framework provides means for parametrically comparing synaptic size fluctuations under different experimental conditions and determining their effects on synaptic size distributions.

In more formal terms, this framework stipulates that for a synapse of size x at time t (x_t), its size (x_t+1) after some discrete time period will be as follows:

where ε_t and η_t are the aforementioned multiplicative downscaling and additive growth parameters. Importantly, ε_t and η_t are not fixed values but random variables drawn independently at each time step from some distribution. Iterations of Process 11 (i.e., x_t+2 = ε_t+1x_t+1 + η_t+1; x_t+3 = ε_t+2x_t+2 + η_t+2; etc.) result in fluctuating size “trajectories” similar to those observed experimentally. Note that expressing the change in synaptic size(Δx_t+1) at t = t+1:

suggests that the Kesten process can be thought of as a combination of myriad, noisy first- and zero-order reactions (for example protein loss/degradation and protein supply/synthesis, respectively) with <ϵ − 1> and <η> (the mean values of these parameters) representing aggregate, effective “rate constants” of such reactions, respectively (Statman et al., 2014).

The mean downscaling factor (<ε>) is an important parameter in this framework, and can be derived in stationary distributions by multiple linear regression analyses of synaptic sizes as a function of time as illustrated in Figure 4D–J (Statman et al., 2014). Derivation of <ε> in this manner revealed that continuous downscaling was substantially weakened in silenced networks compared with active networks, that is <ε> was closer to 1.0 (0.995 and 0.985, silenced and control networks, respectively; Fig. 4J). In addition, this analysis revealed that synaptic configuration erosion rates were approximately halved (Fig. 4K); notably, however, erosion rates were still considerable. Plotting the change in synaptic size (that is, subtracting, for each synapse, its fluorescence at t = 24 from its fluorescence at t = 1) as a function of its size at t = 1 illustrates how lessened downscaling weakens the constraints on synaptic size distributions (Fig. 4L). This weakening might explain the broader distributions of synaptic sizes in silenced networks (Fig. 2A). On the other hand, it remained unclear whether fluctuations with such weak downscaling would be sufficient to generate and maintain the broad, skewed and stable synaptic size distributions observed in silenced networks.

To address this question, we simulated populations of “synapses” whose size fluctuations were modeled as Kesten processes using the experimentally derived values of <ε> and <η> for silenced and control networks. In the first set of simulations, synaptic sizes were initialized using the experimentally measured, normalized PSD-95:EGFP fluorescence values of 2032 and 1922 synapses (data from Fig. 4; silenced and control networks respectively). As shown in Figure 5, excellent fits to the experimental data were obtained for both silenced and control conditions not only in distribution shape and stability (Fig. 5C,F) but also in terms of synaptic configuration erosion rates (compare Figs. 5A,B,D,E, 4F,I,L) and measures of size fluctuations (Fig. 5G–I, 4A–C).

In these simulations, synapses whose sizes were reduced momentarily to zero were treated as “eliminated” and not considered further. Interestingly, rates of synapse “elimination” were greater in simulations based on parameters obtained in silenced networks (Fig. 5J; ∼0.63 ± 0.05% per 24 simulation cycles, silenced networks; 0.06 ± 0.02%, control networks; mean ± SD, 5 runs per condition) indicating that the weaker constraints on intrinsic fluctuations observed in silenced networks might reduce the chances of (small) synapses to escape elimination (see also Holtmaat et al., 2006; Yasumatsu et al., 2008; Minerbi et al., 2009).

In a second set of simulations, we simulated 4000 synapses for each condition, setting the initial size of all synapses to 0.1 (the dimmest synapses identified in our experimental datasets, in normalized units), and followed the evolution of synaptic size distributions using the experimentally derived values of <ε> and <η>. As shown in Figure 5, K and L, in both conditions, size distributions gradually converged to the experimentally measured skewed and stable distributions. Interestingly, however, convergence was much slower in silenced networks, and even after 480 simulated “hours” (20 “days”) convergence was incomplete. Here too, the negative effects of silencing on (small) synapse survival were very evident (Fig. 5M). Collectively, these findings suggest that fluctuations in synaptic sizes measured in chronically silenced networks are sufficient to drive the emergence of the broad, rightward skewed and stable synaptic size distributions observed in these networks.

The Kesten process described is based on the assumption that <ε>, <η> and their noise terms do not depend on momentary synaptic size (as might be expected for simple first and zero-order reactions). In a prior study (Yasumatsu et al., 2008), size fluctuations were modeled using a generic framework that does not necessitate this assumption. Here fluctuations were modeled as a nonlinear Langevin process in which fluctuations were grouped into deterministic [μ(x)] and stochastic terms [σ(x)], both formulated as functions of momentary synaptic size (x_t).

Assuming that the two noise terms in the Kesten Process 12 are distributed normally with SDs of σ_ϵ−1 and σ_η, it can be shown that the Kesten Process 12 can also be formulated as a nonlinear Langevin process (see Materials and Methods). Here, the change in momentary synaptic size Δx_t after some time interval (Δt) is expressed as follows:

with

where N(0,1) is a random variable taken from a normal distribution with a mean of 0 and a variance of 1.

This formulation allowed us to test the aforementioned assumptions: if <ε>, <η> are indeed independent of momentary synaptic size, then plotting the fluctuation magnitude μ(x_t) as a function of synaptic size at that time (x_t) should result in a straight line with a slope of <ϵ − 1> and an intercept of <η> (both scaled by Δt; see Eq. 14). Similarly, if the variances of ϵ and η do not depend on momentary synaptic size, plotting the fluctuation variance [σ²(x_t)] as a function of x_t² should result in a straight line with a slope of σ_ϵ−1² and an intercept of σ_η² (Eq. 15). To test these predictions, size changes measured over 8 h intervals were divided into 20 equally-sized bins according to synaptic size at the beginning of each interval. The average and variance of size changes in each bin were then plotted against average initial synaptic size for that bin. As shown in Figure 6, A and B, excellent linear fits were observed for both the control and silenced conditions, justifying the aforementioned assumptions. The only noticeable deviation was for μ(x_t) for the smallest synapses in the silenced dataset, which might hint that in silenced networks, ϵ and/or η might slightly differ for the smallest synapses.

Linear regression fits of the data in Figure 6, A and B, allowed us to obtain estimates of <ϵ>, <η>, σ_ϵ, σ_η (for 8 h intervals) for control and silenced networks. These estimates were then used to examine whether synaptic size fluctuations modeled as the Langevin process described above give rise to the size distributions measured experimentally. To that end, experimentally measured synaptic sizes (Fig. 5C,F) were evolved for 320 simulated hours (40, 8 h intervals) using Equations 13–15 (see Materials and Methods for further details). As shown in Figure 6, C and D, distributions remained faithful to the experimentally measured distributions for both control and silenced networks. As expected, identical results were obtained when synaptic sizes were evolved as a Kesten process using the same parameters (data not shown).

Collectively these findings suggest that synaptic size distributions, in both active and chronically silenced networks, can arise from size fluctuations that effectively behave as combinations of noisy first and zero-order processes. Interestingly, the Langevin transformation of the Kesten process (Eqs. 13–15) is very similar to the nonlinear Langevin process previously formulated by Yasumatsu et al. (2008) as an effective description of size fluctuations in cultured slices of hippocampal neurons. Thus analytical approaches coming from different directions and theoretical backgrounds, applied to data obtained in different experimental systems, converged to a very similar quantitative description of synaptic size dynamics.

Although synaptic dynamics in both active and silenced networks were well described by stochastic Kesten and Langevin processes (Figs. 4–6), we noted one qualitative deviation in active but not in silenced (or simulated) networks, that is, a minor but conspicuous population of small synapses that exhibited rapid growth over the imaging period (Fig. 4F, shaded area, compare with Fig. 4I). We return to this population later.

Relationships between activity levels, innate molecular dynamics, intrinsic fluctuations, and size distributions

The data described so far suggests that activity-independent, intrinsic size fluctuations are sufficient to generate a full range of synaptic sizes at correct proportions as reflected in the breadth and shape of the resulting size distributions. The source of these fluctuations, however, is not clear. As mentioned in the Introduction, these have been suggested to stem from the innate dynamics of synaptic molecules at synaptic sites. Moreover, network activity levels have been shown to affect these dynamics (for review, see Ziv and Fisher-Lavie, 2014). It is thus plausible that the altered size fluctuations (and consequential changes in synaptic size distributions) observed in silenced networks reflect, at least in part, changes in the underlying dynamics of synaptic molecules associated with low network activity levels.

To obtain a better understanding of the relationships between activity levels, innate molecular dynamics, intrinsic fluctuations, and size distributions, we used a mesoscopic model developed previously to study such relationships (Shomar et al., 2017). Specifically, we used this model to generate hypotheses on the manners by which activity might affect relationships between innate molecular dynamics, intrinsic fluctuations and size distributions, and then tested these hypotheses experimentally. It should be emphasized that the model was used to explore potential explanations, not to generate precise fits to experimental data.

The aforementioned model (Fig. 7A) consists of a neuron with a fixed number of synapses (S) each of which is composed of two components: a postsynaptic “membrane”, modeled as a 50 × 50 matrix of potential binding sites (“slots”) for synaptic scaffold molecules; and synaptic scaffold molecules, which can bind to, or unbind from these slots. The size of a given synapse at any time is defined as the momentary number of occupied slots, that is, the number of scaffold molecules bound to its matrix. In the variant of the model used here, scaffold molecules come from a common (global) pool (N_total), shared and competed over by all synapses. The global amount of free molecules (N_free) at any moment is equal to the total amount of molecules in the cell (N_total) after subtracting all molecules presently bound to synaptic membranes (matrices). Binding and unbinding are modeled as stochastic events characterized by probabilities per unit time. Consequently, the number of molecules binding to a matrix per unit time depends on the binding probability, the number of free molecules (N_free, serving as a proxy of free molecule concentration) and on the number of vacant slots in that matrix. Similarly, the number of molecules dissociating from each matrix per unit time depends on the unbinding probability per unit time and on the number of bound molecules (=occupied slots). In this stochastic description, the binding and unbinding of scaffold molecules result in temporal fluctuations in synaptic sizes, i.e., in the momentary numbers of molecules bound to the matrices, whereas occupancies at all S matrices give rise to momentary synaptic size distributions. The model as described so far is insufficient to explain the rightward skewed, experimentally observed distributions of synaptic sizes. However, when the probabilities of binding to (and unbinding from) each slot depend positively (and negatively) on the number of its immediately neighboring occupied slots (Fig. 7A, right, gray area), synaptic size dynamics and distributions become remarkably similar to those observed experimentally (Shomar et al., 2017). This dependence, justified by the multiplicity of binding sites typical of most synaptic molecules (Won et al., 2017), is essentially a form of cooperativity, and thus both binding and unbinding in this model are cooperative (for a more detailed description of the model, see Materials and Methods).

Prior studies suggest that chronic suppression of network activity can slow the binding and unbinding (exchange) kinetics of synaptic molecules (for review, see Ziv and Fisher-Lavie, 2014). We thus used this model to examine the possibility that reduced synaptic size fluctuations and broader size distributions in silenced networks might stem from slower exchange kinetics. Specifically, we explored the expected consequences of reducing the unbinding probability of molecules bound to “synaptic” matrices. As shown in Figure 7, lower unbinding probabilities would be expected to drive the broadening of synaptic size distributions (7B) increase mean synaptic size (7C), reduce the rate at which the slope declines in plots such as Figure 7D (i.e., drive <ϵ> to values closer to 1.0; 7D,E,G), slow changes in synaptic size configurations (7F), and reduce size fluctuation magnitudes (7H–J), all in good agreement with observations made in real neurons (Figs. 2, 4).

Lower unbinding probabilities also predict slower exchange rates of scaffold molecules at synapses (Fig. 7K). If this hypothesis is correct, experimentally measured exchange rates of PSD-95 might be expected to be slower in chronically silenced networks [due to, for example Ser-295 phosphorylation (Kim et al., 2007) or palmitoylation (Noritake et al., 2009; Sturgill et al., 2009; Fukata et al., 2013)]. To test this prediction, we measured PSD-95:EGFP exchange rates using fluorescence recovery after photobleaching (FRAP) in chronically silenced and control networks. To that end, a small number of well separated PSD-95:EGFP puncta were photobleached by intense laser illumination and subsequently followed by time lapse imaging, initially at 10 min intervals (for the first hour) and then at 1 h intervals, chosen to match to the slow exchange rates of PSD-95 (Sturgill et al., 2009; Zeidan and Ziv, 2012; Fukata et al., 2013). One example is shown in Figure 8A–C. Here, three photobleached PSD-95:EGFP puncta in a chronically silenced network were followed for 90 h after the bleaching procedure. The fluorescence traces obtained here (Fig. 8C) illustrate that over these long time scales, fluorescence recovery measurements are confounded by ongoing changes in synaptic sizes, complicating accurate estimations of recovery kinetics. Nevertheless, pooling measurements over shorter time scales (24 h or less) allowed us to compare mean fluorescence recovery profiles for synapses in chronically silenced (77 synapses from 6 experiments) and control networks (72 synapses from 7 experiments). Surprisingly, mean fluorescence recovery curves for silenced and control networks did not differ significantly (Fig. 8D). These experiments thus did not support the possibility that altered size fluctuations, synaptic sizes and distributions in chronically silenced networks reflect slower unbinding kinetics of PSD-95.

We thus explored an alternative explanation that relates to PSD-95 abundance. As shown in (Fig. 2A,B) mean synaptic PSD-95:EGFP fluorescence was, on average ∼50% greater in chronically silenced networks, possibly indicating that chronic silencing is associated with increased cellular PSD-95 levels due to, for example, effects on synaptic protein synthesis (Schanzenbächer et al., 2016) or degradation (Jakawich et al., 2010). Using the aforementioned model to examine the expected effects of increased scaffold molecule abundance we found that merely increasing N_total by 25% was sufficient to qualitatively recapitulate all of the experimental findings described so far (Fig. 9A–G), including the similar recovery kinetics in FRAP experiments.

To experimentally test this potential explanation, we measured and compared global PSD-95 abundance in chronically silenced and control networks by means of Western blots. Here too, however, the prediction was not supported by the experimental data, as no consistent increases in global PSD-95 abundance were observed in silenced networks (7 replicates from 2 separate experiments; Fig. 9H,I; see also Kim et al., 2007; Lazarevic et al., 2011; Shin et al., 2012).

To examine whether this observation applies to synaptic proteins in general, we used multiplexed SILAC (Stable Isotope Labeling with Amino acids in Cell culture) combined with MS (for review, see Hoedt et al., 2019) to compare synaptic protein quantities in silenced and control preparations. To that end, neurons were prepared and grown in lysine and arginine-free media supplemented with lysine and arginine containing stable, heavy isotopes of carbon and nitrogen. Silenced preparations were labeled with heavy amino acids (Lys8-¹³C₆, ¹⁵N₂ and Arg10-¹³C₆, ¹⁵N₄) whereas control preparations were labeled with medium variants (Lys6-¹³C₆ and Arg6-¹³C₆), which are isotopically separable from both Heavy and unlabeled lysine and arginine. After 21–22 d in culture, during which most of the proteome becomes labeled (Hakim et al., 2016), the preparations were lysed, the extracts mixed together and run on preparative gels, which were subsequently sliced and subjected to MS analysis (see Materials and Methods; Hakim et al., 2016). This method, based on mixing and analyzing samples simultaneously, eliminates much of the variability associated with proteomic approaches; moreover, it provides a H/M ratio reading for each peptide and protein, which reflects the ratio of labeled proteins from silenced and control preparations, respectively. Average H/M ratios were obtained from four replicates (2 separate experiments) using stringent criteria (see Materials and Methods). Stringent H/M ratios obtained for 226 synaptic proteins (categorized as such as in Hakim et al., 2016; 2630 proteins in total) resulted in average and median H/M ratios of 0.89 and 0.86, respectively. Data for 15 and 21 well studied postsynaptic and presynaptic proteins are shown in Figure 9J. Evidently, these data do not support the possibility that chronic silencing increases synaptic protein abundance (if anything, we noted a slight reduction), although confounds related to differences in labeling rates (because of differential metabolism) or cell counts cannot be entirely ruled out.

How could synaptic contents of PSD-95 increase by ∼50% without detectable changes in PSD-95 abundance? One possible explanation is that increased synaptic size in silenced networks was associated with a commensurate decrease in synaptic number (van Huizen et al., 1985; Annis et al., 1994; Kossel et al., 1997; Barnes et al., 2017) resulting is no net change in total PSD-95 levels. Indeed, such decreases were predicted by the simulations shown in Figure 5,J and M.

We thus used the aforementioned mesoscopic model to examine how a reduction in synaptic numbers might affect intrinsic fluctuations and synaptic size distributions. To that end, the number of synapses (matrices) was reduced by 40% (from 4000 to 2400) without changing N_total. As shown in Figure 10A–G the model with these parameters recapitulated the main experimental findings obtained in silenced networks; increased synaptic size, broadening of synaptic size distributions, <ε> values closer to 1.0, reduced magnitudes of synaptic size fluctuations, slower changes in synaptic configurations, and similar FRAP curves.

To examine whether the experimental findings were congruent with this prediction, we revisited the dataset of Figure 2, finding (Fig. 10H) that PSD-95:EGFP puncta counts were indeed reduced in chronically silenced networks (by ∼37%; ∼296 vs ∼470 puncta per field-of-view, 23 fields-of-view in 5 experiments and 20 fields-of-view in 6 experiments, silenced and control networks, respectively). Moreover, the summed (rather than average) fluorescence of PSD-95:EGFP puncta in each field-of-view was practically identical in silenced and active networks (Fig. 10I); in agreement with the explanation proposed above as well as the data of Figure 9H–J. Differences in synaptic numbers were not associated with changes in synaptic density (4.91 ± 1.18 and 5.02 ± 0.87 synapses per 10 μm dendrite length; 11 and 10 fields-of-view from 6 and 5 experiments; silenced and control networks respectively) and thus seem to reflect lessened dendritic arborization in silenced networks (in agreement with van Huizen et al., 1985; Benson and Cohen, 1996). Indeed, the summed length of dendritic segments within each field-of-view was reduced by ∼33% (Fig. 10J; 20 fields-of-view for each condition, p = 1.3 × 10⁻⁷; two-sample t test assuming unequal variances). Moreover, Scholl analysis of reconstructed neurons confirmed that dendritic arborization was substantially reduced (Fig. 11; Benson and Cohen, 1996). Interestingly, whereas PSD-95:EGFP puncta counts in silenced networks were ∼stable over 24 h periods (Fig. 10H), counts in active networks tended to increase slowly over the same time frame (in agreement with Okabe et al., 1999), as did the summed fluorescence of PSD-95:EGFP puncta in active networks (Fig. 10I).

Figure 11.

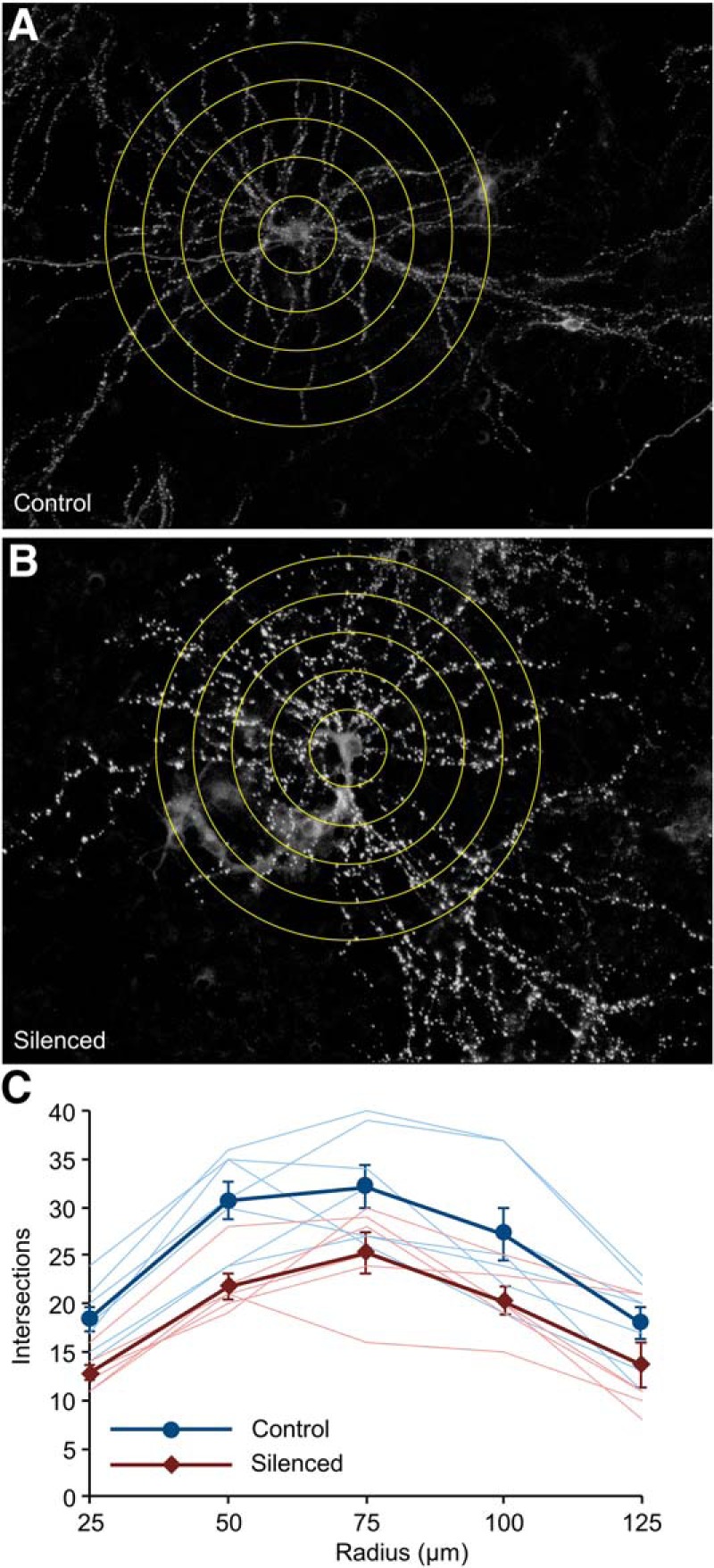
Effects of silencing on dendritic arborization. Neurons sparsely expressing PSD95:EGFP were grown for 3 weeks on glass bottomed Petri dishes (to avoid the occasional obscuring of neuronal structure by MEA electrodes) in the presence or absence of TTX, CNQX, and AP5. Images of live neurons were collected at low magnification (10 sections/image), and individual neurons were reconstructed off-line. A, B, Sholl analysis of two neurons performed at 25 μm intervals as illustrated. C, Intersections measured for all neurons (7 and 6 neurons, control and silenced, respectively) at increasing distances from somata as well as averages (±SEM) for neurons in both groups. Analysis at remote locations and total dendrite length estimations were confounded by the presence of neighboring labeled neurons. Nevertheless, visual inspection indicated that neurons in silenced networks tended to be more compact than those in control networks.

These findings are thus most congruent with an interpretation suggesting that synaptic enlargement in chronically silenced networks, as well as broader size distributions, subdued size fluctuations and <ε> values closer to 1.0, might be attributed to the redistribution of PSD-95 (and probably other synaptic molecules) among the fewer synaptic connections formed in the absence of network activity (Fig. 12A).

Figure 12.

Reciprocal relationships between synaptic sizes, size dynamics, and synaptic numbers. A, Illustration of the effects of chronic silencing on dendritic arborization, manifested as fewer dendritic branches and synapses compared with neurons developing in active networks. B, Mean expected size change plotted against present size using values of <ε> and <η> measured in silenced and active networks. To allow this comparison, both plots are in units of the control condition. Note that the crossing points with the abscissa, which define mean synaptic sizes, differ under the two conditions. Also note that in silenced networks and for particularly small synapses (shaded area) growth expectancy is lower, increasing chances of small synapses to be eliminated in the course of stochastic size fluctuations. C, Small synapse survival probability is reduced in silenced networks. Dim PSD-95:EGFP puncta were selected and then tracked for 24 h. During this period, puncta occasionally disappeared; the percentage of remaining puncta is plotted as a function of time. Time t = 0 represents the beginning of the imaging session. D, An illustration of potential relationships between synaptic numbers, synaptic molecule levels, intrinsic size fluctuations, and synapse survival chances. Note the positive feedback these relationships seem to entail.

Relationships between activity levels and synaptic numbers

Why are less synapses formed in chronically silenced networks? Our data provides potentially interesting clues, although, as we show later, interpretation is not as straightforward as it might seem at first sight.

We note that in active (Fig. 4D), but not in silenced networks (4I), a minor population of synapses (∼1–2% per day) exhibited rapid growth in manners not predicted by any of the models explored here. In a prior study (Minerbi et al., 2009) we found that this phenomenon reflects the rapid formation and enlargement of (post)synaptic sites during periods of particularly strong, synchronous network activity, which presumably drives strong presynaptic activation and possibly long-term potentiation associated spine formation and growth (Smith and Jahr, 1992; Engert and Bonhoeffer, 1999; Maletic-Savatic et al., 1999; Matsuzaki et al., 2004; Kwon and Sabatini, 2011; Bosch et al., 2014; Meyer et al., 2014; Sigler et al., 2017; Hobbiss et al., 2018; for review, see Andreae and Burrone, 2014). Conversely, acute suppression of network activity was found to abruptly arrest and even reverse trends of synaptic proliferation (Minerbi et al., 2009). It thus seems that network silencing might suppress activity-dependent forms of synapse formation (in line with prior predictions; Yasumatsu et al., 2008), ultimately resulting in lower synaptic numbers. This, in turn, would negatively affect dendritic arborization (for review, see Cline and Haas, 2008) potentially explaining the major findings as described.

Our data also indicates, however, that causal relationships between synaptic numbers and network activity might be more complex. The increase in PSD-95 availability and synaptic size associated with reduced synaptic numbers (Fig. 12A) is also associated with changes in size fluctuation characteristics, specifically in <ε> and <η> (Fig. 4J). When expected size change is plotted against present synaptic size using experimentally measured, absolute values of <ε> and <η> (Fig. 12B) it becomes apparent that for particularly small synapses (gray shading), the bias toward growth is weaker in silenced networks (see also Fig. 6A). Consequently, the chances of small synapses to persist in silenced networks is lowered, and thus more synapse elimination (or less stabilization of nascent synapses) is expected, as predicted by the simulations of Figure 5, J and M. This bias is not affected by recalculating <ε> and <η> for active networks after removing the population of rapidly growing synapses from the dataset, although this does not preclude the possibility that some of this bias is created by activity-dependent potentiation of nascent synapses.

To test this prediction, we returned to the time-lapse images obtained in control and silenced networks, focusing this time on small (dim) PSD-95:EGFP puncta. As shown in Figure 12C, tracking such synapses revealed greater rates of puncta loss in silenced networks (5.7 vs 12.6% in 24 h; 17/299 and 41/324, 4 control and 4 silenced networks, respectively). In further agreement with this prediction, lost puncta were particularly dim (333 ± 147 and 373 ± 125; arbitrary fluorescence units at first time point, average ± SD, control and silenced networks, respectively) compared with the entire synaptic population (600 ± 357 and 911 ± 558).

These predictions (Figs. 5J,M, 12B) and findings (10H–J, 12C) suggest that synaptic loss might be both the cause and the product of altered synaptic size dynamics. Stated differently, innate molecular dynamics, intrinsic size fluctuations and synaptic sizes might be related reciprocally, possibly in self-reinforcing fashion as illustrated in Figure 12D, potentially obscuring simple cause and effect relationships between these phenomena.

Discussion

Here we set out to determine the contributions of activity dependent and independent processes to excitatory synapse size diversity. To that end, we pharmacologically silenced networks of cortical neurons from the time of plating and then examined synaptic size distributions and remodeling dynamics using PSD-95:EGFP fluorescence as a proxy of synaptic size. We found that even in networks with no history of activity, size diversity was extensive and size distributions were broad, stable, and rightward skewed. Comparisons with spontaneously active networks revealed that silencing was associated with a broadening of synaptic size distributions and a significant (∼50%) increase in mean synaptic size, yet distribution shapes were similar when scaled by mean synaptic size. Silencing was associated with reductions in size fluctuation magnitudes, as well as considerable weakening of constraints on size distributions. Nevertheless, these fluctuations and constraints were still sufficient to generate broad, skewed and stable size distributions. To better understand relationships between activity levels, size fluctuations, size distributions and innate dynamics of synaptic molecules, we used a previously published mesoscopic model to derive potential explanations, which were then tested experimentally. Explanations attributing the effects of chronic silencing to changes in PSD-95 binding/unbinding kinetics or expression levels were not supported by FRAP experiments, Western blots or quantitative proteomics. Conversely, the experimental findings fully supported the possibility that changes in synaptic size dynamics and distributions primarily reflect PSD-95 redistribution among fewer synapses. These findings thus suggest that intrinsic, activity-independent size fluctuations are sufficient to give rise to full repertoires of synaptic sizes at appropriate proportions. Moreover, they are suggestive of reciprocal and possibly self-reinforcing relationships between synaptic size fluctuations, size distributions, and synaptic counts mediated by the innate dynamics of synaptic molecules as they continuously move in, out, and between synapses

The source of broad and rightward skewed synaptic size distributions

As mentioned, broad, rightward skewed distributions of synaptic sizes are ubiquitously observed. Explanations have typically fallen into two classes:

The first attributes their emergence to various activity-dependent, synaptic plasticity processes (van Rossum et al., 2000; Song et al., 2005; Lefort et al., 2009; Gilson and Fukai, 2011; Zheng et al., 2013; Buzsáki and Mizuseki, 2014; Effenberger et al., 2015; Scheler, 2017; Uzan et al., 2018). Given that synaptic diversity was not reduced or distribution shapes grossly affected in chronically silenced networks (Fig. 2; Harms and Craig, 2005; Harms et al., 2005), this class of explanations would seem to be somewhat unsatisfactory. Indeed, recent studies reported that in chronically silenced mouse forebrains (Sando et al., 2017) and in hippocampal organotypic cultures prepared from Munc13–1 and Munc13–2 knock-out mice (which are essentially devoid of presynaptic release; Sigler et al., 2017), spine types (mushroom, thin, stubby) are present at normal proportions.

A second explanation class attributes these distributions to intrinsic size fluctuations that contain multiplicative (and additive) components (Yasumatsu et al., 2008; Loewenstein et al., 2011; Kaufman et al., 2012; Statman et al., 2014; Rubinski and Ziv, 2015; Ishii et al., 2018, Humble et al., 2019; Ziv and Brenner, 2018). Most of such explanations are based on descriptive models in which size fluctuations are treated statistically without addressing their sources. One exception is the mesoscopic model of Shomar et al., 2017 used here (Figs. 7, 9, 10), which showed how cooperative, stochastic binding and unbinding of synaptic molecules can drive intrinsic size fluctuations that shape synaptic size distributions (see also Ranft et al., 2017; Triesch et al., 2018). Here we extended these findings, showing that changes in synaptic molecule abundance or synapse numbers can affect the magnitude of intrinsic fluctuations and ultimately synaptic diversity (Figs. 9, 10), in good agreement with the recent modeling study of Triesch et al. (2018). These findings thus suggest that activity-independent, intrinsic size fluctuations, whose source can be traced to the innate dynamics of synaptic molecules, contribute enormously to excitatory synapse size diversity (Yasumatsu et al., 2008). In fact, they indicate that synaptic size distributions might be primarily shaped by activity-independent processes, with activity levels mainly setting the scale, rather than the shape of these distributions.

Synaptic size distribution scaling in silenced networks

The finding that chronic suppression of network activity increases average synaptic size and scales up synaptic size distributions resembles the homeostatic scaling-up of synaptic strengths and sizes often observed following acute suppressions of network activity (for review, see Turrigiano, 2008; Pozo and Goda, 2010; Chowdhury and Hell, 2018). In most such studies, both in culture and in vivo, manipulations of activity levels were performed in networks in which numerous synapses had already formed (Turrigiano et al., 1998; Murthy et al., 2001; Minerbi et al., 2009; Sun and Turrigiano, 2011; Keck et al., 2013; Barnes et al., 2017; Hobbiss et al., 2018) and thus the observed scaling presumably reflected changes in preexisting synaptic populations. This was clearly not the case in our experiments, as activity was suppressed long before synapses had formed and thus the semblance is somewhat superficial. Nevertheless, the larger synapses and broader size distributions in chronically silenced networks are in line with prior suggestions that synaptic sizes are continually constrained by activity-dependent processes, and that silencing-associated relaxation of these constraints results in synaptic enlargement (Minerbi et al., 2009; Kaufman et al., 2012; Statman et al., 2014; Ziv and Brenner, 2018). Indeed, a recent study (Sando et al., 2017) reported a 30–40% enlargement of spines (and presynaptic boutons) in chronically silenced mouse forebrains analyzed by light- and electron-microscopy. Interestingly, synapse enlargement was associated with comparable reductions in synaptic counts and arbor complexity in some (although not all) forebrain regions. Similarly, spine enlargement in sensory deprived animals was recently shown to be preceded by, and correlate with spine loss in the same dendritic branches (Barnes et al., 2017) further supporting our observations on reciprocal relationships between synaptic sizes and numbers. Understanding how relaxed constraints might reduce synaptic numbers is less intuitive, but can be understood by appreciating how the weaker bias toward growth increases the likelihood of small synapses to become even smaller and ultimately lost (Fig. 12). The putative intermediate, a shared pool of synaptic building blocks (Fig. 12), is in line with many reports on synaptic competition over limited resources (Harms et al., 2005; Mondin et al., 2011; Ramiro-Cortés et al., 2014; Levy et al., 2015; Ryglewski et al., 2017; Triesch et al., 2018). Obviously, the process proposed in Figure 12D is not the only determinant of synaptic numbers and dendrite arborization, because large numbers of synapses ultimately form on relatively stable dendritic trees even in silenced networks. This might be expected given that synaptogenesis is governed by many processes not touched on here. Moreover, while dendritic extension and arborization are influenced by synaptogenesis (Cline and Haas, 2008), these typically precede synaptogenesis and do not strictly depend on it.

In this study we found no evidence that silencing slows PSD-95 exchange kinetics. Other molecules, however, might be affected differently. For example, prolonged silencing was shown to slow the exchange kinetics of Shank3/ProSAP2 and Munc13–1 (Kalla et al., 2006; Tsuriel et al., 2006); thus, relationships between molecular dynamics and size distributions might differ among synaptic molecules. Finally, many additional mechanisms have been implicated in synaptic size/strength distribution scaling (Turrigiano, 2008; Pozo and Goda, 2010; Chowdhury and Hell, 2018) including mechanisms directly involving PSD-95 (Sun and Turrigiano, 2011; Chowdhury et al., 2018) further highlighting the explanatory challenges these phenomena pose.

Activity-dependent and -independent determinants of synaptic sizes

In vivo studies consistently report substantial fluctuations in spine volume or PSD size over hours to day time scales (Grutzendler et al., 2002; Zuo et al., 2005; Holtmaat et al., 2006; Loewenstein et al., 2011; Cane et al., 2014; Ishii et al., 2018). Moreover, a recent study (using PSD-95:EGFP) suggests that nanoscale PSD organization in the mouse visual cortex undergoes remarkable “morphing” over these time scales (Wegner et al., 2018). As these studies were performed in live animals, it was not possible to separate intrinsic fluctuations from activity-dependent synaptic remodeling. In fact, it was recently proposed that synaptic size fluctuations are the product of ongoing potentiation and depression caused by external stimuli and internal neuronal activity, which ride on top of synaptic scaling related to changes in activity levels (Keck et al., 2017). Our findings suggest, however, that PSD morphing, size fluctuations, size distributions and their scaling are tightly interconnected phenomena, whose root causes relate, at least in part, to the innate dynamics of synaptic molecules. Interestingly, the size dynamics these produce, noisy additive growth offset by noisy multiplicative downscaling inherently “solve” one of the thorny issues of Hebbian forms of synaptic plasticity, that is the requisite for continuous synaptic size normalization (Zenke et al., 2017). Of course, these dynamics introduce thorny issues of their own, such the poor preservation of size relationships during this normalization process (Minerbi et al., 2009; Kaufman et al., 2012; Statman et al., 2014). For now, reconciliation of these thorny issues with common notions on synaptic plasticity still awaits resolution (Chambers and Rumpel, 2017; Mongillo et al., 2017; Ziv and Brenner, 2018).