Abstract
Initial lymphatic vessels are made up of overlapped endothelial cells that act as unidirectional valves enabling one-way drainage of tissue fluid into the lumen of the initial lymphatics when there is a favourable pressure gradient. Initial lymphatics subsequently drain this fluid into the collecting lymphatics. This paper describes a computational model for a network of passive rat mesenteric lymphatic vessels with sparse secondary valves. The network was simulated with the secondary valves both operational and non-operational. The effects on the cycle-mean outflow-rate from the network of both inflammation and the resistance of the surrounding interstitium were considered. The cycle-mean outflow-rate is sensitive to vessel stiffness. If the influence of primary valve resistance is reduced relative to that of interstitial resistance and intravascular resistance, there is no absolute advantage of extrinsic pumping, since maximum outflow-rate occurs when vessels are rigid. However there is relative advantage, in that the outflow-rate at intermediate stiffness is higher with the secondary valves functioning than when they are deactivated. If primary-valve resistance dominates, then extrinsic pumping of non-rigid vessels provides absolute advantage. The nonlinear relation between pressure drop and flow-rate of the endothelial primary valves, combined with downstream compliance and pulsatile external pressure, constitutes a separate mechanism of pumping. By enabling the consideration of interactions between multiple phenomena (primary valves, secondary valves, a real network geometry with multiple branches, deformable vessel walls, interstitial resistance, and external pressures), the model offers a perspective for delineating physiological phenomena that have not yet been fully linked to the biomechanics of fluid flow through initial lymphatic networks.
Keywords: lymph flow, fluid-structure interaction, numerical model, extrinsic pumping
1. Introduction
The lymphatic vascular system maintains homeostasis by transporting excess interstitial fluid from the tissue space, via lymph nodes, back to the venous system. The lymphatics also play a key role in immune surveillance, helping to purge undesirable materials and toxins from the body. In contrast to the cardiovascular system, the lymphatic vascular system has no central pump, and hence the transport of fluid against gravity relies on local intrinsic and extrinsic pumping (McHale and Roddie, 1976; Quick et al., 2007). Intrinsic pumping uses the muscular contractions of lymphatic wall muscle, whereas extrinsic pumping happens as a result of the squeezing of lymphatic vessels by adjacent tissues. This occurs because of the intermittent relative motion of adjacent structures, thanks to use of skeletal muscles, respiration, peristalsis of organs including the oesophagus, intestines and ureters, pulsation of arterial blood vessels, etc. (Guyton & Coleman, 1968; Hogan & Unthank, 1986; Swartz et al., 1996).
There are two main types of lymphatic vessels, initial and collecting. Initial lymphatics are arranged in converging networks that drain lymph into first pre-collecting then collecting lymphatic vessels. Excluding those of the bat wing, initial lymphatics and pre-collectors are passive vessels, devoid of muscle, in which the only mode of pumping is extrinsic. The wall of these vessels comprises a monolayer of endothelial cells with an incomplete basement membrane. The endothelial cells overlap, and are attached to surrounding connective tissue by anchoring filaments. Unlike endothelial cells elsewhere, they do not form tight junctions. This architecture amounts to a system of primary valves (PVs), facilitating one-way flow of interstitial proteins, fluid, and particles into the lumen of the initial lymphatics; see the reviews by Breslin et al. (2019) and Moore & Bertram (2018). The PVs close when the pressure in the initial lymphatic exceeds that outside, and open when it falls below the local interstitial pressure. Fluid entry (i.e. lymph formation) is thus opportunistic, occurring whenever the transmural pressure difference is favourable (Trzewik et al., 2001).
By definition (see Breslin et al., 2019), initial lymphatics end where the first intra-vascular valves define pre-collector vessels, the wall of which is still an endothelial cell monolayer. However, with distance along the pre-collectors, the cells increasingly form the tight junctions that characterise conduit vessels.
Compared with collecting lymphatics, relatively few theoretical models have been formulated for initial lymphatics (and none to our knowledge has been devoted to pre-collectors). Reddy (1974) developed the first model of an idealized initial lymphatic vessel, as part of a computational model of the lymphatic vascular system of the whole human body. Elhay and Casley-Smith (1976) proposed equations to model the initial lymphatics based on the assumption that influx of lymph into the lumen is due to colloidal osmotic pressure exerted by protein molecules in the lumen, but later work has not supported this oncotic mechanism. The Reddy model eventually became the partial differential equation model of Reddy & Patel (1995), analysing variation of interstitial swelling and pulsatile initial lymphatic flow as a result of time-varying pressure at the outlet of the lymphatic vessel. Roose and Swartz (2012) applied homogenization theory to the regular hexagonal arrangement of initial lymphatic vessels that they found in the skin of the mouse tail, showing that this layout was more efficient than other regular arrangements. The analysis by Causey et al. (2012) of lymph formation in skeletal muscle, building on the work of Mazzoni et al. (1990), shows how extrinsic variation in initial lymphatic cross-sectional area is the result of blood vessel volume change and voluntary muscle contraction and stretch.
Sloas et al. (2016) estimated the pressure drop required to drive lymph through an initial lymphatic network. Their model assumed the network to have impermeable walls, with inflow only through the blind ends of the network-tip twigs. This is contrary to established findings that initial lymphatics are permeable (Leak, 1971). They did not take into account the PVs, and assumed that the network was non-compliant. Negrini and Moriondo (2011) showed that the initial lymphatics of the diaphragm exhibit a linear pressure-volume relationship. However, these vessels are atypical initial lymphatics, with size more akin to normal collecting vessels. Reddy & Patel (1995) estimated the pressure-radius relation of initial lymphatics based on linear elasticity theory.
The primary valves have attracted their own share of modelling (Mendoza & Schmid-Schönbein, 2003; Galie & Spilker, 2009). Experiments showed no reflux through the primary valves under normal conditions, but extensive leaking during inflammation (Lynch et al., 2007). Heppell et al. (2013) modelled fluid flow all the way from blood capillaries through the porous interstitium and into the lymphatics via the PVs. Heppell et al. (2015) formulated a model for a sliding PV of initial lymphatics, where the degree of opening was controlled by the extent of interstitial swelling.
In this paper, we seek to understand how interstitial resistance, primary valves, and inflammation affect transport of lymph through a specific rat mesenteric network of passive lymphatic vessels under time-varying external pressure. We applied this oscillating pressure uniformly across the network, on the assumption that the length scale of the moving surrounding tissue structures giving rise to the time-varying pressure is much greater than the dimensions of the specific network we model. We used a published image of a lymphatic network from “the thin translucent connective tissue in between the mesenteric arterial/venous vessels feeding the bowel” (Murfee et al., 2007). The network arrangement is accordingly conveniently two-dimensional. By analysis of the image we obtained the piece-wise vessel centre-lines, and hence the lengths and diameters of all the branches, data which we fed into the model along with the overall network topology.
Following Heppell et al. (2013), we incorporate the interstitial resistance using Darcy’s law. Extrinsic pumping is simulated by applying time-varying pressure at the notional exterior boundary of a thick cylinder of interstitium wrapping each lymphatic vessel. The interstitial thickness, i.e. the distance through which interstitial fluid must pass, is equated to our estimate of half the average distance between the lymphatics in the imaged network. Pressure boundary conditions were chosen to give cycle-mean flow-rate of the order of those experimentally observed in initial lymphatics by Swartz et al. (1996). The walls of the vessels exhibit one-way PV function, with total valve aperture corresponding to the calculated length of endothelial cell perimeter for cells tiling the vessel walls. How such fully porous initial lymphatics give way downstream to less porous pre-collecting vessels before draining into fully impermeable collecting vessels has not been investigated. We therefore modelled two cases, one with the maximum density of endothelial valve uniformly distributed over all vessels, and a second with the PV density depending on the generation of the vessel in the network such that the valve density reduces in the downstream direction. We investigate how inflammation changes the lymph flow by altering the PV model to incorporate leakage.
Collecting lymphatics are normally regarded as distinguished from initial lymphatics both by muscular walls and by rather regular subdivision into short lymphangions by intravascular secondary valves (SVs). In turn pre-collectors are distinguished from initial lymphatics only by the presence of irregular SVs. Very little imaging of lymphatic vessels (Munn & Padera, 2014) provides sufficient detail to show the location of SVs, although their positions in collecting vessels can sometimes be inferred from the bulging of valve sinuses perfusion-fixed at high pressure (Suami et al. 2012). The imaging by Murfee et al. (2007) is the exception, clearly showing the existence of sparse SVs through the unicellular wall of the lymphatics in the particular tissue which they investigated. We accordingly incorporate SVs in the modelled network in their anatomically correct positions, using a model of SV function taken from modelling of collecting lymphatics (Bertram et al., 2011; Jamalian et al., 2016). It is not known whether these intravascular valves are functional or not, so we investigate network fluid flow both with the SVs operational and with them switched off, i.e. set to present only a low constant hydraulic resistance corresponding to their minimum resistance when open. Since the effective stiffness of initial lymphatics and pre-collectors is so little known, we regard this as a principal disposable parameter, which we vary widely around a baseline estimated value to see how it affects the flow-rates in the network. Essentially no data exist on the variation of initial lymphatic vessel stiffness with location, but since initial lymphatics and pre-collectors both lack muscle, we take all the vessels in the network to have the same pressure-diameter slope.
In section 2, we formulate a mathematical framework for the network and give the values of the model parameters. In section 3, we present the results of the computational model. In section 4, we discuss the findings from the model and consider their physiological significance. Section 5 contains our conclusions.
2. Methods
The anatomical network of passive lymphatic vessels which we set out to model is shown in Figure 1.
Figure 1.
A network of initial lymphatics and pre-collectors from a rat mesentery. The image is adapted from fig. 1 of Murfee et al. (2007); blood vessels have been removed, except where they cross lymphatic vessels, where they show up as dark diagonal tracks. The network contains secondary valves labelled V1 to V9 (blue). E1 is the outlet and E2 to E11 (green) are the inlets of the network (assumed impermeable), B1 to B19 (cyan) are the network branch numbers, and the length and spatial-average diameter (in pixels, where 1 pixel = 3.2 μm) are printed (in red) on each of the branches. Green lines indicate approximately the outer edge of the interstitium at radius ris across which fluid must percolate. Scale bar: 100 μm.
Using in-house software coded in Matlab, we segmented the vessels of the network to a binary image, then calculated the local vessel diameter at a dense series of local axial distances (every 30 μm) along the centre-line of each vessel. For the lumped-parameter model, these data were reduced to a single value of length and diameter for each anatomical vessel segment, defined as that part between the nearest network tip or network junction and the next junction or the network exit. If an anatomical segment includes a SV, we treat it for numerical purposes as consisting of two model segments, giving us 28 model segments from 19 anatomical segments. We ignored any changes in direction of a segment, on the basis that the creeping flow in these tiny vessels has insignificant momentum. Rather than the simple average of the measured diameters for each segment, we used the conductance-averaged diameter (see equations below). In a tube of varying diameter, this more accurately reflects the overall relation between pressure difference and flow-rate, which is dominated by the high resistance of the narrowest part(s).
2.1. Mathematical formulation
We developed the computational model by adapting an existing lumped-parameter model (Bertram et al., 2011; Jamalian et al., 2016). The equations of the model are as follows. Table 1 gives the definition of all time-dependent variables, and Table 2 the definitions and values of all parameters.
Table 1.
Time-dependent variables used in the model.
| variable | description | units |
|---|---|---|
| Di | diameter of segment i | cm |
| Qi | flow-rate into segment i from segment i – 1 | ml s−1 |
| Qis,i | flow-rate through interstitium of segment i | ml s−1 |
| Qw,i | transmural flow-rate into segment i | ml s−1 |
| p1,i | pressure at inlet of segment i | dyn cm−2 |
| pm,i | pressure at mid-point of segment i | dyn cm−2 |
| p2,i | pressure at outlet of segment i | dyn cm−2 |
| pow,i | pressure just outside the wall of segment i | dyn cm−2 |
| pe | time-varying external pressure | dyn cm−2 |
| Δptm,i | transmural pressure for segment i | dyn cm−2 |
| ΔpV,i | pressure difference across secondary valve i | dyn cm−2 |
| Rpv,i | resistance of primary valve = f(Δptm,i) | g cm−4 s−1 |
| RV,i | resistance of secondary valve = f(ΔpV,i) | g cm−4 s−1 |
Table 2.
Algebraic parameters used in the model and their values.
| param | description | value | units | source |
|---|---|---|---|---|
| μ | fluid viscosity | 0.01 | g cm−1 s−1 | Bertram et al. (2011) |
| Li | length of vessel segment i | 0.081–1.123 | mm | measured |
| D0,i | conductance-averaged diameter of segment i | 0.021–0.068 | mm | measured |
| f | frequency of sinusoidal external pressure | 0.5 | Hz | estimated |
| Ap | amplitude of sinusoidal external pressure | 0.5 | cmH2O | estimated |
| mean of sinusoidal external pressure | 1.5 | cmH2O | estimated | |
| pout | network outlet pressure | 1.4 or 1.6 | cmH2O | estimated |
| m | slope of ptm − D relationship | 2.1 × 103 to 2.1 × 107 | dyn cm−3 | - |
| ris | radius of surrounding interstitium | 0.03 | cm | estimated |
| κ | permeability of surrounding interstitium | 7.6 × 10−11 | cm2 | Heppell et al. (2013) |
| a | fit constant for primary-valve model | 7.8867 × 10−8 | cm2 dyn−1 | estimated |
| b | fit constant for primary-valve model | 7.1125 × 10−5 | cm2 dyn−1 | estimated |
| dec | characteristic endothelial cell dimension | 2 or 20 | μm | estimated |
| Rpv0 | unit conversion constant | 1 | g cm−3 s−1 | by definition |
| G | network generation number | 1–7 | - | - |
| Δpo | secondary-valve opening/closing pressure | −15 | dyn cm−2 | Bertram et al. (2011) |
| so | secondary-valve opening/closing slope | 0.4 | cm2 dyn−1 | Jamalian et al. (2016) |
| RVn | minimum secondary-valve resistance | 0.5 × 106 | g cm−4 s−1 | Bertram et al. (2011) |
| RVx | maximum secondary-valve resistance | 9.9 × 109 | g cm−4 s−1 | Bertram et al. (2011) |
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
Eqn. 1 describes conservation of mass for a segment; the four terms are the volume change due to diameter change, the inflow from any preceding segments, the outflow to the following segment, and the inflow through the wall via the primary valves. Eqns. 2 and 3 describe conservation of momentum in each of the two compartments comprising a segment, using the Poiseuille formulation. Eqn. 4 is the constitutive relation, representing a balance of forces at the vessel wall. Reddy & Patel (1995) suggested a constitutive relation based on linear elasticity theory that is strain-softening, whereas collecting lymphatics display prominent strain-hardening (Rahbar et al., 2012). In the absence of better information about initial lymphatics, we prescribed a linear relation between transmural pressure and diameter Di with slope m. The intercept at zero transmural pressure, D0,i, is the conductance-averaged diameter for segment i, defined as
| (14) |
where dj is an individual local measurement of diameter at segment axial location j, and n is the total number of such determinations along segment i.
Eqn. 5 prescribes momentum conservation for the flow through the porous interstitium, using the Darcy formulation. The particular form of the equation occurs because the flow is radially inward through the permeable cylinder. Eqn. 6 is again conservation of mass; the trans-interstitial flow-rate must equal the flow-rate in through the primary valves for a given segment. Eqn. 7 prescribes momentum conservation for the flow through a primary valve in generalised notation.
Eqn. 8 specifies the nonlinear function that is the PV resistance; it is shown graphically in Figure 2. Constants a and b fit the model to the data points computed by Galie & Spilker (2009). The driving pressure difference, −Δptm,i, which is minus the transmural pressure (eqn. 9), becomes pe − pm,i if the interstitial thickness is zero. The function is dimensionless, and must be multiplied by an implicit constant q0 with unit value and the units cm2/s to represent 2D flow-rate per unit length of endothelial valve. The conversion from 2D flow-rate to 3D flow-rate for the entire segment depends on the amount of endothelial cell perimeter per unit area of segment wall. This we estimated as follows. Whether endothelial cells be approximated as square or as hexagonal tiles, the length of cell perimeter per unit area of vessel wall is 2/dec, where dec is a nominal endothelial cell diameter1, but can be used to describe the endothelial cell perimeter per unit area of segment wall irrespective of cell shape. The area of vessel wall is πLiD0i, so the 3D flow-rate is 2πLiD0i/dec times the 2D flow-rate given by Fig. 2. Unless otherwise stated, we used dec = 2 μm, but we also consider dec = 20 μm. Constant Rpv0 = p0/q0, where implicit constant p0 has unit value and units dyn/cm2, provides the units of resistance. G is the number of the generation that the vessel occupies in the lymphatic network; see Figure 3. The inclusion of this factor provides a progressive reduction in the area density of primary valves towards the downstream end of the network, so that upstream vessels admit more interstitial fluid than downstream ones. For simulations with uniform PV density everywhere, the factor G is omitted from eqn. 8. Leakage flow during inflammation (Fig. 2, blue curve) is achieved by allowing reverse flow at one-fifth of the forward flow-rate.
Figure 2.
Pressure-drop/flow-rate relationship for a simulated primary lymphatic valve. The data-points are taken from Galie and Spilker (2009). The red curve fits their data. The blue curve incorporates primary-valve leakage.
Figure 3.
A schematic of the 19-segment network shown in Fig. 1, showing network generation numbers, and diameter, inflow-rate and outflow-rate for each anatomic segment. Where a segment (e.g. 15) includes a secondary valve, it is dealt with computationally as two segments (numbered 15a and 15b); thus a total of 28 model segments is defined. Secondary valves are identified by the flow-rate through them, e.g. Q2a.
Eqn. 10 prescribes the sinusoidal variation of external pressure pe between 1 and 2 cmH2O, at a frequency of 0.5 Hz. Given the powerful sources of tissue relative motion in vivo (skeletal muscle contraction, intestinal peristalsis, ventilation, transient compression by body weight, etc.) and in the physiology lab. (passive limb movement), variation of pe over 1 cmH2O is very conservative. Sinusoidal variation is of course a simplification, and indeed some sources will vary pseudo-randomly with time. With mean pe thus fixed at 1.5 cmH2O, we set the constant outlet pressure to be either 1.4 cmH2O or 1.6 cmH2O, providing a time-average pressure difference of ±0.1 cmH2O to drive the flow across the network. Two further values of time-average pressure difference are also explored below in one specific context, that of defining the extent of use of each SV.
Eqns. 11–13 describe the SVs. We used a sigmoidal function (Bertram et al., 2011) to model their resistance, whereby valve state (open or closed) was determined according to whether the pressure difference across the valve was above or below the prescribed valve-opening pressure-difference threshold. Note that this valve description excludes the hysteresis and pressure-dependence of transvalvular offset incorporated in the model described by Bertram et al. (2014a, b).
The model organization can be summarised schematically as in Figure 4, which shows a network consisting of a single Y-branching. The full model applies this same scheme to the 19-segment lymphatic network shown anatomically in Fig. 1 and schematically in Fig. 3.
Figure 4.
A schematic single-Y-branch network with vessel walls that are permeable to inflow only, through primary valves (red). The green outline shows the outer extent of the interstitium draining to each vessel. The distance between the green and red lines represents the thickness of the interstitium through which fluid must percolate to reach the vessel wall (green arrows).
The model equations form a differential-algebraic equation system which was coded in Matlab and solved using the routine ode15s. The majority of simulations were run on a laptop computer, but repeated runs involving variation of a single parameter were accomplished in parallel using the Artemis high-performance computing facility at University of Sydney (https://informatics.sydney.edu.au/services/artemis/#artemis).
3. Results
3.1. Flow-rate and diameter waveforms for outlet branch
Waveforms of the time-varying outflow-rate and diameter of the outlet branch of the network, and external pressure, are shown in Figure 5 over one 2s cycle after start-up transients have died away (8–10s), for both non-leaky and leaky PVs, and for both uniform and downstream-decreasing PV density. As pe(t) increases, the diameter reduces under the compression, increasing again when pe decreases. With uniform PV density throughout the network, Qout(t) becomes positive slightly earlier with non-leaky PVs than with leaky ones, but in both cases well before pe(t) > pout. The reason for this is that the intravascular secondary valves close before pe(t) reaches pout, which then leads to pressure in the lumen increasing beyond pout, causing forward flow. For both leaky and non-leaky PVs, Qout(t) becomes negative again shortly after 9.2s, even though pe(t) > pout, as the outlet branch (and other vessels) starts to refill. The overall diameter change is less with leaky PVs, because of reflux back to the interstitium during positive transmural pressure. With decreased PV density in downstream generations, overall outlet-branch diameter change, and maximum positive and negative Qout, are essentially unchanged, but Qout becomes negative earlier in the cycle: about 40% sooner after peak pe than with uniform PV density. Negative Qout occurs during a portion of the cycle, indicating that the outlet vessel refills from downstream, where the constant pout provides no resistance, when pe(t) reduces. In vivo, this behaviour would likely be counteracted by the closure of valves in collecting lymphatics downstream.
Figure 5.
External pressure, outlet diameter and outlet flow-rate vs. time for the network with spatially uniform (red and blue curves) or tapering (green and grey curves) PV density and non-leaky (red and green curves), or leaky (blue and grey curves) PVs. The period of oscillation is 2s, pout =1.4 cmH2O (magenta line), and pe(t) varies between 1 and 2 cmH2O with mean 1.5 cmH2O; ris = 300 μm, and m = 2.1 × 105 dyn cm−3. Solid vertical lines indicate when pe(t) crosses pout. Dashed vertical lines indicate when Qout(t) crosses zero.
3.2. Cycle-mean flow-rate vs. steady flow-rate
The effect of pulsatile external pressure, representing extrinsic pumping, is shown in Figure 6, for both scenarios of primary-valve spatial distribution and for both non-leaky and leaky PVs, under conditions of favourable mean pressure gradient . Time-varying pe leads to much higher time-average network-outlet flow-rate Qcyc-av than constant pe: comparing the blue bar heights with the yellow bar heights shows a factor of 5–6 difference in mean Q through the outlet branch for both the uniform and the tapered PV distribution. The reason for this is the closure of the SVs downstream when the trans-valvular pressure difference is less than the critical threshold. Lymph trapped in downstream vessels increases luminal pressure which distends the compliant vessels. Even while the instantaneous overall network pressure gradient is still unfavourable, the trapped fluid is expelled from the outlet branch once the local unfavourable gradient reverses. With pulsatile pe, and uniform PV density, leaky PVs decrease Qcyc-av by some 6%. When pe is constant, the network segments operate in a state of negative transmural pressure, which leads to diameter reduction and increase in resistance to flow. In the case of constant favourable overall pressure gradient as here, the SVs provide no benefit but instead a small detriment, as they add to the resistance of the network, leading to further decrease in outflow.
Figure 6.
Comparison of Qcyc-av in the outlet branch when pe varied between 1 and 2 cmH2O with mean 1.5 cmH2O (blue bars), with the steady flow-rate when pe was constant at 1.5 cmH2O (yellow bars), for both uniform and spatially tapering PV function, and both non-leaky and leaky PVs. Parameters: pout = 1.4 cmH2O, ris = 300 μm, m = 2.1 × 105 dyn cm−3.
3.3. Effect of inflammation on the cycle-mean flow-rate
We explored two PV scenarios: (1) uniformly maximal PV density, and (2) PV density tapering lower downstream. For both distributions, Qcyc-av in the outlet branch is greater when there is no inflammation (no back-flow through PVs), as shown in Figure 7. For uniform PV density, we investigate two different values of pout: (1) , similar to an oedema condition, and (2) , since the pressure in the interstitium can be sub-atmospheric. There is a small decrease in flow-rate during inflammation when , as seen in the difference in bar height between the blue bars in columns 1 and 2; this difference is greater when .
Figure 7.
Comparison of Qcyc-av exiting the network between (blue bars) and (yellow bars) for uniform and spatially tapering PV function. External pressure varied between 1 and 2 cmH2O with mean 1.5 cmH2O, for both non-leaky and leaky PVs. Parameters: ris = 300 μm, m = 2.1 × 105 dyn cm−3.
With reduced PV density downstream, there is no significant change in outlet Qcyc-av during inflammation when pout = 1.6 cmH2O, i.e., when . When , there is no effect of inflammation.
3.4. Effect of interstitial resistance on flow distribution in the network
Interstitial resistance favours fluid take-up by longer segments. We investigate this by comparing the uptake of fluid by each vessel of paired Y-branch tips. There are three such pairs in the network. We compare the mean flow-rate exiting network-tip twigs as a function of the twig length, with or without interstitial resistance. Figure 8 shows that in the absence of interstitium (brown), two (8–9 and 18–19) out of the three pairs display more outlet flow-rate from the shorter member of the pair2. Conversely, when the interstitium is included (blue), all three pairs display more outlet flow-rate from the longer member of the pair. In the absence of interstitial resistance, the vessel hydraulic resistance controls the flow through the twig. Since the shorter twig has less hydraulic resistance, there is more flow through it than through the longer one. However, once interstitial resistance is present, it controls the flow-rate. Since interstitial resistance is inversely proportional to segment length, flow-rate in the longer twigs will be greater than in the shorter ones. Decreasing the interstitial permeability, or increasing PV resistance, accentuates the tendency for long segments to admit higher flow-rate than short ones.
Figure 8.
Mean branch outflow-rate vs. branch length, compared in all three pairs of Y-converging terminal branches, with (blue) and without (brown) 300 μm of interstitium.
3.5. State of secondary valves during contraction
Figure 9 shows waveforms of the pressure difference across each of the SVs in the network during a cycle of external pressure variation, for four different values of the overall cycle-average pressure difference across the network. The four values, ranging from favourable to adverse, were achieved by setting pout to 1.4, 1.5, 1.6 and 1.7 cmH2O. For these simulations the interstitial thickness was set to 300 μm, the PV density was uniformly maximal, and the PVs were non-leaky. When the trans-valvular pressure is less than the constant pressure-difference threshold value (shown by a dashed line in each panel of Fig. 9), the valves close.
Figure 9.
The trans-valvular pressure difference (Δpsv) across the secondary valves in the four generations (2, 3, 5 and 6) where they are located, for four different values (−0.1, 0, +0.1, +0.2 cmH2O) of time-average overall network pressure difference . Refer to Fig. 3 for branch and generation numbers. Dashed horizontal line: the trans-valvular pressure difference (−0.015 cmH2O) at which closure/opening occurs. Parameters: ris = 300 μm, m = 2.1 × 105 dyn cm−3.
Referring to Fig. 3, secondary valve 17a, in network generation 2, remains always open, at all four values of . Valve 15a, in generation 3, closes briefly only when . In generation 5 there are six SVs. Valves 4b and 5a operate at all four values of . Valves 4a and 7a operate only when . Valves 6a and 7b never close under any of the four values of . In generation 6, the sole valve 2a operates at all four values of .
A clear pattern of behaviour is thus manifest. SVs exposed to the network exit always operate, i.e. they close and open at some point during the contraction cycle, regardless of actual distance from the exit, and regardless of whether or not there are further valves upstream. In two anatomic segments there are two valves in series, but whereas valve 4b is exposed to the exit and always operates, its equivalent in the other vessel, valve 7b, never operates, being ‘protected’ from downstream influences by valve 2a and from upstream influences by valve 7a. The only other valves which do not operate are 17a, located uniquely far from the exit in generation 2 and with four other valves (2a, 7a, 7b and 15a) in the path between itself and the exit, and 6a, which is isolated from the exit by valve 2a downstream and like 17a is located in a terminal twig. The two ‘upstream’ valves in the two segments with two valves, 4a and 7a, operate only when the network is facing the maximum adverse Δp, as does valve 15a, with three valves between itself and the exit. Thus in general valves in upstream positions are less likely to operate, because the retrograde flow-rate needed to develop the necessary negative Δpo to close them is limited by the closure of valves downstream.
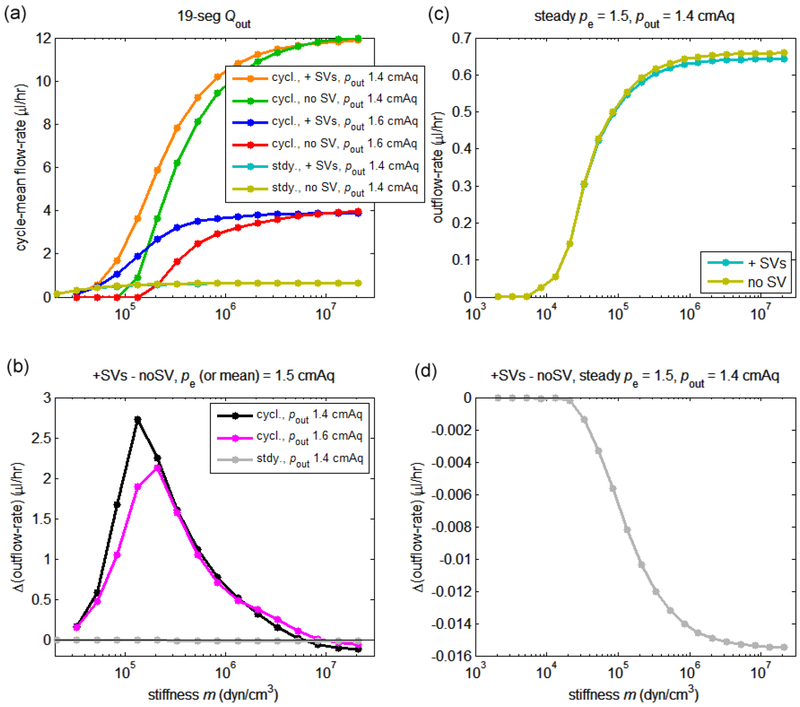
3.6. Effect of vessel stiffness on the cycle-mean flow-rate
In general we predict that the network outflow-rate will tend to a constant value when the slope m of the linear Δptm-D relationship given in eqn. 4 is large, i.e. vessels are effectively rigid. We also predict that outflow-rate will tend to a constant value when m is so small that no further qualitative change in vessel response is possible; one or both of these limiting behaviours may well be unphysiological, albeit a valid solution of the model equations. The computed results bear out these predictions; see Figure 10. Results are shown for both favourable (pout = 1.4 cmH2O) and adverse (pout = 1.6 cmH2O) overall network Δp, for both pulsatile and constant pe, and for both operating and deactivated SVs. For these simulations the interstitial thickness was set to zero.
Figure 10.
Variation of the network-outlet cycle-mean flow-rate Qcyc-av with the slope m of the constitutive relation in eqn. 4, for ris = 300 μm. (a) Qcyc-av with operational and with deactivated SVs for pout = 1.4 cmH2O and 1.6 cmH2O. (b) Difference between Qcyc-av with operational and Qcyc-av with deactivated SVs, for pout = 1.4 cmH2O and 1.6 cmH2O. (c) Outlet Q under steady pe, with operational and with deactivated SVs, for pout = 1.4 cmH2O and 1.6 cmH2O. (d) Difference between Q with operational and with deactivated SVs, at pout = 1.4 cmH2O. Outflow (and outflow difference) is much less at most values of m when pe is steady; to illustrate this, the data from panels c and d are also shown in panels a and b respectively.
Panel a of Fig. 10 shows that the time-average network outflow-rate Qcyc-av was higher when the overall network was favourable than when it was adverse (a point already made by Fig. 6); compare orange with blue, and green with red curves. The panel also shows the effect of stiffness on Qcyc-av when the SVs were operational vs. when they were deactivated, for favourable and adverse . Somewhat surprisingly, under all circumstances examined, maximum outflow-rate occurs when m is large, i.e. when the vessels are stiff. Thus no absolute advantage of extrinsic pumping is evident, but panel b shows a relative advantage of extrinsic pumping, in that Qcyc-av at intermediate values of m, i.e. when the network is somewhat compliant and extrinsic pumping is possible, is higher with SVs operational than with SVs deactivated. However, when the network becomes so stiff that the vessels no longer vary in diameter significantly, the SVs no longer provide this advantage, and in fact their resistance diminishes the outflow-rate, so that the network with non-operational SVs has slightly higher outflow-rate. The disadvantage created by the resistance of the SVs is seen where the black and magenta curves cross the zero line. Depending on the value of , the optimal value of m in terms of creating extrinsic pumping advantage is between 1 and 2 × 105 dyn/cm3. The maximum advantage gained with operational SVs is greater when is favourable than when it is adverse.
With steady pe, there is no network outflow when is adverse (not shown). When is favourable (pout = 1.4 cmH2O), the outflow-rate is close to zero when the network is compliant (panel c), because all vessels in the network are operating under negative transmural pressure, and hence their diameter reduces and their resistance increases. When the stiffness increases, the steady outflow-rate increases, but only reaches some 5.5% of the equivalent maximum value with pulsatile pe. The network with deactivated SVs admits more flow-rate than that with operational SVs, because SV resistance diminishes the flow-rate (panel d).
3.7. Effect of interstitial thickness on mean outflow-rate
The cycle-mean flow-rate decreases with increasing interstitial thickness, but the effect of equal extra increments of thickness decreases, so that the cycle-mean outflow-rate ultimately tends to a non-zero limiting value of around 2.5 μl/hr, as seen in Figure 11.
Figure 11.
Cycle-mean network outflow-rate Qcyc-av vs. m and ris, with pout = 1.4 cmH2O and pe = 1−2 cmH2O. (a) Qcyc-av vs. m for values of interstitium thickness ris from zero to 300 μm. (b) Qcyc-av vs. ris for various values of the vessel stiffness m.
The curves of Qcyc-av vs. m with finite interstitial thickness were explored only down to a minimum value of m = 2.1 × 105 dyn/cm3, because solutions for lower m would have taken impractically long to compute, owing to very long start-up transients. Over the range explored, the curves display qualitatively the same tendency to rise to a maximum value of Qcyc-av with increasing m, but the asymptotic value is reached at lower values of m when the interstitial thickness is greater.
3.8. Effect of available PV length on mean flow-rate
Besides the vessel stiffness, the other parameter for the model that is subject to much uncertainty is the value of dec, which inversely sets the available length of endothelial primary valve per unit vessel wall area (independently of any spatial taper in PV density with vessel generation). Recall that the PV model (Galie & Spilker, 2009) is two-dimensional, predicting the 2D flow-rate vs. pressure difference; it is only when this is multiplied by length in the third dimension that volume flow-rate is obtained. While we have not varied dec systematically over a wide range as with the vessel stiffness parameter m, we have calculated the effect of reducing the PV availability, by setting3 dec = 20 μm; see Figure 12.
Figure 12.
Upper panel: as for Fig. 11, but with dec = 20 μm. The additional curve cutting across the rest is for ris = 0 with the SVs disabled. Lower panel: the difference between cycle-mean Q for ris = 0 with SVs active and with them disabled.
The increase in dec reduces the total length of PV available per unit of vessel wall area by a factor of ten, increasing the PV component of the total resistance to inflow by this same factor and changing the relative importance of interstitial, PV and vessel resistances. The result is that the cycle-mean network outflow-rates are reduced relative to those in Fig. 11, by some three-fold at low ris, two-fold at maximum ris. In addition the shape of the curves changes; there is now maximum (reduced) outflow-rate at intermediate values of vessel stiffness, centred around m-values of about 4 to 8 × 105 dyn/cm3 (the exact value increases slightly as ris decreases). Thus there is now absolute benefit of extrinsic pumping, since the peak flow-rates exceed those at high m. That the mechanism of the benefit is indeed extrinsic pumping (as opposed to that involving just the PVs and downstream compliance) is shown by comparing the curves for ris = 0 with SVs enabled (blue) and deactivated (pink); as for dec = 2 um (Fig. 10), there is substantial advantage to having the SVs in action, with maximal advantage occurring at about m = 2.7 × 105 dyn/cm3. Only at high m (> 1.33 × 107 dyn/cm3) does the added resistance of active SVs create a slight disadvantage.
4. Discussion
All simulations with primary-valve density tapering towards zero at the downstream end of the network resulted in less overall network flow-rate than the corresponding situation with uniformly maximal primary-valve density (Figs. 6 and 7). Comparing corresponding bars in Figs. 6 and 7, the reduction due to tapered density ranged between 46 and 62%. It is likely that this is a cost which is anatomically necessitated by gradual transition from one vessel type to another along network paths in vivo. Outflow was also greatly reduced when the outlet pressure exceeded the mean external pressure: comparing adjacent bars in Fig. 7, the adverse pressure difference reduced outflow by between 39 and 61%. By comparison, the effect of leaky primary valves (representing inflammation) was much less, with a maximum outflow reduction of 32% under adverse pressure difference and uniform primary-valve density.
Outlet-branch mean flow-rate is even more sensitive to whether the mean pressure difference − pout across the network is favourable or adverse when the network vessels are stiff. If m takes sufficiently high values that vessel diameter change becomes insignificant, the flow-rate decreases by a factor of three with an adverse difference (Fig. 10a).
The effect of inflammation (leaky primary valves) is more pronounced when the mean external pressure is less than the outlet pressure (Fig. 7—the difference between blue and yellow bars is greater in columns 2 and 4 than in columns 1 and 3), because the mean adverse pressure drives flow back to the upstream vessels. The secondary valves in the downstream vessels close when the transvalvular pressure difference surpasses the critical threshold value. This creates a build-up of fluid in the vessel which increases the luminal pressure, pm, such that it can exceed the outside-wall pressure pow. In the inflammatory condition, this then causes reflux of fluid back to the interstitium. With spatially tapering primary-valve density, leaky primary valves make less difference, because the downstream vessels are then less permeable than the upstream vessels, and they have secondary valves to prevent backward flow. Hence, lymph only builds up in the less-permeable downstream vessels, decreasing the reflux back to the interstitium. It may be that this advantage of tapering primary-valve density in mitigating the effects of inflammation compensates in vivo for the cost discussed above. There is essentially no effect of inflammation when the external pressure is constant, because these transient conditions for reflux through the primary valves do not occur. However, this is not true when the secondary valves are assumed inoperative; there is then nothing to prevent reflux through all vessels if the outlet pressure exceeds the outside-wall pressure. Likewise, under the same pressure conditions, inflammation would lead to reflux in initial lymphatic networks that lacked secondary valves.
Under conditions of favourable overall pressure difference across the network, constant external pressure leads to five or more times lower cycle-mean network outflow-rate than time-varying external pressure having the same mean value (Fig. 6). This is true whether or not secondary valves are operational (Fig. 10a). With operational secondary valves, there is no flow in the network for outlet pressures greater than the constant external pressure (not illustrated). Such large outflow-rate increases with oscillating external pressure are striking, since little extrinsic pumping as usually defined was found when a large primary-valve length per unit wall area was assumed; only the excess of outflow-rate with secondary valves operating over that with secondary valves deactivated shown in Fig. 10b qualifies. However, significant benefit from extrinsic pumping was found when less primary-valve length per unit wall area was assumed (Fig. 12)4. Extrinsic pumping is normally defined as the intermittent squeezing of compliant lymphatic vessels containing at least two valves in series, so that the transient compression closes the inlet valve and opens the outlet valve, forcing fluid past the outlet of the chamber so formed. In our model, the greatest mean outflow-rates occurred at large values of m, i.e. when the vessels were no longer compliant. And they occurred both with and without operational secondary valves, i.e. in a situation where only the primary valves were available to secure advantage for oscillatory external pressure. Primary valves cannot occur in series, but they suffice to cause lymph formation and transport, even where inertial effects of the fluid are explicitly ruled out (eqns. 2 and 3), against an adverse mean network pressure difference, and in the absence of secondary valves in collecting lymphatic vessels downstream (Schmid-Schönbein, 2003). The mechanism of such pumping is simply the positive curvature of the primary-valve characteristic for forward flow (Fig. 2), which gives rise to a much greater mean transmural inflow-rate in response to a sinusoidal transmural pressure difference than in response to a steady transmural pressure difference having the same (favourable) mean. This mechanism also relies on there being sufficient compliance downstream. The assumed outflow boundary condition of constant pressure amounts to assuming that the missing collecting lymphatics downstream present unlimited compliance, ensuring that the mechanism can still operate if the vessels in the network here are effectively rigid. Any flexibility in the network vessels further adds to the compliance downstream of the primary valves.
We have assumed a linear relationship between transmural pressure and vascular diameter as a starting point, due to the paucity of experimental data on the constitutive relationship of initial lymphatics or pre-collectors. Varying the slope of this relationship, we find two qualitatively different optima for time-varying external pressure (Figs. 10–12). One is simply sufficient vessel stiffness that the vessels do not vary their diameter and act as rigid tubes. With high PV density (dec = 2 μm) everywhere, this situation leads to maximum network outflow-rate in almost all instances examined, failing only at maximum interstitial resistance. The other occurs at a specific non-zero degree of vessel compliance, allowing the oscillating external pressure to work in concert with the primary and secondary valves to effect extrinsic pumping as conventionally defined (Schmid-Schönbein, 2003). At dec = 2 μm this latter situation is a relative optimum only, in that the network outflow-rates so produced are inferior to those produced by making the vessels rigid. But at lower PV density (dec = 20 μm) it becomes an absolute optimum, albeit the optimum outflow-rate is much reduced. This latter optimum is likely to be physiologically attainable, whereas the optimum associated with rigid vessels may be incompatible with the anatomical properties of initial lymphatic vessels. Further investigation of this matter will necessarily have to involve measurement of the real pressure/diameter relationship of initial lymphatics in a range of tissues, something that has so far proved beyond experimenters. It is likely that the relationship will be found to be more a function of the surrounding tissue than of the properties of the endothelial cells which constitute the initial lymphatic wall, in view of the anchoring filaments joining the cells to the surrounding matrix and the open junctions between cells which constitute the primary valve system.
The model indicates that extrinsic pumping as strictly defined is not necessarily the dominant mechanism behind flow through the initial lymphatics. This is partly a question of definition; we here make a distinction between extrinsic pumping and the mechanism involving only the primary valve nonlinearity, pulsatile external pressure, and sufficient outlet compliance, which has not perhaps been recognized previously in the lymphatic literature. However it also reflects the fact that stiff vessels resulted in high network outflow-rates. This is intriguing, since to our knowledge it does not correspond to any known physiology. The cause is the absence of vessel collapse to small cross-sectional area when external pressure exceeds internal, which otherwise increases the viscous resistance to flow of individual vessels and limits the network outflow. However, in reality, initial lymphatics may be incapable of avoiding collapse.
Secondary valves were found to be somewhat concentrated in the downstream part of the anatomical network (Figs. 1 and 3), indicating that generations 5 and above constitute pre-collecting vessels. Although the network we examined is rather small, and the spread of valve locations also rather small, in our simulations we discovered definite evidence of more widespread operation of those secondary valves topologically closer to the downstream end of the network than of the more distant valves. By more widespread, we mean that the downstream valves were more likely to be operating at a given value of overall network mean pressure difference, and continued to operate until lower values of favourable pressure difference. We speculate that the anatomic positioning of the valves may reflect just this: that the further downstream a secondary valve is located, the more use it is, and the more use it will see. According to Sabine et al. (2012), unless a secondary valve operates frequently, transcription factors such as Foxc2 and Gata2 which are required to maintain the valve structure are down-regulated, resulting in valve degeneration.
The model is based on a specific small network of initial lymphatic and precollector vessels from the translucent mesenteric membrane of a rat, a tissue confined between two almost flat planes. While the confinement is not thought to have a bearing on the properties of the initial lymphatics in the network, it caused us to ‘invent’ cylinders of interstitium around each vessel in order to produce a model of more typical anatomical situations where each initial lymphatic drains a region around itself which is in principle homogeneous and isotropic. The actual topology of initial lymphatic networks varies greatly from one tissue to another, including the hexagonal arrangement in rat tail (Roose & Swartz, 2012), and arrangements of relatively straight vessels with many parallel short cul-de-sacs at right angles, subcutaneously in mouse hind thigh (CDB, personal observation in the Davis lab.). The imaging of rat small intestine by Unthank & Bohlen (1988) offers further examples of how much the initial-lymphatic topology can vary, even within one organ. Although our model would need quantitative adaptation to fit each of these structures, qualitatively the interactions between model components that we have documented here would not change.
5. Conclusions
Non-leaky primary valves led to higher mean outflow-rate than was found with leaky valves imitating inflammation. The disparity in mean flow-rate was more obvious when the outlet pressure exceeded the mean of the external pressure.
Steady external pressure led to much lower mean outflow-rate than external pressure oscillating around the same mean, for both uniform and tapering primary-valve area density. If the outlet pressure was greater than the mean of the time-varying external pressure, there was still forward flow, whereas the outflow was zero if outlet pressure exceeded steady external pressure.
The extent of diameter change of the outlet vessel was greater when the primary valves were non-leaky than when inflammation was simulated with leaky valves.
Interstitial resistance led to higher cycle-mean flow-rate out of longer network-tip branches than out of shorter branches.
The mean network outflow-rate increased with vessel stiffness until it reached an asymptote. The secondary valves in the network were advantageous when the network was compliant, but became marginally disadvantageous when the network was stiff.
When interstitial thickness was increased, the mean network flow-rate became less sensitive to the vessel stiffness.
We speculate that lesser utility may be the reason why there were fewer secondary valves in the upstream part of the imaged network than downstream.
Acknowledgements
We acknowledge the facilities, and the scientific and technical assistance of the Sydney Informatics Hub at the University of Sydney and, in particular, access to the high performance computing facility Artemis. BI was supported by NIH grant U01-HL-123420, which also funded the research.
Footnotes
Conflict of interest: the authors declare that they have no conflict of interest.
For a square unit cell of side length dec, forming part of an infinite tiling of the plane with such cells, the unique perimeter (avoiding counting tile borders twice over) is 2dec, and the area is dec2. Thus the perimeter per unit area is 2/dec. The same result holds for a tiling with regular hexagons, side dec/√(3), i.e. width dec.
In the case of the exception (branches 13–14), the effect of the shorter branch having smaller diameter outweighs the effect of branch length.
On the basis of our analysis of initial-lymphatic endothelial cell images (Zöltzer, 2003), we estimate that the true value lies in the range 12–25 μm. The uncertainty relates less to the perimeter per unit area of initial-lymphatic endothelial cells, than to the fraction of that inter-cell length which is actually devoted to non-bonded endothelial cell junctions (Baluk et al., 2007).
In fact close examination of the lowest curve in Fig. 11, that for ris = 300 μm, reveals that there is a shallow local maximum of network outflow-rate at m = 7 × 105 dyn/cm3. Thus extrinsic pumping becomes more evident when either primary-valve resistance or interstitial resistance increases relative to intravascular resistance.
References
- Baluk P, Fuxe J, Hashizume H, Romano T, Lashnits E, Butz S, Vestweber D, Corada M, Molendini C, Dejana E, and McDonald DM (2007) Functionally specialized junctions between endothelial cells of lymphatic vessels. Journal of Experimental Medicine 204(10), 2340–2362. DOI: 10.1084/jem.20062596 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertram CD, Macaskill C, and Moore JE jr. (2011) Simulation of a chain of collapsible contracting lymphangions with progressive valve closure. Journal of Biomechanical Engineering 133(1), 011008–1–011008–10. DOI: 10.1115/1.4002799 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertram CD, Macaskill C, and Moore JE jr. (2014a) Incorporating measured valve properties into a numerical model of a lymphatic vessel. Computer Methods in Biomechanics and Biomedical Engineering 17(14), 1519–1534. DOI: 10.1080/10255842.2012.753066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertram CD, Macaskill C, Davis MJ, and Moore JE jr. (2014b) Development of a model of a multi-lymphangion lymphatic vessel incorporating realistic and measured parameter values. Biomechanics and Modeling in Mechanobiology 13(2), 401–416. DOI: 10.1007/s10237-013-0505-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breslin JW, Yang Y, Scallan JP, Sweat RS, Adderley SP, and Murfee WL (2019) Lymphatic vessel network structure and physiology. Comprehensive Physiology 9, 207–299. DOI: 10.1002/cphy.c180015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casley-Smith J (1982) Mechanisms in the formation of lymph. International Review of Physiology 26, 147–187. [PubMed] [Google Scholar]
- Elhay S, and Casley-Smith J (1976) Mathematical model of the initial lymphatics. Microvascular Research 12(2), 121–140. [DOI] [PubMed] [Google Scholar]
- Galie P, and Spilker RL (2009) A two-dimensional computational model of lymph transport across primary lymphatic valves. Journal of Biomechanical Engineering 131(11), 111004–1–111004–9. DOI: 10.1115/1.3212108 [DOI] [PubMed] [Google Scholar]
- Guyton AC, and Coleman TG (1968) Regulation of interstitial fluid volume and pressure. Annals of the New York Academy of Sciences 150(3), 537–547. DOI: 10.1111/j.1749-6632.1968.tb14705.x [DOI] [PubMed] [Google Scholar]
- Heppell C, Richardson G, and Roose T (2013) A model for fluid drainage by the lymphatic system. Bulletin of Mathematical Biology 75(1), 49–81. DOI: 10.1007/s11538-012-9793-2 [DOI] [PubMed] [Google Scholar]
- Heppell C, Roose T, and Richardson G (2015) A model for interstitial drainage through a sliding lymphatic valve. Bulletin of Mathematical Biology 77(6), 1101–1131. DOI: 10.1007/s11538-015-0078-4 [DOI] [PubMed] [Google Scholar]
- Hogan RD, and Unthank JL (1986) Mechanical control of initial lymphatic contractile behavior in bat’s wing. American Journal of Physiology – Heart and Circulatory Physiology 251(2), H357–H363. [DOI] [PubMed] [Google Scholar]
- Jamalian S, Davis MJ, Zawieja DC, and Moore JE jr. (2016) Network scale modeling of lymph transport and its effective pumping parameters. PloS One 11(2), e0148384.(18 pages). DOI: 10.1371/journal.pone.0148384 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leak LV (1971) Studies on the permeability of lymphatic capillaries. Journal of Cell Biology 50(2), 300–323. DOI: 10.1083/jcb.50.2.300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch PM, DeLano FA, and Schmid-Schönbein GW (2007) The primary valves in the initial lymphatics during inflammation. Lymphatic Research and Biology 5(1), 3–10. DOI:0.1089/lrb.2007.5102 [DOI] [PubMed] [Google Scholar]
- McHale N, and Roddie I (1976) The effect of transmural pressure on pumping activity in isolated bovine lymphatic vessels. Journal of Physiology 261(2), 255–269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendoza E, and Schmid-Schönbein GW (2003) A model for mechanics of primary lymphatic valves. Journal of Biomechanical Engineering 125, 407–414. [DOI] [PubMed] [Google Scholar]
- Moore JE jr. and Bertram CD (2018) Lymphatic system flows. Annual Review of Fluid Mechanics 50, 459–482. DOI 10.1146/annurev-fluid-122316-045259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munn LL, and Padera TP (2014) Imaging the lymphatic system. Microvascular Research 96, 55–63. DOI: 10.1016/j.mvr.2014.06.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murfee WL, Rappleye JW, Ceballos M, and Schmid-Schönbein GW (2007) Discontinuous expression of endothelial cell adhesion molecules along initial lymphatic vessels in mesentery: the primary valve structure. Lymphatic Research and Biology 5(2), 81–90. DOI: 10.1089/lrb.2007.1005 [DOI] [PubMed] [Google Scholar]
- Negrini D, and Moriondo A (2011) Lymphatic anatomy and biomechanics. Journal of Physiology 589(12), 2927–2934. DOI: 10.1113/jphysiol.2011.206672 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quick CM, Venugopal AM, Gashev AA, Zawieja DC, and Stewart RH (2007) Intrinsic pump-conduit behavior of lymphangions. American Journal of Physiology – Regulatory, Integrative and Comparative Physiology 292(4), R1510–R1518. DOI: 10.1152/ajpregu.00258.2006 [DOI] [PubMed] [Google Scholar]
- Rahbar E, Weimer J, Gibbs H, Yeh AT, Bertram CD, Davis MJ, Hill MA, Zawieja DC, and Moore JE jr. (2012) Passive pressure-diameter relationship and structural composition of rat mesenteric lymphangions. Lymphatic Research and Biology 10 (4),152–163. DOI: 10.1089/lrb.2011.0015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddy N (1974) A discrete model of the lymphatic system. PhD thesis, Texas A&M University. [Google Scholar]
- Reddy N, and Patel K (1995) A mathematical model of flow through the terminal lymphatics. Medical Engineering & Physics 17(2), 134–140. [DOI] [PubMed] [Google Scholar]
- Roose T, and Swartz MA (2012) Multiscale modeling of lymphatic drainage from tissues using homogenization theory. Journal of Biomechanics 45 (1), 107–115. DOI: 10.1016/j.jbiomech.2011.09.015 [DOI] [PubMed] [Google Scholar]
- Sabine A, Agalarov Y, Maby-El Hajjami H, Jaquet M, Hägerling R, Pollmann C, Bebber D, Pfenniger A, Miura N, Dormond O, Calmes J-M, Adams RH, Mäkinen T, Kiefer F, Kwak BR, and Petrova TV (2012) Mechanotransduction, PROX1, and FOXC2 cooperate to control connexin37 and calcineurin during lymphatic-valve formation. Developmental Cell, 22(2), 430–445. DOI: 10.1016/j.devcel.2011.12.020 [DOI] [PubMed] [Google Scholar]
- Schmid-Schönbein GW (2003) The second valve system in lymphatics. Lymphatic Research and Biology 1(1), 25–29; discussion 29–31. [DOI] [PubMed] [Google Scholar]
- Sloas DC, Stewart SA, Sweat RS, Doggett TM, Alves NG, Breslin JW, Gaver DP, and Murfee WL (2016) Estimation of the pressure drop required for lymph flow through initial lymphatic networks. Lymphatic Research and Biology, 14(2), 62–69. DOI: 10.1089/lrb.2015.0039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suami H, Shin D, and Chang DW (2012) Mapping of lymphosomes in the canine forelimb: comparative anatomy between canines and humans. Plastic and Reconstructive Surgery 129(3), 612–620. DOI: 10.1097/PRS.0b013e3182402c6d [DOI] [PubMed] [Google Scholar]
- Swartz MA, Berk DA, and Jain RK (1996) Transport in lymphatic capillaries. I. Macroscopic measurements using residence time distribution theory. American Journal of Physiology – Heart and Circulatory Physiology, 270(1), H324–H329. DOI: 10.1152/ajpheart.1996.270.1.H324 [DOI] [PubMed] [Google Scholar]
- Trzewik J, Mallipattu S, Artmann GM, Delano FA, and Schmid-Schönbein GW (2001) Evidence for a second valve system in lymphatics: endothelial microvalves. FASEB Journal 15(10), 1711–1717. [DOI] [PubMed] [Google Scholar]
- Unthank JL, and Bohlen HG (1988) Lymphatic pathways and role of valves in lymph propulsion from small intestine. American Journal of Physiology – Gastrointestinal and Liver Physiology 254 (3), G389–G398 [DOI] [PubMed] [Google Scholar]
- Zöltzer H (2003) Initial lymphatics — morphology and function of the endothelial cells. Lymphology 36, 7–25. [PubMed] [Google Scholar]