Electroenzymatic Glutamate Sensing at Near the Theoretical Performance Limit

Abstract

The sensitivity and response time of glutamate sensors based on glutamate oxidase immobilized on planar platinum microelectrodes have been improved to near the theoretical performance limits predicted by a detailed mathematical model. Microprobes with an array of electroenzymatic sensing sites have emerged as useful tools for the monitoring of glutamate and other neurotransmitters in vivo; and implemented as such, they can be used to study many complex neurological diseases and disorders including Parkinson’s disease and drug addiction. However, less than optimal sensitivity and response time has limited the spatiotemporal resolution of these promising research tools. A mathematical model has guided systematic improvement of an electroenzymatic glutamate microsensor constructed with a 1-2 μm-thick crosslinked glutamate oxidase layer and underlying permselective coating of polyphenylenediamine and Nafion reduced to less than 200 nm thick. These design modifications led to a nearly 6-fold improvement in sensitivity to 320 ± 20 nA μM⁻¹ cm⁻² at 37 °C and a ~10-fold reduction in response time to 80 ± 10 ms. Importantly, the sensitivity and response times were attained while maintaining a low detection limit and excellent selectivity. Direct measurement of the transport properties of the enzyme and polymer layers used to create the biosensors enabled improvement of the mathematical model as well. Subsequent model simulations indicated that the performance characteristics achieved with the optimized biosensors approach the theoretical limits predicted for devices of this construction. Such high-performance glutamate biosensors will be more effective in vivo at a size closer to cellular dimension and will enable better correlation of glutamate signaling events with electrical recordings.

Graphical Abstract

Optimized sensors will enable more accurate monitoring of glutamate signaling in vivo.

Introduction

As was articulated clearly several years ago,¹ an understanding of information processing in the brain can be had only by unraveling of the interrelated roles of chemical neurotransmission and neuronal electrical activity. Great strides have been made in recording activity simultaneously from large numbers of interconnected neurons through millisecond timescale measurements of action potentials or intracellular Ca²⁺ changes.^2-7 However, corresponding tools to monitor chemical neurotransmission with the cellular-scale spatial resolution and the single-digit millisecond timescale of synaptic signaling events have yet to emerge.^8-11 This spatiotemporal mismatch has made problematic the desired correlation of chemical neurotransmission with neuronal activity. The problem is made particularly challenging by the broad array of chemical species involved that must be detected selectively against the complex background of brain extracellular fluid. Microdialysis and related techniques have been valuable tools for neurotransmitter measurements, although the typical minute-to-minute time resolution limits the detection of rapid neurotransmission events which are known to be much faster.^{12, 13} Electrochemical devices based on microelectrode arrays (MEAs) with electroenzymatic sensing sites on silicon or ceramic microprobes have emerged as useful tools for the monitoring of glutamate and choline (as surrogate for acetylcholine) in vivo. Our group and others have successfully demonstrated the feasibility of MEAs with response times in the ~1 s range for use in the study of complex neurological diseases and disorders including Parkinson’s disease and drug addiction.^14-16 Yet historically, these sensors have lacked the temporal resolution to associate unambiguously release events with local field potentials, and certainly not action potentials. Further, sensitivity limitations have required sensing sites on probes to be much larger than cellular dimension, thereby limiting spatial resolution. This report addresses these challenges through several-fold improvement in the design of a selective electroenzymatic sensor for the important excitatory neurotransmitter, glutamate (Glut).

An electroenzymatic Glut sensor consists of an electrode upon which one or more permselective films are deposited as well as an immobilized enzyme (Fig. 1). Typically, glutamate oxidase (GlutOx) serves as the enzyme and selective molecular recognition element that catalyzes Glut oxidation to α-ketoglutarate with production of hydrogen peroxide (H₂O₂). This recognition event is transduced into an electrical current signal most often through the electrooxidation of H₂O₂ by an underlying Pt electrode poised at oxidizing potential. In this way, Glut concentration may be correlated with measured current magnitude. However, the Pt electrode generally must be coated with permselective films to allow H₂O₂ to pass but to reject electrooxidizable interfering species common to brain extracellular fluid such as ascorbic acid (AA) that could give rise to false signals. Due to the restricted diffusion of Glut through the immobilized GlutOx layer and H₂O₂ through both the enzyme layer and the underlying permselective films, biosensor performance is impacted significantly by sensor construction. A variety of polymeric materials have been used as permselective films including polypyrrole (PPy), polyphenylenediamine (PPD) and Nafion.^17-19 GlutOx is most commonly immobilized on the electrode by spreading a mixture of enzyme and bovine serum albumin (BSA) on the coated electrode surface followed by crosslinking with glutaraldehyde (GAH).^{9, 11, 15, 16, 19-22}

Fig. 1.

Schematic of an electroenzymatic glutamate (Glut) sensor with permselective flims and a glutamate oxidase (GlutOx) enzyme layer.

Our previous simulations of then currently representative Glut sensors of the type illustrated in Fig. 1 suggested that the majority of the Glutd if fusing into the enzyme layer is consumed near its outer edge, and that the H₂O₂ concentration in the layer peaks closer to the bulk solution than to the Pt electrode surface.²³ The steeper H₂O₂ concentration gradient in the direction of the bulk solution and the larger corresponding flux indicated that the vast majority of H₂O₂ generated by the GlutOx-catalyzed Glut oxidation reaction escapes from the sensor site and is not available at the Pt electrode surface to give rise to a current signal. These simulations strongly suggest that reducing the enzyme layer thickness while maximizing active enzyme concentration to improve H₂O₂ capture would be an effective strategy to reduce response time and to improve sensitivity.

This report describes sensors fabricated with thinner permselective films and enzyme layers based on the guidance of our simulations. In order to characterize these new sensors, the mass transport properties of H₂O₂ within these permselective and immobilized enzyme films were evaluated experimentally using rotating disk electrodes (RDEs). These values provided improved parameter estimates for our mathematical model, and enabled demonstration that the new Glut biosensors had been improved to near the theoretical performance limit.

Experimental

Reagents

Nafion (5 wt% in lower aliphatic alcohols and 15-20% water), m-phenylenediamine (PD), pyrrole (Py), bovine serum albumin (BSA) lyophilized powder, glutaraldehyde solution (GAH), L-glutamic acid (Glut), L-ascorbic acid (AA), 3-hydroxytyramine (dopamine, DA), sodium phosphate dibasic, sodium chloride, HCl (36.5-38%), and hydrogen peroxide solution (30%) were purchased from Sigma-Aldrich (St. Louis, MO). L-Glutamate oxidase (EC 1.4.3.11) was obtained from US Biological. Bis(sulfosuccinimidyl)suberate (BS3) was purchased from Thermo Fisher Scientific (Pittsburgh, PA). Ag/AgCl glass-bodied reference electrodes with NaCl electrolyte (3M) and a 0.5-mm-diameter Pt wire auxiliary electrode were obtained from BASi (West Lafayette, IN). Sodium phosphate buffer (PBS, pH 7.4) was composed of 50 mM sodium phosphate dibasic and 100 mM sodium chloride. Four-inch silicon wafers (p-type boron doped; orientation h100i; thickness 150 μm) were purchased from Silicon Valley Microelectronics (Santa Clara, CA). The platinum rotating disk electrodes (RDEs) (5.0 mm disk, 12.0 mm OD PEEK shroud) were purchased from Pine Research (Durham, NC). Microcloth (PSA, 2-7/8’’) for electrode polishing was purchased from Buehler (Lake Bluff, Illinois).

Instrumentation

The RDE system (model AFMSRX) was purchased from Pine Research (Durham, NC). Microsensors were calibrated using a Versatile Multichannel Potentiostat (model VMP3) equipped with the ‘p’ low current option and N’Stat box driven by EC-LAB software (Bio-Logic USA, LLC, Knoxville, TN) in a three-electrode configuration consisting of the sensing electrode, a Pt wire auxiliary electrode, and a Ag/AgCl reference electrode. The film thicknesses on microelectrodes and RDEs were measured using a SEM (Nova 600 SEM/FIB System), a Dektak 8 stylus profilometer, and/or a Wyko NT300 optical profiling system.

Sensor preparation

The silicon-based microelectrode arrays used in this work were manufactured in house using microelectromechanical system (MEMS) techniques. The fabrication and array details are described in our previous work.¹¹ The microelectrode array probes were 150 μm thick, 140 μm wide and 9 mm long, with four, 6000 μm² (40 μm × 150 μm) Pt recording sites arranged in pairs at the tip (Fig. 2). A PPD film first was electrodeposited on Pt microelectrodes from a 5 mM PD solution in phosphate-buffered saline (0.1 M PBS) by holding the voltage constant at 0.85 V vs. Ag/AgCl until the desired total charge was transferred (7.6 × 10⁻⁷ coulombs). Alternatively, a PPy film was electrodeposited from 200 mM pyrrole in PBS at 0.85 V vs. Ag/AgCl for 5 mins. A Nafion layer then was applied by dip-coating a 2% Nafion solution (diluted from stock with 4:1 IPA:water) 3× for PPy/Nafion and only 1× for PPD/Nafion, followed by annealing at 115 °C for 20 min (115 °C-Nafion) or 180 °C for 4 min (180 °C-Nafion). Next, an immobilized GlutOx coating was deposited manually by loading a GlutOx and BSA mixture (dissolved in PBS) on the microelectrodes and crosslinking with 174 mM BS3 or 5% GAH vapor for 1 min. After the final crosslinking step, sensors were stored dry at 4 °C for 48 h prior to testing.

Fig. 2.

Scanning electron microscopy (SEM) image of the microelectrode array probe.

Electrochemical measurement

To determine sensor selectivity and sensitivity, a constant potential of 0.7 V vs. Ag/AgCl was applied to the sensors in stirred PBS buffer solution. After current stabilization, AA, DA, Glut or H₂O₂ were added to give final concentrations of 250 μM AA, 10 μM DA, 20-60 μM Glut and 20 μM H₂O₂. The selected concentrations of AA and DA were chosen to be reflective of those found in vivo.^24-26 To test the response time of the Glut microsensors, two peristaltic pump-driven streams of solution (PBS buffer and analyte) flowing from separate pipette tips were positioned close to the microprobe tip (Fig. 3). Rapid step changes in analyte concentration at the microsensors were achieved by alternating between PBS buffer and analyte streams by turning pumps on and off.²²

Fig. 3.

Testing set-up for microsensor response time. Rapid switching of solution flow onto the microprobe was controlled by alternating between pumped streams of PBS buffer and analyte solution.

Diffusion coefficient measurement

Diffusion of H₂O₂ within the PPD, Nafion or immobilized enzyme coatings was determined using a Pt RDE. The Pt RDE was polished using a microcloth and a 0.05 μm particle suspension, followed by rinsing with DI water and sonication in isopropyl alcohol. Next, a PPD, Nafion or enzyme film was deposited onto the electrode surface in the same way described in the sensor preparation section above. Linear sweep voltammetry (LSV) from 0.2 V to 0.9 V vs. Ag/AgCl was used as well as constant potential amperometry with varied rotation rate (see Results and Discussion). Aftermath software was used for collection of voltammetric data (Pine Research, Durham, NC).

Mathematical Model and Simulations

Simulations of sensor performance were generated using an established model for electroenzymatic sensors with updated values for transport parameters based on this work, adjusted for temperature dependence.²³ In the model, sets of partial differential equations describe the one-dimensional transport and reaction rates of Glut, O₂, and H₂O₂ within separately considered PPD, Nafion, and immobilized enzyme coatings. Boundary conditions simulate a step-change in Glut concentration from 0 to 20 μM on the microsensor surface at t = 0. Numerical solutions of model equations were generated using COMSOL (COMSOL, Inc. Los Angeles).

Results and Discussion

Optimization of permselective films

Our published Glut sensor modeling study showed that permselective film thicknesses and transport properties are important parameters to address in sensor optimization.²³ Dopamine (DA) and ascorbic acid (AA) are two common, electroactive interferents found in brain extracellular fluid at relatively high concentration that should be rejected by permselective films coated on the sensing electrode surface (Fig. 1). For what we will refer to as the base-case microsensor in this study, a PPy film and a Nafion overlayer annealed at 180 °C for 4 min (180 °C-Nafion) were used to reject DA and AA, respectively, yet to permit transport of H₂O₂ to the Pt electrode surface.¹¹ However, this PPy/180 °C-Nafion combination resulted in slow H₂O₂ diffusion to the electrode surface and low Glut sensitivity, mostly due to the overly thick Nafion coating necessary for adequate AA rejection, which was measured by SEM at 304 ± 87 nm (n = 3). Alternatively, when PPD was used as the underlying permselective film, a much thinner 180°C-Nafion coating (96 ± 10 nm (n = 5)) was adequate, thereby improving H₂O₂ sensitivity ~3-fold from 121 ± 52 nA μM⁻¹ cm⁻² (n = 4) to 372 ± 70 nA μM⁻¹ cm⁻² (n = 15) (Fig. 4).

Fig. 4.

(a) Comparison of H₂O₂ sensitivity among sensors prepared with PPy/180 °C-Nafion, PPD/180 °C-Nafion, and PPD/115 °C-Nafion. (b) The Nafion thicknesses corresponding to the three different sensor preparations. Inset: SEM image of a Nafion film on Pt. (c) Representative current responses of PPD/115 °C-Nafion coated sensors to 250 μM AA, 5 μM DA, and H₂O₂ administered in 20 μM concentration increments. (Error bars shown are 95% confidence intervals.)

The Nafion annealing temperature also impacts sensor performance significantly. In order to improve the mechanical stability of Nafion coatings and to reduce water solubility, dip-coated Nafion films normally must be heated above the glass transition temperature (T_g = 109 °C for protonated Nafion) to anneal them.^{27, 28} However, the choice of annealing temperature and duration of the annealing process also affects Nafion properties. As illustrated in Fig. 4, we found that lowering the annealing temperature from 180 °C to 115 °C while increasing the baking time from 4 min to 20 min resulted in a further improvement of the H₂O₂ sensitivity by ~25% to 536 ± 69 nA μM⁻¹ cm⁻² (n = 15). The improved annealing process resulted in an even thinner final Nafion layer thickness of 71 ± 11 nm (n = 5) while retaining excellent selectivity against AA. This result is in agreement with the recently published work of Leppänen et al. showing that very thin Nafion films can retain effective anion exclusion properties.²⁹

Hydrogen peroxide diffusion coefficient in permselective films and the crosslinked GlutOx layer

In addition to electrode coating thicknesses, measurements of H₂O₂ diffusivities in the permselective films and crosslinked enzyme layers are needed to improve the accuracy of sensor simulations and to better guide sensor optimization. There are three “resistances” that can limit the rate of H₂O₂ oxidation at the coated Pt electrode: (1) the transport of H₂O₂ in the external diffusion boundary layer just above the coated electrode surface, (2) the diffusion of H₂O₂ within the deposited films and (3) the H₂O₂ electrooxidation kinetics at the Pt surface. The overall current density can be described in terms of these serial resistances by a form of the Koutecky-Levich equation,^{17, 30-35}

$$\frac{1}{I}=\frac{1}{I_k}+\frac{1}{I_f}+\frac{1}{I_l}$$ (1)

where I is the measured current, I_k is the current in the absence of any mass transfer limitations, I_f is the current when limited totally by diffusion in a film deposited on the electrode and I_l is the current when limited totally by mass transfer through the liquid boundary layer on the coated or uncoated electrode surface. Further, I_l can be modeled using the Levich equation, and eq. 1 then becomes³⁵

$$\frac{1}{I}=\frac{1}{I_k}+\frac{1}{I_f}+\frac{1}{B_L{\omega }^{1∕2}C}$$ (2)

where B_L is the Levich constant, ω is the electrode rotation rate (radians/sec), and C is the bulk concentration of H₂O₂. The Levich constant is a function of H₂O₂ diffusivity in the bulk liquid, D_l, and the kinematic viscosity of the liquid medium, ν, such that³⁵

$$B_L=0.62nFA{D}_I^{2∕3}{\nu }^{-1∕6}$$ (3)

where n is the stoichiometric number of electrons transferred in the electrode reaction, F is Faraday’s constant, and A is the electrode surface area.

Representative current-potential (I-E) curves corresponding to bare Pt and Nafion-coated Pt RDEs in 0.2 mM H₂O₂ are shown in Fig. 5 and 6, respectively. The anodic current increases initially as the voltage and the electrode rotation rate are increased as expected, while water dissociation occurs in the potential region above 0.85-1.0 V vs. Ag/AgCl. The limiting current condition (plateau current) on bare Pt (Fig. 5) is achieved when the current is limited by the rate at which H₂O₂ is transported to the Pt electrode surface. When Nafion films are deposited on the Pt surface, these films ultimately limit the current achievable; and the electrode rotation rate, which influences external transport, has little to no impact (Fig. 6a). These results also show that diffusion of H₂O₂ was more hindered in 180 °C-Nafion than 115 °C-Nafion.

Fig. 5.

Representative current vs. potential curves showing the charge transfer, mass transport controlled and water dissociation regions at a bare Pt RDE using a potential sweep rate of 20 mV/s with rotation rates of 100, 200, 400, 800, 1600 rpm in PBS and 0.2 mM H₂O₂ solution.

Fig. 6.

(a) Oxidation of 0.2 mM H₂O₂ in PBS (pH 7.4) at Nafion-coated Pt RDEs annealed at 180 °C and 115 °C using a potential sweep rate of 20 mV/s with rotation rates of 100, 200, 400, 800, 1600, 2400 rpm. (b) Koutecky-Levich plot of data for a bare Pt RDE (gray trace) and for 180 °C-Nafion/Pt (blue trace) and 115 °C-Nafion/Pt (red trace) RDEs. Current data were obtained at 0.7 V vs. Ag/AgCl.

In order to obtain estimates for the diffusivities in Nafion, the current was set at 0.7 V vs. Ag/AgCl while the electrode rotation rate was varied. The plot of the inverse of the recorded current versus the inverse square root of the electrode rotation rate shows a linear relationship as expected from Eq. 2. Since the bathing solution (0.2 mM H₂O₂ in PBS) is unchanged during the whole experiment, the slopes of the lines are about the same (Fig. 6b). For the bare Pt RDE, extrapolation to infinite rotation rate yields an inverse current intercept close to zero, which indicates that the system was limited by mass transfer through the liquid boundary layer. Thus, to a good approximation, I_f may be obtained directly from the plot intercept for the coated electrodes assuming that external mass transport to the coated electrodes is approximately the same as that for bare Pt. Since I_f can be defined as a function of Nafion film thickness, δ, and the H₂O₂ effective diffusivity in the Nafion film, D_f, according to,³⁵

$$I_f=nFA{D}_{f}C∕\delta$$ (4)

an estimate for D_f may be calculated from the intercept of the Koutecky-Levich plot.

For the larger RDE electrodes, the thickness difference between the dip-coated 180°C-Nafion and 115°C-Nafion films were more obvious at ~2 μm and ~1 μm, respectively, than what was observed for our micromachined microelectrode array probes, probably due to the substantial differences in geometry. The average values of D_f were found to be (1.7 ± 0.2) × 10⁻⁷ cm² s⁻¹ (n = 3) for 180°C-Nafion and (1.3 ± 0.2) × 10⁻⁷ cm² s⁻¹ (n = 3) for 115°C-Nafion. Since these effective diffusivities are approximately the same, these results highlight the importance of the thinner 115°C-Nafion films that still show excellent selectivity against interferents. Also, these results are in rough agreement with literature values for effective diffusivity of the slightly smaller O₂ molecule in Nafion in the range of ~2 × 10⁻⁷ cm² s⁻¹ - ~2 × 10⁻⁶ cm² s⁻¹.^{31, 36, 37} The broad range of values is due primarily to the different preparation conditions for the films and membranes studied.

The data and estimated diffusivities were further examined by comparing the values of I_k and the slope (1/B_L) to expected values. Specifically, I_k is the current limited by the kinetics of the electrooxidation of H₂O₂ on Pt, assuming no mass transfer limitations, so the value of I_k should match the value calculated using published reaction kinetics.³⁸ RDE data gave I_k = 0.208 mA, in general agreement with that derived from published data of 0.273 mA. The measured slope was validated by checking consistency with the known value of H₂O₂ diffusivity at room temperature in water, 1.43 × 10⁻⁵ cm² s⁻¹.³⁹ Based on the measured slope and eq. 3, a comparable diffusivity of 0.94 × 10⁻⁵ cm² s⁻¹ was obtained. Thus, this RDE analysis appears to be giving at least semiquantitative results that are well within an order of magnitude of those expected.

A similar experimental procedure was followed to obtain estimates for H₂O₂ effective diffusivities in the PPD film and in the crosslinked GlutOx deposit. For the PPD film, the mean value of the H₂O₂ diffusion coefficient was found to be (1.7 ± 0.3) × 10⁻⁸ cm² s⁻¹ (n = 3), based on the measured film thickness of ~20 nm. This result is in agreement with literature data for H₂O₂ diffusivity in overoxidized polypyrrole (OPPy) (10⁻⁸ cm² s⁻¹), which is a similar polymer.¹⁷ The average estimated value for the effective H₂O₂ diffusion coefficient in the GAH-crosslinked GlutOx layer on the Pt RDE was found to be ~1.6 × 10⁻⁶ cm² s⁻¹, which is about an order of magnitude less than that in free solution due to a deposit porosity less than unity as well as its substantial tortuosity. The effective diffusivities of Glut and O₂ in permselective films and the GlutOx layer were obtained from the H₂O₂ effective diffusivities scaled by the ratio of the molecular diffusivities with that of H₂O₂. These measured values for deposit thicknesses and effective diffusivities provide improved parameters for our simulation studies described below.

Effect of Enzyme loading and Activity

Most commonly, GlutOx is immobilized on electrodes by spreading a mixture of GlutOx and BSA on the electrode surface and crosslinking with GAH. However, the many variations of methods used produces layers of different compositions and thicknesses that directly affect the sensor performance. Typical reported immobilized enzyme layer thicknesses have been in the 10-20 μm range. However, our simulation results suggest immobilized GlutOx layers 1-3 μm thick may be optimal to ensure high sensitivity while achieving rapid response time (if GlutOx activity is well preserved during the immobilization process).²³ Therefore, our experimental strategy was first to improve enzyme activity retention during the immobilization process, and then to optimize systematically the layer thickness.

Homobifunctional crosslinker, BS3, which like GAH also reacts with amine groups, appeared to be a good alternative due to its longer spacer arm, 11.4 Å vs. 5 Å. We hypothesized that this longer spacer arm would result in less enzyme crowding and better access to enzyme active sites. Also, the BS3-crosslinked enzyme layer might be more permeable overall. Crosslinking conditions for both BS3 and GAH were investigated individually before making comparisons. GAH concentrations and vapor exposure times were varied as were BS3 concentrations to find the best conditions for use of each crosslinker. After this simple optimization procedure, sensors made with enzyme crosslinked via BS3 showed ~1.5-fold improvement in sensitivity compared to those crosslinked via GAH, which showed sensitivity of 259 ± 25 nA μM⁻¹ cm⁻² (n = 11) and 196 ± 24 nA μM⁻¹ cm⁻² (n = 11), respectively. Further, the importance of permselective film and enzyme layer thicknesses on sensor performance should be evident here again. Compared to our base-case sensors, a ~4-fold improvement in Glut sensitivity was achieved merely by applying a thinner permselective film and halving the enzyme layer thickness to ~5 μm even while using the inferior crosslinker, GAH. (Fig. 7)

Fig. 7.

(a) Representative current response of Glut sensors crosslinked via BS3 (red trace) and GAH (blue trace) to interferents (250 μM AA and 5 μM DA), followed by three 20 μM step increases in H₂O₂ concentration. (b) Glut sensitivity comparison between BS3 and GAH crosslinked GlutOx sensors with error bars giving 95% confidence intervals. In all cases, the mass ratio of GlutOx to BSA was 1 : 4 and the enzyme layer was less than 5 μm thick.

For our existing sensor designs, a direct investigation of the effect of deposited enzyme concentration on sensor performance can be performed easily by changing the relative proportion of GlutOx and BSA without changing enzyme layer thickness. The protein mass fraction of GlutOx (f_glutox) was varied from 0.02 to 0.95 for the sensors coated optimally with PPD and 115 °C-Nafion and crosslinked with BS3. Based on the experimental results shown in Fig. 8, Glut sensitivity goes through a peak at f_glutox = ~0.4. Theoretically, as GlutOx mass fraction decreases for thicker enzyme layers, more Glut diffuses deeper into the layer before being oxidized resulting in more penetration of H₂O₂ to the electrode surface, less loss back to the bulk medium, and a greater current signal.^{23, 40} However, for the very thin enzyme layers explored here, an optimum f_glutox is expected. At low enzyme mass fraction, decreased Glut sensitivity was observed due to insufficient active enzyme available to consume Glut at a high rate. On the other hand, high enzyme concentration corresponding to f_glutox ≥ 0.5 was found not to be preferable either due to the fact that GlutOx does not have an abundance of surface lysines available for crosslinking, unlike BSA. The relatively low BSA concentration at high f_glutox led to poor crosslinking, an unstable enzyme layer, and great difficulty in gathering data for Fig. 8 at high enzyme concentration. As a result, f_glutox = 0.2 was chosen as the target level for future work since there is little compromise in sensitivity in exchange for excellent stability.

Fig. 8.

Effect of GlutOx concentration on the Glut sensitivity, where f_glutox is varied from 0.02 to 0.95. In all cases, sensors were crosslinked with BS3 and the layer thickness was less than 5 μm. Error bars represent 95% confidence intervals.

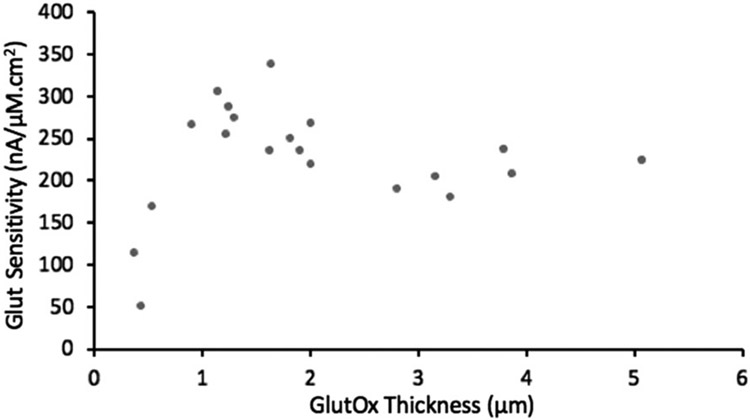
Optimal enzyme layer thickness

Our experimental results of Fig. 9 show the expected result that Glut sensitivity goes through an optimum with regard to enzyme layer thickness. The Glut sensitivity drops sharply for GlutOx layer thickness less than a micron and remains a roughly constant value over the 1-2 μm thickness range. These results match stimulations well (see below) and are consistent with other published experimental reports showing that very thin enzyme layers realized by electropolymerization result in low sensitivity.^{40, 41} As discussed earlier, the decrease in Glut sensitivity with thickness for thicker GlutOx layers is due to the greater diffusional mass-transfer limitation and the loss of the majority of H₂O₂ generated in the enzyme layer back to the bulk solution. Also, the added mass-transfer resistance of a thick enzyme layer leads to a slower response time.

Fig. 9.

Sensor sensitivity based on the linear range of calibration curves (0-60 μM Glut) versus immobilized GlutOx layer thickness. In all cases, f_glutox = 0.2, and sensors were crosslinked with BS3.

Comparison in performance between our optimized and previously reported sensors

Sensors with the optimal permselective film (PPD/115 °C-Nafion) topped with an enzyme layer of optimal thickness of 1-2 μm with mass fraction of GlutOx (f_glutox) = 0.2 and crosslinked with BS3 led to excellent sensitivity of 320 ± 19.6 nA μM⁻¹ cm⁻² (n = 18), which is a ~6-fold improvement compared with our previously reported design (51 ± 1.96 nA μM⁻¹ cm⁻²) without sacrificing selectivity and detection limit(signal-to-noise ratio equal to 3).¹¹ The detection limit for the improved sensors and those previously reported are 0.70 ± 0.08 μM (n = 18) and 0.79 ± 0.31, respectively (Fig. 10). Noise limited improvement in detection limit despite the large increase in sensitivity achieved with the optimized sensors.

Fig. 10.

(a) Sensor sensitivity and (b) detection limit based on the linear range of the calibration curves (0-60 μM Glut) for the improved (current) and previously published (old) (ref. 11) Glut sensors. Error bars represent 95% confidence intervals.

Response time

Response time is defined here as the time for the current signal to reach 90% of its steady-state value in response to a step change in Glut from zero to 40 μM under conditions where external mass transfer is essentially eliminated. Our previous results and other published response times are in the ~1 s range,^{11, 42} mostly due to the overly thick enzyme and permselective layers thought to be needed for high sensitivity and selectivity. Our improved sensors having thin enzyme and polymer layers enabled a faster response time of 0.080 ± 0.012 s (n = 5), which is a ~10-fold improvement over prior work (Fig. 11).¹¹ The fact that the bare Pt response to H₂O₂ appears as a near step change as expected given very rapid electrooxidation kinetics suggests that this method for measuring response time essentially eliminates the external mass transfer resistance. In contrast, the intrinsic response of our optimized Glut biosensor is obscured by the rate of external mass transfer when the measurement is attempted in a stirred beaker or a simple flow cell. However, the response time measurement method, whether using a stirred beaker or pump-driven buffer streams (Fig. 3), was not seen to affect sensor calibration and therefore the determination of sensitivity. In fact, essentially the same response time was measured for our early Glut sensor design using the pump-driven buffer streams (Fig. 11). The higher temporal resolution exhibited by the optimized Glut sensor will enable better correlation of Glut signaling in vivo with local field potentials, which occur at <100 Hz.⁴ Straightforward correlation with single-unit action potentials will require improvement of response time to the single-digit millisecond range, which may be attainable without sacrificing sensitivity by further optimization of these biosensors (see below).

Fig. 11.

Representative sensor response to a 0-40 μM step-change in Glut concentration for base-case Glut sensor (blue trace), the improved Glut sensor (orange trace) and a step-change in H₂O₂ for bare Pt sensor (grey trace) as reference. Dimensionless response is the current divided by the steady-state current.

Simulation Results

Using the newly measured values of coating thicknesses and transport parameters, a mathematical model for Glut sensor performance in vitro was updated to estimate the theoretical limits of sensitivity and response time for these improved sensors.²³ For the simulations, an external mass transfer coefficient of 0.05 cm/s and the currently optimized permselective film thicknesses were used. Note that at this mass transfer coefficient value and above, there is little or no impact on predicted sensor reponse time. Also, an appropriate range of f_glutox and enzyme layer thicknesses were chosen for comparison with experimental work (Fig. 12). As expected, simulations predict that increasing f_glutox increases sensitivity and reduces the optimal enzyme layer thickness. The comparison with representative experimental data suggest that improvements to sensor design described here have brought performance near the theoretical sensitivity limit of ~375 nA μM⁻¹ cm⁻² for this sensor construction at f_glutox = 0.2. As suggested by the simulations shown in Fig. 12, even higher sensitivities of ~450 nA μM⁻¹ cm⁻² at f_glutox = 0.4 and ~550 nA μM⁻¹ cm⁻² at f_glutox = 1.0 (data not shown) are possible if stable enzyme layers can be created at these concentrations and all activity is retained upon immobilization. Theoretically, sensitivities well above 1000 nA μM⁻¹ cm⁻² are possible, although such results would require additional hypothetical improvements including better transport properties of the immobilized enzyme layer, essentially no mass transfer resistance of the permselective films, and improved H₂O₂ electrooxidation kinetics.

Fig. 12.

Simulations of sensor sensitivity to Glut as a function of GlutOx mass fraction in the enzyme layer (f_glutox) and enzyme layer thickness.

Experimental results are consistent with simulated results in terms of optimal enzyme layer thickness and sensitivity for simulated values of f_glutox in the range of ~0.02 to <0.2, given measured thicknesses and transport properties of microelectrode coatings. The observation that most experimental results correspond to simuations at lower f_glutox values than the experimental preparation of 0.2 suggests that enzyme activity was reduced substantially upon immobilization. It is suspected that amine crosslinking negatively impacts immobilized enzyme activity both through direct inactivation of the active site and steric hindrance effects, so that actual active f_glutox after crosslinking is less than the f_glutox used to prepare the sensor.

Response time predictions showed little dependence on f_glutox, and fell within the range of ~8-10 ms for sensors with optimal enzyme layer thicknesses (1-2 μm). The discrepancy between experimental and simulated response time may be due to key differences in the experimental and model sensors. In particular, the model assumes a perfectly planar, rigid sensor surface, whereas SEM images show that the surface is rough and probably soft. Thus, external mass transport from the bulk liquid in vitro to the sensor surface likely is impacted. Also, the model does not account for the likely possibility that Glut adsorbs to sites in the immobilized enzyme layer and that there likely are dead-end pores as well. Both of these possibilities could contribute to the longer response times observed experimentally but would not necessarily affect sensitivity. In any case, the value of these response times measured in vitro where an effort is made to reduce the impact of external mass transfer on the measurement is clear in comparing sensors, but the relevance to utility in practice is not so straightforward since the surrounding medium is essentially quiescent in the brain. The true value of these improved sensors may best be assessed from performance in vivo. Recently, data was reported showing excellent recording of ms-scale Glut signals in vivo using an innovative Glut biosensor with a thin GlutOx layer.⁴³ Although the response time and sensitivity were not measured in vitro, these results offer promising evidence of the utility of high-performance Glut biosensors as neuroscience research tools going forward.

Conclusions

Guided by a detailed mathematical model of electroenzymatic Glut sensors based on crosslinked GlutOx immobilized on planar Pt microelectrodes coated with permselective polymer films, a ~6-fold improvement in sensitivity from ~50 to ~320 nA μM⁻¹ cm⁻² and a ~10-fold improvement in response time from ~0.8 s to ~80 ms was achieved while maintaining a low detection limit of ~0.70 μM and excellent selectivity against AA and DA. The transport properties of the enzyme layer and polymer films used to construct the biosensors were measured directly so as to improve the predictive capability of the mathematical model. Subsequent model simulations showed that the experimentally attained biosensor performance approaches the theoretical limits of sensitivity (~550 nA μM⁻¹ cm⁻²) and response time (~8-10 ms) achievable with electroenzymatic Glut sensors of this construction using this enzyme. Such high-performance biosensors will enable monitoring of Glut signaling with near cellular-scale spatial resolution and at a temporal resolution closer to that of electrical recordings, particularly local field potentials.⁴