Abstract
The design of a composite material structure is often challenging as it is driven by the trade-off between lightweight performance and production costs. In this paper, the boundaries of this design trade-off and its implications on material selection, geometrical design and manufacturability are analysed for a number of design strategies and composite material systems. The analysis is founded on a methodology that couples weight-optimization and technical cost modelling through an application-bound design cost. Each design strategy is evaluated for three levels of bending and torsional stiffness. The resulting stiffness-versus cost-range together constructs the design envelope and provides guidelines on the suitability and improvement potential of each case. Design strategies researched include monolithic, u-beam-, sandwich-insert- and sandwich-stiffened plates. Considered material systems include carbon-, glass, recycled carbon-, lignin- and hemp-fibre reinforced composites. Optimized sandwich designs are shown to have lowest design cost. Glass-, recycled carbon-, lignin- and hemp-fibre reinforced composite materials are all shown to reduce costs but at lower stiffness performance. Ultimately, the case study demonstrates the importance of early structural design trade-off studies and material selection and justifies introducing novel fibre systems in low-cost applications of moderate stiffness levels.
Keywords: Aerospace engineering, Mechanical engineering, Composite materials, Computer-aided engineering, Manufacturing engineering, Materials processing, Carbon fibres, Sandwich structures, Natural fibres, Recycled carbon fibres
Aerospace engineering; Mechanical engineering; Composite materials; Computer-aided engineering; Manufacturing engineering; Materials processing; Carbon fibres; Sandwich structures; Natural fibres; Recycled carbon fibres
1. Introduction
Environmental demands and fuel economy are key driving forces behind the use of lightweight design and advanced lightweight material systems in the aeronautical and automotive sector [1], [2], [3]. Advanced composite materials, such as carbon-fibre reinforced polymers (CFRP), combine high specific stiffness with design flexibility and therefore have particularly high weight-reduction potential. In aerospace applications the use of CFRP-materials can result in lifetime -reductions of 14-20% [4], well on the way to reach future emission targets [5]. Similarly, lightweight design and advanced composite materials have promising environmental benefits for fossil-fuel-based automotive applications [6] as well as pure electric vehicles, where the reduced structure weight counterbalances added battery weight [7].
However, as fibre-reinforced composite materials are complex systems, consisting of tailored, load-carrying, fibre layers and connective matrix, their production and design are often challenging, slow and costly [8], [9]. The material cost of the reinforcing fibres in themselves is also often an issue. Carbon fibre for example, are available at high prices of 20-60 €/kg [10] depending on stiffness grade. Furthermore, production cost studies have shown that material cost becomes a dominating cost driver when producing CFRP components either at high production rates or in large structural adaptions [8], [9], [11], [12].
Some of the production challenges have been addressed by recent manufacturing technology advancements such as additive manufacturing (AM), or 3D-printing, [13], [14], [15], out-of-autoclave curing [16], [17] and 3D-weaving [18], [19]; but slow production rates and high costs of composite production persist. This is especially true in applications that demand excellent structural performance, where quality requirements and validations often still limits industry to certified traditional methods. Apart from improving available manufacturing technologies, productions costs and involved material costs can be addressed through developing and implementing smart geometry design focused on using the expensive material system efficiently. In composite structures, such smart geometry designs can for example be stiffened shells and self-supporting structures such as sandwich structures.
Aeronautical stiffened plates have shown to be more cost-efficient if densely populated by several smaller stiffeners [20], [21], [22]. Automotive stiffened geometries on the other hand, have shown more cost- and weight-promise through implementing more automotive-friendly manufacturing methods such as compression moulding and hot stamping [23]. Self-supporting structures such as sandwich construction [24], as well as multi-functional structures [25] have also shown great promise in automotive applications [26], [27].
These smart geometrical designs also bring further manufacturing and production challenges. Fully weight-optimized stiffened plates for example often implement part integration. Part integration, or the method of combining seperate composite sections to one large part through either co-curing or later-stage co-bonding [28], is often reported to reduce production costs [29] given its slimmed subsequent assembly process. The strategy is not without downsides however. For one, an integrated structure represents higher risk and value as flaws or imperfections that arise requires the full structure to be repaired or even replaced in its entirety. Then, pure co-bonded structures are not admissable in the aeronautical industry where bonded joints must be coupled with additional fasteners in order to be certified [28]. In addition, integrated structures tend to be challenging to inspect. In either case, the actual impact of integration on production cost has been challenged by the authors, as their recent case-study has shown the effect to be moderate [8].
To address the high material cost of the reinforcing fibres, introducing low-cost material systems such as glass fibres, ligning-based carbon fibres, natural fibres as well as novel recycled CFRP can be promising alternatives. Glass fibres have a cost of 1-15%[30] and a density of about 30% that of CFRP and is thus a reasonable cost versus weight trade-off material. Lignin-based carbon fibres have the potential to cost as little as 4 €/kg at a possible stiffness of 172 GPa [31], [32], [33]. Natural fibres [34], [35] such as for example flax [36] or hemp [37] are even more inexpensive, with hemp fibre costs being as low as 0.5-0.75 €/kg [38] at fibre stiffness levels similar to glass fibre. Recycled carbon fibres show promise as it costs less to recycle than to manufacture virgin CFRP [10], [39], [40], [41]. In fact, a recent parallel study by the authors [42] has shown that the use of recycled carbon fibres as opposed to virgin CFRP can result in 50% cost reductions. Other factors promoting recycled CFRP are recent recycling legislations [43], [44], that pushes increased use of recyclable materials in new transport designs, and the release of an AS/EN9100 quality management system certificated material grade [45]. In addition, the recently established partnership between Boeing and ELG Carbon Fibre Ltd aims to consistently supply the market with recycled aviation carbon fibre [46].
However, all new material systems comes with challenges and costs for both aeronautical and automotive applications. In aviation, material certification demands and costs strictly hinder the introduction of new material systems. In contrast, there are no formal material certification demands in automotive applications. However, the break-in costs, or the costs associated with qualifying the material to be used both in the development and manufacturing, must be weighed to that of the cost benefits of a potential new material system. Research and development (R&D) of automotive applications also involve challenges regarding short development cycles of on average 20-30 months, relatively low investment capability and limited number of component level tests available. This results in a development procedure highly driven by computer-aided-engineering (CAE). To accurately describe and simulate fibre-reinforced composites of any certification grade in a CAE-driven development process, a vast amount of characterization is required, which results in high material-related break-in costs. To exemplify, the break-in cost of a new composite material would normally start from 500 000 € when including testing hours required.
In conclusion, it is clear that the conceptual design of a cost-efficient composite structure involves a large set of design decisions, ranging from composite composition and manufacturing selection to smart structural design strategies. In order to make these design decisions on a sound foundation, research focused on multi-objective analyses of composite composition, manufacturing selection and representative design strategies is needed. As the design decisions ultimately represents costs, technical cost assessments becomes valuable guiding tools to govern required multi-objective analyses.
Some examples of recent cost assessment research are; the combination of life-cycle-analysis (LCA) and life cycle costing (LCC) for a cargo aircraft elevator [47], stiffness performance versus estimated service lifetime and maintenance cost of a wind turbine blade [48] and frequency performance versus stacking cost for hybrid composite laminates [49]. In addition, a few LCA-studies [26], [50] defines a methodology connecting material selection to lightweight design. Furthermore, the authors have previously shown that quantitative production cost studies including the identification of production cost drivers and cost reduction strategies can be used to identify non-value adding processes [8], [51] and propose design guidelines [9], [23]. For early conceptual development however, aforementioned cost studies does not provide overarching design guidance spanning application, performance and material system. Indeed, in an early conceptual development stage, wider generic design maps such as Ashby charts [52] and other types of causality maps between involved mechanical properties [53] can prove more useful. However, there is a lack of studies focusing on charting and drawing such design maps connecting the full design boundaries and applicability of generic lightweight design strategies connected to competitive production cost. This gap is the basis for the research presented in this work.
In this paper, a quantative methodology and case study that charts the design envelope of representative lightweight design strategies are proposed and analysed with respect to material selection, geometrical design and manufacturability. The proposed methodology couples weight-optimization and technical cost modelling through an application-bound design cost. The case study treats a number of design strategies, all evaluated for a selection of composite material systems. Each design strategy is evaluated for three stiffness levels; low, intermediate and high, of bending and torsional stiffness respectively. The three stiffness levels combined constructs the design envelope for each design strategy, where the governing axises are stiffness and cost. The design envelope provides guidelines on the suitability and improvement potential of each case. Chosen design strategies and composite material systems are justified by design traditions as well as current, and up-coming, trends to generate weight-driven performance and low-cost designs. Four smart design stiffening strategies are included, first is a single shell, second is a geometrically stiffened plate, third is a sandwich plate and forth is a plate using chamfered sandwich inserts. Composite material systems analysed range from traditional CFRP and glass fibre to promising alternative low-cost materials, including lignin-based CFRP, natural fibres, and most recently, recycled CFRP. Concluding discussion focus on industry impact of not only specified design cases, but also general industry impact in relation to future design strategies, incorporating both traditional materials and studied alternative low-cost materials and beyond.
2. Methodology and definitions
2.1. Methodology
The design study presented in this paper compares the structure weight potential to production cost of four different geometrical design strategies using a number of different composite material systems. Each geometrical design strategy is designed for three stiffness levels, from low to upper, with respect to a representative bending stiffness and torsional stiffness respectively. Specific geometry of each design strategy is generated through weight-optimization and their individual production cost is estimated using an updated composite cost estimation tool previously developed by the authors. [8], [9], [54]. The cost-and-weight-potential of each individual design strategy is rated using a proposed application-bound design cost that is based on the weighted sum of minimized structure weight, value-of-weight and production cost. Composite material systems included in this research include traditional carbon fibre composites and glass fibre as well as recycled carbon fibre reinforced alternatives. Lignin-based carbon fibres and hemp-based biocomposites are ranked and discussed in comparison to the main material systems.
2.2. Geometrical design strategies
The considered geometrical design strategies are presented in Fig. 1, and are; a monolithic plate (M), a plate with integrated u-beam stiffeners (USP), a plate with sandwich inserts (SWI) and finally, a sandwich plate (SW). The monolithic single plate (M) and the sandwich plate design case (SW) are generic designs, whilst the design of case USP and SWI draw on aeronautical and automotive applications respectively. The sandwich insert plate (SWI) addresses a design scenario where there are thickness limitations, and the design strategy of a full sandwich plate (SW) is not possible.
Figure 1.
Design strategies and optimization variables, see Table 1 for description of individual optimization variables. From left to right: monolithic plate (M), stiffener-reinforced plate (USP), sandwich insert-reinforced plate (SWI) and sandwich plate (SW).
2.3. Design cost
In order to provide an internal ranking in between all geometrical designs, a design cost (D) is introduced. An optimal design strategy is a design that minimizes this design cost. The design cost function is defined as a sum of the minimized structure weight, , an application-bound value-of-weight V, and the structure production cost, C, according to
| (1) |
The minimized structure weight and its resulting production cost are generally conflicting arguments. The production cost is in itself a function of weight, , in this study determined through a predictive technical cost model further detailed in upcoming section 2.3.2. In order to compare weight and cost, a value-of-weight constant [52], V, is introduced that translates weight into cost. The value-of-weight constant is tailored to application in order to reflect usage phase benefits, such as decreased fuel costs and emissions, of lower structure weight.
Given eq. (1), two designs can be compared to each other through identifying their design cost break-even-point. The break-even-point becomes the value-of-weight value, , at which two designs are of equal design cost such as
| (2) |
Thus, the alternative design, a, is better than the initial design, i, as long as . Note that if the alternative design is both lighter and of a lower structure production cost or both heavier and of higher structure production cost, no meaningful break-even value-of-weight exists (eq. (2) ) as such a design is either consistently better or worse than that of the initial design, regardless of value-of-weight.
2.3.1. Minimized structure weight,
The minimized structure weight of each design strategy, , is the lowest achievable weight of a design strategy while still fulfilling prescribed stiffness requirement. In this paper, the minimized structure weight is found through an optimization scheme where prescribed stiffness requirement is implemented using a penalty function according to
| (3) |
where is the size of the violation of each prescribed stiffness requirement. The parameter ν normalizes the violation with respect to weight. The parameter further increases the size of the violation if needed. The design variables x, see Table 1, define the geometry of each specific design strategy, and therefore also its current weight, w.
Table 1.
List of optimization design variables.
| M | USP | SWI | SW | |
|---|---|---|---|---|
| Design variables x | Plate thickness | Plate thickness Stiffener thickness Stiffener width Stiffener flange height | Plate thickness Center insert width Center insert skin thickness Fixed edge insert width Fixed edge insert skin thickness Free edge insert width Free edge insert skin thickness | Plate skin thickness Plate core thickness |
Optimized design variables describe final, minimized structure weight . The optimization is performed using the Nelder-Mead simplex algorithm, defined in the open-source SciPy library for Python [55]. This heuristic optimization algorithm is chosen to introduce a reasonable amount of randomness to the optimization. The extra randomness is needed in particular for the u-beam stiffened-plate (USP), where traditional gradient-based optimization algorithms result in local minima entrapment. Geometry stiffness response is calculated in each iteration using respective parametric FE model in Abaqus [56]. Each parametric model has a tailored, scalable, mesh as defined in Fig. 2. Thin, composite, layers are meshed using shell elements while thick, core, layers are either meshed using continuous shell elements or solid brick elements. In the sandwich case, SW, where solid brick elements are used, 4 elements are used throughout the thickness of the plate in order to reach sufficient accuracy.
Figure 2.
Parametric FE element setup for treated design strategies.
2.3.2. Structure production cost,
The structure production cost is a function of optimized weight as previously stated in section 2.3. Structure production cost is a function of structure geometry, chosen manufacturing method and specified annual production volume. A technical cost model developed by the authors [8], [9], [11], [54] as a stand-alone package in Python, is used to estimate the production costs for all optimized design strategies. The technical cost model follows a bottom-up approach and performs the following:
-
•Estimates required process times, t, as a function of process-specific layup rate, r, component complexity, , and characteristic size (area, volume, length etc.), L, according to
(4) -
•Determines and sizes required equipment park for required manufacture, assembly and available work time, , subjected to annual production volume, n, according to
(5) -
•Calculates tooling costs, , as a function of the cost per projected flat area, , and average milling factor, for included tooling features according to
(6) -
•Calculates material cost, as a function of material cost per kg, , component weight, w, and the process specific production scrap fraction, according to
(7) -
•
Calculates labour, investments and facility costs as a function of calculated leadtimes and sized equipment park
-
•
Summarizes all costs and returns cost per part, , as well as process times and required equipment park
More details on the general methodology of the technical cost model developed are detailed in other work [8], [9], [54].
3. Case study
Two individual stiffness requirements are considered, bending stiffness and torsional stiffness, derived from representative aeronautical and automotive adaptions respectively. In short, the stiffness requirement is either bending stiffness through simple out-of-plane deflection or torsional stiffness . Each stiffness requirement is considered on three levels; representing a lower, intermediate, and upper bound. As a whole, the stiffness levels provide a stiffness range. The stiffness levels for maximum out-of-plane deflection u and minimum torsional stiffness are given in Table 2.
Table 2.
Allowed stiffness criteria.
| Allowed deflection, u [mm] | Minimal torsional stiffness [] |
|---|---|
3.1. Bending stiffness and deflection
A cut-out-section of a blended-wing-body shape, see Fig. 3, is subjected to an uniaxial edge compression and an uniform pressure over the section width. The size of the compression load is derived from that of highest pressure differential of a traditional circular fuselage section [57], [58], [59]. The compression load scales with thickness for each studied design case while the fuselage radius is considered constant at 3.5 m. In order to compare the considered flat stiffened plate to a traditional fuselage, considered out-of-plane deflection range follows data reported in literature [57]. Going forward, the bounding deflection values presented in Table 2 are given as a rough representative bending stiffness with respect to applied uniform load p, loading area A and allowed deflection u, according to
| (8) |
Figure 3.
Considered loading cases with respect to prescribed bending (left) and torsional stiffness (right) respectively. Note that the axis denoted as 1 represents the principal loading direction.
3.2. Torsional stiffness and angular deflection
The automotive vehicle frame, the chassis, is subjected to torsional motion through varied contact between wheels and road through steering and terrain. In classic torsion, the twist of the front axis section as a result of reaction forces on the full wheelbase, see Fig. 3, is described as
| (9) |
where is the torque applied on front axle and ϕ is the resulting angle between rear and front axle when the rear axle is clamped [60], [61]. The size of the torsional stiffness of the full frame, the torsional rigidity, often falls between 10-20 kNm/degree and is dimensioned with respect to driver comfort. A higher rigidity generally means a higher driver comfort but also a higher frame weight [62]. A car floor section must carry a certain part of this full torsional stiffness. Here, the chosen torsional stiffness range is set in order to represent a design range, where the lower stiffness bound, 1.4 kNm/deg [63], represents a vehicle design where the stiffness is thoroughly shared throughout the vehicle frame while the upper stiffness bound, 14 kNm/deg, represents a vehicle design where the floor panel carries a large part of the torsional stiffness of the frame.
3.3. Composite and sandwich materials
The first two, composite-dominated, design strategies (SP and USP) are evaluated using traditional composite material systems as well as low-cost glass fibre reinforced plastic (GFRP) and recycled CFRP, while the sandwich design strategies (SWI and SW) are evaluated using only traditional composite material systems and appropriate, application-bound, core material. Details on evaluated material systems are given in Table 3 and Table 4 for composite and core material respectively. Composite prepreg configuration follows a stacking sequence of [0/+45/-45/90], where the 0-direction is parallel with the principal loading directions of each loading case. The laminate is dominated by the 0 and the 90 degree plies, while the +45/-45 plies are limited to 10% of the full laminate thickness individually.
Table 3.
Properties of standard CFRP prepreg laminate material system and alternative low-cost material systems.
| Traditional material systems | ρ [kg/m3] | [GPa] | [GPa] | Poisson's ratio | €/kg |
|---|---|---|---|---|---|
| Aerospace-graded CFRP [20], [24], [64] | 1600 | 180/10 | 5.4/3.1 | 0.3 | 110 |
| Automotive CFRP [23] | 1500 | 180/10 | 5.4/3.1 | 0.3 | 37.5 |
| Low-cost material systems | ρ [kg/m3] | [GPa] | [GPa] | Poisson's ratio | Cost compared to traditional material system [%] |
| Automotive GFRP | 1940 | 45/10 | 4.4 | 0.3 | 1-15 [30] |
| Recycled CFRP | 1600 | 80-100% of aerospace-graded CFRP [42] | 5.4/3.1 | 0.3 | 50 [42] |
Table 4.
Properties of core materials.
3.4. Production cost of studied design strategies and material systems
To determine the production cost, reasonable production process flows for all four design strategies must be established. Considered production schemes and process times are given for all design strategies in Fig. 4. Manufacturing and assembly methods are selected based on conclusions and guidelines found in previous work, regarding cost-effectiveness in relation to part size and complexity [8], [9] and required production volume. Here, the manufacture and assembly vary depending on set stiffness requirement. In the scope of this study, inspection costs are neglected as the level of required inspection varies highly in-between industry application.
Figure 4.
Production schemes and process times of analysed design strategies, where some process times are estimated within used cost estimation model as a function of part size, f(A) detailed in previous work [8], [9], [11].
For the bending stiffness design strategies the composite material is placed through automatic tape layup (ATL) and formed to final shape through hot-drape-forming (HDF). The mounting of the individual stiffeners in the bending stiffness USP design strategy is performed using wet stiffeners. The tacked structure is then bagged and cured in an autoclave. The USP design strategy therefore essentially represents a co-cured part-integrated aeronautical structure. Co-curing is similarly implemented in the bending stiffness sandwich design strategy (SW) where the milled-to-shape core material is placed in between wet ATL-formed skins, bagged and cured in autoclave. More details on the manufacture and costs of integrated aeronautical composite structures is thoroughly described in previous work [8], [9].
For the torsional stiffness design strategies the composite material is stacked through a pick-and-place method using an industrial robot and formed to final shape in a hydraulic press. The used double-shaped mould is heated and kept closed throughout the curing process. For the torsional stiffness USP and sandwich design strategies (SW, ISW), individual stiffeners and skins are mounted and connected to the main skin and core material respectively through adhesive joining. The adhesive is spread on connecting faces by the means of an industrial robot, allowed to set and then mounted. More details on automotive-related production methods are described in [11].
3.5. Value-of-weight in aeronautical and automotive applications
In aerospace adaptions low weight is paramount in order to reduce fuel costs. In automotive adaptions low weight is primarily related to emission legislation. To that end, aeronautical applications provide an upper bound value-of-weight value whilst automotive applications provide a lower bound. Given representative industry values in Table 5, a value-of-weight bound, V in eq. (1), of €/kg is considered.
Table 5.
Representative value-of-weight values sorted on industry application.
4. Results
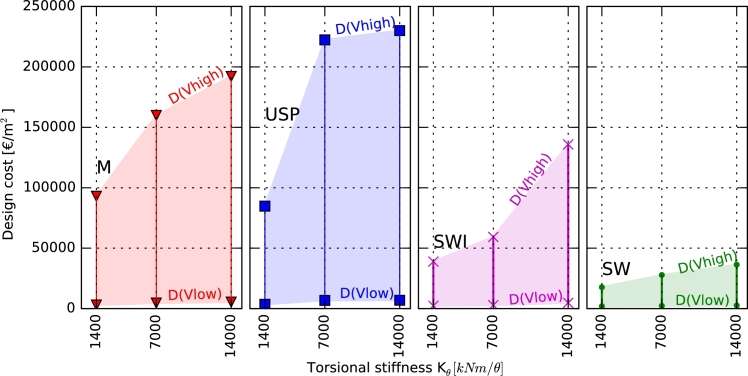
The detailed results from the optimization of the considered design strategies are given in Table 6. Thereafter, the results are further evaluated for bending stiffness and torsional stiffness respectively. As the designs are optimized with regards to three stiffness levels for each stiffness requirement (see optimization data in Table 6), presented data revolves around three specific data points. However, as the stiffness levels are chosen to represent a lower, intermediate and upper component stiffness, see definition in section 3, an interpolated design range in-between the drawn data points can be filled. This design range is illustrated through a coloured area in-between data points and is done in cost versus stiffness figures, see Fig. 5b and 7b, and design cost versus stiffness figures, see Fig. 6 and 8.
Table 6.
Optimization results, x⁎ (in millimeters).
|
x⁎ | |||
|---|---|---|---|
| M |
USP |
SWI |
SW |
| [mm] | |||
| [8.0] | - | ||
| 7 stiffeners in simulation () | Optimization discontinued. (Refer to design strategy SW.) | ||
| [mm] | |||
| [59.7] | - | ||
| 10 stiffeners in simulation | see SW | ||
| [mm] | |||
| [194.0] | - | ||
| 3 stiffeners in simulation | For . | ||
| Several alternative design solutions exist - Here, the design strategy using less stiffeners is used to minimize production cost | see SW | For x⁎ when only skin thickness increases. Optimization discontinued | |
| [] | |||
| [40.0] | |||
| 2 stiffeners in simulation | |||
| [] | |||
| [69.0] | |||
| 17 stiffeners in simulation | |||
| [] | |||
| [83.0] | |||
| 15 stiffeners in simulation | |||
Figure 5.
Detailed production cost with respect to considered high performance bending stiffness strategies.
Figure 7.
Detailed results considered torsional stiffness strategies.
Figure 6.
The design cost range (per m2) of considered high performance bending stiffness strategies for larger annual manufacturing volumes (n > 1000), given low and high value-of-weight, 1.5 ≤ V ≤ 1500. From left to right, monolithic, u-beam reinforced and sandwich plate design. Note that the coloured areas in between stiffness levels are for visual aid only.
Figure 8.
The design cost range (per m2) of considered high performance bending stiffness strategies for larger annual manufacturing volumes (n > 1000), given low and high value-of-weight, 1.5 ≤ V ≤ 1500. From left to right, monolithic, u-beam reinforced, sandwich inserts and sandwich plate design. Note that the coloured areas in between stiffness levels are for visual aid only.
4.1. High performance bending stiffness design strategies
Production costs as a function of annual manufacturing volume and as a function of bending stiffness are given in Fig. 5a and 5b respectively. For illustrative purposes, only the production cost of the intermediate stiffness criteria is shown in Fig. 5a. The sandwich design strategy, SW, is least expensive to produce. However, as the prescribed bending stiffness increases the sandwich design strategy, SW, reaches unreasonable skin versus core thickness ratio. This indicates that considered available honeycomb densities are not sufficient to achieve the higher bending stiffness levels. Therefore, the sandwich design strategy only covers part of the considered bending stiffness range. The bending stiffness sandwich inserts design strategy, SWI, was shown to strive towards that of a pure sandwich plate in order to handle the distributed load. Therefore, the design strategy coincides with that of the pure sandwich design strategy, SW, in the figure. The monocoque design strategy, M, is most expensive as the bending stiffness and annual production volume increases. The traditional u-beam stiffened design strategy, USP, is the most cost-competitive and high-performing design for intermediate to upper bending stiffness levels.
Coupling these results with specific value-of-weight range, (), the design cost calculated according to Eq. (1) provides the design cost range, (), in Fig. 6. The monocoque design is clearly both expensive and heavy. The u-beam stiffened design, USP, and the sandwich design, SW, are most efficient with regards to prescribed bending stiffness levels. The design cost of the sandwich design strategy, SW, is marginally lower than that of the u-beam stiffened design strategy, USP, for comparable prescribed bending stiffness level. For intermediate to upper bending stiffness levels however, only the u-beam stiffened design strategy, USP, and the monocoque design strategy, M, proves sufficient to fulfill required performance.
4.2. Torsional stiffness design strategies
Production costs as a function of annual manufacturing volume and as a function of torsional stiffness are given in Fig. 7a and 7b respectively. The sandwich design strategy, SW, is also here the least expensive to produce and the sandwich inserts design strategy, ISW, falls between that of pure sandwich and the monocoque design strategy, M. The u-beam stiffened design, USP, is the most expensive design strategy.
The design cost range of the torsional stiffness dimensioned designs, Fig. 8, follows the same trends as that of pure production costs in Fig. 7a and 7b, even for high value-of-weight.
4.3. Cost drivers
In order to improve cost-efficiency and decrease the design cost of considered design strategies, detailed cost drivers must be reviewed, see Fig. 9. For design strategies M and USP, dominating cost driver is the material cost. For the bending stiffness pure sandwich design strategy, SW, dominating cost driver is also material cost, and then specifically cost due to the costly nomex honeycomb material. For the torsional stiffness pure sandwich, SW, and the sandwich insert design strategy, ISW, material and tooling costs dominate.
Figure 9.
Cost drivers for prescribed stiffness requirements.
4.4. Effect of introducing alternative low-cost materials in M and USP design strategies
As material costs are dominating cost driver for design strategies M and USP, see Fig. 9, the cost- and weight-impact of introducing alternative low-cost material systems, glass fibre and recycled carbon fibre, are further investigated. The potential of substituting used skin material in the sandwich design strategies (SW and SWI) is not considered here. This is justified by the fact that the material cost of these design strategies is either dominated by the cost of honeycomb or minor in comparison to the tooling cost, see Fig. 9.
Glass fibre has a low production cost reduction potential for the monolithic design strategy, M, for high-performance bending stiffness, see Fig. 10. For USP and high-performance bending stiffness, the design becomes more expensive if glass fibres are introduced due to lower mechanical performance and higher density. In torsional stiffness however, glass fibre is shown to have clear production cost reduction potential, see Fig. 11. In all design strategies however, the increased density of glass fibres makes the designs heavier.
Figure 10.
Production cost as a function of bending stiffness for design strategies M and USP, carbon and glass-fibre. Note that the coloured areas in between stiffness levels are for visual aid only.
Figure 11.
Production cost as a function of torsional stiffness for design strategies M and USP, carbon and glass-fibre. Note that the coloured areas in between stiffness levels are for visual aid only.
Recycled carbon fibres show significant production cost potential and generates cost reductions of up to 50% for both bending stiffness and torsional stiffness, see Fig. 12 and 13 respectively. However, as a 10% stiffness reduction is estimated for recycled CFRP as opposed to virgin CFRP, each design becomes slightly heavier through the use of the material.
Figure 12.
Production cost as a function of bending stiffness for design strategies M and USP, carbon and recycled carbon fibre. Note that the coloured areas in between stiffness levels are for visual aid only.
Figure 13.
Production cost as a function of torsional stiffness for design strategies M and USP, carbon and recycled carbon fibre. Note that the coloured areas in between stiffness levels are for visual aid only.
4.5. Design cost break-even-points
The value-of-weight break-even-points in between different design schemes are given in Table 7.
Table 7.
Value-of-weight break-even-point for studied stiffness levels, where (+) means no break-even-point exist as the alternative design reduces both cost and weight while (-) means no break-even-point exists as the alternative design increases both cost and weight. When a break-even-point exists, and V < Vai, the alternative design is more advantageous than the original design. For comparative values, representative value-of-weight span used in performed case study is 1.5 < V < 1500.
| Break-even-point [€/kg] |
||||||
|---|---|---|---|---|---|---|
| Design comparison | K |
KT |
||||
| Original/alternative | Low | Intermediate | High | Low | Intermediate | High |
| MC/M | 568 | 783.7 | 728 | 788.3 | 181.9 | 67.3 |
| MC/MG | - | 6.3 | 4.7 | 4.5 | 4.5 | 3.4 |
| MC/SW | + | + | NA | + | + | + |
| MC/USPC | 211 | + | + | - | - | - |
| USPC/USP | 1345 | 649 | 661.8 | 28.2 | 28.2 | 28.2 |
| USPC/USPG | - | - | - | 1.4 | 35.8 | 14.8 |
| USPC/SW | + | + | + | + | + | + |
| SW/M | - | - | NA | - | - | - |
| SW/MG | - | - | NA | - | - | - |
| SW/USP | - | - | NA | - | - | - |
| SW/USPG | - | - | NA | - | - | - |
Break-even-points in relation to the monocoque design scheme shows that sandwich is always more cost- and weight-efficient while alternative materials; glass and recycled carbon fibres, produce break-even-points. With regards to alternative materials, sandwich is still more efficient than both glass and recycled carbon fibres, both with respect to weight and cost for applicable stiffness levels.
5. Discussion
This paper has presented a thorough weight- and production cost study of representative composite stiffening strategies. Proposed design cost approach has enabled a common quantification metric of each individual stiffness strategy potential. The use of an industry-based value-of-weight has also produced a comparative metric that indicates how appropriate different design strategies could be for different applications.
The sandwich-stiffened design has been shown most weight- and production-cost efficient for low to intermediate bending stiffness range and for full torsional stiffness range. However, for high bending stiffness the sandwich design tends to thicker skins in relation to core. Essentially, this corresponds to a pure composite plate design, which indicates that sandwich becomes less appropriate for considered upper high bending stiffness level. Moreover, comparing the two pure composite designs, the u-beam stiffened plate is shown more efficient than the monocoque for the upper bending stiffness levels.
The production cost of the monocoque and u-beam stiffened design can be reduced through addressing the dominating cost driver, i.e. the material cost. Exchanging used carbon fibre prepreg to considered low-cost materials, glass fibre prepreg and recycled carbon fibre prepreg, reduces cost but adds weight. Glass fibre prepreg is shown efficient in the monocoque design with a break-even-point value, see definition in equation (2) in section 2.3, between 3-6 €/kg for intermediate to upper stiffness levels. This means the material system will be cost-efficient for a conventional combustion engine, see Table 5. Glass fibre prepreg in the u-beam stiffened design is efficient only in torsional stiffness cases, returning break-even-points between 1-36 €/kg. Note however that the u-beam stiffened design is structurally inefficient as the applied twisting moment falls so that bounded locked edges carry all the load. This means a structural re-design most likely will have higher effect than that of simply exchanging material systems. Combining both re-design and use of low-cost material would most likely give highest total effect. Recycled carbon fibre prepreg is shown efficient in both monocoque and u-beam stiffened design, for full bending and torsional stiffness range and produces break-even-points of between 28-1345 €/kg. This break-even-point range translates into a great application-width, ranging from medium weight-sensitive aeronautical adaptions for upper bending stiffness level to highly weight-sensitive automotive adaptions. Despite the fact that the introduction of alternative low-cost material systems give high production cost reductions of both monocoque and u-beam stiffened design, sandwich design represents the best combination of both cost and stiffness.
To summarize the results, the Ashby methodology [52], [71] of comparing representative performance metrics is applied. A weight versus stiffness performance of each design ( and ) is compared to the normalized cost () of each design strategy, and given in Fig. 14. In the figure, a design becomes more efficient the closer to origo it is placed. To quantify and compare the rough potential of natural fibres and lignin-based CFRP these material systems are compared to evaluated GFRP design strategy and drawn using dashed lines in Fig. 14. Both bio-based fibre systems are shown highly cost-efficient. Hemp fibres perform less in bending stiffness, but at similar level in torsional stiffness compared to CFRP. In torsional stiffness, hemp fibres is most cost-efficient of all material systems and design strategies. Lignin-based CFRP can perform less in bending stiffness, but at a similar level in torsional stiffness. Comparative data presented in Fig. 14 again highlight the combined high cost-efficiency and lightweight-performance of the sandwich construction design strategy.
Figure 14.
The most cost- and weight-efficient design reduces both cost and weight versus stiffness performance. Here data is normalized with respect to the monolithic design, or carbon fibre plate (blue). Note that left and right part of the figure correspond to bending and torsional performance respectively.
Apart from considering the cost potential of each material system and stiffness strategy, it is important to consider material certification issues and break-in costs for aeronautical and automotive applications respectively. In the case of a sandwich composite for example, the break-in cost would be considerably higher as required material characterization would involve three materials, namely the skin, the core and the interface between the skin and core.
Furthermore, it is important to note that the investigation herein has focused on large composite components where material costs has been shown to dominate, however, for smaller geometries, the importance of individual processing costs increases. Not only as less material is used but also due to the fact that automated composite methods like automatic tape and fibre layup are less efficient and involves more start-and-stop actions for smaller sizes. Therefore, the discussions made here will likely differ when smaller geometries are studied.
The efficiency of the holistic design framework presented in this work justifies further research. Upcoming future work expands upon the design framework, and will couple the cost-efficient process - and material-selection to sustainability, energy and CO2-impact. The upcoming expanded design framework will be implemented in sustainability studies that will prove interesting towards understanding necessary changes to bridge the gap to circular economy and environmental demands.
6. Conclusions
This paper has presented a comparative analysis of the structure weight potential to production cost of four different geometrical design strategies using a number of different composite material systems. Method and proposed application-bound comparative value-of-weight metrics, including design cost break-even-points, have enabled a solid discussion of the strengths and weaknesses of researched design strategies. The discussion put forward has furthermore provided a basis for future design recommendations. Some major conclusions are:
-
•
Sandwich structures are weight- and cost-efficient in low to intermediate bending stiffness scenarios and torsional applications
-
•
U-beam stiffened panels are weight- and cost-efficient for upper stiffness levels.
-
•
A lower-cost material system of higher density is beneficial for large structures in low- to intermediate weight-sensitive applications
-
•
The use of recycled carbon fibre prepreg or glass fibre prepreg can result in general cost-reductions of up to 50%
-
•
Lignin-based CFRP are shown to reduce cost by 50-90% at low to intermediate bending stiffness and torsional stiffness respectively
-
•
Hemp fibres are shown to reduce cost with as much as 80% at comparable torsional stiffness levels
Declarations
Author contribution statement
M.K. Hagnell: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
S. Kumaraswamy and T. Nyman: Contributed reagents, materials, analysis tools or data.
M. Åkermo: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.
Funding statement
This work was financially funded by The initiative for Excellence in Production Research (XPRES) and The strategic innovation programme LIGHTer (provided by VINNOVA, the Swedish Energy Agency and Formas). Additional financial support was also supplied by the centre for ECO2 Vehicle Design (funded by VINNOVA, Grant Number 2016-05195).
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
We also wish to acknowledge valuable review comments and ideas from Professor Dan Zenkert, Lightweight Structures at KTH, Royal Institute of Technology.
References
- 1.European Commission Reducing CO2 emissions from passenger cars. 2017. https://ec.europa.eu/clima/policies/transport/vehicles/cars_en
- 2.European Commission Reducing emissions from aviation. 2017. https://ec.europa.eu/clima/policies/transport/aviation_en
- 3.Chu S., Majumdar A. Opportunities and challenges for a sustainable energy future. Nature. 2012;488:294–303. doi: 10.1038/nature11475. [DOI] [PubMed] [Google Scholar]
- 4.Timmis Andrew J., Hodzic Alma, Koh Lenny, Bonner Michael, Soutis Constantinos, Schäfer Andreas W., Dray Lynnette. Environmental impact assessment of aviation emission reduction through the implementation of composite materials. Int. J. Life Cycle Ass. 2015;20:233–243. [Google Scholar]
- 5.European Commission Clean sky 2: developing new generations of greener aircraft. 2014. https://ec.europa.eu/research/press/jti/factsheet_cs2-web.pdf
- 6.Fontaras G., Samaras Z. On the way to 130 g CO2/km-estimating the future characteristics of the average European passenger car. Energy Policy. 2009;38:1826–1833. [Google Scholar]
- 7.Luk Jason M., Kim Hying Chul, Kleine Robert De, Wallington Timothy J., Maclean Heather L. Review of the fuel saving, life cycle ghg emission, and ownership cost impacts of lightweighting vehicles with different powertrains. Environ. Sci. Technol. 2017:8215–8228. doi: 10.1021/acs.est.7b00909. [DOI] [PubMed] [Google Scholar]
- 8.Karlsson Hagnell M., Åkermo M. Cost efficiency, integration and assembly of a generic composite aeronautical wing box. Compos. Struct. 2016;152:1014–1023. [Google Scholar]
- 9.Karlsson Hagnell Mathilda, Åkermo Malin. A composite cost model for the aeronautical industry: methodology and case study. Composites, Part B, Eng. 2015;79:254–261. [Google Scholar]
- 10.Carberry William. Airplane recycling efforts benefit Boeing operators. Boeing Aeromag. 20082008 https://www.boeing.com/commercial/aeromagazine/articles/qtr_4_08/article_02_1.html [Google Scholar]
- 11.Karlsson M. KTH, School of Engineering Sciences (SCI), Aeronautical and Vehicle Engineering, Lightweight Structures; 2013. The development of a technical cost model for composites - adapted to the automotive industry. Master's thesis. [Google Scholar]
- 12.Mårtensson P., Zenkert D., Åkermo M. Method for the cost-efficient and weight-efficient material diversity and partitioning of a carbon fibre composite body structure. Proc. Inst. Mech. Eng., Part D, J. Automob. Eng. 2016;230(1):49–60. [Google Scholar]
- 13.Sugiyama Kentaro, Matsuzaki Ryosuke, Ueda Masahito, Todorokic Akira, Hirano Yoshiyasu. 3D printing of composite sandwich structures using continuous carbon fiber and fiber tension. Composites, Part A, Appl. Sci. Manuf. 2018;113:114–121. [Google Scholar]
- 14.Wang Xin, Jiang Man, Zhou Zuowan, Gou Jihua, Hui David. 3d printing of polymer matrix composites: a review and prospective. Composites, Part B, Eng. 2017;110:442–458. [Google Scholar]
- 15.Brooks Hadley, Molony Samuel. Design and evaluation of additively manufactured parts with three dimensional continuous fibre reinforcement. Mater. Des. 2016;90:276–283. [Google Scholar]
- 16.Kwak M., Robinson P., Bismarck A., Wise R. Microwave curing of carbon-epoxy composites: penetration depth and material characterisation. Composites, Part A, Appl. Sci. Manuf. 2015;75:18–27. [Google Scholar]
- 17.Lee Jeonyoon, Ni Xinchen, Daso Frederick, Xiao Xianghui, King Dale, Sánchez Gómez Jose, Blanco Varela Tamara, Kessler Seth S., Wardle Brian L. Advanced carbon fiber composite out-of-autoclave laminate manufacture via nanostructured out-of-oven conductive curing. Compos. Sci. Technol. 2018;166:150–159. [Google Scholar]
- 18.Kazemahvazi S., Khokar N., Hallstrom S., Wadley H.N.G., Deshpande V.S. Confluent 3d-assembly of fibrous structures. Compos. Sci. Technol. 2016;127:95–105. [Google Scholar]
- 19.Mountasir A., Hoffmann G., Cherif C., Löser M., Großmann K. Competitive manufacturing of 3d thermoplastic composite panels based on multi-layered woven structures for lightweight engineering. Compos. Struct. 2015;133:415–424. [Google Scholar]
- 20.Kaufmann Markus, Zenkert Dan, Åkermo Malin. Material selection for a curved c-spar based on cost optimization. J. Aircr. 2011;48(3):797–804. [Google Scholar]
- 21.Kaufmann M., Zenkert D., Wennhage Per. Integrated cost/weight optimization of aircraft structures. Struct. Multidiscip. Optim. 2010;41(2):325–334. [Google Scholar]
- 22.Moors Gunther, Kassapoglou Christos, Frascino Müller de Almeida Sergio, Augusto Eça Ferreira Clovis. Weight trades in the design of a composite wing box: effect of various design choices. CEAS Aeronaut. J. 2018:1–15. [Google Scholar]
- 23.Mårtensson Per, Zenkert Dan, Åkermo Malin. Integral versus differential design for high-volume manufacturing of composite structures. J. Compos. Mater. 2015;49(23):2897–2908. [Google Scholar]
- 24.Zenkert Dan. KTH Engineering Sciences; Stockholm: 2005. An Introduction to Sandwich Structures. [Google Scholar]
- 25.Jacques Eric, Kjell Maria H., Zenkert Dan, Lindbergh Göran. Piezo-electrochemical effect in lithium-intercalated carbon fibres. Electrochem. Commun. 2013;35(Supplement C):65–67. [Google Scholar]
- 26.Poulikidou S., Schneider C., Björklund A., Kazemahvazi P., Wennhage S., Zenkert D. A material selection approach to evaluate material substitution for minimizing the life cycle environmental impact of vehicles. Mater. Des. 2015;83:704–712. [Google Scholar]
- 27.O'Reilly C.J., Göransson P., Funazaki A., Suzuki T., Edlund S., Gunnarsson C., Lundow J-O., Cerin P., Cameron C.J., Wennhage P., Potting J. Life cycle energy optimisation: a proposed methodology for integrating environmental considerations early in the vehicle engineering design process. J. Clean. Prod. 2016;135:750–759. [Google Scholar]
- 28.Kruse Thomas. Bonding of CFRP primary aerospace structures. ICCM19; Montreal; 2013. [Google Scholar]
- 29.Patterson Jacob B., Grenestedt Joachim L. Manufacturing of a composite wing with internal structure in one cure cycle. Compos. Struct. 2018;206:601–609. [Google Scholar]
- 30.Hexcel Hexply® prepreg technology. 2015. http://www.hexcel.com/Resources/DataSheets/Brochure-Data-Sheets/Prepreg_Technology.pdf
- 31.Baker D.A., Rials T.G. Recent advances in low-cost carbon fiber manufacture from lignin. J. Appl. Polym. Sci. 2013:713–728. [Google Scholar]
- 32.Mainka Hendrik, Täger Olaf, Körner Enrico, Hilfert Liane, Busse Sabine, Edelmann Frank T., Herrmann Axel S. Lignin - an alternative precursor for sustainable and cost-effective automotive carbon fiber. J. Mater. Res. Technol. 2015;4:283–296. [Google Scholar]
- 33.Mannberg Peter. Structural carbon fibre from kraft lignin. 28th SICOMP Conference on Manufacturing and Design of Composites; Piteå; 2017. [Google Scholar]
- 34.Wu Yingji, Xia Changlei, Cai Liping, Garcia Andres C., Shi Sheldon Q. Development of natural fiber-reinforced composite with comparable mechanical properties and reduced energy consumption and environmental impacts for replacing automotive glass-fiber sheet molding compound. J. Clean. Prod. 2018;184:92–100. [Google Scholar]
- 35.Bourmaud Alain, Beaugrand Johnny, Shah Darshil U., Placet Vincent, Baley Christophe. Towards the design of high-performance plant fibre composites. Prog. Mater. Sci. 2018;97:347–408. [Google Scholar]
- 36.Xu Jun, Gao Xiang, Zhang Chong, Yin Sha. Flax fiber-reinforced composite lattice cores: a low-cost and recyclable approach. Mater. Des. 2017;133:444–454. [Google Scholar]
- 37.Faruk Omar, Bledzki Andrzej K., Fink Hans-Peter, Sain Mohini. Biocomposites reinforced with natural fibers: 2000-2010. Prog. Polym. Sci. 2012;37:1552–1596. [Google Scholar]
- 38.Carus Michael. European Industrial Hemp Association (EIHA); 2017. The European hemp industry: cultivation, processing and applications for fibres, shivs, seeds and flowers. Technical report. [Google Scholar]
- 39.ELG Carbon fibre Ltd Recycled carbon fibre as an enabler for cost effect lightweight structures. Global Automotive Lightweight Materials; Detroit; 2016. [Google Scholar]
- 40.Meng Fanran, McKechnie Jon, Pickering Steve J. An assessment of financial viability of recycled carbon fibre in automotive applications. Composites, Part A, Appl. Sci. Manuf. 2018;109:207–220. [Google Scholar]
- 41.Dong Phuong Anh Vo, Azzaro-Pantel Catherine, Cadene Anne-Laure. Economic and environmental assessment of recovery and disposal pathways for cfrp waste management. Resour. Conserv. Recycl. 2018;133:63–75. [Google Scholar]
- 42.Hagnell M.K., Åkermo M. The economic and mechanical potential of closed loop material usage and recycling of fibre-reinforced composite materials. J. Clean. Prod. 2019;223:957–968. [Google Scholar]
- 43.European Commission End of life vehicles. 2014. http://ec.europa.eu/environment/waste/elv/index.htm
- 44.European Commission - DG Environment Ex-post evaluation of certain waste stream directives - final report. 2014. http://ec.europa.eu/environment/waste/pdf/target_review/Final%20Report%20Ex-Post.pdf
- 45.ELG Carbon fibre Ltd. ELG carbon fibre ltd demonstrates commitment to quality standards through as/en9100 certification.
- 46.Boeing Boeing, ELG carbon fibre find new life for airplane structure material in groundbreaking partnership. 2018. https://boeing.mediaroom.com/2018-12-05-Boeing-ELG-Carbon-Fibre-find-new-life-for-airplane-structure-material-in-groundbreaking-partnership
- 47.Calado Elcin Aleixo, Leite Marco, Silva Arlindo. Selecting composite materials considering cost and environmental impact in the early phases of aircraft structure design. J. Clean. Prod. 2018;186:113–122. [Google Scholar]
- 48.Sohouli A., Yildiz M., Suleman A. Cost analysis of variable stiffness composite structures with application to a wind turbine blade. Compos. Struct. 2018;203:681–695. [Google Scholar]
- 49.An Haichao, Chen Shenyan, Huang Hai. Multi-objective optimal design of hybrid composite laminates for minimum cost and maximum fundamental frequency and frequency gaps. Compos. Struct. 2019;209:268–276. [Google Scholar]
- 50.Poulikidou Sofia, Jerpdal Lars, Björklund Anders, Åkermo Malin. Environmental performance of self-reinforced composites in automotive applications - case study on a heavy truck component. Mater. Des. 2016;103:321–329. [Google Scholar]
- 51.Andersson Frida, Hagqvist Astrid, Sundin Erik, Björkman Mats. Design for manufacturing of composite structures for commercial aircraft-the development of a dfm strategy at saab aerostructures. Proc. CIRP. 2014;17:362–367. [Google Scholar]
- 52.Ashby M.F. Multi-objective optimization in material design and selection. Acta Mater. 2000;48(1):359–369. [Google Scholar]
- 53.An Haichao, Singh Jasveer, Pasini Damiano. Structural efficiency metrics for integrated selection of layup, material, and cross-section shape in laminated composite structures. Compos. Struct. 2017;170:53–68. [Google Scholar]
- 54.Karlsson Hagnell Mathilda, Åkermo Malin. Cost and weight efficient assembly of aeronautical composite structures. 20th International Conference on Composite Materials; Copenhagen, 19–24 July 2015; 2015. [Google Scholar]
- 55.The Scipy community Minimization of scalar function of one or more variables using the nelder-mead algorithm. 2016. https://docs.scipy.org/doc/scipy-0.18.1/reference/optimize.minimize-neldermead.html
- 56.Abaqus . Dassault Systèmes; Providence, RI, USA: 2014. Abaqus documentation. [Google Scholar]
- 57.Mukhopadhyay V., Sobieszczanski-Sobieski J., Kosaka I., Quinn G., Vanderplaats G.N. Analysis, design, and optimization of noncylindrical fuselage for blended-wing-body vehicle. J. Aircr. 2004;41:925–930. [Google Scholar]
- 58.Mukhopadhyay V. Blended-wing-body (bwb) fuselage structural design for weight reduction. 46th AIAA/ASME/ASCE/AHS/SC Structure, Structural Dynamics and Materials Conference; Texas; 18-21 April 2005, 2005. [Google Scholar]
- 59.Boni L., Fantaria D. Finite-element-based assessment of analytical methods for the design of fuselage frames. Proc. Inst. Mech. Eng., G J. Aerosp. Eng. 2006;220:387–398. [Google Scholar]
- 60.Helsen J., Cremers L., Mas P. Global static and dynamic car body stiffness based on a single experimental modal analysis test. International Conference on Noise and Vibration Engineering; Leuven, 20-22 September 2010; 2010. [Google Scholar]
- 61.Gauchia A., Diaz V., Boada M.J.L., Boada B.L. Torsional stiffness and weight optimization of a real bus structure. Int. J. Autom. Technol. 2010;11:41–47. [Google Scholar]
- 62.Ferrara Michael. Chassis 201: maximizing torsional rigidity. 2015. http://dsportmag.com/the-tech/chassis-201-maximizing-torsional-rigidity-1/
- 63.Mårtensson P., Zenkert D., Åkermo M. Cost and weight efficient partitioning of composite automotive structures. Polym. Compos. 2015:2174–2181. [Google Scholar]
- 64.Hexcel Hexply® M21 product data. 2015. http://www.hexcel.com/user_area/content_media/raw/HexPly_M21_global_DataSheet.pdf
- 65.Hexcel Hexweb® HRH-10 aramid fibre/phenolic honeycomb. 2015. https://www.hexcel.com/Resources/DataSheets/Honeycomb
- 66.Hexcel Hexweb honeycomb sandwich design technology. 2000. http://www.hexcel.com/user_area/content_media/raw/Honeycomb_Sandwich_Design_Technology.pdf?w=500
- 67.Rinaldi R IM.A.TEC, Hexweb® HRH-10 aramid fibre/phenolic honeycomb quote and general information, personal communication March 2017.
- 68.Diab Divinycell H. 2017. http://www.diabgroup.com/en-GB/Products-and-services/Core-Material/Divinycell-H
- 69.Fiberglass Supply Core materials - h-100 divinycell. 2017. http://www.fiberglasssupply.com/Product_Catalog/Core_Materials/core_materials.html
- 70.Taub Alan I., Luo Alan A. Advanced lightweight materials and manufacturing processes for automotive applications. Mater. Res. Soc. Bull. 2015;40(12):1045–1054. [Google Scholar]
- 71.Ashby M.F. Criteria for selecting the components of composites. Acta Metall. Mater. 1993;5:1313–1335. [Google Scholar]