Propagation analysis and prediction of the COVID-19

Abstract

Based on the official data modeling, this paper studies the transmission process of the Corona Virus Disease 2019 (COVID-19). The error between the model and the official data curve is quite small. At the same time, it realized forward prediction and backward inference of the epidemic situation, and the relevant analysis help relevant countries to make decisions.

1. Introduction

At the end of 2019, the new coronavirus (COVID-19) spread widely in China, and a large number of people became infected. At present, the domestic outbreak has been effectively controlled, while the new coronavirus is spreading rapidly in other areas. Currently, Europe has become the center of the current outbreak of new pneumonia. Meanwhile, on March 11, the World Health Organization (WHO) declared a new pneumonia outbreak a "global pandemic." The new coronavirus has caused a great threat to the health and safety of people all over the world due to its amazing spreading power and potential harm. The research on the domestic and international epidemics and the future development trend has become a hot topic of current research. At present, many teams have studied the transmission law and preventive measures of the COVID-19 (Corman et al., 2020; Hui et al., 2020; Rothe et al., 2020), and many meaningful results have been obtained (Mizumoto & Chowell, 2020; Riou & Althaus, 2020; Shao & Wu, 2020).

According to the transmission characteristics of epidemic at different stages, this paper uses Gaussian distribution theory to construct a new model of coronavirus transmission. By simulating the propagation process of the COVID-19, we found that the curves of proposed model well simulate the official data curves of Hubei, Non-Hubei area of China and also South Korea, Italy, and Iran. The study points out the key factors that affect the spread of the virus, such as the basic reproduction number, virus incubation period, and daily infection number. At the same time, we predict the development trend of epidemics in different regions and infer the time of the initial cases. Furthermore, we analyzed the impact of different control times on the spread of the epidemic. Relevant models and data analysis can provide some basis and guidance for the related countries about epidemic prevention and control.

The main contributions of this paper can answer the following 11 questions and be summarized as:

• ✓
  Epidemic situation in Hubei Province of China:

  • 1).
    When will more than 10,000 confirmed coronavirus cases be completely cured in Hubei ?

The model predicts that almost all cases will be cured before April 1 (Fig. 1).

• 2).When was the earliest case in Hubei?

Fig. 1.

The comparison between the official epidemic data and simulation data of Hubei Province (The curve a - Number of simulated infections. The curve b - Number of officially confirmed infections. The curve c - Number of simulated cures. The curve d - Number of officially cures. The curve e - Number of simulated deaths. The curve f- Number of officially deaths.) There are three stages in the simulation. The first stage is before January 23, when Wuhan is not closed; the second stage is from January 23 to February 10; the third stage is after February 10, when Wuhan starts to close the community.

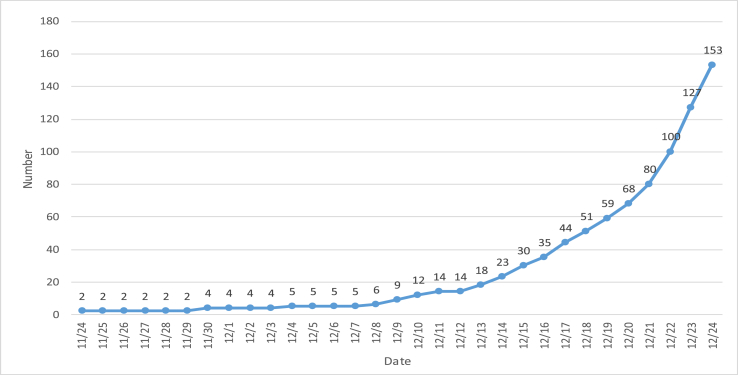
We find that there was already infections on November 24 (Fig. 2).

• 3).How many people are infected per person (Basic reproduction number)?

Fig. 2.

Backward graph of initial epidemic curve.

It is 3.8 when not under control, 0.5 after closing Wuhan city and 0.1 after closing of Wuhan community (Fig. 3).

• 4).What is the average incubation period of the virus?

Fig. 3.

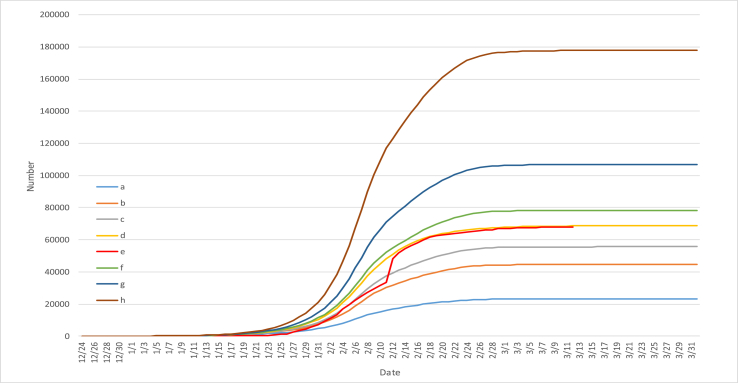
Comparison of the basic reproduction number. (The basic reproduction number a = 3, b = 3.5, c = 3.7, d = 3.8, f = 3.9, g = 4.1, h = 4.6, respectively. The curve e - Number of officially confirmed infections.)

6 days (Fig. 4).

• 5).If it is controlled 5 days in advance, how much is the infection? What if control is lagging 5 days?

Fig. 4.

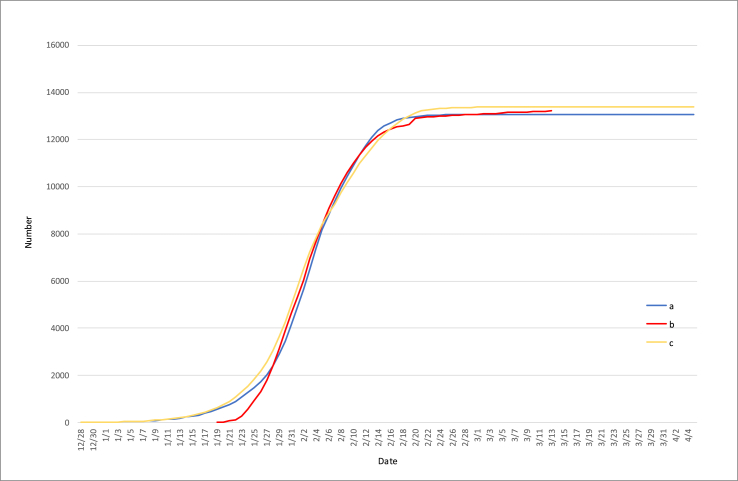
Comparison of the average latency. (The average latency a = 3, b = 5, c = 6, e = 7, f = 9, respectively. The curve d - Number of officially confirmed infections.)

If 5 days in advance, the number of infected people will be 28,000, 42% of the current number of confirmed cases. If the control is delayed for 5 days, it will reach 156,000 people, 2.26 times of the current level. (68,000 in Hubei at March 13) (Fig. 5).

• 6).What distribution does the daily infection curve satisfy, which day reaches the peak, is February 12?

Fig. 5.

Comparison of epidemic control at different times (The curve a - 5 days in advance. The curve b - Control by actual days. The curve c - Number of officially confirmed infections. The curve d - 5 days delayed.).

The distribution satisfy Normal distribution, the actual peak appeared on February 8. In the official data, because the clinical diagnosis was not added before the February 12, the data surged on the February 12 (jump to 14,840 people, cumulative results), indicating that the previously published data did not reflect the actual infection situation in Hubei (Fig. 6).

• 7).The average number of days from diagnosis to cure?

Fig. 6.

Change curve of daily new infections. (The curve a - Simulated curve. The curve b - Smoothed curve. The curve c - Number of officially confirmed infections.)

In the stage of Hubei epidemic, it takes an average of 21 days for patients from diagnosis to cure (Fig. 1).

• ✓
  Epidemic situation in non-Hubei areas of China:

  • 8).
    What is the law of transmission in non-Hubei areas?

The epidemic transmission curve of non-Hubei area is similar to that of Hubei area, which was controlled 10 days in advance (on January 13). (Fig. 7).

• ✓
  International epidemic situation except China

  • 9).
    How to predict the epidemic situation in South Korea?

Fig. 7.

Correlation analysis of epidemic data in non-Hubei area (The curve a - Simulated number of non-Hubei infections, the curve b - Actual number of non- Hubei confirmed cases, the curve c - Number of simulated infections in Hubei when control was ten days in advance).

At present, the epidemic situation in South Korea is basically under control. According to the model, South Korea will be basically under control by the end of March. It was found on January 7 that there was infection in South Korea (confirmed by official broadcast January 20. In addition, we found that the basic reproduction number before the control was 4.2 in Korea and 0.1 after the control (Fig. 8).

Fig. 8.

Comparison of Korean epidemic simulation data and official data. (The curve a-Number of simulated infections. The curve b-Number of officially confirmed infections.)

In March 13, 15,000 people in Italy are infected. If not controlled, it will increase dramatically. It will reach 250,000 by the end of March. In fact, Italy began to control on March 8. According to China’s basic reproduction number 0.5 (when city is closed), it will reach 100,000 by the end of March. The basic reproduction number in Italy is 3.8 before control. According to the model inversion, the infection was found on January 10 in Italy (2 cases were confirmed by the official broadcast January 31). (Fig. 9).

Fig. 9.

Comparison of Italy epidemic simulation data and official data. (The curve a-Number of simulated infections (uncontrol). The curve b-Number of simulated infections (partial control). The curve c-Number of officially confirmed infections.).

In March 13, 11,000 people are infected in Iran. Our model predicts that it will reach 33,000 people at the end of March, through backward inference of the epidemic situation, we found that Iran had an infection on January 11 (officially reporting that two cases died on February 20, and there was no official data before). The model found that the basic reproduction number in Iran before the control was 3.8 (Fig. 10).

Fig. 10.

Comparison of Iran epidemic simulation data and official data. (The curve a-Number of simulated infections. The curve b-Number of officially confirmed infections.)

2. Specific analysis of the epidemic situation model

The epidemic data of Hubei Province is large (http://wjw.hubei.gov.cn/), more in line with the statistical law, and the statistical model is more able to reflect the process of virus transmission, so we build a statistical model for the epidemic situation of Hubei Province (see the method section later for details). Based on the data provided by National Health Commission of China (NHCC), we have carried out accurate simulation. By comparing the simulation results with the real data, we analyze the propagation process and its influencing factors.

2.1. Simulation comparison of epidemic model in Hubei Province

According to the comparison between the official epidemic data and simulation data of Hubei Province (see Fig. 1 for details), we can see that the model simulation curve of the number of confirmed infections, the number of cured people and the number of dead people matches the official data curve very well. According to the curve of simulated number of infected persons and the curve of official number of infected persons, we can see that there is a certain gap between the number of infected persons before February 12, and the others are basically the same. (after the official announced the method of clinical diagnosis of pneumonia on February 12, the data on that day surged to 14,000, indicating that the official data had some omissions before February 12, and our model give a more accurate response to the number of actual cases).

2.2. Simulation of the number of infected people

According to the curve of simulated infection number, we infer that by the end of March (yellow line + light blue line = dark blue line: Number of simulated cures + Number of simulated deaths = Number of simulated infections), all cases will be basically treated, that is to say, more than 10,000 cases in Hubei will be basically cured and cleared. Note: the number of cases of infection on December 24 is not zero. Because the data in Fig. 1 is too large, small data cannot be displayed. For this reason, according to the same distribution curve, we also give the simulation data results before December 24, and the simulation found that the initial infected people had existed as early as November 24 (see Fig. 2 for details). The first confirmed infection was reported on December 8 (http://www.stdaily.com/).

2.3. Simulation of the number of the average infected people

The basic regeneration number has a great influence on the spread of the outbreak. As the number of basic regeneration increases, the total number of people infected will also increase; and the greater the number of basic regeneration, the faster the disease will spread. As in the previous simulation, there are three phases. The first phase is an uncontrolled phase. Through a large number of simulations, we found that the basic regeneration number is 3.8, and the second and third phases are controlled phases. The basic regeneration numbers are respectively It is 0.5 and 0.1 (see the yellow line in Fig. 3). The simulated curve (yellow line) can be closer to the official diagnosis curve (red line) in Hubei. The first stage is the free propagation stage, and we also give other simulation results of the basic regeneration number in the range of 3–4.6 (the second and third stages remain unchanged). The effect of transmission is significant, with the most accurate final infections being obtained only at 3.8. As for the basic regeneration number in the stage of free propagation, some scholars have proposed that it should be between (2.8,3.9) or (3.6,7.4) (Read et al., 2020). Obviously, these expressions are either inaccurate or too wide.

2.4. Simulation of the average latency

Fig. 4 shows the comparison chart of the average incubation period. We simulated the days in the range of 3–9 respectively, and found that when the average incubation period was set to 6 days, it could better fit the official curve, while the other simulated values are quite different from the official curves. It is also found that the shorter the incubation period, the faster the virus spreads and the greater the total number of infections. David mentioned that the incubation period of the virus is 3–6 days, which is not accurate.

According to the previous analysis, the disease develops on average after 6 days of incubation, and it takes an average of 5 days from the morbidity to the diagnosis (data from CHCC) (http://www.labour-daily.cn), that is, 5 + 6 = 11 days from the initial infection and incubation to the diagnosis and isolation after the morbidity. Obviously, not all 11 days are contagious. Simulations show that when the average time for contagion is set to 8 days, it fits the official curve best.

2.5. The simulation test of the epidemic control

We know that epidemic control at different times (such as closing city) will have an important impact on the spread of the epidemic, obviously the earlier the better. Combined with the actual situation of Wuhan’s closure from January 23, we simulated the comparison of the spread of the epidemic situation on January 18 and January 28, as shown in Fig. 5. The red curve and the orange curve in the figure respectively represent the official curve and the simulation curve (when the "cities were closed" measures were taken on January 23). Obviously, the two curves match well, and the simulated final number of infected people is 69,000, which is also close to the actual situation. If the control is started five days in advance, that is, on January 18, the blue line shows that the number of infected people is about 28,000, which is 0.42 times of the number of confirmed cases. If the measures are delayed for 5 days, it can be seen from the yellow line that the number of people will be as high as 156,000, about 2.26 times of the current number of patients. Zhong Nanshan’s team once predicted that if the closure measures were delayed for five days, the number of patients would reach three times of the current number, i.e. 210000 (Heymann, 2020). Our results are more optimistic. It can be seen from this figure that it is necessary to take timely measures to control the spread of the epidemic, which can also be used as a reference for some overseas countries.

2.6. The simulation of daily new infections

We also studied the curve of the daily increase in the number of people (Fig. 6). Because the official did not include the imaging features of pneumonia in the clinical diagnosis into the diagnosis conditions for statistics before February 12, 2020, the omission and inaccuracy of the previous data caused the official data to jump on the February 12 (the number of newly diagnosed patients in Hubei was 14,840 people). As shown in Fig. 6, our simulation data meet the normal distribution, at this time, the daily new infection data peaked on February 8, with the number of 4500. However, the published data, due to not timely included in the clinical diagnosis image test (red line), many patients were not diagnosed, but the curve has become a downward trend, data deviation. For this reason, we smoothed the clinical diagnosis data on February 12, 13 and 14, and used the Gauss function of latent period. These three days were chosen because of the sudden increase of the number of clinical diagnosis in these three days. It can be seen from the figure that the smooth number of official daily infected persons (black line) and the simulation curve (blue line) fit very well.

3. Data analysis of non-Hubei regions

Due to the large liquidity before the Spring Festival in China, Hubei Province has produced case output. We have also conducted research on non-Hubei area, which is also divided into three stages: the first stage is before January 26 (30 provinces and cities in the country enter the first level of combat readiness on January 26), the second stage is from January 26 to February 5 (the whole country starts to close the community in early February, here we take No. 5 for simulation), the third stage is after February 5. A large number of simulations found that the regeneration numbers in the three stages were 3.8, 0.5, and 0.1, respectively. At this time, the simulation curve (blue line) and the actual curve (red line) fit well. Another interesting phenomenon is that we found that if Hubei ’s transmission was controlled 10 days in advance (Hubei began to control on January 13), its propagation curve (yellow line) is highly similar to the propagation curve in non-Hubei regions.

On January 24th, 235 cases were confirmed in non-Hubei province, with an accumulation of 1052 cases in Hubei province, accounting for about 20%. Finally, it was officially announced that non-Hubei 13,220 and Hubei 67,786 were infected, which was also basically in line with the proportion of 20%. In other words, there is a high degree of similarity between the initial and final transmission ratios in Hubei and non-Hubei areas.

4. The prediction of foreign epidemic

4.1. Analysis of Korea data

From March 2, South Korea began to implement large-scale measures to prevent and control the epidemic situation (https://www.best73.com). At present, the epidemic situation in South Korea is basically under control. Our model simulates the actual data well, and it is found through model prediction (Fig. 8). That South Korea will be basically controlled by the end of March. We inferred from the curve and found that there was an infection in South Korea on January 7 (the official broadcast confirmed the diagnosis at January 20). We found that before the control, the basic reproduction number of virus transmission in Korea was 4.2, and the basic reproduction number after control was 0.1. (The basic reproduction number reached 4.2. We suspect that some churches in South Korea ignored the spread of the epidemic in the early stage.)

4.2. Analysis of Italian data

In March 13, 15,000 people are infected in Italy. Through simulation, we find that (Fig. 9), if we do not control (blue line) at all, it will grow explosively, reaching 250,000 at the end of March. In fact, Italy began to control population flow on March 8. According to the basic reproduction number (0.5) after China’s city control, our model predicts that by the end of March, the number of confirmed cases in Italy will reach 100,000 (yellow line). At present, the basic reproduction number in Italy is 3.8. According to the model inversion, there were infected persons in Italy on January 10 (2 cases were confirmed in Italian official broadcast January 29 (https://tech.sina.com.cn/)). (The reproduction number reaches 3.8, which is similar to the date of the early stage in china.)

4.3. Analysis of Iranian data

In March 13, 11,000 people are infected in Iran. According to the simulation, as shown in Fig. 10, the infection data is expected to reach 33,000 by the end of March, and then it will be basically controlled by the beginning of April. It was found that Iran had infection on January 11 (Officially announced 2 cases died on February 20, no previous official data) (https://www.huxiu.com/). The model found that the basic reproduction number of virus transmission in Iran before control was 3.8, and the basic reproduction number after control was 1. (the Iranian government took many control measures in early March. The basic reproduction number after control is 1, indicating that the control effect is not ideal.)

5. Model and description

5.1. Transmission of the virus

Many studies have shown that virological transmission usually satisfies the Gaussian distribution, so this article uses the Gaussian distribution to analyze the transmission of viruses (Yang and Niu, 2018, 2019). When we use Gaussian distribution to simulate, the main influence is the average value, but the standard deviation has little influence, so we will take the best accord with the objective fact variance to simulate. The basic reproduction number is the number of people infected by a patient during the average illness period when all are susceptible at the morbidity of the disease. The Gaussian distribution function of $\text{ D}1~\text{ N}(\text{x}1,\text{y}1)$ is used to represent the propagation ability of the virus. This formula indicates that a single infected person can infect ×1 person on average in the first stage. At this stage, ×1 has a value range of $(1,+\infty )$, and a standard deviation of $\text{y}1=1.5$.

With the development of a series of effective measures, the daily increase of the number of infected people also decreased to a certain extent, and the transmission ability of the disease in the population decreased. For the ability to spread disease through this process, we still use the Gaussian distribution. When a single infected person at this stage is able to infect an average of ×2 individuals, the formula for the capacity to transmit is, $\text{ D}2~\text{ N}(\text{x}2,\text{y}2)$. At this stage, the value range of ×2 is general $(\mathrm{0,1}]$, standard deviation of ×2 is $\text{y}2=2\text{∗x}2$. Because the medical condition of affected area and the degree of people’s activity intention directly decide the basic regeneration number in this stage. The better the health care, the less active the population, the smaller the ×2.

In the course of disease transmission, the patient from being infected to the morbidity of disease, we call it incubation period. We assume that it takes ×3 days for people to get infected and become aware of the disease, then the incubation period follows $\text{D}3~\text{N}(\text{x}3,\text{y}3)$. In this model $\text{x}3=6.0$, the standard deviation $\text{y}3=2.0$.

In addition, patients can transmit the virus to other people, so we assume that the average time from infection to transmission is ×4 days, which follows $\text{D}4~\text{N}(\text{x}4,\text{y}4)$. According to the previous analysis, the disease develops after an average of six days of incubation, and it takes an average of five days from morbidity to diagnosis (according to NHCC), that is, 5 + 6 = 11 days from the initial incubation of infection to post-morbidity isolation. Clearly, not all 11 days are infectious, and simulations show that setting the average number of infectious days to 8 best fits the official curve. In this model $\text{x}4=8.0$, the standard deviation $\text{y}4=1.5$.

5.2. Cure the discharge process

The cure time of the patient is the difference between the time of hospital discharge and the time of diagnosis, set to ×5. During the epidemic period, the cure time of patients was expressed by Gaussian distribution, that is, $\text{D}5~\text{N}(\text{x}5,\text{y}5)$, which means that it takes an average of ×5 days for a single individual to be cured and discharged from hospital. During the early and late stages of the epidemic, depending on the medical condition and level of vigilance, there will be small changes to the ×5. As the epidemic continued, people’s awareness of self-protection became stronger, and hospital treatment became more effective in the late stage of the outbreak, the patient’s recovery time became shorter and shorter. In Hubei Province, the average time from diagnosis to cure was 21 days.

5.3. Death toll

Relative to the spread of previous diseases, the early mortality rate of this disease is also very high, mainly due to the lack of understanding of the new virus, and secondly, the new crown virus transmission is very strong, leading to the collapse of the medical system in the epidemic area. Due to the continuous improvement of medical conditions and other reasons, the mortality rate of the disease has continued to ease. We assume that the mortality rate is ×6, then the mortality distribution follows $\text{ D}6~\text{N}(\text{x}6,\text{y}6)$. The mortality rate will change in stages depending on medical conditions. According to the CHCC, Hubei Province’s current mortality rate is 4.5 percent.

6. Conclusion

In this paper, through analyzing the existing data of Hubei epidemic situation, the corresponding model is established, and then the simulation is carried out. Here, we studied the main factors affecting the spread of COVID-19, such as the number of basic regenerations, the incubation period and the average number of days of cure. What’s more, we predicted the evolution trend of the existing epidemic data, and found that imposing controls would have important impact on the epidemic. In addition, according to the existing data abroad, we also make bold predictions of the epidemic development trends in South Korea, Italy, and Iran, pointing out the possible outbreaks and the corresponding control time, and tracing the earliest transmission dates of countries. Finally, we hope that this article can make some contributions to the world’s response to this epidemic and give some references for future research.

Declaration of competing interest

None.

Handling Editor: Dr. J Wu

Appendix.

A. Methods

A1. Data

We obtained the data from the NHC of China, 2020. The data information includes the cumulative confirmed cases, the cumulative number of deaths, newly confirmed cases and the cumulative number of cured cases for Hubei and non-Hubei provinces from January 26 to March 10. We also used the data on the recent diagnoses in South Korea, Iran, and Italy, it includes the data from the January 20 (the first confirmed diagnosis) to March 13 (the epidemic stabilized) in South Korea, the data from the January 31 (the first confirmed case) to March 20 in Italy and the data from the February 20 (the first confirmed case) to March 20 in Iran, and here, the data comes from official notifications from various countries.

A2. Parameter estimation process

In different control stages, the Basic reproduction number changes greatly and it affects the intensity of control directly. In addition, the incubation period of the virus affects the speed of transmission directly. These two parameters need to be estimated. Current literature shows that the uncontrolled Basic reproduction number fluctuates between [2.8, 7.4] (Read et al., 2020). Therefore, we chose the valuation range in the corresponding range. For the controlled Basic reproduction number, the range of valuation was selected in the range of [0, 1.5]. At the same time, due to the incubation period of NHCC is given in 3–7 days, so we put the estimates of the incubation period interval in the 3–9 days. The average time for contagion of individuals is also an important parameter. In this paper, according to the data of NHCC, we know that it takes 5 days from the onset to the diagnosis of isolation, and the first three days of the onset are infectious (Xia et al., 2020), so the average time for contagion in this paper is 3 + 5 = 8.

The Monte Carlo method was used in the building stage of the model, and we used the programming language-C++ for modeling. In this model, a single individual may be in the following four states, latency, illness, health, or death. According to the different control stages of the specific regions, (such as Hubei regions, non-Hubei regions in China, Italy, et al.). We set up different Gaussian distributions for propagation simulation. By selecting the optimal estimated parameters to fit the official curve, we use the Particle Swarm optimization algorithm to optimal the model. Then, we predict the future development trend based on the obtained parameter values. The infection time of the initial case was reversed by the model. The simulation results are shown in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10.