Rapid, Phase-free Detection of Long Identity-by-Descent Segments Enables Effective Relationship Classification

Abstract

Identity-by-descent (IBD) segments are a useful tool for applications ranging from demographic inference to relationship classification, but most detection methods rely on phasing information and therefore require substantial computation time. As genetic datasets grow, methods for inferring IBD segments that scale well will be critical. We developed IBIS, an IBD detector that locates long regions of allele sharing between unphased individuals, and benchmarked it with Refined IBD, GERMLINE, and TRUFFLE on 3,000 simulated individuals. Phasing these with Beagle 5 takes 4.3 CPU days, followed by either Refined IBD or GERMLINE segment detection in 2.9 or 1.1 h, respectively. By comparison, IBIS finishes in 6.8 min or 7.8 min with IBD2 functionality enabled: speedups of 805–946× including phasing time. TRUFFLE takes 2.6 h, corresponding to IBIS speedups of 20.2–23.3×. IBIS is also accurate, inferring ≥7 cM IBD segments at quality comparable to Refined IBD and GERMLINE. With these segments, IBIS classifies first through third degree relatives in real Mexican American samples at rates meeting or exceeding other methods tested and identifies fourth through sixth degree pairs at rates within 0.0%–2.0% of the top method. While allele frequency-based approaches that do not detect segments can infer relationship degrees faster than IBIS, the fastest are biased in admixed samples, with KING inferring 30.8% fewer fifth degree Mexican American relatives correctly compared with IBIS. Finally, we ran IBIS on chromosome 2 of the UK Biobank dataset and estimate its runtime on the autosomes to be 3.3 days parallelized across 128 cores.

Introduction

Recent efforts in human genetics have focused on generating and analyzing large-scale samples, including data from up to ∼500,000 individuals,¹ with more projects underway. Because every pair of samples has the potential to be related, and as the number of pairs in a study grows quadratically, the proportion of samples with at least one close relative also grows rapidly with sample size.^1,2 Indeed, as datasets continue to increase in size, nearly all individuals will eventually have one or more close relatives within a given study.³

While massive datasets contain many close relatives, identifying these relatives accurately and in a computationally efficient manner is currently challenging. The fastest methods rely on allele frequencies,^4,5 but these approaches are less accurate than those based on identity-by-descent (IBD) segments.⁶ Furthermore, many allele frequency-based methods, including the fastest approaches, are biased in admixed samples because of admixture linkage disequilibrium (LD).^{7, 8, 9} In contrast, IBD segment-based approaches^{10, 11, 12, 13} have high accuracy⁶ and are not subject to the same biases in admixed samples because they utilize shared haplotypes rather than allele frequencies from (assumed) independent markers. Nevertheless, the most commonly used IBD detection methods are computationally expensive because they either perform haplotype phasing internally or require pre-phased data.

Besides relatedness classification, IBD segments are themselves useful for a wide range of analyses, including studies of population history,^{14, 15, 16} analyses of mutation rate,^17,18 disease gene mapping,¹⁹ and fitting disease architecture models.²⁰ Moreover, for relationship classification, approaches that leverage IBD segments from multiple samples provide refined estimates of the degree of relatedness among individuals²¹ and can uncover specific pedigree relationship types (instead of only relatedness degrees) that are otherwise ambiguous.²²

Here we outline a method, Identical by Descent via Identical by State (IBIS), that efficiently and accurately detects IBD segments and infers degrees of relatedness in both admixed and unadmixed samples. IBIS works by identifying long stretches of allele sharing between samples using unphased genotype data and leverages bit sets to store which markers each sample carries in a homozygous state. This method is related to the long-range phasing work of Kong et al.²³ and the IBD detection method described by Henn et al.,²⁴ but here we provide publicly available software and details on the efficient bit-level algorithm we use for detection. We find that IBIS can reliably identify segments ≥7 centiMorgans (cM) in length and can use these segments to infer sixth degree or closer relatives at comparable accuracy rates to Refined IBD and GERMLINE, two of the most accurate IBD segment-based approaches for relatedness classification.⁶

IBIS supports detection of segments designated IBD1 or IBD2, corresponding to regions that have the indicated number (one or two) of shared haplotypes between two individuals. In what follows, the unqualified term “IBD” represents regions where the number of shared segments is undetected. Regions that are not identical by descent on either haplotype are also useful for some analyses, and we refer to these as IBD0.

We evaluated IBIS using a combination of simulated unadmixed and real admixed samples, the latter from the San Antonio Mexican American Family Studies (SAMAFS).^{25, 26, 27} The SAMAFS data contain nearly 2,500 samples in numerous pedigrees, and we used its thousands of real relatives to test the inference accuracy of IBIS, Refined IBD,¹¹ KING,⁵ GERMLINE,¹² and TRUFFLE,²⁸ the last of which is a recently developed method that also detects IBD segments in unphased data.

Material and Methods

IBIS works by searching for regions where two individuals share one or more alleles at successive genotyped markers within an interval of at least a user-defined length. It also tolerates errors that may induce a lack of allele sharing at a few markers across such a region.

The key feature underlying IBIS is its use of sets that indicate which markers are homozygous within a given sample, with one set for each of the two possible alleles at each site. (Multi-allelic variants are also feasible to use by representing them as a series of biallelic variants, one for each allele at the site.) Using this encoding, IBIS searches for IBD segments by performing set operations between these values, obtaining regions in which a given pair of individuals is potentially identical by descent.

Since the method does not utilize phase information, a series of shared alleles may not represent a true identical haplotype, as the shared alleles can fall on different haplotypes at each site. However, the probability of sharing alleles at adjacent sites by chance and not due to a shared IBD segment drops rapidly as the number of such sites increases. We have found that while the algorithm is likely to falsely infer segments <7 cM long, the segments ≥7 cM long that IBIS detects between relatives are typically real (Results). Such long segments enable accurate relationship classification and other similar downstream analyses.²²

IBIS uses a few user-specified parameters for detecting and printing segments, as described below. These include a minimum segment length in centiMorgans, the minimum number of markers a segment must span to be considered real, and an error threshold corresponding to the maximum fraction of sites IBIS tolerates as being inconsistent with IBD sharing in any segment. Additionally, a user may limit printing to sample pairs whose inferred kinship coefficient is above a given minimum value, which decreases the space needed to store IBIS’s results.

Algorithm Overview

We first explain how the algorithm detects IBD regions in general, where we do not distinguish the segments as being IBD1 or IBD2, and later describe an extension to make this distinction. IBD2 information is especially useful for detecting full siblings, and as such IBD2 calling is included as an option, yet use of IBD0 regions (the inverse of those inferred IBD) also enables this classification.^5,6

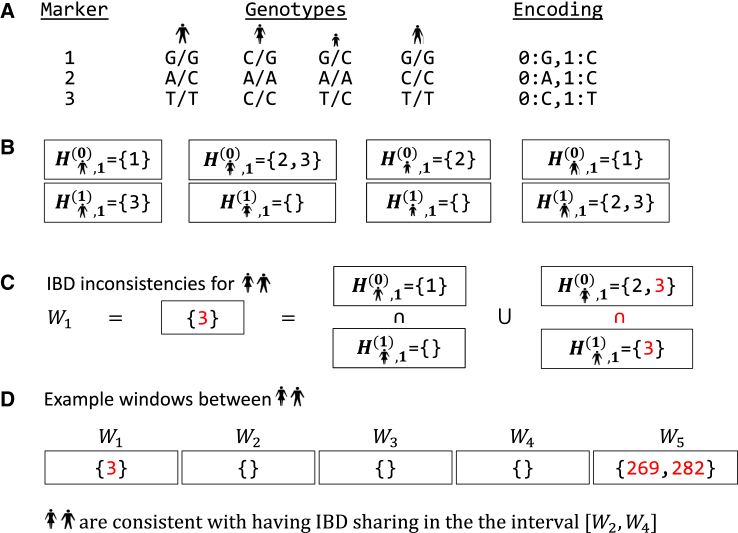
IBIS centers its analysis on non-overlapping windows of markers in which it determines, for a given window, which of its markers are inconsistent with being identical by descent between a pair of individuals. The algorithm begins by taking the input genotype data and generating homozygous marker sets $H_s^{\left(0\right)}$ and $H_s^{\left(1\right)}$ for alleles 0 and 1 and each sample s (Figures 1A and 1B). The 0 and 1 allele encoding is based on the input and has no effect on the results of the analysis. The method then analyzes subsets of H that contain information only for the markers within a given window i, denoted $H_{s,i}^{\left(a\right)}$ for allele a and sample s. These windows are of fixed length (64 SNPs, as explained later) and speed up the comparisons between individuals beyond that of evaluating each marker individually. Additionally, while use of windows in principle leads to lower resolution of segment bounds, determining end points is difficult, and IBIS’s segment starts and ends have similar distances to the true values compared to the other methods we evaluated (Results).

Figure 1.

Example Genotype Data and IBIS Processing

(A) Genotype data at three markers for four samples (stick figures). The input encodes the alleles at each site as a zero or one, as indicated.

(B) Sets $H_{s,1}^{\left(0\right)}$ and $H_{s,1}^{\left(1\right)}$ for each sample s contain the markers that are homozygous for alleles 0 and 1, respectively.

(C) The set operations to construct W₁ for two of the samples yields one marker where these individuals are homozygous for opposite alleles.

(D) Example W_i values across five windows for a given pair. IBIS detects potential IBD segments as a series of windows where the first and last windows have no inconsistencies and where $\left|W_i\right|\le 1$ for all other windows i. Such a region with no inconsistent genotypes spans windows two through four in the figure.

After delineating windows, IBIS performs its primary analysis, iterating over each pair of individuals and each window i, and generating W_i, the set of markers where the current pair of samples do not share an allele in window i (Figure 1C). The algorithm calculates this for samples s₁ and s₂ as

$$W_i=\left(H_{s_1,i}^{\left(0\right)}\cap H_{s_2,i}^{\left(1\right)}\right)\cup \left(H_{s_1,i}^{\left(1\right)}\cap H_{s_2,i}^{\left(0\right)}\right).$$ (Equation 1)

The two intersections above produce a set of markers that are homozygous for opposite alleles in s₁ and s₂, with their union accounting for the two possible homozygous genotype states that lead to this case. Thus, W_i contains all markers that are inconsistent with IBD sharing between s₁ and s₂, as opposite homozygous genotypes are the only way a pair of samples can have such an inconsistency. More specifically, heterozygous markers share an allele with all other genotypes, and we assume universal allele sharing for missing data sites.

During the calculation of the W_i values, IBIS determines where potential IBD segments start and end (Figure 1D). Segment starts manifest as a window b in which $W_b=\varnothing$, i.e., where there are no inconsistencies. In order to account for potential errors, the method allows for up to one marker that is inconsistent with IBD sharing per window, so that segments span windows with $\left|W_i\right|\le 1$. While tracking an ongoing segment, IBIS calculates the fraction of mismatching sites across its length. If this fraction exceeds a user-given threshold, or if the segment reaches the end of the chromosome, the algorithm terminates the segment and chooses the last mismatch-free window as its end point. When a segment ends, the algorithm determines whether its cM length and overall marker counts are greater than the user-defined minimums for these values, and if so, IBIS considers the segment to be real.

When IBIS completes its analysis of a pair of individuals, it calculates their kinship coefficient from their IBD segments, as described below. Then, it determines whether this kinship coefficient is higher than a user-given minimum. If so, or under the default minimum kinship coefficient of 0, it prints the IBD segments that pair shares; otherwise, it discards them.

Detecting IBD1 and IBD2 Segments

The process for detecting IBD1 and IBD2 regions is similar to the general IBD detection method described above, and when run with IBD2 detection enabled, IBIS performs analyses for both general IBD and IBD2 side by side, tracking ongoing potential segments for each. The algorithm treats segments recovered via the approach outlined just above that do not meet additional criteria for IBD2 segments as IBD1.

Since potential IBD2 sharing requires samples to have the same genotypes—i.e., to share two alleles per marker—IBD2 segments have greater evidence of being truly identical by descent than an IBD1 segment of the same length possesses. Therefore, IBIS accepts shorter IBD2 segments as real, with a default minimum length of 2 cM (Results). It also allows for up to two markers with inconsistent genotypes per window in IBD2 regions. As an optimization, IBIS avoids the below IBD2 calculations for windows i where $\left|W_i\right|>1$; i.e., it only considers the possibility of IBD2 sharing within windows that have the potential to be identical by descent using the approach from the previous subsection.

IBIS performs the following set operations to produce $W_i^{\left(2\right)}$, the set of sites in window i that are inconsistent with IBD2 sharing:

$$W_i^{\left(2\right)}={\left(M_{s_1,i}\cup M_{s_2,i}\right)}^c\cap \left(\left(H_{s_1,i}^{\left(0\right)}\oplus H_{s_2,i}^{\left(0\right)}\right)\cup \left(H_{s_1,i}^{\left(1\right)}\oplus H_{s_2,i}^{\left(1\right)}\right)\right).$$ (Equation 2)

Here, M_s,i is the set markers within window i where sample s is missing data. The first operation, the union of these two sets for s₁ and s₂, therefore includes markers that are consistent with IBD2 sharing, and we complement this to exclude those sites from $W_i^{\left(2\right)}$. The other terms identify sites where the samples have different genotypes, and in particular, those where one sample is homozygous for a given allele and the other sample is not. This works using the exclusive-or operator $\oplus$ applied to the two sets of markers at which s₁ and s₂ are both homozygous for one of the alleles, each allele in turn. As this operator retains all markers that appear in exactly one of the two sets, but not those in both or neither, the result is markers that differ in their homozygous genotypes between s₁ and s₂. This takes heterozygosity into account, because if both samples are heterozygous, they will not appear in either of the H sets and will therefore (appropriately) not be included in $W_i^{\left(2\right)}$. However, if either sample is heterozygous and the other is homozygous, the exclusive-or operator will return the site and it will appear in the $W_i^{\left(2\right)}$ set.

General IBD regions can include sub-regions that are either IBD2 or IBD1, and as such, the algorithm separates the IBD2 segments from the IBD1 regions before it produces output. If a putative IBD2 region is above the IBD2 marker count and length thresholds, the method considers it to be real. However, if the region does not meet these thresholds, IBIS can still infer a larger IBD segment containing a rejected IBD2 region as IBD1 if the full segment meets the length and marker count criteria for a standard IBD segment. IBIS also infers regions of IBD that flank an inferred IBD2 segment as IBD1 regardless of their length, as the IBD2 segment lends support to their being real.

Filter for Segments that Span Gaps in Marker Coverage

In order to filter out IBD segments in regions that have unrealistically high sharing rates—which tend to include locations where a few adjacent SNPs are separated by sizable genetic distances—we added a maximum SNP distance parameter. When using this option, IBIS stores an internal genetic map where the distances between SNPs are capped at the user-supplied parameter value, thus imposing a maximum SNP distance and reducing the internally stored length of some segments. This filter is effective, though it can lead to reduced sensitivity (Results), so it is disabled by default. IBIS always prints segments with genetic positions taken from the input genetic map but bases its decisions for whether a segment is sufficiently long on the reduced, internal map positions.

IBIS Implementation

We implemented IBIS in C++, including support for multithreading, and released it with open source (Web Resources). IBIS reads PLINK binary ped format⁴ (i.e., bed, bim, and fam files), which uses two bits to store each genotype, and it outputs IBD segments using either a human-readable text format (with optional gzip compression) or a smaller binary format.

One of the main optimizations underlying IBIS’s speed is that it uses bit-level parallelism such that all set operations apply to 64 markers simultaneously. Specifically, the method stores any set for a given window as a single 64-bit value, where each bit represents one marker and a bit value of 1 indicates set membership. In this formulation, set union takes the form of a bitwise OR—yielding ones for all bits that are nonzero in either of two sets—while set intersection takes the form of bitwise AND—returning ones only for bits that are nonzero in both sets. This bit-level encoding also allows efficient bitwise counting of the number of inconsistent markers in the W sets using the popcount instruction available on most modern Intel CPUs.

Relatedness Classification

After inferring IBD1 and IBD2 segments for a pair, IBIS calculates their kinship coefficient as $\phi =\left(1/4\right)k^{\left(1\right)}+\left(1/2\right)k^{\left(2\right)}$, where k⁽¹⁾ and k⁽²⁾ are the fractions of their genome (from cM genetic lengths) in IBD1 and IBD2 segments, respectively. It then maps these coefficients to degrees of relatedness using the same bounds as KING.^5,6 When using IBIS to call only generic IBD segments, it utilizes the IBD0 fraction k⁽⁰⁾ to classify relatives using bounds also specified by the KING authors.^5,6 This yields similar results to using the distinguished segment types (Results), including for differentiating first and second degree relatives.

For analyses of algorithms other than IBIS, we calculated kinship coefficients φ using the IBD segments they each inferred and then mapped these coefficients to degrees of relatedness as described above. One exception is KING, which does not infer IBD segments, and we used the kinship coefficients from its output to infer relatedness degrees. We derived genetic positions for the inferred segments from their physical positions based on either the genetic map we used to simulate²⁹ (for the simulated data; below), or from the HapMap2 map³⁰ (for the SAMAFS data).

By default, IBIS infers segments that are ≥7 cM long, which means that for more distant relatives, it does not detect some number of real (shorter) IBD segments. This affects the inference of degrees of relatedness, and, in order to help in this classification, we add a factor of 0.00138 to the kinship coefficient (roughly 18–20 cM of additional IBD1 length) for each pair, and an equivalent factor for k⁽⁰⁾-based analyses. This represents one-quarter of the size of the interval KING uses to classify sixth degree relatives.^5,6 Our empirical results in both simulated and real data suggest that this is an effective way to account for missing segments (Results). This choice may not be optimal for all settings (such as inputs with much higher or lower marker counts) and is a user-modifiable parameter.

Accuracy and Runtime Tests with Simulated Data

To evaluate IBIS’s accuracy for relationship classification, we used Ped-sim³¹ v.0.99.3 to simulate 4,000 pairs of first cousins (in two batches of 2,000 pairs) and 4,000 pairs of second cousins (in four batches of 1,000 pairs). We retained the default genotyping error and missingness rates of 10⁻³ per site and utilized both sex-specific genetic maps²⁹ and crossover interference modeling^32,33 in the simulations. We provided Ped-sim a set of European-descent samples³⁴ to serve as founders, which were phased²¹ with Beagle³⁵ 4.1 (8 June 2017 release). Prior to phasing, these data were quality control filtered as previously described.²¹ In brief, samples and SNPs were filtered to those used in the original study,³⁴ and SNPs that failed a test of Hardy-Weinberg equilibrium (p < 10⁻⁵) or had >5% missingness were removed. Further, to prevent close relationships among the founders, samples were filtered to be no more closely related than fifth degree. The final dataset input to Ped-sim comprises 8,955 individuals genotyped at 462,828 SNPs. We analyzed the simulated samples using IBIS v.1.19, KING⁵ v.2.2.3, and TRUFFLE²⁸ v.1.38. KING requires LD filtered markers, and we used PLINK⁴ version 1.90b5.4 with the option --indep-pairwise 1000 25 0.25 in order to filter.

The options we used to run each algorithm for the above simulated and the real data analyses are in Table S1. We used IBIS’s default plain text output format for all analyses except for the UK Biobank runtime test (below).

To perform runtime analyses, we again used Ped-sim to simulate samples with a mix of different relationship types in proportions resembling a natural distribution of relationship degrees. This dataset contains a total of 4,500 samples built out of 1,500 families, each with three individuals: two unrelated (nth great-) grandparents that are the ancestors (a couple) of a third individual. More specifically, the dataset includes 25 families containing two second degree relatives (two grandparents and one grandchild), 200 families with two third degree relatives, 800 with fourth degree relatives, and 475 families with fifth degree relatives. We used the same Ped-sim settings as those for the accuracy evaluation. To check the runtime performance on different sized inputs, we randomly sub-sampled the resulting dataset to 100, 500, 1,000, 2,000, and 3,000 individuals. We timed the performance of IBIS, KING, and TRUFFLE, and the runtime for phasing with Beagle 5 (12 July 2019 version) followed by IBD detection with either Refined IBD¹¹ (16 May 2019 version) or GERMLINE¹² v.1.5.3.

For our comparative runtime analyses, we used machines with four Xeon E5 4620 2.20 GHz processors and 256 GB RAM. We also restricted all algorithms to one full core (two hyperthreaded cores) to ensure the times are not inflated by the overhead of thread management or non-parallel steps. To get an accurate estimate of each program’s runtime on the shared compute cluster we used for testing, we ran each program except KING and Beagle 10 times on data for each chromosome. We then calculated an average of the three lowest of these times and report the total time as the sum of the per-chromosome averages. KING analyzes data from all chromosomes jointly, so we performed 10 tests of it using data from all the autosomes, and we again report the average of the three lowest times. For Beagle, we performed three tests per chromosome, and for the tests of 1,000 individuals or greater, if one run was >20% slower than the other two, we ran another trial. We report Beagle’s time as the average runtime of the resulting three runs, summing these averages over the autosomes. All runtimes we report are wall clock times.

In order to test the quality of the output IBD segments from each method, we simulated a similar dataset to the one for the runtime analyses but added 10 more families with first degree relationships (two parents and their child) for additional long segments. This dataset totals 4,530 samples, and we phased these jointly using Beagle 5 for input to Refined IBD and GERMLINE. We overlapped the called segments from each algorithm with the Ped-sim true segments and calculated quality metrics for segments with lengths in each of the following segment size bins: [1 cM, 3 cM), [3 cM, 5 cM), [5 cM, 7 cM), [7 cM, 10 cM), [10 cM, 13 cM), [13 cM, 15 cM), [15 cM, 20 cM), [20 cM, $\infty$).

One quality metric we measured for each algorithm is its positive predictive value (PPV),³⁶ the fraction of the total length of all inferred IBD segments (within a given length bin) that overlap any true segment of any size. Another metric is sensitivity, or the fraction of the total length of all true IBD segments (in a length bin) that an algorithm calls as identical by descent, considering all called segments of any size. These calculations include segments inferred as either IBD1 or IBD2 for algorithms that make this distinction, though we treat these as generic IBD segments for this analysis, and we merge them into one contiguous region when they are immediately adjacent. Note that for the PPV metric, we assign segments to length bins based on their inferred length, which need not correspond to the same bin as the true segments these overlap; at the same time, for sensitivity, we map segments to bins according to their true lengths. Besides PPV and sensitivity, we calculate the distances between the called and the true segments’ start and end points, reporting the means and standard deviations of these quantities for each algorithm. Additionally, when two or more inferred segments overlap one contiguous true segment, we calculated the mean size of the gaps between the adjacent called segments, and we report the fraction of true segments that have any inferred gaps.

Lastly, we further evaluated IBIS on data with 611,324 SNPs to determine its inference accuracy at this higher SNP density. To that end, we generated a set of 1,000 pairs of double cousins via Ped-sim using an input set of 13,686 genotyped samples. We used this to test IBIS’s PPV and sensitivity for generic IBD segments (the union of true IBD1 and IBD2 regions) and for IBD2 segments only. To obtain the Ped-sim input samples, we used Eagle³⁷ 2.4 to phase 62,508 UK Biobank samples consisting of (1) 50,000 samples that are more distant than third degree relatives of each other¹ and evenly distributed across 174 territorial (NUTS3) regions; (2) a subset of the parent-child pairs from the full sample; (3) individuals either born near the Bristol assessment center or in NUTS3 regions with low population density (<150 individuals per km²) and who have at least one genotyped third degree relative; and (4) samples born in NUTS3 regions with low population density and whose distance from their place of birth to place of residence (POB-POR) is ≤20 km. The subset of 13,686 individuals we used to simulate are those with a POB-POR distance of >20 km and who KING infers as having a more distant than fifth degree relationship with each other. After phasing, we filtered the genotypes of these samples to those with minor allele frequency (MAF) >0.005 (note that Eagle performs internal SNP filters that applied to this set of markers).

Accuracy and Runtime Tests with Real Data

To perform accuracy comparisons in real data, we used genotypes from the SAMAFS^{25, 26, 27} (dbGaP:phs000333.v1.p1, phs000462.v1.p1) in which quality control filtering was carried out previously.^{25, 26, 27,38} The filters are fairly detailed and included mapping SNP probe sequences to GRCh37. Following this, we removed SNPs with greater than 2% missing calls, and individuals with more than 10% missing sites. The full set consists of 2,485 individuals genotyped at 521,184 SNPs. Table 1 lists the numbers of pairs of individuals self-reported to have degrees of relatedness ranging from first to sixth in this dataset, and the number of pairs without a reported relationship and assumed unrelated, which constitute the target relationships for our analysis. (We also included 73 pairs labeled as seventh degree relatives in the “unrelated” class and five reported monozygotic [MZ] twin pairs as first degree relatives.) As in prior work,²¹ we excluded 2,618 pairs of individuals with evidence of bi-lineal relatedness even though they are reported as related through one lineage. In these data, we compared the rate at which a program correctly detects each pair’s reported degree of relatedness using IBIS, Refined IBD, KING, GERMLINE, and TRUFFLE. (IBIS classifies MZ twins as degree zero relatives, but we consider these as first degree pairs for this analysis.) Although the SAMAFS relationships are self reported, the pedigrees have undergone substantial quality control checks in prior work.^{25, 26, 27} Nevertheless, some discrepancies may remain, and we conducted an analysis of reported first and second degree pairs the tools consistently misclassify.

Table 1.

Counts of Pairs Reported to be First through Sixth Degree Relatives in the SAMAFS Genotype Data

Degree	Count of Pairs
First	4,969
Second	6,625
Third	8,241
Fourth	7,636
Fifth	3,794
Sixth	818
Unrelated	3,051,669

The unrelated pair count includes pairs with no reported relationship and seventh degree relatives, and the first degree pairs include reported monozygotic twins. These counts follow after the quality filters described in Material and Methods.

To assess the potential for running IBIS on massive datasets, we also ran it on the SNP array data from chromosome 2 of the UK Biobank¹ using 16 threads. This analysis used IBD2 detection, binary output format, and a maximum SNP distance of 0.12 cM. The server we used has four Intel Xeon E5 4620 v2 2.60 GHz processors and 512 GB RAM, had no other processes running during the test, and stored the input/output data on a solid-state drive. The analysis comprised 50,265 markers following filtering out of sites with MAF <0.005 and SNPs not used in the original phasing of the data.¹ We scaled the resulting wall clock time to estimate the time to perform autosome-wide IBD detection in the UK Biobank assuming linear scaling in number of markers, and we report times for running using 128 threads.

Results

We analyzed the ability of IBIS and several other methods to infer degrees of relatedness among sample pairs using both simulated and real data, where the simulated individuals are formed from European-descent samples³⁴ (Material and Methods). All the methods we evaluated are well tuned to handle such data. In contrast, the real relatives are drawn from the SAMAFS and comprise admixed Mexican American samples that can confound some methods for inferring relationships.⁶ Besides relationship classification, we also measured the quality of the IBD segments each tool generates, considering their PPV and sensitivity (Material and Methods) and also the inferred segment breakpoints compared to the true starts and ends.

Relationship Inference Accuracy in Simulated Data

We initially compared IBIS, KING, and TRUFFLE using simulated first and second cousins (third and fifth degree relatives, respectively), with a total of 4,000 pairs for each relationship type. We did not include Refined IBD or GERMLINE in this analysis to avoid issues of phasing in slightly low sample sizes—the 4,000 second cousins are divided into four batches of 1,000 pairs each. However, we did compare to the true IBD sharing rates for each pair, which is provided by the simulator. KING analyzes the genotypes of each pair of samples at each site to infer the expected proportion of their genome two samples share IBD. This statistic—while derived from a formula that uses allele frequencies—does not in fact directly incorporate allele frequencies and therefore avoids potential biases arising from incorrect allele frequency estimation⁵ (e.g., in the presence of cryptic relatives or samples from multiple populations). On the other hand, TRUFFLE detects segments in a similar way to IBIS, considering the number of identical by state genotypes that occur at successive positions while also accounting for potential genotyping errors.²⁸

Figure 2 shows the fraction of relative pairs that each of the methods classifies as one of several degrees of relatedness, including classification using the true IBD segments. The results for TRUFFLE use non-default options (Table S1) as its default settings underperform due to low sensitivity for segments <20 cM long (see below). Despite perfect information in the true IBD sharing data, not all pairs’ realized kinship coefficients map to the simulated degree of relatedness, particularly for the fifth degree relatives. This is due to the stochastic nature of IBD sharing: the ranges of kinship coefficients overlap between relatedness degrees.

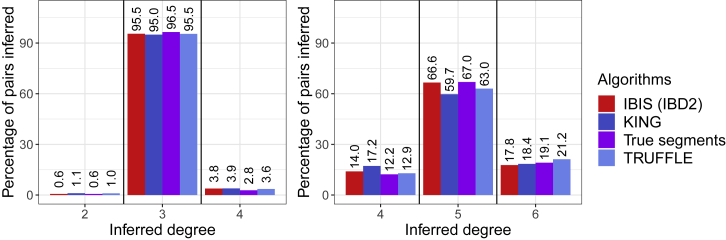
Figure 2.

Rates of Classifying Simulated Third (left) and Fifth (right) Degree Relatives to Various Degrees of Relatedness

Third degree relatives shown on left; fifth degree relatives shown on right. Includes rates from IBIS (with IBD2 detection), KING, the true IBD segments generated by the simulator, and TRUFFLE. The center set of bars in each plot represent correct inference, and the set of bars to the left and right represent inferring one degree closer and one degree more distant than the truth, respectively.

Considering first cousins, IBIS, TRUFFLE, and KING correctly infer 95.5%, 95.5%, and 95.0% of pairs as third degree relatives, respectively, or are fairly comparable to one another. These inference rates are somewhat below the 96.5% obtained using the true IBD segments. For second cousins, the performances are more distinct, with IBIS, TRUFFLE, and KING classifying 66.6%, 63.0%, and 59.7% of these pairs as fifth degree relatives, respectively. KING’s reduced accuracy for classifying these relatives may be due to its use of only independent markers instead of the IBD segments IBIS and TRUFFLE use. Overall, IBIS performs well, with a classification rate for fifth degree relatives close to the 67.0% rate using the true IBD segments.

IBIS Segment Calling Accuracy in Simulated Data

Using simulated data consisting of relatives ranging from first to fifth degree (Material and Methods), we created a truth set of IBD regions and analyzed the quality of the segments IBIS infers within these relative pairs. This analysis also includes any IBD segments IBIS detects between the unrelated parent/great-grandparent couples in a given family (1,510 pairs out of the 4,530 pairs analyzed), which we treat as false. We consider the PPV and sensitivity metrics, which form a trade-off in terms of the portion of the segments IBIS calls that are true (PPV) and the portion of the true segments that it infers as identical by descent (sensitivity) (see Material and Methods).

Our first analysis explores IBIS’s performance across a range of parameterizations in order to determine recommended settings. Figure S1 plots the PPV and sensitivity of the segments IBIS infers for different combinations of its minimum segment length and marker count options, subdivided across several segment length bins. The PPVs for segments shorter than a given minimum segment length—which IBIS will never infer—are always 1, as lack of any false segments of these sizes trivially gives optimal PPV. The sensitivity for 1–3 cM segments is poor, even for input parameterizations that detect such segments, as IBIS requires segments to start in a window without errors, and in such small segments, a window with an error may represent a large fraction of its length. In the next 3–5 cM bin, IBIS’s sensitivity can be far better (up to 0.72), but for the settings that achieve sensitivity above 0.50, the PPV remains too low (0.17–0.28) to justify meaningful attempts at inference. For the 5–7 cM bin, lower minimum segment lengths recover a fair number of regions (0.61–0.85 sensitivity with a 3 cM minimum, and 0.57–0.74 for a 5 cM minimum), but to be capable of this, the highest PPV is only 0.85, which can lead to overestimated relatedness.

For true segments ≥7 cM long, running IBIS with short minimum segment lengths (i.e., 1–5 cM) consistently yields higher sensitivity than longer minimums, but this has the drawback of poor PPV for shorter segment lengths. A 7 cM minimum segment length produces good PPV and sensitivity for these longer segments. Turning to the minimum marker count option, the performance is most differentiated in the 7–10 cM window. There, a minimum of 448 markers represents a slightly better PPV (0.93) than 384 markers (0.91), with only slightly reduced sensitivity (0.80 versus 0.81, respectively). We conclude that using IBIS with a minimum segment length of 7 cM and a minimum marker count of 448 produces ≥7 cM segments of high quality. These are the default parameter values that IBIS adopts, and which we used for all other analyses (including that of Figure 2).

We also evaluated the PPV and sensitivity of IBIS under varied settings of its error threshold parameter (Figure S2). This analysis uses the default minimum segment length and marker counts identified above, and with these defaults, IBIS detects few 1–7 cM segments, so the error threshold parameter makes relatively little difference in the corresponding bins. For segments ≥7 cM long, a pattern emerges in which an error threshold of 0.004 is at or near the most balanced value in terms of trading off PPV and sensitivity. This represents a compromise that has reasonable performance for both metrics, and we therefore chose this as the default for IBIS.

We experimented with IBIS’s performance when employing maximum SNP distances as well (Material and Methods; Figure S3). This parameter has the greatest effect on PPV and sensitivity for segments of sizes near the minimum length threshold (7 cM). In particular, for any of a range of values of this parameter (0.27–0.07 cM), the sensitivity for 7–10 cM segments decreases (losses from 0.02 to 0.36). However, the benefit to using this option is in terms of PPV, and while the PPV values in this analysis improve only modestly (a gain of 0.02 PPV in the 7–10 cM bin for all maximum SNP distances we tested), the number of segments inferred between members of different families improves more substantially (39%–91% of between-family segments removed, considering all segment lengths).

When presented with a higher density SNP set (611,324 markers versus 462,828 for the other analyses), IBIS’s sensitivity under its default settings improves across all ≥7 cM segment length bins (Figure S4; Material and Methods). For example, in the 7–10 cM bin, IBIS has a good PPV of 0.93 and also a high sensitivity of 0.96. For each successively larger segment length bin, IBIS’s PPV and sensitivity both improve slightly, and in the largest ≥20 cM long bin, its PPV is 0.99 and its sensitivity is 1.0.

Figure S5 shows the results of an additional analysis of IBIS’s performance using this higher density data, this time considering only true and inferred IBD2 segments, in order to determine the quality of IBIS’s IBD2 segment inference. Due to greater information provided by the IBD2 signal, we tested lower minimum thresholds for both the marker count and segment length parameters. Varying these parameters results in very little noticeable effect in bins with segments ≥5 cM, which have PPVs ranging from 0.99 to 1.0 and sensitivities from 0.91 to 0.98. For shorter length bins, lower minimum length thresholds produce increased sensitivity, with comparatively little penalty to the PPV. For the 1–3 cM bin, IBIS’s sensitivity is between 0.04 and 0.54, with high PPVs of 0.95–0.99, and for 3–5 cM segments, the sensitivity varies from 0.78 to 0.87, with PPV remaining high at 0.99. We chose a default minimum segment length of 2 cM and a marker count minimum of 192 for IBD2 segments, resulting in sensitivities of 0.33 and 0.86 for the 1–3 and 3–5 cM bins, and PPVs of 0.97 and 0.99 for these bins, respectively. The uniformly high PPVs over the range of parameters are such that users may wish to reduce these thresholds in order to improve sensitivity. Lastly, we set the default error rate threshold within IBD2 segments to 0.008, which is double the generic IBD segment value; we found that this produces a good trade-off between sensitivity and PPV (not shown).

Segment Calling Accuracy Comparison between Methods

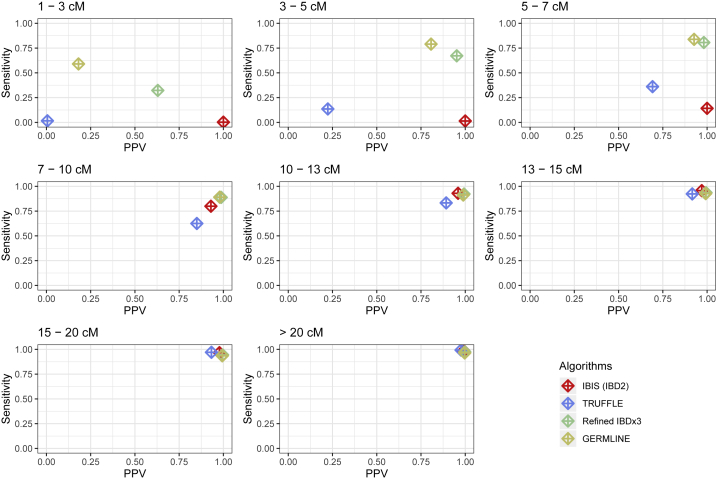
To put IBIS’s segment quality in perspective, we plot its PPV and sensitivity together with that of the other methods we tested in Figure 3, again reporting metrics within bins of cM lengths. These results are from the lower SNP density dataset and include segments detected in its first through fifth degree relatives and the unrelated ancestral couple of each family, as before. Considering the 1–3 cM bin, Refined IBD×3 (i.e., three independent runs of Refined IBD, the author recommendation) and GERMLINE have limited sensitivity and low PPV (sensitivities of 0.32 and 0.59, respectively; PPVs of 0.63 and 0.18, respectively), while TRUFFLE infers very few segments in this range (average of 0.027 segments per pair) that are of poor quality (sensitivity 0.02; PPV 0.01). IBIS does not attempt to infer <7 cM long segments, yielding PPVs of 1.0 for segment of these sizes, and sensitivities near 0.0 for 1–5 cM segments, but slightly higher at 0.14 for segments with true lengths of 5–7 cM. Refined IBD×3 has better sensitivity at 0.67 and 0.81 for the 3–5 cM and 5–7 cM bins, respectively, and high PPVs of 0.95 and 0.98 for these bins, respectively. GERMLINE also has high sensitivity at 0.79 and 0.84 for the 3–5 cM and 5–7 cM bins, respectively, and fair to good PPVs of 0.81 and 0.93, respectively. These results highlight the utility of methods that leverage phased data, which are likely to continue to be useful for detecting IBD segments of these moderate sizes. In turn, TRUFFLE, the most comparable method to IBIS in its approach, is more sensitive than IBIS in these two bins (0.13 and 0.36, respectively), but its PPVs for the bins are low at 0.22 and 0.69, respectively.

Figure 3.

PPV and Sensitivity of IBD Segments for the Tested Methods, Subdivided across Several Bins of Segment Lengths

We calculate PPV using segments that have an inferred length within a given bin and sensitivity using segments that have a true length within a given bin (Material and Methods).

Turning to segments ≥7 cM long, IBIS performs comparably to Refined IBD×3 and GERMLINE, with a slightly lower PPV (IBIS PPV 0.93–0.99 for 7–20 cM segments compared to 0.99–1.0 using Refined IBD×3 and 0.98–1.0 in GERMLINE) and, for segments ≥10 cM long, slightly higher sensitivity than these methods (IBIS sensitivity 0.93–0.99 for 10–20 cM segments compared to 0.92–0.97 with Refined IBD×3 and 0.89–0.96 in GERMLINE). GERMLINE has the highest sensitivity of all methods for the 7–10 cM bin, outperforming IBIS and Refined IBD×3 (0.891 compared to 0.799 by IBIS and very slightly higher than the Refined IBD×3 value of 0.888). By comparison, TRUFFLE has lower PPV (0.85–0.92) and sensitivity (0.62–0.93) for 7–15 cM segments (Figure 2). However, its sensitivity and PPV are high for segments ≥15 cM long, with slightly higher sensitivity than the other methods (0.97–1.0), though the lowest PPV of these approaches (0.93–0.98).

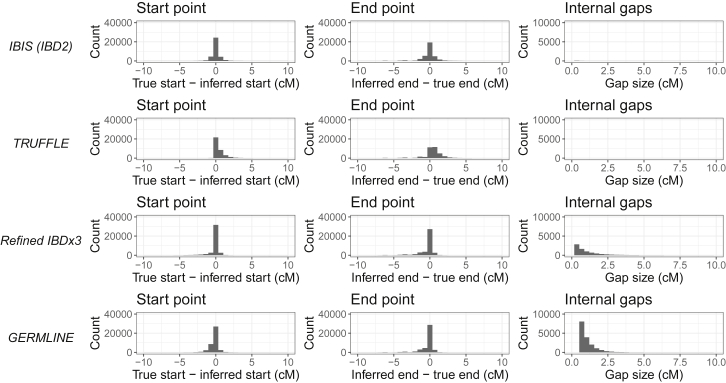
We further evaluated the quality of the inferred segments by calculating the difference between their true and inferred start and end positions and also the sizes of any internal gaps of non-detected IBD regions within a true segment (i.e., between two inferred segments that overlap one true segment). Figure 4 shows the distributions of these quantities for each of the algorithms. All methods have a peak near 0 for the distance between the true and inferred start and end positions, but their mean values differ from this ideal. In particular, TRUFFLE tends to infer segments that start physically before and end physically after the true segment bounds, with positive differences between the inferred and true start and end points that average 0.68 cM for both directions, and standard deviations of 3.7 and 3.8 cM, respectively. Refined IBD×3 and GERMLINE, by contrast, under-call starts and ends, with Refined IBD×3 inferred starts and ends averaging −0.14 and −0.22 cM from the true values, respectively, and GERMLINE’s corresponding average distances being −0.23 cM and −0.33 cM, respectively. GERMLINE’s start and end point standard deviations are 0.69 and 1.1 cM, respectively—the lowest of the algorithms—while Refined IBD has corresponding standard deviations of 0.92 and 1.2 cM. IBIS has a fairly balanced distribution, with mean start and end distances of 0.04 and −0.13 cM, respectively, and somewhat higher standard deviations than Refined IBD and GERMLINE at 1.5 and 1.6 cM for start and end positions, respectively.

Figure 4.

Distances between the True and Inferred Segment Start and End Positions and the Sizes and Numbers of Gaps between Inferred Segments that Span a Contiguous True IBD Interval

With regards to gaps between inferred segments that overlap a contiguous true segment, TRUFFLE performs optimally, having no gaps among all segments it detects that overlap a true segment. IBIS does produce internal gaps, but only 0.35% of the true segments it detects have one or more inferred gaps, with a mean gap size of 0.47 cM. Refined IBD×3 is known to infer many broken up segments that cover one large segment,³⁶ and the fraction of broken up true segments we observe is high at 46.4%; despite this, their mean gap size is the smallest, at 0.30 cM. Under the settings we used, GERMLINE infers gaps in 59.4% of true segments, with a mean gap size of 0.46 cM.

We also tested GERMLINE under two additional settings, first with its genotype extension mode, wherein it initially locates potential IBD segments via identical haplotypes in a window (as in all settings), and following this, it extends these regions across adjacent identical by state genotypes (the latter being similar to IBIS). In this mode, GERMLINE produces segments with no internal gaps that are over-called in length, i.e., with segment properties similar to TRUFFLE (Figure S6). This approach yields very poor PPV, but, as might be expected, the highest sensitivity of all the approaches presented (Figure S7). Nevertheless, such low PPVs make this setting untenable, though note that we used GERMLINE’s default minimum segment length of 3 cM, and increasing this is likely to improve the results. The other setting we tested is the default haplotype extension mode, which has lower sensitivity in long segment bins by comparison to -haploid mode (Figure S7). We chose -haploid for all other GERMLINE analyses due its superior performance in relationship inference (not shown).

Furthermore, as noted above, we found that TRUFFLE’s relationship classification performance was poor using its default settings (not shown), so we examined the effect of varying its sensitivity threshold L and of filtering the input markers. As shown in Figure S8, setting L to 0.5 improves its sensitivity for <20 cM long segments, and this also leads to improved relatedness classification results. On the other hand, filtering markers significantly decreases TRUFFLE’s sensitivity with little to no improvement in its PPV, as shown in Figure S9. In fact, the non-default option that disables TRUFFLE’s internal marker filters markedly improves its sensitivity. Given these findings, we set TRUFFLE’s sensitivity parameter L to 0.5 and disabled its marker filters in all other analyses (including all figures in the main text; Table S1). Notably, TRUFFLE’s runtime (below) makes it less competitive with IBIS, so we did not further test its performance.

Runtime Comparisons

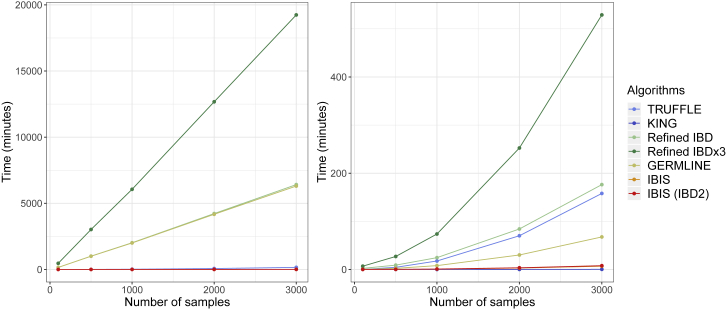
We benchmarked the runtime of the methods using a simulated set of 4,500 European-descent samples that contains 3,000 second through fifth degree relative pairs (Material and Methods). Refined IBD and GERMLINE require the input data to be phased, and we used Beagle 5 to perform phasing.

Figure 5 depicts the runtimes for analyzing random subsets of the 4,500 individuals ranging in size from 100 to 3,000 samples using IBIS, IBIS with IBD2 detection, Refined IBD, Refined IBD×3, GERMLINE, and TRUFFLE. For the set of 100 samples, IBIS runs in 1.3 s, and IBIS including IBD2 detection runs in 1.4 s. In turn, TRUFFLE requires more time at 12.8 s. The other two methods need the input data to be phased, and Beagle 5 takes 152.2 min to run on these 100 samples, which far exceeds the runtime of any of the individual IBD detection methods. Ignoring this prerequisite time, Refined IBD itself takes 2.3 min, while performing three independent runs of Refined IBD requires triple this amount of time and also requires three separate runs of Beagle with different random seeds. GERMLINE completes this inference in 14.0 s, which is slightly longer than TRUFFLE, but also requires phased data. KING, which does not detect IBD segments, runs in only 0.04 s.

Figure 5.

Runtimes of IBD Segment Detection Algorithms on Subsets of 4,500 Simulated Individuals

Left plot includes the runtime for Beagle for methods that require phased data, and the right omits this time.

On the set of 3,000 individuals, IBIS requires only 6.8 min to complete, and using IBD2 detection, 7.8 min. These times are considerably faster than TRUFFLE, which takes 2.6 h to finish when run without filtering the input markers (corresponding to a 20.2–23.3× speedup by IBIS), whereas filtering speeds this up slightly to 2.4 h. Here again, the time to phase the samples dominates the total runtime of both Refined IBD and GERMLINE, as it takes 4.3 days to perform one run of Beagle. Without accounting for the phasing time, Refined IBD still requires 2.9 h to finish, or 22.5–26.0 times longer than IBIS. Also ignoring the time to phase, GERMLINE requires 1.1 h to complete in this sample. The fastest method is again KING, at 16.8 s.

In total, considering the time to phase the 3,000 samples, IBIS and IBIS with IBD2 detection are 946 and 819 times faster, respectively, than one run of the combined Beagle 5 and Refined IBD times. This highlights the great efficiency gains inherent in IBIS’s approach. When running Refined IBD×3, these speedups each increase 3-fold. The time comparisons with GERMLINE including phasing are similar, with IBIS being 805–930× faster.

As a proof of concept in a large dataset, we ran IBIS with IBD2 detection on the SNP array genotypes from chromosome 2 of the UK Biobank. Parallelized across 16 cores, the wall clock time required to process this chromosome is 2.1 days. Given this, we estimate that, when parallelized across 128 cores, IBIS will complete an analysis of the 626,997 autosomal genotypes (following filtering) in only 3.3 days. IBIS’s memory footprint for this analysis is low at 8.9 GB, and, because this chromosome has the most markers, analysis of the other chromosomes will require less memory. Thus IBIS enables IBD detection in biobank-scale samples using resources available on a moderate compute cluster.

Relatedness Classification in the Real SAMAFS Pairs

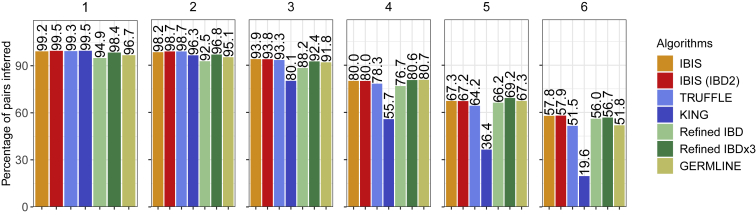
Finally, we evaluated the accuracy of IBIS and the other methods in classifying real relatives from the SAMAFS pedigrees, with inference rates for reported first through sixth degree relatives shown in Figure 6. All algorithms perform well at inferring first degree relationships, with IBIS (IBD2 enabled), TRUFFLE, and KING correctly inferring 99.5% of these pairs. IBIS (without IBD2) also has a high classification accuracy of 99.2% first degree relatives correctly detected, but, lacking IBD2 information, its inference rates are slightly reduced. Refined IBD×3 comes next at 98.4% of first degree pairs detected, and Refined IBD and GERMLINE correctly detect 95.3% and 96.7% of these pairs, respectively. The algorithms follow a similar trend for classifying second degree relatives, with 98.2%–98.7% of pairs inferred correctly by IBIS with IBD2, IBIS, and TRUFFLE. Refined IBD×3 and KING have slightly lower accuracy for these relatives, correctly classifying 96.3%–96.8% of pairs. Standard Refined IBD and GERMLINE perform poorer here, with respectively 93.2% and 95.1% of these pairs correctly classified.

Figure 6.

Rates of Classifying the Real SAMAFS Relatives to Their Reported Degree of Relatedness, Subdivided by This Degree

Includes output from IBIS with and without IBD2 detection, combined segments from three independent runs of Refined IBD (Refined IBD×3), and other methods, as indicated.

Notably, a prior analysis using an older version of Refined IBD on these same SAMAFS individuals had better results than those in this evaluation.⁶ At that time, Refined IBD was incorporated into a single program with Beagle 4.1 and may have had access to a more complete phasing model that improved its detection. GERMLINE’s current results are also distinct from that analysis, with lower performance for close relatives but slightly better or comparable classification rates for third through sixth degree pairs. Further analysis is needed to understand the source of these differences, which may stem from the updated Beagle 5 phasing model.

We analyzed pairs of first degree relatives that are consistently inferred as a different degree by all the algorithms to determine whether the pedigree relationships may be mislabeled. Overall, 23 of the first degree pairs are mis-inferred by all methods, and each of these pairs are reported to be full siblings. IBIS detected few or no IBD2 segments between these pairs, and this, coupled with the fact that IBIS infers their IBD1 sharing fractions to be between 43% and 63%, imply that these samples may truly be half-siblings. KING, IBIS with IBD2, and TRUFFLE are discrepant on a small number of pairs, as KING infers only the common 23 pairs as second degree relatives; IBIS with IBD2 infers one additional pair as second degree (a reported full sibling pair whose IBD2 sharing rate is only 8.5%); and TRUFFLE calls ten additional pairs as second degree relatives (reported full sibling pairs with IBD2 rates from IBIS of 10%–22%). Refined IBD and GERMLINE each infer >100 first degree pairs as more distant degrees.

There are also a set of 12 second degree pairs that IBIS (with IBD2), TRUFFLE, and KING each infer as first degree relatives. Of these, nine have 10%–30% IBD2 sharing, although they are labeled as half-siblings. Some of these pairs may be full siblings or may be three-quarter siblings.⁶ An additional two of these pairs are labeled as avuncular but share nearly 100% of their genome IBD1, consistent with parent-child pairs. These miscategorized avuncular pairs involve two full siblings and the same reported aunt, so represent the same signal, and although we lack genotype data for the reported mother, the aunt may be her monozygotic twin. Each of these methods infers a total of 13 reported second degree pairs as first degree relatives, with IBIS (IBD2) and TRUFFLE agreeing on these inferences, and KING detecting one pair as first degree that IBIS and TRUFFLE do not (for a total of two pairs discrepant between IBIS and KING).

Overall, these results suggest that the SAMAFS relationships may be mis-labeled for 23 first degree pairs and 10 second degree pairs (excluding the noted two avuncular pairs) based on support from multiple methods. Still, we retained the original labels for the analyses in this work.

Returning to the evaluation of relatedness inference across methods, for third degree and more distant relatives, KING’s performance is considerably diminished compared to other approaches. As noted earlier, the SAMAFS are composed of admixed Mexican American samples wherein admixture LD has the potential to confound methods that rely on independent SNPs for analysis. These results underscore the utility of IBD segments for relatedness classification in admixed samples, as the other methods we analyzed have higher classification rates that are more comparable to each other. Notably, KING performs much better in simulated unadmixed (European-descent) first and second cousins than in these admixed samples (Figure 2).

IBIS and IBIS with IBD2 detection perform the best among the methods we considered for third degree relative inference, detecting 93.8%–93.9% of these pairs, whereas TRUFFLE infers 93.3% and Refined IBD$\times$3 identifies 92.4%. For fourth through sixth degree pairs, the classification rates of IBIS and IBIS-IBD2 are within 0.0%–2.0% of those of either of the Refined IBD procedures. These slight accuracy reductions likely stem from the fact that IBIS identifies only segments ≥7 cM long. Surprisingly, Refined IBD×3 has lower accuracy than Refined IBD for sixth degree relatives; however, these current Refined IBD×3 classification rates are below those of from tests that used an older version of the tool.⁶ As in the analysis of simulated relatives, TRUFFLE’s performance is lower than the other IBD segment-based methods for classifying fourth through sixth degree pairs, which is possibly an artifact of its low PPV and sensitivity for 3–13 cM segments (Figure 3).

A final factor is the false positive rate, or the rate at which each method classifies unrelated pairs as related. Figure S10 shows these rates, specifically how often each method calls unrelated pairs as third through sixth degree relatives. KING infers 0.5% of the pairs as fifth degree relatives and 2.1% as sixth degree, suggesting lower reliability for inferred pairs of these degrees. In turn, GERMLINE over-calls 2.3% of unrelated pairs as having a sixth degree relationship. Both Refined IBD×3 and Refined IBD infer 0.2% of unrelated samples to be sixth degree relatives; this is higher than the rates from TRUFFLE and IBIS, which infer only 0.1% of these pairs as sixth degree relatives.

While not shown here, we also tested IBIS’s relationship classification scores using a maximum SNP distance of 0.12 cM. This option produces the same correct first degree inferences as the default, and the proportion of correctly detected unrelated pairs also does not change up to the level of our reported significant figures. However, under this setting, IBIS’s rates of detecting relationships, in order from second to sixth degree, decrease marginally, by the following quantities: 0.03%, 0.27%, 0.14%, 0.11%, and 0.01%, respectively. This is a result of its reduced sensitivity for 7–10 cM segments when using this option (above and Figure S3).

Overall, IBIS’s rates of classifying relatives to their reported degree are high, with low rates of miscalling unrelated pairs as related. As its runtime is several orders of magnitude lower than combined phasing and either Refined IBD or GERMLINE segment detection (Figure 5), IBIS is attractive to apply in order to detect relatives. Notably, IBIS also has better accuracy than KING, a method that was previously used to detect first through third degree relatives in the UK Biobank.¹ We anticipate IBIS will find utility in large datasets and that the need for fast methods will increase as genetic datasets continue to grow in size.

Discussion

Detecting IBD segments is a long-standing problem in population genetics,³⁹ with some of the most popular methods currently available either phasing samples themselves or requiring prephased data to perform inference. When the phased haplotypes are of good quality, these methods have access to precise information with which to resolve segments. However, this added information comes at the cost of substantial amounts of computation time.

We presented IBIS, an algorithm that does not require phased data to detect IBD segments and that reliably and efficiently locates long segments (Figures 3 and 5). For the purposes of relatedness inference, IBIS’s performance is comparable to or, for third degree or closer relatives, sometimes better than phase-enabled algorithms including Refined IBD and GERMLINE (Figure 6). These latter two methods have previously been found to be among the top-performing approaches (roughly equal with one other method).⁶ Thus IBIS is effective for relatedness inference and represents a good balance between speed and accuracy, making it well suited to the very large genetic datasets currently available. Even so, analysis of the algorithms’ runtimes requires consideration not just of their speeds in the datasets we used, but also their overall runtime scaling, particularly in large samples. Methods that use phased data can perform hashing^12,40 and other techniques^41,42 that enable them to avoid explicit comparison of every pair of samples, improving their runtimes. (Despite this, since the number of sample pairs in a dataset grows quadratically in sample size, the number of IBD segments is also expected to increase at this same scale, leading to a commensurate increase in output required of all detection methods.) So while IBIS does perform faster than phase-based approaches in the tests we performed, it is possible that in larger samples, phasing techniques and newer phase-based IBD detection approaches^{40, 41, 42} will have better runtimes than the algorithm presented here.

Besides its speed, IBIS’s use of unphased data means that its segments are not subject to phasing errors, an artifact that can induce lower sensitivity in methods that condition on haplotypes (Figure 3). Additionally, its results remain the same regardless of sample size, so it performs equally well in small datasets, whereas phasing accuracy depends on sample size.⁴³ Furthermore, IBIS’s error model enables it to detect segments that are typically contiguous, whereas our analyses of Refined IBD and GERMLINE found that a large fraction of the segments these methods detect contain internal gaps (Figure 4). Segments with gaps, if not corrected, may adversely affect the performance of relatedness inference methods that leverage segment lengths in their analysis.⁴⁴

While IBIS maintains high accuracy, such that it performs well for inferring degrees of relatedness, we determined that it is most effective at identifying segments ≥7 cM long. The potential exists to detect shorter segments in unphased data, though doing so may require calculating probabilities of allele sharing, likely using allele frequencies or a haplotype model. Performing these analyses may require a significant runtime cost that is inconsistent the goals IBIS is designed to achieve.

Here we have focused on IBIS’s inference of pairwise degrees of relatedness, yet the IBD segments it detects are also useful in the context of other, more powerful relationship analyses. This includes recent approaches that combine IBD signals from multiple related individuals to increase accuracy.²¹ Another recently introduced method, CREST, uses multi-way IBD sharing from IBIS’s output to more precisely characterize not just degrees of relatedness, but pedigree relationships²² (e.g., avuncular versus half-sibling pairs). CREST further relies on IBIS’s largely contiguous segments to detect the sex of the parent that links two second degree relatives, demonstrating another advantage of having few internal gaps in inferred segments. Each of these applications makes use of IBD segments—instead of the estimated IBD fractions produced by more computationally efficient relatedness approaches—highlighting the importance of new methods that enable IBD segment detection.

Declaration of Interests

The authors declare no competing interests.

Published: March 19, 2020

Web Resources

• IBIS, https://github.com/williamslab/ibis/