The airborne transmission of infection between flats in high-rise residential buildings: A review

Abstract

The inter-flat airborne cross-transmission driven by single-sided natural ventilation has been identified recently in high-rise residential buildings, where most people live now in densely populated areas, and is one of the most complex and least understood transport routes. Given potential risks of infection during the outbreak of severe infectious diseases, the need for a full understanding of its mechanism and protective measures within the field of epidemiology and engineering becomes pressing. This review paper considers progress achieved in existing studies of the concerned issue regarding different research priorities. Considerable progress in observing and modeling the inter-flat transmission and dispersion under either buoyancy- or wind-dominated conditions has been made, while fully understanding the combined buoyancy and wind effects is not yet possible. Many methods, including on-site measurements, wind tunnel tests and numerical simulations, have contributed to the research development, despite some deficiencies of each method. Although the inter-flat transmission and dispersion characteristics can be demonstrated and quantified in a time-averaged sense to some extent, there are still unanswered questions at a fundamental level about transient dispersion process and thermal boundary conditions, calling for further studies with more advanced models for simulations and more sound experiments for validations.

Highlights

• •Progress in understanding inter-flat dispersion in multi-storey high-rise residential buildings is reviewed.
• •Transport of gaseous pollutants and quantification of re-entry possibility are indicated by tracer gas.
• •Dispersion routes and infection risks under different physical conditions are evaluated and summarized.
• •Methodologies and models with different research priorities are introduced and analyzed.
• •The transient dispersion process and thermal boundary condition are discussed and recommended for future works.

Nomenclature

C

tracer gas concentration (ppm)

C^*

number of infection cases

H_c

recirculation cavity height (m)

I

number of infectors

k

turbulent kinetic energy (m²/s²)

L

length of the building (m)

L_r

distance of the recirculation zone (m)

M_i–j

mass fraction

P

probability of infection

p

pulmonary ventilation rate of a person (m³/h)

Q

room ventilation rate (m³/h)

Q_e

a portion of the infected airflow which escapes from the upper part window of the lower room

q

quanta generation rate

R

scaling length that characterizes the building's influence on wind flow (m)

R_k

re-entry ratio (%)

S

number of susceptibles

t

exposure time interval (h)

U_H

mean speed of wind approaching the building at H (m/s)

v₁, v₂, v₃, v₄

approaching wind speed (m/s)

V

flat volume (m³)

Greek symbol

ε

turbulence viscous dissipation rate (m²/s³)

θ

incident wind angle (°)

ν

kinematic viscosity (m²/s)

Abbreviation

ACH

hourly air exchange rate (h⁻¹)

CFD

computational fluid dynamics

HRR

high-rise residential

IAQ

indoor air quality

LES

large-eddy simulation

MERS

middle east respiratory syndrome

RANS

Reynolds-averaged Navier–Stokes

RNG

renormalization group

SARS

severe acute respiratory syndrome

Subscript

i

source flat

j

target flat

1. Introduction

Since people spend about 80%–90% of their time indoors [1], [2], [3], the indoor air quality (IAQ) affected by particulate matter and gaseous concentration level is of great importance for human health. Poor IAQ may cause various health problems leading to morbidity, disability, disease, or even death [4], [5]. In addition to indoor contaminant sources, incursion of outdoor pollutants through ventilation or infiltration is another significant factor in IAQ [5], especially for natural ventilation through open windows in residential buildings [6]. Meanwhile, many new environmental problems has emerged in densely populated areas because of the increasing presence of high-rise residential (HRR) buildings, even though the housing problem is solved to some extent [7]. A good understanding of the mechanism and characteristics of airborne pollutant transmission and dispersion in and around the building is thus the perquisite for architects and building managers to employ effective indoor air pollution control strategies [8], particularly during the outbreak of severe infectious diseases.

Airborne transmission is known to be a long-range route of infection, which refers to the situation that agents may be carried long distances, within a room or even between rooms (generally greater than 1 m), by airflows [9]. It is reported to be a major person-to-person respiratory transmission route by many epidemiological and engineering studies [10], [11], [12], [13], [14]. Besides, recent outbreaks of SARS [15], [16], bird flu [17], A(H1N1) influenza [18] and MERS [19] have increased the scientific attention to airborne transmission in the built environment, especially in high density communities.

A special airborne transmission route called inter-flat (or inter-unit) transmission, namely air cross-contamination between flats within the same building, was identified during the outbreak of SARS in Hong Kong and started to be investigated in 2003. Using epidemiologic analysis, experimental studies and airflow simulations, Yu et al. [20] first revealed the high probability of an airborne spread of the SARS virus in one residential block. Then, Li et al. provided further analyses in an HRR building [21] and a hospital [22], where the largest outbreak happened, to show the dispersion through interior doors and window leakage. On the other hand, smaller-scale SARS clusters occurred in several other HRR buildings, such as in Wing Shui House and Hing Tung House [23], where the most affected households were located along the same vertical blocks on different floors. Similar case can also be observed in Germany [24], and it is common for residents to detect the cooking odors from neighbors. Based on these facts, Niu et al. [25] first proposed the possible transmission of inter-flat air cross-contamination under the condition of single-sided natural ventilation through openings. Such single-sided case usually exists in densely occupied residential buildings where there may be only one open window for one small cellular room. This inter-flat transmission and dispersion, driven by wind turbulence and/or temperature differences between indoor and outdoor air, may be a valid route due to the short dispersion distances between flats and the large openings involving considerable airflow exchanges.

Since then, the proposed dispersion through open windows within the same building has attracted increasing attention. Previous on-site measurements [25], [26] and numerical simulations [27], [28], [29], [30] on buoyancy-dominated inter-flat transmission well explained and quantified the upward vertical transport of gaseous pollutants. Later, a series of wind tunnel tests [31], [32], [33], [34] and numerical simulations [35], [36], [37], [38], [39], [40] was carefully performed to study the inter-flat airborne transmission and dispersion dominated by wind effect. In addition, a few studies [26], [29], [39] provided some preliminary work on the dispersion mechanism driven by combined buoyancy and wind effect.

In general, the inter-flat transmission and dispersion presented above involves two basic problems:

• ●coupled indoor and outdoor airflow driven by single-sided natural ventilation
• ●gaseous dispersion in and around a naturally ventilated building

This paper presents a systematic review of existing literature on this kind of inter-flat transmission and dispersion in terms of these two basic problems. In the following content, Section 2 introduces the evaluation indexes used for related investigations. Then, Section 3 illustrates the transmission mechanisms with different driving forces under various scenarios in detail. Finally, discussions and future works regarding the current research are provided in Section 4, and corresponding conclusions are given in Section 5. This review work is expected to be useful in understanding the proposed transmission and dispersion mechanisms in and around the built environment, and in assisting to implement more effective measures and designs for control of infectious respiratory diseases.

2. Evaluation index

The transmission and dispersion pattern characterized by the airflow field is commonly investigated by generating tracer gas in the pre-defined sources. The rationality of tracer gas technique has been discussed by many researchers considering the size and behavior of respiratory droplet nuclei [12], [13], [30], [41], [42], [43]. In the early time, Duguid [42] revealed that the respiratory droplet nuclei commonly range from 1 to 2 μm in diameter. Recently, a review by Morawska [43] pointed out that viruses are usually between 0.02 and 0.3 μm in diameter, and simulations by Gao et al. [30] suggested that the aerosols with diameters less than 2.5 μm act like gaseous pollutants. Besides, the evaporation of droplet with an initial diameter smaller than 20 μm can be treated as an instantaneous process [12], [43]. Generally, small aerosols may suspend in air for long periods, transport over great distances, and deposit in the lower respiratory tract [13], [14], which will cause significantly negative effects on human health. Considering these findings, it is supported that the coagulation, reflection, re-suspension and phase-change of small pathogens-carrying particles can be ignored in the dispersion of droplet nuclei.

Passive tracer gases, such as carbon dioxide (CO₂), sulfur hexafluoride (SF₆), propane (C₃H₈) and haze-fog (HF), have been successfully and widely used in experimental and numerical studies of the inter-flat transmission and dispersion [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40]. The reason lies in the similarity of their aerodynamic behaviors to those various gaseous pollutants and fine aerosols. Therefore, the dispersion route can be visualized and the re-entry phenomenon can be quantified by analyzing the tracer gas concentration distribution at different flats. Corresponding evaluation indexes are introduced in this section.

2.1. Mass fraction

The mass fraction was first proposed by Niu and Tung [26] and further developed by Ai et al. [37] to quantitatively estimate the potential inter-flat flow based on a three-zone airflow and mass-balance model, whose detailed deduction can be found in Ref. [26]. The mass fraction, M _i–j, is defined as the mass fraction of air that originates from the source flat i and is present in another flat j. It can be directly calculated from the measured or predicted tracer gas concentrations:

$$M_{i-j}=\frac{C_j}{C_i}$$ (1)

It is worth mentioning that the values of tracer gas concentrations may be varied, depending on the assumption made by researchers for specific purposes. Thus, the physical characteristics of corresponding mass fraction can be varied according to different research priorities.

2.2. Re-entry ratio

The re-entry ratio is another quantifying index to evaluate the potential inter-flat dispersion, i.e., the re-entry possibility, proposed by Niu and Tung [26]. The re-entry ratio, R _k, is defined as the fraction of the exhaust air from the source flat i that re-enters another flat j. It is calculated as follows:

$$R_k=M_{i-j}\frac{V_j{\left(ACH\right)}_j}{V_i{\left(ACH\right)}_i}$$ (2)

where the values of ACH are calculated using the methods from Refs. [44], [45], [46].

Similarly, the physical meaning of re-entry ratio can be different based on various assumptions and research priorities.

2.3. Wells–Riley model

The possible mass fraction values can serve as a basis for further infection risk analysis in the concerned problems. Based on the knowledge of infection dose, the Wells–Riley model [47] can be used to assess the cross-infection risks:

$$P=\frac{C^{\text{*}}}{S}=1-\exp \left(-\frac{Iqpt}{Q}\right)$$ (3)

Exposure to one quantum of infection gives an average probability of (1-e ⁻¹) to get infected. The model is established based on the assumptions of a well-mixed and steady-state condition, but it can also incorporate spatially distributed infection risk by tracer gas technique, which do not require such assumptions [48].

Some risk assessment studies regarding the concerned airborne transmission have successfully used the Wells–Riley model to estimate the infection risk, by employing numerical simulations [29] and wind tunnel tests [33], [34]. Although the combination of engineering and epidemiological studies is quite encouraging, the assessment need further investigation because many characteristics of indoor infectious droplets are still in question [43].

3. Airborne transmission mechanism

Natural ventilation is generally created by pressure differences between indoor and outdoor. Its detailed flow mechanics has been thoroughly studied by Linden [49]. There are two main natural ventilation types: cross and single-sided ventilation. Single-sided ventilation is more acceptable and common than cross ventilation due to many security and privacy concerns. The focus of this review is on single-sided natural ventilation with single opening.

In this ventilation mode, differences between indoor and outdoor temperatures and/or differences in wind pressure along the façade can create an air exchange, which plays an important role in the contamination transmission [50]. Thus, the airborne transmission under single-sided natural ventilation is mainly driven by buoyancy effect, wind effect, or combined buoyancy and wind effect. The transmission and dispersion characteristics depend on the strength and direction of these forces, whose physical processes are complex and hard to predict. Based on related results and conclusions in existing literature, this section illustrates how these forces create different ventilation modes and further influence the inter-flat transmission and dispersion process.

3.1. Transmission driven by buoyancy effect

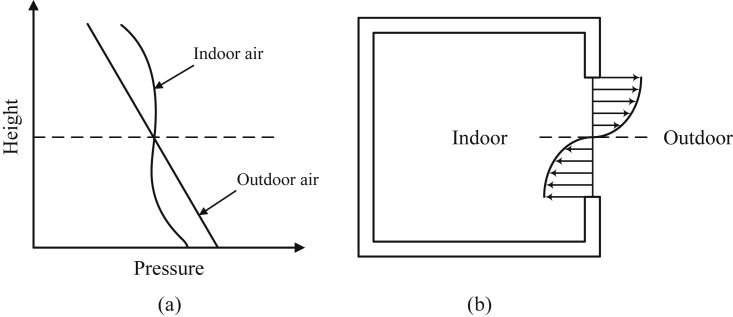
For a flat under natural ventilation, a difference between indoor and outdoor air temperatures can cause a density difference, where the warm air is lighter than the cold air. In such case, a pressure difference between indoor and outdoor air occurs, as shown in Fig. 1(a). As a result, the buoyancy (or stack) effect is created, where the higher interior pressure at the upper part drives outflows while the lower interior pressure at the lower part drives inflows. When the indoor and outdoor air temperatures equalize, the pressure difference is nearly zero and thus no driving force is produced for ventilation. For the natural ventilation with a single opening, as shown in Fig. 1(b), the lower part of the opening becomes the inlet while the upper part acts as the outlet.

Fig. 1.

Buoyancy effect (or stack effect) on single-sided natural ventilation.

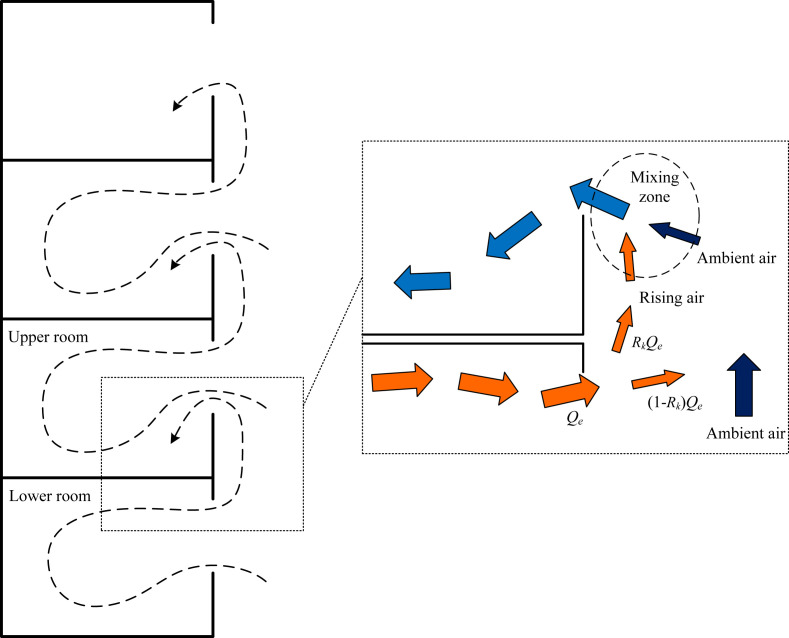
During the SARS epidemic period in Hong Kong, the temperature of outdoor environment was mildly low, with a mean value of about 20 °C [51]. Based on the analysis of the meteorological information from the nearby stations of the building with SARS clusters, low wind speeds (<3 m/s) can be observed, especially during evening and dawn time (around 0.1 m/s) [26]. Such windless case indicates that the buoyant plume is the dominant driving force for building ventilation. Besides, local residents are likely to open windows for night-time cooling instead of using air conditioners during that season. In view of these facts, Niu et al. [25] first proposed the hypothesis that on windless days, the warm airflow escaping from the upper part of the window in the lower floor may mix with outdoor fresh airflow and partially re-enter the lower part of the window in the upper floor, as shown in Fig. 2 . A further hypothesis was also proposed by Niu et al. [25] that for multi-storey HRR buildings, there exists a “cascade” inter-flat flow starting from the lower floor and ending at the top floor when buoyancy effects dominate (Fig. 2).

Fig. 2.

Inter-flat airborne transmission route under single-sided ventilation driven by buoyancy (stack) effects. (Revised from: Niu and Tung [26]).

The buoyancy-driven (or temperature-driven) single-sided natural ventilation through large openings has been widely investigated earlier regarding air exchange rate [52], IAQ and comfort level [53] by theoretical predictions [54], experimental studies [55] and numerical simulations [56]. Unfortunately, nearly no attention has been paid to the fate of the exhaust air with respect to the re-entry possibility. In particular, pure buoyancy-driven single-sided natural ventilation through a lower and upper opening in a three-storey building was simulated by Allocca et al. [57], who found that the indoor temperature level in each flat increased slightly with height, although the flats were physically and thermally isolated from one another. They related such phenomenon with the outside thermal plume from the openings underneath. However, this kind of vertical cascade effect was not further discussed in their study, and the potential transmission path was not mentioned either.

Since the vertical transmission hypothesis was proposed, increasing consideration has been taken into the concerned issue by many researchers recently [25], [26], [27], [28], [29], [30], as elaborated in Table 1 . It can be seen that, despite various assumptions and purposes in these studies, the possible transmission path has been demonstrated qualitatively and quantitatively. An indoor contaminant source at a lower flat can be a considerable contributor to concentrations in the vertical adjacent upper flat under certain meteorological conditions. In general, both on-site measurements [26] and numerical simulations [29] have revealed that, when buoyancy effects dominate, the re-entry ratio of exhaust air from a lower flat to the adjacent upper flat can reach up to about 7%. This is equivalent to an infectious risk of nearly 2% according to the Wells–Riley model, based on an assumed condition made by Gao et al. [29].

Table 1.

Studies on the inter-flat airborne transmission of infection driven by buoyancy effect.

Reference	Method	Mathematical model	Main result and conclusion	Remark
Niu et al. [25]	Tracer gas measurement (SF6) & CFD modeling	Standard k-ε model	Both tracer gas measurement and preliminary CFD simulation results well supported the hypothesis that a vertical upward movement of fine droplets is possible on windless days.	The study was quite preliminary and the accuracy of the CFD simulation need to be validated.
Niu and Tung [26]	On-site tracer gas measurement (SF6 & CO2)	A three-zone airflow and mass-balance model	The room air could contain up to7% of the exhaust air from the lower floor, and this occurs at low wind conditions with a combination of the indoor/outdoor temperature difference.	No residents were allowed in the rooms and no mechanical ventilation was operating during one continuous measurement;A quasi-steady airflow process was assumed.
Liu et al. [27], [28]	CFD modeling	RNG k-ε model with CO2 asa tracer & an assessment index	Under specific weather conditions, the presence of pollutants in the immediate upper floor originating from the lower floor is generally2 orders of magnitude lower than that in the lower floor;A window ledge between the two floors and the individual mechanical exhaust can probably reduce the contaminants spread by such inter-flat air flow.	The sampled rooms were simplified; The outside horizontal wind speed was neglected;A low wind speed of0.1 m/s was set as the inlet velocity at the lower horizontal boundary; The temperatures of the internal walls were set to be constant.
Gao et al. [29]	CFD modeling	RNG k-ε model with CO2 asa tracer & Wells–Riley equation	Ona windless day, around 7.5% of the exhaust air can be re-entrained into upper room; The concentration level is generally2 orders of magnitude lower in the adjacent upper room than in the lower source room, but the risk of infection is only1 order of magnitude lower and is still significantly high when it is assessed using the Wells–Riley model.	The gravity effect on the aerosols was neglected; All thermophysical properties were assumed to be constant except the air density; The multiple numerical solutions of unstable airflows were not considered; Only the transmission between two adjacent flats was discussed.
Gao et al. [30]	CFD modeling with Eulerian and Lagrangian approaches	RNG k-ε model with drift-flux and discrete random walk (DRW) model	Both simulation approaches revealed that the cascade effect exists for particulate pollutants; The particle concentration in the upper floor is2 to3 orders of magnitude lower than that in the lower floor, depending on the particle sizes;1.0 μm particles disperse like gases. Strong deposition at solid surfaces and gravitational settling of particles larger than20.0 μm greatly limit the upward transport of them.	Particle coagulation, reflection at walls, re-suspension, and phase-change such as evaporation were ignored; The unsteady flows and the instantaneously fluctuating velocities on the air exchange between indoor and outdoor spaces were not considered; The effect of particle source location in the lower floor and initial particle velocities were not taken into consideration.

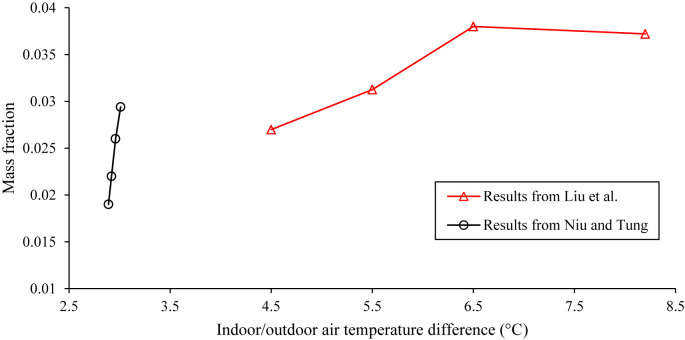
Fig. 3 shows the mass fractions of tracer gas at a lower and adjacent upper room in a slab-like building with various indoor/outdoor air temperature differences, obtained from Niu and Tung [26] and Liu et al. [28]. In spite of different assumed conditions and definitions of the resulting mass fractions, both experimental and simulation studies have found that the concentration level is generally lower by about two orders of magnitude in the upper room than in the lower room. Similar results can also be observed from Gao et al. [30], who further investigated the dispersion of expiratory aerosols in such case through Lagrangian and Eulerian approaches. In addition, as the temperature difference increases within a reasonable range, the corresponding mass fraction will increase (Fig. 3), which can be attributed to the stronger buoyancy forces. On the other hand, the concentrations of the upper flat did not change linearly according to the increase of temperature differences, and the mass fraction may stop increasing as the temperature difference exceeds a specific threshold. This can be explained by the dual roles of natural ventilation in built environments, namely a positive role of dilution and a negative role of transmission [28].

Fig. 3.

Mass fraction of tracer gas in the immediate upper room from the source at a lower floor in a slab-like building with various indoor/outdoor air temperature differences. For the results from Niu and Tung [26], SF₆ was released at a rate of 3 ml/s, and the mass fraction is the mass fraction of pollutant that originates from the upper opening of the lower room. For the results from Liu et al. [27], [28], CO₂ was released at a rate of 5 ml/s, and the mass fraction is the ratio of volume-average concentration in the upper room to that in the lower room.

Although the presented studies have provided some positive achievements regarding the inter-flat transmission with buoyancy-dominated case, all the results were limited to the upward transmission between two vertically adjacent flats due to the scope of building models. Actually, the pollutants from a lower flat may re-enter into other flats further above [29]. As for a multi-storey HRR building, the cascade transport driven by buoyant plumes has not been studied and discussed either. Besides, for the existing CFD simulations, the airflow field was generally obtained based on steady-state models with heat released constantly from the internal walls, while the buoyancy-driven natural ventilated flows are inherently unsteady [30]. Thus, more sophisticated modeling, including the location of heat source, is needed to provide more accurate predictions, which is expected to be explored in the future.

3.2. Transmission driven by wind effect

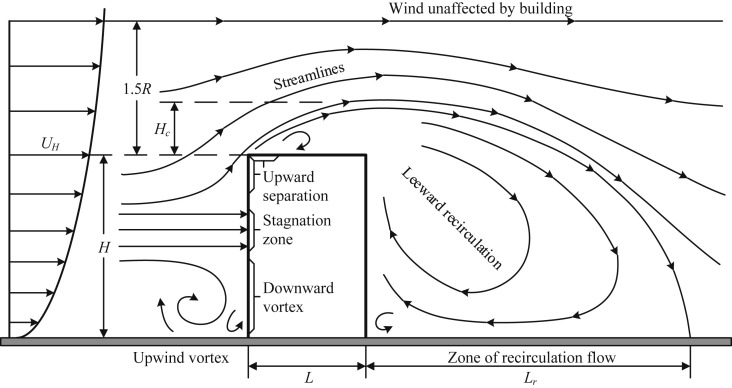
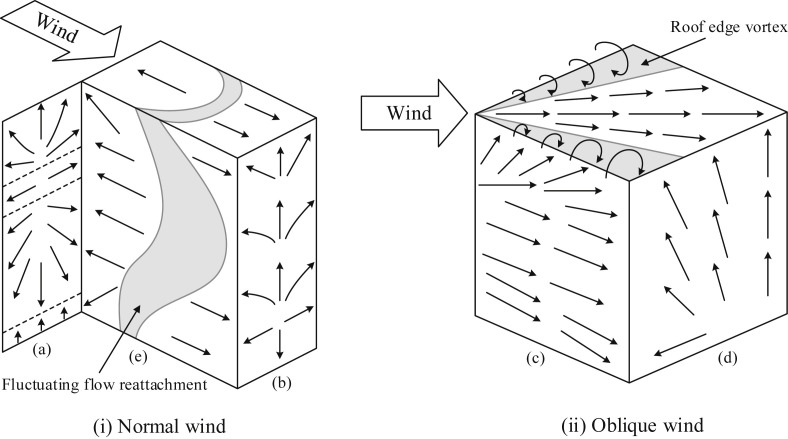
Compared with the buoyancy-dominated case, the inter-flat transmission driven by wind effects in HRR buildings is much more complicated. Fig. 4 shows the general airflow pattern around a bluff body, which has been thoroughly examined by many researchers [58], [59]. As wind impinges a building, airflow separates at building edges, generating recirculation zones over downward surfaces and extending into the downwind wake. The flow pattern near the windward wall is divided into three regions: a front stagnation region at about two-third of the building height, an upward separation region above it, and a downward vortex region below it. At leeward walls, a kind of vertical vortices is formed with a general flow direction from bottom to top. In general, various flow patterns, such as impingement, separation, reattachment, recirculation, vortex-shedding, etc., are involved along the building surface. Therefore, unlike the unidirectional transmission process in the buoyancy-dominated case, the wind-driven inter-flat transmission behaviors can be varied depending on the pollutant source location and the contaminant concentration distribution along the building surface.

Fig. 4.

Schematic airflow pattern around a bluff body. (Mainly from: ASHRAE Handbook, 2011, Section 45.3 [59]).

A large number of previous studies have been conducted on pollutant dispersion near and around built environments, such as street canyons [60], [61], [62], urban areas [63], [64], [65] and an isolated building [66], [67], [68], [69] through experimental measurements and numerical simulations. However, these studies focused mainly on the concentration distribution in a group of buildings, in a built-up environment, or in the vicinity of a building, but to a less extent on the airborne cross-contamination around a building itself.

Recently, many researchers have contributed a lot to the particular interest in this study, as summarized in Table 2 . A series of wind tunnel experiments by Liu et al. [31] and Wang et al. [32] on scaled HRR models with a cross (#) floorplan have revealed that the wind-dominated inter-flat dispersion may occur along both horizontal and vertical directions. Then, Liu et al. further designed detailed experiments to investigate such dispersion mechanism regarding mean concentrations with residents' behavior of window opening [33] and concentration fluctuations [34]. Considering the uncontrollable atmospheric conditions during on-site measurements and the scale problems of wind tunnel tests [70], [71], Ai et al. performed numerical simulations to study the wind-dominated inter-flat dispersion in a multi-storey slab-like building in terms of mean process using the optimized RNG model with the two-layer near-wall model [37], [38], and transient process using LES model [40]. Besides, Ai et al. [37], [38], [40] further investigated the effects of balcony on the dispersion behavior, which is out of the scope of this paper.

Table 2.

Studies on the inter-flat airborne transmission of infection driven by wind effect.

Reference	Method	Building model	Tracer gas		Main conclusion	Remark
			Source location	Wind direction
Liu et al. [31]	Wind tunnel test	A10−storey HRR building witha scale of1:30	9F, 6F and 3F	0° and90°	In the so-called re-entrance spaces, the pollutant can spread in both vertical directions, not only in the upward direction, but also in the downward direction; Dispersion can also occur in the horizontal direction; Generally, the upper floors at the leeward havea relatively higher risk of cross-contamination than that of the lower floors.	Provided data to validate CFD models in the future work; Did not study the dispersion features with oblique wind conditions
Wang et al. [32]	Wind tunnel test	A30−storey HRR building witha scale of1:150	26F,16F and 6F	0°,45°,90°,135° and180°	The upper floors would havea relatively higher risk of being contaminated than the lower floors when the pollutant source was located at the upper part of the building. However, when the source is located in the lower part of the building, the apartments in the floors below on the windward side would havea higher risk of infection than the upper floors.	Focused mainly on the characteristics along the vertical direction with different source locations and wind directions
Cheng et al. [33]	CFD modeling (standard k-ε model)	27 buildings with the re-entrant bays of different dimensions	N/A	0° and90°	The bays on the building side face are much worse ventilated than the windward or leeward bays but their ventilation efficiency is not affected by the building height which playsa governing effect on the pollutant dispersion for the later two types of re-entrance bays; In general, air exchange and pollutant dispersion are the worst in taller and deeper bays.	Focused mainly on the effect of wind directions and dimensions of the re-entrant bay on pollutant dispersion in view of the entire building
Liu et al. [34]	Wind tunnel test	A10−storey HRR building witha scale of1:30	9F, 6F and 3F	0°,45°,90° and180°	Both the vertical and horizontal dispersion revealed in Ref. [31] under closed-window condition can still be found when the windows are open, but the overall concentration level is clearly reduced under open-window condition; The spatial distribution of infection probabilities shows that the risk of airborne transmission in neighboring households is not negligible.	Further studied the wind effect on dispersion with the residents' behavior of window opening based on the results in Ref. [31] and evaluated the exposure risks
Liu et al. [35]	Wind tunnel test	A10−storey HRR building witha scale of1:30	9F, 6F and 3F	0°,45°,90° and180°	The wind-induced cross-contamination around the studied type of HRR building should not be overlooked; Variations in fluctuation intensity are quite sensitive to both the source location and the wind direction; The fluctuating concentrations should be paid attention to particularly during the evaluation ofa potential contamination risk.	Focused mainly on the behavior of concentration fluctuation during the hazardous gas dispersion process
Liu et al. [36]	CFD modeling (standard, RNG and realizable k-ε model)	The HRR building studied in Ref. [32]	26F,16F and 6F	0° and45°	Dispersion in both vertical and horizontal directions could be illustrated from the simulated results; The agreement between the numerical simulations and wind-tunnel measurements was good in the case under normal wind direction, while larger discrepancies were observed in the case under oblique wind direction.	Further assessed the accuracy of three numerical models in studying the wind effect on dispersion based on the experimental data in Ref. [32]
Ai et al. [37], [38]	CFD modeling (RNG k-ε and two-layer near-wall model)	Two1:30 scaled 5−story buildings with balconies in one of them	The end, middle, top units and the stagnation region	0° [37],45° and90° [38]	Undera normal incident wind, the pollutant disperses mainly downwards on the windward side and upwards on the leeward side, respectively; Under an oblique incident wind, the pollutant disperses mainly towards its downstream units on the windward side and upstream units on the leeward side, respectively; Under a parallel incident wind, the pollutant disperses mainly towards its upper and upstream units; The presence of balconies results ina more turbulent near-wall flow field, which significantly changes the re-entry characteristics.	Focused mainly on the dispersion characteristics of the slab-like building and compared some results with previous results in Ref. [29], [31]
Zhang et al. [39]	CFD modeling (standard k-ε model)	The HRR building studied in Ref. [31]	3F	Windward and leeward	For the windward emission, due to the downwash of wind in the re-entry area, pollutant migrated predominantly downwards and spread horizontally after reaching the ground. For the leeward emission, air pollutant migrated upwards within the re-entry before discharging downstream.	Focused mainly on the dispersion characteristics when pollutant is emitted ata low position through a numerical model based on the results in Ref. [31]
Ai and Mak [40]	CFD modeling (LES model)	Two1:30 scaled 5−story buildings with balconies in one of them	The upstream-end, middle, downstream-end units at 2F and 3F	0°,45° and90°	The main dispersion routes always vary with time, implying that the incursion of pollutants into a specific unit is intermittent; Secondary dispersions are observed; For pre-stable periods, the timescales ofa unit are influenced negligibly by distance from the source unit and the approaching wind direction, which are generally shorter on the windward sides than the leeward sides; For dynamically stable periods,a unit witha very small mean re-entry ratio could occasionally experience very large re-entry ratios, and the presence of balconies helps shrink and broaden the infectious scope on the windward and leeward sides, respectively.	Further studied the interunit transient dispersion based on the results in Ref. [37], [38]

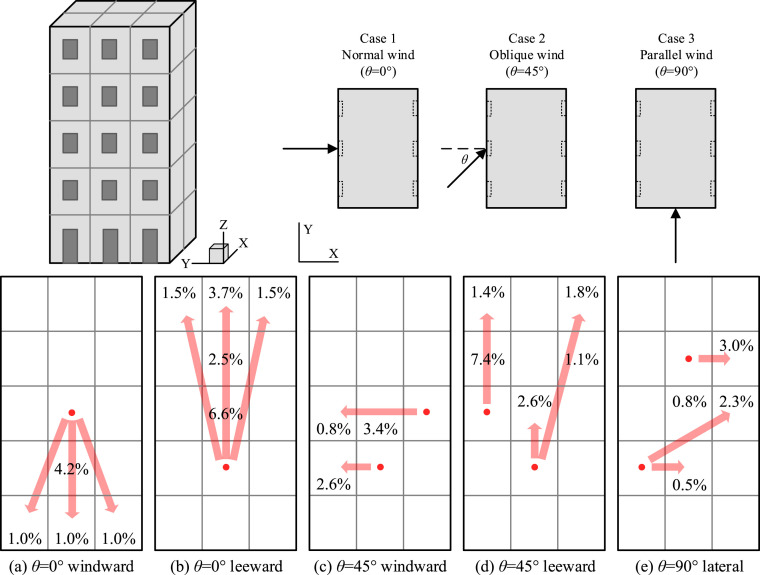
As mentioned above, the inter-flat airborne dispersion dominated by wind effects is highly dependent on the surface airflow pattern and the pollutant source location. Flats at different locations may experience different incident wind characteristics, resulting in a different airflow pattern even though all other factors are the same. The surface flow patterns along rectangular buildings for normal and oblique winds are shown in Fig. 5 . Besides, Fig. 6 depicts the partial results summarized from Ai et al. [37], [38] of dispersion patterns and re-entry ratios around a slab-like multi-storey building with different conditions. Detailed analysis and discussions regarding comparisons between Fig. 5, Fig. 6 are given as follows.

Fig. 5.

Surface flow patterns for normal and oblique winds. (Mainly from: ASHRAE Handbook, 2011, Section 45.3 [59]).

Fig. 6.

Typical dispersion patterns and re-entry ratios of tracer gas from different sources around a slab-like multistory building with different wind directions. Red dot: tracer gas source. (From: Ai et al. [37], [38]). The wind-dominated pollutant dispersion is studied by Ai et al. [37], [38] considering a wind speed of 1 m/s at roof height; The threshold used to exclude results is: re-entry ratio <0.1%. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

For a normal wind (0°) on the windward side, the flow pattern is generally characterized by an upward separation, a stagnation zone, a downward vortex and a ground-level upwind vortex, as shown in Fig. 5(a). When the gaseous pollutant is released at the bottom flat, only lateral dispersions result. When the pollutant source is located below the stagnation zone, most momentum is transferred to the vertical and oblique downward flows. The pollutant is thus carried to the lower region, leading to larger re-entry ratios for lower flats, as shown in Fig. 6(a). When the pollutant is emitted in the stagnation region, dispersions in all directions can be observed, while the downward and lateral cases dominate. When the pollutant source is located at the top flat, the pollutant directly disperses downstream and may not re-enter other flats due to the upward flow. Generally, the pollutant disperses mainly downwards on the windward side under a normal incident wind.

For a normal wind (0°) on the leeward side, the flow pattern is generally characterized by a large building-height recirculation flow and a small corner recirculation flow near the bottom floor, as shown in Fig. 5(b). The pollutant generated from the bottom floor can only affect the lowest floors. When the pollutant is emitted from the middle floors, it will disperse around all adjacent upper flats before entering the main downstream, causing a large scope of contamination and a high risk of infection, as shown in Fig. 6(b). Finally, the pollutant from the top floor can be directly diluted by the upward flow on the leeward side and the horizontal flow from the upstream, indicating a very low possibility of re-entry into other flats. Generally, the pollutant disperses mainly upwards on the leeward side under a normal incident wind.

For an oblique wind (45°) on the windward side, the flow pattern is generally dominated by a strong sweeping flow from the upstream to the downstream flats, as shown in Fig. 5(c). A unidirectional dispersion with high concentration flows dominates, see Fig. 6(c), instead of the bilateral dispersion as found under normal wind direction. It is worth mentioning that special cases can be observed at the top or bottom floor, where the combination of the relatively weak sweeping flow and the corner recirculation near the roof or ground results in an upward or downward dispersion. Generally, the pollutant disperses mainly towards its downstream flats on the windward side under an oblique incident wind.

For an oblique wind (45°) on the leeward side, the flow pattern is generally characterized by the combination of an upward flow, a horizontal reverse flow from downstream to upstream flats and a weak reattachment flow, as shown in Fig. 5(d). The pollutant generated from upstream flats can be directly diluted without re-entry due to the strong reverse flow. The pollutant dispersion in the middle flats is controlled by the upward, reverse and reattachment flows. As the height increases, the momentum of the reverse flow will gradually transferred to the reattachment flow in the horizontal direction, resulting in a general upward and oblique dispersion, as shown in Fig. 6(d). Similar case can also be found when the pollutant is generated from downstream flats, where the pollutant is gradually diluted into the downstream with the increase of the building height, as shown in Fig. 6(d). Generally, the pollutant disperses mainly towards its upstream flats on the leeward side under an oblique incident wind.

For a parallel wind (90°) on the lateral side, the flow pattern is mainly characterized by a reverse flow, a sweeping flow and a fluctuating reattachment flow, as shown in Fig. 5(e). In general, the pollutant disperses towards its upstream or downstream flats horizontally and obliquely due to the complex interaction between these flows. However, the flow pattern in such case simulated by Ai and Mak [38] was reported to be characterized by the combination of an upward flow and a strong reverse flow, see Fig. 6(e), which is quite different from the results in Fig. 5(e). Such discrepancy may be attributed to the different geometrical sizes of these two building models. Further studies are required to explore the details of the dispersion process in such case.

It can be seen that the typical mean dispersion patterns simulated by Ai et al. [37], [38] are generally consistent with the mean surface flow patterns in Ref. [59] under different conditions, except the lateral side case with a parallel wind. Thus, a nearly full understanding of distinctive mean dispersion routes when the pollutant is emitted in different flats on different facades under different wind directions can be deduced. Moreover, the simulated re-entry ratios may provide an implication of the dispersion scope and extent under a certain case.

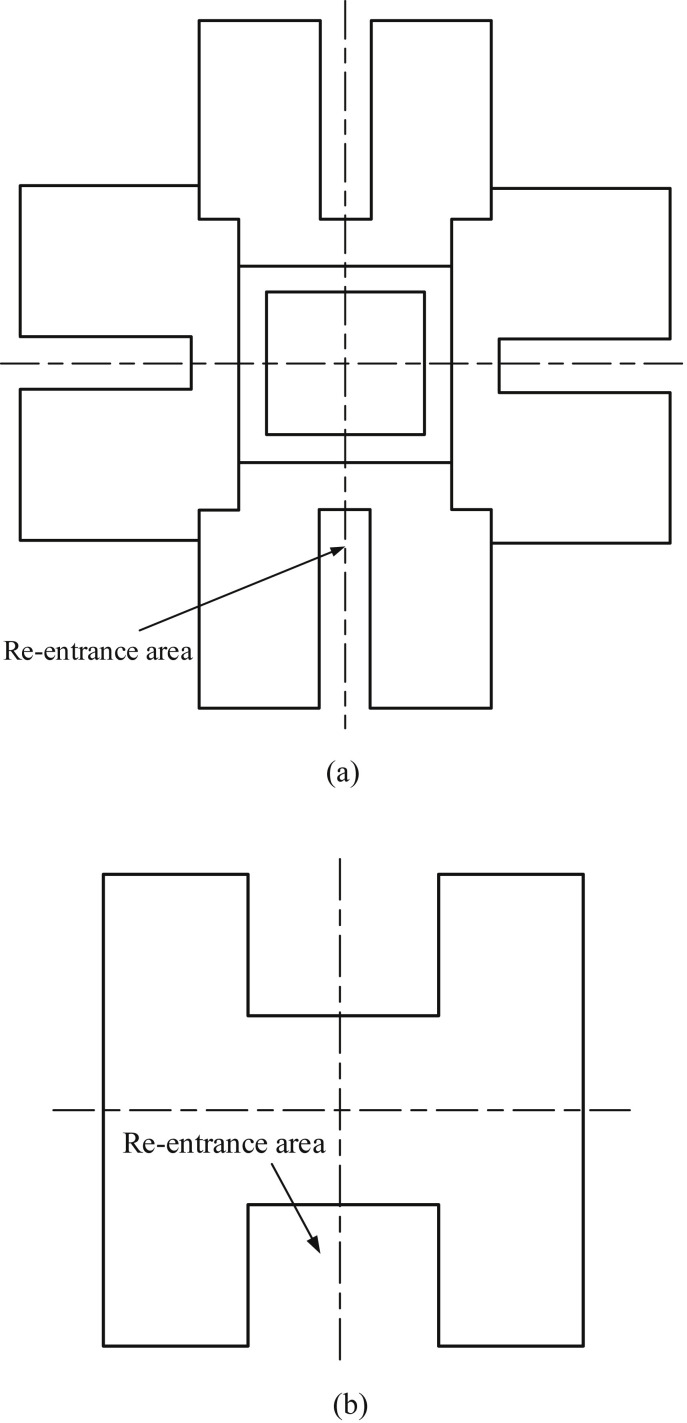
Similar dispersion characteristics can also be observed in other related studies (Table 2) when more complicated HRR building models were investigated with a cross (#) floorplan shape [31], [32], [33], [34], [36], [39] and an H-like floorplan shape [35], as shown in Fig. 7 . In particular, these studies focused mainly on the pollutant dispersion features in the so-called “re-entrance area”, which was identified as the major air-route of SARS spread in one residential block (the Amoy Garden) during the epidemic period in Hong Kong [20], [21]. In densely populated cities (e.g. Hong Kong) such re-entrance area is typical, which is designed to maximize the availability of daylighting and natural ventilation to the flats for fulfilling local building code requirements [21].

Fig. 7.

Schematic plan view of the studied building models: (a) the cross floorplan; (b) the H-like floorplan.

However, the dilution speeds and ACH values obtained in the wind tunnel tests [31], [32], [33], [34] are significantly lower than in the simulation studies [37], [38]. One reason for the difference may lie in the different building models. The two lateral boundaries of the re-entrance area will confine the horizontal dispersion, resulting in a high concentration level. While there is no obstruction effect for either vertical or horizontal directions in the slab-like building. In addition, such difference may also be attributed to the distinct assumed conditions in these studies. The simulations were based on a complex and turbulent near-wall airflow field, presenting a real situation, while the wind tunnel tests were conducted using a simplified solid model. Therefore, different building types may experience different possibilities of inter-flat cross-contamination, calling for distinctive control strategies and ventilation measures as appropriate.

3.3. Transmission driven by combined buoyancy and wind effect

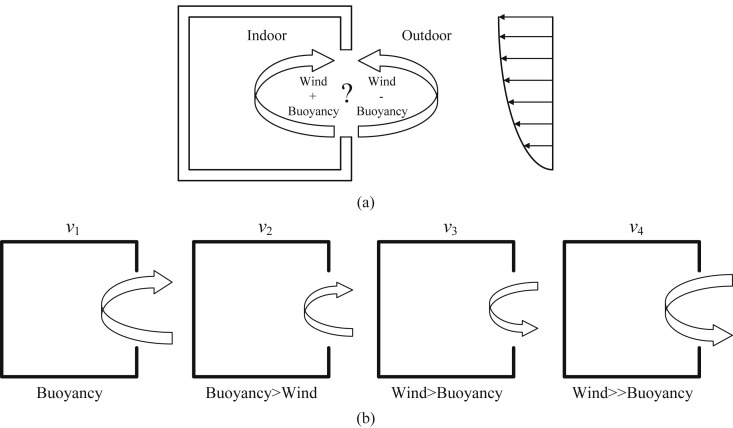
In most real cases, buoyancy- and wind-driven flows exist simultaneously. The simultaneous effect of temperature and wind on the air exchange and ventilation process at an opening is very complicated, especially for the single-sided case. Although many experimental and numerical studies have been conducted to understand the single-sided natural ventilation driven by the combined buoyancy and wind effects regarding the airflow rate [57], [72], [73], [74], [75], [76], such understanding is yet limited for application. In particular, after the SARS outbreak in Hong Kong, many researchers have tried to address the mechanisms of disease spread [20], [21], [26]. Nevertheless, it still remains unclear whether the buoyancy or wind effect played a more significant role. Hence, a full understanding of the single-sided natural ventilation under combined buoyancy and wind effects is extremely important to reveal the inter-flat airborne transmission mechanisms.

As shown in Fig. 8(a), the wind and buoyancy forces may reinforce or counteract each other according to various characteristics of the approaching wind, the indoor/outdoor temperature, and the opening. Such ambiguity makes it hard to observe consistent trends and to deduce general airflow processes. Nevertheless, some encouraging results have been obtained from Allocca et al. [57] by tracking the velocity patterns through a room at a range of wind speeds, as shown in Fig. 8(b). At a low wind speed (v ₁), buoyancy effects dominate and drive air in through the lower part and out through the upper part. At a wind speed of v ₂ (v ₂ > v ₁), such buoyancy effects diminish as the wind forces increase, resulting in a smaller airflow rate. When the wind speed increases to v ₃ (v ₃ > v ₂), the wind forces become dominant and drive a counterclockwise flow. As the wind speed continues to increase (v ₄), the wind forces further grow stronger and the buoyancy effects are nearly negligible. Similar changes between the wind- and buoyancy-dominated cases can also be observed in other studies [74], [75], [76], which further investigated the effects of indoor/outdoor temperature differences and opening conditions. Thus, it is important to note that the combined effect should be studied case by case due to the complicated interaction between related parameters.

Fig. 8.

Combined wind and buoyancy effect on single-sided natural ventilation: (a) Uncertainty about the reinforcing or counteracting effect; (b) Combined effect with different wind speeds. (Revised from: Allocca et al. [57]).

It has been found from both numerical simulations [29] and experimental studies [75], [77] that the effect of weak wind is multiple and complex in the single-sided natural ventilation. Firstly, wind may increase the intensity of outdoor turbulence and further increase the interfacial mixing between incoming and outgoing airstreams at the middle of the opening [75], [77]. Such mixing layer tends to increase the airflow rate. Secondly, the approaching wind speed profile may attenuate the net pressure difference across the opening, indicating a counteraction between wind and buoyancy forces [29], [75]. Thirdly, wind turbulent fluctuations may contain high frequency energy, which can reinforce the air exchange through the opening [78]. Thus, the general behavior of weak wind in terms of the single-sided natural ventilation is far from clear at the current stage.

Despite the complexities of such effects, some preliminary results regarding the inter-flat cross-contamination have been obtained, as illustrated in Table 3 . Generally, it depends on the assumed condition whether the buoyancy forces or wind turbulences will dominate the dispersion process.

Table 3.

Studies on the inter-flat airborne transmission of infection driven by combined buoyancy and wind effect.

Reference	Method	Study object	Main result	Related conclusion	Remark
Niu and Tung [26]	On-site tracer gas measurement (SF6 & CO2)	Two adjacent units on 1F and 2F at Wing Shui House in Hong Kong	Ona windless day the ratio of the SF6 concentration in the upper room to the lower room ranged from 2.9% to7%, depending on the locations, and the re-entry ratio was 4.8%; Outside wind speed, when increased from 0−0.03 to 2.48 m/s, could lower the maximum concentration ratio to 3.6% and re-entry ratio to 0.6%.	For the studied building configurations and an indoor/outdoor temperature difference of 3–5°C, the mass fraction is influenced by the temperature differences at the wind speed range of 0–0.07 m/s. While the turbulence effect ofa wind speed over0.9 m/s will overwhelm the thermal force.	Smoke visualization showed that the airflow along the façade was fairly turbulent and flow directions varied drastically. But most of the time, upward vertical airflow dominated, though downward or horizontal movement was occasionally observed.
Gao et al. [29]	CFD modeling (RNG k-ε model with CO2 asa tracer)	Two adjacent units on 2F and 3F ina slab-like building	For an indoor/outdoor temperature difference of5°C, the re-entry ratio was 7.5% ona windless day. As wind speed ascended from 0.5 to2.0 m/s, the re-entry ratio increased up to 16.3%. If the wind speed increased further to 4.0 m/s, the re-entry ratio was the lowest (3.5%).	For the studied case, a gentle wind forces the warm polluted plume to enter into the upper window by its horizontal momentum. But high-speed winds may function like an air curtain, suppressing the convective spread of pollutants between flats.	Only the transmission between two adjacent flats was discussed; Only wind normal to the window is taken into account; The finding still needs more experimental validations.
Zhang et al. [39]	CFD modeling (standard k-ε model)	A typical residential building witha cross floorplan	The HF (haze-fog) studies, where the pollutant density was adjusted to be heavier (+50%), same and lighter (−50%) than air, showed that the pathway of HF migration in the re-entrant area of the studied building for both windward and leeward discharge remain unchanged when compared with the case dominated by wind-structure interaction.	With the approaching wind speed at the building height (1 m) of3.27 m/s, the air pollutant dispersion around the building model is dominated by wind-structure interaction and buoyancy effect associated with the pollutant specific weight within the range tested only playsa minor role in the dispersion process.	Only the vertical air pollutant dispersion in the re-entry area of the specific building for the windward and leeward case was studied; The inter-flat transmission driven by the combined buoyancy and wind effect need further investigations.

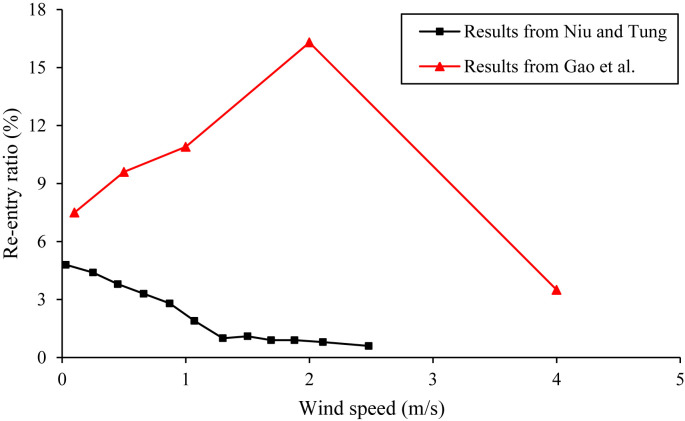
Fig. 9 shows the re-entry ratio of the tracer gas from a lower flat to the adjacent upper flat in a slab-like building with various wind speeds, obtained from Niu and Tung [26] and Gao et al. [29]. In spite of the slight difference in their assumptions, some positive findings can be deduced from the comparison. Firstly, both studies have demonstrated the re-entry possibility, namely the inter-flat cross-contamination within the same building exactly exists no matter what physical effects drive the ventilation. Secondly, when the wind speed is extremely low or high, both results show the same order of magnitude in re-entry ratios, indicating that both experimental and numerical studies can quantitatively describe the consistent trends under buoyancy- or wind-dominated cases. Thirdly, when the buoyancy effect is comparable to the wind effect, a large discrepancy can be observed. Gao et al. [29] revealed that the wind may first reinforce the upward transport and then suppress such spread as the speed increases, while the on-site measurements by Niu and Tung [26] did not capture such reinforcing phenomenon. There are two explanations regarding this discrepancy in addition to the complexity of weak wind effects as discussed above. One reason may lie in the modeling simplification of real conditions. In the simulations, only the wind normal to the window with heat released constantly from the internal walls was taken into account by Gao et al. [29], while the real airflow along the façade was fairly turbulent and flow directions varied drastically, as reported by Niu and Tung [26]. The three-dimensional nature of airflows and the vertical temperature gradients are incompatible with simple assumptions such as one-dimensional flows and constant temperatures in both flats, as explained by Heiselberg et al. [79]. In addition, the inherent inability of the RNG k-ε model used by Gao et al. [29] to reveal the turbulent fluctuations and instantaneous air exchanges through the opening may be another reason for such discrepancy.

Fig. 9.

Re-entry ratios of tracer gas from the source at a lower floor in a slab-like building with various wind speeds. The wind speeds were taken at 10 m above the ground level by Gao et al. [29], while the wind speeds were obtained based on the wind data monitored outside the window, 1.6 m away from the façade of the building by Niu and Tung [26].

In general, the research of the inter-flat airborne cross-contamination under single-sided natural ventilation driven by combined buoyancy and wind effects is quite preliminary at the current stage. There is a particular lack of detailed information on this dispersion process in HRR buildings. Due to the complexity and ubiquity of such effect, more experimental studies are needed for further validations and more advanced models are needed for simulation optimizations.

4. Discussions and future works

4.1. Transient inter-flat dispersion process

In general, the mean concentration and dispersion patterns have been widely studied, particularly under stable atmospheric conditions. However, such mean behavior may not be sufficient for investigating the dispersion of odorant, flammable and highly toxic gases, which are related to odor perception, combustion and severe health effects [80], [81]. The reason lies in the fluctuating and stochastic nature of turbulent flows, calling for further investigations on the fluctuation characteristics in unsteady environments. Although some studies have been carried out to examine these situations [61], [82], [83], [84], [85], a lack of full understanding and unclear data interpretation regarding turbulent flow characteristics can still be observed.

For the inter-flat airborne cross-contamination, the experimental results from Liu et al. [34] suggested that the infection risk caused by instantaneous peak concentration can be neglected. However, their conclusion may only be implemented to similar HRR buildings with a cross (#) floorplan, as shown in Fig. 7(a). Moreover, simulation results by Ai and Mak [40] using LES on a slab-like building pointed out that: 1) the incursion of pollutants into a specific flat is intermittent, 2) secondary dispersions are observed, and 3) a flat with a very low mean re-entry ratio could occasionally experience extremely high re-entry ratios. These findings further extend the dispersion scope and highlight the dispersion uncertainty for inter-flat cross-contamination, which were unfortunately ruled out by the inherent time-averaged treatment of previous RANS models [27], [28], [29], [30], [37], [38]. Thus, more transient investigations are needed to fully describe the inter-flat dispersion process.

The infectious risk of a susceptible person is influenced by the number of infectious quanta from infector(s) and the duration of exposure time, according to the Wells–Riley model [47]. For a specific flat, the number of infectious quanta can be provided by the re-entry portion of infected air generating from the source flat. The re-entry portions in various scenarios are reviewed and analyzed in Section 3. However, existing studies have not provided a general secure threshold for the re-entry ratio to quantitatively evaluate the infectious risk for a specific flat by this kind of cross-contamination. This is due to the diverse pathogen types and different physical conditions of susceptible people [40]. Although previous researchers [42], [86] have studied the possibility of causing disease by pathogens, the results are shown to be strongly case-dependent. When exposed to a certain concentration level of a specific pathogen, isolating infectors as early as possible is nevertheless an effective method to reduce exposure time and control infection.

Another factor influencing the airborne infectious risk is the comparison of two timescales: the time needed to accumulate a quantum and the survival time of a pathogen. An airborne infection is caused based on the prerequisite that at least one quantum produced by an infector must remain airborne and survive to be inhaled by a susceptible person [9]. If the survival time of a pathogen is shorter than the time required for quantum accumulation in a target flat, the occupants in this flat are safe and thus need no protective measures. Unfortunately, many pathogens can survive airborne for long periods, such as 24 h for influenza viruses [87], 7 days for SARS coronavirus [88], etc., which are longer than the timescale of inter-flat dispersion. On the other hand, many factors may affect the survival time of a pathogen [9], [43]. To the authors' knowledge, the two timescales have not been systematically compared and analyzed to evaluate the infectious risk with the concerned inter-flat dispersion. Therefore, the need to analyze the two timescales for a specific pathogen is meaningful to obtain more accurate risk estimations in a certain built environment.

Based on a brief epidemiological discussion above, the infection risk with the inter-flat airborne cross-contamination cannot be accurately assessed due to the lack of detailed information about the corresponding factors. Since these factors are strongly related to concentration fluctuations during the dispersion, more transient investigations should be carried out with the combination of engineering and epidemiological analyses.

4.2. Atmospheric thermal boundary condition

The inter-flat transmission and dispersion has been examined in a steady atmospheric boundary layer using wind tunnel experiments and numerical simulations, as shown in Section 3. However, a building in reality is subject to solar heating, which may increase the turbulent exchange significantly. Furthermore, large horizontal thermal gradients in the vicinity of walls heated by solar radiation [89] and intermittent heat transfer within the wall boundary layer [90] have been observed in some field studies. Unfortunately, existing studies [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40] have not accounted for the buoyancy effects caused by wall heating, which may affect the airflow pattern and dispersion behavior near walls, especially for the inter-flat case under weak wind conditions. Due to the ignorance or the lack of atmospheric thermal boundary input data in the existing models, it still remains a mystery whether and to what extent will this kind of buoyancy effects influence the inter-flat dispersion characteristics.

Quantification of the buoyancy effects caused by wall heating is extremely challenging due to the involvement of various complex processes:

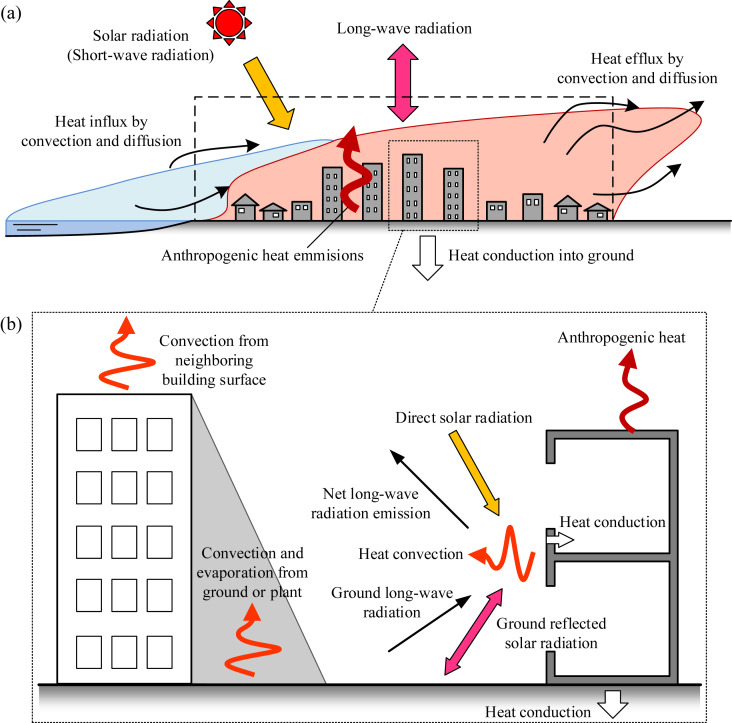
• ●The building surface temperature is strongly related to the urban surface condition, which is determined by the energy balance between: 1) the sensible and latent heat fluxes transferred to the air, 2) the received net radiation (short-wave and long-wave), 3) the heat storage into the building materials and the ground, and 4) anthropogenic heat sources [91], [92], [93], as shown in Fig. 10(a).
• ●The energy-balance characteristics mentioned above vary with latitude of the city, built form, urban geometry, and surface materials [94], [95], [96].
• ●The heat transfer around a building in the residential microclimate is affected by: 1) heat convection between outdoor air, building surfaces, ground and plants, 2) radiation including solar radiation, sky long-wave radiation and long-wave radiation between ground and building surfaces, 3) heat conduction into the building and ground, and 4) latent heat transfer in the residential environment [97], as shown in Fig. 10(b).

Fig. 10.

Concept of heat balance in urban environment: (a) Heat balance of urban surface layer (Mainly from: Ooka et al. [93]); (b) Heat balance in thermal environment around buildings (Revised from: Li et al. [97]).

Therefore, different surfaces may generate turbulence and transfer energy, momentum and moisture at different rates, causing the overlying airflows and boundary layer structure to be highly stochastic and dynamic. In order to evaluate the wall thermal boundary condition around a building, it is necessary to consider the total (atmosphere + buildings + ground) thermal energy balance and their interactions. However, there has been less conclusive work on this case, partly due to the difficulty in resolving or parameterizing the thermal boundary layers on building surfaces in simulations [98], and the challenges in capturing heat transfer processes on the building and district scales [99]. Nevertheless, it is important to address these technical issues because of the increased emphasis on accurate modeling of building and ground surface temperature and near-ground atmospheric boundary layer.

Many field observations and numerical modeling have been made in order to understand the effects of building surface heating in the urban canopy on the canyon flow and pollutant dispersion [89], [100], [101], [102], [103], [104], [105], although some ambiguous or even opposing conclusions can be found. It is important to note that a thin thermally-driven updraft was demonstrated near the walls [89], and the thermal effects on the flow pattern and dispersion were suggested to be considerable in the location very near the heated walls [101], [102].

Since the inter-flat dispersion routes are mainly embedded in the flows near the building surfaces, the buoyancy effects caused by heated walls may largely affect the re-entry phenomenon and alter the inter-flat dispersion characteristics. Therefore, in order to take care of the thermal boundary condition and accurately predict the re-entry possibility, grid resolution in the computations need to be extremely fine and advanced near-wall models (e.g. wall functions) need to be further developed.

4.3. Future works

In addition to the transient dispersion process and the atmospheric thermal boundary conditions, several recommendations are introduced for a better understanding of the inter-flat airborne cross-transmission mechanism.

There has been insufficient research to elucidate the inter-flat dispersion process in HRR buildings driven by combined buoyancy and wind effects. Due to the complexity and ubiquity of such effects, a systematic series of studies should be performed for further investigation. Besides, building models with more floors and more flats per floor should be developed for studying the cascade effect.

It is recommended to develop more accurate and reliable CFD models in predicting pollutant dispersions. Considering some deficiencies existed in RANS modeling, LES modeling is expected to simulate complex physical processes and capture unsteady characteristics.

The current study focuses on an isolated building, while the impact introduced by neighboring HRR buildings is ignored. The further step should be to consider the situation with building groups. The assessment of cross-contamination should be extended to building arrays. Correspondingly, the pollutant generating from one flat can be assumed from the neighboring building.

Finally, practical solutions and strategies of how to avoid the inter-flat airborne cross-contamination in HRR buildings are not yet fully available based on the current understanding, which requires more explorations.

5. Conclusions

Progress in understanding the inter-flat airborne transmission and dispersion driven by single-sided natural ventilation in high-rise residential buildings has been reviewed, and specific conclusions and discussions regarding different research priorities with various study methods are drawn at the end of each subsection.

Modeling and testing the inter-flat dispersion mechanisms under either buoyancy- or wind-dominated conditions has been more successful. While there has been less conclusive work on combined buoyancy and wind effect on flow and dispersion within the proposed issue. Due to the complexity and ubiquity of such combined effect, more progress is expected to be achieved with further investigations in the near future.

In general, mean inter-flat airborne transmission and dispersion can be demonstrated and elucidated, and the re-entry possibility can be quantified and evaluated in a time-averaged sense to some extent by many researchers. However, there are still unanswered questions at a fundamental level about transient dispersion process and thermal boundary conditions. Since these two factors are strongly related to the inter-flat dispersion behavior, it is important to emphasize on these research priorities for a more accurate estimation and a more profound understanding.