Abstract
This paper investigated the transmission of respiratory droplets between two seated occupants equipped with one type of personalized ventilation (PV) device using round movable panel (RMP) in an office room. The office was ventilated by three different total volume (TV) ventilation strategies, i.e. mixing ventilation (MV), displacement ventilation (DV), and under-floor air distribution (UFAD) system respectively as background ventilation methods. Concentrations of particles with aerodynamic diameters of 0.8 μm, 5 μm, and 16 μm as well as tracer gas were numerically studied in the Eulerian frame. Two indexes, i.e. intake fraction (IF) and concentration uniformity index RC were introduced to evaluate the performance of ventilation systems. It was found that without PV, DV performed best concern protecting the exposed manikin from the pollutants exhaled by the polluting manikin. In MV when the exposed manikin opened RMP the inhaled air quality could always be improved. In DV and UFAD application of RMP might sometimes, depending on the personalized airflow rate, increase the exposure of the others to the exhaled droplets of tracer gas, 0.8 μm particles, and 5 μm particles from the infected occupants. Application of PV could reduce RC for all the three TV systems of 0.8 μm and 5 μm particles. PV enhanced mixing degree of particles under DV and UFAD based conditions much stronger than under MV based ones. PV could increase the average concentration in the occupied zone of the exposed manikin as well as provide clean personalized airflow. Whether inhaled air quality could be improved depended on the balance of pros and cons of PV.
Keywords: Exhaled droplets, Ventilation strategy, Aerosol transmission, Eulerian drift-flux method
1. Introduction
Aerosol is one of the main sources of air pollutants indoors. It may act as an agent of infectious diseases through exhaled droplets of patients. More and more evidences have identified the transmission route of infectious diseases through respiratory droplets in enclosed environments [1], [2], [3]. Li et al. [4] made a multidisciplinary review of the relationship between infectious airborne transmission and ventilation in built environment. They believed that there is a strong and sufficient evidence of the association between spread of infectious agent (including measles, tuberculosis, chickenpox, influenza, smallpox, and severe acute respiratory syndrome (SARS)) and ventilation and airflow pattern indoors. With the successive outbreaks of SARS, avian influenza and recently A/H1N1 influenza, understanding of infectious aerosol transmission behaviors between occupants in typical ventilation rooms becomes not only important but also emergent.
The effects of ventilation airflow patterns on the dispersion of exhaled droplets indoors have been studied before. Gao et al. [5] studied spatial concentration distribution and temporal evolution of exhaled and sneezed/coughed droplets within the range of 1.0–10.0 μm in an office room with mixing ventilation (MV), displacement ventilation (DV) and under-floor air distribution (UFAD). To et al. [6] and Wan et al. [7] studied dispersion and deposition of expiratory aerosol experimentally and numerically under typical airflow patterns in an aircraft cabin. Chao et al. [8] investigated transport and removal characteristics of expiratory droplets in a three bed hospital ward with MV under different ventilation rates and coughing orientations. Richmond [9] numerically studied dispersion of exhaled pathogen-laden droplets by a patient through both continuous breathing and single coughing in an airborne infection isolation room with MV. Mui et al. [10] investigated transmission of exhaled droplet nuclei between a polluting manikin and a receiver under MV and DV in an empty room. These investigations mainly focus on the dispersion characteristics of exhaled droplets under different total volume (TV) ventilation systems. However, the effect of using personalized ventilation (PV) on protecting occupants against exhaled droplets as virus carriers is less studied.
The main purpose of PV is to provide clean and cool air close to each occupant [11]. If the clean core region of PV airflow could effectively reach the breathing zone of occupants, the inhaled pollutant concentration would decrease significantly [11]. Pantelic et al. [12] found the protective role of PV for an exposed manikin against droplets released from a ‘coughing machine’ in three distances experimentally. They found that PV combined with TV could both reduce the peak aerosol concentration levels in the breathing zone and shorten the exposure time compared with TV alone. However, when the occupant using PV is infected, the PV airflow would help promote infectious exhaled droplets mixing with TV airflows and would enhance their spread indoors. These could cause a higher infection probability of other people in the same room. Cermak and Melikov [13], [14], [15] studied the transmission of infectious agents between two occupants under different total volume ventilation strategies combined with two types of PV using tracer gas method in a full-scale test room. However, the diameters of exhaled droplets may span a wide range from O(1 μm) to O(1000 μm) [16]. In a recent experimental study carried out by Morawska et al. [17], the exhaled droplets for all respiratory activities were most in the mode with diameters below 0.8 μm. Speech activity produced additional particles in modes near 3.5 and 5 μm. Whereas Chao et al. [18] reported that the geometric mean diameter of exhaled droplets was 13.5 μm from coughing and 16.0 μm for speaking using the same experimental system and interferometric Mie imaging (IMI) technique for droplet size measurement. For fine particles smaller than 1 μm, tracer gas may be a good surrogate due to the aerodynamic characteristics of fine particles. But for coarse particles, this method may cause significant difference.
In this study, the transmission behaviors of exhaled aerosols between two occupants under three different TV systems, i.e. MV, DV, and UFAD combined with a PV system using round movable panel (RMP) as the air terminal device (ATD) were investigated numerically using an Eulerian drift-flux method. One person acted as a polluting source and the other was exposed. Particle sizes of 0.8 μm, 5 μm, and 16 μm as well as tracer gas were studied. Two indexes, i.e. intake fraction (IF) and concentration uniformity index R C were used to evaluate the performance of ventilation systems.
2. Numerical methods
2.1. Airflow model
In order to model particle dispersion and deposition accurately, a good simulation of airflow field is crucial. Mass, momentum, and energy equations were solved in a finite-volume method with the aid of a commercial software Fluent [19]. The general form of the governing equations is as follows:
| (1) |
Here ϕ represents each of the three air velocity components u, v, and w, the turbulence kinetic energy k, the turbulence dissipation rate ɛ, and the temperature T. When ϕ is unity, Eq. (1) represents conservation of mass. is air velocity vector, ρ is air density, Γϕ is the effective diffusion coefficient, and Sϕ is the source term of the general form in the governing equations.
Considering the complexity of combined buoyant flow and forced convective flow indoors, although no turbulence model can precisely predict such a complex airflow motion [20], the RNG k–ɛ turbulence model with the standard wall function was used to enclose the Navier–Stocks equations. The predictions of airflow field by the RNG k–ɛ model in indoor environments were validated in previous studies [21], [22], [23]. A surface-to-surface radiation model was used to take radiative heat transfer into account. Incompressible ideal gas law was adopted to reflect the change of air density to temperature in the momentum equations. The convection and diffusion term for all variables were discretized by second order upwind and second order central difference scheme, respectively, except for pressure by PRESTO. The SIMPLE algorithm was used to couple the pressure and momentum equations. The turbulence kinetic energy k and turbulence dissipation rate ɛ employed in air inlets and outlets were calculated by Eqs. (2), (3), (4) [19].
| (2) |
| (3) |
| (4) |
where u avg refers to the mean flow velocity, I is the turbulence intensity, Dh is the hydraulic diameter, and Cμ = 0.09.
2.2. Particle transmission model
A simplified Eulerian method, i.e. a drift-flux model was employed which incorporated the effects of Brownian motion, turbulent diffusion, and gravitational settling effect to predict particle dispersion in enclosed environment [22]. The governing equation of the particle concentration is similar to Navier–Stokes equations, except that it integrates the gravitational settling effect of particles into the convection term:
| (5) |
Here C is the particle concentration, is the particle velocity, and μ eff is the effective viscosity which is the sum of molecular and turbulent viscosity. σC is the Prantl number and is often set as 1.0. The gravitational settling velocity of particles is calculated by Stokes equation [24]. Eq. (5) was discretized directly into algebraic equation in the frame of finite-volume method with second order accuracy.
To consider particle deposition process at solid boundaries, a semi-empirical deposition model proposed by Lai and Nazaroff was used [25]. The model calculates the particle deposition rate as a function of particle density, diameter, and near-wall airflow condition characterized by the friction velocity.
The drift-flux model is not a fully-coupled multi-phase model. In the calculation of particle concentration, indoor airflow and temperature fields were solved firstly. When the convergence was reached, Eq. (5) with the semi-empirical deposition model as boundary conditions at solid walls was solved separately based on the one-way coupling assumption. The drift-flux model was incorporated into Fluent through a user-written sub-program.
3. Model validation
Jin et al. [26] measured the heterogeneity of particle concentrations in a ventilated scaled-chamber with dimensions of width × depth × height = 1 m × 1 m × 0.3 m (Fig. 1 ). One inlet and three outlets (named outlet O1, O2 and O3) with the same rectangular size of 0.2 × 0.3 m2 were installed. At each experimental run, the inlet and one of the outlets were opened to produce different airflow patterns. Poly-dispersed particles with a density of about 2100 kg/m3 were mixed with the supply airflow at the speed of 1.5 m/s and 0.5 m/s. Nine measuring points were uniformly located in the center plane of z direction as a 3 × 3 arrangement. They used a laser particle counter (CLJ–BII) to measure particle concentrations. Aerosol particle sizes were classified into five groups: 0.3–0.5 μm, 0.5–1.0 μm, 1.0–3.0 μm, 3.0–5.0 μm, and 5.0–10.0 μm.
Fig. 1.
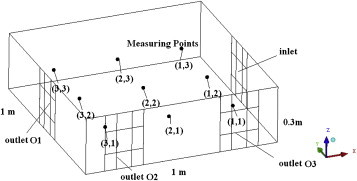
Geometry of the ventilated chamber.
According to the particle diameters distribution curve, two peak diameters (0.9 μm and 5 μm) were selected to validate the numerical model. The simulated chamber was of the same size with the experiments and was divided into 71,858 hexahedral cells. Particle concentrations at the measuring points in steady state in three cases (case a: outlet O1 opened, inlet air velocity 0.5 m/s; case b: outlet O2 opened, inlet air velocity 0.5 m/s; case c: outlet O2 opened, inlet air velocity 1.5 m/s) are shown in Fig. 2 .
Fig. 2.
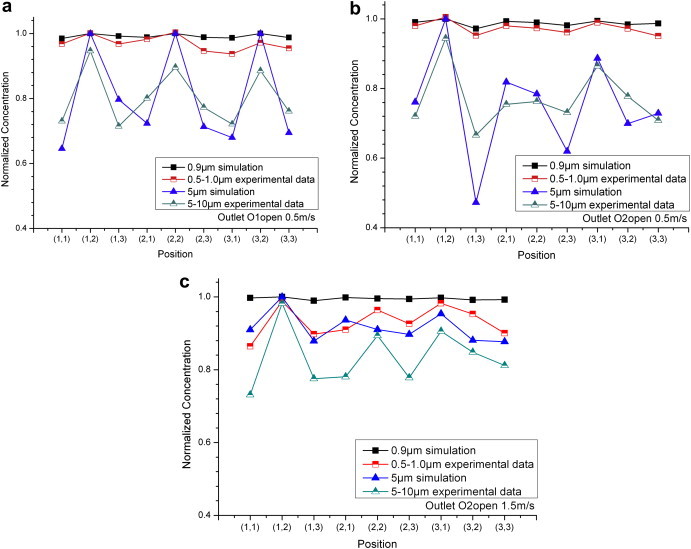
Comparisons of simulated and experimental particle concentrations at the measuring points (a: outlet O1 opened, inlet air velocity 0.5 m/s; b: outlet O2 opened, inlet air velocity 0.5 m/s; c: outlet O2 opened, inlet air velocity 1.5 m/s).
It is observed that the numerical values agreed with the experimental data reasonably. In case a, average relative errors of the nine measuring points were 2.3% for 0.9 μm particles and 9.5% for 5 μm particles. Maximum relative errors were 5.0% for 0.9 μm particles and 13.1% for 5 μm particles. In case b, average relative errors and maximum relative errors were 1.5% and 3.6% for 0.9 μm particles and 10.8% and 40.9% for 5 μm particles respectively. In case c, average relative errors and maximum relative errors were 6.4% and 13.3% for 0.9 μm particles and 9.0% and 19.7% for 5 μm particles. Given that the measuring errors of the experiments are unknown, simulation results with average relative errors below 10% for all the cases are acceptable. It indicates that the present numerical method can reasonably predict indoor particle concentrations.
4. Case descriptions
4.1. Case set-up and boundary conditions
The simulation model was set-up as a combination of experimental conditions of Cermak and Melikov [13], [14], [15]. The dimensions of the simulated office room were width (X) 4.8 m × length (Y) 5.4 m × height (Z) 2.6 m. The origin of the coordinate system was selected at the center of the floor plane (Fig. 3 ). Two numerical thermal manikins (75 W each) were identical in shape and were seated upright at the tables inside the office. Table 1 shows the detail of the geometry and center coordinates of the numerical thermal manikins used in this study. Constant heat-flux boundary conditions were set for the skins of the manikins. The front one was a polluting source (denoted as P) which exhaled infected airflow at 6 l/min and 35 °C [14] through the mouth (20 × 10 mm) [27] at 45° downward [22]. The back one was an exposed person (denoted as E) which inhaled airflow at 6 l/min through the mouth (20 × 10 mm) at 45° upward. Although the breathing rate is various in different studies [20], the experimental results of Rim and Novoselac [28] indicated that breathing of a sedentary manikin has little influence on the airflow field in the breathing zone and it has very small impact on the occupant’s thermal plume. The experimental results of Pantelic [12] also demonstrated that droplets concentrations measured in the breathing zone of a thermal manikin were similar with and without a normal breathing process. Therefore, the fixed breathing rate set in the current simulation instead of transient breathing curve is rational in regard to the evaluation of inhaled concentration of the exposed manikin and spatial distributions of pollutants.
Fig. 3.
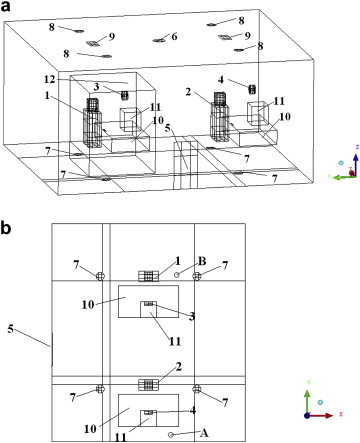
Configuration of the simulated office, a: three-dimensional view; b: top view (room width (X) 4.8 m, length (Y) 5.4 m, height (Z) 2.6 m; 1-the exposed person; 2-the polluting person; 3-RMP-E d = 190 mm; 4-RMP-P d = 190 mm; 5-DV inlet 500 × 1000 mm; 6-MV inlet d = 254 mm; 7-UFAD inlets d = 200 mm; 8-outlets d = 200 mm; 9-lamps; 10-tables; 11-monitors; 12-the exposed manikin’s occupied zone; A and B-measurement positions).
Table 1.
Geometry and center coordinates of the numerical thermal manikins (unit: m).
| Part | Dimensions (x × y × z) | Center coordinate of the polluting manikin (x, y, z) | Center coordinate of the exposed manikin (x, y, z) |
|---|---|---|---|
| Head | 0.168 × 0.200 × 0.249 | (0, −1.30, 1.31) | (0, 1.40, 1.31) |
| Body | 0.486 × 0.262 × 0.719 | (0, −1.30, 0.82) | (0, 1.40, 0.82) |
| Mouth | 0.01 × 0.02 | (0, −1.40, 1.22) | (0, 1.30, 1.22) |
Two monitors (198 W each) and two lamps (18 W each) were set as other heat sources. A round swirling diffuser (d = 254 mm) in the center of the ceiling was for MV inlet. A rectangular opening (500 × 1000 mm) as DV inlet was located at one side wall and four swirling diffusers (d = 200 mm) located at the floor were UFAD inlets. The air terminal devices of PV were two round movable panels (RMP) and the diameters of the RMPs were both 190 mm. One was used for the polluting manikin and the other for the exposed one. The distance between the center of the RMP-P (RMP-E) and the center of the mouth of the polluting (exposed) thermal manikin was 0.586 m. The room air was exhausted from four outlets on the ceiling. A rectangular exposed manikin’s occupied zone was chosen to investigate the pollutant concentration in the vicinity of him. The supply air temperature was 20 °C and total flow rate was 80 l/s (corresponding to 4.27 air changes per hour) for all the ventilation strategy combinations. Detailed conditions are listed in Table 2 . Totally fifteen airflow patterns were studied.
Table 2.
Detailed boundary conditions for TV and PV systems.
| Case | TV |
TV + RMP |
TV + RMP |
TV + RMP |
TV + RMP |
|---|---|---|---|---|---|
| alone | P7 + E7 | P15 + E15 | P0 + E15 | P15 + E0 | |
| MV Inlet | FR: 80 l/s | FR: 66 l/s | FR: 50 l/s | FR: 65 l/s | FR: 65 l/s |
| VA = 1.58 m/s | VA = 1.30 m/s | VA = 0.99 m/s | VA = 1.28 m/s | VA = 1.28 m/s | |
| VT = 3.16 m/s | VT = 2.61 m/s | VT = 1.98 m/s | VT = 2.57 m/s | VT = 2.57 m/s | |
| DV Inlet | FR: 80 l/s | FR: 66 l/s | FR: 50 l/s | FR: 65 l/s | FR: 65 l/s |
| V = 0.16 m/s | V = 0.13 m/s | V = 0.10 m/s | V = 0.13 m/s | V = 0.13 m/s | |
| UFAD Inlet × 4 | FR: 80 l/s | FR: 66 l/s | FR: 50 l/s | FR: 65 l/s | FR: 65 l/s |
| VA = 0.64 m/s | VA = 0.53 m/s | VA = 0.40 m/s | VA = 0.52 m/s | VA = 0.52 m/s | |
| VT = 0.64 m/s | VT = 0.53 m/s | VT = 0.40 m/s | VT = 0.52 m/s | VT = 0.52 m/s | |
| RMP-E | N/A | FR: 7 l/s | FR: 15 l/s | FR: 15 l/s | N/A |
| V = 0.25 m/s | Vy = 0.53 m/s | Vy = 0.53 m/s | |||
| Vz = −0.17 m/s | Vz = −0.17 m/s | ||||
| RMP-P | N/A | FR: 7 l/s | FR: 15 l/s | N/A | FR: 15 l/s |
| V = 0.25 m/s | Vy = 0.53 m/s | Vy = 0.53 m/s | |||
| Vz = −0.17 m/s | Vz = −0.17 m/s | ||||
Note: FR: flow rate; VA: Axial-velocity; VT: Tangential-velocity. The fifteen cases are: MV80 + P0 + E0, MV66 + P7 + E7, MV50 + P15 + E15, MV65 + P0 + E15, MV65 + P15 + E0, DV80 + P0 + E0, DV66 + P7 + E7, DV50 + P15 + E15, DV65 + P0 + E15, DV65 + P15 + E0, UFAD80 + P0 + E0, UFAD66 + P7 + E7, UFAD50 + P15 + E15, UFAD65 + P0 + E15, UFAD65 + P15 + E0. Here for example, MV50 + P15 + E15 means the supply airflow rate for MV is 50 l/s, for PV of the polluting manikin 15 l/s, and for PV of the exposed manikin 15 l/s.
Morawska et al. [17] found that non-equilibrium droplet evaporation was not detectable for particles between 0.5 and 20 μm and implied that evaporation to the equilibrium droplet size occurred within 0.8 s of the exhalation process. Chen and Zhao [29] also studied evaporation processes of human exhaled droplets numerically. They found that when particle diameters were below 100 μm the results of droplets transmission indoors were quite similar with and without the evaporation process. Based on these findings, we chose to simulate 0.8 μm, 5 μm, 16 μm droplets as well as tracer gas exhaled from the mouth of the polluting manikin. The density of particles was 1000 kg/m3 and the evaporation process of droplets was not considered.
4.2. Grid generations and independence test
Due to the complex geometry of the simulated model, hybrid mesh scheme was used to generate grid systems. The unstructured tetrahedral meshes were created in the occupied zone of the manikins whereas the hexahedral mesh style was used for the rest of the room. Two mesh systems were generated to test grid independence. The coarse system contained 416,752 cells and the fine one 994,634 cells.
Because the complex flow pattern involving natural convection and forced convection in the room, grid convergence test is really a great challenge. Direct comparisons of velocity magnitude at four vertical lines close to the manikins are presented in Fig. 4 . The discrepancies of velocity magnitude for coarse and fine meshes were in an acceptable range. With a comprehensive consideration of computational accuracy and cost, the coarse mesh was selected in this research.
Fig. 4.
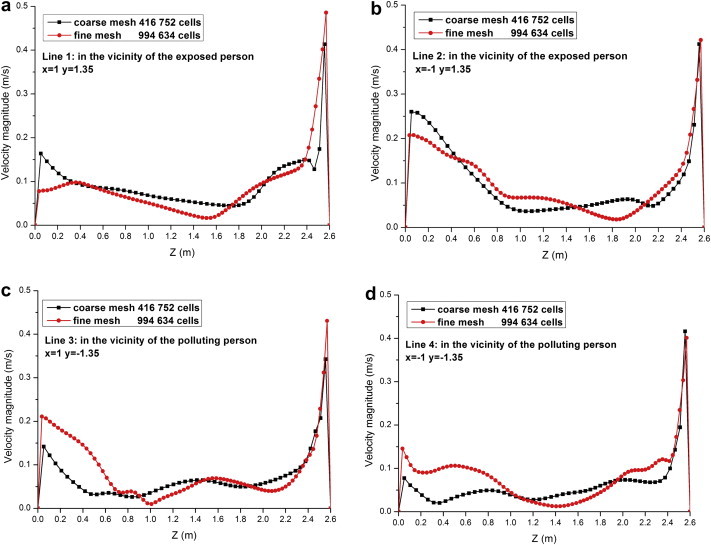
Comparisons of velocity magnitude at four vertical lines close to the manikins (a, b in the vicinity of the exposed manikin; c, d in the vicinity of the polluting manikin.).
4.3. Evaluation index
The exposure was evaluated by intake fraction (IF) [30]. Intake fraction is defined as the proportion of pollutant mass emitted from a source that is inhaled by an individual. For the current situation it can be expressed as:
| (6) |
in which C E, C P are area-weighted average concentrations of pollutant at the mouth of the exposed and the polluting manikin, respectively. M E is the mass flow rate inhaled by the exposed manikin, and M P is the mass flow rate exhaled by the polluting manikin. M E equals to M P here.
For tracer gas, due to mass conservation, the average gas concentration at outlets was the same for all the cases. Intake fraction therefore can be converted to ventilation effectiveness (VE) which is used to assess the performance of ventilation systems popularly [13], [14], [15], [31]. Ventilation effectiveness is defined as:
| (7) |
where C in, C out and C E are area-weighted average concentrations of tracer gas at inlet, outlet, and the mouth of the exposed manikin, individually. Since the supply air is free of contamination, C in = 0. VE can be rewritten as:
| (8) |
and .
For particles, because of deposition processes, particle concentrations at outlets in different settings were case-dependent. It is more reasonable to use intake fraction instead of ventilation effectiveness to evaluate the performance of ventilation systems.
Since steady-state simulation was performed in this paper, a steady-state concentration uniformity index R C was proposed (similar to that defined by Mage and Ott [32] in unsteady-state mixing process) to estimate the level of pollutant mixing for different ventilation strategies. R C is defined as:
| (9) |
where Ci is the concentration in each control volume and is the volume average concentration of the office room. N cell is the total cell number in the computational domain. If the concentration is uniform in the room, Ci equals to at every cell and R C = 0. A high value of R C represents weak mixing of pollutants and significant concentration differences.
5. Results and discussions
5.1. Overall concentration distributions of the three TV systems (MV, DV and UFAD)
Fig. 5 demonstrates the average normalized concentrations (by the value in the exhaled air of the polluting manikin) in horizontal planes across the room at different height levels of MV, DV and UFAD. Concentrations of tracer gas and particles were almost uniformly distributed along room height in MV, which showed a well-mixed phenomenon. With the increase of particle size, the concentration level decreased. This is because particles in this study were among the accumulation model and coarse model [30]. Particle deposition amount is much more significant for large particles than small ones. There was a peak concentration value for all particles and tracer gas at the height of 1.1–1.4 m above the floor because this is the height of exhalation of the polluting manikin.
Fig. 5.
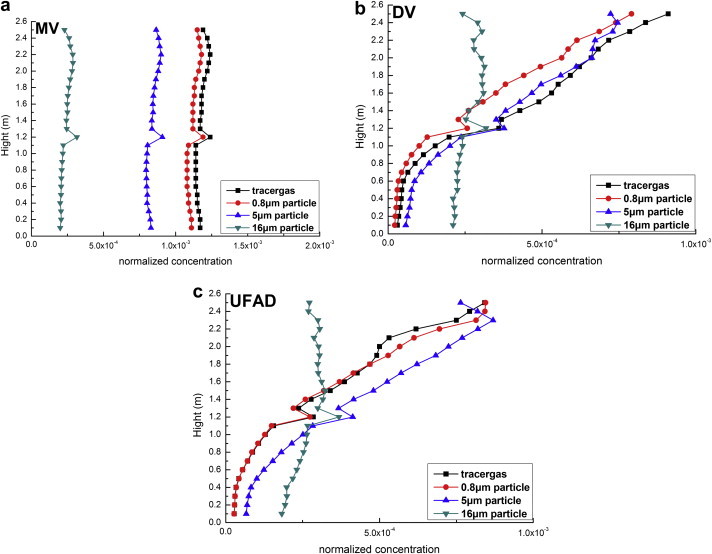
Average normalized concentrations in horizontal planes across the room at different height levels of a: MV, b: DV and c: UFAD. The concentration of the exhaled air from the polluting manikin is denoted as 1.0.
For DV and UFAD, concentration distributions for tracer gas, 0.8 μm, and 5 μm particles were similar and obeyed the general stratification principle of DV and UFAD, in which there is a clean zone in the lower level of the room and a pollution zone in the upper level. The two zones were separated at the height of about 1.1–1.4 m.
For 16 μm particles, particle concentrations were uniform and were approximately the same under the three TV strategies due to their large gravitational force. This finding indicates that for 16 μm and larger particles DV and UFAD may lose their advantages in providing better indoor air quality in the occupied zone than MV. In other words, the stratification phenomenon disappears. However, in these cases the intensive deposition is self-cleaning mechanism.
Fig. 6 compares simulated concentrations of tracer gas to experimental data obtained from Cermak and Melikov [13] under DV at two measuring positions near the polluting and the exposed manikins (A and B in Fig. 3). It was found that the profiles of the simulated results and the measured ones show a similar tendency. The discrepancies are mainly due to that the exact coordinates of the measuring positions and boundary conditions in the literature [13] are not clearly presented.
Fig. 6.
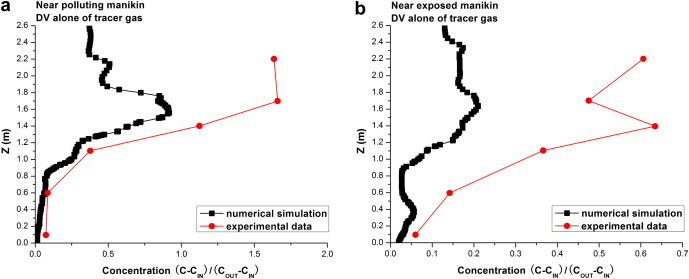
Comparisons of simulated concentrations of tracer gas to experimental ones under DV at two measuring positions near the polluting manikin (a) and the exposed manikin (b).
5.2. Performance of different ventilation strategies on protecting the exposed manikin
5.2.1. Performance of TV systems
Fig. 7 illustrates intake fraction of all the fifteen cases in Table 2 for tracer gas and particles of the exposed manikin. For tracer gas, 0.8 μm particles, and 5 μm particles, IF of MV alone was about one order of magnitude higher than that of DV and UFAD. Generally, IF of UFAD alone for 0.8 μm particles and 5 μm particles were slightly higher than that of DV. This is because UFAD is a partial stratified ventilation system. High momentums from swirling diffusers of UFAD enhance mixing of pollutants in the lower region of the room which results in relatively higher concentrations in the occupied zone of the exposed manikin (also shown in Fig. 10). It could be envisaged that weak mixing and strong stratification in the occupied zone is able to restrict lateral dispersion of particles and consequently protect the occupants. For 16 μm particles, IFUFAD > IFMV > IFDV. UFAD held the highest IF for 16 μm particles because the upward swirling airflows hinder local deposition and promote mixing of heavy 16 μm particles greatly in the lower region near the exposed manikin. DV system performed best of all on protecting the exposed manikin from pollutants exhaled by the polluting manikin.
Fig. 7.
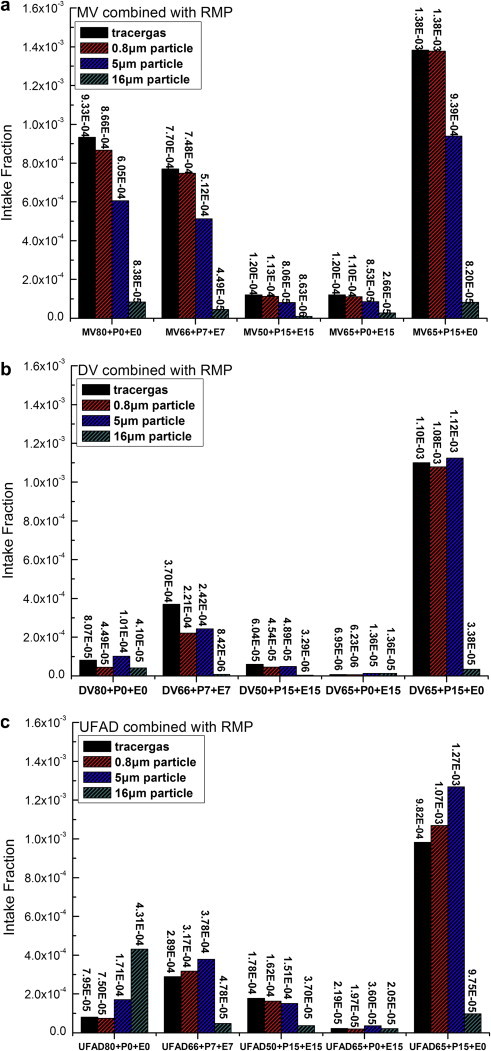
Intake fraction of PV in conjunction with MV (a), DV (b), and UFAD (c) for tracer gas and particles of the exposed manikin.
Fig. 10.
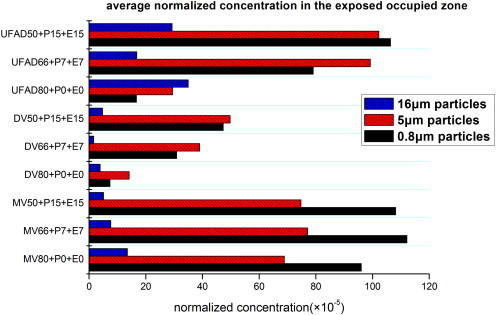
Average normalized concentrations in the exposed occupied zone. The concentration of the exhaled air from the polluting manikin is denoted as 1.0.
5.2.2. Performance of MV based PV systems
In the three MV based cases, when the exposed manikin using RMP, the inhaled air quality would be improved for both tracer gas and particles. The degree of RMP on improving inhaled air quality of the exposed manikin depends on its airflow rate. Large airflow rate of RMP, e.g. 15 l/s performed best because it could maintain the jet core region of clean personalized air to the breathing zone. Fig. 8 demonstrates the velocity vectors at the vicinity of the exposed manikin. It could be seen that the velocity magnitude at the mouth of the exposed manikin at the PV flow rate of 15 l/s was around 0.55 m/s to 0.40 m/s. This agreed well with the result of about 0.48 m/s by Cermak and Melikov [13]. The velocity magnitude at the PV flow rate of 7 l/s was around 0.21 m/s to 0.09 m/s. The personalized air jet was much weaker and the trajectory was clearly bended due to the negative buoyancy.
Fig. 8.
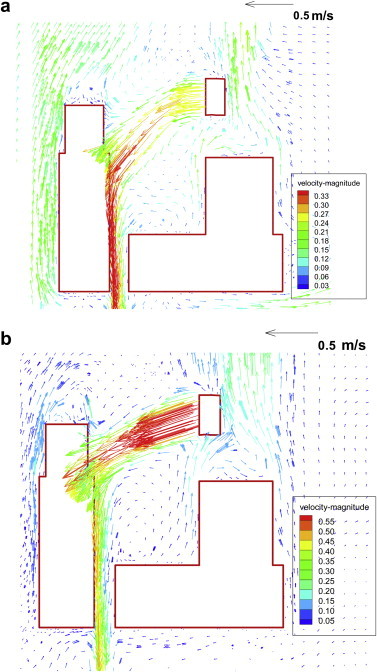
Velocity vectors at the vicinity of the exposed manikin under MV based conditions (a) MV66 + P7 + E7; (b) MV50 + P15 + E15.
When RMP for the exposed manikin was switched on, such as the case MV65 + P0 + E15 and MV50 + P15 + E15, IF was similar whether RMP for the polluting manikin was used or not. When RMP for the exposed manikin was switched off and RMP for the polluting manikin switched on, IF of the exposed manikin was the highest for tracer gas, 0.8 μm and 5 μm particles.
5.2.3. Performance of DV and UFAD based PV systems
When RMP combines with DV, the results of using PV for the exposed manikin are not always optimistic. For tracer gas, 0.8 μm, and 5 μm particles, when both the exposed and the polluting manikin used RMP at 7 l/s, IF of the exposed manikin was much higher than that of DV alone. When PV airflow rate was 15 l/s each, IF of the exposed manikin was a little smaller than using DV alone. This is because personalized air promotes dispersion of the exhaled particles as well as protects the exposed manikin by direct supply of fresh air in the breathing zone. Whether IF of the exposed manikin would decrease or increase depends on the balance of these two factors, one of which is positive and the other is negative. Fig. 9 illustrates normalized concentration contours of 0.8 μm particles in the center plane of x-direction under DV based conditions. It was observed that in stratified DV based conditions using RMP for the polluting manikin could increase particle concentrations around the exposed one greatly. The jet of PV airflow at 7 l/s decayed remarkably before it reached the breathing zone of the exposed manikin. Generally the effect of providing a small flow rate of clean personalized air cannot counteract the increment of concentration in the occupied zone. At the flow rate of 15 l/s, the effect of local fresh air supply almost matched the concentration augment caused by the personalized air of the polluting manikin. Therefore, the IF values in case DV50 + P15 + E15 and DV alone in Fig. 7(b) are comparable. The worst situation appeared if RMP for the polluting manikin opened and for the exposed manikin closed. In the case DV65 + P15 + E0, the exposure reached two orders of magnitude higher than in DV alone.
Fig. 9.
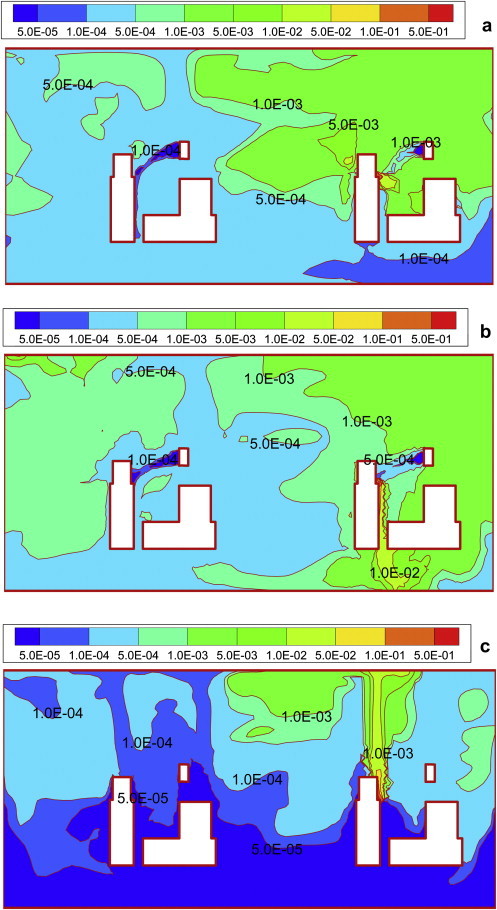
Normalized concentration contours of 0.8 μm particles at the center plane of x-direction under DV based conditions (a) DV66 + P7 + E7; (b) DV50 + P15 + E15; (c) DV alone.
For 16 μm particles, downward airflow from RMP could suppress large particles, improved their deposition onto the floor, and thus decreased the ambient concentration. Therefore, application of RMP could always protect the exposed manikin from large particles. The IFs of the exposed manikin under UFAD based conditions were similar with DV based conditions except that they were slightly higher.
5.3. Influence of PV airflow on droplet concentration uniformities and distributions
Table 3 lists concentration uniformity index R C in the room under different TV and PV combinations. Concentration uniformity index R C was used to quantitatively evaluate the mixing degree of exhaled droplets. In this paper, low R C means well mixing and it could lead to high infection probability of the exposed manikin without PV airflow protection. For 0.8 μm particles, R C s of DV and UFAD were almost the same and were about 2.6 times higher than R C of MV. For 5 μm particles, R C s of DV and UFAD were also similar but only about 1.2 times higher than R C of MV. For 16 μm particles, R C of the three TV systems were nearly the same, which agreed with the results in Fig. 5. It implies that with the increasing of particle size the influence of different TV airflow patterns on indoor particle concentration uniformity becomes less significant.
Table 3.
Concentration uniformity index RC under different TV and PV combinations.
|
RC |
|||
|---|---|---|---|
| 0.8 μm | 5 μm | 16 μm | |
| MV80 + P0 + E0 | 11.58 | 15.38 | 51.41 |
| MV66 + P7 + E7 | 6.66 | 9.24 | 55.88 |
| MV50 + P15 + E15 | 5.86 | 8.09 | 61.59 |
| DV80 + P0 + E0 | 41.75 | 33.99 | 45.43 |
| DV66 + P7 + E7 | 9.04 | 8.71 | 35.30 |
| DV50 + P15 + E15 | 7.68 | 7.95 | 33.26 |
| UFAD80 + P0 + E0 | 43.70 | 34.04 | 50.45 |
| UFAD66 + P7 + E7 | 8.85 | 7.89 | 31.11 |
| UFAD50 + P15 + E15 | 6.39 | 7.06 | 33.74 |
Using PV for both the pollutant and the exposed manikin resulted in lowering R C for 0.8 μm and 5 μm particles for all the three TV systems, with various degrees of reduction under different TV conditions. For 0.8 μm particles, R C in the case DV66 + P7 + E7 and UFAD66 + P7 + E7 was only about 20% of that in DV80 + P0 + E0 and UFAD80 + P0 + E0, respectively. R C of MV66 + P7 + E7 was about 57% of that in MV80 + P0 + E0. The trend of R C reduction for 5 μm particles was similar in the corresponding conditions, although it was less pronounced. Table 3 also shows that using PV led to much higher reductions of R C for DV and UFAD than for MV. This is reasonable, because DV and UFAD are stratified ventilation systems whereas MV is a well-mixed system. Therefore, additional mixing caused by PV would promote the concentration uniformity much more strongly for DV and UFAD than for MV, compared to the cases without PV. R C changed by a small value in all the cases when the total PV flow rates increased from 14 l/s to 30 l/s. For 16 μm particles, the influence of additional mixing through using personalized air was not obvious for all the cases.
R C is an overall index to estimate the level of pollutant mixing in the whole office. In present study, using PV can reduce R C which could increase pollutant concentration in the office room. However, generally speaking, since in essence R C is a normalized value and has the characteristics of a standard deviation, there is no certain relationship between R C and the concentration level. Fig. 10 illustrates average normalized concentrations in the occupied zone of the exposed occupant (see Fig. 3). Total amount of inhaled pollutants of the exposed manikin can be expressed as follows:
| (10) |
in which C E is area-weighted average concentration of pollutant at the mouth of the exposed manikin, C A is volume averaged concentration in the exposed occupied zone, C PV is pollutant concentration in the PV airflow which is zero in the current study. f is the mass fraction of personalized air in the total inhaled air. Fig. 10 shows that using RMP for both manikins always increased C A except for 16 μm particles. Whether C E could be decreased or increased depends on the balance of pros and cons of using PV. For example, for 0.8–5 μm particles, in the case MV66 + P7 + E7 and MV50 + P15 + E15, C A was just slightly higher than in MV80 + P0 + E0 due to the well-mixed characteristic of MV. The positive effect of f could always overcome the negative influence of increased C A.
6. Conclusions
This study used an Eulerian drift-flux method to investigate the transmission of exhaled droplets through breathing process between two occupants both of whom were equipped with PV systems in a full-scale office room. One manikin acted as a polluting source and the other was exposed. Particle sizes of 0.8 μm, 5 μm, and 16 μm as well as tracer gas were studied. The main conclusions are as follows:
-
1.
Concentrations of tracer gas and particles were nearly uniformly distributed in MV. Intensive deposition effect of coarse particles resulted in a lower concentration level than fine particles and tracer gases. Concentration stratification in DV and UFAD was found for tracer gas and particles up to 5 μm in the current study. As to 16 μm particles, the stratification phenomenon disappeared.
-
2.
For tracer gas and particles smaller than 5 μm, the intake fraction (IF) of the exposed manikin was almost an order of magnitude higher in MV than in DV and UFAD. Performance of DV was slightly better than UFAD. However, for 16 μm particles, IFUFAD > IFMV > IFDV. The stirring effect in the lower zone of the room caused by the swirling supply flow may limit the settlement of 16.0 μm particles and lead to a longer suspension of them.
-
3.
For MV based conditions, in present study when the exposed manikin using RMP the inhaled air quality could be improved. Large airflow rate of RMP performed better than small flow rate. For DV and UFAD based conditions, however, PV has the possibility to increase the intake fractions for tracer gas, 0.8 μm particles, and 5 μm particles, which is contrary to the original intention to use PV.
-
4.
Momentum of personalized air will reduce R C of 0.8 μm and 5 μm particles for all the three TV systems. Further, PV enhanced mixing degree of particles under DV and UFAD much stronger than under MV. R C did not change a lot for all cases when the total PV airflow increased from 14 l/s to 30 l/s. For 16 μm particles, the effect of promoting mixing by the personalized air was not obvious for all the cases.
-
5.
Application of PV can increase C A as well as increase f. Whether the exposure could be decreased or increased depended on the balance of pros and cons of PV.
In this paper, we modeled the normal breathing process of the polluting manikin. However, coughed/sneezed airflow with a high initial velocity may result in different transport behavior of exhaled droplets in the circumstance where PV is used. It could be envisaged that relative locations of the manikins also play a key role in the exposure. These are worthy of further studies.
Acknowledgement
This study was financially supported by the Research Grant Committee, Hong Kong, China, under the project No. RGC GRF 526508, the National Natural Science Foundation of China under the project No. 50808133, and Program of Young Excellent Teachers in Tongji University.
References
- 1.Mangili A., Gendreau M.A. Transmission of infectious diseases during commercial air travel. Lancet. 2005;365:989–996. doi: 10.1016/S0140-6736(05)71089-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Han K., Zhu X.P., He F., Liu L.G., Zhang L.J., Ma H.L. Lack of airborne transmission during outbreak of pandemic (H1N1) 2009 among tour group members, China, June 2009. Emerging Infectious Diseases. 2009;15:1578–1581. doi: 10.3201/eid1510.091013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wagner B.G., Coburn B.J., Blower S. Calculating the potential for within-flight transmission of influenza A (H1N1) BMC Medicine. 2009;7 doi: 10.1186/1741-7015-7-81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Li Y., Leung G.M., Tang J.W., Yang X., Chao C.Y.H., Lin J.Z. Role of ventilation in airborne transmission of infectious agents in the built environment – a multidisciplinary systematic review. Indoor Air. 2007;17:2–18. doi: 10.1111/j.1600-0668.2006.00445.x. [DOI] [PubMed] [Google Scholar]
- 5.Gao N., Niu J., Morawska L. Distribution of respiratory droplets in enclosed environments under different air distribution methods. Building Simulation. 2008;1:326–335. [Google Scholar]
- 6.To G.N.S., Wan M.P., Chao C.Y.H., Fang L., Melikov A. Experimental study of dispersion and deposition of expiratory aerosols in aircraft cabins and impact on infectious disease transmission. Aerosol Science and Technology. 2009;43:466–485. [Google Scholar]
- 7.Wan M.P., To G.N.S., Chao C.Y.H., Fang L., Melikov A. Modeling the fate of expiratory aerosols and the associated infection risk in an aircraft cabin environment. Aerosol Science and Technology. 2009;43:322–343. [Google Scholar]
- 8.Chao C.Y.H., Wan M.P., To G.N.S. Transport and removal of expiratory droplets in hospital ward environment. Aerosol Science and Technology. 2008;42:377–394. [Google Scholar]
- 9.Richmond-Bryant J. Transport of exhaled particulate matter in airborne infection isolation rooms. Building and Environment. 2009;44:44–55. doi: 10.1016/j.buildenv.2008.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mui K.W., Wong L.T., Wu C.L., Lai A.C.K. Numerical modeling of exhaled droplet nuclei dispersion and mixing in indoor environments. Journal of Hazardous Materials. 2009;167:736–744. doi: 10.1016/j.jhazmat.2009.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Melikov A.K. Personalized ventilation. Indoor Air. 2004;14:157–167. doi: 10.1111/j.1600-0668.2004.00284.x. [DOI] [PubMed] [Google Scholar]
- 12.Pantelic J., Sze-To G.N., Tham K.W., Chao C.Y.H., Khoo Y.C.M. Personalized ventilation as a control measure for airborne transmissible disease spread. Journal of the Royal Society Interface. 2009;6:S715–S726. doi: 10.1098/rsif.2009.0311.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cermak R., Melikov A.K., Forejt L., Kovar O. Performance of personalized ventilation in conjunction with mixing and displacement ventilation. International Journal of Heating, Ventilating, Air-Conditioning and Refrigerating Research. 2006;12:295–311. [Google Scholar]
- 14.Cermak R., Melikov A.K. Protection of occupants from exhaled infectious agents and floor material emissions in rooms with personalized and underfloor ventilation. International Journal of Heating, Ventilating, Air-Conditioning and Refrigerating Research. 2007;13:23–38. [Google Scholar]
- 15.Melikov AK, Cermak R, Kovar O, Forejt L. Impact of airflow interaction on inhaled air quality and transport of contaminants in rooms with personalized and total volume ventilation. Proceedings of Healthy Buildings 2003, Singapore 2003. p. 592–7.
- 16.Nicas M., Nazaroff W.W., Hubbard A. Toward understanding the risk of secondary airborne infection: emission of respirable pathogens. Journal of Occupational and Environmental Hygiene. 2005;2:143–154. doi: 10.1080/15459620590918466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M., Mengersen K., Corbett S. Size distribution and sites of origin of droplets expelled from the human respiratory tract during expiratory activities. Journal of Aerosol Science. 2009;40:256–269. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chao C.Y.H., Wan M.P., Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. Journal of Aerosol Science. 2009;40:122–133. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fluent. Fluent 6.3 User’s Guide. Lebanon, NH 03766, USA; 2006.
- 20.Gao N.P., Niu J.L. CFD study of the thermal environment around a human body: a review. Indoor and Built Environment. 2005;14:5–16. [Google Scholar]
- 21.Chen F.Z., Yu S.C.M., Lai A.C.K. Modeling particle distribution and deposition in indoor environments with a new drift-flux model. Atmospheric Environment. 2006;40:357–367. [Google Scholar]
- 22.Gao N.P., Niu J.L. Modeling particle dispersion and deposition in indoor environments. Atmospheric Environment. 2007;41:3862–3876. doi: 10.1016/j.atmosenv.2007.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhang Z., Chen Q. Prediction of particle deposition onto indoor surfaces by CFD with a modified Lagrangian method. Atmospheric Environment. 2009;43:319–328. [Google Scholar]
- 24.Hinds W.C. 2nd ed. A Wiley-Interscience Publication; New York: 1998. Aerosol technology: properties, behavior, and measurement of airborne particles. [Google Scholar]
- 25.Lai A.C.K., Nazaroff W.W. Modeling indoor particle deposition from turbulent flow onto smooth surfaces. Journal of Aerosol Science. 2000;31:463–476. [Google Scholar]
- 26.Jin H.H., Li Q.P., Chen L.H., Fan J.R., Lu L. Experimental analysis of particle concentration heterogeneity in a ventilated scale chamber. Atmospheric Environment. 2009;43:4311–4318. [Google Scholar]
- 27.Lai A.C.K., Cheng Y.C. Study of expiratory droplet dispersion and transport using a new Eulerian modeling approach. Atmospheric Environment. 2007;41:7473–7484. doi: 10.1016/j.atmosenv.2007.05.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rim D., Novoselac A. Transport of particulate and gaseous pollutants in the vicinity of a human body. Building and Environment. 2009;44:1840–1849. [Google Scholar]
- 29.Chen C., Zhao B. Some questions on dispersion of human exhaled droplets in ventilation room: answers from numerical investigation. Indoor Air. 2010;20:95–111. doi: 10.1111/j.1600-0668.2009.00626.x. [DOI] [PubMed] [Google Scholar]
- 30.Nazaroff W.W. Indoor particle dynamics. Indoor Air. 2004;14:175–183. doi: 10.1111/j.1600-0668.2004.00286.x. [DOI] [PubMed] [Google Scholar]
- 31.Nielsen P.V. Control of airborne infectious diseases in ventilated spaces. Journal of the Royal Society Interface. 2009;6:S747–S755. doi: 10.1098/rsif.2009.0228.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mage D., Ott W. Accounting for nonuniform mixing and human exposure in indoor environments. In: Tichenor Bruce A., editor. Characterizing sources of indoor air pollution and related sink effects. American Society for Testing and Materials; 1996. [Google Scholar]


