Abstract
Focus a laser on dissolved particles and analyze the scattered light to reveal their size. This well established principle is used in dynamic light scattering (DLS), or also called photon-correlation spectroscopy, which is a widely popular and highly adaptable analytical method applied in different fields of life and material sciences, as well as in industrial quality control processes.
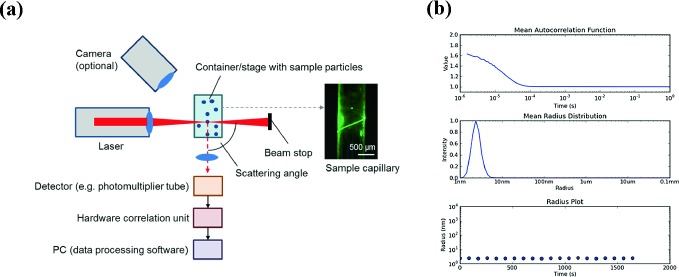
Focus a laser on dissolved particles and analyze the scattered light to reveal their size. This well established principle is used in dynamic light scattering (DLS), or also called photon-correlation spectroscopy, which is a widely popular and highly adaptable analytical method applied in different fields of life and material sciences, as well as in industrial quality control processes. Fluctuations of elastic laser light scattering due to the particle’s individual Brownian motion in a solvent can be utilized to determine particle size distributions in real-time. DLS usually uses non-invasive visible laser light that is focused on a sample solution, suspension, emulsion or aerosol inside a sample container, commonly a cuvette or a capillary. Besides, a few more general components are required for a typical DLS device, as shown in Fig. 6.1.
Fig. 6.1.
a Scheme of a light scattering setup. Light scattered by the particles over time at a scattering angle θ is focused onto a detector or detector-connected fiber cable for further downstream data processing. b Exemplary DLS data of an L-form DNAzyme (5′-GAAGTTAGCAACATCGATCGGAGGCGG-3′) in solution containing MES buffer as evaluated by the accompanying software. Autocorrelation function, half-logarithmic mean particle radius distribution and particle radius plot of the molecules are indicating a homogeneous monodisperse solution and a hydrodynamic radius of 2.4 ± 0.1 nm. Details about data processing are described in the following sections
The method DLS and underlying principles are known for several decades already (Mueller and Givens 1961; Cummins et al. 1964; Chu 1970; Fujime 1972), whereas the development of single-mode fiber cables, improvement of detection optics, variation of sample containers and introduction of affordable diode-pumped solid-state lasers as light source advanced the applications of DLS tremendously later on and particularly during the last years (Brown 1987; Dhadwal and Chu 1989; Brown and Smart 1997; Minton 2016). In terms of data processing, digital autocorrelators (Foord et al. 1970), the monomodal cumulant analysis (Koppel 1972) and the CONTIN algorithm (Provencher 1982) are a few of the milestones.
After briefly explaining the physical principles and requirements of light scattering techniques, different biological samples, recently established setups for in situ DLS experiments and selected applications will be introduced. An additional section will provide practical guidelines and hints for sample preparation. Further a short section is summarizing selected complementary analytical methods. The chapter overall focuses on exemplary biochemical sample solutions and the respective applications, even though all principles are well applicable to other fields of natural sciences targeting nano particles. Areas of applications and especially much further physical detail of light scattering and data processing were covered for example by Berne and Pecora (2000) and within the series of Light Scattering Reviews books edited by Kokhanovsky (2006). Exemplary biological applications were discussed in addition more recently (Minton 2016).
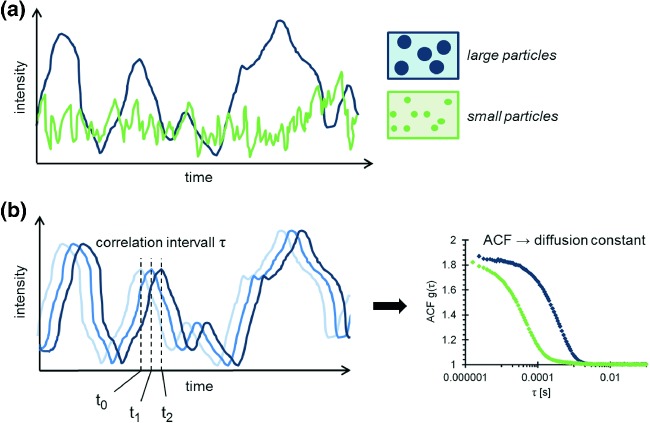
In general, all kinds of particles scatter electromagnetic waves in all directions, depending on their size isotropically or anisotropically. The laser light that is scattered by the particles inside a small focal volume of a DLS sample is continuously recorded and quantified by a photon-counting detector positioned at a specific angle; if not hindered by other geometrical restraints, an angle of 90° might be suitable for the experimental setup. The number of photons hitting the detector, which can be a photo-multiplier tube, is fluctuating over time. This is explained by Brownian motion of particles in and around the sample volume that is in focus of the laser (Fig. 6.2), which results in characteristic size-dependent fluctuation intervals of the electric field component of the scattered light. Scattering intensity pattern are correlated with themselves (auto-correlation) after short delay intervals of time (τ) to monitor the continuous decay of correlation. Depending on how fast particles are diffusing, the correlation decay time constants, which are derived from the exponential auto-correlation function (ACF) are individually different. Decay time constants of small particles are shorter in agreement with the dependency of diffusion speed on particle mass (Fig. 6.2). The ACF can be evaluated by the CONTIN algorithm according to Provencher (1982), which allows to fit even a complex decay of correlation in polydisperse solutions to calculate the respective diffusion constants (D) and process the data. As for most measurements the temperature T is kept constant and the viscosity η of the sample solution is known, or can be determined rather easily, this translational diffusion constant D can be used to determine the hydrodynamic radius rh of a corresponding spherical particle, according to the Stokes-Einstein equation (Eq. 6.1). This relationship between diffusion and size was established in 1906 and is also useful for complementary methods like Taylor-Dispersion analysis or nano particle tracking analysis (kB is the Boltzmann constant 1.380648 × 10−23 J K−1):
| 6.1 |
Fig. 6.2.
DLS determines particle sizes based on the velocity of Brownian motion: a Generalized illustration of the time-dependent intensity of light scattered by particles, which is fluctuating due to Brownian motion. Mixtures of small and large particles would result in a weighted average of the two displayed scattering intensity pattern. b Schematic illustration of the auto-correlation. Depending on the particle size, the diffusion speed and hence the time scale of the correlation coefficient decay is varying. Accordingly two auto-correlation functions (g(τ)) for a small (green) and a larger (blue) particle species are shown on the right side
Depending on the implemented auto-correlation unit (and a few other parameters of the setup), particles in a wide range of hydrodynamic radii, typically from below 1 nm up to a few µm, which corresponds to a molecular weight range from approx. 10 kDa to several MDa for compact globular macromolecules, can be investigated. Further, all changes of D over time for given particles, typically due to particle size changes, can also be followed in real time. DLS is very often used in preparation and systematic optimization of sample solutions (pH-value, ionic strength, solvent etc.) to meet strict requirements of particle homogeneity and long-term stability in further structural investigation of macromolecules, see e.g. Borgstahl (2006) in terms of X-ray crystallography or exemplified for RNA-protein complexes (Stetefeld et al. 2016). In this context DLS is frequently used in combination with other scattering techniques or mass spectrometry. For example small-angle X-ray scattering (SAXS), NMR spectroscopy and crystallization experiments usually require a high degree of particle size homogeneity, i.e. a monodisperse solution (Jeffries et al. 2016). Today, individual light scattering techniques and setups allow to manipulate the solution composition during the experiment (Meyer et al. 2012), investigate sample solutions in flow, to investigate a sample suspension at different neighboring positions in parallel (Falke et al. 2018), determine the net surface charge of molecules (Ware 1974) or even allow to obtain limited shape and structure information in situ (Cantor and Schimmel 1980; Minton 2007; Haghighi et al. 2013; Schubert et al. 2015) as outlined in following sections of this chapter. Especially for in situ DLS instruments with freely adjustable laser probe the alignment of the optics, i.e. the superposition of the focal points of the laser and the focal point of the lens that focusses the scattered light on a receiver fiber should be verified via a set of screws with µm precision to obtain optimal performance.
Principles of Light Scattering
In contrast to methods like Raman spectroscopy, DLS is based on elastic electromagnetic scattering of the dispersing particles. The electric field component of laser light waves is interacting with sample molecules by inducing oscillating (point source) electric dipoles within the molecule at the same frequency, resulting in the emission of light. Light is scattered spherically in all directions, while maintaining nearly constant energy of the photons. Most samples of interest for a biochemist, like proteins in solution, are much smaller than the wavelength of the applied DLS laser (<0.1λ) allowing light penetration and isotropic scattering according to the laws of Rayleigh scattering (Barnett 1942) named after the British physicist Lord Rayleigh. The scattered light is typically not coherent and the spherical waves interfere with each other. The intensity of scattered light I depends on other setup parameters such as the wavelength λ, the scattering angle θ, the distance from the scattering particle s, the refractive index n of the medium and the particle radius r:
| 6.2 |
The average value of I over all scattering angles is commonly called scattering cross section. The scattering intensity is notably inverse proportional to the forth power of the laser wavelength, which makes a shorter wavelength very attractive for the detection of otherwise weakly scattering molecules. However, an increased intensity of “background” reflections of laser light can obviously reduce the sensitivity of the instrument again. Further, the focal lengths of lenses should be shortened as possible, according to I ~ s−2. Also probe position and fiber cables should be optimized accordingly. For additional optimization, glass surfaces may be coated with a thin layer of MgF2 or a similar solid material with low refractive index, to minimize reflection of laser light. Further, the light scattering intensity depends on the sixth power of the particle diameter. Consequently, larger particles contribute to the total scattering intensity exponentially more with increasing size, making DLS particularly sensitive for clustering (very large oligomers or unspecific large aggregates) compared to smaller molecules. When the diameter of the particles increases to the size regime of the laser wavelength, the particles create shape dependent anisotropic Mie scattering (referring to the German physicist Gustav Adolf Mie) distorted in forward direction (Mie 1908). One example is sun light scattered by spherical lipid droplets in diluted milk. For particles significantly larger than the wavelength, surface reflection becomes predominant and the scattering cross section, which determines how much light is scattered by the particle, only weakly depends on the light frequency.
Accordingly, it is important to consider a suitable scattering angle for an experimental DLS setup. DLS measurements of inhomogeneous and therefore polydisperse solutions with large particles should ideally be expanded to measurements at different scattering angles exploiting multi-angle light scattering (MALS) (Fernández and Minton 2009). MALS is beneficially combined with size-exclusion chromatography, which can optionally be equipped with a UV absorbance and refractive index detector for a most accurate approximation of the molecular weight M (Graewert et al. 2015; Minton 2016) of unknown biological macromolecules using scattering intensity I and refractive index RI:
| 6.3 |
| 6.4 |
Scattering Data Processing
As illustrated by Fig. 6.2, an ACF of scattered light at time point t, depending on the correlation time delay τ, is generated during a DLS experiment. A second order ACF is generally given by:
| 6.5 |
The additional brackets indicate averaging over time of the respective intensity value products in a single measurement. For experiments that use different scattering angles and therefore different values for the scattering vector q, g depends on τ and q, as summarized by Provencher and Štêpánek (1996). In good approximation a DLS ACF can also be expressed and fitted as the following exponential function (or multiple exponential functions), where b∞ is the ACF baseline value at infinite values of time delay, b0 is the maximum ACF value at a time delay of nearly zero and Γ is a measure for the decay rate (Chu 1991):
| 6.6 |
In principle this exponential ACF function can be evaluated using an algorithm in order to obtain values for D and a mean radius distribution with multiple particle species, e.g. in a sample suspension: Γ is proportional to the diffusion constant D for a given DLS setup (Eq. 6.7), n0 is the solvent’s refractive index, θ the scattering angle and λ the wavelength in vacuum.
| 6.7 |
The scattering vector q is used to determine D, which allows to calculate rh based on the Stokes-Einstein equation (Eq. 6.1). D and subsequently rh values with standard deviations can be directly obtained from the CONTIN algorithm (Provencher 1982), which is solving the inverse Laplace transform of the ACF for the size distribution analysis. As an alternative, a cumulant analysis of the ACF (Frisken 2001) can be applied, which provides polydispersity index (PDI) and the intensity weighted Z-average size value. PDI can express the homogeneity of the radii: For a Gaussian size distribution of a single particle species the width or standard deviation (σ) of an individual rh peak is squared and divided by the square of the mean size to yield the PDI. The distribution of rh values can commonly be weighted by molecular mass, volume, particle number or scattering intensity.
Assuming that the investigated particle is spherical, the molecular weight (M) of dissolved macromolecules might be approximated as following, which is explained in more detail elsewhere (Cantor and Schimmel 1980). VS is the specific particle density, the hydration is represented by h (mass of water per mass of protein) and NA is the Avogadro constant:
| 6.8 |
For non-globular particles the mass equivalent spherical radius is usually smaller than the determined rh. The Perrin factor F, which is the ratio of the frictional coefficients of the mass equivalent solid sphere (fs) and the sphere corresponding to the measured rh (fh), provides a first estimate about the degree of elongation of an ellipsoid particle. The frictional coefficients are derived from Stokes law as specified by Eq. 6.9, with the inclusion of Eq. 6.8, with l being the thickness of a single solvent layer:
| 6.9 |
Sample Preparation and Selected Results
The capability of DLS to determine particle size distributions in a wide size range and to roughly compare the quantity of particles in different samples via the scattering intensity opens applications for a variety of different samples. Further, indirectly it is also possible to determine the solution viscosity applying a sample with known hydrodynamic radius rh, which is shifting to a higher or lower rh value proportional to the viscosity difference according to the Stokes-Einstein equation.
In preparation of samples even minor amounts of artificial large environmental particles need to be removed due to their disturbing scattering properties, i.e. a “shielding” effect of the weaker scattering of smaller particles (Eq. 6.2) and the limited size-resolution in a typical DLS experiment (Ruf 1993; Karow et al. 2015). Next to other optical parameters those environmental particles also hinder the characterization of particles larger than approx. 1 µm. Most commonly sample solutions are simply filtered or centrifuged at the time of the experiment or fractionated according to their size by chromatographic methods. Also extensive optimization of solution additives or ultra-centrifugation typically helps to minimize polydispersity and undesired peak broadening. High-throughput additive screens for optimization of the solution dispersity are supported by experiments in multi-well plates, which are ideally covered by transparent oil rather than by foils to hinder evaporation of aqueous solutions. Cleanness of optical and quartz glass components can be maintained by removing dust particles by pressured air and other remaining material by diluted nitric acid.
Hydrodynamic radii of some exemplary proteins and other biological samples investigated by DLS are listed in Table 6.1. To also ensure that rh is not concentration dependent, typically in an artificial manner, the diffusion constant D can be determined at different concentrations. Those diffusion constants should be evaluated by a Debye plot. A linear dependency of D on the concentration allows to extrapolate D to a value at infinite dilution (unbiased by attractive or repulsive interactions), similar to the extrapolation of size parameters in X-ray scattering data processing. A high correlation value of the ACF at correlation time values of nearly zero (y-axis intercept), which is considered as an essential “signal-to-noise ratio” parameter, will obviously improve the accuracy of the ACF evaluation. However, if the sample concentration is too high or the solution becomes nearly non-transparent, the ACF and the applicability of DLS will suffer from multiple photon scattering. The calculation of an ACF can generally be completed in around 2 s. Nonetheless, static DLS experiments are typically running for 10–30 s and are repeated several times for averaging and verification. Scattering intensity data of weakly scattering molecules can to some extend be statistically improved by prolonging the measurement time. Required minimum concentrations heavily depend on several parameters of the instrumentation, most obviously laser intensity and detector sensitivity. Commonly, a monomeric protein of 30–40 kDa has a sufficient scattering intensity at concentrations of around 1–2 g l−1 (or around 50 µM) in a typical cuvette DLS instrument. For larger proteins the concentration can be reduced according to I ~ r6.
Table 6.1.
Hydrodynamic radii of selected exemplary biological particles with different shape in a broad molecular weight range
| Sample particle | MWa (kDa) | Structure/composition | rh (nm) | Sample container | Experiment reference |
|---|---|---|---|---|---|
| n-docecyl-β-D-maltopyranoside | – | Globular micelles forming in aqueous solutions | 3.3 ± 0.5 | Quartz cuvette | Meyer et al. (2015) |
| Influenza virus particles | – | Enveloped virus particles, Influenza A (H5N1) | 59 ± 4 | Quartz cuvette | Vajda et al. (2016) |
| Aprotinin | 6.5 | 58 amino acids, Kunitz-type serine protease inhibitor, 3 disulfide bonds | 1.8 ± 0.1 | Quartz cuvette | Stetefeld et al. (2016) |
| Prion (hPrPc; amino acids 121-231) | 13 | Soluble partially unfolded monomeric domain of recombinant human prion protein in acetate buffer | 1.9 ± 0.1 | Quartz cuvette | – |
| RNase A | 14 | 154 amino acids, typically monomeric, nearly globular ribonuclease | 2.0 ± 0.2 | Capillary | Falke et al. (2018) |
| 2.2 ± 0.1 | Quartz cuvette | Falke et al. (2018) | |||
| OvEC-SOD | 40 | Dimeric extracellular Onchocerca volvulus super oxide dismutase (Monomer: 20 kDa) | 3.5 ± 0.1 | Quartz cuvette | – |
| West Nile virus RNA 5′-translated region | 48 | Elongated RNA; the non-globular shape is indicated by nearly identical values for rh and radius of gyration (rg) | 5.1 ± 0.1 | Quartz cuvette | Deo et al. (2014) |
| BSA | 66 | 383 amino acids, predominantly monomeric, acidic pI; dissolved in phosphate buffered saline | 3.5 ± 0.4 | Quartz cuvette | Falke et al. (2018) |
| SARS Coronavirus main protease | 69 | Dimeric protease cleaving pre-processed polyproteins | 4.2 ± 0.1 | Multi-well plate | – |
| SARS Coronavirus main protease R298A | 34 | Predominantly monomeric and reduced in catalytic activity due to the point mutation | 3.5 ± 0.1 | Multi-well plate | – |
| S-layer protein slp-B53 | 116 | Elongated surface layer protein from Lysinibacillus sphaericus; monomeric state | 4.9 ± 1.1 | Multi-well plate | Liu et al. (2017) |
| Nidogen-1 | 139 | Protein of the extra-cellular matrix | 6.8 ± 0.1 | Quartz cuvette | Patel et al. (2014) |
| Aldolase | 158 | Heterotetrameric glycolytic enzyme; 50 mM Tris, 150 mM NaCl, pH8.0 | 5.0 ± 0.1 | Quartz cuvette | Stetefeld et al. (2016) |
| Apoferritin | 440 | 24-meric globular complex, one function is iron storage | 7.8 ± 0.3 | Capillary | Falke et al. (2018) |
| Human thyroglobulin | 670 | Dimeric globular protein of the follicular cells; 50 mM Tris, 150 mM NaCl, pH8.0 | 8.7 ± 0.2 | Quartz cuvette | Stetefeld et al. (2016) |
aTotal molecular weight expected for the oligomeric state in solution and the respective solution composition
Based on the considerations before, DLS is most suitable to study macromolecule degradation, disassembly, homo- and hetero-oligomerization, polymerization (also enzyme-catalyzed), clustering and amplification in real-time. Examples are the pH-dependent dissociation and hydrolysis of Apoferritin (Jaenicke 1987), human prion protein (PrP) aggregation upon specific proteolytic cleavage or UV irradiation (Georgieva et al. 2004; Redecke et al. 2009) stages of protein crystallization (Dierks et al. 2008; Meyer et al. 2012; Oberthuer et al. 2012; Schubert et al. 2017), monitoring density of cell culture (Loske et al. 2014), assembly of lipid nano discs (Petrache et al. 2016) and pharmaceutical kinetics (Fávero-Retto et al. 2013). For some of these experiments the option to adjust the temperature is essential and also allows to investigate and optimize the thermal stability or assembly of a native biological macromolecule. Figures 6.3 and 6.6 further display DLS data of crystallization processes exemplified by the protein mistletoe lectin I (ML-I) from Viscum album and ferritin. After addition of the precipitant solution larger clusters and nanocrystals are forming while the smaller protein oligomers observed in the beginning are still highly abundant. Typically 2–4 major fractions of particles sizes are observed in parallel towards later stages of crystal growth, recognized for different proteins with different solution composition.
Fig. 6.3.
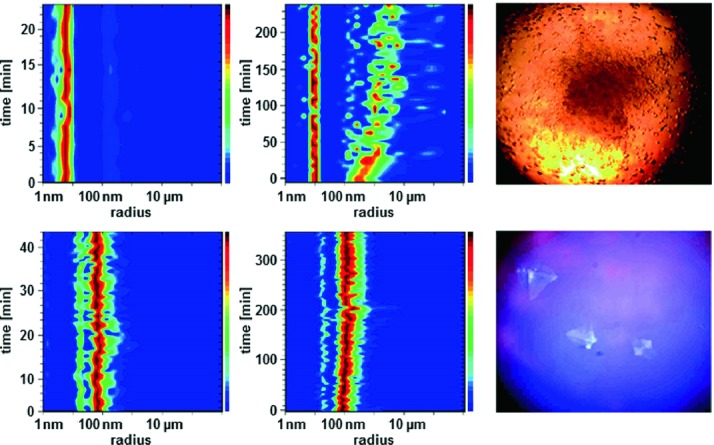
The half-logarithmic size distribution plots on the left were recorded applying ML-I (top left) and ferritin (bottom left) in solution respectively. The plots in the middle display the respective size-distribution over time after mixing with an appropriate crystallization solution. The abundancy of radii is color-coded from blue (low) to red (high). The pictures obtained from a microscope show crystals grown upon long-term incubation. The displayed ferritin crystals (bottom right), which are >100 µm in all dimensions in size, are exposed to UV-light as well to confirm the intrinsic fluorescence of the protein.
Reproduced from Dierks et al. (2008), Crystal Growth and Design with permission of the American Chemical Society, copyright 2008
Fig. 6.6.
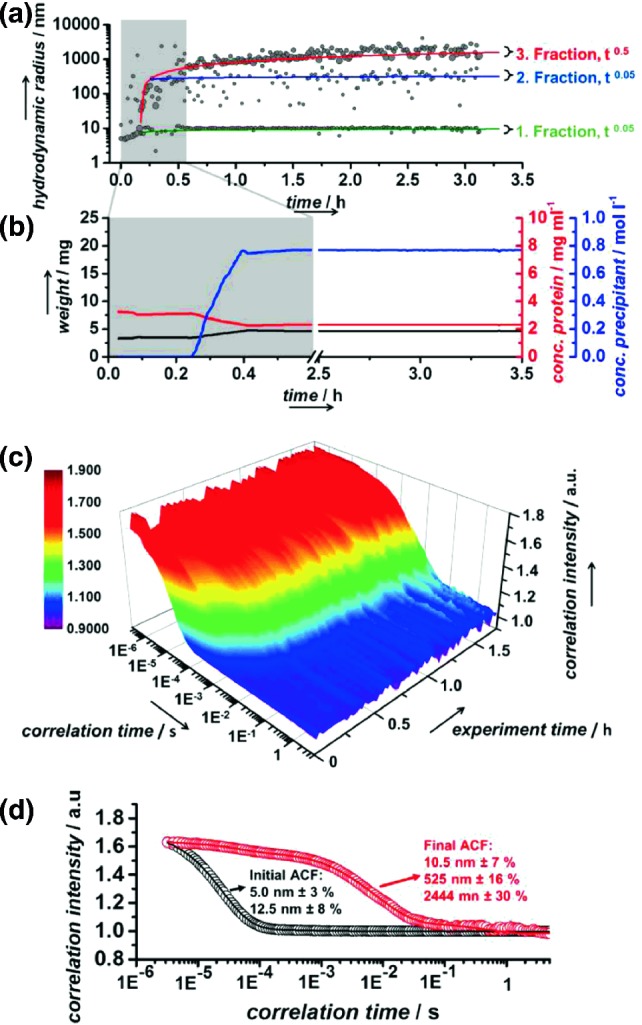
Induction and characterization of ML-I nucleation utilizing in situ DLS according to Fig. 6.5. a Radius plot of the experiment showing the time course of the hydrodynamic radii. After adding the precipitant solution to supersaturate the protein solution and induce crystal nucleation three distinct radius fractions are detected indicated by the green, blue and red line respectively. b The solution composition and precipitant addition is actively regulated by piezo pumps and monitored over the experiment as displayed. c 3D plot of ACFs indicating increasing polydispersity due to multimodal correlation decay in later stages of the experiment. d Comparison of initial (black) and final (red) ACF visualizing also the particle species composition during a later stage of ML-I crystal growth.
Reproduced from Schubert et al. (2017), Crystal Growth and Design with permission of the American Chemical Society, copyright 2017
In Flow DLS
As DLS is determining particle sizes based on Brownian motion, it is not self-evident that sample solutions can be analyzed while they are flowing. However, it is well established that below a critical velocity the ACF of scattering particles for a nearly laminar flow is dominated by Brownian motion and the resulting hydrodynamic radii are consequently not significantly different compared to static samples. The application of DLS under shear flow conditions and in a microfluidic channel, both mathematically and via an initial experimental approach with regard to flow channel dimensions, shear rate, velocity profile of the Poiseuille flow and Doppler shift interferences has been verified (Destremaut et al. 2009). The obtained theoretical approximation of an ACF with some geometrical restrains underlined the applicability of DLS in flow mode. The DLS experiments in this study were performed in a widened channel segment of a microfluidic PDMS chip with dimensions of 500 by 700 µm. Further stopped-flow DLS experiments have already been performed to study stages of protein folding (Gast et al. 1997) and characterize spherical latex particles in flow utilizing a specific fiber optic laser probe (Leung et al. 2006). This experimental setup is potentially indicating a huge variety of further applications to count and determine the size of macromolecules in place and in flow.
To properly design innovative DLS instrumentation for characterization of samples in flow, orientation of the scattering vector as well as velocity profile of the sample need to be taken into account. Moreover, the focal volume of the laser should be minimized in order to minimize the time required for the particles to pass the scattering volume at a certain flow rate (Taylor and Sorensen 1986). The applicability of sample solutions in shear flow to DLS is also interesting due to the altered oligomerization, fiber formation or aggregation of protein molecules recognized under shear flow stress, which is still lacking some understanding (Bekard et al. 2011; Dobson et al. 2017).
Latest Methods and Experimental DLS Setups
As discussed, DLS is a highly adaptable technique, which can be applied in situ to characterize samples in various sample containers in different phase states and under different physico-chemical environments, as well as in flow. Besides, DLS setups were expanded and varied even further.
Cross-Correlation and Multi-channel DLS
Light scattering samples with a very high particle concentration or otherwise not perfectly transparent samples are more prone to multiple light scattering (Fernández and Minton 2009). The respective data sets can be analyzed by utilizing a particular 3D cross correlation DLS setup (Medebach et al. 2007; Block and Scheffold 2010). It contains a split laser beam, which essentially hits the sample particles typically at two different angles with the same scattering vector. A potential contribution of multiple scattering is expected to vary for the two scattering pattern recorded in parallel, whereas the contribution of single scattering remains constant. Thereby, a cross-correlation of two intensity pattern can identify and suppress multiple scattering. Alternatively, for highly dense colloidal suspensions, gels or biological media, which scatter even stronger, diffusing-wave spectroscopy is most suitable (Zakharov et al. 2006).
In contrast to cross-correlation DLS, the term multi-channel DLS was recently used for a setup that allows to record multiple DLS data sets in parallel (Falke et al. 2018). The setup uses one laser and records the scattering data in different neighboring and statistically independent positions of a sample solution close to the focal point of the laser. Each data set is processed by an individual detector. This is most time efficient and also allows to see local differences at different positions of a solution or suspension.
Electrophoretic Light Scattering
In combination with a homogeneous electric field, DLS can be utilized to determine the electrophoretic mobility and thus the Debye-Hückel-Henry charge of unknown particles, which is called electrophoretic light scattering (Ware 1974; Minton 2016). The underlying principle is the quantification of the Doppler effect of the light scattered by particles migrating in the electric field: The light scattered by particles in the direction of migration, i.e. towards the oppositely charged electrode, is upshifted in its frequency, while the frequency in the opposite direction is downshifted. At equal intensity of incident light, the difference of these frequencies is proportional to the electrophoretic mobility.
Depolarized Dynamic Light Scattering (DDLS)
Some DLS setups investigate intrinsic birefringence or form birefringence (Allen 1996), i.e. anisotropy of the individual molecule, or a crystal lattice, in order to obtain valuable additional information on structure and shape of dissolved particles. The DDLS method quantifies depolarization of the scattered light using additional optical components, e.g. as essentially described before (Schubert et al. 2015; Rifaie-Graham et al. 2018) as well as illustrated by Fig. 6.4. This is particularly challenging due to rather low intensities of depolarized light and multiple scattering of light which perhaps kept the method from being more common till now. In addition to the translational diffusion constant (Eq. 6.1) the rotational diffusion constant Drot is calculated to evaluate the ACF of the depolarized light scattering according to the similar Stokes–Einstein–Debye equation:
| 6.10 |
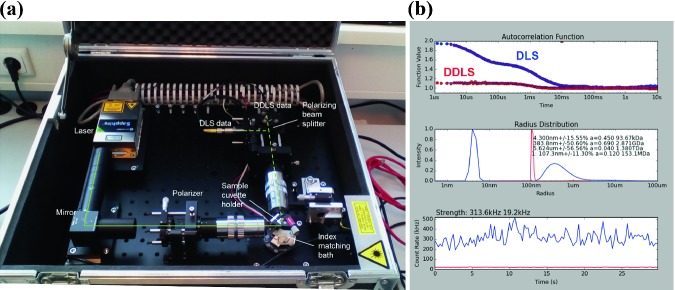
Fig. 6.4.
a Portable DDLS cabinet. The path of the laser beam is indicated by green lines; light scattered by particles inside the cuvette is represented by dashed lines. A CPU is attached for data processing and display. b A single exemplary 20 s measurement to monitor the oligomerization process of the bacterial β-lactamase CTX-M14 (30 kDa) in an early stage of crystallization. The DLS autocorrelation function (blue spheres and lines) indicates a polydisperse sample solution containing a mixture of small oligomers with a radius of approximately 4 nm and larger particles with a radius of a few hundred nm. The intensity of scattered light that is depolarized is quantified by a separate detector (red spheres and lines)
A combination of both diffusion constants allows to calculate the dimensions of both half axes of elongated particles, e.g. fibers, virus particles or synthetic nano particles or tubes, considered as rotational ellipsoids (Glidden and Muschol 2012). Based on the birefringence of crystals, DDLS was also utilized to distinguish between protein nano and micro crystals and amorphous precipitation, e.g. for glucose isomerase (Schubert et al. 2015). Rod-shaped gold particles are frequently used for calibration. Besides, oxygen-binding Limulus polyphemus hemocyanin, which is forming large hexa-, dodeca- and 24-mers were applied as well as the oblate membrane-bound photosystem I for which dimensions of 10 by 26 nm were determined in good agreement with X-ray diffraction data (Chayen et al. 2004; Beltramini et al. 2005). The method was discussed to be ideally suitable for scoring of protein crystal suspensions used at X-ray free-electron laser (XFEL) sources also in combination with second order harmonic generation (SHG) microscopy.
“Combinatory” Devices for Online Sample Scoring
As discussed DLS is most suitable to verify sample homogeneity to match a high standard of sample quality in nano particle sample preparation towards imaging and manufacturing techniques. Consequently, a few setups and devices have been developed to continuously monitor and score the sample quality in situ and in parallel to other experimental procedures, including growth of macromolecular crystals (Meyer et al. 2012), SAXS (Schwamberger et al. 2015; Falke et al. 2018), asymmetrical field flow fractionation (Sitar et al. 2017) and to score nanocrystal suspensions to be measured at XFEL radiation sources in the future as well as in context of other experimental procedures in biochemistry, genetics, material science, sorting and chemical synthesis.
In order to induce, optimize and study the crystal nucleation of the protein ML-I in detail and analyze complex liquid-liquid phase separation and phase transition mechanisms in general, the DLS setup shown in Fig. 6.5 was utilized. The time-resolved development of nuclei in this experiment is summarized as an example in Fig. 6.6, starting with a single drop of protein solution positioned on a glass cover slip in a humidity-controlled environment.
Fig. 6.5.
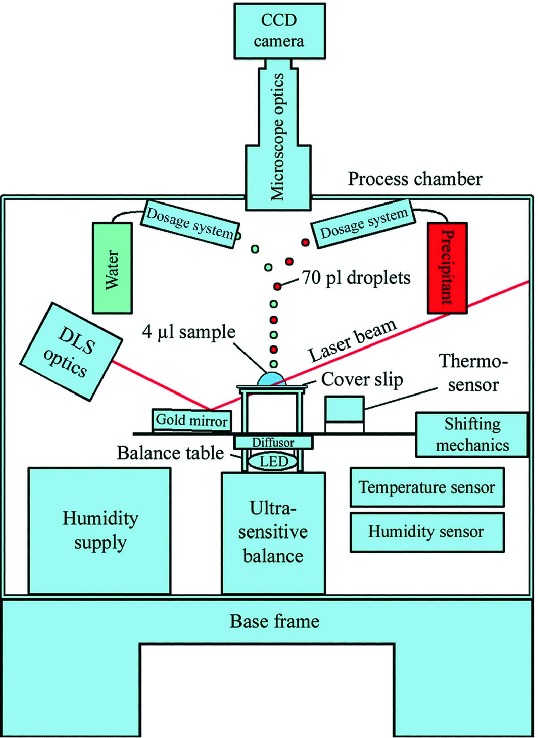
Schematic representation of a setup to monitor individual solution drops and the micromanipulation towards optimized macromolecule crystallization using in situ DLS and a highly sensitive balance.
Reproduced from Meyer et al. (2012), Acta Crystallographica with permission of the International Union of Crystallography, https://journals.iucr.org/, copyright 2012
Complementary Techniques and Conclusion
A technique that is closely related to DLS and is not in focus of this chapter is static light scattering (SLS), which allows to record the scattering intensity as an average over time. Data recorded for a serial dilution and at different detector angles can be visualized by Zimm plots (Hashim et al. 2014) and are combined in order to determine the shape-dependent radius of gyration (rg), the second virial coefficient B2 and also molecular weight as well as to verify ideal diffusion. The ratio of rg and rh also called shape factor can reveal shape information as well. The expected shape factor for globular particles is the square root of 0.6, which means rg/rh ≈ 0.775. The second virial coefficient is highly useful in analyzing intermolecular interactions, e.g. in crystallography—a negative B2 value is indicating repulsion, as explained and summarized in more detail elsewhere, e.g. Yadav et al. (2011).
Further, X-ray photon correlation spectroscopy, which is using an X-ray beam, i.e. a much shorter wavelength, and is otherwise highly similar to DLS, should be mentioned (Sutton et al. 1991). Moreover, a variety of distinct techniques to complement data based on light scattering is available, including but not limited to Taylor dispersion analysis, microscopic nano particle tracking, SAXS or small-angle neutron scattering (SANS), native mass spectrometry, native gel electrophoresis, analytical ultracentrifugation or analytical size exclusion chromatography to obtain certain size information of (biological) particles (see for example Boivin et al. 2016). SAXS and SANS as well as electron microscopy techniques or even native ion-mobility mass spectrometry are superior in analyzing the shape of molecules at moderately low resolution in solution, Taylor dispersion analysis is capable of determining the size of small compounds, also <1 kDa, and native mass spectrometry is known for high mass accuracy. However, DLS (and SLS) has huge advantages in terms of sample preparation/consumption, experimental effort, particle size range or instrumental adaptability respectively, especially for long-term time-resolved experiments and in an authentic solution environment for biomolecules. Some of the described in situ DLS instruments can monitor sample volumes around or even below 2 µl. A strongly curved drop surface for very small solution volumes might hinder the laser alignment in those cases. The option to apply DLS to solutions and suspensions in nearly laminar flow—with some restraints as mentioned—is another mayor benefit in combination with chromatographic purification, automated analytical pipelines and high-throughput or iterative sample analysis.
In this context, applications of DLS further include preparation of ceramic nano particles (Sōmiya 2013), size determination in SiO2 particle suspensions (Wojciechowski et al. 2018), conjugation of gold nano particles and proteins (Jans et al. 2009), liposomes used in cosmetics and medical research (Hupfeld et al. 2006), monitoring of the gelation of milk related to food quality control (Dalgleish and Hallett 1995) or gelation of organic-inorganic hybrid polymers (Norisuye et al. 1999). Moreover, the applicability of DLS and scattering intensity measurements to hydrogel environments was evaluated (Rochas and Geissler 2014). Dynamic light scattering can also be applied to verify oligomerization and crystallization of Macromolecules in preparation for experiments under microgravity conditions. Studying macromolecular interactions and symmetry under microgravity conditions has always been attractive, e.g. to obtain crystals of superior size, lattice homogeneity and maximized diffraction capability (Drebes et al. 2016). Gels or microfluidic chips, which are “down to earth” tools to partially mimic microgravity conditions, can be combined with in situ DLS as mentioned before to follow the crystal growth. Further, time-resolved experiments in outer space like at the International Space Station could be monitored by DLS in this context. A National Aeronautics and Space Administration research institute applied a DLS technique to detect clinical eye cataract in an early stage (Ansari et al. 2000).
Those individual examples and applications in structural biology as discussed before underline the expectation that the applications of light scattering techniques will even expand in the near future using further improved instrumentation modules.
Acknowledgements
The corresponding research and complex instrument development activities have been supported by the Cluster of Excellence ‘Advanced Imaging of Matter’ of the Deutsche Forschungsgemeinschaft (DFG) - EXC 2056 - project ID 390715994 and DFG project BE1443/29-1, by the German Aerospace Center (DLR) via project 50WB1423 and BMBF via project 05K16GUA. Further, the authors acknowledge helpful and critical discussion with all colleagues and cooperation partners in all aspects of DLS.
Contributor Information
Alice S. Pereira, Phone: +351351212948300, FAX: +351351212948550, Email: masp@fct.unl.pt
Pedro Tavares, Phone: +35135121299659, FAX: +351351212948550, Email: pedro.tavares@fct.unl.pt.
Paulo Limão-Vieira, Phone: +351351212948576, Email: plimaovieira@fct.unl.pt.
Sven Falke, Email: Falke@chemie.uni-hamburg.de.
Christian Betzel, Email: Christian.Betzel@uni-hamburg.de.
References
- Allen G (1996) Comprehensive polymer science and supplements. In: Chapter 33: Optical microscopy. Elsevier, New York
- Ansari RR, Datiles III MB, King (2000) New clinical instrument for the early detection of cataract using dynamic light scattering and corneal topography. In: Rol PO, Joos KM, Manns F (eds). San Jose, CA pp. 38–49
- Barnett CE. Some applications of wave-length turbidimetry in the infrared. J Phys Chem. 1942;46:69–75. doi: 10.1021/j150415a009. [DOI] [Google Scholar]
- Bekard IB, Asimakis P, Bertolini J, Dunstan DE. The effects of shear flow on protein structure and function. Biopolym. 2011;95:733–745. doi: 10.1002/bip.21646. [DOI] [PubMed] [Google Scholar]
- Beltramini M, Colangelo N, Giomi F, Bubacco L, Di Muro P, Hellmann N, Jaenicke E, Decker H. Quaternary structure and functional properties of Penaeus monodon hemocyanin: P. monodon hemocyanin structure and function. FEBS J. 2005;272:2060–2075. doi: 10.1111/j.1742-4658.2005.04634.x. [DOI] [PubMed] [Google Scholar]
- Berne BJ, Pecora R (2000) Dynamic light scattering: with applications to chemistry, biology, and physics. Dover Publications, Mineola, NY
- Block ID, Scheffold F. Modulated 3D cross-correlation light scattering: Improving turbid sample characterization. Rev Sci Instrum. 2010;81:123107. doi: 10.1063/1.3518961. [DOI] [PubMed] [Google Scholar]
- Boivin S, Kozak S, Rasmussen G, Nemtanu IM, Vieira V, Meijers R. An integrated pipeline for sample preparation and characterization at the EMBL@PETRA3 synchrotron facilities. Methods. 2016;95:70–77. doi: 10.1016/j.ymeth.2015.08.003. [DOI] [PubMed] [Google Scholar]
- Borgstahl GEO. In: Macromolecular crystallography protocols. New Jersey: Humana Press; 2006. How to use dynamic light scattering to improve the likelihood of growing macromolecular crystals; pp. 109–130. [DOI] [PubMed] [Google Scholar]
- Brown RG. Dynamic light scattering using monomode optical fibers. Appl Opt. 1987;26:4846–4851. doi: 10.1364/AO.26.004846. [DOI] [PubMed] [Google Scholar]
- Brown RG, Smart AE. Practical considerations in photon correlation experiments. Appl Opt. 1997;36:7480–7492. doi: 10.1364/AO.36.007480. [DOI] [PubMed] [Google Scholar]
- Cantor CR, Schimmel PR. The behavior of biological macromolecules. San Francisco: W. H. Freeman; 1980. [Google Scholar]
- Chayen N, Dieckmann M, Dierks K, Fromme P. Size and shape determination of proteins in solution by a noninvasive depolarized dynamic light scattering instrument. Ann N Y Acad Sci. 2004;1027:20–27. doi: 10.1196/annals.1324.003. [DOI] [PubMed] [Google Scholar]
- Chu B. Laser Light Scattering. Annu Rev Phys Chem. 1970;21:145–174. doi: 10.1146/annurev.pc.21.100170.001045. [DOI] [Google Scholar]
- Chu B. Laser light scattering 2e: basic principles and practice. Oxford: Elsevier Science; 1991. [Google Scholar]
- Cummins HZ, Knable N, Yeh Y. Observation of diffusion broadening of Rayleigh scattered light. Phys Rev Lett. 1964;12:150–153. doi: 10.1103/PhysRevLett.12.150. [DOI] [Google Scholar]
- Dalgleish DG, Hallett FR. Dynamic light scattering: applications to food systems. Food Res Int. 1995;28:181–193. doi: 10.1016/0963-9969(94)00053-B. [DOI] [Google Scholar]
- Deo S, Patel TR, Dzananovic E, Booy EP, Zeid K, McEleney K, Harding SE, McKenna SA. Activation of 2′ 5′-oligoadenylate synthetase by stem loops at the 5′-end of the West Nile virus genome. PLoS ONE. 2014;9:e92545. doi: 10.1371/journal.pone.0092545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destremaut F, Salmon JB, Qi L, Chapel JP. Microfluidics with on-line dynamic light scattering for size measurements. Lab Chip. 2009;9:3289. doi: 10.1039/b906514h. [DOI] [PubMed] [Google Scholar]
- Dhadwal HS, Chu B. A fiber-optic light-scattering spectrometer. Rev Sci Instrum. 1989;60:845–853. doi: 10.1063/1.1140333. [DOI] [Google Scholar]
- Dierks K, Meyer A, Einspahr H, Betzel C. Dynamic light scattering in protein crystallization droplets: adaptations for analysis and optimization of crystallization processes. Cryst Growth Des. 2008;8:1628–1634. doi: 10.1021/cg701067r. [DOI] [Google Scholar]
- Dobson J, Kumar A, Willis LF, Tuma R, Higazi DR, Turner R, Lowe DC, Ashcroft AE, Radford SE, Kapur N, Brockwell DJ. Inducing protein aggregation by extensional flow. Proc Natl Acad Sci. 2017;114:4673–4678. doi: 10.1073/pnas.1702724114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drebes J, Künz M, Windshügel B, Kikhney AG, Müller IB, Eberle RJ, Oberthür D, Cang H, Svergun DI, Perbandt M, Betzel C, Wrenger C. Structure of ThiM from Vitamin B1 biosynthetic pathway of Staphylococcus aureus—insights into a novel pro-drug approach addressing MRSA infections. Sci Rep. 2016;6:22871. doi: 10.1038/srep22871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falke S, Dierks K, Blanchet C, Graewert M, Cipriani F, Meijers R, Svergun D, Betzel C. Multi-channel in situ dynamic light scattering instrumentation enhancing biological small-angle X-ray scattering experiments at the PETRA III beamline P12. J Synchrotron Rad. 2018;25:361–372. doi: 10.1107/S1600577517017568. [DOI] [PubMed] [Google Scholar]
- Fávero-Retto MP, Palmieri LC, Souza TACB, Almeida FCL, Lima LMTR. Structural meta-analysis of regular human insulin in pharmaceutical formulations. Eur J Pharm Biopharm. 2013;85:1112–1121. doi: 10.1016/j.ejpb.2013.05.005. [DOI] [PubMed] [Google Scholar]
- Fernández C, Minton AP. Static light scattering from concentrated protein solutions II: Experimental test of theory for protein mixtures and weakly self-associating proteins. Biophys J. 2009;96:1992–1998. doi: 10.1016/j.bpj.2008.11.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foord R, Jakeman E, Oliver CJ, Pike ER, Blagrove RJ, Wood E, Peacocke AR. Determination of diffusion coefficients of haemocyanin at low concentration by intensity fluctuation spectroscopy of scattered laser light. Nature. 1970;227:242–245. doi: 10.1038/227242a0. [DOI] [PubMed] [Google Scholar]
- Frisken BJ. Revisiting the method of cumulants for the analysis of dynamic light-scattering data. Appl Opt. 2001;40:4087–4091. doi: 10.1364/AO.40.004087. [DOI] [PubMed] [Google Scholar]
- Fujime S. Quasi-elastic scattering of laser light. A new tool for the dynamic study of biological macromolecules. Adv Biophys. 1972;3:1–43. [PubMed] [Google Scholar]
- Gast K, Nöppert A, Müller-Frohne M, Zirwer D, Damaschun G. Stopped-flow dynamic light scattering as a method to monitor compaction during protein folding. Eur Biophys J. 1997;25:211–219. doi: 10.1007/s002490050033. [DOI] [Google Scholar]
- Georgieva D, Koker M, Redecke L, Perbandt M, Clos J, Bredehorst R, Genov N, Betzel C. Oligomerization of the proteolytic products is an intrinsic property of prion proteins. Biochem Biophy Res Commun. 2004;323:1278–1286. doi: 10.1016/j.bbrc.2004.08.230. [DOI] [PubMed] [Google Scholar]
- Glidden M, Muschol M. Characterizing gold nanorods in solution using depolarized dynamic light scattering. J Phys Chem C. 2012;116:8128–8137. doi: 10.1021/jp211533d. [DOI] [Google Scholar]
- Graewert MA, Franke D, Jeffries CM, Blanchet CE, Ruskule D, Kuhle K, Flieger A, Schäfer B, Tartsch B, Meijers R, Svergun D. Automated pipeline for purification, biophysical and X-ray analysis of biomacromolecular solutions. Sci Rep. 2015;5:10734. doi: 10.1038/srep10734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haghighi M, Plum MA, Gantzounis G, Butt H-J, Steffen W, Fytas G. Plasmon-enhanced dynamic depolarized light scattering. J Phys Chem C. 2013;117:8411–8419. doi: 10.1021/jp400358a. [DOI] [Google Scholar]
- Hashim H, El-Mekawey F, El-Kashef H, Ghazy R. Determination of scattering parameters of polyvinyl alcohol by static laser scattering. Beni-Suef Univ J Basic Appl Sci. 2014;3:203–208. doi: 10.1016/j.bjbas.2014.10.005. [DOI] [Google Scholar]
- Hupfeld S, Holsæter AM, Skar M, Frantzen CB, Brandl M. Liposome size analysis by dynamic/static light scattering upon size exclusion-/field flow-fractionation. J Nanosci Nanotechnol. 2006;6:3025–3031. doi: 10.1166/jnn.2006.454. [DOI] [PubMed] [Google Scholar]
- Jaenicke R. Folding and association of proteins. Prog Biophys Mol Biol. 1987;49:117–237. doi: 10.1016/0079-6107(87)90011-3. [DOI] [PubMed] [Google Scholar]
- Jans H, Liu X, Austin L, Maes G, Huo Q. Dynamic light scattering as a powerful tool for gold nanoparticle bioconjugation and biomolecular binding studies. Anal Chem. 2009;81:9425–9432. doi: 10.1021/ac901822w. [DOI] [PubMed] [Google Scholar]
- Jeffries CM, Graewert MA, Blanchet CE, Langley DB, Whitten AE, Svergun DI. Preparing monodisperse macromolecular samples for successful biological small-angle X-ray and neutron-scattering experiments. Nat Protoc. 2016;11:2122–2153. doi: 10.1038/nprot.2016.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karow AR, Götzl J, Garidel P. Resolving power of dynamic light scattering for protein and polystyrene nanoparticles. Pharm Dev Technol. 2015;20:84–89. doi: 10.3109/10837450.2014.910808. [DOI] [PubMed] [Google Scholar]
- Kokhanovsky Alexander A., editor. Light Scattering Reviews. 2006. [Google Scholar]
- Koppel DE. Analysis of macromolecular polydispersity in intensity correlation spectroscopy: the method of cumulants. J Chem Phys. 1972;57:4814–4820. doi: 10.1063/1.1678153. [DOI] [Google Scholar]
- Liu J, Falke S, Drobot B, Oberthuer D, Kikhney A, Guenther T, Fahmy K, Svergun D, Betzel C, Raff J. Analysis of self-assembly of S-layer protein slp-B53 from Lysinibacillus sphaericus. Eur Biophys J. 2017;46:77–89. doi: 10.1007/s00249-016-1139-9. [DOI] [PubMed] [Google Scholar]
- Loske AM, Tello EM, Vargas S, Rodriguez R. Escherichia coli viability determination using dynamic light scattering: a comparison with standard methods. Arch Microbiol. 2014;196:557–563. doi: 10.1007/s00203-014-0995-x. [DOI] [PubMed] [Google Scholar]
- Medebach M, Moitzi C, Freiberger N, Glatter O. Dynamic light scattering in turbid colloidal dispersions: a comparison between the modified flat-cell light-scattering instrument and 3D dynamic light-scattering instrument. J Colloid Interface Sci. 2007;305:88–93. doi: 10.1016/j.jcis.2006.09.013. [DOI] [PubMed] [Google Scholar]
- Meyer A, Dierks K, Hilterhaus D, Klupsch T, Mühlig P, Kleesiek J, Schöpflin R, Einspahr H, Hilgenfeld R, Betzel C. Single-drop optimization of protein crystallization. Acta Crystallogr Sect F: Struct Biol Cryst Commun. 2012;68:994–998. doi: 10.1107/S1744309112024074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer A, Dierks K, Hussein R, Brillet K, Brognaro H, Betzel C. Systematic analysis of protein–detergent complexes applying dynamic light scattering to optimize solutions for crystallization trials. Acta Crystallogr F Struct Biol Commun. 2015;71:75–81. doi: 10.1107/S2053230X14027149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mie G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann Phys. 1908;330:377–445. doi: 10.1002/andp.19083300302. [DOI] [Google Scholar]
- Minton AP. Static light scattering from concentrated protein solutions, I: General theory for protein mixtures and application to self-associating proteins. Biophys J. 2007;93:1321–1328. doi: 10.1529/biophysj.107.103895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minton AP. Recent applications of light scattering measurement in the biological and biopharmaceutical sciences. Anal Biochem. 2016;501:4–22. doi: 10.1016/j.ab.2016.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller PK, Givens RG. Dynamic calibration and data interpretation of a light-scattering instrument. J Air Pollut Control Assoc. 1961;11:576–580. doi: 10.1080/00022470.1961.10468040. [DOI] [PubMed] [Google Scholar]
- Norisuye T, Shibayama M, Tamaki R, Chujo Y. Time-resolved dynamic light scattering studies on gelation process of organic–inorganic polymer hybrids. Macromolecules. 1999;32:1528–1533. doi: 10.1021/ma981306h. [DOI] [Google Scholar]
- Oberthuer D, Melero-García E, Dierks K, Meyer A, Betzel C, Garcia-Caballero A, Gavira JA. Monitoring and scoring counter-diffusion protein crystallization experiments in capillaries by in situ dynamic light scattering. PLoS ONE. 2012;7:e33545. doi: 10.1371/journal.pone.0033545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel TR, Bernards C, Meier M, McEleney K, Winzor DJ, Koch M, Stetefeld J. Structural elucidation of full-length nidogen and the laminin–nidogen complex in solution. Matrix Biol. 2014;33:60–67. doi: 10.1016/j.matbio.2013.07.009. [DOI] [PubMed] [Google Scholar]
- Petrache AI, Machin DC, Williamson DJ, Webb ME, Beales PA. Sortase-mediated labelling of lipid nanodiscs for cellular tracing. Mol BioSyst. 2016;12:1760–1763. doi: 10.1039/C6MB00126B. [DOI] [PubMed] [Google Scholar]
- Provencher SW. CONTIN: a general purpose constrained regularization program for inverting noisy linear algebraic and integral equations. Comput Phys Commun. 1982;27:229–242. doi: 10.1016/0010-4655(82)90174-6. [DOI] [Google Scholar]
- Provencher SW, Štêpánek P. Global analysis of dynamic light scattering autocorrelation functions. Part Part Syst Charact. 1996;13:291–294. doi: 10.1002/ppsc.19960130507. [DOI] [Google Scholar]
- Redecke L, Binder S, Elmallah MIY, Broadbent R, Tilkorn C, Schulz B, May P, Goos A, Eich A, Rübhausen M, Betzel C. UV-light-induced conversion and aggregation of prion proteins. Free Radic Biol Med. 2009;46:1353–1361. doi: 10.1016/j.freeradbiomed.2009.02.013. [DOI] [PubMed] [Google Scholar]
- Rifaie-Graham O, Hua X, Bruns N, Balog S (2018) The kinetics of β-hematin crystallization measured by depolarized light scattering. Small e1802295 [DOI] [PubMed]
- Rochas C, Geissler E. Measurement of dynamic light scattering intensity in gels. Macromolecules. 2014;47:8012–8017. doi: 10.1021/ma501882d. [DOI] [Google Scholar]
- Ruf H. Data accuracy and resolution in particle sizing by dynamic light scattering. Adv Coll Interface Sci. 1993;46:333–342. doi: 10.1016/0001-8686(93)80047-F. [DOI] [Google Scholar]
- Schubert R, Meyer A, Dierks K, Kapis S, Reimer R, Einspahr H, Perbandt M, Betzel C. Reliably distinguishing protein nanocrystals from amorphous precipitate by means of depolarized dynamic light scattering. J Appl Crystallogr. 2015;48:1476–1484. doi: 10.1107/S1600576715014740. [DOI] [Google Scholar]
- Schubert R, Meyer A, Baitan D, Dierks K, Perbandt M, Betzel C. Real-time observation of protein dense liquid cluster evolution during nucleation in protein crystallization. Cryst Growth Des. 2017;17:954–958. doi: 10.1021/acs.cgd.6b01826. [DOI] [Google Scholar]
- Schwamberger A, De Roo B, Jacob D, Dillemans L, Bruegemann L, Seo JW, Locquet JP. Combining SAXS and DLS for simultaneous measurements and time-resolved monitoring of nanoparticle synthesis. Nucl Instrum Methods Phys Res Sect B. 2015;343:116–122. doi: 10.1016/j.nimb.2014.11.049. [DOI] [Google Scholar]
- Sitar S, Vezočnik V, Maček P, Kogej K, Pahovnik D, Žagar E. Pitfalls in size characterization of soft particles by dynamic light scattering online coupled to asymmetrical flow field-flow fractionation. Anal Chem. 2017;89:11744–11752. doi: 10.1021/acs.analchem.7b03251. [DOI] [PubMed] [Google Scholar]
- Sōmiya S (ed) (2013) Handbook of advanced ceramics: materials, applications, processing, and properties, 2nd edn. Academic Press, imprint of Elsevier, Amsterdam; Boston
- Stetefeld J, McKenna SA, Patel TR. Dynamic light scattering: a practical guide and applications in biomedical sciences. Biophys Rev. 2016;8:409–427. doi: 10.1007/s12551-016-0218-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton M, Mochrie SGJ, Greytak T, Nagler SE, Berman LE, Held GA, Stephenson GB. Observation of speckle by diffraction with coherent X-rays. Nature. 1991;352:608–610. doi: 10.1038/352608a0. [DOI] [Google Scholar]
- Taylor TW, Sorensen CM. Gaussian beam effects on the photon correlation spectrum from a flowing Brownian motion system. Appl Opt, AO. 1986;25:2421–2426. doi: 10.1364/AO.25.002421. [DOI] [PubMed] [Google Scholar]
- Vajda J, Weber D, Brekel D, Hundt B, Müller E. Size distribution analysis of influenza virus particles using size exclusion chromatography. J Chromatogr A. 2016;1465:117–125. doi: 10.1016/j.chroma.2016.08.056. [DOI] [PubMed] [Google Scholar]
- Ware BR. Electrophoretic light scattering. Adv Coll Interface Sci. 1974;4:1–44. doi: 10.1016/0001-8686(74)80001-1. [DOI] [Google Scholar]
- Wojciechowski T, Shopa YI, Derkachov G, Jakubczyk D, Kolwas K, Woźniak M (2018) Application of dynamic light scattering for studying the evolution of micro- and nano-droplets. In: Angelsky OV (ed). SPIE, p 84
- Yadav S, Scherer TM, Shire SJ, Kalonia DS. Use of dynamic light scattering to determine second virial coefficient in a semidilute concentration regime. Anal Biochem. 2011;411:292–296. doi: 10.1016/j.ab.2010.12.014. [DOI] [PubMed] [Google Scholar]
- Zakharov P, Cardinaux F, Scheffold F. Multispeckle diffusing-wave spectroscopy with a single-mode detection scheme. Phys Rev E. 2006;73:011413. doi: 10.1103/PhysRevE.73.011413. [DOI] [PubMed] [Google Scholar]