Multiclass Disease Classification from Microbial Whole-Community Metagenomes

Abstract

The microbiome, the community of microorganisms living within an individual, is a promising avenue for developing non-invasive methods for disease screening and diagnosis. Here, we utilize 5643 aggregated, annotated whole-community metagenomes to implement the first multiclass microbiome disease classifier of this scale, able to discriminate between 18 different diseases and healthy. We compared three different machine learning models: random forests, deep neural nets, and a novel graph convolutional architecture which exploits the graph structure of phylogenetic trees as its input. We show that the graph convolutional model outperforms deep neural nets in terms of accuracy (achieving 75% average test-set accuracy), receiver-operator-characteristics (92.1% average area-under-ROC (AUC)), and precision-recall (50% average area-under-precision-recall (AUPR)). Additionally, the convolutional net’s performance complements that of the random forest, showing a lower propensity for Type-I errors (false-positives) while the random forest makes less Type-II errors (false-negatives). Lastly, we are able to achieve over 90% average top-3 accuracy across all of our models. Together, these results indicate that there are predictive, disease-specific signatures across microbiomes that can be used for diagnostic purposes.

1. Introduction

In the past few years, there has been an immense interest towards developing statistical methods to predict phenotypes, such as disease, from metagenomic sequencing of a microbiome.¹ One of the challenges in achieving this goal is the problem of separating out signals for different diseases from each other. Many studies that have looked for signatures of individual diseases in the microbiome have produced conflicting results,² and there is evidence that there are general signatures of dysbiosis common to all diseases.³ Thus, the standard protocol of comparing samples from a disease of interest against healthy controls, with the goal of identifying features of predictive for that disease, may instead be identifying more general features that signal a diseased or healthy microbiome. This problem can arise if the microbiome signals associated with dysbiosis are stronger than those specific to a given disease. The classifier will then have no mechanism to discriminate between general dysbiosis and the specific signatures of the disease. This is problematic if we want to understand the differences between diseases on a microbial level and/or make specific diagnoses. For example, in a clinical setting, a classifier for a certain disease that has not been trained against a diverse range of conditions may produce false positives when applied on a patient who has a different disease.⁴

We propose that approaching this problem as a multiclass classification can alleviate this issue by forcing the classifier to find features in the input that are specific for discriminating between a given class and every other class in the dataset. Additionally, this approach allows us to use a larger dataset containing samples from more conditions, potentially alleviating biases due to batch effects. Making accurate predictions becomes much harder in this setting, because output is much more specific (random guesses are now correct with probability $\frac{1}{n}$ rather than $\frac{1}{2}$). Here, we quantify the performance of three machine learning approaches to address this problem: random forests due to their popularity and ease-of-use, deep neural networks as a baseline for a deep-learning approach, and a novel graph convolutional network architecture which incorporates microbiome phylogeny to improve performance over the baseline deep net. We use these models to demonstrate that the multiclass disease classification problem is tractable given the amount of publicly available metagenomic data, and we posit this tractability will only improve over time as more data becomes available.

2. Previous Work

Two previous works have attempted to encode the graph structure of phylogenetic trees in order to enhance microbiome-disease predictions using publicly available data from healthy and diseased patients. Reiman et al. implemented a CNN by embedding phylogenetic trees into ${ℝ}^2$ and used two-dimensional convolutional layers to construct a body-site classifier.⁵ Fioravanti et al. developed a model to discriminate between subtypes of inflammatory bowel disease (IBD) and healthy by projecting samples into a two-dimensional space using Multi-Dimensional Scaling with the patristic distance between phylogenetic trees as the distance metric.⁶ However, both papers mapped phylogenetic data to a Euclidean domain to perform convolutions instead of operating in the original tree topology, as we do in this study.

We also show that this problem is tractable in a multi-class setting, whereas most previous studies have focused on discriminating between individual diseases and healthy. For example, there have been meta-analyses^3,7,8 that have tried to identify disease-specific signatures which generalize beyond individual studies, but the results presented in these papers have all been for disease vs. healthy scenarios. Our major contribution here is to present three machine learning models that can make multiclass disease predictions, including a novel convolutional architecture which exploits the tree structure of bacterial phylogenies.

3. Problem Setup

There are many moving targets that make machine learning in bioinformatics particularly challenging, and one major problem is the paucity of standardized datasets. Data pre-processing, particularly in the relatively new microbiome field, involves numerous components that are each active areas of research, and thus being continually improved; for metagenomics data, this includes new assembly methods, decontamination algorithms, sequencing libraries, annotation methods, reference genomes and so on.^9–11 Additionally, new studies are published every month, resulting in an ever-increasing catalog of potential data points to utilize for model training. In an effort to promote usage of a ‘standard dataset’ instead of constructing our own from scratch, we drew our training data from a recently published database containing annotated metagenomic data from multiple studies called curatedMetagenomicData.¹²

3.1. Dataset Construction

We constructed a dataset containing 5643 samples with 4885 from stool, 403 from skin, 254 from oral cavity, 93 from nares (nasal cavity), and 8 from maternal milk (healthy babies from Asnicar et al.³³) by including diseases that had at least 15 unique samples (table 3.1). One of the challenges we faced is that some samples have multiple disease labels due to the way the original studies were run. We approached this problem as a multiclasss (one correct label) as opposed to a multilabel (k possible correct labels) problem and thus sought to avoid conflicts due to multiple labeling. Multiple labeling was present in four of our disease sets: Atopic Dermatitis (atopic rhinitis (28), asthma (12)); C. difficile (pneumonia (15), cellulitis (2), osteoarthritis (1), ureteral stone (1)); Adenoma (fatty liver (28), hypertension (19), Type 2 Diabetes (6), Hypercholesterolemia (2), metastases (1)); and Hepatitis B (Schistosoma (1), Hepatitis E (7), Hepatic encephalopathy (2), Hepatitis D (5), Wilson’s disease (1), Cirrhosis (97), Ascites (48)). Additionally, depending on how an individual study was annotated, some samples in the original dataset have no disease label or are instead labeled as ”control”. We chose to be conservative in our construction and only included as ”healthy” samples where the disease column in the curatedMetagenomicData database was ”healthy”. Thus, we define ‘healthy’ in our study as those samples coming from patients who were explicitly considered to be healthy in the original study that the sample came from.

3.2. Graph Convolutional Neural Networks

Convolutional neural networks (CNNs) have been extremely successful in the field of machinevision.³⁴ Intuitively, their effectiveness derives from their ability to encode geometric properties of images such as translation-invariance in order to learn a better representation of the data.³⁵ In recent years, there has been interest in developing neural architectures that can capture analogous symmetries on non-Euclidean domains such as graphs and manifolds in order to extend the success of CNNs to those domains.³⁶

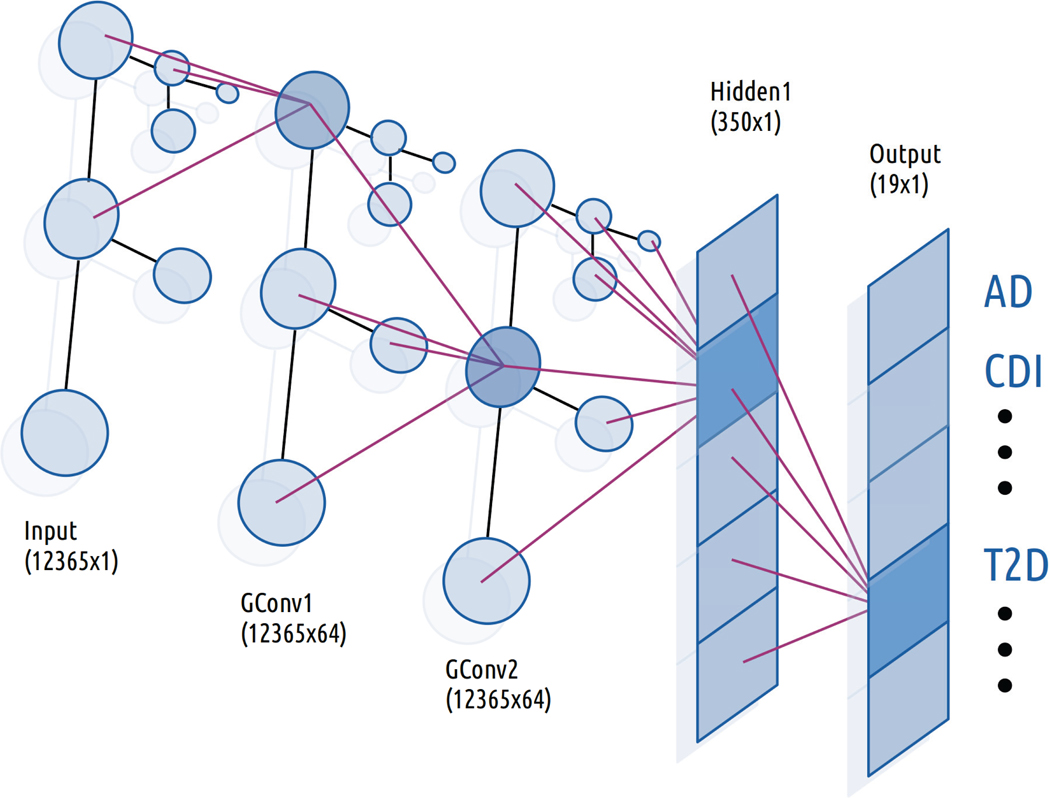
There are many architectures for doing this, and we chose to use the method outlined by Kipf and Welling,³⁷ which is a computationally simple method to generalize the convolution operation to graphs (Figure 1). The method falls into the category of spectral methods, which model convolutions as multiplication by a filter operator g_θ in the Fourier domain against input $x\in {ℝ}^n$, where g_θ is a diagonal matrix with parameters $\theta \in {ℝ}^n$. The multiplication takes place with respect to the Fourier basis of eigenvectors U of the graph Laplacian $L=I_N-D^{-\frac{1}{2}}A{D}^{\frac{1}{2}}$, where D is the diagonal matrix of vertex degrees, and A is the adjacency matrix of the graph (in our case, A is the adjacency matrix of the phylogenetic tree used in our model). In Euclidean domains, U is the Eigenbasis of the Laplacian operator in ${ℝ}^n$, which is the standard Fourier basis $\left\{e^{2\pi ik\cdot x}:k\in {\mathbb{N}}^n,x\in {ℝ}^n\right\}$ .

Fig. 1.

Architecture of Graph Convolutional Classifier. Purple lines indicate the flow of information from the previous to the highlighted neuron in each layer. In the convolutional layers, each neuron receives information only from its immediate neighbors in the preceding layer.

$$g_{\theta }\star x=U{g}_{\theta }{U}^{\top }x$$

Instead of considering all Fourier modes, we choose a cutoff K and use the first K Laplacian Eigenvectors when constructing U in order to simplify computation. However, this operation is still very expensive on graphs because there is no general analogue of Fast Fourier Transforms outside of a Euclidean domain (meaning we would have to perform direct matrix multiplications). The method of Kipf and Welling overcomes this problem by setting K = 1 and reformulating the above operation to get

$$g_{\theta }\star x\approx \theta \left(I_N+D^{-\frac{1}{2}}A{D}^{\frac{1}{2}}\right)x$$

The choice of cutoff specifies that all nodes up to K edges away from a given node contribute to the output of the convolution operator at that node. Thus, K = 1 implies that the output at each node is a function of that node and its immediate neighbors. By stacking layers of this form together (after applying a non-linearity at each level), we can integrate information from increasingly farther nodes. Each individual convolution layer can thus be written as

$$x^{\prime }=\sigma \left(g_{\theta }\star x\right)$$

for some non-linear activation function σ. Lastly, this framework can be extended to incorporate more than one input / output channel per layer by adding an additional channel dimension to each of these parameters (see original paper for details).

3.3. Models

We implemented three types of classifiers for comparison: a feed-forward deep neural network (DNN), a graph convolutional neural network (GCN), and a random forest (RF). We constructed the GCN model by stacking two convolutional layers with 64 channels each followed by a fully-connected linear layer with 350 nodes. The DNN model consisted of two fully connected linear layers with 1000 and 350 neurons respectively. We used exponential linear units (eLU) as our activations between each layer in either model and a sigmoid activation at the top level for classifications.³⁸ Additionally, the GCN model was initialized with the adjacency matrix of the phylogenetic tree corresponding to the taxa present in our 12365-dimensional input vector. All three classifiers took such a 12365-dimensional abundance vector as input and produced a 19-dimensional output (number of classes). We implemented our neural networks using PyTorch along with the PyTorch Geometric library for the GCN components.^39,40 Lastly, our random forest model was constructed using the default settings from the random forest module in the Python package Scikit-learn⁴¹ except for the number of trees, which was set to 1000. We settled on these configurations after manual experimentation. We found that increasing the number of trees improved generalization performance of the random forest up to a certain point, and the size of hidden layers in our networks did not make a dramatic difference in performance.

3.4. Training

The biggest challenge in this study was dealing with the extreme class imbalance caused by more than half of the samples in our dataset coming from healthy patients and many diseases having only a few dozen samples. Resampling the dataset to artificially balance it is one way to deal with this problem. Many resampling methods have been shown to perform similarly, so we used a simple oversampling protocol.⁴² For each experiment, we oversampled the training set by computing the size of the largest class (healthy) and randomly resampling from every class until each class had the same number of samples.⁴³

We augmented this by assigning each class a weight of $1-\frac{1}{n}$, where n is the number of classes, and training our neural networks in a one-vs-all manner for each class (using a binary cross-entropy loss function).⁴⁴ To compute the top prediction of the classifier, we ran the outputs of the network through a softmax function and returned the index of the highest class. This is a commonly used technique in multiclass classification, because it reduces the difficult problem of discriminating between n classes to n easier problems of discriminating between two classes.⁴⁵ We used a $1-\frac{1}{n}$ weight in order to address a new class imbalance problem that arises in this setting; if there are m examples of each class in the dataset after oversampling, then each binary classifier will see m positive examples and mn negative examples. A $1-\frac{1}{n}$ weight magnifies the importance of the positive samples for each class to compensate.

Next, we trained our classifiers. We used a 70–30 split between training and test set, generated a new split for each training run, and ran 30 iterations of the GCN model, 30 of the DNN, and 20 of the random forest. Data preprocessing, ingest, and analysis for our neural networks was performed using Fireworks, a PyTorch-based library that we previously developed to facilitate common machine learning tasks.⁴⁶ The GCN and DNN were trained using the Adam optimizer with $2*{10}^{-5}$ and $1*{10}^{-4}$ respective learning rates, 40 and 100 respective batch sizes, weight decay parameter set to 1, binary cross-entropy loss, and an early stopping condition when the loss dropped to 2. We performed an analogous procedure with our random forest classifier by assigning the same class weights and using the same over-sampled training set as with the neural network.

4. Results

We evaluated our classifiers by measuring their accuracy, AUC (area-under-receiver-operating-characteristic (ROC)), and AUPR (area-under-precision-recall-curve (PRC)). The average accuracy varied widely by disease and classifier, indicating the difficulty of this problem given the number of positive samples for each category (Table 2). In general, the convolutional net performed on par with or better than the deep net in terms of accuracy, AUC, and AUPR, implying that the graph structure of the data is useful for making classifications. Both of these models had higher accuracy than the RF for most diseases. The RF excelled in the healthy vs. disease task, producing an impressive 99% accuracy. Because healthy was also the largest component of the test set (66.9% of samples on average), it was responsible for the bulk of the RF’s weighted accuracy measurement. However, overall accuracy can be biased by the distribution of the test set (ie. if there were more samples for the classes that a given classifier excelled at, then that classifier would benefit). When we weighted each class equally, then the GCN had the highest average accuracy (46% vs 34.6% for random forest and 44.9% for DNN), indicating that it was more accurate across a broader range of diseases than the RF model.

Table 2:

Percent accuracy by disease for each model.Boldface indicates the model(s) with the highest score in the category.

	Accuracy (%)
Disease	GCN (n=30)	DNN (n=30)	RF (n=20)
Healthy	91 ± 1	87 ± 1	99 ± 0
Colorectal Cancer (CRC)	36 ± 2	35 ± 2	19 ± 2
Type 2 Diabetes (T2D)	39 ± 3	40 ± 3	08 ± 1
Rheumatoid Arthritis (RA)	73 ± 4	79 ± 2	80 ± 3
Hypertension	56 ± 3	55 ± 3	56 ± 3
Inflammatory Bowel Disease (IBD)	40 ± 3	40 ± 3	07 ± 1
Adenoma	15 ± 2	13 ± 2	04 ± 1
Otitis	12 ± 3	13 ± 2	00 ± 0
Hepatitis B Virus (HBV)	62 ± 3	59 ± 3	80 ± 4
Fatty Liver	32 ± 4	22 ± 2	02 ± 1
Psoriasis	67 ± 4	63 ± 4	51 ± 5
Type 1 Diabetes (T1D)	37 ± 7	41 ± 7	25 ± 6
Metabolic Syndrome	52 ± 6	50 ± 4	08 ± 3
Impaired Glucose Tolerance (IGT)	12 ± 3	18 ± 3	00 ± 0
Periodontitis	93 ± 2	93 ± 3	93 ± 3
Atopic Dermatitis (AD)	80 ± 6	78 ± 6	82 ± 6
C dificile infection (CDI)	67 ± 7	53 ± 5	54 ± 9
Infectious Gastroenteritis	08 ± 4	09 ± 5	01 ± 2
Bronchitis	02 ± 3	05 ± 4	0 ± 0
Average	46 ± 27	45 ± 12	35 ± 14

Next, we computed ROCs, which plot the tradeoff between true-positive-rates and false-positive-rates for a model⁴⁷ (Table 3). This statistic is important because it is invariant to class distribution, and is thus useful for models that try to rule-in a diagnosis, because a high AUC (area-under the ROC plot) score implies that the model can achieve a high true-positive rate while generating few false-positives. We generated ROCs for our neural nets by varying the bias threshold of the final layer and evaluating their true positive and false positive rate on the test set, and for the random forest by using the sklearn.metrics.roc_curve function on the test set predictions. We found that the GCN model had higher or statistically equivalent AUCs across all labels than both the random forest and the deep net. In particular, we achieved an average AUC of 89.5% for T2D, which previous studies have found to be a particularly challenging task⁸ (AUCs typically range in the 60s).

Table 3:

Percent area-under-precision-recall (AUPR) and area-under-ROC (AUC) by disease for each model. Boldface indicates the model(s) with the highest score in the category.

	AUC (%)			AUPR (%)
Disease	GCN	DNN	RF	GCN	DNN	RF
Healthy	84 ± 1	82 ± 0	83 ± 0	73 ± 8	88 ± 1	93 ± 0
CRC	84 ± 1	81 ± 2	50 ± 0	41 ± 4	35 ± 3	53 ± 0
T2D	90 ± 1	86 ± 1	50 ± 0	40 ± 5	31 ± 2	52 ± 0
RA	98 ± 1	99 ± 0	85 ± 2	73 ± 4	74 ± 3	85 ± 2
Hypertension	94 ± 1	92 ± 1	66 ± 1	51 ± 5	44 ± 3	60 ± 2
IBD	94 ± 2	90 ± 1	50 ± 1	41 ± 4	36 ± 2	52 ± 0
Adenoma	81 ± 2	75 ± 2	50 ± 0	15 ± 3	12 ± 1	51 ± 0
Otitis	86 ± 2	74 ± 2	50 ± 0	18 ± 3	10 ± 1	51 ± 0
HBV	97 ± 1	96 ± 1	69 ± 2	64 ± 5	58 ± 3	70 ± 2
Fatty Liver	89 ± 2	80 ± 2	5 ± 2	35 ± 7	20 ± 3	51 ± 0
Psoriasis	98 ± 1	93 ± 2	73 ± 3	74 ± 3	57 ± 4	62 ± 3
T1D	98 ± 0	97 ± 1	53 ± 3	47 ± 7	48 ± 7	53 ± 2
Metabolic Syndrome	98 ± 1	97 ± 1	51 ± 1	63 ± 8	55 ± 3	51 ± 1
IGT	95 ± 1	88 ± 2	50 ± 0	22 ± 3	16 ± 1	50 ± 0
Periodontitis	99 ± 0	99 ± 0	96 ± 2	95 ± 2	93 ± 2	96 ± 2
AD	99 ± 0	99 ± 0	88 ± 3	89 ± 4	78 ± 5	85 ± 3
CDI	99 ± 0	91 ± 4	64 ± 3	75 ± 4	64 ± 8	62 ± 3
Infectious Gastroenteritis	88 ± 3	70 ± 1	50 ± 0	21 ± 4	14 ± 1	50 ± 0
Bronchitis	78 ± 4	74 ± 6	50 ± 0	13 ± 3	13 ± 2	50 ± 0
Average	92 ± 3	88 ± 12	62 ± 7	50 ± 11	45 ± 12	62 ± 7

In a clinical context, class-imbalance is the norm because because most patients do not have a given disease. Thus, for screening purposes, we want a classifier with a low false-negative rate in order to avoid under-diagnosing patients. To evaluate this, we computed AUPR values, which summarize the relationship between positive-predictive-value and true-positive rate.⁴⁸ A high AUPR implies that a model can accurately identify positive labels while avoiding false-negatives. For most diseases, the random forest performed much better than the neural network models with respect to AUPR. This result, along with its superior accuracy on healthy patients, implies that the random forest would be more useful as a screening tool for identifying dysbiosis in general, while the neural networks are more useful as a diagnostic tool for ruling-in a specific disease in patients that have already been screened.

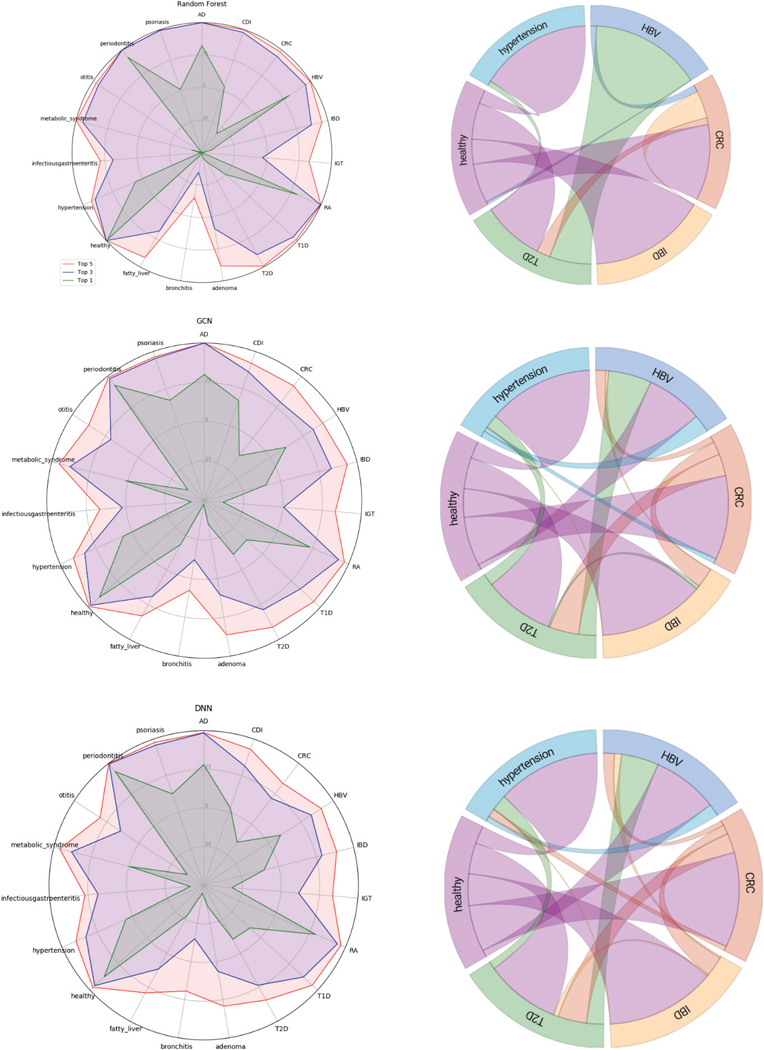
Next, we analyzed the ranking of predictions by our models. A ranked ordering of probabilities may be more useful to a physician than a single output, because that information can be integrated with the entire patient examination to generate a differential diagnosis. We examined the accuracy of the top-3 and top-5 predictions for each classifier (Figure 2). Most diseases were correctly identified within the top-3 classifications, and almost almost every disease was correctly present with at least 90% of the time in the top-5 classifications for each model. We measured which classes were most often predicted for a given label when an incorrect prediction was made for a subset of the labels (ie. how often the model confused a given disease for another disease). Healthy was often misclassified as T2D or CRC, and every disease was often misclassified as healthy. These patterns were also consistent across the three models. These errors may simply be due to the limited size of the dataset or noise in the system. But it could also indicate that the concept of a ‘healthy microbiome’ is vacuous due to the broad of range of microbiomes that a healthy individual can have. Additionally, diseases can manifest with a broad range of severities, which may result in different metagenomic signatures which would all get grouped under a single label.

Fig. 2.

(left) Accuracy at top-1,3, and 5 levels for (top to bottom) Random Forest, GCN, DNN. (right) Chord diagram showing (for a subset of labels) the most common classification made when an incorrect classification was made for a given class.

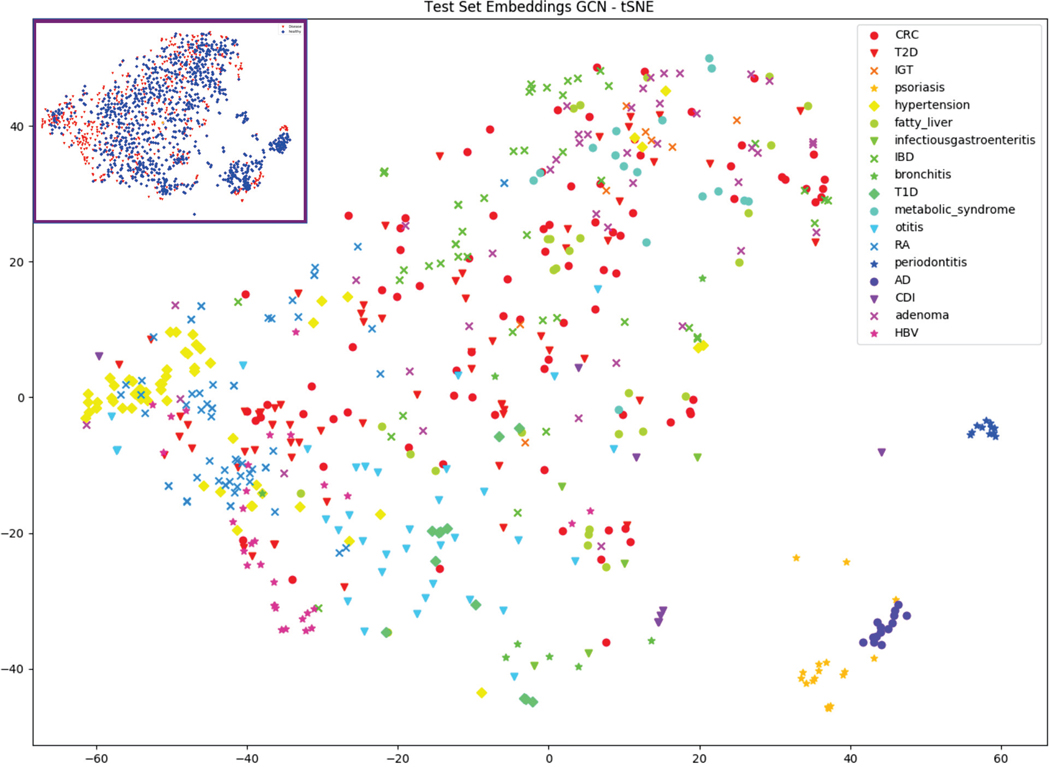
Lastly, we visualized the hidden layer activations of our GCN model on the test set using tSNE to see how different diseases cluster (Figure 3). We found that the skin conditions AD and psoriasis clustered together, separate from the other diseases which were evaluated on stool samples. Periodontitis, which was represented via oral microbiome samples, also clustered independently. Some other conditions, such as hypertension, adenoma, and otitis weakly clustered in some regions of the graph. We also visualized healthy and disease using the same tSNE and found that healthy microbiomes scattered throughout the plot alongside disease, consistent with the idea that there is a broad range of possible healthy microbiomes.

Fig. 3.

tSNE visualization of the final layer activations of the GCN model (excluding healthy). Inset shows the same tSNE labeled by healthy (blue) and disease (red).

5. Conclusion

We have extended the results of previous work on microbiome-phenotype prediction here by demonstrating that multiclass disease prediction from whole community metagenomes, a clinically relevant task for machine learning, is a tractable problem and is improved by using the taxonomic structure of bacterial communities. We implemented multiple classifiers that were able to discriminate between 18 different diseases and healthy with greater than 70% accuracy on a dataset of over 7000 samples. Moreover, while the GCN model generally outperformed the DNN, the RF excelled on a completely different set of metrics, indicating that these two models could potentially complement one another. RF based models, achieving 99% accuracy on healthy vs. not-healthy, could be used as a screening test to identify dysbiosis in general, while GCNs could potentially then be used to discriminate between individual diseases. Additionally, the success of the GCN model implies that the geometric structure entailed in microbial phylogeny contains meaningful information for disease classification. This is a particularly exciting result, because graph and tree structures are ubiquitous in systems biology, so GCN architectures may be applicable to many other biological problems.⁴⁹

While there are obvious clinical applications of a successful phenotype classifier, there are many questions that still need to be answered before these techniques can be deployed to the clinic. For example, we need to understand why the model makes certain predictions in order to give physicians more confidence in its diagnoses. Recently, a class of algorithms called attribution methods have emerged which can identify predictive features in the input on a per-sample basis.^50,51 Attribution methods could be useful from a personalized genomics standpoint by helping explain which bacteria are contributing to dysbiosis in an individual patient and potentially suggesting probiotic interventions to alleviate the dysbiosis. We will perform attribution analysis for our models to consider such questions in a future study.

There are also shortcomings stemming from the available data. For example, we are not aware of any method to infer causality between the microbiome and disease (ie. if the disease signatures the model detects are a cause or effect of the disease). Large-scale causal inference is typically done using time-series or interventional data,⁵² which unfortunately there is very little of in this field.⁵³ Additionally, there is a great deal of patient metadata, such as gender, age, and body site, along with study-specific metadata that may be useful for making these predictions and could be explored in a future work. In general, there is no ‘standardized-dataset’ for this problem, making it difficult to compare different models. To make this exercise easier for other researchers, we have made our code available on Github, which contains not only our models and training scripts, but also our scripts for downloading and pre-processing the data. We believe that the results shown here will be improved upon in the future as more studies are added to curatedMetagenomicData and better models and training procedures emerge. We hope that the code we provide will help other researchers attack this problem and similar problems involving machine learning with metagenomics.

Table 1:

Overview of dataset samples.

Disease	Count	Site	Studies
Atopic Dermatitis (AD)	38	Skin	Chng13
Adenoma	143	Stool	Thomas,7 Feng,14 Hannigan,15 Zeller16
Bronchitis	18	Stool	Yassour17
C. difficile Infection (CDI)	33	Stool	Vincent18
Colorectal Cancer (CRC)	273	Stool	Vogtmann,2 Yu,19 Feng,14 Zeller,16 Hannigan15
Fatty Liver	94	Stool	Loomba,20 Feng14
Hepatitis B Virus (HBV)	99	Stool	Qin21 (2014)
Healthy	3808	All	25 Studies
Hypertension	169	Stool	Thomas,7 Feng,14 Li22
Inflammatory Bowel Disease (IBD)	148	Stool	Nielsen23
Impaired Glucose Tolerance (IGT)	49	Stool	Karlsson24
Infectious Gastroenteritis	20	Stool	David,25 Yassour17
Metabolic Syndrome	50	Stool	Vrieze26
Otitis	107	Stool	Yassour17
Periodontitis	48	Oral	Shi27
Psoriasis	74	Skin	TettAJ28
Rheumatoid Arthritis (RA)	194	Stool	Chengping29
Type 1 Diabetes (T1D)	55	Stool	HeintZ-Buschart,30 Kostic31
Type 2 Diabetes (T2D)	223	Stool	Qin32 (2012), Karlsson24