Reflection on modern methods: five myths about measurement error in epidemiological research

Abstract

Epidemiologists are often confronted with datasets to analyse which contain measurement error due to, for instance, mistaken data entries, inaccurate recordings and measurement instrument or procedural errors. If the effect of measurement error is misjudged, the data analyses are hampered and the validity of the study’s inferences may be affected. In this paper, we describe five myths that contribute to misjudgments about measurement error, regarding expected structure, impact and solutions to mitigate the problems resulting from mismeasurements. The aim is to clarify these measurement error misconceptions. We show that the influence of measurement error in an epidemiological data analysis can play out in ways that go beyond simple heuristics, such as heuristics about whether or not to expect attenuation of the effect estimates. Whereas we encourage epidemiologists to deliberate about the structure and potential impact of measurement error in their analyses, we also recommend exercising restraint when making claims about the magnitude or even direction of effect of measurement error if not accompanied by statistical measurement error corrections or quantitative bias analysis. Suggestions for alleviating the problems or investigating the structure and magnitude of measurement error are given.

Introduction

Epidemiologists are often confronted with datasets to analyse which contain data errors. Settings where such errors occur include, but are not limited to, measurements of dietary intake,^1–3 blood pressure,^4–6 physical activity,^7–9 exposure to air pollutants,^10–12 medical treatments received^13–15 and diagnostic coding.^16–18 Mismeasurements and misclassifications, hereinafter collectively referred to as measurement error, are mentioned as a potential study limitation in approximately half of all the original research articles published in highly ranked epidemiology journals.^19,20 The actual burden of measurement error in all of epidemiological research is likely to be even higher.¹⁹

Despite the attention given to measurement error in the discussion and limitation sections of many published articles, empirical investigations of measurement error in epidemiological research remain rare.^19–21 Notably, statistical methods that aim to investigate the impact of measurement error or alleviate their consequences for the epidemiological data analyses at hand continue to be rarely used. Authors instead appear to rely on simple heuristics about measurement error structure, e.g. whether or not measurement error is expected to be nondifferential, and impact on epidemiological data analyses, e.g. whether or not the measurement error creates bias towards null effects, despite ample warnings that such heuristics are oversimplified and often wrong.^22–27 As we will illustrate, the impact of measurement error often plays out in a way that counters common conceptions.

In this paper we describe and reply to five myths about measurement error which we perceive to exist in epidemiology. It is our intention to clarify misconceptions about mechanisms and bias introduced by measurement error in epidemiological data analyses, and to encourage researchers to use analytical approaches to investigate measurement error. We first briefly characterize measurement error variants before discussing the five measurement error myths.

Measurement error: settings and terminology

Throughout this article (except for myth 5) we assume that measurement error is to occur in a non-experimental epidemiological study designed to estimate an exposure effect, that is the relationship between a single exposure (denoted by $A$, e.g. adherence versus non-adherence to a 30-day physical exercise programme) and a single outcome (denoted by $Y,$ e.g. post-programme body weight in kg), statistically controlled for one or more confounding variables (e.g. age, sex and pre-programme body weight). Some simplifying assumptions are made for brevity of this presentation.

It is assumed that the confounders are adequately controlled for by conventional multivariable linear, risk or rate regression (e.g. ordinary least squares, logistic regression, Cox or Poisson regression), or by an exposure model (e.g. propensity score analysis).²⁸ Besides measurement error, other sources that could affect inferences about the exposure effect are assumed not to play an important role, e.g. no selection bias.²⁹ Unless otherwise specified, we assume that the measurement error has the classical additive form: Observation = Truth + Error, shortened as O = T + E, where the mean of E is assumed to be zero, meaning that the Observations do not systematically differ from the Truth. Alternative and more complex models for measurement error relevant to epidemiological research, such as systematic and Berkson error models,³⁰ are not considered here. We also assume that there is an agreed underlying reality (T) of the phenomenon that one aims to measure and an imperfectly measured representation of that reality (O) subject to measurement error (E). This identifiable measurement error assumption is often reasonable in epidemiological research but may be less so in some circumstances, for instance with the measurement of complex diseases. For in-depth discussion on the theories of measurement we refer to the work by Hand.³¹

In the simplest setting, we may assume (or in rare cases, know) that the measurement error is univariate, that is to say that measurement error occurs only in a single variable. Measurement error in an exposure variable (${\mathrm{E}}_{\mathrm{A}}$) is further commonly classified as nondifferential if error in the measurement error is independent of the true value of the outcome (${\mathrm{T}}_Y,\mathrm{ }$i.e. ${\mathrm{E}}_A⫫{\mathrm{T}}_Y$) and differential otherwise. Likewise, error in the measurement of the outcome (${\mathrm{E}}_Y$) is said to be nondifferential only if the error is independent of the true value of the exposure (${\mathrm{T}}_A,\mathrm{ }$i.e. ${\mathrm{E}}_Y⫫{\mathrm{T}}_A$),^32–35 or in an alternative notation if for each possible outcome status y of $T_Y$, Pr(${\mathrm{O}}_Y$ = y| ${\mathrm{T}}_Y$ = y, ${\mathrm{T}}_A=a)=c,\mathrm{ }\mathrm{where}\mathrm{ }c$ is a constant for all possible values a of ${\mathrm{T}}_A$. (Note that nondifferential error sometimes refers to a broader definition that includes covariates; for a single covariate L with true values, the assumption can then be specified by Pr(${\mathrm{O}}_Y$ = y| ${\mathrm{T}}_Y$ = y, ${\mathrm{T}}_A=a,\mathrm{ }{\mathrm{T}}_l=l)=c$.)

Reconsider the hypothetical example of the relation between the exposure physical exercise programme adherence and post-programme body weight. Differential exposure measurement error would mean that mismeasurement of programme adherence occurs more frequently or more infrequently in individuals with a higher (or lower) post-programme body weight. For the binary exposure programme adherence, nondifferential error simplifies to assuming that the sensitivity and specificity of measured programme adherence are the same for all possible true values of post-programme body weight.

If two or more variables in the analysis are subject to measurement error, we may speak of multivariate (or joint) measurement error. When two variables are measured with error, measurement error (which may be differential or nondifferential for either variable) is said to be independent if the errors in the one error-prone variable are statistically unrelated to the errors in the other error-prone variable and dependent otherwise, i.e. multivariate measurement error in A and Y is said to be independent if ${\mathrm{E}}_Y⫫\mathrm{ }{\mathrm{E}}_A.$^32–34 Dependent measurement error may for instance occur in an exposure variable when error on exposure becomes more (or less) likely for units that are misclassified on the outcome variable. In the hypothetical example, if both adherence to a physical activity programme and post-programme body weight were self-reported, we may expect error in both exposure and outcome measurements. Further, we may also anticipate that respondents who misreport adherence to the exercise programme also misreport their post-programme body weight, which would result in multivariate dependent measurement error.

Five myths about measurement error

In this section we discuss five myths about measurement in epidemiological research, in particular as regards the impact of measurement error on study results (myths 2 and 5), solutions to mitigate the impact (myths 1 and 4) and the mechanisms of measurement error (myth 3). Each myth is accompanied by a short reply that is substantiated in a more detailed explanation.

Myth 1: measurement error can be compensated for by large numbers of observations

Reply: no, a large number of observations does not resolve the most serious consequences of measurement error in epidemiological data analyses. These remain regardless of the sample size.

Explanation: one intuition is that measurement error distorts the true existing statistical relationships between variables, analogous to noise (the measurement error) lowering the ability to detect a signal (the true statistical relationships) that can be picked up from the data. Continuing on this thought, increasing the sample size would amplify the signal to become better distinguishable from the noise, thereby compensating for the measurement error. Unfortunately, this signal to noise analogy rarely applies to epidemiological studies.

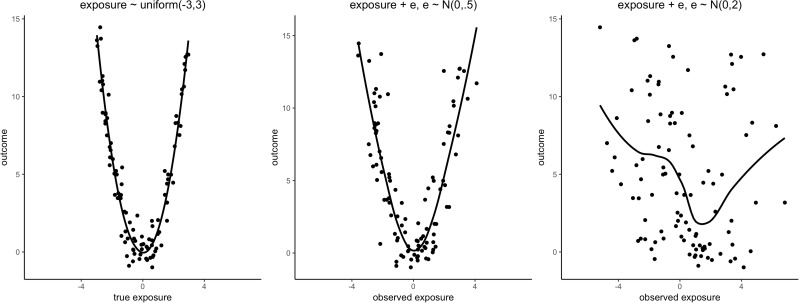
Measurement error can have impact on epidemiological data analyses in at least three ways, as summarized by the Triple Whammy of Measurement Error.³⁰ First, measurement error can create a bias in the measures of the exposure effect estimate. Second, measurement error affects the precision of the exposure effect estimate, often by reducing it, reflected in larger standard errors and widening of confidence intervals for the exposure effect estimates, and a lower statistical power of the significance test for the null exposure effect. Biased exposure effect estimates may, however, be accompanied by smaller rather than larger expected standard errors and conserved statistical power.³⁶ Third, measurement error can mask the features of data, such as non-linear functional relationships between the exposure and outcome variables. Figure 1 illustrates feature masking by univariate nondifferential measurement error.

Figure 1.

Illustration of Whammy 3: Measurement error may mask a functional relation. True model: outcome = 3/2*exposure^2 + e, e∼N(0, 1). Measurement error model: observed exposure value = true exposure value + exposure error. Line is a LOESS curve.

Key Messages

• The strength and direction of effect of measurement error on any given epidemiological data analysis is generally difficult to conceive without appropriate quantitative investigations.

• Frequently used heuristics about measurement error structure (e.g. nondifferential error) and impact (e.g. bias towards null) are often wrong and encourage a tolerant attitude towards neglecting measurement error in epidemiological research.

• Statistical approaches to mitigate the effects of unavoidable measurement error should be more widely adopted.

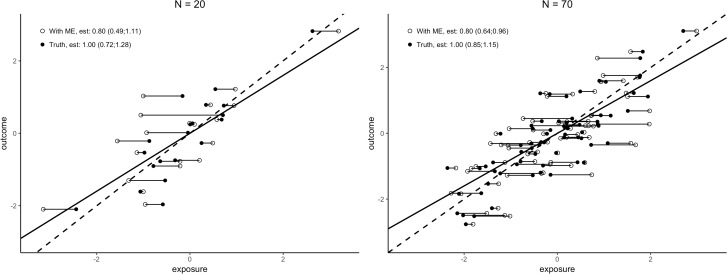
With sample size increasing and assuming all else remains equal, exposure effect estimates will on average be closer to their limiting expected values, while not necessarily closer in distance to their respective true values. A large sample size thus improves the assurance that the exposure effect estimate comports to the expected value under the measurement error mechanism, affecting the second Whammy of Measurement Error (precision) but not directly the first (bias) (Figure 2). A larger sample size may thus compensate for the loss in precision and power which is due to the presence of measurement error. The compensation needed for studies with data that contain measurement error can be a 50-fold or more increase of the sample size when the reliability of measurement is low.^37,38 In consequence, even a dataset of a spectacularly large size containing measurement errors may or may not yield more precise estimates and more powerful testing than a much smaller dataset without measurement error.

Figure 2.

Illustration of Whammy 1 (bias) and Whammy 2 (precision, see width confidence intervals) of measurement error. Dashed is regression line without measurement error (Truth), solid line is regression line with measurement error (With ME). N = sample size. Lines, point estimates and confidence intervals based on 5000 replicate Monte Carlo simulations (Truth: outcome = exposure + e, e∼N(0, 0.6), exposure∼N(0, 1), With ME: Truth + er, er∼N(0, 0.5)). Plotted points the first single simulation replicate.

Myth 2: the exposure effect is underestimated when variables are measured with error

Reply: no, an exposure effect can be over- or underestimated in the presence of measurement error depending on which variables are affected, how measurement error is structured and the expression of other biasing and data sampling factors. In contrast to common understanding, even univariate nondifferential exposure measurement error, which is often expected to bias towards the null, may yield a bias away from null.

Explanation: more than a century ago, Spearman³⁹ derived his measurement error attenuation formula for a pairwise correlation coefficient between two variables wherein at least one of the variables was measured with error. Spearman identified that this correlation coefficient would on average be underestimated by a predictable amount if the reliability of the measurements was known. This systematic bias towards the null value, also known as regression dilution bias, attenuation to the null and Hausman’s iron law, is now known to apply beyond simple correlations to other types of data and analyses.^25,40–42

It is, however, an overstatement to say that—by iron law—the exposure estimates are underestimated in any given epidemiological study analysing data with measurement error. For instance, selective filtering of statistically significant exposure effects in measurement error-contaminated data estimated with low precision is likely to lead to substantial overestimation of the exposure effect estimates for the variables that withstand the significance test.²⁶ Even if one is willing to assume that measurement error is the only biasing factor, a simplifying assumption that we make in this article for illustration purposes only, statistical estimation is subject to sampling variability. The distance of the exposure effect estimate relative to its true value varies from dataset to dataset. In a particular dataset with measurement error, exposure effects may be overestimated only due to sampling variability, illustrations of which are found in Hutcheon et al. and Jurek et al.^22,43 Hence, a defining characteristic of the iron law is that it applies to averages of exposure effect estimates, e.g. after many hypothetical replications of a study with the same measures.

This is not to argue that measurement error in itself cannot, in principle, produce a bias in a predictable direction. The iron law does come with many exceptions. For instance, the law does not apply uniformly to univariate differential measurement error in any variable (which may produce bias in the exposure effect estimate away or towards null^27,44–46), nor to univariate nondifferential error in the outcome variable (which may not affect bias in the exposure effect in case the outcome is continuous²⁵) nor to univariate nondifferential measurement error in one of the confounding variables (which may create a bias in the exposure effect estimate away or towards null due to residual confounding^27,44,47). For multivariate measurement error in any combination of exposure, outcome and confounders, bias in the exposure can be in either direction, with the exception of (strictly) independent and nondifferential measurement error in dichotomous exposure and outcome.³⁴

There are also exceptions to the iron law in cases of univariate nondifferential exposure measurement error. Particularly, nondifferential misclassification of a polytomous exposure variable (i.e. with more than two categories) may create bias that is away from null for some of the exposure categories and towards null for others.^29,48,49 Measurement error of any kind, including nondifferential exposure measurement error, also hampers the evaluation of exposure effect modification,^44,50 interaction^51,52 and mediation,^53,54 creating bias away or towards null.

Myth 3: exposure measurement error is nondifferential if measurements are taken without knowledge of the outcome

Reply: no, exposure measurement error can be differential even if the measurement is taken without knowledge of the outcome.

Explanation: differential exposure measurement error is of particular concern because of its potentially strong biasing effects on exposure effect estimates.^29,35,55 Differential error is a common suspect in retrospective studies where knowledge of the outcome status can influence the accuracy of measurement of the exposure. For instance, in a case-control study with self-reported exposure data, cases may recall or report their exposure status differently from controls, creating an expectation of differential exposure measurement error. Differential exposure measurement error may also arise due to bias by interviewers or care providers who are not blinded to the outcome status, or by use of different methods of exposure measurement for cases and controls.

Differential exposure measurement error is often not suspected in prospective data collection settings where the measurement of exposure precedes measurement of the outcome. Measurement of exposure before the outcome is nonetheless insufficient to guarantee that exposure measurement error is nondifferential. For example, as White⁵⁶ noted: in a prospective design, differential measurement error in the exposure ‘family history of disease’ may be due to a more accurate recollection of family history among individuals with strong family history who are at a higher risk of the disease outcome. The nondifferential exposure measurement assumption is violated, as the measurement error in exposure is not independent of the true value of the outcome (i.e. ${\mathrm{E}}_A⫫{\mathrm{T}}_Y$ is violated) despite that the exposure was measured before the outcome could have been observed.

Measurement error structures are also not invariant to discretization and collapsing of categories. For instance, discretization of a continuous exposure variable measured with nondifferential error into a categorical exposure variable can create differential exposure measurement error within the discrete categories.^48,57,58 A clear numerical example of this is given in Wacholder et al., their second table.⁵⁹ Although discretization in broader categories may be perceived as more robust to measurement error-induced fluctuations, the possible change in the mechanism of the error may do more harm than good for the estimation of the exposure effect.

Myth 4: measurement error can be prevented but not mitigated in epidemiological data analyses

Reply: no, statistical methods for measurement error bias-corrections can be used in the presence of measurement error provided that data are available on the structure and magnitude of measurement error from an internal or external source. This often requires planning of a measurement error correction approach or quantitative bias analysis, which may require additional data to be collected.

Explanation: a number of approaches have been proposed which examine and correct for the bias due to measurement error in analysis of an epidemiological study, typically focusing on adjusting for the bias in the exposure effect estimator and corresponding confidence intervals. These approaches include: likelihood based approaches⁶⁰; score function methods⁶¹; method-of-moments corrections⁶²; simulation extrapolation⁶³; regression calibration⁶⁴; latent class modelling⁶⁵; structural equation models with latent variables⁶⁶; multiple imputation for measurement error correction⁶⁷; inverse probability weighing approaches⁶⁸ and Bayesian analyses.⁶⁹ Comprehensive text books^{30,62,69–71} and a measurement error corrections tutorial⁷² are available. Some applied examples are given in Table 1.

Table 1.

Examples of measurement error corrections, models and bias analyses

Measure with error	Methods	Applied example	Ref.
Serum measurement of Vitamin D	Regression calibration	To account for measurement error, serum measurements were calibrated to assay measurements (the preferred reference standard) using data from an earlier study containing measurements of both assay and serum of Vitamin D	73
Smoking status reported by health care providers	Multiple imputation	Clinical assessments of smoking status were available only for an internal validation subgroup. Multiple imputation was used to account for the potential measurement error in health care provider-reported smoking status for the remaining patients	74
Low-density lipoprotein cholesterol (LDL-c) measurement	SIMEX	Effect estimate of LDL-c on coronary artery disease was corrected for bias in the error contaminated LDL-c measurements using the Simulation Extrapolation (SIMEX) method	75
Self-reported dietary fibre intake	Regression calibration	Repeated measurement of error-prone self-reported dietary feedback was used to estimate within-person variation to correct for measurement error via regression calibration	76
Diagnostic tests for pulmonary tuberculosis (PTB)	Latent class analysis	Results from six diagnostic tests for PTB were available which were considered error-contaminated measurements of PTB infection. A latent class model was developed to estimate diagnostic accuracy in the absence of a gold standard	77
Self-reported influenza vaccination status	Quantitative bias analysis	Monte Carlo simulations were performed to evaluate the impact of measurement error in the relation between vaccination status of pregnant women and preterm birth, assuming a range of plausible accuracy values for self-reported influenza vaccination	78

Measurement error correction methods⁷⁹ require information to be gathered about the structure and magnitude of measurement error. These data may come from within the study data that are currently analysed (i.e. internal validation data) or from other data (i.e. external validation data). If an accurate measurement procedure exists (i.e. a gold standard), either external or on an internal subset, a measurement error validation study can be conducted to extract information about the structure and magnitude of measurement error. If no such gold standard measurement procedure exists, a reliability study can replicate measurements of the same imperfect measure (e.g. multiple blood pressure measurements within the same unit), or alternatively, observations on multiple measures that aim to measure the same phenomenon (e.g. different diagnostic tests for the same disease within the same unit). Different measurement error correction methods, and the ability of the bias correction to return an estimate nearer to the truth, may be more or less applicable depending on the data sources available for the measurement error correction.

The impact of measurement error on study results can also be investigated by a quantitative bias analysis,^79,80 even in the absence of reliable information about structure and magnitude. In brief, a quantitative bias analysis is a sensitivity analysis that simulates the effect of measurement error assuming a certain structure and magnitude of that error. Since some degree of uncertainty about measurement error generally remains, in particular about error structure, sensitivity analyses can also be useful following the application of measurement error correction methods mentioned above.

Myth 5: certain types of epidemiological research are unaffected by measurement error

Reply: no, measurement error can affect all types of epidemiological research.

Explanation: measurement error affects epidemiology undoubtedly beyond the settings we have discussed thus far, i.e. studies of a single exposure and outcome variable statistically controlled for confounding. For instance, measurement error has also been linked to issues with data analyses in the context of record linkage,^81,82 time series analyses,^10,11 Mendelian randomization studies,⁸³ genome-wide association studies,⁸⁴ environmental epidemiology,⁸⁵ negative control studies,⁸⁶ diagnostic accuracy studies,^87,88 disease prevalence studies,⁸⁹ prediction modelling studies^90,91 and randomized trials.⁹²

It is worth noting that types of data and analyses can be differently affected by measurement error. This means that even when measurement error is similar in structure and magnitude, the error can have a different impact depending on the analyses conducted. For example, consider a two-arm randomized trial with univariate differential measurement error in the outcome variable. If it is not possible to blind patients and providers to the treatment assignment, then the accuracy of assessment of some outcomes may depend on the assigned treatment arm. In this setting, bias in the exposure (treatment) effect estimate can be in either direction and inflate or deflate both Type I and Type II error for the null hypothesis significance test of no effect of treatment.⁹² The impact the measurement error has on the inferences made from the trial’s results depends on whether the trial is a superiority, equivalence or non-inferiority trial.⁹³

Concluding remarks

Our discussion of five measurement error-related myths adds to an already extensive literature that has warned against the detrimental effects of neglected measurement error, a problem that is widely acknowledged to be ubiquitous in epidemiology. We suspect that these persistent myths have contributed to the tolerant attitude towards neglecting measurement error found in most of the applied epidemiological literature, as evidenced by the slow uptake of quantitative approaches that mitigate or investigate measurement error.

We have shown in this paper that the effect that measurement error can have on a data analysis is often counter-intuitive. Whereas we encourage epidemiologists to deliberate about the structure and potential impact of measurement error in their analyses, for instance via graphical approaches such as causal diagrams,^33,45,94 we also recommend exercising restraint when making claims about the magnitude or even direction of bias of measurement error if not accompanied by analytical investigations. With the increase of collection and use of epidemiological data that are primarily collected without a specific research question in mind, such as routine care data,⁹⁵ we anticipate that attention to measurement error and approaches to mitigate it will only become more important.

Funding

R.H.H.G. was funded by the Netherlands Organization for Scientific Research (NWO-Vidi project 917.16.430). T.L.L. was supported, in part, by R01LM013049 from the US National Library of Medicine.