Layer-resolved ultrafast extreme ultraviolet measurement of hole transport in a Ni-TiO₂-Si photoanode

Ultrafast charge carrier migration through all the layers of a nanojunction is observed and quantified.

Abstract

Metal oxide semiconductor junctions are central to most electronic and optoelectronic devices, but ultrafast measurements of carrier transport have been limited to device-average measurements. Here, charge transport and recombination kinetics in each layer of a Ni-TiO₂-Si junction is measured using the element specificity of broadband extreme ultraviolet (XUV) ultrafast pulses. After silicon photoexcitation, holes are inferred to transport from Si to Ni ballistically in ~100 fs, resulting in characteristic spectral shifts in the XUV edges. Meanwhile, the electrons remain on Si. After picoseconds, the transient hole population on Ni is observed to back-diffuse through the TiO₂, shifting the Ti spectrum to a higher oxidation state, followed by electron-hole recombination at the Si-TiO₂ interface and in the Si bulk. Electrical properties, such as the hole diffusion constant in TiO₂ and the initial hole mobility in Si, are fit from these transient spectra and match well with values reported previously.

INTRODUCTION

Metal oxide semiconductor (MOS) junctions are foundational to electronic devices. In solar energy research, oxide-passivated junctions have led to record photoconversion efficiencies for semiconductor solar cells and photoelectrodes (1–3). In a solar cell, one role of the metal oxide–passivated junction is to control surface recombination velocities, slowing the recombination at the metal-semiconductor contacts (4). In photoelectrochemical cells, the metal oxide layer also acts as a corrosion barrier (5–9). Even in solar photocatalytic reduction of CO₂, the MOS junction has proven critical by acting as a proton transport layer (10, 11). Despite the critical applications of MOS junctions, the femtosecond-to-picosecond charge transfer processes that occur within a photoinitiated MOS junction are still debated. It is established that field-induced tunneling dominates thin <5-nm junctions. However, in photoelectrochemical junctions, thicker barriers often lead to better performance (5). In addition, an amorphous or defect-rich oxide will often outperform a crystalline material. It has therefore been proposed that in p-type MOS junctions with TiO₂, the Ti³⁺ defect states support efficient hole or proton conduction (6, 12, 13).

Ultrafast x-ray studies have recently brought element specificity to time-resolved dynamics (14, 15). One approach to producing ultrafast x-ray probes is using high harmonic generation. In high harmonic generation, extreme ultraviolet (XUV) or soft x-ray pulses are produced by a noble gas using a tabletop laser (16). The broadband x-ray pulses can have a bandwidth of 10 to 100 eV, allowing for multiple elements to be temporally correlated. However, interpreting the measured x-ray dynamics in terms of ground-state electronic properties is made difficult by the positive core-hole that is produced by the core-level probe transition. Advances in theory have led to accurate interpretation of atomic and molecular dynamics, but the many-body state created by the core-hole in a solid makes the theoretical interpretation of the spectral features challenging (17, 18). Nevertheless, recent progress in approximate methods has led to extraction of the electron and hole dynamics in semiconductors. The fit dynamics accurately correspond to scattering pathways within the material’s band structure (19–22).

Here, we use the element specificity of transient XUV spectroscopy to measure the charge transfer kinetics of a Ni-TiO₂-Si junction with band alignment as shown in Fig. 1A. First, a near-infrared pump photoexcites the 200-nm-thick Si in the MOS junction. Then, a broadband XUV pulse created by high harmonic generation in Ar (30 to 60 eV) or He (60 to 110 eV) probes the photoexcited changes in the Ti M_2,3 edge at 33 eV, the Ni M_2,3 edge at 66 and 68 eV, and the Si L_2,3 edge at 100 eV from femtoseconds to 200 ps. The increased absorption feature normally ascribed to photoexcited holes in pure Si is not measured immediately in the junction. The electron spectral feature of Si is consistent with photoexcited Si alone. A subsequent negative shift in the Ni edge energy is measured within 100 fs, which is attributed to excess holes opening up transitions to states below the Fermi energy. No change is measured for the Ti edge on this short time scale. On a picosecond time scale, the Ni edge energy returns to its equilibrium value while a positive energy shift of the Ti edge is measured, attributed to an increase in the Ti oxidation state from back diffusion of excess holes. On a time scale of tens to hundreds of picoseconds, the Ti peak shift reaches its maximum, and then it begins to decay in sync with the decay of the electron signature in Si.

Fig. 1. Characterization and measurement of the Ni-TiO₂-Si junction.

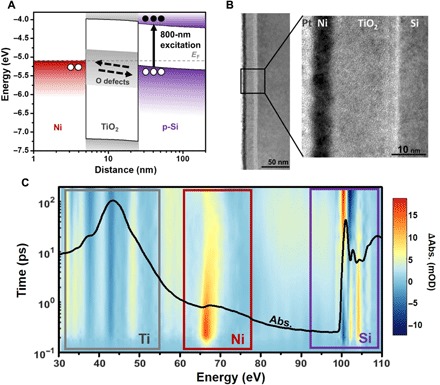
(A) The energy level alignment for the metal, oxide, and semiconductor is shown, along with the expected photoexcited hole transfer in the p-type MOS junction. The Si is p-type–doped by boron at 10¹⁵ per cm³. The presence of oxygen defect levels (n-type) in the TiO₂ layer was previously confirmed by photoemission spectroscopy of a Si-TiO₂ junction (23). The band bending is calculated using the drift-diffusion equation (27). (B) A TEM measurement of the thickness of the TiO₂ and Ni, which are 19 ± 0.6 nm and 5.6 ± 0.6 nm, respectively. The TiO₂ is amorphous, and an ~1-nm SiO₂ interface is measured where the TiO₂ and Si contact. (C) The black line overlay is the ground-state XUV absorption. The regions that correspond to the Ti M_2,3 edge, the Ni M_2,3 edge, and the Si L_2,3 edge are indicated by the colored boxes. The differential XUV absorption that results from photoexcitation is shown as the background color map, with the scale on the right of the graph. Each peak is observed to have a unique response to the photoinitiated charge transfer, which will be discussed in the main text.

The initial hole transport from Si to Ni in the junction is fit and compared with the fitted hole transport time in a Ni-Si sample. The average hole transit time is delayed in the junction by 33 ± 8 fs, and the hole quantum yield is measured to be 42 ± 6%. Accounting for the TiO₂ thickness, the hole tunneling velocity in the TiO₂ is 5.8 ± 1.4 × 10⁷ cm/s. For the built-in electric field (1.5 × 10⁵ V/cm) of the MOS junction, this implies a hole mobility of 390 ± 100 cm²/V·s in Si, which matches measured Si hole mobilities. The value suggests ballistic transfer because it is unchanged by scattering in the TiO₂. After the tunneling process, the holes back-transfer through the TiO₂ with a fit diffusion constant of 1.2 ± 0.1 cm²/s. The recombination of holes in the TiO₂ with nontransferred electrons in the Si, or injection of holes from TiO₂ to Si, is fit to a surface recombination/injection velocity of >200 cm/s.

RESULTS

The Ni-TiO₂-Si thin films (Fig. 1A) were prepared via physical vapor deposition under ultrahigh vacuum conditions using home-built evaporators. Filaments of the Ti and Ni metals were evaporated with and without oxygen, respectively, onto a purchased silicon membrane. The 19 ± 0.6 nm of TiO₂ and 5.6 ± 0.6 nm of Ni were grown on a 200-nm-thick p-doped (B at 10¹⁵ per cm³) Si membrane. The surface oxide of the Si could not be etched because of the fragility of the membrane, as attempts to perform Ar sputtering destroyed them. The ~1-nm SiO₂ layer can be seen in the transmission electron microscope (TEM) image of Fig. 1B and may act as a thin tunneling barrier; its presence is consistent with previous Ni-TiO₂-Si photoanode studies (5, 23). The topmost Pt layer was used for TEM imaging purposes. The TEM cross section confirms the amorphous nature of the TiO₂. For this sample, the presence of the oxygen defect levels in the TiO₂ was previously quantified during growth of the Si-TiO₂ junction to have a density of states of approximately 6% of the O 2p density of states via photoemission spectroscopy (24). The resulting Ti³⁺ defect states in the amorphous TiO₂ are generally accepted to be >1 eV below the conduction band of TiO₂ and span a range of 1 to 2 eV (13, 25, 26).

The band bending in Fig. 1A is calculated on the basis of a drift-diffusion model using the experimentally measured thicknesses (27). Calculations were performed with the AFORS-HET (automat for the simulation of heterostructures) program, setting the electron affinity of the p-Si to 4.05 eV and the n-TiO₂ to 4.0 eV. More details of this calculation can be found in the Supplementary Materials. Note that in a Si-TiO₂ junction alone, the band energetics promote photoexcited electron transport from the Si to TiO₂ (28). This is because the approximately 0.1-eV difference in Fermi level between the n-TiO₂ and p-Si creates an electron accumulation layer in Si and, in turn, a negative field that transports the photoexcited electrons. The Ni layer has an electron affinity nearly 1 eV below that of both TiO₂ and Si, which creates the opposite direction field in the total device junction. Holes accumulate in the TiO₂ at the TiO₂/Ni interface, but this layer is so thin that additional holes accumulate in the Si. The Si and TiO₂ bands both bend upward, producing a positive 1.5 × 10⁵ V/cm field across the TiO₂ layer promoting hole transport, as shown in Fig. 1A.

The ground-state XUV absorption (black line overlay in Fig. 1C) contains the Ti M_2,3 edge at 32.6 eV, the Ni M_2,3 edges at 66.2 and 68 eV, and the Si L_2,3 edges at 99.2 and 99.8 eV. The XUV range of 30 to 150 eV is created by high harmonic generation in Ar or He. An Al or Zr metal filter prevents second-order diffraction modes from being observed at the XUV camera. The residual 800-nm driving laser for the high harmonic generation process is removed using a microchannel plate filter before the camera (29). The full details of the technique are found in the Materials and Methods. The ground-state absorption amplitude for each elemental edge is determined by the film thickness (Fig. 1B) and the absorption transition probability of the element. This is why the absorption magnitude of the ~20-nm TiO₂ film, which has 10 empty 3d levels, is larger than the 200-nm-thick Si, which has partially occupied and sp–hybridized valence bands. Similarly, the Ni M_2,3 edge has the smallest amplitude in the static spectra because only two unoccupied 3d orbitals can absorb the XUV radiation in the relatively thin ~5-nm film.

Charge transfer in the MOS junction is photoinitiated by a 50-fs 800-nm laser pulse from a Ti:sapphire regenerative amplifier. The Si thin film primarily absorbs the 800-nm radiation, photoexciting electrons and holes by an indirect transition to the Δ valley. The photoexcitation density is restricted to 1 × 10²⁰ carriers/cm³ to minimize multiphoton absorption by using 800-nm pulse energy densities of approximately 2 mJ cm⁻² (30). The resulting changes to the XUV absorption spectrum are shown as the background color map of Fig. 1C. The blue color represents a decrease in absorption after photoexcitation, while the red color indicates an increase in absorption. The change in absorption is displayed from tens of femtoseconds to 200 ps on a logarithmic time scale. The time scale is offset for visualization, with zero delay between pump and probe occurring at 100 fs. The absorption features in Fig. 1C and their evolution in time represent the underlying photoexcitation, charge transfer, and heat transfer processes in the junction.

The differential absorption versus photon energy of Si and Ni at 100 fs and Ti at 1 ps is shown in the bottom row of Fig. 2. The top row of Fig. 2 shows the ground-state absorption plus the differential absorption, scaled for visualization. This information is plotted for each element in the junction (solid lines) as well as for Si, Ni, and TiO₂ photoexcited on their own (dashed lines). The full differential absorption plots for the elements alone are shown in fig. S1. For the alone samples, conditions are arranged to obtain a similar transient absorbance as for the junction. In Si, this is simply measuring a blank membrane at the same 800-nm photoexcitation density as the junction. To measure TiO₂ alone, a TiO₂ layer on a diamond substrate is measured and the pump wavelength is changed to 266 nm (approximately 1 mJ cm⁻²) to excite above the ~3.2-eV bandgap (30). The 266-nm single-photon absorption probability of TiO₂ is 10⁵ times larger than the three photon absorption at 800 nm needed to excite above the bandgap, so any excitation of TiO₂ by 800-nm light can be neglected in the junction. To measure Ni alone, a diamond substrate supporting a Ni layer of the same thickness as the junction is not a good comparison. When this sample is excited by 800-nm light to the same carrier density as Si (approximately 0.3 mJ cm⁻²), no signal from Ni is observed within the experimental noise (see fig. S2). The Ni in the junction has a 0.03 optical density (OD) absorption magnitude from the pre-edge to the peak. Instead, a thicker layer of Ni with an absorption of 0.6 OD from the pre-edge to peak is used (fig. S2). When the thicker Ni is photoexcited with the same density of 800-nm light, a change in absorption of ~25 milli-OD or milli-optical density (mOD) is measured. This change would be obscured in the thinner sample, as the 20× decrease in absorbed 800-nm light would be below the few mOD noise. In addition, an immediate rise time is not measured for the Ni in the junction, as it is for Ni alone, as discussed in the section ‘Comparing ultrafast dynamics between the junction and lone layers’.

Fig. 2. Photoexcited changes in the Si, TiO₂, and Ni separately and in a junction.

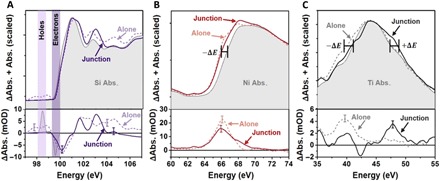
The differential absorption versus photon energy from Fig. 1C is plotted in the bottom row, while the top row shows the differential absorption scaled and added to the ground-state absorption. The solid lines represent the excited-state change for the elements in the junction for (A) Si 100 fs after photoexcitation, (B) Ni 100 fs after photoexcitation of the Si, and (C) TiO₂ 1 ps after the photoexcitation of Si. The same time differential absorption versus photon energy is shown for photoexcitation of each element alone as a dashed line. As discussed in the text, different excitation wavelengths and thicknesses were required to photoexcite the elements alone as compared to the junction. A representative error bar of the experimental few mOD noise is shown at key comparison energies.

Interpreting the differential XUV spectra at the Si, Ni, and Ti edges

The core-hole excited by the XUV transition perturbs the final state in the core-level transition, masking the ground-state density of states. The strength of the core-hole interaction depends on the element’s orbital occupation and bonding. The stronger the core-hole interaction, the more the ground-state density of states is masked, and thus the information that can be obtained from the measured photoexcited state is altered. For example, the core-hole in Si is well screened, and the critical points are only slightly shifted from the ground-state band structure (fig. S3A). Changes in the Si L_2,3 edge are therefore representative of the underlying carrier and lattice dynamics, as shown by the L_2,3 edge absorption of different Si oxidation states in fig. S4A. After photoexcitation, the differential absorption features above 101 eV are known to correspond to structural changes (30). Below 101 eV, a signature of the photoexcited electron and hole populations is present at approximately 100 and 99 eV, respectively, as shown in the bottom panel of Fig. 2A. When the Si alone is photoexcited (dashed line in Fig. 2A), an increased absorption is measured below 99 eV (holes) and above 101 eV (structural). A decreased absorption is measured around 100 eV (electrons). Following photoexcitation of the Si in the junction, an increased absorption is not measured below 99 eV, while a decreased absorption is still measured at 100 eV. In other words, the spectral signature of photoexcited holes is not observed within the signal-to-noise ratio of the experiment in the junction, but the electron signature is present. Above 101 eV, a slightly different structural change is also measured, as would be expected when comparing the strain dynamics of the free-standing 200-nm Si film versus the more rigid junction. Together, the Si edge measurement suggests that holes have left the Si but the electrons remain, as expected for the operation of this MOS junction (Fig. 1A).

Unlike the Si edge, the metallic Ni M_2,3 edge does not closely correspond to the underlying density of states (fig. S3B). The core-hole perturbs the final-state wave function, and the resultant many-body interaction exponentially increases the number of states at energies near the Fermi level. This leads to the sharp absorption feature around 66 eV in the ground-state XUV spectrum. Any photoexcited changes in the edge therefore mostly relate to changes in occupation near the Fermi level. Following photoexcitation of the Ni alone with 800-nm light, the M_2,3 edge shifts to lower absolute energies and increases in absorption (dashed line Fig. 2B). A similar, but slightly broader, change occurs when the Ni is photoexcited in the junction. Photoexcitation of Ni alone promotes electrons from the Fermi level to a higher lying conduction band, shifting the quasi-Fermi level to lower energy. The presence of more holes near the Fermi level also allows for more XUV transitions to be possible near the Fermi level. Correspondingly, a negative energy shift and gain in absorption is measured in Fig. 2B. The photoexcited electrons are too high in energy to affect the many-body state near the Fermi level. In the junction, the same negative shift is measured when 800-nm light excites the Si, indicating that holes have been added to the Ni near the Fermi level. Thus, while holes are not directly observed in the Si, their rapid movement into the Ni is observed. The appearance of holes on the Ni corresponds to the absence of holes measured on Si. For reference, the hole spectral signature is also observed when comparing the static ground-state absorption of Ni⁰ to Ni²⁺ in NiO (fig. S4B).

The measurements in Fig. 2 (A and B) indicate that holes are transferred from the Si to the Ni within the first 100 fs of optical excitation. No transient signal is measured for TiO₂ in this same time period, as can be seen in the color map in Fig. 1C. Instead, the dynamics in TiO₂ start only after 1 ps and represent a shift and broadening (Fig. 2C). The Ti M_2,3 core-hole has a strong interaction with the localized Ti 3d orbitals in TiO₂. Little screening of the core-hole occurs, and as a result, the measured spectrum is distorted from the ground-state density of states by atomic multiplet splitting (fig. S3C). When the TiO₂ is photoexcited alone at 266 nm, a small negative shift in the edge energy is observed. The negative energy shift occurs immediately after photoexcitation because an electron is promoted from the O 2p orbital to the Ti 3d orbital, lowering the Ti oxidation state. The added electron helps screen the strong core-hole interactions on the Ti such that the overall edge shift is negative. When the junction is photoexcited, a small positive shift to larger absolute energy is observed after 1 ps. This opposite shift when the Si is photoexcited is interpreted to mean that the Ti oxidation state has increased or that holes have been added instead of electrons. The positive and negative shifts can again be confirmed by comparing the ground-state absorption of different Ti charge states (fig. S4C). The spectral shifts assigned to holes have opposite signs in the Ni and TiO₂ because the predominant core-hole effects are different. The excess holes increase the Ti oxidation state, decreasing the core-hole screening and shifting the peak positively. The excess holes on the Ni perturb the many-body state at the transition edge, shifting the quasi-Fermi level and opening up new transitions.

Comparing ultrafast dynamics between the junction and alone layers

The fit kinetics for the electrons and holes on Si, as well as the Ti and Ni edge shifts, are shown in Fig. 3. The fit procedure qualitatively mirrors the discussion of Fig. 2 and is described in more depth in the Supplementary Materials. Briefly, the ground-state absorption is modeled (fig. S3) using the Bethe-Salpeter equation with density functional theory for the Si and TiO₂ while using an analytic many-body theory expression for the Ni. The photoexcited data are then fit at each time point as equilibrium changes to the ground state. For the Si, the electron and hole signatures are fit based on previous analysis (Fig. 3A) (22, 30). For the Ni and Ti, the edge shifts are fit since no distinct spectral signature exists for the photoexcited electrons and holes (Fig. 3B). For reference, all fit quantities are shown in fig. S5. In Fig. 3, the error bars of the fit process are shown on the symbols in the graphs, and the data for the material alone are shown as the gray symbols.

Fig. 3. Comparing the fit kinetics separately and in a junction.

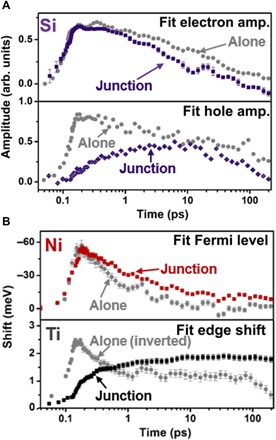
The spectral signatures described by Fig. 2 are fit to extract the excited-state kinetics, shown here. In each case, the error bars correspond to the nonlinear fit standard error from a robust fit weighted by the experimental uncertainty. For each plot, the junction fit parameters are shown as the colored symbols, while the gray symbols are for the isolated material. The time scale is logarithmic with a 100-fs offset for visualization. (A) The amplitude of electron spectral signature in the junction (purple symbols) has a similar rise time compared to the isolated material but has an increased decay rate. In the isolated Si, the amplitude of the hole spectral feature (gray symbols in bottom panel) follows the same kinetics as the electrons. In the junction, the hole signature slowly grows until 10 ps, suggesting that the initial photoexcited hole population was transferred out from the Si. (B) Top: The fit Fermi level of Ni decreases when the Si in the junction is excited with 800-nm light or when a 20× thicker Ni film alone is excited with 800-nm light. The fit Fermi level then decays on a longer time scale in the junction. The amplitudes are scaled for comparison of the rise times. Bottom: When TiO₂ alone is excited with 266-nm light, a decrease in the fitted edge energy is observed because of the ligand-to-metal charge transfer. In the junction, the Ti edge fit energy increases on a time scale that matches the decay of the Fermi level in Ni.

The fit kinetics confirm and quantify the qualitative observations of Fig. 2. Specifically, following photoexcitation, holes are absent on the Si in the junction, while the photoexcited electrons exist in the same magnitude as Si alone. An initial change is not measured in the Ti edge. However, an edge shift that correlates with increased holes in the Ni is measured on a sub–100-fs time scale, in agreement with the expected photoexcited tunneling of holes for the p-type MOS junction. For the first approximately 100 fs, while holes are still being transferred from the Si to the Ni, a small hole population is still present in Si. No signature of these holes is reported because of the extremely low signal-to-noise ratio of the Si (<3 mOD signal) hole population at this excitation density, while holes are more readily observed in Ni (>20 mOD signal), as can be seen in the error bars in the bottom panels of Fig. 2 (A and B).

After a few hundred femtoseconds, the fit edge shift of the Ni decreases in magnitude, while the positive edge shift of the Ti begins to rise on a similar time scale. This observation correlates with the transferred holes leaving the Ni by back-diffusing through the TiO₂. The fit kinetics at >100 ps are further consistent with the arrival of holes at the Si/TiO₂ interface and the following injection into the Si bulk or surface recombination with the excited electrons left on the Si. This is evidenced by the similar time scales of the decay of the fit Si hole and electron amplitudes as the decay of the Ti fit edge shift.

DISCUSSION

The hole transfer, diffusion, and surface recombination can be quantified using the fit kinetics of Fig. 3 by taking advantage of the fact that the relative timing between the Ti and Ni or Si peaks is maintained in the spectra and fit kinetics. This is possible because at least two different elemental edges are measured simultaneously for each transient experiment. The Ti and Ni edges are measured simultaneously using Ar high harmonics, and the Si and Ni edges are measured simultaneously using He high harmonics. For all fitted values, the error bars are in terms of the standard error of the mean as calculated through the Jacobian and covariance of a multistart fit (MATLAB 2018b, MultiStart) of the experimental data within a 500% range of the final value. The few mOD experimental error is reflected by the scatter of the points on each plot.

The calculation of the charge carrier dynamics is developed as follows. First, the transit time for holes through the TiO₂ layer is quantified by fitting the magnitude of the Ni edge rise time to an error function that is convoluted with the 50 ± 5–fs pump pulse width (Fig. 4A). Convolving the fit with the pulse duration accounts for the instrument response time. This fit for the Ni-TiO₂-Si junction sample is compared to a separate Ni-Si sample. The Ni-Si junction is used instead of Ni alone as the reference so that any delay from carrier transport within the Si is included. The full differential absorption following photoexcitation of the Si side is shown in fig. S6. In the Ni-TiO₂-Si junction, the transfer time determined by convoluting the 50 ± 5–fs pulse with an error function is delayed by 50 ± 6 fs relative to the excitation pulse, while in the Ni-Si junction, it is delayed by 17 ± 5 fs. These error bars are the standard error of the fit, which includes the pump pulse duration and its error. The ~20-nm TiO₂ therefore delays the arrival of holes at the Ni by 33 ± 8 fs, which, by using the measured thickness of the TiO₂, gives an average hole velocity of 5.8 ± 1.4 × 10⁷ cm/s for the tunneling process. The calculated built-in field of 1.5 × 10⁵ V/cm after photoexcitation would therefore imply a hole mobility during tunneling of 390 ± 100 cm²/V·s, similar to the accepted value for 10¹⁵ per cm² p-doped Si of 450 to 500 cm²/V·s (31).

Fig. 4. Quantifying the photoinitiated hole tunneling and diffusion in the junction.

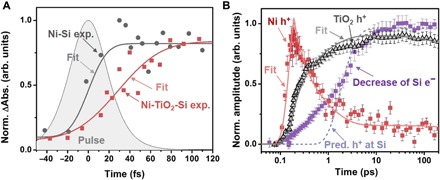
(A) The square light red symbols represent the magnitude of the measured rise time of the Ni edge in the junction; their scatter represents the error of the experimental measurement. The gray circles represent the rise time of the Ni in a Si-Ni junction with no TiO₂ spacer. Fitting the experimental data to an error function (solid lines) convoluted with the excitation pulse gives a delayed rise of 17 ± 5 fs for the Si-Ni and 50 ± 6 fs with the TiO₂ layer. The transit time in the TiO₂ is therefore obtained as 33 ± 8 fs. (B) The edge shift kinetics, which, as noted previously, indicate the hole kinetics, measured for the TiO₂ (gray triangles) and the Ni (red squares) in the junction are compared to the increase in electron recombination (or decrease in electron signature at the Si edge) in the junction (purple squares). The solid line is a fit to the diffusion equation with a diffusion constant of 1.2 ± 0.1 cm²/s and a surface recombination velocity of 200 ± 50 cm/s. The decrease in electron density qualitatively tracks the diffusion of holes through the TiO₂. The dashed line represents the predicted (Pred.) arrival of holes at the Si-TiO₂ interface based on the fit diffusion kinetics.

From the unchanged hole mobility in the TiO₂ with respect to the Si at early times, which implies no scattering of the holes in the TiO₂, and the lack of a measurable hole signal in the TiO₂ during tunneling, the hole transport through the TiO₂ is therefore suggested to be ballistic. The injection efficiency of the tunnel junction is also quantifiable as 42 ± 6% from the excitation density and the fit Fermi level change in the Ni. This relationship was calibrated by the Fermi level shift of Ni alone for a given photoexcitation density and matches the expected shift calculated for a parabolic band. This injection efficiency is reasonable for the junction (32). The approximately 60% remaining holes in Si are beneath the noise of the spectrum in that region (Fig. 2A, bottom). Note that the peak laser field intensity is 170 GW/cm², which would correlate with an electric field of 5.8 × 10⁶ V/cm. This pulse energy is one order of magnitude less than that needed for optical field–induced tunnel ionization or for optical field–induced changes in the band structure (33–35). Although not comparable to AC modulations at the optical field frequency, the DC dielectric breakdown values for Si and TiO₂ are >10⁷ V/cm (36).

To test the accuracy of the element-specific kinetics, the hole back diffusion rate through the TiO₂ layer is quantified by fitting the Ni and Ti edge shifts, which represent the hole kinetics, to the diffusion equation (Fig. 4B). The fit uses the Si-to-Ni hole transfer kinetics in Fig. 3A as the source and is discretized over the junction. The boundary condition is fit to a constant representing the surface hole arrival velocity, which can include both surface recombination and hole injection into the Si bulk. More details can be found in the “Statistical analysis” section of Materials and Methods. The fit gives a diffusion constant of 1.2 ± 0.1 cm²/s, close to the value of 0.4 cm²/s estimated in an annealed thin film of amorphous TiO₂ nanoparticles (36). The surface recombination or injection velocity from the fit is 200 ± 50 cm/s, which is also similar to previous measurements of >200 cm/s (28, 37). The fit surface recombination velocity should only be taken as qualitative since the scan time range of 200 ps is too short for substantial recombination to occur. There is little dependence between the two fit parameters because they have such differing time scales. In Fig. 4B, the measured increase in recombination for electrons on Si (purple squares) is also compared to the number of holes at the Si-TiO₂ interface as predicted by the fit diffusion equation (dashed purple line). Again, although a qualitative comparison, the arrival of holes at the interface predicted by the diffusion rate appears to correlate with the recombination of electrons on the Si. The primary source of error in these quantities is approximating the kinetics by a simple diffusion equation, rather than the experimental error or the fit standard error. This model is presented to give context to the measured dynamics in terms of the known values and is not intended to be absolute.

In conclusion, element-specific transient XUV spectroscopy is used to quantify the photoinitiated charge transfer in a Ni-TiO₂-Si junction. An initial ballistic hole tunneling from Si to Ni is observed on a <100-fs time scale. The injection efficiency of photoexcited carriers was measured to be 42 ± 6%. On a picosecond time scale, a back diffusion of holes from the Ni to the Si through the TiO₂ is measured. As the holes arrive at the Si-TiO₂ interface, a decrease in the electron population is measured on the Si in the junction relative to the Si alone. The drift and diffusion values quantified from the transient XUV measurement also match previously reported values, confirming transient XUV as a highly versatile analysis tool for measuring charge transfer in multiple-element materials and junctions.

MATERIALS AND METHODS

Experimental design

The objectives of this research were twofold. One goal was to simultaneously observe charge carrier dynamics separately in each layer of a layered thin-film junction. Second, the aim was to understand the ultrafast dynamics of charge carriers in a MOS junction following photoexcitation and to determine the time scales of charge transport. We hypothesized an initial fast tunneling of holes from the Si to Ni from simple drift-diffusion calculations. To test this hypothesis, a Si-TiO₂-Ni junction sample is studied with XUV spectroscopy. This sample is compared with control samples of pure Si, TiO₂ film supported on diamond, and Ni film supported on diamond. In addition, a Ni-Si junction is used as a control on the effects of the TiO₂ layer.

Each measurement consists of a pump-on and pump-off trace of 61 logarithmically spaced time points, and each time point is the Weiner-filtered average of thousands of laser pulses. The number of pulses used was chosen to maximize the signal-to-noise ratio of the experiment, as the stability of the high harmonic generation process decreases over the course of the measurement. An acquisition time of approximately 6 hours, or 125,000 pulses, is optimal. Measurements that resulted in obvious damage to the samples and measurements that were cut short by equipment malfunctions were excluded.

Thin-film growth and characterization

The physical vapor deposition method was used to grow TiO₂ and Ni films onto a 200-nm-thick <100> silicon membrane (Norcada), using home-built evaporators containing Ti (99.98% pure, from Kurt J. Lesker Company) and Ni (99.98% pure, from Kurt J. Lesker Company) filaments. To make the layered sample studied here, first Ti was evaporated on the silicon membrane under an oxygen (99.998% pure) atmosphere of 7.4 × 10⁻⁹ to 8.0 × 10⁻⁹ torr with the Ti filament at ~1157°C. After 7.5 hours of Ti deposition, the oxygen was pumped off, and Ni was evaporated at a temperature of ~1000°C for 3.5 hours. A cross-sectional TEM of the sample can be seen in Fig. 1B. The samples with the TiO₂ and Ni alone were deposited on 50-nm-thick diamond membranes.

High harmonic generation

The near-infrared pump pulses used in this experiment are a portion of the 3.5-mJ, 40-fs pulses centered at 800 nm produced by a 1-kHz Ti:sapphire chirped pulse amplifier (Spitfire Pro, Spectra-Physics). The 266-nm pump pulses used to photoexcite the TiO₂ are produced via third harmonic generation of the 800-nm pulses. XUV probe pulses are produced by high harmonic generation of 2.5 mJ of the 800-nm pulses, a portion of which is converted to 400 nm using an in-line second harmonic generation scheme (38). This allows for the production of both even and odd harmonics. High harmonic generation occurs in a semi-infinite gas cell (40 cm) filled with either 250-torr (approximately 3.3 × 10⁴ Pa) helium gas for the Ni M_2,3 and Si L_2,3 edges or 40-torr (approximately 5.3 × 10³ Pa) argon for the Ti M_2,3 edge. The residual near-infrared and visible light is blocked by a 0.5-mm-thick 5-μm pore size glass capillary array (or microchannel plate), which transmits the XUV onto the sample (29). The XUV pulses transmitted through the sample are spectrally dispersed by a variable line spacing grating (35 to 110 eV) and captured using a charge-coupled device camera (PIXIS-400, Princeton Instruments).

The XUV probe spot size is approximately 200 μm at the sample; the samples are raster-scanned in 100-μm steps between each time delay, and a stream of dry nitrogen is flowed over the sample to dissipate heat to avoid thermal damage. Approximately 500 pulses are coadded together to produce a camera image of XUV light versus photon energy. Pump-on and pump-off camera images comprise a single time delay, with the delays spaced logarithmically after time zero (61 delay times, −2.50 to +200 ps about time zero). Approximately 250 such scans are averaged together to produce each transient absorption measurement. Static absorbances are reported as the logarithm of the ratio of XUV photon flux between no sample and the sample. Differential absorbance is reported as the difference between the absorbance measured with the pump on versus the pump off, with outlier measurements removed with Weiner filtering. The pump spot size is approximately 250 μm at the sample, which encompasses the entire probe spot. Pump power densities are approximately 2 mJ cm⁻² for all excitations of the Si edge (junction sample, Si-Ni sample, and Si alone sample), approximately 1 mJ cm⁻² for the TiO₂ alone sample, and approximately 0.3 mJ cm⁻² for the Ni edge excitations (Ni alone sample and thin sample in fig. S2B).

Statistical analysis

The fitting routines reported in Discussion and shown in Fig. 4 all use a robust, nonlinear fit procedure. Error bars reported represent the sum of the experimental variance, including uncertainty in the pulse width, and the standard error of the fit, which includes cross terms between all fit parameters. In addition, a multistart fit procedure was performed on all fitted parameters within a range of 500% of the final value, and the resulting parameter variances were within bounds of the standard error, as expected. The multistart fit was performed using the MATLAB MultiStart algorithm. For the rise time fit, an error function is used, fitting the amplitude and time constant to the experimental data, as shown in Fig. 4A. For the diffusion equation fit, $\frac{\mathrm{\partial }{n}_h}{\mathrm{\partial }t}=\frac{\mathrm{\partial }}{\mathrm{\partial }z}\left(D_h\frac{\mathrm{\partial }{n}_h}{\mathrm{\partial }z}\right)+S(t,z)$, the one-dimensional diffusion equation is solved with the diffusion constant (D_h) and surface recombination/injection velocity at the Si-TiO₂ interface held as fit parameters, as shown in Fig. 4B. The hole population is represented by n_h. The source of holes S(t,z) is the error function fit to the Ni rise time and is taken as one boundary condition. The other boundary condition includes the surface recombination/injection velocity to replicate the interface with Si. Since the hole diffusion and injection/recombination occur on such differing time scales, these parameters have very little cross-talk.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/14/eaay6650/DC1