We describe a groundbreaking approach to generate long-lived bulk nanobubbles in water by external electric fields.
Abstract
Nanobubbles (NBs) are nanoscopic gaseous domains than can exist on solid surfaces or in bulk liquids. They have attracted substantial attention due to their long-time (meta)stability and a high potential for real-world applications. Using an approach not previously investigated, we exploit surface-electrostatic NB formation and stabilization via application of external electric fields in gas-liquid systems, with the marked result of massively increased gas uptake into the liquid in NB form. The de facto gas solubility enhancement (over many months) ranges from 2.5-fold for oxygen to 30-fold for methane vis-à-vis respective Henry’s law values for gas solubility; the more hydrophobic the gas, the more spectacular the increase. Molecular dynamics simulations reveal that the origin of NBs’ movement lies in dielectrophoresis, while substantial NB stabilization arises from a surface-polarization interaction.
INTRODUCTION
Nanobubbles (NBs) are nanoscopic gaseous domains than can exist on solid surfaces or in bulk liquids. It is generally thought that bulk NBs are present in most aqueous solutions, possibly created constantly by agitation and cosmic radiation (1). They have attracted significant attention in the past decade (1–3) due to their long-time (meta)stability and high potential for real-world applications. Among these applications, NBs can be applied toward nanoscopic cleaning (4), control of boundary slip in microfluidics (5), wastewater treatment (6), heterocoagulation (7), and medical applications (8). Although surface NBs have been formed and observed using various experimental methods, bulk liquid NBs have been much less investigated. It has been conjectured that NBs’ long-lived presence is due to negative-charge buildup at the bubble/liquid interface, with the surface having a strong electron affinity (9): An opposing Coulombic force to surface tension slows the bubbles’ dissipation. They have negative zeta potentials (≈ −25 to −40 mV), independent of NB diameter; resultant mutual repulsions between NBs in water are usually sufficiently large to prevent coalescence and slow any buoyancy rise (10). NB surface charge depends strongly on the pH and dissolved salt concentrations; increased ionic strength reduces zeta potential (10). Insoluble gases may form NBs that are stable almost indefinitely in water (11); for soluble gases, the pressure inside gas cavities is inversely proportional to diameter by the Laplace equation, with this thought to be correct down to about a nanometer (12). Intra-NB pressure is affected by other factors and is possibly much lower than Laplace equation expectations: Their gas-liquid interface may be coated with surface-active materials, such as protein or detergent, lowering surface tension and excess pressure, thereby affording stabilization. The presence and concentration of surface-active agents can regulate NBs’ size; coated bubbles are used as ultrasound-contrast agents or for targeted drug delivery (13). Despite early theoretical calculations showing NB persistence for microseconds only (14), they have been observed to be long lived experimentally (15). It is hypothesized that NB clusters are stabilized by ionic solutes and magnetic fields (16).
Bearing in mind NBs’ pH-, ionic-, and magnetic field–sensitive nature, governed fundamentally by surface electrostatics, an open question in NB science is whether externally applied electric fields can manipulate—dictate, control, and enhance—NB formation. If so, what might be the energy cost and electroinduced alterations, if any, in NB thermodynamics and kinetics, as well as overall gas accommodation levels in aqueous solutions, whether in NB or solvated form? Here, we directly tackle these pressing and fundamental questions, finding massive and rapid enhancement of metastable NB gas accommodation in water with low electric energy application. Naturally, the fundamental question arises as to whether this previously unknown observed NB generation phenomenon realizes NBs primarily in the bulk liquid or at the liquid interface; as we will discuss below, we find that it is bulk NBs that are generated, and we have used a bulk-probing NB detection/diagnostic tool to both investigate and confirm this.
RESULTS
We placed deionized water in a pressure vessel and fed pure gas therein to ~90 bar (after cleaning and purging air—cf. Materials and Methods), closing the vessel (i.e., constant-volume operation). The system temperature was regulated to 20.0°C via a surrounding jacket. Upon reaching the Henry’s law gas-solubility level (within 2 hours), we activated an external, sustained static electric field (~12 kV/m) inside the liquid water with a 60-V DC source (cf. Materials and Methods and Fig. 1—with no direct wire-water contact, eliminating completely electrolysis). Very markedly, within 3 hours, or less, greatly elevated gas uptake plateaux were reached in the water (cf. Fig. 2)—there was a flux of gas molecules from the bulk gas phase into the liquid during NB formation, which caused the pressure drop, typically up to several bar. The results for methane and oxygen indicated stored gas levels of ~30 and 2.5 times higher than Henry’s law solubility in water (0.0013 and 0.0014 mol kg−1 bar−1) (17, 18), respectively. The energy required to form NBs using electric fields was found to be exceedingly low (cf. fig. S3)—over 24 hours, no more than ~29 mJ (cf. the Supplementary Materials). This is a notably small energy provision for only 20 ml of liquid, pointing to extraordinarily high levels of energy efficiency (19). On the basis of these measurements, the required energy can be reported as 0.3 W hour/m3, which is much lower than available advanced systems in, say, the wastewater industries (with typical aeration energies of ~40 W hour/m3). Taking wastewater as a further example, typical aeration levels point to typically no more than ~1 to 2 mg/liter dissolved oxygen; in contrast, the use of NBs achieves ~25 to 35 mg/liter at standard temperature and pressure (STP), metastable for months.
Fig. 1. Schematic of pressure vessel rig.

(A) The four main sections are gas supplier, distribution terminal, the pressure cell itself, and temperature regulation jacket. High-purity (N5-level) gases (methane and O2) are supplied to the 0.34-liter, 200-bar–rated stainless steel and rocker-mounted vessel through the distribution terminal, with line cleaning before purging the desired gas, by way of a mass flow controller and accurate measurement of gas loading into the deionized water-loaded vessel. The system operates under constant volume modes, with the inlet valve closed upon reaching the desired pressure (~90 bar), and pressure logged digitally every second for the experiment’s duration. A temperature control system operates in a jacket around the vessel (held at 20°C). A 60-V DC electric current supply was introduced via sheath-covered wires (preventing direct wire-water contact) into a three-dimensional–printed plastic (B), horizontally mounted holder immersed in water (cf. fig. S2, with discussion on the resultant electric field distribution inside the pressure cell). (Photo credit: Mohammad Reza Ghaani.)
Fig. 2. Gas uptake as a function of time.
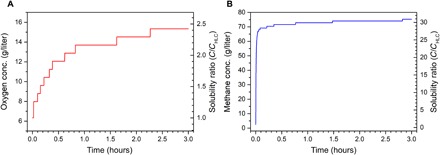
Results shown for oxygen (A) and methane (B) at 60 V (with average field intensity of 12 kV/m), expressed as a multiple of their respective HLCs (right axis) and in g/liter (left axis) at prevailing background pressures of ~90 bar; plateaux occurred within less than 3 hours.
With a view to exploring further the underlying molecular mechanisms of the startling gas accommodation increase in water, we have used nonequilibrium molecular dynamics (NEMD); more complete details can be found in Materials and Methods. Here, we also found NB formation in gas-liquid milieux and subsequent stability enhancement in applied static electric fields, as witnessed reproducibly in the pressure vessel rig (cf. Fig. 1A). Given the more spectacular comparative increase [versus Henry’s law constant (HLC)] in de facto methane solubility vis-à-vis oxygen (albeit in NB form, as opposed to molecular dissolution), it appears that the more hydrophobic the gas, the more accentuated the electric field effect in amplifying massive increases in the propensity to form bulk NBs. Given very similar methane and oxygen HLCs, the significant comparative increase in de facto methane solubility vis-à-vis oxygen suggests that the NB formation process may be kinetically dominated. Given that we observed, visually, small, stable gas (micro- to macroscopic) bubbles forming at the polytetrafluoroethylene (PTFE) electrodes (Fig. 1B), we have evidence of molecular gas adsorption there. The hydrophobic nature of methane-PTFE interactions serves to enhance local adsorbed methane concentration thereat vis-à-vis O2, before field application—explaining differing comparative extents of field-induced NB nucleation at these surfaces; we note that electric field intensity is maximized at this surface (cf. fig. S1).
To clarify both NB generation and stability mechanisms, we ran NEMD simulations for both propane and methane in water, given methane’s greater level of experimental gas uptake and propane’s similarity in terms of hydrophobicity to methane—observing similar results for both. It was necessary to apply external fields of much greater intensity than the ~12 kV/m of the experiments to observe tangible field effects (in the sense of a “signal-to-noise” ratio) over million-atom NEMD spanning tens of nanoseconds (cf. Materials and Methods and section S5). In Fig. 3A, as an example, we started with individually solvated propane molecules in water and found that application of static electric fields in NEMD led to NB formation and competitive aggregation, in a manner akin to Ostwald ripening, especially in more intense electric fields. In Fig. 3B, the evolution of the water-accessible NB surface area shows NB formation, with enhanced stability evident. The more intense fields, e.g., 1.0 V/nm, promote NB formation readily, with a higher surface area and elongated aspect ratio (cf. fig. S5 and explanation).
Fig. 3. NB formation and ensuing stability enhancement via applied static electric fields in NEMD.
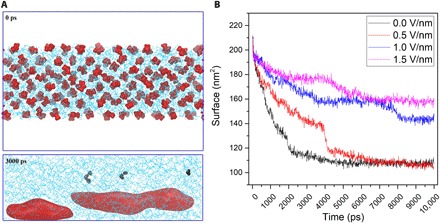
(A) Starting with individually solvated propane molecules in water (top), field application leads to NB formation: The bottom panel shows NBs within 3 ns in a field (1.5 V/nm). (B) Evolution of the accessible bubble surface area to water molecules; increasing NB stability is evident—1.5 V/nm readily promotes NB formation, with a higher surface area, stable for more than 10 ns.
In the literature, long-lived NB stability is well known (1–3). Therefore, here, this motivates us to study the metastability of NBs upon field removal and exposure to ambient pressure, 20°C conditions. Bubble-size distributions with a nonfield “control” run (Fig. 4), featuring no NBs. To address the abovementioned fundamental question of whether NBs are localized at surfaces or distributed in the bulk, we remark that dispersive light scattering (DLS) is a bulk-probing method, and we detected NBs throughout the bulk of the liquid. For oxygen NBs, the O2 mass loss was measured for the first 50 hours upon field removal under ambient conditions. Extra oxygen “loaded” from the bulk gas phase as larger, microsized bubbles in the system during field-induced NB formation was released more rapidly during the first hours of gas unloading upon removal of electric field and depressurization (cf. stage I in Fig. 5A) for ambient pressure/temperature storage in a container sealed for fugitive water vapor emissions. However, as remarked above, we also witnessed visually transient micro- to macrosized bubbles at the PTFE surface (Fig. 1B), born of nano- to micrometer-sized bubble nucleation thereat upon application of electric field; this was also a source of bulk phase. In any event, in Fig. 5A, two regimes were observed in the O2 mass loss graph, which support this hypothesis: The extra O2 water/gas surface–localized (micro-) bubbles destabilized mechanically within ~6 hours, and then, a limited bulk-bubble loss over 6 to 50 hours was observed (cf. Fig. 5A). Over a period of 4 months, the bubbles enlarged somewhat in size (cf. Fig. 5B), determined from DLS (20). The population of NBs themselves remained stable over months, as evidenced by DLS measurements (vide supra). Bearing in mind the role of microbubbles dissipating in stage I gas mass release (upon field removal and depressurization), we took the DLS bubble-size distributions in Fig. 4 ~12 to 24 hours after pressure release and field removal (unlike tracking from that very instant in Fig. 5A), by which point the visually detected macrosized bubbles have left the liquid (cf. Fig. 5A); this explains the lack of a micrometer-sized bubble signature in Fig. 4.
Fig. 4. NB detection via dynamic light scattering (Malvern Zetasizer Pro); this uses fluctuations in laser light scattering traveling through the sample solution.
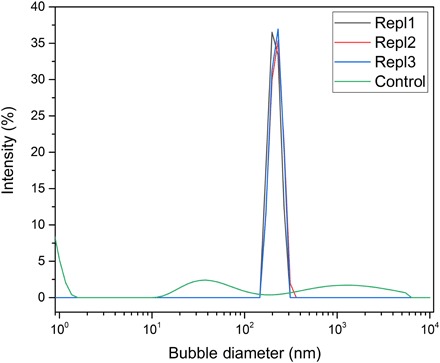
The measurements are all done after 12 to 24 hours after depressurizing and field removal. The measurement repeated three times on three samples for better accuracy. A control sample was also measured with the same experimental process except in the absence of field.
Fig. 5. NB evolution under ambient, STP conditions after field removal.
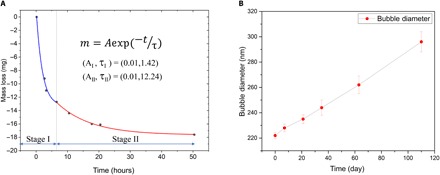
(A) Dual-regime mass loss during the first 50 hours upon field removal and storage under ambient temperature/pressure conditions. (B) Evolution in methane-bubble Sauter mean diameter over a 4-month period (three replicas for each measurement); very slow bubble growth is seen.
DISCUSSION
Having assessed the largely kinetic effect of NB formation, we now turn to the matter of rationalizing NB stability. In the main, NB stabilization arises from the polarization at its water surface, and the force contributions arise from this important interaction (vide infra; see also mechanistic theory in section S3). It has been well established by both experiments (e.g., sum-frequency generation) (21) and simulations (22) that gas-water interfaces constitute uniquely structured molecular environments. Using both classical models and ab initio representations, simulations have predicted that the interface environment gives rise to preferred water-molecule orientations (i.e., hydrogen bond arrangements). It will be sufficient here to ascribe a set of surface dipole moments to this effect (see figs. S3 and S4—with nonlinear field response readily evident in surface orientational distributions in fig. S4). For spherical NBs, the interactions between these surface dipoles are sufficient to generate a repulsive force, with the same dependence on bubble size, sufficient to counter Laplace pressure effects (cf. the Supplementary Materials). Thus, one need not invoke accumulation of surface charge to stabilize NBs [as typically used; (23)]. Moreover, while zeta potential measurements for NBs are frequently used as supporting evidence that anions (OH−) accumulate at an NB’s surface, recent work (24) has demonstrated that zeta potentials can be ascribed to gas-water interface polarization. It has also been observed that small uncharged particles can be made to move in nonuniform electric fields (25). This phenomenon—dielectrophoresis—arises from a net force due to the interaction of a polarizable particle with a nonuniform (i.e., spatially varying) field. (22) For NBs, an analogous effect can be expected to arise because of the nonlinear polarization response of the gas-water interface to uniform field [see (22) and mechanistic theory development in the Supplementary Materials]. The displacement of NBs in a uniform electric field is also confirmed by NEMD simulation results reported in the Supplementary Materials, with drift velocity results in fig. S7 only becoming statistically meaningful and responding nonlinearly in the applied field direction for 5-nm bubbles for larger field strengths (confirming that a reasonably large bubble size is required for physical realism and that this effect is suppressed for small bubbles). Consequently, both NBs’ stability and their movement in electric fields do not require the presence of surface charge, but rather only the presence of surface polarization at the gas-water interface. External field removal leads to the gradual growth of bubbles (cf. Fig. 5B), although this effect takes place over time scales exceeding several months.
We conjecture that the field-induced genesis per se of NBs may be explained by the realization of regions of negative pressure in a dielectric liquid, created by the applied field’s electrostrictive forces (26); this leads to cavitation at the liquid interface (e.g., with PTFE surface or with bulk gas) and “void” formation in a local negative-pressure region thereat—allowing gas at the interface to enter this locale, as we observe in the experiment and the NEMD simulation (cf. Figs. 2 and 3). An analysis of external and intrinsic field intensities, reflective directly of applied and intrinsic Coulombic forces, is provided in section S5. Following such cavitation-based birth, the incipient growth of the NBs is of spherical shape. However, for the NEMD simulations using necessarily larger field intensities, reported further in the Supplementary Materials, it was observed that the bubbles become oval shaped along the external field axis, with an aspect ratio larger than unity (cf. fig. S6). This may be rationalized by (27), which shows the angular interplay of intrinsic and externally applied fields in the environs of voids (cf. the Supplementary Materials for further details) (27). In fig. S2, it is evident that the largest field intensity is at the electrode surface itself, where the hydrophobic, plastic surface accentuates the presence of gas in any event, enhancing still further NB “electrogenesis” itself.
In closing, we have established prima facie evidence of static electric fields enhancing bulk-NB formation at massively elevated levels far in excess of Henry’s law solubility, with a greater enhancement apparent for more hydrophobic gases. This discovery is expected to have large ramifications in the process, fermentation, brewing, and wastewater treatment industries, in addition to accelerating gas (diffusion)–limited processes. Further work is under way to clarify the mechanistic features of the kinetics of NB generation, as well as the nature of NB stabilization, after generation. In effect, drawing on the concept of porous, or “holey,” liquids (28), we realize here “nanoporous liquids” in the form of gas NBs in a simple and facile manner, with highly elevated surface-to-volume ratios, aside from much higher gas accommodation levels per se.
MATERIALS AND METHODS
NB formation and gas uptake determination in water
The experimental apparatus for NB formation used a pressure vessel fabricated using 316 stainless steel with internal volume of approximately 340 cm3 (cf. fig. S1). The vessel was agitated using a tilting shaker. A pressure transducer with an uncertainty of 0.02 MPa was used to measure pressure, while a thermocouple with an accuracy of ±0.1 K was inserted into the cell to measure the inner temperature, with temperature/pressure readings every 1 s.
Before starting the experiments, the cell was washed, cleaned, and dried completely using an air stream. Afterward, the cell was examined for leakage by injecting nitrogen at a pressure of 1 MPa. Inert gas was then purged, and a vacuum pump was used for about 30 min to evacuate all trapped gases from the cell. In all NB proof-of-concept experiments, a volume of 20 cm3 of deionized water was fed into the cell. Cell pressure was increased by injecting the selected gas (oxygen or methane) until the desired pressure (~90 bar) was reached. The loaded water was saturated after about 2 hours of gas-water contact, in the presence of slow rocking of the vessel to enhance gas-water contact, with temperature held at 20°C via the reactor jacket (cf. Supporting Information, fig. S1). Then, a 60-V DC electric voltage was applied, achieving sustained externally electric field intensity (~12 kV/m) in the liquid water (with no direct wire-water contact, eliminating completely electrolysis)—cf. figs. S1 and S2 (Supporting Information). The pressure and temperature were logged every second, with 20°C held steady. Within around 3 hours, or less, gas uptake plateaux were reached in the water (cf. Fig. 2).
In terms of mass balance–based determination of gas uptake in water, this is calculated on the basis of the number of absorbed moles of gas into the liquid phase (i.e., by monitoring gas-phase pressure drop continuously on a mass balance basis). Naturally, the first step in this number-of-gas-phase-moles-from-pressure determination lies in accurately defining the compressibility factor of methane and oxygen, as well as their HLCs (17). During in-field NB formation runs, mass balances on the thus-inferred gas-phase-number-of-moles data (from gas-phase pressure) allowed determination of the number of absorbed moles of gas.
Dynamic light scattering
Dynamic light scattering (Malvern Zetasizer Pro) was used to measure the size of NBs. The refractive index of bubble’s gas content and the water as dispersant was set to 1 and 1.33, respectively. In measurement, Stokes-Einstein equation was used to calculate the particle size based on the velocity of bubbles by monitoring the undulation of scattered laser light. All measurements were done at ambient temperature and pressure (25°C and 1 atm) by loading 5 ml of the sample to the plastic cell. Each reading repeated three times for each sample and averaged to determine particle diameter. The measurement range of the selected machine is 0.3 nm to 10 μm. A control sample was also measured with a same experimental process, except in the absence of field. The recorded data of one sample including the data for a control run are presented in Fig. 4. The measurement repeated three times on three samples for better accuracy.
Nonequilibrium molecular dynamics
Individually solvated propane and methane molecules were placed in a liquid water slab in a simulation box (cf. Fig. 3A for propane simulation)—with a high degree of supersaturation. The TIP4P/2005 model (29) was used for water, while propane molecules were parameterized by general Amber force field (30). The methane molecule was modeled considering all the hydrogens, using OPLS-AA (All-Atom Optimized Potentials for Liquid Simulations) force field (31). The cutoff radius for Lennard-Jones interaction parameters was 11.0 Å, while the smooth particle mesh Ewald method was used to handle long-range electrostatics (32). These water-propane interactions have been validated in (33) in terms of accurate prediction of propane-hydrate melting points and latent heats (33). The velocity Verlet scheme was used for molecular dynamics under periodic boundary conditions with a time step of 2 fs (32). For extended-system dynamics to maintain constant temperature and pressure conditions, a relaxation time of 0.1 ps was applied. Parrinello-Rahman pressure coupling system was used to keep the pressure of the system at ambient pressure (1 bar) with 2.0-ps relaxation time (32). We ran NEMD for various static electric field intensities up to 1.4 V/nm along the X direction, using fi,E = qi E for the externally applied static field forces acting on charge sites (34). Given that the necessarily limited time scales of these computationally intensive, million-atom NEMD simulations are of the order of 50 to 100 ns, as opposed to over hours in ~12 kV/m experiments, it was necessary to apply electric fields in NEMD simulation of intensity several orders of magnitude greater than in experiments. From (34), it is known that applied field intensities of the order of ~1 V/nm and larger often lead to structural and dynamical effects in condensed-phase systems, verging into nonlinear response territory with applied field forces being several percent of those intrinsic to the liquid water system. In the present work, the upper limit of applied field intensity in NEMD (i.e., 1.4 V/nm) corresponds to nonlinear field effects becoming apparent, e.g., in terms of dipole distribution and translational, dielectrophoretic response (cf. section S3); a more full discussion of comparative external and intrinsic electric field intensities is provided in section S5. Each field was simulated for 50 ns in four replicas to improve the accuracy and reproducibility of the results. Although the initial slab construction (cf. Fig. 3A) can allow for propane “escape” into the surrounding vacuum space, to serve as a potential, putative bulk gas phase, it was observed that the propane retained its heavily supersaturated level, albeit in the form of NBs (cf. Fig. 3).
To study further size effects on NB behavior, NEMD simulations for both propane and methane bubbles were ran in two bubble diameters for propane—2.5 and 5 nm and 5 nm for methane, with one (initially spherical) NB per simulation box. The simulation box for the big-bubble system was 33.14 nm by 16.77 by 16.77 nm and was 15.64 nm by 7.82 nm by 7.82 nm for the small-bubble system. Further details may be found in table S1 (section S3).
Supplementary Material
Acknowledgments
Funding: M.R.G. thanks the Irish Research Council for a Government-of-Ireland postdoctoral fellowship (GOIPD/2016/365). N.J.E. and M.R.G. thank P. Dobbyn and Particular Sciences and Aqua-B (http://www.aqua-bubble.com/) for technical assistance. P.G.K. is grateful for the financial support of the Natural Sciences and Engineering Research Council of Canada (RGPIN-2016-03845). Author contributions: N.J.E. and M.R.G. conceived the study conceptually. N.J.E. and M.R.G. designed and built the pressure vessel rig with electric field setup therein. M.R.G. carried out the NB formation experiments and post-field characterization at ambient STP, as well as performing NEMD simulations. P.G.K. and N.J.E. contributed importantly with interpretation of results and microscopic mechanisms. N.J.E. wrote the initial draft of the manuscript, with subsequent important edits from P.G.K. and M.R.G. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/14/eaaz0094/DC1
REFERENCES AND NOTES
- 1.Seddon J. R. T., Lohse D., Ducker W. A., Craig V. S. J., A deliberation on nanobubbles at surfaces and in bulk. ChemPhysChem 13, 2179–2187 (2012). [DOI] [PubMed] [Google Scholar]
- 2.Lohse D., Zhang X., Surface nanobubbles and nanodroplets. Rev. Mod. Phys. 87, 981–1035 (2015). [Google Scholar]
- 3.Alheshibri M., Qian J., Jehannin M., Craig V. S. J., A history of nanobubbles. Langmuir 32, 11086–11100 (2016). [DOI] [PubMed] [Google Scholar]
- 4.Zhu J., An H., Alheshibri M., Liu L., Terpstra P. M. J., Liu G., Craig V. S. J., Cleaning with bulk nanobubbles. Langmuir 32, 11203–11211 (2016). [DOI] [PubMed] [Google Scholar]
- 5.Wang Y., Bhushan B., Boundary slip and nanobubble study in micro/nanofluidics using atomic force microscopy. Soft Matter 6, 29–66 (2010). [Google Scholar]
- 6.Agarwal A., Ng W. J., Liu Y., Principle and applications of microbubble and nanobubble technology for water treatment. Chemosphere 84, 1175–1180 (2011). [DOI] [PubMed] [Google Scholar]
- 7.Mishchuk N., Ralston J., Fornasiero D., Influence of very small bubbles on particle/bubble heterocoagulation. J. Colloid Interface Sci. 301, 168–175 (2006). [DOI] [PubMed] [Google Scholar]
- 8.Modi K. K., Jana A., Ghosh S., Watson R., Pahan K., A physically-modified saline suppresses neuronal apoptosis, attenuates tau phosphorylation and protects memory in an animal model of Alzheimer’s disease. PLOS ONE 9, e103606 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ahmed A. K. A., Sun C., Hua L., Zhang Z., Zhang Y., Marhaba T., Zhang W., Colloidal properties of air, oxygen, and nitrogen nanobubbles in water: Effects of ionic strength, natural organic matters, and surfactants. Environ. Eng. Sci. 35, 720–727 (2018). [Google Scholar]
- 10.Ruckenstein E., Nanodispersions of bubbles and oil drops in water. Colloids Surface A Physicochem. Eng. Asp. 423, 112–114 (2013). [Google Scholar]
- 11.Yarom M., Marmur A., Stabilization of boiling nuclei by insoluble gas: Can a nanobubble cloud exist? Langmuir 31, 7792–7798 (2015). [DOI] [PubMed] [Google Scholar]
- 12.Fraxedas J., Verdaguer A., Sanz F., Baudron S., Batail P., Water nanodroplets confined in molecular nanobeakers. Surf. Sci. 588, 41–48 (2005). [Google Scholar]
- 13.Peyman S. A., McLaughlan J. R., Abou-Saleh R. H., Marston G., Johnson B. R. G., Freear S., Coletta P. L., Markham A. F., Evans S. D., On-chip preparation of nanoscale contrast agents towards high-resolution ultrasound imaging. Lab Chip 16, 679–687 (2016). [DOI] [PubMed] [Google Scholar]
- 14.Ljunggren S., Eriksson J. C., The lifetime of a colloid-sized gas bubble in water and the cause of the hydrophobic attraction. Colloids Surfaces A Physicochem. Eng. Asp. 129–130, 151–155 (1997). [Google Scholar]
- 15.Bunkin N. F., Ninham B. W., Ignatiev P. S., Kozlov V. A., Shkirin A. V., Starosvetskij A. V., Long-living nanobubbles of dissolved gas in aqueous solutions of salts and erythrocyte suspensions. J. Biophotonics 4, 150–164 (2011). [DOI] [PubMed] [Google Scholar]
- 16.Usanov A. D., Ulyanov S. S., Ilyukhina N. S., Usanov D. A., Monitoring of changes in cluster structures in water under AC magnetic field. Opt. Spectrosc. 120, 82–85 (2016). [Google Scholar]
- 17.R. Sander, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69 (National Institute of Standards and Technology, Gaithersburg MD, 2018), p. 20899; 10.18434/T4D303. [DOI]
- 18.Wilhelm E., Battino R., Wilcock R. J., Low-pressure solubility of gases in liquid water. Chem. Rev. 77, 219–262 (1977). [Google Scholar]
- 19.M. R. Ghaani, N. J. English, A system, method and generator for generating nanobubbles or nanodroplets, UK IPO, 1816766.8 (2018).
- 20.Wang Q., Zhao H., Qi N., Qin Y., Zhang X., Li Y., Generation and stability of size-adjustable bulk nanobubbles based on periodic pressure change. Sci. Rep. 9, 1118 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang H.-F., Velarde L., Gan W., Fu L., Quantitative sum-frequency generation vibrational spectroscopy of molecular surfaces and interfaces: Lineshape, polarization, and orientation. Annu. Rev. Phys. Chem. 66, 189–216 (2015). [DOI] [PubMed] [Google Scholar]
- 22.Cipcigan F. S., Sokhan V. P., Jones A. P., Crain J., Martyna G. J., Hydrogen bonding and molecular orientation at the liquid–vapour interface of water. Phys. Chem. Chem. Phys. 17, 8660–8669 (2015). [DOI] [PubMed] [Google Scholar]
- 23.Nirmalkar N., Pacek A. W., Barigou M., Interpreting the interfacial and colloidal stability of bulk nanobubbles. Soft Matter 14, 9643–9656 (2018). [DOI] [PubMed] [Google Scholar]
- 24.Vácha R., Marsalek O., Willard A. P., Jan Bonthuis D., Netz R. R., Jungwirth P., Charge transfer between water molecules as the possible origin of the observed charging at the surface of pure water. J. Phys. Chem. Lett. 3, 107–111 (2011). [Google Scholar]
- 25.Amah E., Janjua M., Singh P., Direct numerical simulation of particles in spatially varying electric fields. Fluids 3, 52 (2018). [Google Scholar]
- 26.Shneider M. N., Pekker M., Cavitation in dielectric fluid in inhomogeneous pulsed electric field. J. Appl. Phys. 114, 214906 (2013). [DOI] [PubMed] [Google Scholar]
- 27.Shneider M. N., Pekker M., Pre-breakdown processes in a dielectric fluid in inhomogeneous pulsed electric fields. J. Appl. Phys. 117, 224902 (2015). [DOI] [PubMed] [Google Scholar]
- 28.Giri N., Del Pópolo M. G., Melaugh G., Greenaway R. L., Rätzke K., Koschine T., Pison L., Gomes M. F. C., Cooper A. I., James S. L., Liquids with permanent porosity. Nature 527, 216–220 (2015). [DOI] [PubMed] [Google Scholar]
- 29.Abascal J. L. F., Vega C., A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 123, 234505 (2005). [DOI] [PubMed] [Google Scholar]
- 30.Wang J., Wolf R. M., Caldwell J. W., Kollman P. A., Case D. A., Development and testing of a general amber force field. J. Comput. Chem. 25, 1157–1174 (2004). [DOI] [PubMed] [Google Scholar]
- 31.MacKerell A. D. Jr., Bashford D., Bellott M., Dunbrack R. L., Evanseck J. D., Field M. J., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., Reiher W. E., Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiórkiewicz-Kuczera J., Yin D., Karplus M., All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 102, 3586–3616 (1998). [DOI] [PubMed] [Google Scholar]
- 32.M. P. Allen, D. J. Tildesley, Computer Simulation of Liquids (Oxford Univ. Press, 2017). [Google Scholar]
- 33.Ghaani M. R., English N. J., Molecular dynamics study of propane hydrate dissociation: Nonequilibrium analysis in externally applied electric fields. J. Phys. Chem. C 122, 7504–7515 (2018). [Google Scholar]
- 34.English N. J., Waldron C. J., Perspectives on external electric fields in molecular simulation: Progress, prospects and challenges. Phys. Chem. Chem. Phys. 17, 12407–12440 (2015). [DOI] [PubMed] [Google Scholar]
- 35.Vácha R., Rick S. W., Jungwirth P., de Beer A. G. F., de Aguiar H. B., Samson J.-S., Roke S., The orientation and charge of water at the hydrophobic oil droplet–water interface. J. Am. Chem. Soc. 133, 10204–10210 (2011). [DOI] [PubMed] [Google Scholar]
- 36.Vácha R., Marsalek O., Willard A. P., Bonthuis D. J., Netz R. R., Jungwirth P., Charge transfer between water molecules as the possible origin of the observed charging at the surface of pure water. J. Phys. Chem. Lett. 3, 107–111 (2012). [Google Scholar]
- 37.Tang F., Ohto T., Hasegawa T., Xie W. J., Xu L., Bonn M., Nagata Y., Definition of free O–H groups of water at the air–water interface. J. Chem. Theory Comput. 14, 357–364 (2018). [DOI] [PubMed] [Google Scholar]
- 38.Wilson M. A., Pohorille A., Pratt L. R., Surface potential of the water liquid–vapor interface. J. Chem. Phys. 88, 3281–3285 (1988). [DOI] [PubMed] [Google Scholar]
- 39.Sokhan V. P., Tildesley D. J., The free surface of water: Molecular orientation, surface potential and nonlinear susceptibility. Mol. Phys. 92, 625–640 (1997). [Google Scholar]
- 40.Cendagorta J. R., Ichiye T., The surface potential of the water–vapor interface from classical simulations. J. Phys. Chem. B 119, 9114–9122 (2015). [DOI] [PubMed] [Google Scholar]
- 41.Kathmann S. M., Kuo I.-F. W., Mundy C. J., Schenter G. K., Understanding the surface potential of water. J. Phys. Chem. B 115, 4369–4377 (2011). [DOI] [PubMed] [Google Scholar]
- 42.Leung K., Surface potential at the air−water interface computed using density functional theory. J. Phys. Chem. Lett. 1, 496–499 (2010). [Google Scholar]
- 43.Baer M. D., Stern A. C., Levin Y., Tobias D. J., Mundy C. J., Electrochemical surface potential due to classical point charge models drives anion adsorption to the air–water interface. J. Phys. Chem. Lett. 3, 1565–1570 (2012). [DOI] [PubMed] [Google Scholar]
- 44.Remsing R. C., Baer M. D., Schenter G. K., Mundy C. J., Weeks J. D., The role of broken symmetry in solvation of a spherical cavity in classical and quantum water models. J. Phys. Chem. Lett. 5, 2767–2774 (2014). [DOI] [PubMed] [Google Scholar]
- 45.Sellner B., Valiev M., Kathmann S. M., Charge and electric field fluctuations in aqueous NaCl electrolytes. J. Phys. Chem. B 117, 10869–10882 (2013). [DOI] [PubMed] [Google Scholar]
- 46.Kusalik P. G., Patey G. N., On the molecular theory of aqueous electrolyte solutions. IV. Effects of solvent polarizability. J. Chem. Phys. 92, 1345–1358 (1990). [Google Scholar]
- 47.Yasui K., Tuziuti T., Kanematsu W., Mysteries of bulk nanobubbles (ultrafine bubbles); stability and radical formation. Ultrason. Sonochem. 48, 259–266 (2018). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/14/eaaz0094/DC1


