Profiling Dialysis Facilities for Adverse Recurrent Events

Summary

Profiling analysis aims to evaluate health care providers, such as hospitals, nursing homes, or dialysis facilities, with respect to a patient outcome. Previous profiling methods have considered binary outcomes, such as 30-day hospital readmission or mortality. For the unique population of dialysis patients, regular blood works are required to evaluate effectiveness of treatment and avoid adverse events, including dialysis inadequacy, imbalance mineral levels, and anemia among others. For example, anemic events (when hemoglobin levels exceeds normative range) are recurrent and common for patients on dialysis. Thus, we propose high-dimensional Poisson and negative binomial regression models for rate/count outcomes and introduce a standardized event ratio (SER) measure to compare the event rate at a specific facility relative to a chosen normative standard, typically defined as an “average” national rate across all facilities. Our proposed estimation and inference procedures overcome the challenge of high-dimensional parameters for thousands of dialysis facilities. Also, we investigate how overdispersion affects inference in the context of profiling analysis. The proposed methods are illustrated with profiling dialysis facilities for recurrent anemia events.

1. Introduction

Due to kidney failure, patients with end-stage renal disease (ESRD) require long-term renal replacement therapy with dialysis or kidney transplantation to sustain life. Compared to other morbid populations, dialysis patients have much higher mortality and morbidity. At the end of 2015, there were over 700,000 cases of ESRD, which included over 124,000 incident ESRD patients in the United States (US).¹ Patients receiving dialysis are monitored regularly. For example, patients receiving dialysis care at over 6,000 dialysis facilities typically dialyze three times per week and they are monitored regularly with respect to patient outcomes, including dialysis adequacy (sufficient removal of waste from blood); bone and mineral disorder (e.g., to prevent high calcium in the blood or hypercalcemia); phosphorous level; regulation of blood pressure; and hemoglobin (Hb) to manage anemia among other conditions. Management of anemia, for instance, contributes to improved cardiovascular health, reduced risk of hospitalization, and prevention of fatigue.

Therefore, monitoring or profiling of dialysis facilities (or more generally of health care providers, including hospitals, nursing homes etc.) with respect to specific patient outcomes, contributes to the national goal of ensuring safe and adequate delivery of health care to patients (CMS [Center for Medicare and Medicaid Services]).² For example, the CMS have implemented quality of care measures for 30-day hospital readmission based on profiling models, which compare the performance of a specific heath care provider, such as a hospital or dialysis facility, to the national average rate of readmission.^3–6 Because patients are nested within providers and the patient outcome variables, such as hospital readmission or mortality, are binary outcomes, profiling models previously considered were hierarchical logistic regression models with provider random effects^5,7–9 for the general population and providers as hospitals, for example. For profiling dialysis facilities (providers), high-dimensional fixed effects (FEs) models (with providers as fixed effects) have been advanced by researchers from the University of Michigan Kidney Epidemiology and Cost Center (UM-KECC).^10,11 Part of CMS new initiative for quality of care for dialysis facilities is based on the methodology works from UM-KECC.¹² Our own works^13–16 also focuses on FEs profiling models for the dialysis population where outcomes are typically not sparse. For example, in our application the overall anemic rate is 5.6 per person-year. For binary outcomes, the choice of fixed versus random dialysis facility effects was previously examined.^11,15 As previously noted, random effects models have smaller average absolute error in estimation, although this is achieved through average gain in the center of the distribution of the outcomes. In profiling analysis where focus is on identifying extreme facilities (e.g., facilities with extremely high rate of patients with out of target Hb level), high-dimensional fixed effects (FEs) models has been reported to be effective in flagging/identifying extreme facilities¹⁰ and at the same time avoids confounding between patient risk factors and facility effects ^9,11 (which is inherent in random facility effects). However, when the outcome is highly sparse, such as profiling hospital readmission in the general population, shrinkage to stabilize estimates via RE models is needed.⁹

In this work we develop FEs models for profiling with respect to rate/count outcomes. This is particularly relevant to the dialysis patients, where routine (e.g., weekly or monthly) blood works are performed to evaluate effectiveness of treatment, including dialysis adequacy, calcium, parathyroid hormone, and hemoglobin (Hb) among others. For each marker, a normal range is targeted. For instance, for hemoglobin in red blood cells the target range is Hb between 9 and 11 g/dL. Thus, the outcome for patient k in facility i, denoted Y_ik, is defined as the number of times Hb is out of target range during the follow-up time, denoted by t_ik. More specifically, first, we develop a high-dimensional FEs Poisson regression model that accommodates thousands of facility-level parameters needed for profiling and the model estimation is achieved via an efficient Newton-Raphson algorithm, inspired by the seminal work of.¹⁰ Second, we investigate the effect of overdisperson on profiling, and also propose a negative binomial (NB) regression model that accounts for overdispersion when needed. For profiling facilities with a count outcome, we introduce the standardized event ratio (SER) measure for each facility, which is the ratio of the expected number of events (e.g., # of Hb out of target) for patients treated at a given facility to the expected number of events if these same patients were treated at an “average” facility, i.e., a national reference standard. The SER reduces to the standardized readmission ratio or standardized mortality ratio when the profiling model is for a binary outcome. We note that to date profiling facilities with respect to rate of adverse events have not been considered in the literature.

The remainder of the paper is organized as follows. The high-dimensional FEs Poisson and NB regression models along with the definition of SER, estimation algorithm, and inference (hypothesis testing) procedure are presented in Section 2. In Section 3, we present simulation studies to demonstrate the efficacy of the proposed estimation and inference procedure and the effect of ignoring overdisperson on inference. Profiling of dialysis facilities with respect to the rate of anemia events is illustrated in Section 4 and we conclude with a brief discussion in Section 5.

2. Profiling Models for Rate/Count Outcomes

2.1. High-dimensional Log-Linear Regression Model

Let i = 1, …, I index dialysis facilities and k = 1, …, N_i index patients receiving dialysis treatment at facility i with N_i total number of patients. The outcome variable Y_ik counts the number of adverse recurrent events for patient k, such as the number of anemic events (e.g., when Hb level exceeds target range) during follow-up time t_ik. In profiling models, it is critical to adequately risk-adjust for patient-level factors and avoid inclusion of variables (e.g., facility-level or patient-level variables) that are related to the process of care. (For instance, erythropoiesis stimulating agents and iron therapy used to manage anemia should not be included in the risk adjustment). Denote the patient risk adjustment factors for patient k in facility i by the vector Z_ik = (Z_1ik, …, Z_rik)^T, where r is the number of risk adjustment variables. In our application, risk adjustment included age, sex, body mass index (BMI), diabetes as the cause of ESRD, years on dialysis, past-year comorbidities, nephrology care prior to initiation of dialysis, and if the patient experienced Hb outside the target range in the prior year to the start of follow-up. We propose the following log-linear model to profile dialysis facilities with respect to a rate/count outcome:

$$\log \{E(Y_{ik}|Z_{ik},t_{ik})\}=\log ({\mu }_{ik})=\log (t_{ik})+{\gamma }_i+Z_{ik}^T\beta ,i=1,\dots ,I,$$ (1)

where Y_ik is the number of adverse events for patient k in facility i during follow-up time t_ik, ${\mu }_{ik}=E(Y_{ik}|Z_{ik},t_{ik})=\exp \{\log (t_{ik})+{\gamma }_i+Z_{ik}^T\beta \}$, γ_i is facility i effect, and β = (β₁, …, β_r)^T is a vector of parameters for patient-level risk adjustment factors. We emphasize that the model shown in (1) is not a collection of individual models (i.e., not one for each facility), but rather a single model with high-dimensional parameters and requires simultaneous estimation for thousands of facility-level effects parameters (γ_i’s). For our application, the dimension of γ = (γ₁, …, γ_I)^T is 6,188 and the dimension of β is 39.

Under model (1) with outcomes assumed to follow a Poisson or NB distribution, we present estimation procedures that overcome the challenges associated with the high-dimensional parameters in Section 2.3 and 2.5, respectively. We first introduce the standardized event ratio (SER) as a measure to flag extreme (“outlier”) facilities under profiling model (1) in the next section.

2.2. Standardized Event Ratio Measure

To assess the performance of the ith facility relative to a reference (e.g., national median/average) that account for patient-level risk adjustment, we introduce the following standardized event ratio (SER) measure

$$SE{R}_i=\frac{{\sum }_{k=1}^{N_i}{\mu }_{ik}}{{\sum }_{k=1}^{N_i}{\mu }_{ik,M}}.$$ (2)

In the denominator, ${\mu }_{ik,M}=\exp \{\log (t_{ik})+{\gamma }_M+Z_{ik}^T\beta \}$ with γ_M denoting the median of {γ₁, …, γ_I}, and ${\Sigma }_{k=1}^{N_i}{\mu }_{ik,M}$ is the expected total number of events for facility i if patients in that facility were treated at a national “average” facility (taken over the population of all facilities). The numerator is the expected total number of events at facility i. For example, with respect to Hb outcome, SER_i is the ratio of the expected total number of anemia events for all patients at facility i relative to the expected total number of anemia events for the same patients based on the national reference. We note that for binary outcome, such as hospital readmission and mortality, the SER_i measure reduces to the standardized readmission ratio and standardized mortality ratio, respectively. A natural estimator of SER_i is

$${\widehat{SER}}_i=\frac{{\sum }_{k=1}^{N_i}{\widehat{\mu }}_{ik}}{{\sum }_{k=1}^T{\widehat{\mu }}_{ik,M}},$$ (3)

where ${\widehat{\mu }}_{ik}=\exp \{\log (t_{ik})+{\widehat{\gamma }}_i+Z_{ik}^T\widehat{\beta }\}$ and ${\widehat{\mu }}_{ik,M}=\exp \{\log (t_{ik})+{\widehat{\gamma }}_M+Z_{ik}^T\widehat{\beta }\}$. Estimates $\widehat{\beta }$ and ${\widehat{\gamma }}_1,\dots ,{\widehat{\gamma }}_I$ of the model parameters are obtained iteratively using a Newton-Raphson algorithm alternating between the estimation of β and γ₁, …, γ_I due to the large number of facility effects in the model. The estimation procedure is detailed in next section.

2.3. Poisson Model and Estimation Procedure

For the log-linear model (1) with Poisson counts, $\mathrm{Pr}(Y_{ik}=y_{ik};{\mu }_{ik})={\mu }_{ik}^{y_{ik}}\exp (-{\mu }_{ik})/y_{ik}!$, the likelihood function is

$$L(\gamma ,\beta )=\prod _{i=1}^I\prod _{k=1}^{N_i}\frac{{\mu }_{ik}^{y_{ik}}\exp (-{\mu }_{ik})}{y_{ik}!}.$$ (4)

Maximization of (4) is challenging when I is large, as in our data application where I is larger than 6,000, and standard software is not feasible due to the size of the design matrix. In profiling binary outcome via logistic regression, He et al. (2013) proposed an iterative algorithm that alternates between estimation of γ_i given β and estimation of β given γ_i using one-step Newton-Raphson updates.¹⁰ We take a similar approach. More precisely, estimation of the high-dimensional parameters (γ, β) is feasible since the likelihood (4) can be written as $L(\gamma ,\beta )={\prod }_i{L}_i({\gamma }_i,\beta )$ where $L_i({\gamma }_i,\beta )={\prod }_k{\mu }_{ik}^{y_{ik}}\exp (-{\mu }_{ik})/y_{ik}!$. Thus, given β, γ_i can be estimated via a Newton-Raphson procedure that depends only on one variable in the maximization of L_i(γ_i, β). The estimation procedure is as follows.

1. Set the initial values β⁽⁰⁾ and ${\gamma }_i^{(0)}=0$ of β and γ_i, respectively. For example, one might choose β⁽⁰⁾ = 0 and ${\gamma }_i^{(0)}=0$ or take β⁽⁰⁾ = 0 and ${\gamma }_i^{(0)}=\log (n_i^{-1}{\sum }_{k=1}^{n_i}{y}_{ik}/t_{ik})$, the log of the average event rate for facility i.

2. The mth maximization step for β is given by

   $${\beta }^{(m)}={\beta }^{(m-1)}-{\left[\frac{{\partial }^2\ell }{\partial \beta \partial {\beta }^{\text{T}}}\{{\gamma }_i^{(m-1)},{\beta }^{(m-1)}\}\right]}^{-1}\frac{\partial \ell }{\partial \beta }\{{\gamma }_i^{(m-1)},{\beta }^{(m-1)}\},$$

   where the partial derivatives evaluated at $\{{\gamma }_i^{(m-1)},{\beta }^{(m-1)}\}$ are provided in the Appendix section.
3. The mth maximization step for γ_i is given by

   $${\gamma }_i^{(m)}={\gamma }_i^{(m-1)}-{\left[\frac{{\partial }^2\ell }{\partial {\gamma }_i^2}\{{\gamma }_i^{(m-1)},{\beta }^{(m)}\}\right]}^{-1}\frac{\partial \ell }{\partial {\gamma }_i}\{{\gamma }_i^{(m-1)},{\beta }^{(m)}\},$$

   where the partial derivatives evaluated at $\{{\gamma }_i^{(m-1)},{\beta }^{(m-1)}\}$ are provided in the Appendix section.

4. The above steps are repeated until convergence, defined by $\underset{i,k}{\max }\left|{\mu }_{ik}^{(m)}-{\mu }_{ik}^{(m-1)}\right|<ϵ$, where ${\mu }_{ik}^{(m)}=\exp \{\log (t_{ik})+{\gamma }_i^{(m)}+Z_{ik}^T{\beta }^{(m)}\}$ and ϵ is some pre-specified tolerance level. Programs in R, sample data, and tutorial are provided as supplemental materials at http://faculty.sites.uci.edu/nguyenlab/supplement/. (Website not yet activated.)

2.4. Hypothesis Testing for Facility Effects: Identifying Extreme Facilities

It is of interest to identify facilities that significantly deviate from the national norm. For a facility with an event rate that does not differ from the national norm, γ_i = γ_M, which implies SER_i = 1. When SER_i > 1 or SER_i < 1, then the event rate for facility i is greater than or less than the national norm, respectively. Thus, testing the null hypothesis H₀ : γ_i = γ_M is of interest and a suitable test statistic is $T_i={\Sigma }_{k=1}^{N_i}{\widehat{\mu }}_{ik}$ when sampling from the null. That is, we assess the probability that the facility would have a count (or rate) of adverse events at least as extreme as what was observed if the null hypothesis was true. For this, we adapt the procedure by He et al. (2013) to be applicable to rate/count outcome.¹⁰

First, note that simultaneously testing the null hypothesis for thousands of facilities is computationally expensive. However, one can take advantage of the fact that β and γ_M can be estimated quite precisely based on the large data from all facilities. Hence, these parameters are estimated only once and fixed throughout the proposed algorithm below which is based on resampling responses under the null hypothesis. Since the global parameters β and γ_M are fixed, model fitting to the resampled data only requires estimation of facility-level effects γ_i. This reduces the computational burden substantially since each γ_i is estimated using only data from each facility separately. The steps of the procedure are:

1. Draw B samples $Y_{ik}^b~Pois(\exp \{\log (t_{ik})+{\widehat{\gamma }}_M+Z_{ik}^{\text{T}}\widehat{\beta }\})$ for b = 1, …, B.

2. Calculate $T_i^b={\sum }_{k=1}^{N_i}\exp \{\log (t_{ik})+{\widehat{\gamma }}_i^b+Z_{ik}^{\text{T}}\widehat{\beta }\}$, where ${\widehat{\gamma }}_i^b$ is the effect estimate of γ_i in sample b.

3. A nominal two-sided p value is calculated as

   $$p_i=2\cdot \min \left[B^{-1}\sum _{b=1}^B\{0.5I(T_i=T_i^b)+I(T_i<T_i^b)\},B^{-1}\sum _{b=1}^B\{0.5I(T_i=T_i^b)+I(T_i>T_i^b)\}\right].$$

   We note that in the estimation of ${\gamma }_i^b$ (step 2), ${\sum }_{k=1}^{N_i}\exp \{\log (t_{ik})+{\widehat{\gamma }}_i^b+Z_{ik}^T\widehat{\beta }\}$ equals ${\Sigma }_k{y}_{ik}^b$, which follows from the score equation. Thus, estimation of ${\gamma }_i^b$ is not necessary and we can take $T_i^b={\Sigma }_k{y}_{ik}^b$ in step (2) to reduce computational burden. However, we have presented step 2 in more generality (with total estimated counts from the model fit) so that the procedure will be applicable to other models, such as the NB model for overdispersed data, where the total estimated counts does not equal the observed counts.

2.5. Negative Binomial Model for Data with Overdispersion

When the event counts exhibit overdispersion (variance greater than mean), in which the Poisson distribution cannot naturally accommodate, alternative models, such as the negative binomial, can be used. We consider the following parametrization of the NB model for overdispersed outcome. Consider the conditional distribution Y_ik|θ_ik ~ Pois(θ_ik), where θ_ik ~ Gamma(αμ_ik, α⁻¹) with shape parameter αμ_ik and scale parameter α⁻¹. Thus, the distribution of observed counts, Y_ik, is negative binomial with probability mass function

$$\mathrm{Pr}(Y_{ik}=y_{ik};{\mu }_{ik},\varphi )=\frac{\Gamma (y_{ik}+{\mu }_{ik}\alpha )}{\Gamma ({\mu }_{ik}\alpha )y_{ik}!}{\left(\frac{\alpha }{1+\alpha }\right)}^{{\mu }_{ik}\alpha }{\left(\frac{1}{1+\alpha }\right)}^{y_{ik}},$$ (5)

with E(Y_ik) = μ_ik, Var(Y_ik) = μ_ikϕ, ϕ = (1 + α⁻¹) is the overdispersion parameter, and Γ(·) denotes the gamma function.

Thus, the likelihood function for the log-linear regression model (1) under NB outcome (5) is

$$L(\gamma ,\beta ,\varphi )=\prod _{i=1}^I\prod _{k=1}^{N_i}\frac{\Gamma \{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}}{\Gamma \{{\mu }_{ik}{(\varphi -1)}^{-1}\}{y}_{ik}!}{\varphi }^{-y_{ik}-{\mu }_{ik}/(\varphi -1)}{(\varphi -1)}^{y_{ik}}.$$ (6)

Estimation of the model parameters γ_i, β and ϕ follows same overall estimation steps provided in Section 2.3 for the Poisson regression model, but with appropriate modifications for the NB model. The details of NB model estimation are provided in the Appendix section. The hypothesis testing procedure outlined in Section 2.4 is only modified by resampling from a NB distribution rather than a Poisson distribution in Step (1).

3. Simulation Studies

3.1. Simulation Design

We carried out simulation studies to assess the efficacy of estimation (patient-level and facility effects), hypothesis test of facility effects, and flagging of extreme facilities. Because outcome data with overdispersion is likely to affect the inference procedure, we also considered this in the simulation studies. Three overall settings were considered.

Setting I (Poisson Model):

Data was generated from the regression model (1) with subject baseline covariates Z_ik = (Z_ik1, Z_ik2)^T generated by Z_ik1 ~ Bernoulli(.5) and Z_ik2|Z_ik1 ~ Z_ik1N(−.25, 1) + (1 − Z_ik1 )N(.25,1), where N(a, b) denotes the normal distribution with mean a and variance b. Event counts were generated from the Poisson distribution, Y_ik ~ Pois(μ_ik). A total of I = 5,000 facilities was specified, with facility fixed-effects, γ_i (i = 1, …, I), equally spaced between −0.5 and 0.5 inclusively. The number of subjects in each facility was randomly generated from a truncated Gamma distribution with shape 1.9 and scale 38 over the support [20,600] which paralleled what was observed in the United States Renal Data System (USRDS) data of Section 4. Each dataset generated included 400,000 subjects. Also, subject follow-up times (months), t_ik, were generated from a discrete random variable T, where pr(T = 1) = 0.015, pr(T = 12) = 0.685, and pr(T = t) = 0.03 for t = 2, …, 11. In this setting, expected follow-up time is 10.2 and the standard deviation of follow-up time is approximately 3.2, which are similar to our data application. Also, to mimic the baseline event rate in our data application, a constant of log(0.22) was added so that the data generating model used was $\text{log}({\mu }_{ik})=\text{log}(0.22)+\text{log}(t_{ik})+{\gamma }_i+Z_{ik}^{\text{T}}\beta$ for i = 1, …, I. The Poisson regression model was fitted to each dataset as described in Section 2.3.

Setting II (Negative Binomial Model):

In this setting, data was generated as described by regression model (1) with outcome from the NB distribution (5) with mean μ_ik, variance μ_ikϕ, and overdispersion ϕ = 3 (as detailed in Section 2.5). All other simulation parameters were as described in setting I above. The NB regression model was fitted to each dataset as described in Section 2.5.

Setting III (Ignoring Overdispersion):

In this setting, data with overdispersion was generated via the NB model (as in setting II); however, the Poisson regression model was fitted to ignore overdispersion.

In each setting, 1,000 Monte Carlo datasets were generated.

3.2. Estimation

Table 1A shows that the subject-level parameters, β₁ and β₂, were accurately targeted in Poisson regression ([absolute] bias: <7e-6 and <5e-6), NB regression (bias: 0.001 and 0.001), and when ignoring overdispersion (bias: <2e-4 and <2e-6). The 5,000 facility effect estimates, ${\widehat{\gamma }}_i’\text{s}$, were also well estimated with low bias and small MSE in the three simulation settings: Setting I (max bias and MSE: 0.077 and 0.010), II (max bias and MSE: 0.079 and 0.118), and III (max bias and MSE: 0.084 and 0.131). See Table 1B for details. Finally, our proposed SER_i measure used for inference was also nicely targeted in all settings examined: Setting I (max bias and MSE: 0.076 and 0.010), II (max bias and MSE: 0.125 and 0.027), and III (max bias and MSE: 0.130 and 0.029). We note that, similar to classical Poisson and NB regression models, overdispersion did not affect maximum likelihood estimation in these corresponding high-dimensional model. However, overdispersion does affect inference as illustrated in the next two subsections.

Table 1:

(A) Estimated absolute bias, standard deviation (SD), and mean squared error (MSE) of patient-level parameter estimates in simulation settings I (Poisson model), II (negative binomial model), and III (ignoring overdispersion). (B) 25th, 50th, 75th percentile and maximum of the distribution of bias and MSE for estimation of facility-level effects (γ_i; i = 1, …, I) and standardized event ratio (SER). Results given were based on on 1,000 Monte Carlo datasets.

(A) Patient-level Parameter (Par.) Estimates
I. Poisson Model						II. Negative Binomial Model						III. Ignoring Overdispersion
Par.	True	Mean	SD	Bias	MSE	Par.	True	Mean	SD	Bias	MSE	Par.	True	Mean	SD	Bias	MSE
β1	0.5	0.500	0.002	<7e-6	<4e-6	β1	0.5	0.501	0.001	0.001	<2e-5	β1	0.5	0.500	0.003	<2e-4	<2e-5
β2	−0.5	−0.500	0.001	<5e-6	<7e-7	β2	−0.5	−0.501	0.001	0.001	<4e-6	β2	−0.5	−0.500	0.001	<2e-6	<3e-6
						ϕ	3	2.957	0.008	0.043	0.002
(B) Facility-level (γi’s) and SER Estimates Estimates
I. Poisson Model						II. Negative Binomial Model						III. Ignoring Overdispersion
		25th%	50th%	75th%	Max			25th%	50th%	75th%	Max			25th%	50th%	75th%	Max
$\text{Bias}({\widehat{\gamma }}_i)$		0.049	0.055	0.063	0.077	$\text{Bias}({\widehat{\gamma }}_i)$		0.079	0.089	0.010	0.118	$\text{Bias}({\widehat{\gamma }}_i)$		0.084	0.096	0.109	0.131
$\text{MSE}({\widehat{\gamma }}_i)$		0.004	0.005	0.007	0.010	$\text{MSE}({\widehat{\gamma }}_i)$		0.011	0.014	0.017	0.026	$\text{MSE}({\widehat{\gamma }}_i)$		0.012	0.016	0.021	0.031
$\text{Bias}({\widehat{SER}}_i)$		0.049	0.055	0.062	0.076	$\text{Bias}({\widehat{SER}}_i)$		0.077	0.089	0.102	0.125	$\text{Bias}({\widehat{SER}}_i)$		0.084	0.095	0.107	0.130
$\text{MSE}({\widehat{SER}}_i)$		0.004	0.005	0.007	0.010	$\text{MSE}({\widehat{SER}}_i)$		0.010	0.014	0.018	0.027	$\text{MSE}({\widehat{SER}}_i)$		0.012	0.016	0.020	0.029

3.3. Hypothesis Testing

The hypothesis testing procedure outlined in Section 2.4 (replace ${\widehat{\gamma }}_M$ with γ₀) was carried out to test the null hypothesis H₀ : γ₁ = γ₀ for γ₀ ∈ {−1.0, −0.4, 0.0, 0.4, 1.0} in simulation settings I, II, and III. (These γ₀ values translate to SER of 0.368 to 2.718; see Table 2.) For this, the first facility’s effect, namely γ₁, was set to the value γ₀ and the remaining (4,999) facility effects were set to be equally spaced between −0.5 and 0.5 inclusively. Estimated bias and standard deviation (SD) of our SER_i estimator are summarized in Table 2 as well as acceptance probabilities (AP) based on 1,000 Monte Carlo runs.

Table 2:

Estimated absolute bias, standard deviation (SD), and acceptance probability (AP) for testing H₀: γ₁ = γ₀ for γ₀ ∈ {−1.0, −0.4, 0.0, 0.4, 1.0} in simulation settings I (Poisson model), II (negative binomial model), and III (ignoring overdispersion) based on 1,000 Monte Carlo datasets. (SER, standardized event ratio)

		I. Poisson			II. Negative Binomial			III. Ignoring Overdispersion
γ0	True SER	Bias	SD	AP	Bias	SD	AP	Bias	SD	AP
−1.0	0.368	<6e-5	0.043	0.949	0.001	0.066	0.941	0.005	0.075	0.735
−0.4	0.670	<5e-4	0.059	0.950	0.001	0.095	0.952	<4e-4	0.099	0.747
0.0	1.000	<3e-4	0.075	0.952	0.001	0.120	0.941	<6e-4	0.129	0.726
0.4	1.492	0.005	0.089	0.950	0.005	0.144	0.954	0.003	0.147	0.757
1.0	2.718	0.002	0.122	0.948	0.007	0.197	0.948	0.001	0.202	0.729

Table 2 shows that the true SER₁ was accurately targeted in all simulation settings with small bias and the AP in Settings I and II target the nominal value of 0.95 (AP: 0.941 to 0.952 for setting I and II). However, as expected, in setting III where data with overdispersion was ignored, the AP was degraded substantially to roughly 0.74 (range: 0.726 to 0.757), thus, clearly failing to target the nominal level. Therefore, ignoring overdispersion led to serious inflation of Type I error.

3.4. Flagging Extreme Facilities

We also conducted simulation studies to assess the relative performance of profiling models to identify/flag extreme facilities that under-perform (W: “worse”) or over-perform (B: “better”) relative to the reference standard (e.g., national reference). For this, we considered the hypothesis testing procedure (for H₀: γ_i = γ_M) outlined in Section 2.4 applied to simulation settings I, II, and III with 600 better-performing facilities: γ_i ~ Unif(−ξ −.1, −ξ + .1) for i = 1 … 600; 3,800 facilities performing not different from the reference: γ_i = 0 for i = 601 … 3,800; and 600 worse-performing facilities: γ_i ~ Unif(ξ − .1, ξ + .1) for i = 3, 801 … 5000 for each data set. Results are presented for this case of 12% worse and 12% better performing facilities. (Results were similar for other percentage of “extreme” facilities and those results are not presented.) We examined flagging performance under small, moderate, and large facility effect size defined by ξ ∈ {0.15, 0.25, 0.40} over 200 Monte Carlo datasets for each effect size setting. The percentage of truly worse and better facilities were both 12% (600/5,000), which is similar to the percentage of facilities flagged in the data application; however, results with varying percentage of truly worse and better facilities were similar.

The relative efficacy of the flagging procedure was evaluated by the sensitivity (SEN) or proportion of truly worse facilities identified (“SEN-W”); the sensitivity of truly better facilities identified (“SEN-B”); and the specificity (SPEC) or proportion of facilities truly not different (ND) from the reference (“SPEC-ND”). We note that in the context of FE model profiling, the reader may have a question regarding multiple testing, specifically control of type I error. However, in the context of profiling, this must balanced with type II error. The work from Professors John D. Kalbfleisch and Robert A. Wolfe,¹¹ summarizes this point: “In the context of profiling centers, it seems important to assess each center separately, treating each center and its patients as the population of interest, without regard to the totality of tests being done. Adjustments for multiple testing are typically done to control the overall type I error … But in the context of profiling centers, patient interests suggest that the type II error is at least equally important and that we should have methods which will typically identify a center whose results are relatively extreme.” For these reasons, our current work on profiling (as well as previous works in profiling^14,16) provides performance assessment metrics that focus on the rate of correctly identifying extreme facilities (referred to as “sensitivity-worse” and “sensitivity-better”), but also the rate of correctly identifying non-significant facilities (“specificity - not different”) and these are provided Figure 1, for instance. These are analogous to power (1-type II) and (1-type I) errors in profiling.

Figure 1:

Flagging performance for negative binomial and poisson models for rates of abnormal events based on standardized event rate (SER). Given are sensitivity-worse (under-performing facilities, sensitivity-better (over-performing facilities), and specificity-not different (facilities event rates not different from the reference standard) as a function of effect sizes (A: low; B: moderate; C: large).

Note that facilities assessment policies in practice focus on identifying under-performing (worse) facilities. Results of our simulation studies are summarized in Figure 1 for the Poisson and negative binomial data settings. As expected, the sensitivities to detect truly worse and better performing facilities improves with increasing effect sizes (A: small, B: moderate, C: large; Figure 1). Because of the relatively high number of truly ND facilities (3,800 out of facilities), specificities for both the negative binomial and Poisson models were high at about 95%.

The hypothesis testing described above in Section 3.3 suggests that ignoring overdispersion may affect flagging performance. Indeed this is the case, as illustrated in Figure 2 (effect size fixed at moderate level). Sensitivity for identifying truly under-performing facilities were inflated (mean SEN-W: 84%, SD 2.7%) compared to the optimal negative binomial model (mean SEN-W: 67%, SD 2.6%) at the high cost of substantially reduced specificity ND (optimal mean SPEC-ND: 95%, SD 0.8% vs. mean SPEC-ND: 75%, SD 1.5% for the Poisson model ignoring overdispersion).

Figure 2:

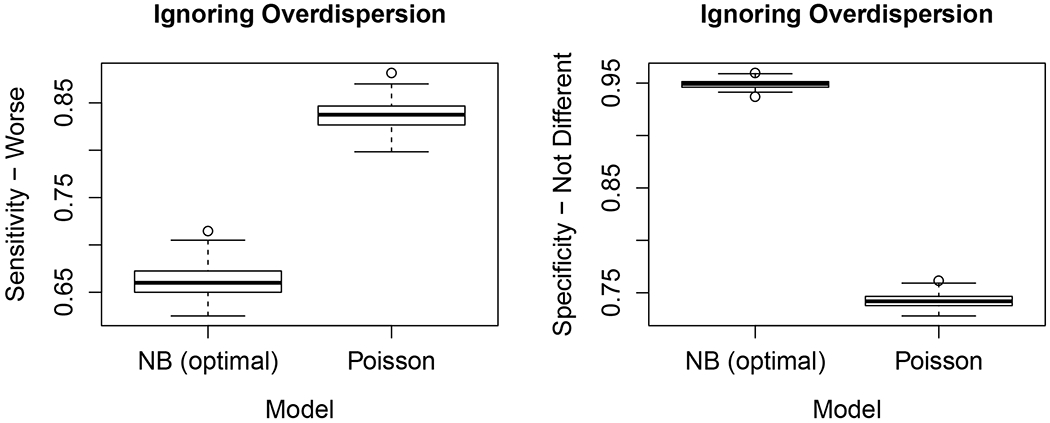
Effect of ignoring overdisperson on flagging performance based on models for standardized event rate (SER). Given are sensitivity-worse (under-performing facilities) and and specificity-not different (i.e., facilities event rates not different from the reference standard) the negative binomial model (optimal) and the Poisson, model that ignores overdispersion.

4. Profiling Dialysis Facilities for Recurrent Anemia Events

4.1. Study Cohort, Follow-up Time, Outcome, and Risk Adjustment

To illustrate the proposed methods, we consider profiling dialysis facilities for the year 2014 using data from the United States Renal Data System (USRDS), a national registry that includes nearly all patients receiving care for ESRD in the US.¹ The study cohort included dialysis patients from January 1, 2014 through December 31, 2014 with Medicare as primary payer in the US. Follow-up for prevalent patients (beginning 1/1/14) and incident patients (beginning from the start of dialysis in 2014) continued until kidney transplant (2.4%), renal function recovery (0.7%), death (14.3%), or to end of 2014 (82.6%). There were 15.4% of patients who switched among facilities during 2014, among which 13.0% patients were in 2 facilities, and 2.4% patients were in 3-4 facilities. Because the profiling analysis aims to assess each dialysis facility’s performance with respect to an outcome of patients treated at the facility, accordingly, for patients who switched between dialysis facilities during 2014, only their follow-up time period at each facility was used. The potential analysis cohort included 464,774 patients and 6,401 facilities. However, an extremely small facility with only several patients may not be reliable for profiling since the object of inference is based on SER, which may not be reliably estimated. (For a more detailed discussion of this issue in the context of binary outcome models, see Ash et al.⁹). Thus, facilities with less than 10 patients were excluded (3.3%). Also, patients with missing baseline covariates were excluded (5.2%, mainly missing BMI and previous year Hb). The final analysis cohort after the above exclusion included 440,107 patients and 6,188 facilities with the number of patients per facility ranging from 10 to 560.

We defined the outcome to be the number of times a patient’s Hb is outside the Hb target range (Hb between 9 and 11 g/dL) and the count is measured monthly. (Thus, the potential count ranges from 0 to 12.) Because the main goal of profiling models is to assess facility effects, the model must carefully adjust for patients risk characteristics. Following previous works on profiling dialysis facilities,^12,13 the risk adjustment included age, sex, body mass index (BMI), diabetes as the cause of ESRD, years on dialysis, past-year comorbidities, past-year high-risk hospitalization, and nephrology care prior to initiation of dialysis. We also included in the risk adjustment whether the patient experienced Hb outside the target range in the prior year to the start of follow-up. (See Table 3.)

Table 3:

Estimated rate ratio (RR: $\text{exp}({\widehat{\beta }}_r)$) and 95% lower and upper confidence limit (LCL, UCL) for patient-level risk adjustment from the negative binomial model. (Results for the Poisson model were very similar; not shown.)

Variable	Groups	Percent (Count)	RR	LCL	UCL
Age group (reference: 45-60)	<25	0.88 (3,683)	1.019	1.002	1.040
	25-45	10.92 (45,835)	1.019	1.013	1.027
	45-60	27.69 (116,207)	Ref
	60-75	38.61 (162,078)	0.954	0.950	0.960
	>75	21.90 (91,930)	0.894	0.889	0.900
BMI (referent: Normal)	Underweight	2.77 (11,641)	1.014	1.002	1.026
	Normal weight	26.31 (110,442)	Ref
	Overweight	27.76 (116,497)	1.015	1.011	1.021
	Obese	43.16 (181,153)	1.040	1.036	1.046
Cause of ESRD: Diabetes		45.73 (191,951)	0.938	0.934	0.942
Prior nephrology care (reference: No)	Yes	56.92 (226,839)	1.007	1.003	1.012
	Missing	19.48 (77,645)	1.015	1.010	1.023
Time on ESRD (years) (reference: < 1)	<1	34.47 (144,688)	Ref
	1 to 2	14.79 (62,071)	0.904	0.899	0.910
	2 to 3	11.96 (50,202)	0.896	0.890	0.903
	3 to 6	22.78 (95,615)	0.894	0.890	0.899
	>6	16.00 (67,157)	0.944	0.938	0.950
Sex: female		43.97 (184,540)	0.861	0.858	0.864
Hemoglobin out of target range in the prior year		91.49 (384,005)	1.302	1.295	1.320
Past-year comorbidities:
Amputation status		5.02 (21,080)	1.006	0.998	1.016
COPD*		12.10 (50,773)	1.013	1.008	1.020
Cardiorespiratory failure/shock		10.32 (43,310)	0.977	0.971	0.983
Coagulopathy		7.66 (32,163)	0.988	0.981	0.995
Drug and alcohol disorders		1.41 (5,922)	0.986	0.971	1.000
End-stage liver disease		1.74 (7,307)	0.987	0.975	1.002
Fibrosis of lung or OCLD*		1.09 (4,578)	0.993	0.976	1.010
Motor disfunction		3.11 (13,061)	0.993	0.983	1.005
Hip fracture/dislocation		1.27 (5,325)	1.000	0.984	1.017
Transplants		0.57 (2,405)	0.913	0.893	0.934
Metastatic cancer		0.46 (1,914)	0.995	0.970	1.020
Severe hematological disorders		0.65 (2,727)	1.089	1.066	1.112
Other infectious disease and pneumonias		20.13 (84,512)	0.986	0.982	0.992
Other cancers		3.73 (15,671)	0.963	0.954	0.974
Pancreatic disease		1.86 (7,818)	0.991	0.977	1.003
Psychiatric comorbidity		14.47 (60,753)	0.991	0.985	0.996
Respirator dependence*		0.45 (1,873)	0.986	0.958	1.012
Arthritis and ICTD*		2.70 (11,340)	0.970	0.958	0.981
Seizure disorders and convulsions		3.64 (15,286)	0.969	0.960	0.978
Septicemia/shock		8.33 (34,973)	1.014	1.007	1.021
Severe cancer		1.49 (6,268)	0.967	0.953	0.983
Severe infection		1.88 (7,893)	0.993	0.981	1.006
Decubitus ulcer or chronic skin ulcer		7.72 (32,399)	1.000	0.992	1.007

^*OCLD: other chronic lung disorder; ICTD: inflammatory connective tissue disease; COPD: chronic obstructive pulmonary disease; respirator dependence/tracheostomy status

4.2. Model Fits and Profiling Results

The distribution of patient follow-up time ranged from 1 to 12 months, with a median follow-up time of 11 months, and the average raw rates of anemia across patients was 0.43 per month (SD 0.07); see Figure 3 (row 1). We fitted both the Poisson and NB models and the rate ratio (RR) estimates ($\text{exp}({\widehat{\beta }}_r)$) are summarized in Table 3 for the NB model. (Results for the Poisson regression were nearly identical and are not shown.) The model goodness-of-fit was assessed by examination of the observed rates vs. model estimated/predicted rates and shown in Supplementary Figure S3. The observed vs. model-based predicted values showed overall good fit, aligning with the 45° line. Not surprisingly, patients who had Hb level out of target range in the year prior to the start of follow-up for the study was associated with the largest estimated increase in rate of anemia over 30% (RR 1.302, 95% confidence interval [CI]: 1.295-1.320). Having hematological disorder as a past year comorbidity was associated with nearly a 9% increase rate of anemia (RR 1.089, 95% CI: 1.066-1.112). Patient factors associated with notably reduced rate of anemia included female (RR 0.861), diabetes as the cause of ESRD (RR 0.938), and longer times on dialysis (e.g., RR 0.896 for 2 to 3 years on ESRD vs. < 1 year). See Table 3 for details of RR estimates for all patient risk factors. Confidence intervals for RR estimates (or ${\widehat{\beta }}_r’\text{s}$) in Table 3 were obtained using bootstrap estimates of standard errors (SEs) based on 200 bootstrap samples at the facility level. (Because the alternating one-step Newton-Raphson estimation algorithm is not classical MLEs, SE estimates obtained from the observed information matrix at convergence generally may not target the true variability of the estimators. Simulation studies documenting this are provided in the Supplementary Materials and Figure S1.)

Figure 3:

Row 1: Distribution of follow-up time and distribution of raw anemia rates. Row 2: Distribution of standardized event rates (SERs) in dialysis facilities flagged/identified as significantly worse, better, and not different relative to the national reference.

The distribution of SERs for facilities flagged as significantly worse (SW), significant better (SB), and not different (ND) compared to the national reference are displayed in Figure 3 (row 2) for the negative binomial model. Mean (SD) of the estimated SERs for SW, ND, and SB dialysis facilities were 1.264 (0.114), 1.010 (0.110), and 0.762 (0.96), respectively. As described in simulation study of Section 3, overdispersed data leads to overflagging of “extreme” facilities. Table 4 shows the flagging results for 6,188 facilities between the Poisson and negative binomial model, with the Poisson model flagging 16.2% (1005) facilities as having SW (standardized) anemia rates compared to 12.5% (774) for the negative binomial model. This was consistent with overdispersion parameter estimate of 1.4. Thus, the negative binomial model results are more appropriate in the presence of overdispersion. Table 5 provides further details of flagging results for the negative binomial model across all facilities and by facilities size (small: 10-55, medium: 56-96, and large: 97-560 patients). The main focus of profiling in practice centers on identifying facilities that are extremely under-performing. We note that of the 774 facilities identified as having anemia rates significantly worse than the national norm, variation in the proportion of facilities flagged for small (9.4%), medium (12.7%), and large facilities (15.4%) was not substantial.

Table 4:

Comparison of dialysis facility flagging between Poisson and negative binomial regression models for 6,188 facilities.

Poisson model
Negative binomial model	Better	Not different	Worse	Total
Better	907	29	0	936 (15.1%)
Not different	137	4108	233	4478 (72.4%)
Worse	0	2	772	774 (12.5%)
Total	1044 (16.9%)	4139 (69.9%)	1005 (16.2%)	6188

Table 5:

Results of identifying extreme dialysis facilities using the negative binomial model among all facilities and by facility size (small: 10-55, medium: 56-96, and large: 97-560 patients).

Facility size	Worse		Not different		Better
Small	194	9.4%	1713	82.7%	164	7.9%
Medium	261	12.7%	1466	71.5%	323	15.8%
Large	319	15.4%	1299	62.8%	449	21.7%
Overall	774	12.5%	4478	72.4%	936	15.1%

Note that the analysis identified 12.5% of facilities have patient anemic rates worse than the national average (Table 5). Consumers of profiling analysis must interpret this result within the context of the specific outcome, the patient population, and stakeholder objectives. More specifically, we point out the following considerations in interpreting this result. (1) First, unlike the general population and most chronic disease conditions, dialysis patients have many serious comorbidities and survival is worse than most malignancies. Conditions/events including anemia, malnutrition, volume overload, mineral metabolism disorders, and dialysis inadequacy (among others) are monitored routinely and they are commonly out of target range and not all are easily controlled in this population, such as Hb level considered in this work. For example, with respect to the outcome considered here, namely anemic events, this occurred 5.6 times per year on average and we are not surprised from our experience with dialysis patients that there are many facilities with rates substantially deviating from the national average. (2) Second, in profiling applications, the total percentage of providers flagged that are used for quality improvement (and/or payment reimbursement policy) is partly determined/set by the policy objective with stakeholder inputs. For example, in the extreme case where the regulatory agency and stakeholders deemed the outcome event of critical importance and the objective may be to motivate/enforce immediate change in the patient care culture, then all under-performing facilities identified (e.g., 12.5%) would be flagged for quality improvement/enforcement, regardless of how many. However, more practically, it is also feasible that the policy objective would set a threshold such as using the top 5% of under-performing facilities identified. (Also, see the Discussion section for further context for interpretation of the results.)

Finally, we note that when the percentage of total truly outlier facilities is small (e.g., 1%-5% usually or at most 10%), flagging extreme facilities based on the empirical null distribution¹⁷ may be preferred to avoid over-flagging of higher volume (size) facilities. This was previously implemented for profiling dialysis facilities with respect to 30-day hospital readmission (a binary outcome) due to the relatively low rate of extreme facilities.^10,11,13 Use of the empirical null distribution procedure may not be appropriate when extreme (outlier) facilities are common (e.g., > 10% as suggested by Efron¹⁷), which may be the case in our application. The empirical null distribution approach is based on a robust regression fit to the empirical null distribution and may suffer from a large proportion of outlier providers and may over estimate the variance of the empirical null distribution. This is an issue that warrants further research in the context of profiling health care providers. For the interested reader, the flagging results based on the empirical null distribution are provided in supplementary Tables S1 and S2.

5. Discussion

In this work, we have presented methods applicable to profiling health care providers with respect to patient outcomes that are rates/counts per unit time. Specifically, high-dimensional FEs Poisson and negative binomial regression were proposed and illustrated with monitoring dialysis facilities with respect to the rate of out of target hemoglobin level in dialysis patients. For simplicity of exposition, we considered Hb between 9 and 11 g/dL as the target range, although there are some debates with respect to the target range and possibly target ranges should be tailored to age groups and sex. The proposed methods would be applicable to such modifications of the outcome with respect to Hb. Also, despite the broad patient-level risk adjustment factors included, indicator of hematological disorders and having Hb out of target range in the prior year were the two factors that were associated with the largest increase in the rate of out of target Hb. Adequate risk adjustment in profiling models is important, and, therefore, refinement to the risk adjustment factors presented in this work may be useful in practice. The “final” profiling model typically includes risk factors selected from various stakeholder perspectives, including from technical/statistical considerations (e.g., using a variety of regression modeling strategies, e.g., see¹⁸), clinical knowledge of the specific outcome considered, and the specific regulatory (CMS) objectives among others. Our main purpose in the data analysis was to illustrate the main aspects of the proposed models and also to use a set of risk adjustment factors that had previously received stakeholder inputs in the dialysis community with respect to dialysis patients and their hospitalizations. Further refinement of the application should consider addition of other relevant factors as well as exclusion of factors found not to contribute to model fit beyond noise.

With respect to the data application, we also note that factors such as erythropoiesis stimulating agents and iron therapy used to manage anemia in dialysis patients were not included in the risk adjustment as these are precisely part of the facility’s process of care (which should be excluded from risk adjustment in profiling). In addition to modeling counts of specific types of events, such as anemia, hypercalcemia, or dialysis adequacy etc., in the dialysis population, in practice, it may be informative to also consider combination of events deemed important for monitoring dialysis facilities. For example, the outcome of interest may be the number of times a patient was inadequately dialyzed who also had anemia, or hypercalcemia, or both, for instance. The proposed profiling models, with suitably chosen risk adjustment, would be useful in such applications.

An important consideration, raised by a reviewer, is the issue of volume-quality relationship in many areas of profiling. Indeed, the inclusion of volume (and other provider characteristics) to stabilize estimates of standardized readmission ratios (SRR) and standardized mortality ratio (SMR) for hospitals has been contentious and discussed in details previously⁹ and also in recent works.^19,20 As discussed in Ash et al.,⁹ inclusion of volume typically centers on the need to stabilize quality measure (SRR, SMR, and in our context here SER) in the context of low volume providers (as high volume providers are largely unaffected). This is naturally achieved within the framework of random effects models (for binary outcomes) which shrinks SRR/SMR estimates towards the national average (SMR, SRR = 1) for very low volume providers and inclusion of volume in such models translate to setting different shrinkage targets for low volume providers. Such an approach/model conceptually can be extended for patient outcomes which are counts. One limitation with current high-dimensional fixed effects models is the inability to handle extremely sparse data inherent in very low volume providers and it is an area of future research. However, we note that volume should not be included in the model for the denominator of SER (the expected rate), similar to SRR and SMR, because volume is potentially both exogenous (“associated with quality but not ‘caused’ by quality”, e.g., “practice makes perfect”) and endogenous (poor quality led to low volume), i.e., volume is on the causal pathway to outcome (see Ash et al.⁹ for details).

In our illustrative data analysis with respect to anemic rates, 12.5% of facilities were identified as having worse rates than the national average and with 9.4%, 12.7%, and 15.4% of facilities flagged from small, medium and large facilities, respectively. The amount of variation in the proportion of facilities flagged by volume may vary (depending on the outcome considered), and consideration of models that incorporate facility characteristics, such as volume, or setting different targets for identifying facilities that depend on volume must balance the specific profiling objective with the aforementioned considerations. However, generally larger facilities are flagged more frequently. This is partly due to the effect of volume (# of patients) on inference (flagging providers), which is essentially a reflection of the issue of effective sample size in inference. This issue has been recognized and extensively discussed in profiling.⁹ Inference in profiling models (as in any statistical model) for providers with larger effective sample sizes (~ higher volume) is improved on average, resulting in typically more providers flagged, as expected due to lower variance (relative to smaller effective sample sizes among low volume providers). However, a cautionary note is that for rare outcomes, large providers may also have low effective sample size (events) due to rare events, but generally among the population of providers, volume and effective sample size are highly related. Nevertheless, there are also complicated issues related to the “process of care” that is generally confounded with the technical impact of volume/effective sample size. Some non-technical effects of volume on patient outcomes have been investigated indirectly. For example, our previous study showed that for-profit dialysis facilities have higher patient hospitalization rates than nonprofit facilities,²¹ and typically for-profit dialysis chains are larger. Furthermore, for-profit (larger facilities) typically employs more patient-care-technicians, which is relatively less costly, and the ratios of registered nurses-to-patients and the ratio of licensed practical nurses-to-patients has been reported to be 35% and 42% lower, respectively, in for-profit dialysis facilities.²² These real effects which potentially could lead to larger facilities being flagged would be confounded with the above technical impact of sample size/volume in profiling. More directly, we recently found that dialysis facilities identified as having significantly worse 30-day unplanned hospital readmission rates using profiling models, indeed on average have lower proportions of nurses-to-total staff and higher patient-to-nurse ratios.¹⁶

Finally, we note that overdispersion in the high-dimensional Poisson model affects the inference procedure (i.e., the ability to identify extreme facilities), but not estimation of the regression coefficients or SER estimates. This is analogous to classical Poisson regression models where overdispersion does not affect parameter estimates, but do lead to incorrect inference (inflated Type I errors) in hypothesis tests. In the context of profiling considered here, ignoring substantial overdispersion leads to “inflated” sensitivity in detecting truly extreme facilities, but at the severe cost of reduced specificity to detect facilities that are not different from the reference standard. To account for overdispersion, the proposed negative binomial regression profiling method may be used instead.

Appendix

We provide maximum likelihood estimation details for the proposed high-dimensional Poisson and negative binomial regression. For the Poisson model, the log-likelihood is

$$\ell (\gamma ,\beta )=\sum _{i=1}^I\sum _{k=1}^{N_i}\{y_{ik}\log ({\mu }_{ik})-{\mu }_{ik}-\log (y_{ik}!)\}$$

where ${\mu }_{ik}=\exp \{\log (t_{ik})+{\gamma }_i+Z_{ik}^T\beta \}$. The partial derivatives are:

$$\frac{\partial \ell }{\partial {\gamma }_i}=\sum _{k=1}^{N_i}(y_{ik}-{\mu }_{ik}),$$

$$\frac{{\partial }^2\ell }{\partial {\gamma }_i^2}=-\sum _{k=1}^{N_i}{\mu }_{ik},$$

$$\frac{\partial \ell }{\partial \beta }=\sum _{i=1}^I\sum _{k=1}^{N_i}(y_{ik}-{\mu }_{ik})Z_{ik},\text{and}$$

$$\frac{{\partial }^2\ell }{\partial \beta \partial {\beta }^{\text{T}}}=-\sum _{i=1}^I\sum _{k=1}^{N_i}{\mu }_{ik}{Z}_{ik}{Z}_{ik}^{\text{T}}.$$

For the negative binomial model, the log-likelihood is

$$\ell (\gamma ,\beta ,\varphi )=\sum _{i=1}^I\sum _{k=1}^{N_i}\left[\log \Gamma \{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}-\log \Gamma \{{\mu }_{ik}{(\varphi -1)}^{-1}\}-\log (y_{ik}!)-\{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}\log (\varphi )+y_{ik}\log (\varphi -1)\right]$$

where ${\mu }_{ik}=\exp \{\log (t_{ik})+{\gamma }_i+Z_{ik}^{\text{T}}\beta \}$ and Γ(·) is the Gamma function. Let ψ(·) to denote the digamma function, i.e., ψ(·) = Γ′(·)/Γ(·). For a given β and ϕ, the maximization of ℓ(γ₁, …, γ_I, β) with respect to γ_i only depends on γ_i reducing a high-dimensional maximization problem to a sequence of maximizations in one dimension. This motivates our one-step Newton-Raphson procedure as follows. Set the initial valued β⁽⁰⁾, ${\gamma }_i^{(0)}$ and ϕ⁽⁰⁾ of β, γ_i and ϕ, respectively. The mth maximization step for β, γ_i and ϕ are given by

$${\beta }^{(m)}={\beta }^{(m-1)}-{\left[\frac{{\partial }^2\ell }{\partial \beta \partial {\beta }^{\text{T}}}\{{\gamma }_i^{(m-1)},{\beta }^{(m-1)}\}\right]}^{-1}\frac{\partial \ell }{\partial \beta }\{{\gamma }_i^{(m-1)},{\beta }^{(m-1)}\},$$

$${\gamma }_i^{(m)}={\gamma }_i^{(m-1)}-{\left[\frac{{\partial }^2\ell }{\partial {\gamma }_i^2}\{{\gamma }_i^{(m-1)},{\beta }^{(m)}\}\right]}^{-1}\frac{\partial \ell }{\partial {\gamma }_i}\{{\gamma }_i^{(m-1)},{\beta }^{(m)}\},\text{and}$$

$${\varphi }^{(m)}={\varphi }^{(m-1)}-{\left[\frac{{\partial }^2\ell }{\partial {\varphi }^2}\{{\gamma }_i^{(m)},{\beta }^{(m)}\}\right]}^{-1}\frac{\partial \ell }{\partial \varphi }\{{\gamma }_i^{(m)},{\beta }^{(m)}\},$$

where the partial derivative are

$$\frac{\partial \ell }{\partial {\gamma }_i}=\sum _{k=1}^{N_i}\left[\psi \{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}-\psi \{{\mu }_{ik}{(\varphi -1)}^{-1}\}-\log (\varphi )\right]{\mu }_{ik}{(\varphi -1)}^{-1},$$

$$\frac{{\partial }^2\ell }{\partial {\gamma }_i^2}=\sum _{k=1}^{N_i}\left[{\psi }^{\prime }\{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}-{\psi }^{\prime }\{{\mu }_{ik}{(\varphi -1)}^{-1}\}\right]{\mu }_{ik}^2{(\varphi -1)}^{-2}+\frac{\partial \ell }{\partial {\gamma }_i},$$

$$\frac{\partial \ell }{\partial \beta }=\sum _{i=1}^I\sum _{k=1}^{N_i}\left[\psi \{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}-\psi \{{\mu }_{ik}{(\varphi -1)}^{-1}\}-\log (\varphi )\right]{\mu }_{ik}{(\varphi -1)}^{-1}{Z}_{ik},$$

$$\frac{{\partial }^2\ell }{\partial \beta \partial {\beta }^{\text{T}}}=\sum _{i=1}^I\sum _{k=1}^{N_i}(\left[{\psi }^{\prime }\{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}-{\psi }^{\prime }\{{\mu }_{ik}{(\varphi -1)}^{-1}\}\right]{\mu }_{ik}^2{(\varphi -1)}^{-2}+\left[\psi \{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}-\psi \{{\mu }_{ik}{(\varphi -1)}^{-1}\}-\log (\varphi )\right]{\mu }_{ik}{(\varphi -1)}^{-1})Z_{ik}{Z}_{ik}^{\text{T}},$$

$$\frac{\partial \ell }{\partial \varphi }=\sum _{i=1}^I\sum _{k=1}^{N_i}(\left[\psi \{{\mu }_{ik}{(\varphi -1)}^{-1}\}-\psi \{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}+\log (\varphi )\right]{\mu }_{ik}{(\varphi -1)}^{-2}-\{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}{\varphi }^{-1}+y_{ik}{(\varphi -1)}^{-1}),\text{and}$$

$$\frac{{\partial }^2\ell }{\partial {\varphi }^2}=\sum _{i=1}^I\sum _{k=1}^{N_i}(\left[{\psi }^{\prime }\{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}-{\psi }^{\prime }\{{\mu }_{ik}{(\varphi -1)}^{-1}\}\right]{\mu }_{ik}^2{(\varphi -1)}^{-4}-2\left[\psi \{{\mu }_{ik}{(\varphi -1)}^{-1}\}-\psi \{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}+\log (\varphi )\right]{\mu }_{ik}{(\varphi -1)}^{-3}+(2{\mu }_{ik}{\varphi }^{-1}-y_{ik}){(\varphi -1)}^{-2}+\{y_{ik}+{\mu }_{ik}{(\varphi -1)}^{-1}\}{\varphi }^{-2}).$$