Abstract
Background
Meta‐analyses based on individual participant data (IPD‐MAs) allow more powerful and uniformly consistent analyses as well as better characterisation of subgroups and outcomes, compared to those which are based on aggregate data (AD‐MAs) extracted from published trial reports. However, IPD‐MAs are a larger undertaking requiring greater resources than AD‐MAs. Researchers have compared results from IPD‐MA against results obtained from AD‐MA and reported conflicting findings. We present a methodology review to summarise this empirical evidence .
Objectives
To review systematically empirical comparisons of meta‐analyses of randomised trials based on IPD with those based on AD extracted from published reports, to evaluate the level of agreement between IPD‐MA and AD‐MA and whether agreement is affected by differences in type of effect measure, trials and participants included within the IPD‐MA and AD‐MA, and whether analyses were undertaken to explore the main effect of treatment or a treatment effect modifier.
Search methods
An electronic search of the Cochrane Library (includes Cochrane Database of Systematic Reviews, Database of Abstracts of Reviews of Effectiveness, CENTRAL, Cochrane Methodology Register, HTA database, NHS Economic Evaluations Database), MEDLINE, and Embase was undertaken up to 7 January 2016. Potentially relevant articles that were known to any of the review authors and reference lists of retrieved articles were also checked.
Selection criteria
Studies reporting an empirical comparison of the results of meta‐analyses of randomised trials using IPD with those using AD. Studies were included if sufficient numerical data, comparing IPD‐MA and AD‐MA, were available in their reports.
Data collection and analysis
Two review authors screened the title and abstract of identified studies with full‐text publications retrieved for those identified as eligible or potentially eligible. A ‘quality’ assessment was done and data were extracted independently by two review authors with disagreements resolved by involving a third author. Data were summarised descriptively for comparisons where an estimate of effect measure and corresponding precision have been provided both for IPD‐MA and for AD‐MA in the study report. Comparisons have been classified according to whether identical effect measures, identical trials and patients had been used in the IPD‐MA and the AD‐MA, and whether the analyses were undertaken to explore the main effect of treatment, or to explore a potential treatment effect modifier.
Effect measures were transformed to a standardised scale (z scores) and scatter plots generated to allow visual comparisons. For each comparison, we compared the statistical significance (at the 5% two‐sided level) of an IPD‐MA compared to the corresponding AD‐MA and calculated the number of discrepancies. We examined discrepancies by type of analysis (main effect or modifier) and according to whether identical trials, patients and effect measures had been used by the IPD‐MA and AD‐MA. We calculated the average of differences between IPD‐MA and AD‐MA (z scores, ratio effect estimates and standard errors (of ratio effects)) and 95% limits of agreement.
Main results
From the 9330 reports found by our searches, 39 studies were eligible for this review with effect estimate and measure of precision extracted for 190 comparisons of IPD‐MA and AD‐MA. We classified the quality of studies as ‘no important flaws’ (29 (74%) studies) or ‘possibly important flaws’ (10 (26%) studies).
A median of 4 (interquartile range (IQR): 2 to 6) comparisons were made per study, with 6 (IQR 4 to 11) trials and 1225 (542 to 2641) participants in IPD‐MAs and 7 (4 to 11) and 1225 (705 to 2541) for the AD‐MAs. One hundred and forty‐four (76%) comparisons were made on the main treatment effect meta‐analysis and 46 (24%) made using results from analyses to explore treatment effect modifiers.
There is agreement in statistical significance between the IPD‐MA and AD‐MA for 152 (80%) comparisons, 23 of which disagreed in direction of effect. There is disagreement in statistical significance for 38 (20%) comparisons with an excess proportion of IPD‐MA detecting a statistically significant result that was not confirmed with AD‐MA (28 (15%)), compared with 10 (5%) comparisons with a statistically significant AD‐MA that was not confirmed by IPD‐MA. This pattern of disagreement is consistent for the 144 main effect analyses but not for the 46 comparisons of treatment effect modifier analyses. Conclusions from some IPD‐MA and AD‐MA differed even when based on identical trials, participants (but not necessarily identical follow‐up) and treatment effect measures. The average difference between IPD‐MA and AD‐MA in z scores, ratio effect estimates and standard errors is small but limits of agreement are wide and include important differences in both directions. Discrepancies between IPD‐MA and AD‐MA do not appear to increase as the differences between trials and participants increase.
Authors' conclusions
IPD offers the potential to explore additional, more thorough, and potentially more appropriate analyses compared to those possible with AD. But in many cases, similar results and conclusions can be drawn from IPD‐MA and AD‐MA. Therefore, before embarking on a resource‐intensive IPD‐MA, an AD‐MA should initially be explored and researchers should carefully consider the potential added benefits of IPD.
Plain language summary
Meta‐analysis using individual participant data or summary aggregate data
Meta‐analysis is a statistical technique to combine results from separate research studies. A meta‐analysis can be performed using summary data published in a study report, referred to as aggregate data (AD), or using data collected on each individual participant in the study, referred to as individual participant data (IPD). A meta‐analysis of individual participant data (IPD‐MA) can take longer and be more expensive than a meta‐analysis of aggregate data (AD‐MA), but the IPD‐MA can be more reliable and can answer much more detailed questions than an AD‐MA.
We searched for studies, published up to 7 January 2016, that compared results of IPD‐MA with AD‐MA. We found that four times out of five, similar conclusions can be drawn, but in one out of five cases the two different types of meta‐analyses gave different results and conclusions. As we could not reliably identify when an IPD‐MA and AD‐MA will differ most using these studies, we recommend that an AD‐MA should be done first before doing an IPD‐MA. If there are shortcomings with the AD‐MA, researchers should then consider the possible benefits of IPD whilst remembering the extra work involved.
Background
Description of the methods being investigated
Meta‐analysis, a statistical technique to combine results from multiple studies addressing similar research questions, is most commonly undertaken using aggregate data (AD) extracted from published trial reports or requested from trialists. Examples of AD include the number of events and number of patients randomised in each treatment group, or published treatment effect estimates such as the odds ratio, risk ratio or hazard ratio. Meta‐analyses based on individual participant data (IPD‐MAs), in which data on all patients in all relevant randomised trials are centrally collected and re‐analysed have been proposed as the gold standard for systematic reviews (Chalmers 1993).
How these methods might work
Compared with aggregate data meta‐analysis (AD‐MA), IPD‐MAs allow more powerful and uniformly consistent analyses of, for example, the time to particular outcomes, different patient subgroups and complex outcomes, as well as better characterisation of these subgroups and outcomes. The extended follow‐up that can often be obtained for IPD can also provide an opportunity to investigate long‐term outcomes. However, IPD‐MAs are often more time‐consuming and resource intensive than other forms of review. It is also possible that an IPD review will not be able to obtain suitable data from all relevant studies and will, therefore, not be able to include these studies fully in the review, which might lead to bias.
Why it is important to do this review
One of the key issues in the research agenda of the Cochrane Individual Participant Data Meta‐analysis Methods Group, and a long‐standing question of interest in evidence synthesis is ‘How do IPD‐MA and AD‐MA results differ’? We present a methodology review of the empirical evidence to address this question. The first methodological comparison was presented at the Oslo Cochrane Colloquium in 1995 followed by an early summary of evidence, presented at the Amsterdam Colloquium in 1997, when five studies had been identified that were relevant to a comparison of IPD with published AD (Clarke 1997). Subsequently, a review of 10 studies was presented at a workshop at the Rome Cochrane Colloquium in 1999 (Williamson 2000). IPD‐MAs of randomised trials were shown to differ in important ways from MAs based on published data alone, and the importance of including as much follow‐up as possible on all randomised participants and data from all relevant trials (not just those that have been published) was confirmed. More recently, a review of 70 empirical comparisons from 25 studies was presented in a German doctorate thesis (Mukhtar 2008), concluding that two thirds of the comparisons showed a tendency to overestimate the effect size and to reduce its precision by AD‐MA in comparison to IPD‐MA. However, the differences between the point estimates of both types of meta‐analysis were small in all comparisons. Indeed, Olkin 1998 and Mathew 1999 have shown that for continuous outcome data the main effect results from IPD‐MA and AD‐MA are theoretically identical if based on identical data from homogenous studies. However, in practice, the differences between datasets that are used for IPD‐MA and AD‐MA are often subtle and it is rarely the case that datasets are identical. For example, an IPD‐MA may re‐instate patients, or may include additional follow‐up data, which were not included in published analyses that are the basis of an AD‐MA.
IPD‐MAs are becoming more common in medical research (Ahmed 2012). Numerous empirical studies comparing their results to corresponding AD‐MA results have been undertaken and reported in the literature. Some of the empirical studies focused on research relating to randomised trials of healthcare interventions have conflicting conclusions making it difficult for researchers, and research funders, to decide whether there are likely to be important differences between IPD‐MA and AD‐MA. There is therefore a need to summarise the existing evidence from empirical studies to inform researchers and to help identify where future methodology research may be required. This review attempts this task, based on a previously published protocol (Clarke 2007).
Objectives
To review systematically empirical comparisons of meta‐analyses of randomised trials based on IPD with those based on AD extracted from published reports, to evaluate the level of agreement between IPD‐MA and AD‐MA and whether agreement is affected by differences in type of effect measure, trials and participants included within the IPD‐MA and AD‐MA, and whether analyses were undertaken to explore the main effect of treatment or a treatment effect modifier.
Methods
Criteria for considering studies for this review
Types of studies
Studies reporting an empirical comparison of the results of meta‐analyses using individual participant data (IPD‐MA) with those using aggregate data (AD‐MA). Abstracts were included if sufficient numerical data were available comparing IPD‐MA and AD‐MA.
Types of data
Meta‐analyses of randomised trials.
Types of methods
Meta‐analyses in which centrally collected, processed and analysed data on each participant in each trial (IPD‐MA) have been used to undertake analyses, compared with meta‐analyses in which analyses are based on aggregate data (AD‐MA) extracted from published reports of the trial or supplied by the people responsible for it. Comparisons of IPD‐MA and AD‐MA in which the AD have been calculated from the IPD were included but those in which the IPD has been estimated or extracted from published reports were excluded. We included comparisons where IPD‐MA and AD‐MA were either based on the same number of studies and participants or not (i.e. the studies included in the IPD‐MA and AD‐MA, although answering the same question, may only partially overlap). However, studies that compared IPD‐MA and AD‐MA from independent sets of studies without any overlap (e.g. to compare results from studies providing IPD with those studies that did not provide IPD) were excluded. We excluded comparisons of network meta‐analysis (NMA) and those in which meta‐analysis methods had been used for the synthesis of data from a single multi‐centre randomised trial.
Types of outcome measures
For each study, we summarised the relevant effect measure estimate and corresponding precision for the IPD‐MA and the AD‐MA. Any type of outcome measure was included.
Search methods for identification of studies
Up to 7 January 2016, a variety of searches were undertaken. An electronic search of the Cochrane Library (including Cochrane Database of Systematic Reviews, Database of Abstracts of Reviews of Effectiveness, CENTRAL, Cochrane Methodology Register, HTA database, NHS Economic Evaluations Database), MEDLINE, and Embase was undertaken in June 2006 followed by updated searches in May 2009 and January 2016 (Appendix 1). Potentially relevant articles that were known to any of the review authors were also added to the list of records to be assessed. Reference lists of retrieved articles (Horsley 2011) and an unpublished review by Mukhtar 2008 were cross‐checked.
Data collection and analysis
See Contributions of authors for details of authors participating in screening, data extraction and quality assessment.
The title and abstract of identified studies were initially screened for inclusion or exclusion by two review authors. Records judged to be potentially relevant were discussed and we erred on the side of inclusion if doubt remained after this discussion. Full‐text publications were retrieved for those identified as eligible or potentially eligible and each was assessed independently by two review authors with any disagreements resolved by involving a third author.
Studies identified as eligible were distributed amongst pairs of review authors and data for every study were extracted independently by the two review authors in each pair. Any disagreements were resolved by involving a third author. The data were extracted using an online data extraction form (Appendix 2) with data stored in an Excel spreadsheet. We did not systematically contact the authors of published empirical comparisons.
A ‘quality’ assessment was undertaken by two review authors independently with disagreements resolved by involving a third author. In the context of this review, quality was measured in terms of the fairness of the comparison between IPD‐MA and AD‐MA. For example, a study which compares IPD‐MA and AD‐MA that were based on very different inclusion criteria might be expected to yield a larger discrepancy in results as compared to a study which compares IPD‐MA and AD‐MA using similar inclusion criteria. Similarly, a study which compares IPD‐MA and AD‐MA undertaken by the same researchers, using the same outcome definitions might be expected to yield smaller discrepancies between IPD‐MA and AD‐MA than studies in which the IPD‐MA and AD‐MA being compared had been done by different researchers using different outcome definitions.
The following questions were considered in the assessment of each included study.
In your opinion, are the inclusion criteria for the IPD‐MA and AD‐MA similar? Yes, No, Unclear
Would you describe the quality of this study as: A = No important flaws; B = Possibly important flaws; C = Major flaws?
Was the comparison of IPD‐MA and AD‐MA a main aim of the study? Yes, No, Unclear
Were the IPD‐MA and AD‐MA done by independent researchers? Yes, No, Unclear
Were the same outcome definitions used for the IPD‐MA and AD‐MA? Yes, No, Unclear
Data have been summarised descriptively for comparisons where an estimate of effect measure (such as the treatment main effect, interaction term, or subgroup treatment effect) and corresponding precision have been provided both for IPD‐MA and for AD‐MA in the study report.
Comparisons have been classified according to whether identical effect measures (yes/no) and identical trials and participants (yes/no) had been used in the IPD‐MA and the AD‐MA. Comparisons were also classified according to whether the analyses were undertaken to explore the main effect of treatment, or to explore a potential treatment effect modifier (for example, by fitting a meta‐regression model with AD or by fitting a regression model including an interaction between treatment and covariate with IPD).
If a study report presented an IPD‐MA compared to multiple AD‐MAs for the same comparison (e.g. IPD‐MA of overall survival summarised with hazard ratio (HR) compared to multiple AD‐MAs summarised with risk ratios at different time points), each comparison has been included to reflect alternative scenarios that may be considered for the AD‐MA. Similarly, if a study report presented comparisons for multiple clinical outcomes, we attempted to extract data for all comparisons where this was possible.
Following the approach described by Michiels 2005, ratio effect measures (hazard ratio (HR), risk ratio (RR), rate ratio, odds ratio (OR)) were transformed to a standardised scale (z scores) by dividing the logarithm of the ratio by the respective standard error. Similarly, weighted mean differences were transformed to a standardised scale by dividing the difference by the respective standard error. Scatterplots of these standardised effects of IPD‐MA versus AD‐MA were generated to allow visual comparisons, but bearing in mind the clustering of comparisons that originate from the same study. For each comparison, the statistical significance (at the 5% two‐sided level) of an IPD‐MA was compared to that for the corresponding AD‐MA and we calculated the number of discrepancies. Bland‐Altman agreement statistics (mean of the differences (IPD‐MA ‐ AD‐MA) and limits of agreement) between IPD‐MA and AD‐MA z scores, log ratio effect measures, and standard errors (of log ratio effects) were calculated for main effect analyses and treatment effect modifier analyses separately. Sensitivity analyses were undertaken to explore the effect of clustering of comparisons from within the same study. For each analysis we selected at random (with replacement) one comparison from each study, calculated agreement statistics, repeated the process 250 times and calculated the mean and standard deviation across the 250 samples.
Results
Description of studies
The PRISMA flow diagram is shown in Figure 1. From a total of 9330 articles retrieved by our searches, we found 39 studies that met the eligibility criteria and extracted an effect estimate (e.g. odds ratio (OR), hazard ratio (HR)) and measure of precision (e.g. 95% confidence interval (CI), standard error (SE)) for 190 empirical comparisons of IPD‐MA and AD‐MA. Twenty studies that mentioned comparing IPD‐AD with AD‐MA but failed to present sufficient numerical data for their comparison were deemed ineligible.
1.
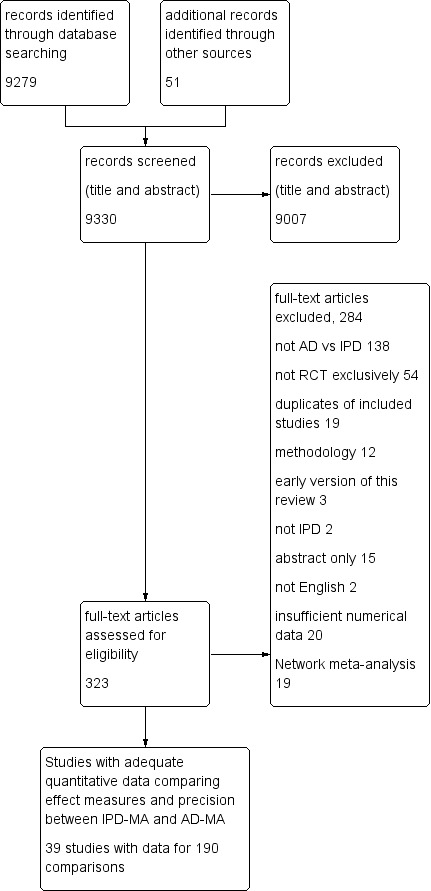
Study flow diagram.
Characteristics of the 39 included studies are shown in Characteristics of included studies. Studies were published as full‐text journal articles (34 (87%)), abstracts (four (10%)), or a letter (one (3%)). All but one of the studies were published in English language journals or conference proceedings. The publication date of studies ranged between 1992 and 2015 with the highest numbers published in the late 1990s and early 2000s (Figure 2). Empirical comparisons were made using randomised trials from a variety of clinical areas. These included oncology (14 (36%)), cardiovascular disease (six (15%)), mixed populations (five (13%)), infectious disease (three (8%)), neurology (three (8%)), nephrology (three (5%)), critical care (two (5%)), rheumatology (one (3%)), gynaecology/obstetrics (one (3%)), and respiratory disease (one (3%)). The outcomes examined in the meta‐analyses also varied, with a large number of studies (26 (67%)) including mortality‐related outcomes. The most common type of outcome data was time‐to‐event, which was included in 23 (59%) studies. Eight of these studies had maintained the time‐to‐event nature of data for the comparison of IPD‐MA and AD‐MA (two of these also included a binary outcome), whilst 15 studies treated the data as binary data for the AD‐MA. The remaining studies had included binary data (nine (23%)), continuous data (six (15%)) and count data (one (3%)) for the outcome measures compared between IPD‐MA and AD‐MA.
2.
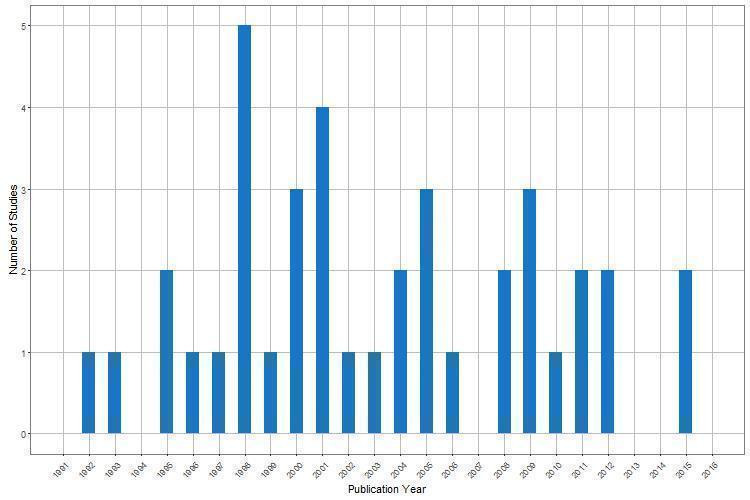
Year of publication for 39 included studies comparing IPD‐MA and AD‐MA
The method of analysis used in the IPD‐MAs varied (Table 1). The most common approach, reflecting the most common type of data analysed, was the stratified log‐rank analysis (11 (28%) studies) and Cox regression model (seven (18%) studies) for time‐to‐event outcomes. Four (10%) studies used a logistic regression model, two (5%) studies used a multilevel Bayesian model, one (3%) study used a longitudinal model and three (8%) studies used continuous outcomes regression models. The method of analysis was unclear in six (15%) studies and five (13%) further studies provided some limited information about method of analysis (e.g. mentioning the use of a “random‐effects model”, or “two‐stage approach”).
1. Methods and conclusions.
| Study | IPD‐MA methods | AD‐MA methods | Main treatment effect, subgroup analyses, both | Main conclusions of the study |
| Berlin 2002 | Logistic regression models, unadjusted and adjusted, with fixed effects and including treatment by covariate interaction terms. | 1) fixed‐effects logistic regression with AD at the level of treatment arm; 2) weighted least‐squares linear regression with the log‐odds ratio and log hazard ratio as the study‐level outcome variable; 3) hierarchical bayesian analysis including random‐effects. For all these analyses the same covariates studied in the IPD analysis were included. |
Subgroup | The IPD analysis revealed a clinically important and statistically significant difference between the effect of treatment among patients whose PRA was >= 20 per cent (compared to patients with PRA < 20 per cent) which the AD analyses failed to identify. |
| Best 2000 | Stratified log‐rank analysis (fixed‐effect) | Risk of death compared at 6, 12, 18, 24 months and the risk of disease progression was compared at 3, 6, 9 and 12 months. | Both | The results of AD and IPD meta‐analyses were broadly similar even if IPD analysis was more reliable and informative. |
| Beveridge 2015 | Two‐stage analysis. For each study, the mean BP values for each group at the final follow‐up were calculated and adjusted for baseline values using analysis of covariance These values were combined using weighted least‐squares random‐effects models. |
Weighted squares method with random‐effects models. For each analysis at the trial level, the mean change from baseline to the last follow‐up reported was compared between groups. |
Both | Results were consistent between the trial‐level and IPD analyses. |
| Brouwer 2009 | Log‐rank tests and Cox proportional hazard models were used to assess outcomes when controlling for relevant baseline characteristics. We included a variable named ‘trial’ to take into account differences between studies/trials such as supplemented dose into account. |
Random‐effects model on hazard ratios (HRs) from the individual studies. | Both | Both our pooled analysis and our meta‐analysis showed that fish oil was not efficacious in patients who entered the studies with a VT. |
| Clarke 1998 | Log‐rank methods (providing odds ratio) and survival curve. | Fixed‐effect model (pooling odds ratios). | Main | The IPD review provides a larger, more significant estimate of treatment effect than would have been found with a review based solely on published data. An IPD review can produce very important results that might not have been obtainable in any other way. Without the ability to analyse data on each of the women who took part in these randomised trials and to update this with follow‐up information collected after the results of some of the trials had been published, the important findings would not have come to light. |
| D'Amico 1998 | Odds ratio, stratified by prognostic factors, were calculated with the fixed‐effect model. | Peto odds ratio (fixed‐effect). | Both | Firstly, this allowed a comprehensive quality check of the data, which, by and large, confirmed the validity of the aggregate analysis. Secondly, the availability of data on individual patients permitted the identification of subgroups more likely to benefit from treatment. |
| Duchateau 2001 | Stratified log‐rank test and Cox regression (hazard ratio); to allow at comparing with the AD meta‐analysis, also odds ratio (at 2 and 5 years) and Mantel Haenszel test. | Odds ratio (at 2 and 5 years) and Mantel Haenszel test. | Main | The IPD and AD results differed substantially: although both the meta‐analyses showed a significant advantage for chemotherapy + loco‐regional treatment versus loco‐regional treatment alone, the size of the treatment effect varied considerably. |
| Fortin 1995 | 1) A 'narrow' analysis on IPD restricted to patients from the studies included in the AD meta‐analysis for each outcome measure, by a mixed‐model analysis of variance with fixed‐effect for treatment and random‐effects for study; 2) A 'broad validation' analysis including IPD from all 10 studies that met the inclusion criteria, studying all the clinical and demographic variables for which data were supplied by primary authors, and using different analytic approaches and more uniform outcome measures (for this second analysis The sites were treated as fixed‐effect). |
Pooled RD with 95% CI was calculated using DerSimonian and Laird method. | Main | The 'narrow' IPD analysis confirmed the results of the AD meta‐analysis on the efficacy of the fish oil treatment to improve the tender joints count and the morning stiffness (no significant effect was found for the other outcome measures); these main results held up also in the broader IPD analysis. The broader IPD analysis allowed exploring the effects of a variety of covariates. |
| Franzosi 1997 | Unclear. | Unclear | Main | IPD meta‐analysis remain the gold standard, mainly when continuous data are used and time‐dependent analyses are the main end point. |
| Ioannidis 1999 | Study stratified proportional hazard models | Pooled odds ratios | Main | In the absence of extensive empirical evidence in the relative validity of meta‐analysis of published literature and meta analysis of IPD, strong statements about their relative importance may be premature. |
| Jeng 1995 | Fixed‐efect and random‐effects methods to obtain a pooled relative live birth ratio, adjusted for maternal age (<3 5 years or others) and number of previous miscarriages (the authors did not explain whether they adjusted for study effect). | Fixed‐effect and random‐effects methods to obtain a pooled relative live birth ratio. | Both | The IPD and AD meta‐analyses provided different results (in particular, AD consistently yielded greater estimates of a treatment benefit). |
| Jones 2009 | Longitudinal model with time as a factor and as a continuous variable, assuming fixed treatment effects across studies. Two approaches were undertaken. The one‐step approach simultaneously models the IPD from all of the studies. The two‐step approach first fits a model to the IPD from each study separately, and then the study parameter estimates are combined using multivariate meta‐analysis. | Study parameter estimates across studies are combined using a multivariate meta‐analysis model. taking a simplistic assumption of common correlation between observations across studies, treatment and time points. a sensitivity analysis was also undertaken on the assumption of correlations values of 0.8, 0.4 and 0 . | Main | It is preferable to obtain IPD from all studies to correctly account for the correlation between repeated observations. When IPD are not available, the ideal aggregate data are model‐based estimates of treatment difference and their variance and covariance estimates. If covariance estimates are not available, sensitivity analyses should be undertaken to investigate the robustness of the results to different amounts of correlation. |
| Kim 2010 | Meta‐analysis was performed using the Mantel‐Haenszel adjusted risk difference method (fixed‐effect). | Meta‐analysis was performed using the Mantel‐Haenszel adjusted risk difference method (fixed‐effect). | Main | This finding was consistent in both trial‐level and patient‐level analyses. |
| Koopman 2008 | Two‐stage meta‐analysis of IPD. One‐stage meta‐analysis of IPD including covariate for study. | Unclear | Subgroup | Conventional meta‐analyses do not allow proper subgroup analyses, whereas IPD meta‐analyses produce more accurate subgroup effects. Conventional meta‐analysis showed larger and smaller subgroup effect estimates and wider confidence intervals than both one‐ and two‐stage IPD meta‐analyses. |
| le Chevalier 1996 | Unclear. | Unclear | Both | The IPD meta‐analysis shows that the advantage of chemotherapy over best supportive care depends on the chemotherapy regimen used. |
| Legg 2003 | Unclear. | Unclear | Main | IPD resulted in more precise estimates of effect with greater statistical significance and less statistical heterogeneity. |
| Lindley 2005 | Logistic regression. | Peto odds ratio | Both | Results on timing influence found in the IPD meta‐analyses had already been suggested by the Cochrane AD meta‐analysis. |
| Lukka 2006 | Unclear. | Unclear | Both | The best evidence came from the largest meta‐analysis based on IPD |
| Michiels 2005 | Stratified log rank test and the overall pooled HR (for each trial, HR and variance were derived from the log rank statistic, then pooled logHR were obtained). | 1) for each trial, logOR and its variance were estimated using Yusuf et al. method; OR of survival at 1‐year was calculated 2) a pooled ratio of median survival times (MR) were calculated by estimating a pooled logMR weighted for variances (inversely proportional); variance for logMR for each trial was estimated using 3 different methods. | Main | Both OR and MR method resulted in under‐ and overestimation of the treatment effect and major loss of statistical power. Furthermore, in 20% of trials included, the log(MR) had an opposite sign to the log(HR). OR method did not perform much better than the MR ratio method when translated into absolute survival differences to compare them with HRs. |
| Myeloma 1998 | Stratified log‐rank analysis | Unclear | Both | There is no good evidence of any difference between the results of trials with IPD and those for which published data were used. |
| Pignon 1992 | Stratified log rank analyses | Unclear | Both | Similar results obtained. |
| Rejnmark 2012 | Unconditional logistic regression incorporating age and sex, which we expected a priori to contribute to variation in mortality Analysis on mortality was performed using a stratified Cox regression model, with the clinical study as stratum, We added treatment allocation and interaction terms to this model too. |
Unclear | Both | Findings from IPD‐MA were supported by a trial level meta‐analysis but there were differences when compared to previously conducted trial level meta‐analyses. |
| Rothwell 2011 | Log‐rank test (stratified by trial) and Cox proportional hazards model stratified by trial. | Unclear | Main | IPD are essential to determine the time course of effects on risk of cancer and other outcomes during trials. Crude meta‐analyses of overall numbers of events from trials of different lengths without stratification by period of follow‐up will be of limited value. |
| Saillourglenisson 2000 | Stratified Hazard Ratio was calculated. | Odds Ratio | Both | AD and IPD meta‐analysis obtained very similar results, demonstrating the absence of a deleterious effect of dapsone on survival, although IPD meta‐analysis was performed only on a subset of trials. |
| Schmid 2004 | A multilevel Bayesian model | Meta‐regression (the multilevel model based on IPD and the meta‐regression based on AD were also compared to a third approach based on meta‐analysis of interaction effects computed by least‐squares regression in each study and then aggregated by meta‐analysis using a non‐informative prior for the distribution of the random interaction effects). | Subgroup | Neither meta‐regression nor combining of study interaction effects by random effects pooling consistently approximated the multilevel model. |
| Shepperd 2009 | Fixed‐effect model. Where at least one event was reported in both study groups in a trial, we used Cox regression models to calculate the log hazard ratio and its standard error for mortality and readmission separately for each data set. We combined the calculated log hazard ratios using fixed‐effect inverse variance meta‐analysis. |
Peto odds ratio method | Main | |
| Spooner 1998 | Weighted mean difference from random‐effects model | Weighted mean difference from random‐effects model. | Both | The results of the IPD analysis did not differ in important ways from the results of the traditional Cochrane meta‐analysis. |
| Stewart 1993 | A stratified by trial Cox regression model (fixed‐effect). In order to compare IPD results to AD results, the HR were translated to an absolute survival estimate at 30 months. | The proportion of patients surviving at a specific time point for each study was usually estimated from the published survival curves (HR were mostly not presented in the published papers. Being not binomially distributed, these data were transformed by adjusting (reducing) the numbers at risk at the beginning of the trial. The estimates for each trial obtained in this way were pooled by the modified Mantel‐Haensezel method (OR). In order to compare IPD results to AD results, the OR were translated to an absolute survival estimate at 30 months. For the additional analyses made in order to investigate the effect of potential sources of bias in an AD MA, the OR were calculated using the IPD from AOCTG database and then pooled. | Main | The AD‐MA gave a result of greater statistical significance and an estimate of absolute treatment effect 3 times as large as the IPD‐MA. |
| Szczech 1998 | Using data from the published reports, we calculated the rate ratios of allograft failure by use of a discrete‐time version of the proportional hazards model for both the subset of studies for which individual patient‐level data were available and the subset for which data were unavailable. | Using data from the published reports, we calculated the rate ratios of allograft failure by use of a discrete‐time version of the proportional hazards model for both the subset of studies for which individual patient‐level data were available and the subset for which data were unavailable. | Main | Even when follow‐up is incomplete, individual patient‐level data can be analysed with survival analysis techniques that yield estimates of true rates of failure over time rather than less informative estimates of risk. In addition, by using individual patient‐level data extended beyond the follow‐up in the published literature, meta‐analyses such as this one can evaluate long‐term survival. We were able to evaluate potential predictors of allograft survival, such as recipient ethnicity and panel reactive antibody levels; this was not possible in our previous meta‐analysis, when used published data. Finally, use of individual patient‐level data allowed us to perform subgroup analyses that were not possible by using original published analyses. |
| Teramukai 2004 | Model 1: Cox regression model, stratified by trial (fixed effect), including interaction term 'treatment x stage'. Model 2: Fixed‐effects exponential risk model where the survival outcome was changed to a binary outcome (alive or dead at the end of the study); interaction term 'treatment x stage' was included | Meta‐regression with risk ratio (RR) as dependent variable (only graphical results are shown for AD‐MA). | Subgroup | Meta‐regression gave a greater P value for interaction term than the IPD‐MA (both the MA gave non statistically significant results). When excluding two studies (including only stage I patients), the direction of the effect found by meta‐regression was inverted. |
| Thompson 2001 | Bayesian two‐ and three‐level models. | They contrast classical (REML) and bayesian analysis to pool the absolute risk difference in each (sub)trial, either two‐ or three‐level models. Meta‐regression for the effect of the time delay. | Both | AD meta‐analyses (classical and bayesian) and IPD meta‐analysis gave very similar results. It is preferable to model individual participant outcome data directly rather than summary statistics to avoid the assumptions that have to be made regarding the summary statistics (of normality and known variance). Furthermore, individual participant level covariates can be introduced to study potential treatment interactions. |
| Tierney 2001 | Unclear | Unclear | Main | Where events happen quickly, HRs from published data and IPD were very similar, although the published data were less convincing. However, where events happen over a prolonged period, the HR of the published data was a poorer approximation of both its IPD equivalent and the full IPD analysis. |
| Tonia 2011 | Unclear | Unclear | Main | This was a review of meta‐analyses. With IPD the limitations of literature‐based meta‐analyses, that have to analyse data as reported in the literature with inconsistencies across studies, can be overcome. |
| Tudur 2001 | Stratified logrank analysis. | Stratified logrank analysis. | Both | AD analysis can be useful in some circumstances. All analyses agreed in overall conclusion and suggested that risk of death was significantly reduced in chemotherapy group. estimates of heterogeneity differ between IPD and AD. |
| Tudur Smith 2005 | Fixed‐effect and random‐effects Cox regression model stratified by trial including covariates. | AD were generated from IPD which was then used to undertake fixed‐effect and random‐effects. meta‐regression | Both | The availability of IPD allowed a thorough investigation into the main effects of each covariate which was not possible using meta‐regression of AD. Age as a potential cause of heterogeneity is detected by both AD and IPD regression models. Time from first ever seizure to randomisation is only identified by some AD models. A more thorough explanation of heterogeneity is obtained from the model using IPD. A pragmatic comparison of results using IPD vs. results using extracted AD was not possible for this example as sufficient data were unavailable directly from trial reports. For the epilepsy example, the clinical interpretation obtained from the final Cox regression models would not have been discovered without IPD. For the empirical comparison presented in the current paper involving a small number of trials, but still reflective of many meta‐analyses in practice, the results suggest that meta‐regression using AD can be accurate if there is evidence for a within study treatment by covariate interaction and sufficient between trial variation for the aggregate value of the covariate. Departures from this condition could mean that meta‐regression results using AD are unreliable. IPD should be used whenever possible to reliably study patient characteristics and investigate heterogeneity. This recommendation is especially important when the number of trials in the meta‐analysis is small and AD approaches are likely to become increasingly more uncertain. Furthermore, if time‐to‐event outcomes are of interest, IPD can be extremely valuable as a result of limitations reporting appropriate summary data. |
| Turner 2000 | Multilevel modelling for binary outcome (based on logistic modelling), with fixed trial effects (using standard logistic regression for fixed treatment effects and additional iterative estimation procedures for random treatment effects) and random trial effects. | Standard methods (fixed‐effect and random‐effects) and multilevel modelling methods (ML and REML). | Main | For the first example, "The fixed and random effects estimates from individual data methods all differed noticeably from the corresponding summary data estimates; each of the latter indicates a smaller treatment effect than its counterpart". For the second example: "differences between summary and IP data estimates of the logOR and between‐trial variance were generally smaller than in the first example". |
| Vansteenkiste 2012 | Cox proportional hazards models stratified by study. |
Random‐effects | Both | By including IPD from both published and unpublished sources, the meta‐analysis study avoids some of these limitations (publication bias). |
| Walwyn 2015 | Fixed‐effect and random effects models accounting for clustering. | Fixed‐effect and random‐effects models accounting for clustering. | Main | Fitting fixed‐effect and random‐effects meta‐analysis models to trials of counselling in primary care, adopting summary‐data and IPD approaches and allowing for these effects, had minimal impact on the pooled estimate and its standard error. Collection of the IPD is made attractive by the potential of meta‐regression analyses for exploring trial‐level, therapist‐level and patient‐level predictors of the treatment effect and of the random‐effects. |
| Williamson 2000 | Stratified log rank analyses | Extracting estimates of the log hazard ratio from publications and combined using stratified log rank analysis. | Main | More empirical data are needed to answer the question whether the extra investment needed for IPD is worthwhile. |
Abbreviations: AD: Aggregate data, AD‐MA: Aggregate data meta‐analysis, AOCTG: Advanced Ovarian Cancer Trialists Group, BP: Blood pressure, IPD: IPD: Individual participant data, PRA: panel reactive antibodies, RD: risk difference, REML: restricted maximum likelihood, VT: ventricular tachycardia
A median of 4 (inter‐quartile range (IQR): 2 to 6) comparisons were made per study. Identical effect measures had been used in the IPD‐MA and corresponding AD‐MA (e.g. an HR was used in both the IPD‐MA and the corresponding AD‐MA) in 115 (61%) comparisons: 59 (31%) based on identical trials and participants, and 56 (29%) based on different data. Different effect measures had been used in the IPD‐MA and corresponding AD‐MA (e.g. an HR had been used for the IPD‐MA and an OR estimated at a specific time‐point in the AD‐MA) in 75 (39%) comparisons: 36 (19%) based on identical trials and participants, and 39 (21%) based on different data. The median number of trials and participants were 6 (IQR: 4 to 11) and 1225 (542 to 2641), respectively for the IPD‐MAs and 7 (4 to 11) and 1225 (705 to 2541) for the AD‐MAs. The majority of IPD‐MAs were based on an equal (103 (54%); 93 (49%)) or a greater (37 (19%); 50 (26%)) number of trials and participants respectively, compared to the corresponding AD‐MAs (Figure 3). One hundred and forty‐four (76%) comparisons were made on the main treatment effect meta‐analysis and 46 (24%) were made using results from analyses to explore treatment effect modifiers.
3.
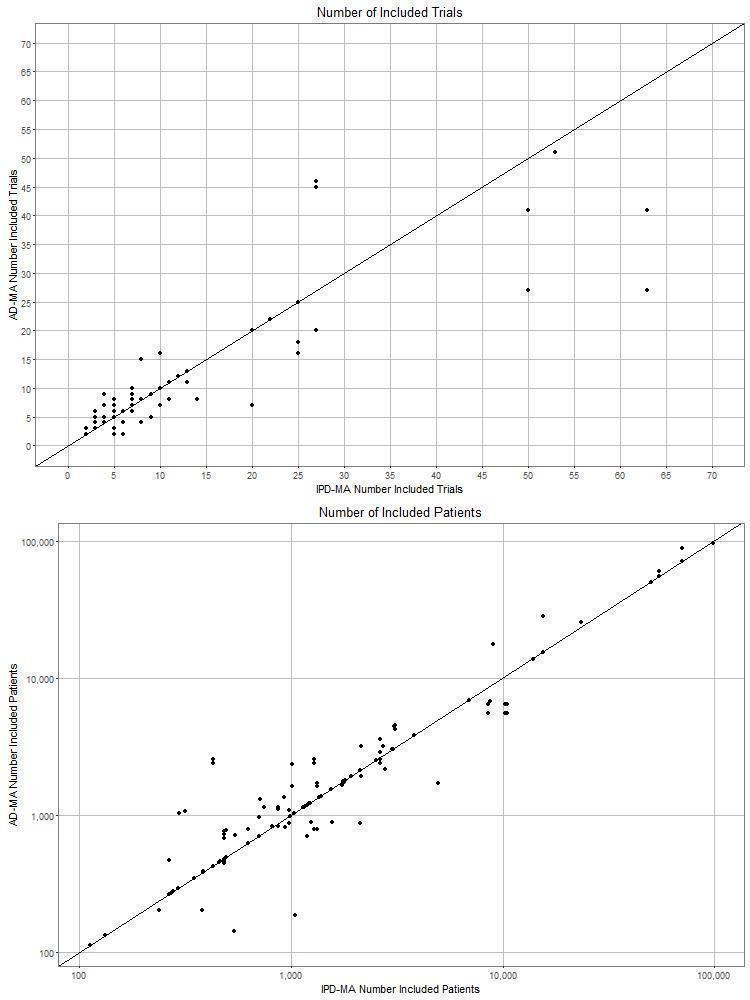
Number of trials and participants in each empirical comparison of IPD‐MA and AD‐MA
Risk of bias in included studies
The assessment of quality in individual studies is summarised in Table 2. The comparison of IPD‐MA versus AD‐MA was the main objective of the publication in 22 (56%) studies. We classified the quality of studies as either ‘no important flaws’ (29 (74%) studies) or ‘possibly important flaws’ (10 (26%) studies). The latter was due to insufficient information provided in abstracts, or lack of detail regarding the statistical methods for undertaking the IPD‐MA and AD‐MA. The IPD‐MA and AD‐MA were undertaken by independent groups in 12 (31%) studies, or by the same group in 24 (62%) studies, with three (8%) studies unclear. The inclusion criteria were similar for the IPD‐MA and AD‐MA in 36 (92%) studies, and similar outcome definitions had been used for the IPD‐MA and AD‐MA in 36 (92%) studies, albeit with some studies using different approaches to analysis and different treatment effect measures. Insufficient details were provided to judge the similarity of inclusion criteria and outcome definitions in two (5%) studies (Franzosi 1997; Legg 2003). For 18 (46%) studies, the empirical comparison of IPD‐MA and AD‐MA had focused on the main effect of treatment, whereas four (10%) studies had compared results of analyses to explore potential treatment effect modifiers and 17 (44%) studies had included comparisons of both main effects and effect modifiers (see Table 1).
2. Summary of quality.
| Study |
Inclusion criteria similar for IPD‐MA and AD‐MA? |
Study quality* |
Comparison of IPD‐MA and AD‐MA a main aim of the study? |
IPD‐MA and AD‐MA done by independent researchers? |
Same outcome definitions for IPD‐MA and AD‐MA? |
| Berlin 2002 | Yes | A | Yes | No | Yes |
| Best 2000 | Yes | A | Yes | No | Yes |
| Beveridge 2015 | Yes | A | No | No | Yes |
| Brouwer 2009 | Yes | B (Insufficient information) | No | No | Yes |
| Clarke 1998 | Yes | A | Yes | No | Yes |
| D'Amico 1998 | Yes | A | Yes | No | Yes |
| Duchateau 2001 | Yes | A | Yes | No | Yes |
| Fortin 1995 | Yes | A | Yes | No | Yes |
| Franzosi 1997 | Unclear | B (Insufficient information) | Yes | Unclear | Unclear |
| Ioannidis 1999 | Yes | A | No | Yes | Yes |
| Jeng 1995 | Yes | A | Yes | No | Yes |
| Jones 2009 | Yes | A | Yes | No | Yes |
| Kim 2010 | Yes | A | No | No | Yes |
| Koopman 2008 | Yes | A | Yes | Yes | Yes |
| le Chevalier 1996 | Yes | B (Statistical methods unclear) | Yes | Yes | Yes |
| Legg 2003 | Unclear | B (Insufficient information) | Yes | Yes | Unclear |
| Lindley 2005 | Yes | A | No | No | Yes |
| Lukka 2006 | Yes | B (Statistical methods unclear) | No | Yes | Yes |
| Michiels 2005 | Yes | A | Yes | No | Yes |
| Myeloma 1998 | Yes | A | No | Unclear | Yes |
| Pignon 1992 | Yes | A | Yes | Yes | Yes |
| Rejnmark 2012 | Yes | A | No | Yes | Yes |
| Rothwell 2011 | Yes | A | No | No | Yes |
| Saillourglenisson 2000 | Yes | A | No | No | Yes |
| Schmid 2004 | Yes | A | Yes | No | Yes |
| Shepperd 2009 | Yes | A | No | No | Yes |
| Spooner 1998 | Yes | B (Insufficient information) | Yes | Yes | Yes |
| Stewart 1993 | Yes | A | Yes | Unclear | Yes |
| Szczech 1998 | Yes | A | No | No | Yes |
| Teramukai 2004 | Yes | A | Yes | No | Yes |
| Thompson 2001 | Yes | A | Yes | Yes | Yes |
| Tierney 2001 | Yes | B (Insufficient information) | Yes | Yes | Yes |
| Tonia 2011 | No | B (Insufficient information) | No | Yes | No |
| Tudur 2001 | Yes | A | No | No | Yes |
| Tudur Smith 2005 | Yes | A | Yes | No | Yes |
| Turner 2000 | Yes | A | Yes | No | Yes |
| Vansteenkiste 2012 | Yes | B (Insufficient information) | No | No | Yes |
| Walwyn 2015 | Yes | B (Insufficient information) | No | No | Yes |
| Williamson 2000 | Yes | A | No | Yes | Yes |
* A = No important flaws; B = Possibly important flaws; C = Major flaws
Abbreviations: AD: Aggregate data, AD‐MA: Aggregate data meta‐analysis, IPD: Individual participant data, IPD‐MA: Individual participant data meta‐analysis
Effect of methods
Summary of numerical comparisons
There is variability in the agreement between the standardised effects (computed for comparisons where effect measures were summarised as hazard ratio (HR), odds ratio (OR), risk ratio (RR), rate ratio and difference in means) for 174 IPD‐MA and AD‐MA comparisons, as shown by the scatter of points around the line of equality in Figure 4 and Figure 5. Missing data prevented calculation of standardised effects for 16 comparisons.
4.
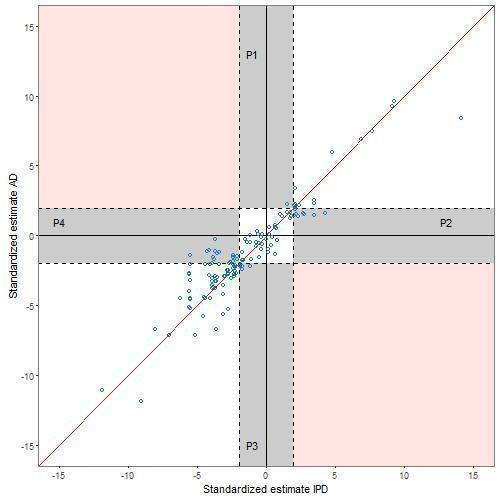
Comparison of standardised effects (z scores ‐ main effect analyses)
5.
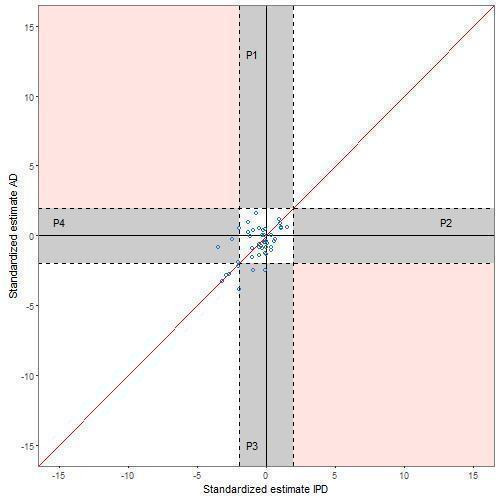
Comparison of standardised effects (z scores ‐ interaction effect analyses)
Across all 190 comparisons, there is agreement on statistical significance (assessed at the 5% level) between the IPD‐MA and AD‐MA for 152 (80%) comparisons (Table 3). For example, Duchateau 2001 present an IPD‐MA of trials of chemotherapy for patients with head and neck cancer which was based on 8523 patients (5201 events) with HR of 0.88 (95% CI: 0.83 to 0.93) compared to an AD‐MA based on 5536 patients (3771 events) with a five‐year mortality OR of 0.78 (95% CI: 0.70 to 0.87). For 23 comparisons with agreement in statistical significance in which both IPD‐MA and AD‐MA were not statistically significant, there is disagreement in the direction of effect. For example, the Myeloma 1998 IPD‐MA based on 20 trials with 4930 patients estimated an OR of 0.98 (95% CI: 0.92 to 1.04) with an AD‐MA estimate of 1.03 (95% CI: 0.83 to 1.25) based on seven trials with 1703 patients.
3. Comparison of statistical significance (at 5% two‐sided level) of IPD‐MA and AD‐MA across 190 comparisons (main effect and effect modifier analyses).
| AD‐MA | ||||
| Not significant | Significant* | Total | ||
| IPD‐MA | Not significant | 77 (41) | 10 (5) | 87 (46) |
| Significant* | 28 (15) | 75 (39) | 103 (54) | |
| Total | 105 (55) | 85 (45) | 190 (100) | |
Abbreviations: AD: Aggregate data, AD‐MA: Aggregate data meta‐analysis, IPD: Individual participant data, IPD‐MA: Individual participant data meta‐analysis
Table entries are number (%) of comparisons.
*Statistical significance determined using standardised effect estimates for 174 comparisons where effect estimates are Hazard Ratio, Risk Ratio, Odds Ratio, Rate Ratio and Mean Difference (plotted in Figure 4 and Figure 5), and using the data as presented for the remaining 16 comparisons (e.g. a study presented results as a regression coefficient with P value).
There is disagreement on statistical significance for 38 (20%) comparisons. For example, Michiels 2005 estimated the HR from an IPD‐MA to be 0.88 (95% CI: 0.78 to 0.99) whereas the OR from the AD‐MA based on identical data was estimated to be 0.84 (95% CI: 0.67 to 1.06). More of these comparisons have a statistically significant IPD‐MA and non‐significant AD‐MA (28 (15%)) compared with 10 (5%) comparisons with a statistically significant AD‐MA and non‐significant IPD‐MA. Alternative graphs were produced (not shown) by including one randomly selected comparison per study to remove the potential correlation caused by including multiple comparisons from within the same study. The patterns were similar. This pattern of disagreement between IPD‐MA and AD‐MA is consistent when considering the main effect analyses (Table 4; Figure 4). However, for the treatment effect modifier analyses, although only based on 46 comparisons, the percentage of comparisons with disagreement in statistical significance is similarly distributed (Table 4;Figure 5). The breakdown of data according to whether or not analyses were based on identical trials and participants, or identical effect measures (Table 5; Figure 6; Figure 7) suggests that conclusions from IPD‐MA and AD‐MA can still differ even when based on identical trials, participants (but not necessarily identical follow‐up) and treatment effect measures (top section of Table 5).
4. Comparison of statistical significance (at 5% two‐sided level) of IPD‐MA and AD‐MA across 190 comparisons according to type of analysis.
| AD‐MA | ||||
| Main effect analysis | Not significant | Significant* | Total | |
| IPD‐MA | Not significant | 42 (29) | 6 (4) | 48 (33) |
| Significant* | 25 (17) | 71 (49) | 96 (67) | |
| Total | 67 (47) | 77 (53) | 144 (100) | |
| Treatment effect modifier analysis | Not significant | Significant* | Total | |
| IPD‐MA | Not significant | 35 (76) | 4 (9) | 39 (85) |
| Significant* | 3 (7) | 4 (9) | 7 (16) | |
| Total | 38 (83) | 8 (17) | 46 (100) | |
Abbreviations: AD: Aggregate data, AD‐MA: Aggregate data meta‐analysis, IPD: Individual participant data, IPD‐MA: Individual participant data meta‐analysis
Table entries are number (%) of comparisons.
*Statistical significance determined using standardised effect estimates for 174 comparisons where effect estimates are Hazard Ratio, Risk Ratio, Odds Ratio, Rate Ratio and Mean Difference (plotted in Figure 4 and Figure 5), and using the data as presented for the remaining 16 comparisons (e.g. a study presented results as a regression coefficient with P value).
5. Comparison of significance (at 5% two‐sided level) of IPD‐MA and AD‐MA across 174 comparisons according to similarity of data and treatment effect type (main effect and effect modifier analyses).
| AD‐MA | ||||
| Same trials and patients, same treatment effect | Not significant | Significant* | Total | |
| IPD‐MA | Not significant | 28 (47) | 5 (8) | 33 (56) |
| Significant* | 4 (7) | 22 (37) | 26 (44) | |
| Total | 32 (54) | 27 (46) | 59 (100) | |
| Same trials and patients, different treatment effect | ||||
| IPD‐MA | Not significant | 8 (22) | 1 (3) | 9 (25) |
| Significant* | 10 (28) | 17 (47) | 27 (75) | |
| Total | 18 (50) | 18 (50) | 36 (100) | |
| Different trials and patients, same treatment effect | ||||
| IPD‐MA | Not significant | 30 (54) | 3 (5) | 33 (59) |
| Significant* | 9 (16) | 14 (25) | 23 (41) | |
| Total | 39 (70) | 17 (30) | 56 (100) | |
| Different trials and patients, different treatment effect | ||||
| IPD‐MA | Not significant | 11 (28) | 1 (3) | 12 (31) |
| Significant* | 5 (13) | 22 (56) | 27 (69) | |
| Total | 16 (41) | 23 (59) | 39 (100) | |
Abbreviations: AD: Aggregate data, AD‐MA: Aggregate data meta‐analysis, IPD: Individual participant data, IPD‐MA: Individual participant data meta‐analysis
Table entries are number (%) of comparisons.
*16 comparisons with insufficient numerical data regarding number of patients have been excluded from this table
6.
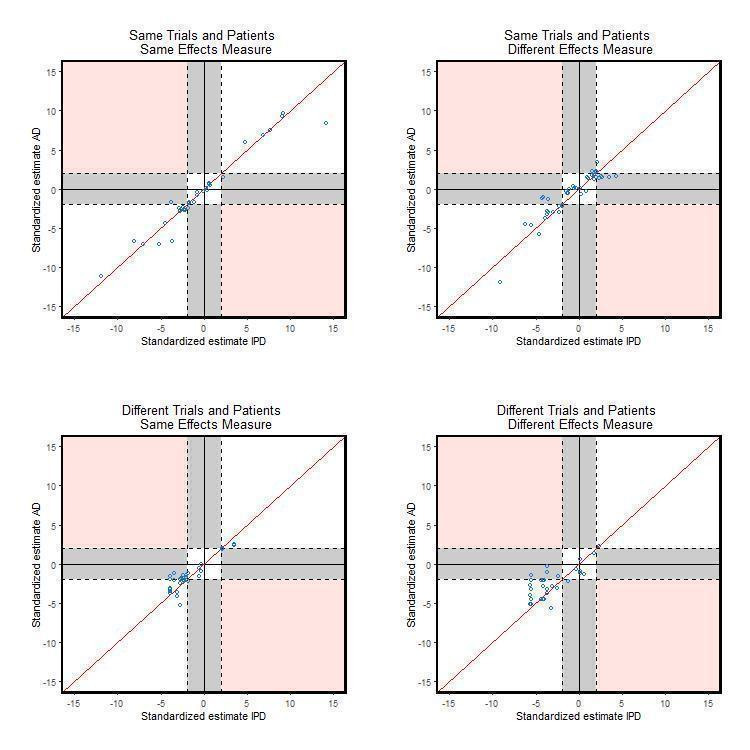
Comparison of standardised effects split by data and effect measure (main effect analyses only)
7.
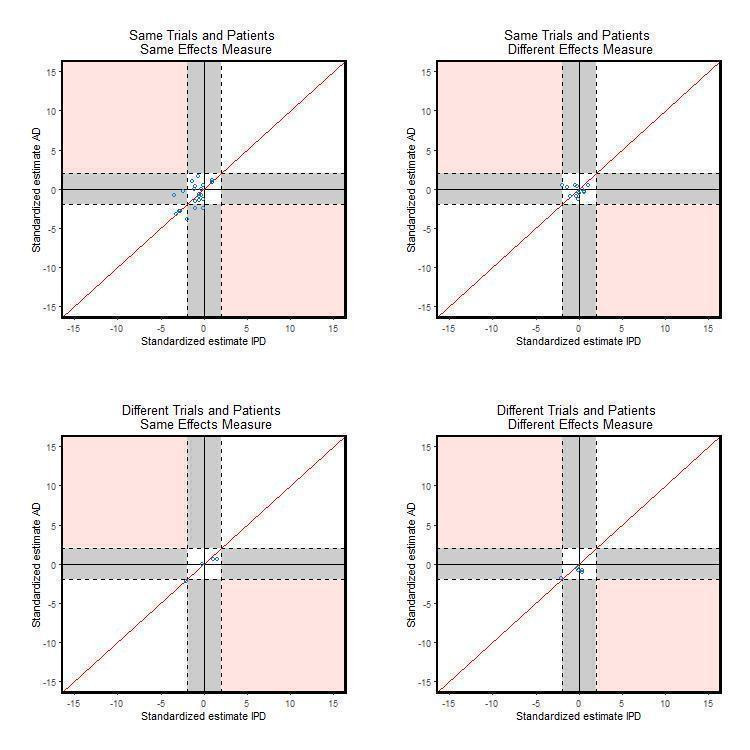
Comparison of standardised effects split by data and effect measure (interaction effect analyses only)
Agreement analyses (Table 6) suggest that on average the IPD‐MA z scores are slightly smaller (‐0.22) than the AD‐MA scores across main effect analyses but approximately 95% of the time the differences lie within limits of agreement of (‐2.84 to 2.40), a range of values that includes important differences in both directions. The average difference in z scores is slightly larger (0.08) for IPD‐MA interaction effect analyses but again with wide limits of agreement (‐2.26 to 2.43). When considering comparisons that focused only on ratio effect analyses the IPD‐MA z scores are on average smaller for main effect analyses (‐0.34) but larger for interaction effect analyses (0.42) whereas for comparisons that focused on difference effects, the IPD‐MA z scores are on average larger for main effect analyses (0.20) and smaller for interaction effect analyses (‐0.44). All these differences are close to zero, suggesting that the IPD‐MA and AD‐MA give similar results on average, however the limits of agreement are wide (Table 6).
6. Agreement.
| Analysis (n) | Average Difference (IPD‐MA –AD‐MA) | 95% Limits of Agreement |
| 1.1. Difference in Z scores MA only (144) | ‐0.22 | ‐2.84 to 2.40 |
| 1.2. Difference in Z scores MR only (46) | 0.08 | ‐2.26 to 2.43 |
| 1.3. Difference in Z scores MA only ratio effects (115) | ‐0.34 | ‐2.87 to 2.19 |
| 1.4. Difference in Z scores MR only ratio effects (25) | 0.42 | ‐1.97 to 2.80 |
| 1.5. Difference in Z scores MA only difference effects (28) | 0.20 | ‐2.64 to 3.05 |
| 1.6. Difference in Z scores MR only difference effects (19) | ‐0.44 | ‐2.46 to 1.57 |
| 2.1. Difference in Log ratio effect estimates MA only (115) | ‐0.004 | ‐0.36 to 0.35 |
| 2.2. Difference in Log ratio effect estimates MR only (25) | ‐0.05 | ‐0.78 to 0.69 |
| 3.1. Log ratio effect standard errors MA only (115) | ‐0.015 | ‐0.14 to 0.11 |
| 3.2. Log ratio effect standard errors MR only (25) | 0.012 | ‐0.55 to 0.57 |
MA: main effect analyses, MR: interaction effect analyses
When considering differences between IPD‐MA and AD‐MA in log ratio effect estimates (e.g. log odds ratio IPD‐MA – log odds ratio AD‐MA), the differences are again close to zero for main effect analyses (‐0.004 on the log scale or 0.996 on the natural ratio scale) and interaction effect analyses (‐0.05 on the log scale or 0.95 on the natural ratio scale) suggesting that on average the IPD‐MA and AD‐MA effects are similar. However, the limits of agreement are wide: approximately 95% of the differences in log ratio effects lie between ‐0.36 and 0.35 [i.e. (0.70 and 1.42) on the ratio of ratios scale] for main effect analyses, and approximately 95% of the differences in log ratio effects lie between ‐0.78 and 0.69 [i.e. (0.46 and 1.99) on the ratio of ratios scale] for interaction effect analyses.
Finally, when considering differences between IPD‐MA and AD‐MA in standard errors of log ratio effect estimates (e.g. SE(log odds ratio IPD‐MA) – SE(log odds ratio AD‐MA)), the differences are again close to zero for main effect analyses (‐0.015) and interaction effect analyses (0.012) suggesting that on average the IPD‐MA and AD‐MA precision is similar. However, the limits of agreement are wide: approximately 95% of the differences lie between ‐0.14 and 0.11 for main effect analyses and even wider (‐0.55 to 0.57) for interaction effect analyses (Table 6).
Sensitivity analyses to examine the effect of clustering of comparisons within studies showed that across 250 samples, each including one comparison selected at random from each study, the mean (SD) of the differences in z scores between IPD‐MA and AD‐MA was 0.033 (0.199) for main effect analyses and ‐0.118 (0.279) for interaction effect analyses. These values are close to zero and the 95% reference range includes our calculated values of ‐0.22 and 0.08, suggesting that conclusions from our agreement analyses are robust.
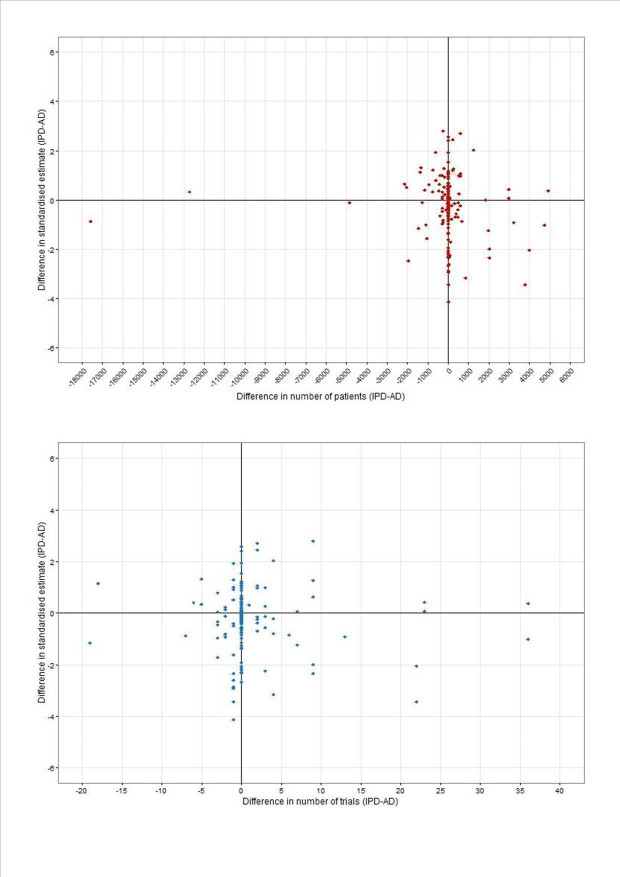
Scatter plots of the difference in standardised effect between IPD‐MA and AD‐MA plotted against the difference (IPD‐AD) in numbers of patients and trials (Figure 8) do not suggest that discrepancies in results expressed as standardised effects between IPD‐MA and AD‐MA increase as the differences between numbers of trials and patients increase.
8.
Difference in standardised estimates (IPD‐AD) versus difference in participants (top panel) and trials (bottom panel) for 174 main effect and effect modifier analyses (IPD‐AD)
Summary of descriptive conclusions
Table 1summarises the main conclusions made in each study in terms of a comparison between IPD‐MA and AD‐MA.
As seen from the summary of numerical comparisons, several studies concluded that results of IPD‐MA and AD‐MA were similar. For example, original authors wrote “results were consistent between the trial‐level and individual patient data analyses” (Beveridge 2015); “both our pooled analysis and our meta‐analysis showed that fish oil was not efficacious in patients …” (Brouwer 2009); “this finding was consistent in both trial‐level and patient‐level analyses” (Kim 2010); “There is no good evidence of any difference between the results of trials with individual patient data and those for which published data were used” (Myeloma 1998); and “AD and IPD meta‐analysis obtained very similar results …” (Saillourglenisson 2000).
Similarly, some studies describe important differences between IPD‐MA and AD‐MA. For example, “The IPD analysis revealed a clinically important and statistically significant difference between the effect of treatment … which the AD analyses failed to identify” (Berlin 2002); “The IPD review provides a larger, more significant estimate of treatment effect than would have been found with a review based solely on published data. An IPD review can produce very important results that might not have been obtainable in any other way” (Clarke 1998); “The IPD and AD results differed substantially … the size of the treatment effect varied considerably” (Duchateau 2001); “The IPD and AD meta‐analyses provided different results (in particular, AD consistently yielded greater estimates of a treatment benefit)” (Jeng 1995); “IPD resulted in more precise estimates of effect with greater statistical significance and less statistical heterogeneity” (Legg 2003); and “The best evidence came from the largest meta‐analysis based on IPD” (Lukka 2006).
Finally, regardless of whether or not differences were noted in statistical significance between IPD‐MA and AD‐MA, a number of benefits of IPD were described across studies. For example, “the availability of data on individual patients permitted the identification of subgroups more likely to benefit from treatment” (D'Amico 1998); “The broader IPD analysis allowed exploring the effects of a variety of covariates” (Fortin 1995); “It is preferable to obtain IPD from all studies to correctly account for the correlation between repeated observations” (Jones 2009); “Conventional meta‐analyses do not allow proper subgroup analyses, whereas IPD meta‐analyses produce more accurate subgroup effects.” (Koopman 2008); “Individual patient data are essential to determine the time course of effects on risk of cancer and other outcomes during trials” (Rothwell 2011); “It is preferable to model individual patient outcome data directly rather than summary statistics to avoid the assumptions that have to be made regarding the summary statistics (of normality and known variance). Furthermore, individual patient level covariates can be introduced to study potential treatment interactions” (Thompson 2001); “The availability of IPD allowed a thorough investigation into the main effects of each covariate which was not possible using meta regression of AD.” (Tudur Smith 2005); and “Collection of the IPD is made attractive by the potential of meta‐regression analyses for exploring trial‐level, therapist‐level and patient‐level predictors of the treatment effect and of the random effects” (Walwyn 2015).
Discussion
We have conducted a meta‐epidemiological study of articles reporting a numerical comparison of meta‐analysis results using individual participant data (IPD) and aggregate data (AD). Due to the variability across comparisons in effect measures used, comparisons were mainly summarised in terms of z scores and discrepancies in statistical significance as a proxy measure for impact on clinical decisions. Our findings show that conclusions from IPD‐MA and AD‐MA can often differ (38 (20%) comparisons) in terms of statistical significance and therefore potentially different clinical conclusions can be expected. It was more common for the IPD‐MA to detect a statistically significant difference that was not confirmed by the AD‐MA (28 (15%)), than the reverse in which a statistically significant difference was found in the AD‐MA but not the IPD‐MA (10 (5%)). Of course, within each of the meta‐analyses, other factors, such as size of effect, balancing benefits and harms, and degree of heterogeneity between trials, would also be taken into account when making clinical decisions rather than necessarily focusing purely on statistical significance. The average difference in z scores, log ratio effect estimates, and standard errors between IPD‐MA and AD‐MA were close to zero, but wide limits of agreement suggest that IPD‐MA and AD‐MA are not always similar and sometimes quite different.
Factors that we expected to lead to important differences between IPD‐MA and AD‐MAs were higher levels of trial exclusion, higher levels of patient exclusion, and greater influence of early follow‐up information for some trials in the AD‐MA compared with the IPD‐MA. We did not find evidence to suggest that differences in the number of included trials and participants would necessarily lead to differences in conclusions, although it is important in some cases. In fact, results from IPD‐MA and AD‐MA can differ when analyses are based on identical trials and participants, and even identical effect measures. Additional follow‐up data for patients included in the IPD‐MA could explain these discrepancies, but a lack of information across the majority of studies made it difficult to explore this reliably. Nevertheless, one of the included studies (Michiels 2005) did specify that the researchers had compared like with like, that is, the same trials, participants, and extended follow‐up in each analysis and they still found discrepancies between IPD‐MA and AD‐MA, as well as across 128 trial level analyses, when analyses were based on different effect measures.
Overall, we found that the proportion of significant results is greater for main effect analyses compared to treatment effect modifier analyses. This is most likely because meta‐analyses have greater power to detect main effect results as statistically significant compared to treatment effect modifier analyses (Lambert 2002).
We focused this review on studies reporting numerical data for empirical comparisons of IPD‐MA against AD‐MA. This naturally implies some type of corresponding AD‐MA is possible. However, IPD is potentially of greatest value in reviews where AD may be unavailable or limited and hence an AD‐MA would not be feasible. Several included studies described additional analyses that could only be undertaken with IPD. For example, D'Amico 1998, Koopman 2008 and Pignon 1992 described subgroup analyses that could only be explored using IPD. Furthermore, studies that did not present numerical data comparing IPD‐MA and AD‐MA but that may have mentioned limitations of previous AD‐MAs as the motivation to conduct an IPD‐MA were not eligible. For example, Cools 2010 collected IPD as previous AD‐MAs had been “difficult to interpret because of heterogeneity in study design, patient characteristics, and outcome definition, and have limitations because interpretations are made on the basis of summary data extracted from published trial reports.” They concluded that their IPD‐MA “provides clinically relevant information about effectiveness and safety of elective use of HFOV in preterm infants with respiratory failure, and improves on past AD‐MA” (Cools 2010). These additional benefits of IPD‐MA are not fully recognised within this current review and further work is required to quantify this additional information, to allow more in‐depth and standardised analyses of the comparisons.
Potential biases in the review process
The identification of conference abstracts, principally from the Cochrane Methodology Register because of the handsearching of conference proceedings (such as the Cochrane Colloquia, Systematic Reviews Symposia, INAHTA and HTAi annual conferences, and the annual meetings of the Society for Clinical Trials) that was used to compile that Register is a strength of this review, because of the increased comprehensiveness of the process for identifying studies. However, despite the comprehensive search strategy and systematic approach to the identification of studies, there is still a possibility of publication bias with reporting of empirical comparisons of IPD‐MA and AD‐MA being suppressed due to the lack of interesting differences between the two approaches whilst a comparison of IPD‐MA and AD‐MA may be more likely to be published when there is a discrepant finding.
Although we present a comprehensive systematic review of empirical comparisons of IPD‐MA and AD‐MA, there are some limitations.
We did not systematically contact the authors of published empirical comparisons but a future update of this review may develop into a collaborative review, in which the original researchers will be asked to conduct common analyses of their data, to allow more in‐depth analyses of the comparisons.
Multiple comparisons presented for the same study have been extracted and compared alongside each other, essentially as independent studies. Whilst results from exploratory analyses randomly selecting one comparison per study gave similar conclusions, results incorporating all 190 comparisons should be considered cautiously because of the potential clustering of comparisons within studies.
We have focused on comparisons of meta‐analysis results from randomised trials. There are examples in the literature of empirical comparisons based on observational studies (e.g. Steinberg 1997) where discrepancies between IPD‐MA and AD‐MA may be expected to be more extreme than those discrepancies observed between meta‐analysis of randomised trials.
We excluded comparisons of network meta‐analysis (NMA) but acknowledge that a comparison of IPD‐NMA against AD‐NMA (e.g. Cope 2012) is an important research question to address given the value of using IPD for NMA (Donegan 2013).
We excluded comparisons that were based solely on simulated data (e.g. Lambert 2002) because our main objective was to examine empirical comparisons of data to capture experiences of what happens in practice.
Agreements and disagreements with other studies or reviews
Results from our review are comparable to those described by Mukhtar 2008 in a German Doctorate thesis which included 25 studies with 70 empirical comparisons of IPD‐MA and AD‐MA of randomised trials. Our review includes 22 of their 25 included studies and an additional 17 studies. Three studies included by Mukhtar were not eligible for our review: one study appeared to include IPD mixed with AD rather than IPD‐MA compared to AD‐MA; one unpublished study did not contain sufficient reliable information; and one study mentioned a comparison of IPD‐AD with AD‐MA but failed to present sufficient numerical data. Mukhtar 2008 concluded that two thirds of the comparisons showed a tendency to overestimate the effect size and to reduce its precision by MA‐APD in comparison to MA‐IPD but the differences between the point estimates of both types of meta‐analysis were small in all comparisons. In a separate review, Cooper 2009 describe the relative benefits of IPD‐MA compared to AD‐MA illustrated by selected studies that have compared the two approaches. They conclude that when both IPD and AD are equally available, IPD‐MA is superior to AD‐MA as IPD permits subgroup analyses, checking of the data and analyses in the original studies, adding new information to the data sets, and the possibility to use different statistical methods. Due to the cost of IPD‐MA and the potential lack of available IPD, they recommend a strategy using both approaches in a complementary fashion such that the first step in conducting an IPD‐MA would be to conduct an AD‐MA (Cooper 2009).
Authors' conclusions
Implication for methodological research.
Further research, incorporating the benefits and costs of IPD‐MA and extending to IPD‐MA of observational studies would be beneficial to support decisions about when IPD‐MA is most valuable. More research is required on the value of IPD in network meta‐analysis (NMA).
History
Protocol first published: Issue 3, 2001 Review first published: Issue 9, 2016
| Date | Event | Description |
|---|---|---|
| 27 December 2007 | Amended | Converted to new review format. |
| 20 February 2007 | New citation required and major changes | Substantive amendment |
Acknowledgements
We thank James Oyee for extracting data for a sample of studies, Eleanor Kotas from the Liverpool Reviews and implementation Group for help with updating the search; Mike Clarke, Jayne Tierney and Lesley Stewart for input into the protocol and an early version of this review, and Lisa Williams for her help with preparation of graphical displays.
Appendices
Appendix 1. Search Strategy
Search undertaken on June 9 2006
| Source | Search terms |
| Cochrane Methodology Register (2006, Issue 3) |
Review methodology – data collection – individual patient data – general methods Review methodology – data collection – individual patient data – IPD vs other types of meta‐analysis Review methodology – data collection – individual patient data – IPD and non IPD “individual patient data” “ipd” [These terms were combined with the Boolean OR] |
| CENTRAL (2006, Issue 2) |
#1 (individual next patient next data) #2 ((individual next patient*) near data) #3 ((individual next patient*) near report*) #4 ((individual next patient*) near outcome*) #5 ipd #6 (#1 or #2 or #3 or #4 or #5) |
|
OvidWeb MEDLINE (1966 to May Week 5 2006) |
1 individual patient data.ti,ab. 2 individual patient report$.ti,ab. 3 individual patient outcome$.ti,ab. 4 (individual patient$ adj6 data).ti,ab. 5 (individual patient$ adj6 report$).ti,ab. 6 (individual patient$ adj6 outcome$).ti,ab. 7 ipd.ti,ab. 8 or/1‐7 |
|
OvidWeb Embase (1980 to 2004 Week 20) |
1 individual patient data.ti,ab. 2 individual patient report$.ti,ab. 3 individual patient outcome$.ti,ab. 4 (individual patient$ adj6 data).ti,ab. 5 (individual patient$ adj6 report$).ti,ab. 6 (individual patient$ adj6 outcome$).ti,ab. 7 ipd.ti,ab. 8 or/1‐7 |
Search undertaken on May 14 2009
|
Search strategies: Individual patient data meta‐analyses compared with meta‐analyses based on aggregate data. MEDLINE OvidSP (MEDLINE In‐Process & Other Non‐indexed citations and MEDLINE (R)) (1950 to Week 2 May 2009); Embase OvidSP (1980 to Week 19 2009) searched 14 May 2009. 1 (individual patient$ adj6 data).tw. 2 (individual patient$ adj6 report$).tw. 3 (individual patient$ adj6 outcome$).tw. 4 (individual patient$ adj6 level$).tw. 5 ipd.tw. 6 (individual subject$ adj6 data).tw. 7 (individual subject$ adj6 report$).tw. 8 (individual subject$ adj6 outcome$).tw. 9 (individual subject$ adj6 level$).tw. 10 (raw patient$ adj6 data).tw. 11 (raw data adj6 patient$).tw. 12 (raw data adj6 individual$).tw. 13 (raw data adj6 subject$).tw. 14 (raw data adj6 participant$).tw. 15 (individual participant$ adj6 data).tw. 16 (individual participant$ adj6 report$).tw. 17 (individual participant$ adj6 outcome$).tw. 18 (individual participant$ adj6 level$).tw. 19 or/1‐18 20 remove duplicates from 19 The Cochrane Library Issue 2 2009 (includes Cochrane Database of Systematic Reviews, Database of Abstracts of Reviews of Effectiveness, CENTRAL, Cochrane Methodology Register, HTA database, NHS Economic Evaluations Database) – searched 14 May 2009. #1 (individual next patient*):ti,ab near6 data:ti,ab #2 (individual next patient*):ti,ab near6 report*:ti,ab #3 (individual next patient*):ti,ab near6 outcome*:ti,ab #4 (individual next patient*) near6 level*:ti,ab #5 ipd:ti,ab #6 (individual next subject*):ti,ab near6 data:ti,ab #7 (individual next subject*):ti,ab near6 report*:ti,ab #8 (individual next subject*):ti,ab near6 outcome*:ti,ab #9 (individual next subject*):ti,ab near6 level*:ti,ab #10 (raw next patient*):ti,ab near6 data:ti,ab #11 (raw next data):ti,ab near6 patient*:ti,ab #12 (raw next data):ti,ab near6 individual*:ti,ab #13 (raw next data):ti,ab near6 subject*:ti,ab #14 (raw next data):ti,ab near6 participant*:ti,ab #15 (individual next participant*):ti,ab near6 data:ti,ab #16 (individual next participant*):ti,ab near6 report*:ti,ab #17 (individual next participant*):ti,ab near6 outcome*:ti,ab #18 (individual next participant*):ti,ab near6 level*:ti,ab #19 #1 or #2 or #3 or #4 or #5 or #6 or #7 or #8 or #9 or #10 or #11 or #12 or #13 or #14 or #15 or #16 or #17 or #18 |
Search undertaken on Jan 7 2016
|
Search strategies: Individual patient data meta‐analyses compared with meta‐analyses based on aggregate data. MEDLINE OvidSP (MEDLINE In‐Process & Other Non‐indexed citations and MEDLINE (R)) (1950 to Week 1 January 2016); Embase OvidSP (1980 to Week 1 2016) searched 7 January 2016. 1 (individual patient$ adj6 data).tw. 2 (individual patient$ adj6 report$).tw. 3 (individual patient$ adj6 outcome$).tw. 4 (individual patient$ adj6 level$).tw. 5 ipd.tw. 6 (individual subject$ adj6 data).tw. 7 (individual subject$ adj6 report$).tw. 8 (individual subject$ adj6 outcome$).tw. 9 (individual subject$ adj6 level$).tw. 10 (raw patient$ adj6 data).tw. 11 (raw data adj6 patient$).tw. 12 (raw data adj6 individual$).tw. 13 (raw data adj6 subject$).tw. 14 (raw data adj6 participant$).tw. 15 (individual participant$ adj6 data).tw. 16 (individual participant$ adj6 report$).tw. 17 (individual participant$ adj6 outcome$).tw. 18 (individual participant$ adj6 level$).tw. 19 or/1‐18 20 remove duplicates from 19 The Cochrane Library Issue 1 2016 (includes Cochrane Database of Systematic Reviews, Database of Abstracts of Reviews of Effectiveness, CENTRAL, Cochrane Methodology Register, HTA database, NHS Economic Evaluations Database) – searched 7 January 2016. #1 (individual next patient*):ti,ab near6 data:ti,ab #2 (individual next patient*):ti,ab near6 report*:ti,ab #3 (individual next patient*):ti,ab near6 outcome*:ti,ab #4 (individual next patient*) near6 level*:ti,ab #5 ipd:ti,ab #6 (individual next subject*):ti,ab near6 data:ti,ab #7 (individual next subject*):ti,ab near6 report*:ti,ab #8 (individual next subject*):ti,ab near6 outcome*:ti,ab #9 (individual next subject*):ti,ab near6 level*:ti,ab #10 (raw next patient*):ti,ab near6 data:ti,ab #11 (raw next data):ti,ab near6 patient*:ti,ab #12 (raw next data):ti,ab near6 individual*:ti,ab #13 (raw next data):ti,ab near6 subject*:ti,ab #14 (raw next data):ti,ab near6 participant*:ti,ab #15 (individual next participant*):ti,ab near6 data:ti,ab #16 (individual next participant*):ti,ab near6 report*:ti,ab #17 (individual next participant*):ti,ab near6 outcome*:ti,ab #18 (individual next participant*):ti,ab near6 level*:ti,ab #19 #1 or #2 or #3 or #4 or #5 or #6 or #7 or #8 or #9 or #10 or #11 or #12 or #13 or #14 or #15 or #16 or #17 or #18 |
Appendix 2. Quality assessment and data extraction items included in the online extraction form
| Study ID |
| Title |
| Journal |
| Year |
| Volume |
| Pages |
| Authors |
| Type of article |
| Language |
| Does the study include both IPD and aggregate data meta‐analyses for the same comparison? |
| Is it a comparison of meta‐analyses of RCTs? |
| Does the study compare the results of the IPD and the aggregate data meta‐analyses? |
| Was a comparison of IPD and aggregate data meta‐analyses one of the main aims of the study? |
| What treatments/interventions are compared in the meta‐analyses? |
| Type of disease |
| What types of patients are studied in the meta‐analyses? |
| What is the outcome measure of the meta‐analyses? |
| Were the meta‐analyses done by independent researchers? |
| Aggregated data obtained (published reports/unclear/neither/trialists/other) |
| In your opinion are the inclusion criteria for the IPD and aggregate data meta‐analyses similar? |
| Are the same outcome definitions used for the IPD and aggregate data meta‐analyses? |
| What methods were used for analysis of IPD? |
| What methods were used for analysis of AD? |
| What were the main conclusions of the study about the comparison of IPD and aggregate data meta‐analysis? |
| What reasons (if any) were given for any differences? |
| Would you describe the quality of this study as (A = No important flaws, B = Possibly important flaws, C = Major flaws) |
| If B or C please describe flaws |
| Is further information required from the authors? |
| Data Included in IPD Analysis ‐ All trials |
| Data Included in IPD Analysis ‐ Published trials only |
| Data Included in IPD Analysis ‐ Unpublished trials only |
| Data Included in IPD Analysis ‐ Updated data |
| Data Included in IPD Analysis ‐ Including excluded participants |
| Data Included in AD Analysis ‐ All trials |
| Data Included in AD Analysis ‐ Published trials only |
| Data Included in AD Analysis ‐ Unpublished trials only |
| Data Included in AD Analysis ‐ Updated data |
| Data Included in AD Analysis ‐ Including excluded participants |
| Other Items |
Characteristics of studies
Characteristics of included studies [ordered by study ID]
Berlin 2002.
| Methods | ||
| Data | Binary | |
| Comparisons | ||
| Outcomes | Renal allograft failure | |
| Notes | Terminal renal failure requiring renal transplant | |
Best 2000.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Overall survival, progression‐free survival | |
| Notes | Locally advanced or metastatic colorectal cancer | |
Beveridge 2015.
| Methods | ||
| Data | Continuous | |
| Comparisons | ||
| Outcomes | SBP and DBP | |
| Notes | Range of study populations with any reported baseline 25OHD level | |
Brouwer 2009.
| Methods | ||
| Data | Time‐to‐event | |
| Comparisons | ||
| Outcomes | Time to first confirmed tachyarrhythmia or death | |
| Notes | Implantable cardioverter defibrillator (ICD) patients | |
Clarke 1998.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Overall survival | |
| Notes | Early breast cancer | |
D'Amico 1998.
| Methods | ||
| Data | Binary | |
| Comparisons | ||
| Outcomes | Respiratory tract infections (both tracheobronchitis and pneumonia) and death | |
| Notes | Critical illness | |
Duchateau 2001.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Overall survival | |
| Notes | Head and neck cancer | |
Fortin 1995.
| Methods | ||
| Data | Count | |
| Comparisons | ||
| Outcomes | Tender joint count, swollen joint count, morning stiffness, grip strength, patient/physician global assessment scale, visual analogue scale | |
| Notes | Rheumatoid arthritis | |
Franzosi 1997.
| Methods | ||
| Data | Binary | |
| Comparisons | ||
| Outcomes | Mortality | |
| Notes | Acute myocardial infarction | |
Ioannidis 1999.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Mortality | |
| Notes | HIV | |
Jeng 1995.
| Methods | ||
| Data | Binary | |
| Comparisons | ||
| Outcomes | Live birthrate | |
| Notes | Recurrent miscarriage | |
Jones 2009.
| Methods | ||
| Data | Continuous | |
| Comparisons | ||
| Outcomes | Cognitive function (measured with mini‐mental state examination (MMSE)) | |
| Notes | Alzheimer’s disease | |
Kim 2010.
| Methods | ||
| Data | Binary | |
| Comparisons | ||
| Outcomes | Mortality | |
| Notes | Range of study populations | |
Koopman 2008.
| Methods | ||
| Data | Binary | |
| Comparisons | ||
| Outcomes | Pain, fever or both at 3 and 7 days | |
| Notes | Acute otitis media | |
le Chevalier 1996.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Overall Survival | |
| Notes | Non‐small cell lung cancer | |
Legg 2003.
| Methods | ||
| Data | Continuous | |
| Comparisons | ||
| Outcomes | Activities of daily living core | |
| Notes | Stroke | |
Lindley 2005.
| Methods | ||
| Data | Binary | |
| Comparisons | ||
| Outcomes | Death or dependency | |
| Notes | Acute ischaemic stroke | |
Lukka 2006.
| Methods | ||
| Data | Time‐to‐event, binary | |
| Comparisons | ||
| Outcomes | Overall survival | |
| Notes | Metastatic prostate cancer | |
Michiels 2005.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Overall survival | |
| Notes | Small‐cell lung cancer | |
Myeloma 1998.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Overall survival | |
| Notes | Multiple myeloma | |
Pignon 1992.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Overall survival | |
| Notes | Limited‐stage small‐cell lung cancer | |
Rejnmark 2012.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Mortality | |
| Notes | Range of study populations | |
Rothwell 2011.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Mortality | |
| Notes | High risk of vascular event | |
Saillourglenisson 2000.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Mortality | |
| Notes | HIV | |
Schmid 2004.
| Methods | ||
| Data | Continuous | |
| Comparisons | ||
| Outcomes | Glomerularfiltration rate, progression to end stage renal disease or any doubling of serum creatinine relative to the baseline level | |
| Notes | Renal disease | |
Shepperd 2009.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Mortality Hospital readmissions |
|
| Notes | Range of study populations | |
Spooner 1998.
| Methods | ||
| Data | Continuous | |
| Comparisons | ||
| Outcomes | FEV1 and PEFR | |
| Notes | Exercise‐induced bronchoconstriction | |
Stewart 1993.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Overall survival | |
| Notes | Ovarian cancer | |
Szczech 1998.
| Methods | ||
| Data | Time‐to‐event | |
| Comparisons | ||
| Outcomes | Allograft failure at 2 years | |
| Notes | Renal disease | |
Teramukai 2004.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Overall survival | |
| Notes | Non‐small‐cell lung cancer | |
Thompson 2001.
| Methods | ||
| Data | Binary | |
| Comparisons | ||
| Outcomes | Mortality | |
| Notes | Myocardial infarction | |
Tierney 2001.
| Methods | ||
| Data | Time‐to‐event | |
| Comparisons | ||
| Outcomes | Overall survival | |
| Notes | Lung cancer and soft tissue sarcoma | |
Tonia 2011.
| Methods | ||
| Data | Time‐to‐event, binary | |
| Comparisons | ||
| Outcomes | Overall survival, red blood cell transfusions, thrombovascular events | |
| Notes | Cancer or myelodysplastic syndrome | |
Tudur 2001.
| Methods | ||
| Data | Time‐to‐event | |
| Comparisons | ||
| Outcomes | Overall survival | |
| Notes | Locally advanced or metastatic colorectal cancer | |
Tudur Smith 2005.
| Methods | ||
| Data | Time‐to‐event | |
| Comparisons | ||
| Outcomes | Time to 12 month remission | |
| Notes | Epilepsy | |
Turner 2000.
| Methods | ||
| Data | Binary | |
| Comparisons | ||
| Outcomes | Respiratory tract infections, pre‐eclampsia | |
| Notes | Critically acute illness and pregnancy | |
Vansteenkiste 2012.
| Methods | ||
| Data | Time‐to‐event (IPD) Binary (AD) |
|
| Comparisons | ||
| Outcomes | Overall survival, progression‐free survival | |
| Notes | Lung cancer | |
Walwyn 2015.
| Methods | ||
| Data | Continuous | |
| Comparisons | ||
| Outcomes | Mental health symptoms | |
| Notes | Counselling in primary care | |
Williamson 2000.
| Methods | ||
| Data | Time‐to‐event | |
| Comparisons | ||
| Outcomes | Treatment failure | |
| Notes | Epilepsy | |
Differences between protocol and review
The protocol for this review planned to explore separately comparisons based on aggregate data extracted from published reports [IPD‐MA versus AD‐MA published], aggregate data collected from the responsible trialists [IPD‐MA versus AD‐MA with trialists' aggregate data], and those based on a combination of aggregate data collected from the responsible trialists and aggregate data extracted from published reports [IPD versus best available aggregate data]. However, due to reporting limitations further work is required to contact authors and request additional analyses to explore fully the effects of differing levels of aggregate data. Therefore, this review summarises comparisons made between IPD‐MA and AD‐MA of all types and further important information may be uncovered by seeking additional information, which is planned in a future update of this review.
We did not compare the cost and resource implications of IPD‐MA and AD‐MA because this was rarely mentioned in the studies. However, this is an important consideration for researchers and further data are required to examine this question.
Contributions of authors
CTS led the review, contributed to screening studies for inclusion, extracted data, performed analyses and drafted the manuscript. PW developed the protocol, screened studies for inclusion and drafted the manuscript. MS, SN, RR, MM, AI and MR contributed to screening of studies, data extraction and drafted the manuscript. MS and SN contributed to analyses and graphical display preparation.
Sources of support
Internal sources
-
University of Liverpool, UK.
Catrin Tudur Smith and Paula Williamson
External sources
-
National Institute for Health Research Cochrane Review Incentive Scheme, UK.
Sarah Nolan received funding
-
National Institute for Health Research Research Methods Fellowship in Medical Statistics, UK.
Maria Sudell received funding
Declarations of interest
All authors are involved in the conduct of meta‐analyses using individual participant data. CTS and PW are responsible for at least one of the studies included in the review.
New
References
References to studies included in this review
Berlin 2002 {published data only}
- Berlin JA, Santanna J, Schmid CH, Szczech LA, Feldman HI, Anti‐Lymphocyte Antibody Induction Therapy Study G. Individual patient‐ versus group‐level data meta‐regressions for the investigation of treatment effect modifiers: ecological bias rears its ugly head. Statistics in Medicine 2002;21(3):371‐87. [DOI] [PubMed] [Google Scholar]
Best 2000 {published data only}
- Best L, Simmonds P, Baughan C, Buchanan R, Davis C, Fentiman I, et al. Collaboration Colorectal Meta‐analysis. Palliative chemotherapy for advanced or metastatic colorectal cancer. Cochrane Database of Systematic Reviews 2000, Issue 1. [DOI: 10.1002/14651858.CD001545] [DOI] [PMC free article] [PubMed] [Google Scholar]
Beveridge 2015 {published data only}
- Beveridge LA, Struthers AD, Khan F, Jorde R, Scragg R, Macdonald HM, et al. Effect of vitamin D supplementation on blood pressure: a systematic review and meta‐analysis incorporating individual patient data. JAMA Internal Medicine 2015;175(5):745‐54. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brouwer 2009 {published data only}
- Brouwer IA, Raitt MH, Dullemeijer C, Kraemer DF, Zock PL, Morris C, et al. Effect of fish oil on ventricular tachyarrhythmia in three studies in patients with implantable cardioverter defibrillators. European Heart Journal 2009;30(7):820‐6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Clarke 1998 {published data only}
- Clarke M, Godwin J. Systematic reviews using individual patient data: A map for the minefields?. Annals of Oncology 1998;9:827‐33. [DOI] [PubMed] [Google Scholar]
D'Amico 1998 {published data only}
- D'Amico R, Pifferi S, Leonetti, Torri V, Tinazzi A, Liberati A. Effectiveness of antibiotic prophylaxis in critically ill adult patients: systematic review of randomised controlled trials. BMJ 1998;316:1275–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
Duchateau 2001 {published data only}
- Duchateau L, Pignon JP, Bijnens L, Bertin S, Bourhis J, Sylvester R. Individual patient‐versus literature‐based meta‐analysis of survival data: time to event and event rate at a particular time can make a difference, an example based on head and neck cancer. Controlled Clinical Trials 2001;22(5):538‐47. [DOI] [PubMed] [Google Scholar]
Fortin 1995 {published data only}
- Fortin PR, Lew RA, Liang MH, Wright EA, Beckett LA, Chalmers TC, et al. Validation of a meta‐analysis: the effects of fish oil in rheumatoid arthritis. Journal of Clinical Epidemiology 1995;48(11):1379‐90. [DOI] [PubMed] [Google Scholar]
Franzosi 1997 {published data only}
- Franzosi MG, Santoro E, Santoro L. Prospective meta‐analysis using individual patient data vs meta‐analysis of published reports: the case of ACE‐inhibitors in myocardial infarction. Controlled Clinical Trials 1997;18:183s. [Google Scholar]
Ioannidis 1999 {published data only}
- Ioannidis JP, Contopoulos‐Ioannidis DG, Lau J. Recursive cumulative meta‐analysis: a diagnostic for the evolution of total randomized evidence from group and individual patient data. Journal of Clinical Epidemiology 1999;52(4):281‐91. [DOI] [PubMed] [Google Scholar]
Jeng 1995 {published data only}
- Jeng GT, Scott JR, Burmeister LF. A comparison of meta‐analytic results using literature vs individual patient data: Paternal cell immunization for recurrent miscarriage. JAMA 1995;274(10):830‐6. [PubMed] [Google Scholar]
Jones 2009 {published data only}
- Jones AP, Riley RD, Williamson PR, Whitehead A. Meta‐analysis of individual patient data versus aggregate data from longitudinal clinical trials. Clinical Trials 2009;6(1):16‐27. [DOI] [PubMed] [Google Scholar]
Kim 2010 {published data only}
- Kim PW, Wu YT, Cooper C, Rochester G, Valappil T, Wang Y, et al. Meta‐analysis of a possible signal of increased mortality associated with cefepime use. Clinical Infectious Diseases 2010;51(4):381‐9. [DOI] [PubMed] [Google Scholar]
Koopman 2008 {published data only}
- Koopman L, Heijden GJ, Hoes AW, Grobbee DE, Rovers MM. Empirical comparison of subgroup effects in conventional and individual patient data meta‐analyses. International Journal of Technology Assessment in Health Care 2008;24(3):358‐61. [DOI] [PubMed] [Google Scholar]
le Chevalier 1996 {published data only}
- Chevalier T. Chemotherapy for advanced NSCLC: Will meta‐analysis provide the answer?. Chest 1996;109(5 Suppl):107s‐9s. [DOI] [PubMed] [Google Scholar]
Legg 2003 {published data only}
- Legg L, Leonardi‐Bee J, Langhorne P, Walker M. Is getting individual patient data for meta‐analyses worthwhile?. XI Cochrane Colloquium: Evidence, Health Care and Culture. 2003.
Lindley 2005 {published data only}
- Lindley RI, Wardlaw JM, Sandercock PA. Alteplase and ischaemic stroke: have new reviews of old data helped?. Lancet Neurology 2005;4(4):249‐53. [DOI] [PubMed] [Google Scholar]
Lukka 2006 {published data only}
- Lukka H, Waldron T, Klotz L, Winquist E, Trachtenberg J. Maximal androgen blockade for the treatment of metastatic prostate cancer‐‐a systematic review. Current Oncology (Toronto, Ont.) 2006;13(3):81‐93. [DOI] [PMC free article] [PubMed] [Google Scholar]
Michiels 2005 {published data only}
- Michiels S, Piedbois P, Burdett S, Syz N, Stewart L, Pignon JP. Meta‐analysis when only the median survival times are known: a comparison with individual patient data results. International Journal of Technology Assessment in Health Care 2005;21(1):119‐25. [DOI] [PubMed] [Google Scholar]
Myeloma 1998 {published data only}
- Myeloma Trialists' Collaborative Group. Combination chemotherapy versus melphalan plus prednisone as treatment for multiple myeloma: an overview of 6,633 patients from 27 randomized trials. Journal of Clinical Oncology 1998;16(12):3832‐42. [DOI] [PubMed] [Google Scholar]
Pignon 1992 {published data only}
- Pignon JP, Arriagada R. Role of thoracic radiotherapy in limited‐stage small‐cell lung cancer: quantitative review based on the literature versus meta‐analysis based on individual data. Journal of Clinical Oncology 1992;10(11):1819‐20. [DOI] [PubMed] [Google Scholar]
Rejnmark 2012 {published data only}
- Rejnmark L, Avenell A, Masud T, Anderson F, Meyer HE, Sanders KM, et al. Vitamin D with calcium reduces mortality: patient level pooled analysis of 70,528 patients from eight major vitamin D trials. Journal of Clinical Endocrinology 2012;97(8):2670‐81. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rothwell 2011 {published data only}
- Rothwell PM, Fowkes FG, Belch JF, Ogawa H, Warlow CP, Meade TW. Effect of daily aspirin on long‐term risk of death due to cancer: analysis of individual patient data from randomised trials. Lancet 2011;377(9759):31‐41. [DOI] [PubMed] [Google Scholar]
Saillourglenisson 2000 {published data only}
- Saillourglenisson F, Chene G, Salmi LR, Hafner R, Salamon R. Effect of dapsone on survival in HIV infected patients: a meta‐ analysis of finished trials [Effet de la dapsone sur la survie des patients infectés par le VIH : une métaanalyse des essais terminés]. Revue d'Epidemiologie et de Sante Publique 2000;48(1):17‐30. [PubMed] [Google Scholar]
Schmid 2004 {published data only}
- Schmid CH, Stark PC, Berlin JA, Landais P, Lau J. Meta‐regression detected associations between heterogeneous treatment effects and study‐level, but not patient‐level, factors. Journal of Clinical Epidemiology 2004;57(7):683‐97. [DOI] [PubMed] [Google Scholar]
Shepperd 2009 {published data only}
- Shepperd S, Doll H, Broad J, Gladman JS, Langhorne P, Richards S, et al. Hospital at home early discharge. Cochrane Database of Systematic Reviews 2009, Issue 1. [DOI: 10.1002/14651858.CD000356.pub3] [DOI] [PMC free article] [PubMed] [Google Scholar]
Spooner 1998 {published data only}
- Spooner C, Rowe BH, Saunders LD, Milner RA. Nedocromil sodium as treatment of exercise‐induced bronchoconstriction: a comparison of results from a meta‐analysis with individual patient data. 6th Cochrane Colloquium. 1998; Vol. A03.
Stewart 1993 {published data only}
- Stewart LA, Parmar MK. Meta‐analysis of the literature or of individual patient data: is there a difference?. Lancet 1993;341(8842):418‐22. [DOI] [PubMed] [Google Scholar]
Szczech 1998 {published data only}
- Szczech LA, Berlin JA, Feldman HI, for the Anti‐Lymphocyte Antibody Induction Therapy Study Group. The effect of antilymphocyte induction therapy on renal allograft survival. Annals of Internal Medicine 1998;128:817‐26. [DOI] [PubMed] [Google Scholar]
Teramukai 2004 {published data only}
- Teramukai S, Matsuyama Y, Mizuno S, Sakamoto J. Individual patient‐level and study‐level meta‐analysis for investigating modifiers of treatment effect. Japanese Journal of Clinical Oncology 2004;34(12):717‐21. [DOI] [PubMed] [Google Scholar]
Thompson 2001 {published data only}
- Thompson SG, Turner RM, Warn DE. Multilevel models for meta‐analysis, and their application to absolute risk differences. Statistical Methods in Medical Research 2001;10(6):375‐92. [DOI] [PubMed] [Google Scholar]
Tierney 2001 {published data only}
- Tierney J, Rydzewska L, Burdett S. Feasibility and reliability of using hazard ratios in meta‐analyses of published time‐to‐event data. 9th Cochrane Colloquium. 2001; Vol. O‐002.
Tonia 2011 {published data only}
- Tonia T, Bohlius J. Ten years of meta‐analyses on erythropoiesis‐stimulating agents in cancer patients. Cancer Treatment and Research 2011;157:217‐38. [DOI] [PubMed] [Google Scholar]
Tudur 2001 {published data only}
- Tudur C, Williamson PR, Khan SA, Best L. The value of the aggregate data approach in meta‐analysis with time‐to‐event outcomes. Journal of the Royal Statistical Society. Series a (General) 2001;164:357‐70. [Google Scholar]
Tudur Smith 2005 {published data only}
- Tudur Smith C, Williamson PR, Marson AG. An overview of methods and empirical comparison of aggregate data and individual patient data results for investigating heterogeneity in meta‐analysis of time‐to‐event outcomes. Journal of Evaluation in Clinical Practice 2005;11(5):468‐78. [DOI] [PubMed] [Google Scholar]
Turner 2000 {published data only}
- Turner RM, Omar RZ, Yang M, Goldstein H, Thompson SG. A multilevel model framework for meta‐analysis of clinical trials with binary outcomes. Statistics in Medicine 2000;19(24):3417‐32. [DOI] [PubMed] [Google Scholar]
Vansteenkiste 2012 {published data only}
- Vansteenkiste J, Glaspy J, Henry D, Ludwig H, Pirker R, Tomita D, et al. Benefits and risks of using erythropoiesis‐stimulating agents (ESAs) in lung cancer patients: study‐level and patient‐level meta‐analyses. Lung Cancer (Amsterdam, Netherlands) 2012;76(3):478‐85. [DOI] [PubMed] [Google Scholar]
Walwyn 2015 {published data only}
- Walwyn R, Roberts C. Meta‐analysis of absolute mean differences from randomised trials with treatment‐related clustering associated with care providers. Statistics in Medicine 2015;34(6):966‐83. [DOI] [PubMed] [Google Scholar]
Williamson 2000 {published data only}
- Williamson PR, Marson AG, Tudur C, Hutton JL, Chadwick D. Individual patient data meta‐analysis of randomized anti‐epileptic drug monotherapy trials. Journal of Evaluation in Clinical Practice 2000;6(2):205‐14. [DOI] [PubMed] [Google Scholar]
Additional references
Ahmed 2012
- Ahmed I, Sutton AJ, Riley RD. Assessment of publication bias, selection bias, and unavailable data in meta‐analyses using individual participant data: a database survey. BMJ 2012;3(344):d7762. [DOI] [PubMed] [Google Scholar]
Chalmers 1993
- Chalmers I. The Cochrane Collaboration: preparing, maintaining, and disseminating systematic reviews of the effects of health care. Annals of the New York Academy of Sciences 1993;703:156‐65. [DOI] [PubMed] [Google Scholar]
Clarke 1997
- Clarke M, Stewart L. Individual patient data or published data meta‐analysis: a systematic review. Proceedings of the Fifth Cochrane Collaboration Colloquium. 1997:94, abstract 019.04.
Cools 2010
- Cools F, Askie L, Offringa M, Asselin M, Calvert JM, Courtney SA, et al. Elective high‐frequency oscillatory versus conventional ventilation in preterm infants: a systematic review and meta‐analysis of individual patients' data. Lancet 2010;375:2082‐91. [DOI] [PubMed] [Google Scholar]
Cooper 2009
- Cooper H, Patall EA. The relative benefits of meta‐analysis conducted with individual participant data versus aggregated data. Psychological Methods 2009;14(2):165‐76. [DOI] [PubMed] [Google Scholar]
Cope 2012
- Cope S, Zhang J, Williams J, Jansen JP. Efficacy of once‐daily indacaterol 75 μg relative to alternative bronchodilators in COPD: a study level and a patient level network meta‐analysis. BMC Pulmonary Medicine 2012;12:29. [DOI] [PMC free article] [PubMed] [Google Scholar]
Donegan 2013
- Donegan S, Williamson P, D'Alessandro U, Garner P, Tudur Smith C. Combining individual patient data and aggregate data in mixed treatment comparison meta‐analysis: Individual patient data may be beneficial if only for a subset of trials. Statistics in Medicine 2013;32(6):914‐930. [DOI] [PubMed] [Google Scholar]
Horsley 2011
- Horsley T, Dingwall O, Sampson M. Checking reference lists to find additional studies for systematic reviews. Cochrane Database of Systematic Reviews 2011, Issue 8. [DOI: 10.1002/14651858.MR000026.pub2; PUBMED: 21833989] [DOI] [PMC free article] [PubMed] [Google Scholar]
Lambert 2002
- Lambert PC, Sutton AJ, Abrams KR, Jones DR. A comparison of summary patient‐level covariates in meta‐regressionwith individual patient data meta‐analysis. Journal of Clinical Epidemiology 2002;55:86–94. [DOI] [PubMed] [Google Scholar]
Mathew 1999
- Mathew T, Nordström K. On the equivalence of meta‐analysis using literature and using individual patient data. Biometrics 1999;55(4):1221‐3. [DOI] [PubMed] [Google Scholar]
Mukhtar 2008
- Mukhtar MA. Incorporation of heterogeneity in meta‐analysis of randomised controlled trials. PhD Thesis 2008.
Olkin 1998
- Olkin I, Sampson A. Comparison of meta‐analysis versus analysis of variance of individual patient data. Biometrics 1998;54:317‐22. [PubMed] [Google Scholar]
Steinberg 1997
- Steinberg KK, Smith SJ, Stroup DF, Olkin I, Lee NC, Williamson GD, et al. Comparison of effect estimates from a meta‐analysis of summary data from published studies and from a meta‐analysis using individual patient data for ovarian cancer studies. American Journal of Epidemiology 1997;145:917‐25. [DOI] [PubMed] [Google Scholar]
References to other published versions of this review
Clarke 2001
- Clarke M, Stewart L, Tierney J, Williamson P. Individual patient data meta‐analyses compared with meta‐analyses based on aggregate data. Cochrane Database of Systematic Reviews 2001, Issue 3. [DOI: 10.1002/14651858.MR000007] [DOI] [Google Scholar]
Clarke 2007
- Clarke MJ, Stewart L, Tierney J, Williamson PR. Individual patient data meta‐analyses compared with meta‐analyses based on aggregate data. Cochrane Database of Systematic Reviews 2007, Issue 2. [DOI: 10.1002/14651858.MR000007.pub2] [DOI] [PMC free article] [PubMed] [Google Scholar]