Optimal and sub-optimal quarantine and isolation control in SARS epidemics

Abstract

This paper discusses the application of optimal and sub-optimal controls to a SEQIJR SARS model via the Pontryagin’s Maximum Principle. To this end, two control variables representing the quarantine and isolation strategies are considered in the model. The numerical optimal control laws are implemented in an iterative method, and the sub-optimal solution is computed using a genetic algorithm. The simulation results demonstrate that the maximal applications of quarantining and isolation strategies in the early stage of the epidemic are of very critical impacts in both cases of optimal and sub-optimal control. Otherwise, the control effect will be much worse. This gives a theoretical interpretation to the practical experiences that the early quarantine and isolation strategies are critically important to control the outbreaks of epidemics. Furthermore, our results also show that the proposed sub-optimal control can lead to performances close to the optimal control, but with much simpler strategies for long periods of time in practical use.

1. Introduction

Severe acute respiratory syndrome (SARS), a new, highly contagious, viral disease, emerged in China late in 2002 and quickly spread to 32 countries and regions, causing in excess of 774 deaths and 8098 infections worldwide [1]. Since there are no valid medicines or vaccines for SARS, measures to control the spread of SARS had to take two major forms: isolation of symptomatic individuals and quarantining and close observation of asymptomatic individuals [2]. It had been shown that quarantining and isolating diseased individuals is a critically important strategy that can control SARS outbreaks, because of a reduction in the contact rate between susceptible and diseased individuals [2], [3], [4]. Moreover, Gumel [3] examines the impact of isolation and quarantine on the control of SARS during the outbreaks in Toronto, Hong Kong, Singapore and Beijing in a mathematical way. It uses a deterministic model that closely mimics the data for cumulative infected cases and SARS-related deaths.

In addition, mathematical models have recently been used to examine the transmission dynamics and to model the control of SARS in the literature [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15]. But most of them are mainly in the purely simulative levels [5], [6], [7], [8], [9], [10]. Wang and Ruan [9] propose a mathematical model consists of six subpopulations, namely susceptible, exposed, quarantined, suspect, probable, and removed, to simulate the SARS outbreak in Beijing. Chowell and Castillo-Chavez [10] use the uncertainty and sensitivity analysis of the basic reproductive number $R_0$ to assess the role that the model parameters play in outbreak control, and the results show that the transmission rate and isolation effectiveness have the largest fractional effect on $R_0$. Shi [11] and Lloyd-Smith [12] present a stochastic dynamic model of SARS spreading, and a stochastic model of a SARS outbreak in a community and its hospital, respectively. Furthermore, small-world networks have been introduced to study the propagation of SARS by Naoki Masuda [13] and Small [14]. It has been shown that if all infectious individuals are isolated as rapidly as they are identified, the severity of the outbreak would be minimal [14]. Moreover, Gumel [3] and Chowell [4] attempt to obtain a threshold for the basic reproductive number $R_0$ for assessing the strategies of quarantine and isolation, and discuss the control of SARS by looking at the role of disease transmission parameters in the reduction of $R_0$ and the prevalence of the disease, while the discrete case has been studied by Zhou and Ma [15]. However, those models do not consider control strategies, since their discussions are based on prevalence of disease at equilibria. In Swan’s work [16], optimal control theory is applied to obtain maximal benefits in terms of social benefits from the parsimonious use of insufficient public funds in the control of epidemics. Moreover, the Pontryagin’s Maximum Principle [17] and the time dependent control strategies are also applied for the studies of HIV models [18], mosquito-borne diseases [19], insect transmitted diseases [20], dengue models [21], tuberculosis models [22] and others [23].

In this paper, we consider the optimal and sub-optimal control strategies associated with quarantining asymptomatic individuals and isolating symptomatic individuals for a SARS SEQIJR model presented by Gumel [3]. The model monitors the dynamics of six sub-populations (classes), namely susceptible, asymptomatic, quarantined, symptomatic, isolated, and recovered individuals. We introduce, for the first time, into this model two control variables representing the rate of quarantining of asymptomatic individuals who have been exposed to the virus, but have not yet developed clinical symptoms, and the rate of isolating of symptomatic individuals, respectively.

The rest of the paper is organized as follows. Section 2 describes the SEQIJR SARS model. The analysis of optimization problems and the sub-optimal solution are presented in Sections 3, 4, respectively. In Section 5, we present the numerical method and the simulation results. Finally, the conclusions are summarized in Section 6.

2. Dynamic model for SARS epidemics

In this section, we use the dynamic SEQIJR model for SARS presented by Gumel [3]. By choosing the proper parameters, the simulation results from such a model fit the available data fairly well (see Section 3 in [3]).

$$\dot{S}=\Lambda -\frac{S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N}-\mu S$$

$$\dot{E}=p+\frac{S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N}-(u_1\left(t\right)+k_1+\mu )E$$

$$\dot{Q}=u_1\left(t\right)E-(k_2+\mu )Q$$

$$\dot{I}=k_{1}E-(u_2\left(t\right)+d_1+{\sigma }_1+\mu )I$$

$$\dot{J}=u_2\left(t\right)I+k_{2}Q-(d_2+{\sigma }_2+\mu )J$$

$$\dot{R}={\sigma }_{1}I+{\sigma }_{2}J-\mu R$$ (1)

with $S\left(0\right),E\left(0\right),Q\left(0\right),I\left(0\right),J\left(0\right),R\left(0\right)$ given. Here, the host population is divided into the following epidemiological classes (state variables):

$S$: Susceptible individuals;

$E$: Asymptomatic individuals who have been exposed to the virus but have not yet developed clinical symptoms of SARS;

$Q$: Quarantined individuals;

$I$: Symptomatic individuals;

$J$: Isolated individuals;

$R$: Recovered individuals;

$$N=S+E+Q+I+J+R\text{.}$$

The model synthesizes some demographic effects by assuming a proportional natural death rate $\mu >0$ in each of the six sub-populations of the model and the constant recruitment rate $\Lambda$. In addition, it also includes a net inflow of asymptomatic individuals into the region at a rate $p$ per unit time. This parameter includes new births, immigration and emigration. Owing to the continuing inflow of travellers into the community during the SARS outbreaks, and the absence of a rapid and effective screening test, it is assumed that some of these travellers are asymptomatically infected and enter the community at a rate $p$ per day. In this work, we set $p$ to zero for simplicity. We assume that a susceptible individual may be infected through contacts with an asymptomatic individual, a quarantined individual, an infected individual, or an isolated individual.

The transmission coefficients for these four classes of infected individuals are $\beta$, ${\epsilon }_E\beta$, ${\epsilon }_Q\beta$, and ${\epsilon }_J\beta$ respectively. Although SARS is believed to be transmitted exclusively by symptomatic individuals, a very low rate of transmission by asymptomatic individuals cannot yet be ruled out. In the model this possibility is depicted by employing the modification parameter ${\epsilon }_E$, where $0⩽{\epsilon }_E<1$.

The modification parameter ${\epsilon }_Q⩾0$ represents varying levels of hygiene precautions during quarantine, and a similar interpretation is given to the modification parameter ${\epsilon }_J$ during isolation [3]. An asymptomatic individual is transferred into the symptomatic class (at a rate $k_1$), and a quarantined individual is transferred into the isolated class (at a rate $k_2$) because of the development of clinical symptoms. $d_1$ and $d_2$ are per-capita disease induced death rates for the symptomatic individuals and isolated individuals, respectively. In addition, ${\sigma }_1$ and ${\sigma }_2$ are per-capita recovery rates for the symptomatic individuals and isolated individuals, respectively.

The control variables, $u_1\left(t\right)$ and $u_2\left(t\right)$, are bounded, Lebesgue integrable functions [22]. The control $u_1\left(t\right)$ represents the rate of quarantining of people who have been in contact with an infected individual by a quarantine program and educational campaigns. The control $u_2\left(t\right)$ represents the rate of isolating of symptomatic individuals by an isolation program. Furthermore, from the epidemiological modeling viewpoint, the transfer rate $u_{1}E$ corresponds to an exponential waiting time $e^{-u_{1}t}$, as the fraction that is still in the asymptomatic class $t$ units after entering this class and to $1/u_1$ as the mean waiting time [24]. And the interpretation of $u_{2}I$ is similar to $u_{1}E$.

3. The optimal control problems

The problem is to minimize the cost function

$$J(u_1,u_2)={\int }_0^{t_f}[B_{1}E\left(t\right)+B_{2}Q\left(t\right)+B_{3}I\left(t\right)+B_{4}J\left(t\right)+\frac{C_1}{2}{u}_1^2\left(t\right)+\frac{C_2}{2}{u}_2^2\left(t\right)]dt$$ (2)

subject to the differential equations (1), where $t_f$ is the final time. This performance specification involves the numbers of individuals of symptomatic, asymptomatic, quarantined, or isolated, respectively, as well as the cost for applying quarantine control ($u_1$) and isolation control ($u_2$). The total cost includes not only the consumption for every individual, but also the cost of organization, management, and cooperation etc. Hence, the cost function should be nonlinear. In this paper, a quadratic function is implemented for measuring the control cost by reference to many papers in epidemic control [18], [19], [20], [21], [22]. The coefficients,$B_1$, $B_2$, $B_3$, $B_4$, $C_1$ and $C_2$, are balancing cost factors due to size and importance of the six parts of the objective function. We seek to find an optimal control pair, $u_1^{\ast }$ and $u_2^{\ast }$, such that

$$J(u_1^{\ast },u_2^{\ast })=\underset{\Omega }{min}J(u_1,u_2)\text{.}$$ (3)

Here $\Omega =\{(u_1,u_2)\in L^1(0,t_f)|a_i⩽u_i⩽b_i,i=1,2\}$ and $a_i,b_i,i=1,2$, are fixed positive constants.

Pontryagin’s Maximum Principle [17] provides the necessary conditions for an optimal control problem. This principle converts (1), (2), (3) into a problem of minimizing a Hamiltonian, $H$, pointwise with respect to $u_1$ and $u_2$:

$$H=B_{1}E\left(t\right)+B_{2}Q\left(t\right)+B_{3}I\left(t\right)+B_{4}J\left(t\right)+\frac{C_1}{2}{u}_1^2\left(t\right)+\frac{C_2}{2}{u}_2^2\left(t\right)+\sum _{i=1}^6{\lambda }_i{f}_i$$ (4)

where $f_i$ is the right hand side of the differential equation of $i$-th state variable. By applying Pontryagin’s Maximum Principle [17], we have the adjoint equations

$$\frac{d{\lambda }_1}{dt}=-\frac{\partial H}{\partial S}\text{,}{\lambda }_1\left(t_f\right)=0\text{,}$$

$$\dots$$

$$\frac{d{\lambda }_6}{dt}=-\frac{\partial H}{\partial R}\text{,}{\lambda }_6\left(t_f\right)=0$$

i.e. 

$${\dot{\lambda }}_1={\lambda }_1\frac{(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)N-S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N^2}-{\lambda }_2\frac{(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)N-S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N^2}$$

$${\dot{\lambda }}_2=-B_1-{\lambda }_1[\mu -\frac{{\epsilon }_E\beta SN-S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N^2}]-{\lambda }_2[\frac{{\epsilon }_E\beta SN-S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N^2}-(u_1\left(t\right)+k_1+\mu )]-{\lambda }_3{u}_1\left(t\right)-{\lambda }_4{k}_1$$

$${\dot{\lambda }}_3=-B_2-{\lambda }_1[\mu -\frac{{\epsilon }_Q\beta SN-S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N^2}]-{\lambda }_2\left[\frac{{\epsilon }_Q\beta SN-S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N^2}\right]+{\lambda }_3(k_2+\mu )-{\lambda }_5{k}_2$$

$${\dot{\lambda }}_4=-B_3-{\lambda }_1[\mu -\frac{\beta SN-S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N^2}]-{\lambda }_2\left[\frac{\beta SN-S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N^2}\right]+{\lambda }_4(u_2\left(t\right)+d_1+{\sigma }_1+\mu )-{\lambda }_5{u}_2\left(t\right)-{\lambda }_6{\sigma }_1$$

$${\dot{\lambda }}_5=-B_4-{\lambda }_1[\mu -\frac{{\epsilon }_J\beta SN-S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N^2}]-{\lambda }_2\left[\frac{{\epsilon }_J\beta SN-S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N^2}\right]+{\lambda }_5(d_2+{\sigma }_2+\mu )-{\lambda }_6{\sigma }_2$$

$${\dot{\lambda }}_6=-{\lambda }_1[\mu +\frac{S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N^2}]+{\lambda }_2\left[\frac{S(\beta I+{\epsilon }_E\beta E+{\epsilon }_Q\beta Q+{\epsilon }_J\beta J)}{N^2}\right]+{\lambda }_6\mu$$ (5)

with transversality conditions

$${\lambda }_i\left(t_f\right)=0\text{,}i=1,\dots ,6\text{.}$$ (6)

By the bounds in $\Omega =\{(u_1,u_2)\in L^1(0,t_f)|a_i⩽u_i⩽b_i,i=1,2\}$, the optimal control is given by

$$u_1\left(t\right)=min\{max\{a_1,\frac{1}{C_1}({\lambda }_2-{\lambda }_3)E\},b_1\}$$ (7)

and

$$u_2\left(t\right)=min\{max\{a_2,\frac{1}{C_2}({\lambda }_4-{\lambda }_5)I\},b_2\}$$ (8)

which are derived from the condition

$$\frac{\partial H}{\partial u_1}=0\text{,}\frac{\partial H}{\partial u_2}=0\text{.}$$

Remark 1

Due to the a priori boundedness of the state and adjoint functions and the resulting Lipschitz structure of the ODEs, we obtain the uniqueness of the optimal control for small $t_f$ [22]. The uniqueness of the optimal control pair follows from the uniqueness of the optimality system, which consists of (1), (5), (6) with characterizations (7), (8). There is a restriction on the length of the time interval in order to guarantee the uniqueness of the optimality system. This smallness restriction on the length on the time interval is due to the opposite time orientations of (1), (5), (6); the state problem has initial values and the adjoint problem has final values. This restriction is very common in control problems (see [18], [22]).

Remark 2

The problem described above is a Two Point Boundary Value Problem (TPBVP), with specified initial conditions for the state equation (1), and terminal boundary conditions (6) for the adjoint equation (5). It can be numerically solved by the iteration method presented in Section 5.

4. A sub-optimal solution

In this section, the sub-optimal solution is obtained by a genetic algorithm which follows the idea of [21]. Let the class of admissible controls be restricted to the collection of functions of type

$$u_k\left(t\right)=\{\begin{array}{c}\hfill u_k^i\text{if }t\in I_i\hfill \\ \hfill 0\text{otherwise ,}\hfill \end{array}k=1,2\text{,}$$ (9)

where $u_k^i\in \Omega$ are constants, and $I_i$ are closed intervals $[t_i,t_i+{\Delta }_i]$ such that $I_i\cap I_j=\varnothing$ if $i\ne j$. Therefore, the restricted class admissible controls consist of pulses of height $u_k^i(k=1,2)$ and width ${\Delta }_i$, starting at time $t_i$.

In order to simplify the actual policy implementation, we assume that the two controls are to be of pulsed form. Let $u_k\left(t\right)=u_k^N\left(t\right)(k=1,2)$ be admissible controls with $N$ pulses, characterized by $(t_1,{\Delta }_1,u_1^1,u_2^1,t_2,{\Delta }_2,u_1^2,u_2^2,\dots ,t_N,{\Delta }_N,u_1^N,u_2^N)$. Therefore, the sub-optimal control problem is to minimize

$$J^{\prime }(t_1,{\Delta }_1,u_1^1,u_2^1,t_2,{\Delta }_2,u_1^2,u_2^2,\dots ,t_N,{\Delta }_N,u_1^N,u_2^N)≔J[u_1^N(\cdot ),u_2^N(\cdot )]$$

where $J[\cdot ,\cdot ]$ is the same as defined in (2).

Let $\pi =(t_1,{\Delta }_1,u_1^1,u_2^1,t_2,{\Delta }_2,u_1^2,u_2^2,\dots ,t_N,{\Delta }_N,u_1^N,u_2^N)\in R^{4N}$ for the case of $N$ pulses, and the sub-optimal control problem is simply

$$\underset{\pi =R^{4N}}{min}{J}^{\prime }\left(\pi \right)\text{.}$$

In this work, the search for a global minimum of $J^{\prime }\left(\pi \right)$ is implemented by an extended method based on the Genetic Algorithm [25]. This extension admits the constraints $t_i+{\Delta }_i=t_{i+1}$, $t_N+{\Delta }_N=t_f$, $t_i⩾0$, ${\Delta }_i⩾0$ and $a_k⩽u_k^i⩽b_k$,$k=1,2$.

5. Numerical simulation

In this section, we investigate the numerical algorithm for optimal control in SARS model. The optimal Quarantine and Isolation Control is obtained by solving the optimality conditions, consisting of twelve ODEs from the state and their adjoint equations. This problem (TPBVP) is solved by using the multiple shooting method (see, for instance, [21], [26], [27]) as follows:

• (1)Select $n$ nodes to divide the interval $[0,t_f]$, or, $0=t_1⩽t_2⩽\cdots ⩽t_n=t_f$.
• (2)Choose $y_i≔[x\left(t_i\right),\lambda \left(t_i\right)]$, $i=1,\dots ,n$.
• (3)Integrate (1), (5) for each time interval $[t_i,t_{i+1})$ using $y_i$ as the initial conditions, and obtaining $y\left(t_{i-1}\right)=[x\left(t_{i-1}\right),\lambda \left(t_{i-1}\right)]$.
• (4)Compute $h≔\left[h_i\right]$ where $h_i≔y_i-y\left(t_i\right)$.
• (5)If $\left|h\right|$ is sufficiently close to a minimum value, then stop; Else modify the initial conditions $y_i$ for the next iteration (using, for instance, the Newton–Raphson algorithm to make $h_i≔y_i^{\mathrm{new}}-y\left(t_i\right)=0$) and go to step (3).

In this work, the optimal control was computed using the multiple shooting method with 30 nodes, up to a tolerance of 10⁻⁵ for $\left|h\right|$. Considering the four weight factors associated with $E$, $Q$, $I$ and $J$, we choose $B_1=B_2=B_3=B_4=1$, $C_1=300$ and $C_2=600$ to illustrate the optimal strategies.

Remark 3

We assume that the weight factor $C_2$ associated with control $u_2$ is much larger than $C_1$, which is associated with control $u_1$. This assumption is based on the following facts: The cost associated with $u_1$ mainly includes the cost of monitoring and quarantining programs, while the cost associated with $u_2$ includes the cost of monitoring and isolating programs, and the hospital treatment resource. The ideal weights are very hard to obtain in practice. It needs a lot of work on data mining, analyzing, and fitting. Hence, the acquisition of appropriate practical weights is a difficult problem and it still remains for further investigations. It should be pointed out that the weights in the simulations here are of only theoretical interest to illustrate the control strategies proposed in this paper.

In the simulation, we study the impact of optimal quarantine and isolation control on SARS during the outbreaks in Beijing. We choose the upper bound of $u_1$ equals 0.50, according to the reasonable case in China that it took at least an average of 2 days to quarantine the asymptomatic individuals who had been exposed to the virus, but had not yet developed clinical symptoms. And the choice of upper bound of $u_2$ is similar to $u_1$. The sub-optimal control was computed for the case $N=3$ and specified time intervals: ${\Delta }_1=60$, ${\Delta }_2=240$ and ${\Delta }_3=60$. Parameters such as population size for the genetic algorithm, generation gap and others were adjusted ad hoc [21]. The data and parameters we used, as shown in Table 1 , are mainly from the published data [3], [9]. In order to evaluate the effect of the uncertainty on the model parameters, simulations were repeated with values of $\beta$, ${\epsilon }_E$, ${\epsilon }_Q$, ${\epsilon }_J$, $\mu$, $k_1$, $k_2$, $d_1$, $d_2$, ${\sigma }_1$ and ${\sigma }_2$, altered by random values in the range ±10% (normal distribution), while the inputs $u_1$ and $u_2$ were kept identical to the computed optimal values.

Table 1.

Values of the model parameters

Parameters	Values	Computational parameters	Values
$\beta$	0.2	$S\left(0\right)$	12 million
${\epsilon }_E$	0.3	$E\left(0\right)$	1565
${\epsilon }_Q$	0	$Q\left(0\right)$	292
${\epsilon }_J$	0.1	$I\left(0\right)$	695
$\mu$	0.000034	$J\left(0\right)$	326
$\Lambda$	$\mu N$	$R\left(0\right)$	20
$p$	0	Final time $t_f$	1 year
$k_1$	0.1	Time step duration $dt$	1 day
$k_2$	0.125	Upper bound for $u_1$	0.50
$d_1$	0.0079	Lower bound for $u_1$	0.05
$d_2$	0.0068	Upper bound for $u_2$	0.50
${\sigma }_1$	0.0337	Lower bound for $u_2$	0.05
${\sigma }_2$	0.0386

Fig. 1 shows the time dependent optimal and sub-optimal quarantine and isolation control laws. In order to minimize the total infected individuals, $E+Q+I+J$, the optimal control $u_1$ is at its upper bound during more than the half of the year, and then $u_1$ is steadily decreased to the lower bound, while the optimal control $u_2$ stays at its upper bound for a short time, about 70 days and then steadily decreases to the lower bound over the rest simulated time. The sub-optimal control laws $u_1$ and $u_2$ stay at the upper bound during the first two time intervals and the first time interval, respectively.

Fig. 1.

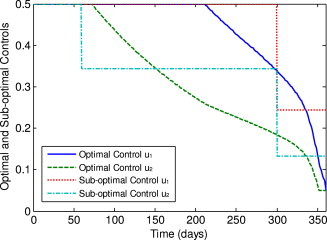
The optimal and sub-optimal control laws.

In fact, at the beginning of simulated time, both the optimal control and sub-optimal control are staying at their upper bounds in order to quarantine and isolate as many as asymptomatic individuals ($E$) and symptomatic individuals ($I$) to prevent the increasing of the number of the infected individuals. For both $u_1$ and $u_2$, the steady decrease to the lower bound in the optimal control case, and the staying at a proper value in the sub-optimal case, are determined by the balance between the cost of the infected individuals and the cost of the controls.

A comparison of the optimal control, the sub-optimal control and the constant controls $u_1\equiv 0.2$ and $u_2\equiv 0.2$ throughout the simulated time are also implemented (Fig. 2 ). It is easy to see that the optimal control and sub-optimal control are much more effective for reducing the number of infected individuals and decreasing the time-span of the epidemic. As normally expected, in the early phase of the epidemic breakouts, keeping the quarantine and isolation controls at their upper bounds will directly lead to decreasing of the number of the infected people. Moreover, Fig. 3 shows that if we take the lower bound values for each control throughout the simulated time, the number of infected individuals would reach about 4.1919×10⁶ (nearly 35% of the total population). This illustrates that the quarantine and isolation strategies are critically important to control the outbreaks of SARS. In addition, in order to illustrate the overall of picture of the epidemic, the number of infected and recovered individuals under the optimal control, the sub-optimal control, the constant control and the lower bound control are shown, respectively, in Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9 .

Fig. 2.

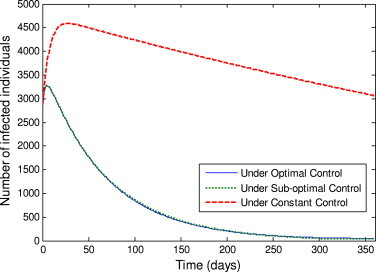
Number of infected individuals under the optimal control, sub-optimal control and constant control.

Fig. 3.

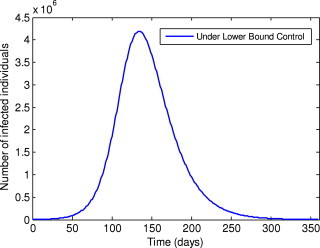
Number of infected individuals under the lower bound control.

Fig. 4.

Number of susceptible individuals under the optimal control and sub-optimal control.

Fig. 5.

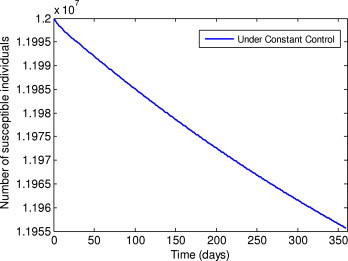
Number of susceptible individuals under the constant control.

Fig. 6.

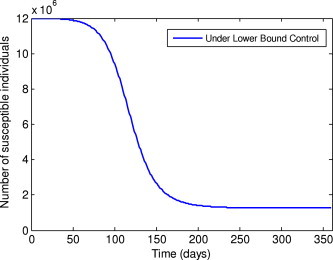
Number of susceptible individuals under the lower bound control.

Fig. 7.

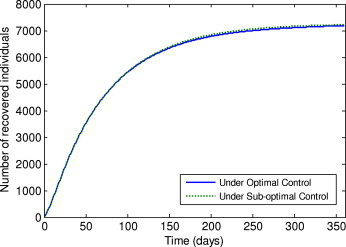
Number of recovered individuals under the optimal control and sub-optimal control.

Fig. 8.

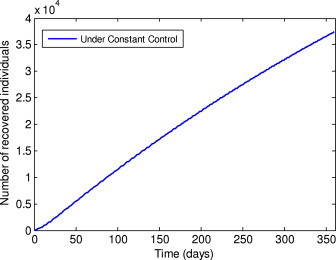
Number of recovered individuals under the constant control.

Fig. 9.

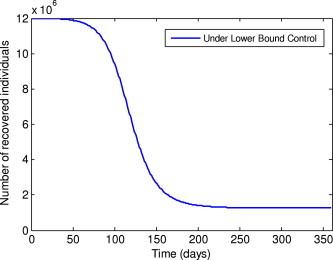
Number of recovered individuals under the lower bound control.

The costs achieved by the optimal control and sub-optimal control are much less than the constant control and the lower bound control, as shown in Fig. 10, Fig. 11 . It is interesting to note that the cost achieved by the sub-optimal control is very close to that of the optimal control, despite the fact that the sub-optimal control is much easier to implement than the optimal control.

Fig. 10.

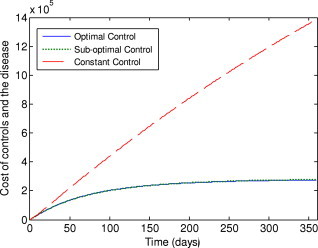
Costs of the controls and the disease under the optimal control, sub-optimal control and constant control.

Fig. 11.

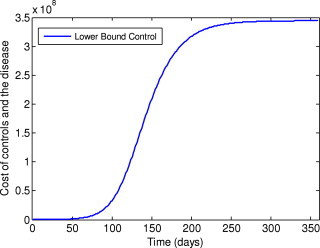
Cost of the control and the disease under the lower bound control.

6. Conclusions

In this paper, we introduced, for the first time, two control variables to represent the quarantine and isolation strategies in epidemic control. The optimal and sub-optimal quarantine and isolation controls for a SEQIJR SARS model were studied. The numerical results show both the optimal and sub-optimal strategy for SARS epidemic control are effective. Furthermore, this idea of introducing these two new control variables is helpful for further discussions on catastrophic epidemic control. It should be pointed out that, as was mentioned in [23], the ideal time-varying optimal strategy might not be applied in practice easily. Nevertheless, it does provide a reference basis on which to design the practical quasi-optimal control strategies or policies, and to assess their effectiveness. However, the proposed sub-optimal control in this paper can provide much simpler strategies, which, as verified by numerical simulations, can also lead to a performance very similar to that achieved by the optimal control. In practical implementations, it is considerably easier to use such a sub-optimal control.