Dynamics of a model with quarantine-adjusted incidence and quarantine of susceptible individuals

Abstract

A new deterministic model for the spread of a communicable disease that is controllable using mass quarantine is designed. Unlike in the case of the vast majority of prior quarantine models in the literature, the new model includes a quarantine-adjusted incidence function for the infection rate and the quarantine of susceptible individuals suspected of being exposed to the disease (thereby making it more realistic epidemiologically). The earlier quarantine models tend to only explicitly consider individuals who are already infected, but show no clinical symptoms of the disease (i.e., those latently-infected), in the quarantine class (while ignoring the quarantine of susceptible individuals). In reality, however, the vast majority of people in quarantine (during a disease outbreak) are susceptible. Rigorous analysis of the model shows that the assumed imperfect nature of quarantine (in preventing the infection of quarantined susceptible individuals) induces the phenomenon of backward bifurcation when the associated reproduction threshold is less than unity (thereby making effective disease control difficult). For the case when the efficacy of quarantine to prevent infection during quarantine is perfect, the disease-free equilibrium is globally-asymptotically stable when the reproduction threshold is less than unity. Furthermore, the model has a unique endemic equilibrium when the reproduction threshold exceeds unity (and the disease persists in the population in this case).

1. Introduction

Quarantine (of individuals feared exposed to a communicable disease) is one of the oldest public health control measures for the spread of communicable diseases in given populations. More recently, this measure was successfully used to combat the spread of some emerging and re-emerging human and animal diseases, such as the severe acute respiratory syndrome (SARS) [1], [2], [3], [4], [5], [6], [7], [8], foot-and-mouth disease [9] and the 2009 swine influenza pandemic [10]. Mathematical models have been designed and used to gain qualitative insights into the spread of diseases in the presence of quarantine of individuals suspected of being exposed to a disease, and the subsequent isolation or hospitalization of those with clinical symptoms of the disease (see, for instance, [1], [2], [3], [4], [5], [6], [7], [8], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21]). In the aforementioned models, with the exception of the models in [2], [5], the dynamics of the quarantined susceptible individuals is not explicitly incorporated into the model (the models only count quarantined individuals who are actually latently-infected, and essentially ignore those who remain susceptible at the end of the quarantine period).

In other words, in the aforementioned models (with the exception of the models in [2], [5]) the class (or compartment) of quarantined individuals contain only those who are latently-infected (and the temporary removal of susceptible individuals from the susceptible pool is not accounted for). The justification given for this assumption (of ignoring the back-and-forth dynamics of quarantined susceptible individuals: from susceptible to quarantine and back to susceptible class if they show no disease symptoms) is that, in general, the fraction of infected contacts that can be traced and quarantined at the time of infection is very small; and that the total population is large in comparison to the size of the infected individuals [13]. In practice, however, quarantine involves the removal of all individuals suspected of being exposed to a given disease (regardless of infection status) from the rest of the population (this often involves a lot of people; the term mass quarantine is often used to describe this process). Those who show disease symptoms during quarantine are hospitalized (or isolated), and those who remain susceptible at the end of the quarantine period are returned to the susceptible class. It is, therefore, instructive to study the impact of the aforementioned assumption (of not explicitly accounting for the quarantine of susceptible individuals) on the transmission dynamics of a disease that is controllable using quarantine.

The purpose of this study is to investigate the qualitative impact of explicitly including the dynamics of quarantined susceptible individuals on the spread of a disease that is controllable by quarantine and isolation. To achieve this objective, a new deterministic model, which includes the dynamics of quarantined susceptible individuals and quarantine-adjusted incidence function, is designed and analyzed. It should be mentioned that quarantined-adjusted incidence has also been used in a number of quarantine models, such as those in [5], [14], [15], [20].

The model to be considered is that for the transmission dynamics of a communicable disease that can be controlled using quarantine and isolation, such as ebola, measles, pandemic influenza and SARS [1], [2], [3], [4], [5], [7], [8], [11], [12], [14], [19], [21]. It is based on splitting the total population at time $t$, denoted by $N\left(t\right)$, into the sub-populations of non-quarantined susceptible ($S\left(t\right)$), quarantined susceptible ($S_q\left(t\right)$), non-quarantined latently-infected (i.e., infected but show no clinical symptoms of the disease) $\left(E\left(t\right)\right)$, quarantined latently-infected ($E_q\left(t\right)$), non-quarantined symptomatic ($I\left(t\right)$), quarantined symptomatic ($I_q\left(t\right)$), hospitalized ($H\left(t\right)$) and recovered ($R\left(t\right)$) individuals, so that

$$N\left(t\right)=S\left(t\right)+S_q\left(t\right)+E\left(t\right)+E_q\left(t\right)+I\left(t\right)+I_q\left(t\right)+H\left(t\right)+R\left(t\right)\text{.}$$

The model is given by the following system of non-linear differential equations (a flow diagram of the model is depicted in Fig. 1 ):

$$\frac{dS}{dt}=\Pi +{\psi }_1{S}_q\left(t\right)+{\psi }_{2}R\left(t\right)-{\lambda }_a\left(t\right)S\left(t\right)-\gamma S\left(t\right)-\mu S\left(t\right)\text{,}$$$$\frac{d{S}_q}{dt}=\gamma S\left(t\right)-r{\lambda }_a\left(t\right)S_q\left(t\right)-({\psi }_1+\mu )S_q\left(t\right)\text{,}$$$$\frac{dE}{dt}={\lambda }_a\left(t\right)S\left(t\right)-({\sigma }_1+\mu )E\left(t\right)\text{,}$$$$\frac{d{E}_q}{dt}=r{\lambda }_a\left(t\right)S_q\left(t\right)-({\sigma }_2+\mu )E_q\left(t\right)\text{,}$$$$\frac{dI}{dt}={\sigma }_{1}E\left(t\right)-({\alpha }_1+{\varphi }_1+\mu +{\delta }_1)I\left(t\right)\text{,}$$$$\frac{d{I}_q}{dt}={\sigma }_2{E}_q\left(t\right)-({\alpha }_2+{\varphi }_2+\mu +{\delta }_2)I_q\left(t\right)\text{,}$$$$\frac{dH}{dt}={\alpha }_{1}I\left(t\right)+{\alpha }_2{I}_q\left(t\right)-({\varphi }_3+\mu +{\delta }_3)H\left(t\right)\text{,}$$$$\frac{dR}{dt}={\varphi }_{1}I\left(t\right)+{\varphi }_2{I}_q\left(t\right)+{\varphi }_{3}H\left(t\right)-({\psi }_2+\mu )R\left(t\right)\text{,}$$ (1)

where ${\lambda }_a$ is the infection rate given by Safi et al. [20]:

$${\lambda }_a\left(t\right)=\frac{\beta \{I\left(t\right)+{\eta }_{1}E\left(t\right)+{\eta }_q[I_q\left(t\right)+{\eta }_2{E}_q\left(t\right)]+{\eta }_{h}H\left(t\right)\}}{N_a\left(t\right)}\text{,}$$ (2)

and $N_a\left(t\right)$ is the total actively-mixing population given by (see also [20])

$$N_a\left(t\right)=S\left(t\right)+E\left(t\right)+I\left(t\right)+{\eta }_q[S_q\left(t\right)+E_q\left(t\right)+I_q\left(t\right)]+{\eta }_{h}H\left(t\right)+R\left(t\right)\text{.}$$ (3)

In (2), $\beta$ is the effective contact rate, and the modification parameters $0\le {\eta }_1,{\eta }_h<1$ accounts for the assumed reduction of infectiousness of exposed and hospitalized individuals, respectively, in relation to the symptomatically-infected (infectious) individuals in the $I$ class. Similarly, $0\le {\eta }_q\le 1$ accounts for the assumed reduction of infectiousness of infected quarantined individuals in relation to individuals in the $I$ class (the parameter $0\le {\eta }_2\le 1$ represents the assumed reduction of infectiousness of exposed quarantined individuals, in the $E_q$ class, in relation to infectious quarantined individuals in the $I_q$ class).

Fig. 1.

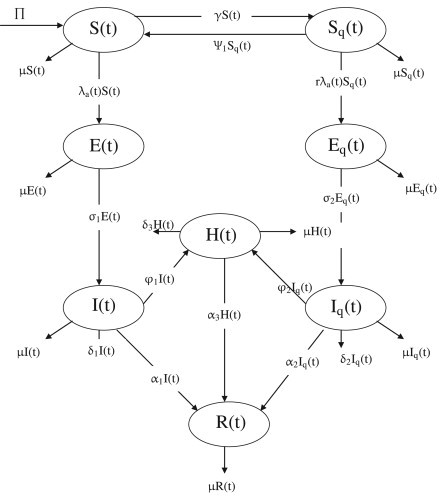
Flow diagram of the model.

In (3), ${\eta }_q$ is a modification parameter that measures the efficacy of quarantine in preventing individuals in quarantine from having contact with members of the general public. If ${\eta }_q=0$, then quarantine is perfectly-implemented (so that individuals in the quarantine classes are not part of the actively-mixing population, and do not transmit infection).

The non-quarantined susceptible population ($S$) is increased by the recruitment of individuals into the community, at a rate $\Pi$. This population is reduced by infection (at the rate ${\lambda }_a$), quarantine (at a rate $\gamma$) and natural death (at a rate $\mu$; populations in all epidemiological compartments are assumed to suffer natural death at this rate). This population is increased by the return of quarantined susceptible individuals at the end of the quarantine period (at a rate ${\psi }_1$) and the loss of natural immunity by recovered individuals (at a rate ${\psi }_2$). The population of quarantined susceptible individuals ($S_q$) is generated by the quarantine of non-quarantined susceptible individuals (at the rate $\gamma$). It is decreased by infection (at a reduced rate $r{\lambda }_a$, with $0<r<1$ accounting for the efficacy of quarantine in preventing infection of quarantined susceptible individuals) and by the reversion to the non-quarantined susceptible class at the end of the quarantine period (at the rate ${\psi }_1$).

Non-quarantined latently-infected individuals ($E$) are generated at the rate ${\lambda }_a$ and decreased by the development of clinical symptoms of the disease (at a rate ${\sigma }_1$). Similarly, the population of quarantined latently-infected individuals ($E_q$) is generated at the rate $r{\lambda }_a$ and decreased by the development of clinical symptoms (at a rate ${\sigma }_2$). Non-quarantined symptomatic individuals ($I$) are generated at the rate ${\sigma }_1$. This population is decreased by hospitalization (at a rate ${\alpha }_1$), natural recovery (at a rate ${\varphi }_1$) and disease-induced mortality (at a rate ${\delta }_1$). The population of quarantined symptomatic individuals ($I_q$) is generated at the rate ${\sigma }_2$ and decreased by hospitalization (at a rate ${\alpha }_2$), recovery (at a rate ${\varphi }_2$) and disease-induced death (at a rate ${\delta }_2$).

The population of hospitalized individuals ($H$) is generated by the hospitalization of non-quarantined and quarantined symptomatic individuals (at the rate ${\alpha }_1$ and ${\alpha }_2$, respectively). It is diminished by recovery (at a rate ${\varphi }_3$) and disease-induced death (at a rate ${\delta }_3<{\delta }_2<{\delta }_1$). The recovered population ($R$) is generated at the rates ${\varphi }_i(i=1,2,3)$ and diminished by loss of natural immunity (at the rate ${\psi }_2$).

The model (1) is an extension of many of the models for quarantine published in the literature (including those in [1], [3], [4], [6], [11], [12], [13], [14], [15], [16], [17], [18]), by considering the dynamics of quarantined susceptible individuals (this entails adding the epidemiological compartments $S_q,E_q$ and $I_q$), in line with the models in [2], [5]. Furthermore, the model (1) extends the model in [5] by:

• (i)including a compartment for hospitalized individuals ($H$);
• (ii)allowing for the infection of quarantined susceptible individuals (at the rate $r{\lambda }_a$; that is, unlike in [5], it is assumed that the efficacy of quarantine to prevent infection of quarantined susceptible individuals is not 100%);
• (iii)allowing for disease transmission by infected quarantined and hospitalized individuals (i.e., it is assumed, unlike in [5], that quarantine and hospitalization are not 100% effective in preventing transmission by infected quarantined or hospitalized individuals).

The model (1) also extends the model in [2] by:

• (a)incorporating demographic parameters (i.e., using an endemic model as against the epidemic model used in [2]);
• (b)using a standard incidence function to model the infection rate (the mass action incidence function was used in [2] by assuming constant total population);
• (c)allowing for the infection of quarantined susceptible individuals (quarantine was assumed to be perfect against infection in [2]);
• (d)allowing for disease transmission by non-quarantined latently-infected individuals.

Furthermore, detailed qualitative analysis of the model will be carried out in this study (this is not done in [2]). The model (1) extends the quarantine models with quarantined-adjusted incidence in [15], [20], by including the dynamics of quarantined susceptible individuals ($S_q$) as well as adding classes for quarantined exposed ($E_q$) and symptomatic ($I_q$) individuals.

The model (1) will now be analyzed to gain insight into its dynamical features.

2. Analysis of the model

2.1. Basic properties

Since the model (1) monitors human populations, all its associated parameters are non-negative. The following basic results can be established using the method in Appendix A of [22].

Theorem 1

The variables of the model (1) are non-negative for all time. In other words, solutions of the model system (1) with positive initial data will remain positive for all time $t>0$ .

Lemma 1

The closed set

$$\mathcal{D}=\{(S,S_q,E,E_q,I,I_q,H,R)\in {\mathbb{R}}_{+}^8:S+S_q+E+E_q+I+I_q+H+R\le \frac{\Pi }{\mu }\}$$

is positively-invariant for the model (1) .

Proof

Adding all the equations of the model (1) gives,

$$\frac{dN}{dt}=\Pi -\mu N-({\delta }_{1}I+{\delta }_2{I}_q+{\delta }_{3}H)\text{.}$$

Since $dN/dt\le \Pi -\mu N$, it follows that $dN/dt\le 0$ if $N\ge \Pi /\mu$. Thus, a standard comparison theorem [23] can be used to show that $N\le N\left(0\right)e^{-\mu t}+\frac{\Pi }{\mu }(1-e^{-\mu t})$. In particular, $N\left(t\right)\le \Pi /\mu$ if $N\left(0\right)\le \Pi /\mu$. Thus, the region $\mathcal{D}$ is positively-invariant. Further, if $N\left(0\right)>\Pi /\mu$, then either the solution enters $\mathcal{D}$ in finite time, or $N\left(t\right)$ approaches $\Pi /\mu$ asymptotically. Hence, the region $\mathcal{D}$ attracts all solutions in ${\mathbb{R}}_{+}^8$.  □

2.2. Local stability of disease-free equilibrium (DFE)

The DFE of the model (1) is given by

$${\mathcal{E}}_0=(S^{\ast },S_q^{\ast },E^{\ast },E_q^{\ast },I^{\ast },I_q^{\ast },H^{\ast },R^{\ast })=(\frac{\Pi (\mu +{\psi }_1)}{\mu (\mu +{\psi }_1+\gamma )},\frac{\Pi \gamma }{\mu (\mu +{\psi }_1+\gamma )},0,0,0,0,0,0)\text{.}$$ (4)

The local stability of ${\mathcal{E}}_0$ will be explored using the next generation operator method [24], [25]. Using the notation in [25], the non-negative matrix, $F$, of the new infection terms, and the $M$-matrix, $V$, of the transition terms associated with the model (1), are given, respectively, by

$$F=\left(\begin{array}{ccccc}\hfill \beta {\eta }_1{\nu }_1\hfill & \hfill \beta {\eta }_2{\eta }_q{\nu }_1\hfill & \hfill \beta {\nu }_1\hfill & \hfill \beta {\eta }_q{\nu }_1\hfill & \hfill \beta {\eta }_h{\nu }_1\hfill \\ \hfill r\beta {\eta }_1{\nu }_2\hfill & \hfill r\beta {\eta }_2{\eta }_q{\nu }_2\hfill & \hfill r\beta {\nu }_2\hfill & \hfill r\beta {\eta }_q{\nu }_2\hfill & \hfill r\beta {\eta }_h{\nu }_2\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\text{,}$$

and,

$$V=\left(\begin{array}{ccccc}\hfill k_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill k_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\sigma }_1\hfill & \hfill 0\hfill & \hfill k_3\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -{\sigma }_2\hfill & \hfill 0\hfill & \hfill k_4\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -{\alpha }_1\hfill & \hfill -{\alpha }_2\hfill & \hfill k_5\hfill \end{array}\right)\text{,}$$

where,

$${\nu }_1=\frac{\mu +{\psi }_1}{\mu +{\psi }_1+{\eta }_q\gamma }\text{,}{\nu }_2=\frac{\gamma }{\mu +{\psi }_1+{\eta }_q\gamma }\text{,}{k}_1={\sigma }_1+\mu \text{,}{k}_2={\sigma }_2+\mu \text{,}$$

$$k_3={\alpha }_1+{\varphi }_1+\mu +{\delta }_1\text{,}{k}_4={\alpha }_2+{\varphi }_2+\mu +{\delta }_2\text{,}{k}_5={\alpha }_3+\mu +{\delta }_3\text{.}$$

It follows that the control reproduction number [26], [27], denoted by ${\mathcal{R}}_q=\rho \left(F{V}^{-1}\right)$, where $\rho$ is the spectral radius, is given by

$${\mathcal{R}}_q=\frac{\beta {\nu }_1[{\eta }_1{k}_2{k}_3{k}_4{k}_5+{\sigma }_1{k}_2{k}_4{k}_5+{\eta }_h{\alpha }_1{\sigma }_1{k}_2{k}_4]}{k_1{k}_2{k}_3{k}_4{k}_5}+\frac{r\beta {\nu }_2[{\eta }_2{\eta }_q{k}_1{k}_3{k}_4{k}_5+{\eta }_q{\sigma }_2{k}_1{k}_3{k}_5+{\eta }_h{\alpha }_2{\sigma }_2{k}_1{k}_3]}{k_1{k}_2{k}_3{k}_4{k}_5}\text{.}$$

Using Theorem 2 in [25], the following result is established.

Lemma 2

The DFE of the model (1) , given by (4) , is locally-asymptotically stable (LAS) if ${\mathcal{R}}_q<1$ , and unstable if ${\mathcal{R}}_q>1$ .

The threshold quantity ${\mathcal{R}}_q$ measures the average number of new infections generated by a single infectious individual in a population where a certain fraction of the susceptible population is vaccinated. Lemma 2 implies that the disease can be eliminated from the community (when ${\mathcal{R}}_q<1$) if the initial sizes of the sub-populations of the model are in the basin of attraction of the DFE (${\mathcal{E}}_0$).

2.3. Backward bifurcation analysis

In this section, the existence of endemic equilibria (that is, equilibria where the infected compartments of the model are non-zero) of the model (1) is established. Let,

$${\mathcal{E}}_1=(S^{\ast \ast },S_q^{\ast \ast },E^{\ast \ast },E_q^{\ast \ast },I^{\ast \ast },I_q^{\ast \ast },H^{\ast \ast },R^{\ast \ast })$$

represents any arbitrary endemic equilibrium point (EEP) of the model (1). Further, define

$${\lambda }_a^{\ast \ast }=\frac{\beta \{I^{\ast \ast }+{\eta }_1{E}^{\ast \ast }+{\eta }_q^{\ast \ast }[I_q^{\ast \ast }+{\eta }_2{E}_q^{\ast \ast }]+{\eta }_h{H}^{\ast \ast }\}}{N_a^{\ast \ast }}\text{,}$$ (5)

(the force of infection of the model (1) at steady-state). It follows, by solving the equations in (1) at steady-state, that

$$S^{\ast \ast }=\frac{\Pi (r{\lambda }_a^{\ast \ast }+{\psi }_1+\mu )}{r{\left({\lambda }_a^{\ast \ast }\right)}^2+[r(\gamma +\mu )+{\psi }_1+\mu ]{\lambda }_a^{\ast \ast }+({\psi }_1+\mu )(\gamma +\mu )-\gamma {\psi }_1}\text{,}$$$$S_q^{\ast \ast }=\frac{\Pi \gamma }{r{\left({\lambda }_a^{\ast \ast }\right)}^2+[r(\gamma +\mu )+{\psi }_1+\mu ]{\lambda }_a^{\ast \ast }+({\psi }_1+\mu )(\gamma +\mu )-\gamma {\psi }_1}\text{,}$$$$E^{\ast \ast }=\frac{{\lambda }_a^{\ast \ast }{S}^{\ast \ast }}{k_1}\text{,}{E}_q^{\ast \ast }=\frac{r{\lambda }_a^{\ast \ast }{S}_q^{\ast \ast }}{k_2}\text{,}$$$$I^{\ast \ast }=\frac{{\lambda }_a^{\ast \ast }{S}^{\ast \ast }{\sigma }_1}{k_1{k}_3}\text{,}{I}_q^{\ast \ast }=\frac{r{\lambda }_a^{\ast \ast }{S}_q^{\ast \ast }{\sigma }_2}{k_2{k}_4}\text{,}$$$$H^{\ast \ast }=\frac{{\lambda }_a^{\ast \ast }{S}^{\ast \ast }{\sigma }_1{\alpha }_1}{k_1{k}_3{k}_5}+\frac{r{\lambda }_a^{\ast \ast }{S}_q^{\ast \ast }{\sigma }_2{\alpha }_2}{k_2{k}_4{k}_5}\text{,}$$$$R^{\ast \ast }=\frac{{\lambda }_a^{\ast \ast }{S}^{\ast \ast }{\sigma }_1{\varphi }_1}{k_1{k}_3{k}_6}+\frac{r{\lambda }_a^{\ast \ast }{S}_q^{\ast \ast }{\sigma }_2{\varphi }_2}{k_2{k}_4{k}_6}+\frac{{\lambda }_a^{\ast \ast }{S}^{\ast \ast }{\sigma }_1{\alpha }_1{\varphi }_3}{k_1{k}_3{k}_5{k}_6}+\frac{r{\lambda }_a^{\ast \ast }{S}_q^{\ast \ast }{\sigma }_2{\alpha }_2{\varphi }_3}{k_2{k}_4{k}_5{k}_6}\text{.}$$ (6)

Substituting the expressions in (6) into (5) shows that the non-zero equilibria of the model satisfy the following quadratic equation (in terms of ${\lambda }_a^{\ast \ast }$):

$$a_0{\left({\lambda }_a^{\ast \ast }\right)}^2+a_1{\lambda }_a^{\ast \ast }+a_2=0\text{,}$$ (7)

where,

$$a_0=r{k}_2{k}_4(k_3{k}_5{k}_6+k_5{k}_6{\sigma }_1+k_5{\sigma }_1{\varphi }_1+k_6{\sigma }_1{\alpha }_1{\eta }_h+{\varphi }_3{\alpha }_1{\sigma }_1)\text{,}$$

$$a_1=r({\eta }_q\gamma k_1{k}_3{k}_4{k}_5{k}_6+{\eta }_q\gamma {\sigma }_2{k}_1{k}_3{k}_5{k}_6+k_1{k}_2{k}_3{k}_4{k}_5{k}_6+\gamma {\sigma }_2{\alpha }_2{\varphi }_3{k}_1{k}_3)+r(\gamma {\sigma }_2{\varphi }_2{k}_1{k}_3{k}_5+{\eta }_h\gamma {\alpha }_2{\sigma }_2{k}_1{k}_3{k}_6)-r\beta ({\eta }_h{\alpha }_1{\sigma }_1{k}_2{k}_4{k}_6+{\eta }_1{k}_2{k}_3{k}_4{k}_5{k}_6+{\sigma }_1{k}_2{k}_4{k}_5{k}_6)+({\psi }_1+\mu )({\alpha }_1{\sigma }_1{\varphi }_3{k}_2{k}_4+{\sigma }_1{\varphi }_1{k}_2{k}_4{k}_5+{\eta }_h{\alpha }_1{\sigma }_1{k}_2{k}_4{k}_6+{\sigma }_1{k}_2{k}_4{k}_5{k}_6+k_2{k}_3{k}_4{k}_5{k}_6)\text{,}$$

$$a_2=k_1{k}_2{k}_3{k}_4{k}_5{k}_6({\eta }_q\gamma +{\psi }_1+\mu )(1-{\mathcal{R}}_q)\text{.}$$

The endemic equilibria of the model (1) can then be obtained by solving for ${\lambda }_a^{\ast \ast }$ from (7), and substituting the positive values of ${\lambda }_a^{\ast \ast }$ into the expressions in (6). The quadratic equation (7) can be analyzed for the possibility of multiple endemic equilibria when ${\mathcal{R}}_q<1$. It should be noted that the coefficient, $a_0$, of the quadratic (7) is always positive and $a_2$ is positive (negative) if ${\mathcal{R}}_q$ is less (greater) than unity. Hence, the following result is established.

Theorem 2

The model (1) has

• (i) a unique endemic equilibrium if $a_2<0\iff {\mathcal{R}}_q>1$;
• (ii) a unique endemic equilibrium if ( $a_1<0$ and $a_2=0$ ) or $a_1^2-4a_0{a}_2=0$;
• (iii) two endemic equilibria if $a_2>0,a_1<0$ and $a_1^2-4a_0{a}_2>0$;
• (iv) no endemic equilibrium otherwise.

Thus, it is clear from Case (i) of Theorem 2 that the model (1) has a unique EEP (of the form ${\mathcal{E}}_1$) whenever ${\mathcal{R}}_q>1$. Furthermore, Case (iii) of Theorem 2 indicates the possibility of backward bifurcation, where a LAS DFE co-exists with a LAS endemic equilibrium when the associated reproduction number ${\mathcal{R}}_q$ is less than unity (see, for instance, [28], [29], [30] for discussions on backward bifurcation) in the model (1). The epidemiological importance of the phenomenon of backward bifurcation is that the classical requirement of having ${\mathcal{R}}_q<1$ is, although necessary, not sufficient for disease elimination. In this case, disease elimination will depend upon the initial sizes of the sub-populations of the model. Thus, the existence of backward bifurcation in the transmission dynamics of a disease makes its effective control difficult. A more rigorous proof of the backward bifurcation property of the model (1), based on using center manifold theory (see, for instance, [25], [29], [31], [32]), is given in the Appendix.

2.3.1. Non-existence of backward bifurcation

In this section, the scenario where the backward bifurcation property of the model can be lost is explored. Consider the model (1) with a perfect quarantine efficacy against infection (so that, $r=0$). In this case, the coefficients $a_0,a_1$ and $a_2$ of the quadratic equation (7) reduce to $a_0=0,a_1>0$ and $a_2\ge 0$ whenever ${\tilde{\mathcal{R}}}_q={\mathcal{R}}_q{|}_{r=0}\le 1$. Thus, for this case, the quadratic equation (7) has one solution (${\lambda }_a^{\ast \ast }=\frac{-a_2}{a_1}\le 0$.) Therefore, the model (1) with a perfect quarantine has no positive endemic equilibrium whenever ${\tilde{\mathcal{R}}}_q<1$. This rules out the possibility of backward bifurcation in this case (since backward bifurcation requires the existence of at least two endemic equilibria whenever ${\tilde{\mathcal{R}}}_q\le 1$ [28], [29], [30]). Furthermore, it can be shown that, for the case when $r=0$, the DFE (${\mathcal{E}}_0$) of the model (1) is globally-asymptotically stable (GAS) under some conditions, as shown below.

Setting $r=0$ in the model (1) gives the following reduced model (it should be noted from (1) that, for the case when $r=0$, $(E_q\left(t\right),I_q\left(t\right))\to (0,0)$ as $t\to \infty$; hence, these variables are omitted from the asymptotic analysis of the model for the special case with $r=0$):

$$\frac{dS}{dt}=\Pi -{\lambda }_1\left(t\right)S\left(t\right)-\gamma S\left(t\right)+{\psi }_1{S}_q\left(t\right)+{\psi }_{2}R\left(t\right)-\mu S\left(t\right)\text{,}$$$$\frac{d{S}_q}{dt}=\gamma S\left(t\right)-({\psi }_1+\mu )S_q\left(t\right)\text{,}$$$$\frac{dE}{dt}={\lambda }_1\left(t\right)S\left(t\right)-({\sigma }_1+\mu )E\left(t\right)\text{,}$$$$\frac{dI}{dt}={\sigma }_{1}E\left(t\right)-({\alpha }_1+{\varphi }_1+\mu +{\delta }_1)I\left(t\right)\text{,}$$$$\frac{dH}{dt}={\alpha }_{1}I\left(t\right)-({\varphi }_3+\mu +{\delta }_3)H\left(t\right)\text{,}$$$$\frac{dR}{dt}={\varphi }_{1}I\left(t\right)+{\varphi }_{3}H\left(t\right)-({\psi }_2+\mu )R\left(t\right)\text{,}$$ (8)

with the associated force of infection ${\lambda }_a={\lambda }_1$, where

$${\lambda }_1={\lambda }_a{|}_{r=0}=\frac{\beta \{I\left(t\right)+{\eta }_{1}E\left(t\right)+{\eta }_{h}H\left(t\right)\}}{S\left(t\right)+{\eta }_q{S}_q\left(t\right)+E\left(t\right)+I\left(t\right)+{\eta }_{h}H\left(t\right)+R\left(t\right)}\text{.}$$ (9)

It can be shown that the reproduction number associated with the reduced model (8), with (9), is given by

$${\tilde{\mathcal{R}}}_q={\mathcal{R}}_q{|}_{r=0}=\frac{\beta {\nu }_1({\eta }_1{k}_3{k}_5+{\sigma }_1{k}_5+{\eta }_h{\sigma }_1{\alpha }_1)}{k_1{k}_3{k}_5}\text{.}$$

Define,

$${\mathcal{D}}_1=\{(S,S_q,E,I,H,R)\in {\mathbb{R}}_{+}^6:S+S_q+E+I+H+R\le \frac{\Pi }{\mu }\}\text{.}$$

The model (8) has a DFE, given by ${\mathcal{E}}_{01}=(S^{\ast },S_q^{\ast },0,0,0,0)$.

Theorem 3

The DFE ( ${\mathcal{E}}_{01}$ ) of the reduced model (8) , with (9) , is GAS in ${\mathcal{D}}_1$ whenever ${\tilde{\mathcal{R}}}_q\le {\nu }_1<1$ .

Proof

Consider the following Lyapunov function

$$\mathcal{F}=\left(\frac{k_5{\tilde{\mathcal{R}}}_q}{{\nu }_1{\eta }_h\beta }\right)E+\left(\frac{k_5+{\eta }_h{\alpha }_1}{k_3{\eta }_h}\right)I+H\text{,}$$

with Lyapunov derivative (where a dot represents differentiation with respect to time) given by

$$\dot{\mathcal{F}}=\left(\frac{k_5{\tilde{\mathcal{R}}}_q}{{\nu }_1{\eta }_h\beta }\right)\dot{E}+\left(\frac{k_5+{\eta }_h{\alpha }_1}{k_3{\eta }_h}\right)\dot{I}+\dot{H}=\frac{k_5{\tilde{\mathcal{R}}}_q}{{\nu }_1{\eta }_h\beta }[\frac{\beta S(I+{\eta }_{1}E+{\eta }_{h}H)}{S+{\eta }_q{S}_q+E+I+{\eta }_{h}H+R}-k_{1}E]+\left(\frac{k_5+{\eta }_h{\alpha }_1}{k_3{\eta }_h}\right)({\sigma }_{1}E-k_{3}I)+{\alpha }_{1}I-k_{5}H\le \frac{k_5{\tilde{\mathcal{R}}}_q}{{\nu }_1{\eta }_h}(I+{\eta }_{1}E+{\eta }_{h}H)-\frac{k_1{k}_5{\tilde{\mathcal{R}}}_q}{{\nu }_1{\eta }_h\beta }E+\frac{{\sigma }_1(k_5+{\eta }_h{\alpha }_1)}{k_3{\eta }_h}E-\frac{(k_5+{\eta }_h\alpha )}{{\eta }_h}I+{\alpha }_{1}I-k_{5}H\text{,}\text{since }S\le S+{\eta }_q{S}_q+E+I+{\eta }_{h}H+R\text{ in }{\mathcal{D}}_1=[\frac{k_5\widetilde{{\mathcal{R}}_q}({\eta }_1\beta -k_1)}{{\nu }_1{\eta }_h\beta }+\frac{{\sigma }_1(k_5+{\eta }_h{\alpha }_1)}{k_3{\eta }_h}]E+({\alpha }_1+\frac{k_5{\tilde{\mathcal{R}}}_q}{{\nu }_1{\eta }_h}-\frac{k_5+{\eta }_h{\alpha }_1}{{\eta }_h})I+k_5(\frac{{\tilde{\mathcal{R}}}_q}{{\nu }_1}-1)H=\frac{k_5}{{\eta }_h}(\frac{{\tilde{\mathcal{R}}}_q}{{\nu }_1}-1)(I+{\eta }_{1}E+{\eta }_{h}H)\le 0\text{whenever }{\tilde{\mathcal{R}}}_q\le {\nu }_1<1\text{.}$$

Since all the parameters and variables of the model (1) are non-negative (Theorem 1), it follows that $\dot{\mathcal{F}}\le 0$ for ${\tilde{\mathcal{R}}}_q\le {\nu }_1$ (it should be noted that ${\nu }_1=\frac{S^{\ast }}{N^{\ast }}<1$) with $\dot{\mathcal{F}}=0$ if and only if $E=I=H=0$. Hence, $\mathcal{F}$ is a Lyapunov function on ${\mathcal{D}}_1$. Thus, it follows, by LaSalle’s Invariance Principle [33], that

$$(E\left(t\right),I\left(t\right),H\left(t\right))\to (0,0,0)\text{as }t\to \infty \text{.}$$ (10)

Since ${lim\; sup}_{t\to \infty }I\left(t\right)=0$ and ${lim\; sup}_{t\to \infty }H\left(t\right)=0$ (from (10)), it follows that, for sufficiently small ${\varpi }^{\ast }>0$, there exist constants $M_1>0$ and $M_2>0$ such that ${lim\; sup}_{t\to \infty }I\left(t\right)\le {\varpi }^{\ast }$ for all $t>M_1$ and ${lim\; sup}_{t\to \infty }H\left(t\right)\le {\varpi }^{\ast }$ for all $t>M_2$. Hence, it follows from the last equation of the model (8) that, for $t>max\{M_1,M_2\}$,

$$\dot{R}\le {\varphi }_1{\varpi }^{\ast }+{\varphi }_3{\varpi }^{\ast }-\mu R\text{.}$$

Thus, by comparison theorem [23],

$$R^{\infty }=\underset{t\to \infty }{lim\; sup}R\le \frac{{\varphi }_1{\varpi }^{\ast }+{\varphi }_3{\varpi }^{\ast }}{\mu }\text{,}$$

so that, by letting ${\varpi }^{\ast }\to 0$,

$$R^{\infty }=\underset{t\to \infty }{lim\; sup}R\le 0\text{.}$$ (11)

Similarly (by using ${lim\; inf}_{t\to \infty }I\left(t\right)=0$ and ${lim\; inf}_{t\to \infty }H\left(t\right)=0$), it can be shown that

$$R_{\infty }=\underset{t\to \infty }{lim\; inf}R\ge 0\text{.}$$ (12)

Thus, it follows from (11), (12) that

$$R_{\infty }\ge 0\ge R^{\infty }\text{.}$$

Hence,

$$\underset{t\to \infty }{lim}R\left(t\right)=0\text{.}$$ (13)

Similarly, it can be shown that

$$\underset{t\to \infty }{lim}S\left(t\right)=\frac{\Pi (\mu +{\psi }_1)}{\mu (\mu +{\psi }_1+\gamma )}=S^{\ast }\text{,}\underset{t\to \infty }{lim}{S}_q\left(t\right)=\frac{\Pi \gamma }{\mu (\mu +{\psi }_1+\gamma )}=S_q^{\ast }\text{.}$$ (14)

Thus, by combining Eqs. (10), (13), (14), it follows that every solution of the equations of the model (8), with initial conditions in ${\mathcal{D}}_1$, approaches ${\mathcal{E}}_0$ as $t\to \infty$ (for ${\tilde{\mathcal{R}}}_q\le {\nu }_1<1$).  □

The above result shows that, for the case when the efficacy of quarantine in preventing infection is perfect (i.e., $r=0$), the disease can be eliminated from the community if the associated reproduction number of the model is less than unity. Furthermore, this result clearly shows that the backward bifurcation property of the model (1) is caused by the imperfect nature of the efficacy of quarantine to prevent infection (see the Appendix).

Conditions for the persistence of the disease in the population will be investigated below.

2.4. Persistence

The model system (1) is said to be uniformly-persistent if there exists a constant $c$ such that any solution $(S\left(t\right),S_q\left(t\right),E\left(t\right),E_q\left(t\right),I\left(t\right),I_q\left(t\right),H\left(t\right),R\left(t\right))$ satisfies [34], [35]:

$$\underset{t\to \infty }{lim\; inf}S\left(t\right)\ge c\text{,}\underset{t\to \infty }{lim\; inf}{S}_q\left(t\right)\ge c\text{,}\underset{t\to \infty }{lim\; inf}E\left(t\right)\ge c\text{,}\underset{t\to \infty }{lim\; inf}{E}_q\left(t\right)\ge c\text{,}$$

$$\underset{t\to \infty }{lim\; inf}I\left(t\right)\ge c\text{,}\underset{t\to \infty }{lim\; inf}{I}_q\left(t\right)\ge c\text{,}\underset{t\to \infty }{lim\; inf}H\left(t\right)\ge c\text{,}\underset{t\to \infty }{lim\; inf}R\left(t\right)\ge c\text{,}$$

provided that $(S\left(0\right),S_q\left(0\right),E\left(0\right),E_q\left(0\right),I\left(0\right),I_q\left(0\right),H\left(0\right),R\left(0\right))\in \mathcal{D}$.

Theorem 4

System (1) is uniformly-persistent in $\mathcal{D}$ if and only if ${\mathcal{R}}_q>1$ .

Proof

The theorem can be proved by using the approach used to prove Proposition 3.3 of [36], by applying a uniform persistence result in [34] and noting that the DFE of the model (1) is unstable whenever ${\mathcal{R}}_q>1$ (Lemma 2).  □

The consequence of this result is that each infected variable ($E,E_q,I,I_q,H$) of the model will persist above a certain threshold value at steady-state, so that the disease will persist (become endemic) in the population. It should be mentioned that some other models for quarantine, which did not explicitly include the dynamics of quarantined susceptible individuals, also showed the presence of a unique endemic equilibrium and disease persistence when the associated reproduction number exceeds unity (see, for instance, [13], [17], [18]).

Conclusions

A new deterministic model for the spread of a disease in a population in the presence of quarantine is designed. A major feature of the model is that it incorporate the dynamics of quarantine-adjusted incidence and the quarantine of susceptible individuals (that is, quarantine is modeled in terms of the temporarily removal of susceptible individuals from the susceptible pool as well as the removal of new infected individuals, detected via the contact tracing of known infectious individuals). Rigorous analysis of the model reveals that it undergoes the phenomenon of backward bifurcation when the associated reproduction number (${\mathcal{R}}_q$) is less than unity. The presence of this phenomenon, which does not arise if the quarantine is 100% effective, implies that the effective control of the spread of the disease, using an imperfect quarantine, depends on the initial sizes of the sub-populations of the model (when ${\mathcal{R}}_q<1$). The model has a unique endemic equilibrium whenever ${\mathcal{R}}_q>1$. Furthermore, it is shown that the disease will persist in the population whenever ${\mathcal{R}}_q>1$.

Submitted by Juan J. Nieto

Appendix. Proof of backward bifurcation property of model (1)

The proof is based on using center manifold theory [31], [32]. In particular, Theorem 4.1 of [32] will be used. It is convenient to make the following change of variables:

$$S=x_1\text{,}{S}_q=x_2\text{,}E=x_3\text{,}{E}_q=x_4\text{,}I=x_5\text{,}{I}_q=x_6\text{,}H=x_7\text{,}R=x_8\text{.}$$

Furthermore, let $X={(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8)}^T$. Thus, the model (1) can be re-written in the form $\frac{dX}{dt}=F\left(X\right)$, with $F={(f_1,f_2,f_3,f_4,f_5,f_6,f_7,f_8)}^T$, as follows:

$$\frac{d{x}_1}{dt}=f_1=\Pi -\frac{\beta [x_5+{\eta }_1{x}_3+{\eta }_q(x_6+{\eta }_2{x}_4+{\eta }_h{x}_7)]x_1}{x_1+x_3+x_5+{\eta }_q(x_2+x_4+x_6)+x_7+x_8}+{\psi }_1{x}_2-(\mu +\gamma )x_1\text{,}$$$$\frac{d{x}_2}{dt}=f_2=\gamma x_1-\frac{r\beta [x_5+{\eta }_1{x}_3+{\eta }_q(x_6+{\eta }_2{x}_4+{\eta }_h{x}_7)]x_1}{x_1+x_3+x_5+{\eta }_q(x_2+x_4+x_6)+x_7+x_8}-(\mu +{\psi }_1)x_2\text{,}$$$$\frac{d{x}_3}{dt}=f_3=\frac{\beta (x_5+{\eta }_1{x}_3+{\eta }_q[x_6+{\eta }_2{x}_4+{\eta }_h{x}_7])x_1}{x_1+x_3+x_5+{\eta }_q(x_2+x_4+x_6)+x_7+x_8}-k_1{x}_3\text{,}$$$$\frac{d{x}_4}{dt}=f_4=\frac{r\beta (x_5+{\eta }_1{x}_3+{\eta }_q[x_6+{\eta }_2{x}_4+{\eta }_h{x}_7])x_1}{x_1+x_3+x_5+{\eta }_q(x_2+x_4+x_6)+x_7+x_8}-k_2{x}_4\text{,}$$$$\frac{d{x}_5}{dt}=f_5={\sigma }_1{x}_3-k_3{x}_5\text{,}$$$$\frac{d{x}_6}{dt}=f_6={\sigma }_2{x}_4-k_4{x}_6\text{,}$$$$\frac{d{x}_7}{dt}=f_7={\alpha }_1{x}_5+{\alpha }_2{x}_6-k_5{x}_7\text{,}$$$$\frac{d{x}_8}{dt}=f_8={\varphi }_1{x}_5+{\varphi }_2{x}_6+{\varphi }_3{x}_7-k_6{x}_8\text{.}$$ (15)

The Jacobian of the system (15), at the associated DFE (${\mathcal{E}}_0$), is given by

$$J\left({\mathcal{E}}_0\right)=\left[M_{4\times 8}{U}_{4\times 8}\right]\text{,}$$

where

$$M=\left(\begin{array}{cccc}\hfill -(\gamma +\mu )\hfill & \hfill {\psi }_1\hfill & \hfill -\frac{\beta {\eta }_1{x}_1^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill -\frac{\beta {\eta }_q{\eta }_2{x}_1^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill \\ \hfill \gamma \hfill & \hfill -({\psi }_1+\mu )\hfill & \hfill -\frac{r\beta {\eta }_1{x}_2^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill -\frac{r\beta {\eta }_q{\eta }_2{x}_1^{\ast }}{x_2^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\beta {\eta }_1{x}_1^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}-k_1\hfill & \hfill \frac{\beta {\eta }_q{\eta }_2{x}_1^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{r\beta {\eta }_1{x}_2^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill \frac{r\beta {\eta }_q{\eta }_2{x}_1^{\ast }}{x_2^{\ast }+{\eta }_q{x}_2^{\ast }}-k_2\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\sigma }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\sigma }_2\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\text{,}$$

$$U=\left(\begin{array}{cccc}\hfill -\frac{\beta x_1^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill -\frac{\beta {\eta }_q{x}_1^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill -\frac{\beta {\eta }_h{x}_1^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill 0\hfill \\ \hfill -\frac{r\beta x_2^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill -\frac{r\beta {\eta }_q{x}_2^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill -\frac{r\beta {\eta }_h{x}_2^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill 0\hfill \\ \hfill \frac{\beta x_1^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill \frac{\beta {\eta }_q{x}_1^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill \frac{\beta {\eta }_h{x}_1^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill 0\hfill \\ \hfill \frac{r\beta x_2^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill \frac{r\beta {\eta }_q{x}_2^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill \frac{r\beta {\eta }_h{x}_2^{\ast }}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}\hfill & \hfill 0\hfill \\ \hfill -k_3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -k_4\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\alpha }_1\hfill & \hfill {\alpha }_2\hfill & \hfill -k_5\hfill & \hfill 0\hfill \\ \hfill {\varphi }_1\hfill & \hfill {\varphi }_2\hfill & \hfill {\varphi }_3\hfill & \hfill -k_6\hfill \end{array}\right)\text{.}$$

Consider the case when ${\mathcal{R}}_q=1$. Furthermore, suppose that $\beta$ is chosen as a bifurcation parameter. Solving for $\beta$ from ${\mathcal{R}}_q=1$ gives

$${\beta }^{\ast }=\frac{k_1{k}_2{k}_3{k}_4{k}_5}{{\nu }_1{M}_1+r{\nu }_2{M}_2}\text{,}$$

where

$$M_1={\eta }_1{k}_2{k}_3{k}_4{k}_5+{\sigma }_1{k}_2{k}_4{k}_5+{\eta }_h{\alpha }_1{\sigma }_1{k}_2{k}_4\text{,}$$

$$M_2={\eta }_2{\eta }_q{k}_1{k}_3{k}_4{k}_5+{\eta }_q{\sigma }_2{k}_1{k}_3{k}_5+{\eta }_h{\alpha }_2{\sigma }_2{k}_1{k}_3\text{.}$$

The transformed system (15), with $\beta ={\beta }^{\ast }$, has a hyperbolic equilibrium point (i.e., the linearized system has a simple eigenvalue with zero real part, and all other eigenvalues have negative real part), so that the center manifold theory [31], [32] can be used to analyze the dynamics of (15) near $\beta ={\beta }^{\ast }$.

It can be shown that the right eigenvector of $J\left({\mathcal{E}}_0\right){|}_{\beta ={\beta }^{\ast }}$, denoted by $w$, is given by $w={(w_1,w_2,\dots ,w_7,w_8)}^T$, where,

$$w_1=\frac{k_2{w}_4+(\mu +{\psi }_1)w_2}{\gamma }\text{,}{w}_2=\left[\frac{-\gamma }{\mu (\mu +\gamma +{\psi }_1)}\right][k_1{w}_3+k_2{w}_4(\mu +\gamma )]\text{,}$$

$$w_5=\frac{{\sigma }_1{w}_3}{k_3}\text{,}{w}_6=\frac{{\sigma }_2{w}_4}{k_4}\text{,}{w}_7=\frac{{\alpha }_1{w}_5+{\alpha }_2{w}_6}{k_5}\text{,}$$

$$w_8=\frac{{\varphi }_1{w}_5+{\varphi }_2{w}_6+{\varphi }_{3}w7}{k_6}\text{,}{w}_3>0\text{,}{w}_4>0\text{.}$$

Similarly, $J\left({\mathcal{E}}_0\right){|}_{\beta ={\beta }^{\ast }}$ has a left eigenvector, $v$ given by $v=(v_1,v_2,\dots ,v_7,v_8)$, where,

$$v_1=0\text{,}{v}_2=0\text{,}{v}_7=\frac{\beta {\eta }_h{x}_1^{\ast }{v}_3}{k_5(x_1^{\ast }+{\eta }_q{x}_2^{\ast })}+\frac{r\beta {\eta }_h{x}_1^{\ast }{v}_4}{k_5(x_1^{\ast }+{\eta }_q{x}_2^{\ast })}\text{,}$$

$$v_6=\frac{{\alpha }_2{v}_7}{k_4}+\frac{\beta {\eta }_q{x}_1^{\ast }{v}_3}{k_4(x_1^{\ast }+{\eta }_q{x}_2^{\ast })}+\frac{r\beta {\eta }_q{x}_1^{\ast }{v}_4}{k_4(x_1^{\ast }+{\eta }_q{x}_2^{\ast })}\text{,}$$

$$v_5=\frac{{\alpha }_1{v}_7}{k_3}+\frac{\beta x_1^{\ast }{v}_3}{k_3(x_1^{\ast }+{\eta }_q{x}_2^{\ast })}+\frac{r\beta x_1^{\ast }{v}_4}{k_3(x_1^{\ast }+{\eta }_q{x}_2^{\ast })}\text{,}{v}_3>0\text{,}{v}_4>0\text{,}{v}_8=0\text{.}$$

Consequently, it follows that the associated bifurcation coefficients, $a$ and $b$ (defined in Theorem 4.1 of [32]), are given, respectively, by

$$a=\sum _{k,i,j=1}^8{v}_k{w}_i{w}_j\frac{{\partial }^2{f}_k(0,0)}{\partial x_i\partial x_j}=(r{\eta }_q{v}_4{w}_4-{\eta }_q{v}_3{w}_4)\left(\frac{\mu +{\sigma }_2}{\mu +{\psi }_1+{\eta }_q\gamma }\right)-\frac{(r{v}_4{x}_2^{\ast }+v_3{x}_1^{\ast })}{k_3{k}_4{k}_5{k}_6}(a_1+a_2+a_3+a_4)\text{,}$$ (16)

$$b=\sum _{k,i=1}^8{v}_k{w}_i\frac{{\partial }^2{f}_k(0,0)}{\partial x_i\partial {\beta }^{\ast }}=\frac{(v_3{x}_1^{\ast }+r{v}_4{x}_2^{\ast })({\eta }_1{w}_3+{\eta }_2{\eta }_q{w}_4+w_5+{\eta }_q{w}_6+{\eta }_h{w}_7)}{x_1^{\ast }+{\eta }_q{x}_2^{\ast }}>0\text{,}$$

where

$$a_1=k_3{k}_4{k}_5{k}_6{w}_3+k_3{k}_4{k}_5{k}_6{\eta }_q{w}_4\text{,}$$

$$a_2=k_4{k}_5{k}_6{\sigma }_1{w}_3+k_3{k}_5{k}_6{\eta }_q{\sigma }_2{w}_4\text{,}$$

$$a_3=k_4{k}_6{\eta }_h{\alpha }_1{\sigma }_1{w}_3+k_3{k}_6{\eta }_h{\alpha }_2{\sigma }_2{w}_4\text{,}$$

$$a_4=k_4{k}_5{\varphi }_1{\sigma }_1{w}_3+k_3{k}_5{\varphi }_2{\sigma }_2{w}_4+k_4{\varphi }_3{\alpha }_1{\sigma }_1{w}_3+k_3{\varphi }_3{\alpha }_2{\sigma }_2{w}_4\text{.}$$

Since the bifurcation coefficient $b$ is always positive, it follows (from Theorem 4.1 of [32]) that the system (15) will undergo backward bifurcation if the bifurcation coefficient $a$ is positive. This result is summarized below.

Theorem 5

The transformed model (15) , or equivalently (1) , exhibits backward bifurcation at ${\mathcal{R}}_q=1$ whenever the bifurcation coefficient, $a$ , given by (16) , is positive.

It should be noted from (16) that the bifurcation coefficient $a$, is positive whenever

$$r>\frac{{\eta }_q{v}_3{w}_4(\mu +{\sigma }_2)}{v_4({\eta }_q{w}_4-x_2^{\ast })(\mu +{\psi }_1+{\eta }_q\gamma )}+\frac{v_3{x}_1^{\ast }(a_1+a_2+a_3+a_4)}{v_4({\eta }_q{w}_4-x_2^{\ast })k_3{k}_4{k}_5{k}_6}=r_c\text{.}$$

Thus, the transformed model (15), exhibits backward bifurcation at ${\mathcal{R}}_q=1$ whenever $r>r_c$. Furthermore, it should be noted that for the case when quarantined susceptible individuals do not acquire infection during quarantine (i.e., $r=0$), the bifurcation coefficient $a$ becomes

$$a=-{\eta }_q{v}_3{w}_4\left(\frac{\mu +{\sigma }_2}{\mu +{\psi }_1+{\eta }_q\gamma }\right)-\frac{v_3{x}_1^{\ast }}{k_3{k}_4{k}_5{k}_6}(a_1+a_2+a_3+a_4)<0$$

since $a_i>0$ for $i=1,\dots ,4$ (since all the model parameters are non-negative). Thus, since $a<0$ in this case, it follows from Theorem 4.1 of [32] that the model (1) will not exhibit backward bifurcation if $r=0$. In other words, this study shows that the backward bifurcation property of the model (1) arises due to the infection of susceptible individuals in quarantine. This result is consistent with Theorem 3 (where it was shown that the DFE of the model (1) with $r=0$ is globally-asymptotically stable).