Abstract
The problem of finding a better immunization strategy for controlling the spreading of the epidemic with limited resources has attracted much attention since its great theoretical significance and wide application. In this letter, we propose a novel and successful targeted immunization strategy based on percolation transition. Our strategy repeatedly looks for the critical nodes for immunizing. The critical node, which leads to the emergence of the giant connected component as the degree threshold increases, is determined when the maximal second-largest connected component disappears. To test the effectiveness of the proposed method, we conduct the experiments on several artificial networks and real-world networks. The results show that the proposed method outperforms the degree centrality strategy, the betweenness centrality strategy and the adaptive degree centrality strategy with 18% to 50% fewer immunized nodes for same amount of immunization.
Keywords: Immunization strategy, Percolation transition, Degree threshold, Critical nodes
Highlights
-
•
We propose a targeted immunization strategy based on percolation transition.
-
•
A degree threshold is developed to find the critical node for immunization.
-
•
The critical node emerges along with the emergence of giant connected component.
-
•
Our method hold the advantage of 18% to 50% compared to other strategies.
1. Introduction
Epidemic spreading and controlling in complex networks has attracted much attention from various research fields [1], [2], [3], [4]. In the real world, there are usually only a few infection sources in the early stage of the spreading process. However, it is possible that these infected sources spread the epidemic to large area in the world within a few days if the epidemic is ineffectively controlled [5], such as the outbreak of severe acute respiratory syndrome (SARS) and swine flu [6]. An immediate concern, therefore, is the development of the effective countermeasures against epidemics, wherein immunization science plays an important, if not critical, role. A feasible and effective immunization strategy can save thousands of human lives with low cost. Over the past decades, many immunization strategies have been extensively investigated [7], [8], [9]. So far, it is still an open problem.
In the complex networks, numerous strategies have been proposed to immunize nodes, such as random immunization strategy [10], target immunization strategy [10], acquaintance immunization strategy [11], [12], active immunization strategy [13] and other related scenarios [14], [15], [16]. For a given fraction of immunized nodes, a good immunization strategy should make the susceptible size, which is always dependent on the largest connected component of a network, as small as possible [17], [6]. It is widely accepted that the most efficient immunization strategies are based on targeted strategies [18], [19], [17]. The target immunization, making use of the network heterogeneity characteristic, is first to identify the importance of each node and then removes the nodes from the highest importance to the lowest until the network reaches the certain immunization fraction.
As degree is the basic and the most accessible property of networks, numerous efficient immunization strategies are directly or indirectly based on it [11], [12], [20], [21], [22]. The degree centrality immunization strategy makes use of the network heterogeneity characteristic and selects nodes with larger degree for immunization [20]. It was also extended to the multilayer networks in [21], [22]. However, those strategies always neglect some important nodes without larger degree, such as in community networks. Recently, percolation transition in complex networks has attracted people's attention, including the universal loopless percolation transition by randomly removing links from networks [23], traffic percolation by decreasing the velocity threshold of the roads [24] and others [25], [26].
In this letter, motivated by Refs. [24], [27], we proposed a novel immunization strategy. Following the percolation transition in Ref. [24] (where the giant cluster of local flows disintegrates when the second largest cluster reaches its maximum), the main idea of the proposed method is to find the critical nodes, which lead to the emergence of the giant connected component, for immunizing. Different from the degree centrality immunization strategy, the proposed method can find the critical nodes which may be not holding the largest degree. In addition, our method works only based on the degree property compared to Refs. [23], [24]. To test the performance of our proposed strategy, we conduct the experiments on Erdős–Rényi (ER) networks [28], scale-free (SF) networks [29] and also several real-world networks. The results show that the proposed method has 18% to 50% improvement than the degree centrality strategy, the betweenness centrality strategy and the adaptive degree centrality strategy (for the networks studied here).
The rest of the letter is organized as follows. In Section 2, the proposed strategy is described; in Section 3, related experiments are conducted and experimental results are evaluated and conclusions are presented in Section 4.
2. Method
Consider a network where N and E are the set of nodes and edges, respectively. For a given degree threshold , let be the subnetwork of G, which is constructed by the whole nodes whose degree values are not larger than and the whole edges where nodes and .
Let and correspond to the largest and the second-largest connected components of , respectively. In this way, the function and of are constructed. The critical degree threshold is determined as follows:
| (1) |
s.t.
| (2) |
Let be the set of incoming nodes which is the node set difference between and where is the node set of . Order the node in as (assign a unique label to each node), and then orderly add them into the network one by one. In this way, the function is constructed and the critical node is defined as:
| (3) |
s.t.
| (4) |
where denotes the number of nodes of the second-largest component of the network composed with the nodes of and the nodes .
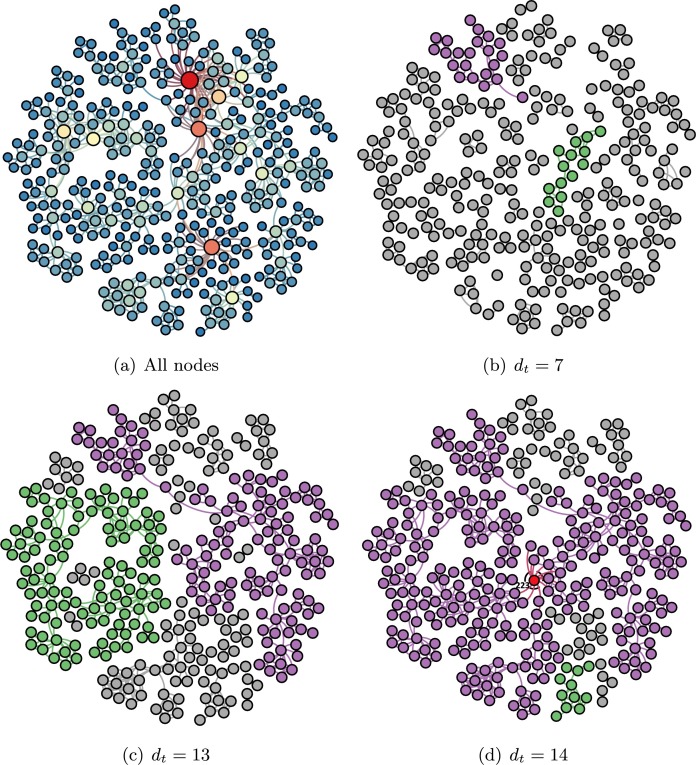
To illustrate how to determine the critical node, the largest connected component of the network of coauthorships between scientists [30], [31] is considered. In order to clearly understand, we obtain the experimental network (Fig. 1 (a)) by removing the little isolated components after the removal of node 51 and node 52. After a node is immunized, id values are renumbered, but the ordering of nodes induced by the ids remains the same as in [31]. From Fig. 1(b) to Fig. 1(c), increases as increases. In Fig. 1(d), the critical degree threshold is obtained, and then the critical node is determined. The details of and of are shown in Fig. 2 where the critical node is that connecting the largest connected component with the maximal second-largest connected component. We also obtain the other critical nodes until the predetermined fraction of nodes to immunize by repeating this process on the largest connected component of the network after the critical node removal.
Fig. 1.
Critical node of the network. (a) A representation of all nodes. The size of a node is proportional to its degree: node 4 holds the largest degree. (b) A representation of subnetwork when . The largest and second-largest connected component are clarified by purple and green, respectively. And others with gray belong to the smaller connected component. (c) A representation of subnetwork when . (d) The critical node (red) is obtained when . (For interpretation of the references to color in this figure, the reader is referred to the web version of this article.)
Fig. 2.
(a) The number of nodes of the largest (LCC) and second-largest (SLCC) connected component (black square) and (red circle) versus the degree threshold . (b) The number of nodes in as a function of and the number of nodes of the second-largest component versus ranked label j. The critical node (223) is determined as the maximal second-largest connected component disappears. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article.)
3. Results
To test the effectiveness of the proposed strategy, critical-node strategy (CNS), we plot F (the fraction of the size of the largest connected component that can be infected) versus q (the fraction of immunized nodes) for several artificial networks (including Erdős–Rényi (ER) networks [28] and Barabási–Albert (BA) model networks [29] in Fig. 3 ) and empirical networks from different fields in Fig. 4 : the electrical power grid of the western United States (Power Grid) [32], [33], [34], a trust network of mutual signing based on the pretty good privacy algorithm (PGP network) [35], [36], [37], [38], collaboration network of arxiv condensed matter (ca-CondMat) [39], [40], and email communication network from Enron (email-Enron) [41], [42], [43]. The detailed information of the networks is shown in Table 1 . Note that we here remove 58 self-loop edges from the source data of ca-CondMat.
Fig. 3.
The fraction F of the size of the largest connected component that can be infected versus the fraction of immunized nodes q for DCS, BCS, ADCS and CNS for (a) ER network with N = 104 and 〈k〉 = 3.50, (b) BA network with N = 104 and 〈k〉 = 4.0. We also show the error bars in F, which are derived from simulating realization.
Fig. 4.
The fraction F of the size of the largest connected component versus the fraction of immunized nodes q for DCS, EGP, ADCS and CNS for (a) the Power Grid network, (b) the PGP network, (c) the ca-CondMat network, (d) the email-Enron network.
Table 1.
Some statistical properties of the real-world networks: network size (n), edge number (m), average degree 〈k〉, maximum degree , degree heterogeneity (), degree assortativity (r), clustering coefficient (〈C〉).
| Network | n | m | H | r | |||
|---|---|---|---|---|---|---|---|
| Power Grid | 4941 | 6594 | 2.6691 | 19 | 1.4504 | 0.0035 | 0.0801 |
| PGP | 10 680 | 24 316 | 4.5536 | 205 | 4.1465 | 0.2382 | 0.2659 |
| ca-CondMat | 23 133 | 93 439 | 8.0784 | 279 | 2.7305 | 0.1340 | 0.6334 |
| email-Enron | 36 692 | 183 831 | 10.0202 | 1383 | 13.9796 | −0.1108 | 0.4970 |
We compare the efficiency of the CNS to the degree centrality strategy (DCS), the betweenness centrality strategy (BCS), the equal graph partitioning strategy (EGP) and the adaptive degree centrality strategy (ADCS). In the ADCS we immunize a node by recalculating the importance of every node after the immunized node removal. For both of ER and BA networks, the CNS exhibits notable advantage of less nodes to be immunized compared to the other strategies. Regarding to threshold point , where F approaches 0 , the CNS shows over 50% improvement than the DCS and BCS, 18% in ER network and 26% in BA network than ADCS. For the real-world networks, the CNS also shows a larger improvement, over 50%, against both DCS, and gives an advantage of over 30% compared to ADCS.
To further evaluate the performance of the proposed strategy, the susceptible-infectious-recovery (SIR) epidemic spreading model [44], [45] is used to evaluate the immunization effectiveness on the BA network, the PGP network, the ca-CondMat network and the email-Enron network. In the SIR model, each node belongs to one state of the susceptible state, the infected state and the recovered state. At the initial stage, the immunized nodes are removed from the network, including the incident links. We set one node that is randomly selected from the remaining network or networks (may be some disconnected subnetworks after immunized) to be infected to investigate the transmissibility of this node, and the others to be susceptible. At each time step, the infected nodes infect its susceptible neighbors with infection rate λ, and they recover with rate η. The recovered nodes are removed from the network. This process is repeated until there is no infected node in the network. The simulation results are shown in Fig. 5 and Fig. 6 . In the simulations we use and for strong infection situation. For all of the networks studied here, the recovered fraction is significantly (42 to 77 times) lower when using the CNS compared to the ADCS with the same fraction of immunization doses.
Fig. 5.
Infected fraction and recovered fraction of time steps for the SIR simulation. Comparison between the CNS and ADCS for (a) immunizing a fraction q = 0.11 of the nodes in the BA network with α = 2.6, N = 104 and 〈k〉 = 4, (b) immunizing a fraction q = 0.045 of the nodes in the PGP network, (c) immunizing a fraction q = 0.12 of the nodes in the ca-CondMat network, (d) immunizing a fraction q = 0.075 of the nodes in the email-Enron network. 104 independent simulation for each network.
Fig. 6.
Final recovered fraction versus the fraction of immunized nodes q for ADCS and CNS for (a) BA network with N = 104 and 〈k〉 = 4, (b) the PGP network, (c) the ca-CondMat network, (d) the email-Enron network. 104 independent simulation for each network.
In Fig. 7 , we also investigate the threshold of the network parameters of ER and BA networks for different immunization strategies. The threshold is defined as the fraction of nodes immunized or removed for which F approaches 0 . In all networks tested here, the proposed strategy exhibits obviously effectiveness of lower compared to the other immunization strategies. Although increases with increasing the average degree , the curves of CNS are far below curves of DCS, BCS and ADCS.
Fig. 7.
The threshold of average node degree 〈k〉 for the DCS, BCS, ADCS and CNS for (a) ER networks with N = 104, (b) BA networks with N = 104.
Finally, comparing Fig. 4(a) and Fig. 4(d), the results show that the proposed method is more effective in assortatively mixed networks where high degree nodes tend to connect to other high degree nodes, which is a common feature for many real networks [46], [47]. In the disassortative networks, high degree nodes mostly have neighbors with a small number of connections. Our strategy identifies the critical node only based on the largest and the second-largest connected components. It is expected that the proposed strategy will immunize or remove some low degree nodes (shown as Fig. 8 (a) where and Fig. 8(b) where ), which is the critical node of two components, at the early stage. However, those components are also connected by some high degree nodes. The immunization threshold is quickly reached after those low degree nodes removal ( on the BA network and on the email-Enron network). To summarize, the proposed method is more effective in assortatively mixed networks. In the disassortative networks, our strategy performs worse than other methods when low immunized fraction of nodes is conducted. However, it will outperform the others if we increase the immunized fraction of nodes.
Fig. 8.
The degree of nodes versus the fraction of immunized nodes q for BCS, ADCS and CNS for (a) the BA network, (b) the email-Enron network, (c) the PGP network, (d) the Power Grid network.
4. Conclusion
In this letter, we have developed and applied a novel method as an efficient network immunization strategy based on the percolation transition. The proposed strategy chooses the immunization fraction of nodes by repeatedly looking for the critical node, which leads to the emergence of the giant connected component as the degree threshold increases, in the largest connected network. To test the performance of the proposed method, we conduct the experiments on several artificial and real-world networks. The results show that the proposed method is more effective in assortatively mixed networks. In the disassortative networks, our strategy performs worse than other methods when low immunized fraction of nodes is conducted. However, it will outperform the others if we increase the immunized fraction of nodes. To summarize, our strategy holds the advantage of 18% to 50% compared to the degree centrality strategy, the betweenness centrality strategy and the adaptive degree centrality strategy.
Acknowledgements
The authors greatly appreciate the reviews' suggestions. The work is partially supported by National Natural Science Foundation of China (Grant No. 61174022), Specialized Research Fund for the Doctoral Program of Higher Education (Grant No. 20131102130002), R&D Program of China (2012BAH07B01), National High Technology Research and Development Program of China (863 Program) (Grant No. 2013AA013801), the open funding project of State Key Laboratory of Virtual Reality Technology and Systems, Beihang University (Grant No. BUAA-VR-14KF-02).
Communicated by C.R. Doering
References
- 1.Pastor-Satorras R., Vespignani A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2001;86:3200. doi: 10.1103/PhysRevLett.86.3200. [DOI] [PubMed] [Google Scholar]
- 2.Saumell-Mendiola A., Serrano M.Á., Boguñá M. Epidemic spreading on interconnected networks. Phys. Rev. E. 2012;86 doi: 10.1103/PhysRevE.86.026106. [DOI] [PubMed] [Google Scholar]
- 3.Zhou J., Xiao G., Cheong S.A., Fu X., Wong L., Ma S., Cheng T.H. Epidemic reemergence in adaptive complex networks. Phys. Rev. E. 2012;85 doi: 10.1103/PhysRevE.85.036107. [DOI] [PubMed] [Google Scholar]
- 4.Buono C., Alvarez-Zuzek L.G., Macri P.A., Braunstein L.A. Epidemics in partially overlapped multiplex networks. PLoS ONE. 2014;9 doi: 10.1371/journal.pone.0092200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Colizza V., Barrat A., Barthelemy M., Valleron A.-J., Vespignani A. Modeling the worldwide spread of pandemic influenza: baseline case and containment interventions. PLoS Med. 2007;4:95–110. doi: 10.1371/journal.pmed.0040013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schneider C.M., Mihaljev T., Havlin S., Herrmann H.J. Suppressing epidemics with a limited amount of immunization units. Phys. Rev. E. 2011;84 doi: 10.1103/PhysRevE.84.061911. [DOI] [PubMed] [Google Scholar]
- 7.Bauch C.T., Earn D.J. Vaccination and the theory of games. Proc. Natl. Acad. Sci. USA. 2004;101:13391–13394. doi: 10.1073/pnas.0403823101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hébert-Dufresne L., Allard A., Young J.-G., Dubé L.J. Global efficiency of local immunization on complex networks. Sci. Rep. 2013;3:2171. doi: 10.1038/srep02171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Vespignani A. Modelling dynamical processes in complex socio-technical systems. Nat. Phys. 2012;8:32–39. [Google Scholar]
- 10.Pastor-Satorras R., Vespignani A. Immunization of complex networks. Phys. Rev. E. 2002;65 doi: 10.1103/PhysRevE.65.036104. [DOI] [PubMed] [Google Scholar]
- 11.Cohen R., Havlin S., Ben-Avraham D. Efficient immunization strategies for computer networks and populations. Phys. Rev. Lett. 2003;91 doi: 10.1103/PhysRevLett.91.247901. [DOI] [PubMed] [Google Scholar]
- 12.Gallos L.K., Liljeros F., Argyrakis P., Bunde A., Havlin S. Improving immunization strategies. Phys. Rev. E. 2007;75 doi: 10.1103/PhysRevE.75.045104. [DOI] [PubMed] [Google Scholar]
- 13.Fu X., Small M., Walker D.M., Zhang H. Epidemic dynamics on scale-free networks with piecewise linear infectivity and immunization. Phys. Rev. E. 2008;77 doi: 10.1103/PhysRevE.77.036113. [DOI] [PubMed] [Google Scholar]
- 14.Lü L., Zhang Y.-C., Yeung C.H., Zhou T. Leaders in social networks, the delicious case. PLoS ONE. 2011;6 doi: 10.1371/journal.pone.0021202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gong K., Tang M., Hui P.M., Zhang H.F., Younghae D., Lai Y.-C. An efficient immunization strategy for community networks. PLoS ONE. 2013;8 doi: 10.1371/journal.pone.0083489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang W., Tang M., Zhang H.-F., Gao H., Do Y., Liu Z.-H. Epidemic spreading on complex networks with general degree and weight distributions. Phys. Rev. E. 2014;90 doi: 10.1103/PhysRevE.90.042803. [DOI] [PubMed] [Google Scholar]
- 17.Chen Y., Paul G., Havlin S., Liljeros F., Stanley H.E. Finding a better immunization strategy. Phys. Rev. Lett. 2008;101 doi: 10.1103/PhysRevLett.101.058701. [DOI] [PubMed] [Google Scholar]
- 18.Holme P., Kim B.J., Yoon C.N., Han S.K. Attack vulnerability of complex networks. Phys. Rev. E. 2002;65 doi: 10.1103/PhysRevE.65.056109. [DOI] [PubMed] [Google Scholar]
- 19.Gallos L.K., Cohen R., Argyrakis P., Bunde A., Havlin S. Stability and topology of scale-free networks under attack and defense strategies. Phys. Rev. Lett. 2005;94 doi: 10.1103/PhysRevLett.94.188701. [DOI] [PubMed] [Google Scholar]
- 20.Cohen R., Havlin S. Cambridge University Press; 2010. Complex Networks: Structure, Robustness and Function. [Google Scholar]
- 21.Zhao D., Wang L., Li S., Wang Z., Wang L., Gao B. Immunization of epidemics in multiplex networks. PLoS ONE. 2014;9 doi: 10.1371/journal.pone.0112018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Buono C., Braunstein L. Immunization strategy for epidemic spreading on multilayer networks. Europhys. Lett. 2015;109:26001. [Google Scholar]
- 23.Kawamoto H., Takayasu H., Jensen H.J., Takayasu M. Precise calculation of a bond percolation transition and survival rates of nodes in a complex network. PLoS ONE. 2015;10 doi: 10.1371/journal.pone.0119979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Li D., Fu B., Wang Y., Lu G., Berezin Y., Stanley H.E., Havlin S. Percolation transition in dynamical traffic network with evolving critical bottlenecks. Proc. Natl. Acad. Sci. USA. 2015;112:669–672. doi: 10.1073/pnas.1419185112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhao J.-H., Zhou H.-J., Liu Y.-Y. Inducing effect on the percolation transition in complex networks. Nat. Commun. 2013;4 doi: 10.1038/ncomms3412. [DOI] [PubMed] [Google Scholar]
- 26.Colomer-de Simón P., Boguñá M. Double percolation phase transition in clustered complex networks. Phys. Rev. X. 2014;4 [Google Scholar]
- 27.Erdős P., Rényi A. On the evolution of random graphs. Magy. Tud. Akad. Mat. Kut. Intéz. Közl. 1960;5:17–61. [Google Scholar]
- 28.Erdős P., Rényi A. On random graphs I. Publ. Math. (Debr.) 1959;6:290–297. [Google Scholar]
- 29.Barabási A.-L., Albert R., Jeong H. Mean-field theory for scale-free random networks. Physica A. 1999;272:173–187. [Google Scholar]
- 30.Newman M.J.E. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E. 2006;74 doi: 10.1103/PhysRevE.74.036104. [DOI] [PubMed] [Google Scholar]
- 31.2015. http://www-personal.umich.edu/~mejn/netdata/
- 32.Watts D.J., Strogatz S.H. Collective dynamics of ‘small-world’ networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 33.Barabási A.-L., Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- 34.2015. https://networkdata.ics.uci.edu/data.php?id=107
- 35.Boguñá M., Pastor-Satorras R., Díaz-Guilera A., Arenas A. Models of social networks based on social distance attachment. Phys. Rev. E. 2004;70 doi: 10.1103/PhysRevE.70.056122. [DOI] [PubMed] [Google Scholar]
- 36.Duch J., Arenas A. Community detection in complex networks using extremal optimization. Phys. Rev. E. 2005;72 doi: 10.1103/PhysRevE.72.027104. [DOI] [PubMed] [Google Scholar]
- 37.Lü Z., Huang W. Iterated tabu search for identifying community structure in complex networks. Phys. Rev. E. 2009;80 doi: 10.1103/PhysRevE.80.026130. [DOI] [PubMed] [Google Scholar]
- 38.2015. https://www.cs.bris.ac.uk/~steve/networks/peacockpaper/
- 39.Leskovec J., Kleinberg J., Faloutsos C. Graph evolution: densification and shrinking diameters. ACM Trans. Knowl. Discov. Data. 2007;1:2. [Google Scholar]
- 40.2015. http://snap.stanford.edu/data/ca-CondMat.html
- 41.Klimt B., Yang Y. Introducing the Enron corpus. Proceedings of the CEAS 2004; Mountain View, CA; 2004. [Google Scholar]
- 42.Leskovec J., Lang K.J., Dasgupta A., Mahoney M.W. Community structure in large networks: natural cluster sizes and the absence of large well-defined clusters. Internet Math. 2009;6:29–123. [Google Scholar]
- 43.2015. http://snap.stanford.edu/data/email-Enron.html
- 44.Newman M.E.J. Spread of epidemic disease on networks. Phys. Rev. E. 2002;66 doi: 10.1103/PhysRevE.66.016128. [DOI] [PubMed] [Google Scholar]
- 45.Castellano C., Pastor-Satorras R. Thresholds for epidemic spreading in networks. Phys. Rev. Lett. 2010;105 doi: 10.1103/PhysRevLett.105.218701. [DOI] [PubMed] [Google Scholar]
- 46.Newman M.E.J. Assortative mixing in networks. Phys. Rev. Lett. 2002;89 doi: 10.1103/PhysRevLett.89.208701. [DOI] [PubMed] [Google Scholar]
- 47.Foster D.V., Foster J.G., Grassberger P., Paczuski M. Clustering drives assortativity and community structure in ensembles of networks. Phys. Rev. E. 2011;84 doi: 10.1103/PhysRevE.84.066117. [DOI] [PubMed] [Google Scholar]