Pacing a small cage: mutation and RNA viruses

Abstract

RNA viruses have an extremely high mutation rate, and we argue that the most plausible explanation for this is a trade-off with replication speed. We suggest that research into further increasing this mutation rate artificially as an antiviral treatment requires a theoretical reevaluation, especially relating to the so-called error threshold. The main evolutionary consequence of a high mutation rate appears to have been to restrict RNA viruses to a small genome; they thus rapidly exploit a limited array of possibilities. Investigating this constraint to their evolution, and how it is occasionally overcome, promises to be fruitful. We explain the many terms used in investigating RNA viral evolution and highlight the specific experimental and comparative work that needs to be done.

The mutation rate of RNA viruses

The single most important feature of RNA viruses is their high mutation rate. Estimates of this rate fall between 0.4 and 1.1 nucleotide errors per genome per round of replication (excluding some outlying retroviruses, which we discuss later) [1]. These mutation rates affect every aspect of virus biology and are at least a hundred-fold higher than those estimated for DNA viruses and other DNA microbes [1]. The difference in rates appears to result from the lack of proofreading by the RNA-dependent polymerases of RNA viruses [2]: the DNA-dependent replicative polymerases of many other organisms have similar misincorporation rates, on the order of 10⁻⁴ to 10⁻⁵ per base per round of replication, but the error rate is then reduced to 10⁻⁵ to 10⁻⁷ by subsequent proofreading [3].

At its simplest, an RNA virus is a single RNA molecule within a protein shell that enters a host cell and is translated, with the resulting proteins initiating viral replication and leading to the production of many more viral particles by the host cell. At present, there are complete genome sequences for ∼500 species of such single-stranded (ss) positive-sense viruses (http://www.ncbi.nlm.nih.gov/genomes/VIRUSES/viruses.html), which infect animals, plants and bacteria (and include poliovirus, foot-and-mouth disease virus [FMDV] and the ‘common cold’ rhinoviruses). The other RNA virus groups, each with ∼100 completely sequenced genomes, are the ss negative-sense viruses (in which the genomic RNA is copied to form mRNA immediately following entry into the cell, and which include influenza, measles, mumps and rabies viruses); the double-stranded viruses (which include the important diarrhoea-causing rotaviruses and the veterinary pest bluetongue); and the retrotranscribing viruses, which convert RNA to DNA as part of their replication cycle (including hepatitis B virus and the retrovirus HIV).

RNA viruses feature prominently in the list of the most serious infectious diseases. The second and sixth biggest killers worldwide are RNA viruses (HIV and measles, respectively), and several RNA viruses contribute significantly to the first and third biggest killers: lower respiratory infections and diarrhoea, respectively [4]. By contrast, although a similar number of DNA viral species are known (whose replication involves DNA to DNA copying), none of these appear in the top 30 of this list.

Here we ask why RNA viruses have such high mutation rates and what are the consequences of these, both for the virus population and their human hosts. We suggest that the most likely cause, and one that is amenable to further empirical study, is a trade-off between replication fidelity and replication speed. An important consequence, which is now exploited therapeutically, is that RNA viruses might be particularly susceptible to further elevation of their mutation rate; however, we argue that explanations for this involving a so-called error threshold might be misleading. The high mutation rate of RNA viruses affects their importance as human pathogens: it can facilitate rapid escape from adaptive immune responses and from drug treatment. However, a less-studied consequence is that high mutation rates are likely to constrain viral evolutionary change. Understanding the nature of this constraint, and perhaps more importantly what enables RNA viruses to occasionally escape it, will lead to valuable insights.

Causes of a high mutation rate

Hypotheses to explain why RNA viruses have such a high mutation rate fall into three main categories.

Life history

Many RNA viruses infect hosts that have adaptive immune systems (defences which learn to recognize and destroy invading pathogens) 5, 6. A high mutation rate might be an adaptation to this mode of life because viruses would be more likely to generate mutations enabling them to remain undetected by the immune system of the host for longer. Such mutations provide a striking exception to the general argument that, because most mutations are harmful, natural selection will cause the mutation rate to decrease to the point where it is balanced by the prohibitive metabolic cost of perfect replication fidelity [7].

Although models for RNA viruses have been proposed that balance beneficial mutations against those with harmful effects [8], there is no good correlation between mutation rate and life history [9]. The mutation rates of RNA viruses that attack bacteria, and hence do not face an adaptive immune response, are also high 1, 10, and many RNA viruses do not use mutation as a means of evading the adaptive immune response; for example, many use a ‘hit-and-run’ strategy of being transmitted from the host before the adaptive immune system can respond [5]. Thus, the high mutation rate of RNA viruses cannot readily be ascribed to their life history.

Evolutionary constraint

The high mutation rate could be an evolutionary constraint for RNA viruses. In other words, the high error rate of RNA-dependent polymerases might be something that RNA viruses have simply been unable to improve upon [1]. Also, unlike DNA viruses, RNA viruses do not have the option of using host polymerases for their replication (there are no RNA-dependent polymerases in the host). This is another tempting explanation but, for the reasons described below, it is most likely incorrect as well.

The natural variation in mutation rates among RNA viruses is incompatible with such a constraint. A low rate of mutation has been reported in the polymerase of yellow fever virus (a per genome rate of 0.002 [11], although this excludes lethal mutations, which, if included, could potentially increase the rate by a factor of two [12]). Furthermore, retroviruses have a broader range of rates than other RNA viruses (extending down to 0.06 mutations per genome per round of replication [13]). Perhaps more significantly, higher-fidelity RNA viral polymerases (which lead to a lower mutation rate) can be created in vitro. For example, repeated passage of poliovirus in the presence of the chemical mutagen ribavirin produced a mutant polymerase, differing by only one base, which showed higher replication fidelity than the wild type [14]. A ribavirin-resistant polymerase has also been selected for in FMDV [15]. Thus, RNA viruses can acquire a lower mutation rate, and it seems reasonable to assume that the option of reducing the mutation rate is open to natural populations, but is selected against.

There is also wide variation in the level of recombination, from several crossovers per round of replication in HIV [16] to effectively clonal replication in some negative-sense viruses [17]. This variation seems inconsistent with a struggle against harmfully high mutation rates, given that, in theory, recombination could alleviate a high mutational load [18].

Trade-off with replication speed

We believe that a more probable explanation for the high mutation rate of RNA viruses lies in a putative fitness cost to replication fidelity. Such a cost could be a reduced replication rate: viruses might be able to replicate either quickly or accurately, but not both [19].

Currently, there are few data on the relationship between these variables for RNA viruses. In support of this hypothesis, in vitro studies of the reverse transcriptase (RT) of HIV-1 showed a negative relationship between the rate of polymerisation and the rate of mutation [20], and vesicular stomatitis virus (VSV) clones with reduced mutation rates had a reduced competitive fitness (lower growth in cell culture compared with the wild type) [21]. There is also evidence for such a trade-off within DNA viruses: mutants of T4 phage differing by only one base pair in their DNA polymerase exhibited variation in mutation rate over four orders of magnitude [22]. This study found evidence for a cost to fidelity in the form of a reduced viral replication rate, with increased proofreading appearing to also lead to the removal of correct nucleotides.

Contrary to this hypothesis, another study of HIV-1 RT found that replacement of a methionine by a valine at one specific position in the same enzyme reduced the mutation rate, whereas replacement by an alanine increased it; however, both mutants showed a higher rate of polymerisation [23]. Also, a mutant poliovirus replicase with increased fidelity did not appear to have a reduced replication rate [24].

Consequences of a high mutation rate

We propose that the high mutation rate of RNA viruses has three main consequences for their evolution.

Population viability

Given that most mutations are harmful, high mutation rates might pose a problem for RNA viruses, and artificially raising the mutation rate even further could represent a viable antiviral strategy. This is the reasoning behind so-called lethal mutagenesis therapy 25, 26. The chemical ribavirin is used to treat several viral infections in humans including hepatitis C virus (HCV) and respiratory syncytial virus (RSV), and it is thought (although not conclusively demonstrated) that its effect is due to its being a known mutagen [27]. Chemical mutagens have also been shown to reduce the growth of at least another six RNA viral species in cell culture [25].

The idea that artificially elevating mutation rates could be a useful therapy is given weight by the existence of natural antiviral hypermutagens. In primates, some APOBEC proteins act as a defence against retroviral pathogens by causing additional mutations in them; in response, one of the accessory proteins of HIV-1, Vif, acts to neutralise APOBEC3G [28].

Although the potentially therapeutic effect of elevating already high mutation rates might seem intuitive, there is not a good quantitative understanding of what is happening and why. Historically, the reasoning behind lethal mutagenesis appears to have emerged from population dynamic models in which the mutation rate is crucial – so-called quasispecies models 29, 30. Increasing the mutation (error) rate in these models causes unwelcome effects for the viral population. However, we believe that the common use of the term error threshold (or error catastrophe) to explain lethal mutagenesis therapy might be misleading. In Box 1 , we show how the error threshold could be an artifact caused by unrealistic model assumptions and how lethal mutagenesis (that is, population extinction) can be explained solely in terms of viral growth and mutation rates. Bull et al. [25] recently presented a formal theory of this.

Box 1. A simple quasispecies model.

Consider a viral population composed of a wild-type (i.e. fittest) sequence X and all its mutants Y. We model its growth as follows (Equations I and II; see online Supplementary Material for details).

$$\frac{dx}{dt}=\alpha Q{x}_t-\delta x_t$$ [Equation I]

$$\frac{\text{d}y}{\text{d}t}=\alpha (1-Q)x_t+\beta y_t-\delta y_t\text{,}$$ [Equation II]

where x _t and y _t are the population sizes of wild type and mutant at time t, respectively, α and β are the replication rates of wild type and mutant, respectively (note, α > β), δ is a uniform death rate and Q is the probability of error-free replication.

We derive two thresholds involving Q.

First, the fittest sequence is maintained only if Q > β/α. That is to say, the wild-type virus must be able to copy itself without error with a probability (Q) at least equal to its advantage in replication rate over that of the mutant (β/α). This is called the error threshold and a population that passes this threshold suffers an error catastrophe and loses its fittest sequence (the population also ceases to be centered upon the wild-type sequence and loses its consensus). In addition to being used to explain lethal mutagenesis, the error threshold offers an apparent explanation of why a typical RNA virus has a genome size of 10⁴ bases and a mutation rate of 10⁻⁴ errors per base per round of replication [47]. We represent Q by the proportion of progeny that have no mutations in a Poisson distribution:

$$Q=e^{-mp}\text{,}$$ [Equation III]

where p is the probability of mutation per base and m is the sequence length in bases.

At the error threshold, Q = β/α. Thus,

$$\frac{\beta }{\alpha }=e^{-mp}\text{.}$$ [Equation IV]

Rewriting Equation IV, we get the following:

$$m=\frac{\ln \left(\frac{\alpha }{\beta }\right)}{p}\text{.}$$ [Equation V]

Given that the experimental data suggest that ln(α/β) ≈ 1 [12], the predicted maximum length of the virus is the inverse of its mutation rate, which is approximately what is observed.

The error threshold is not biologically plausible, however. Our model assumes that (i) only the mutations that occur in the fittest sequence are deleterious and (ii) they are non-lethal (i.e. the virus has a fitness landscape as shown in Figure Ia). The empirical data for RNA viruses [12] suggest that their fitness landscape is more similar to that in Figure Ib, and several theoretical studies have shown that, if a more realistic fitness landscape is used, there is no error threshold (i.e. the fittest sequence always maintains itself) 46, 48, 49, 50.

Figure I.

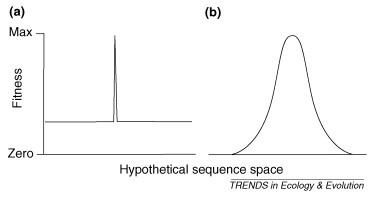
Possible fitness landscapes. Profile (a) is assumed by the basic quasispecies model, whereas empirical evidence suggests the landscape is closer to profile (b).

We argue that the possible absence of an error threshold is not important. If β < δ (the mutants have a negative growth rate), the second threshold in our model, Q > δ/α, determines whether the population as a whole survives. Here, the wild-type virus must be able to copy itself without error with a probability (Q) at least equal to the difference between its replication and death rates (δ/α). Artificially increasing the mutation rate to reduce Q below this value will lead to extinction of the population (lethal mutagenesis). Alternatively, in the absence of δ, extinction can be achieved by introducing additional mutant categories with growth rates below one into the model [29]. It is therefore not necessary to invoke an error threshold to explain either the small genomes of RNA viruses (as they get larger, Q will decrease in the absence of greater per base fidelity) or their sensitivity to artificially increased mutation rates (reducing Q directly).

Mutational robustness

The high mutation rate of RNA viruses might be expected to be associated with genomes that are mutationally robust, that is, can tolerate high levels of mutation. As with lethal mutagenesis, although perhaps intuitive, application of this idea to viruses has usually been framed in terms of quasispecies theory. In quasispecies models, at high mutation rates the fitness of sequences that are mutationally close to the fittest (wild type) are crucially important [31].

Mutational robustness can also be considered graphically as follows. If the relative fitnesses of different genomes within the same species is represented by a simple two-dimensional fitness landscape with a single peak, then the mutational robustness of the virus is the gradient around that peak: a flatter fitness profile represents a more mutationally robust genome. In silico competition experiments have shown that a slower replicator can outcompete a faster replicator if (i) the former is more robust to mutations, and (ii) the mutation rate is high – a process described as the ‘survival of the flattest’ (in reference to the famous ‘survival of the fittest’) [32]. In vitro competition experiments using VSV have shown that the competitive advantage of a faster-replicating clone over a more mutationally robust clone can be reversed by adding a chemical mutagen [33].

A small genome

The genomes of RNA viruses are small, typically only 10 kb long, with the largest (coronavirus) at 30 kb and the smallest (levivirus) at only 4 kb (Figure 1 ). However, it is not the small size of RNA viruses that is striking, but rather the observation that none of them have evolved to be larger. DNA viruses can be as small as RNA viruses but their genome sizes range over three orders of magnitude, with some DNA virus genomes being larger than the genomes of some endosymbiont bacteria.

Figure 1.

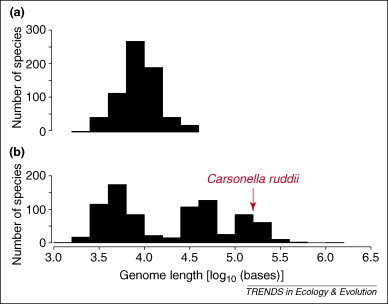
Genome lengths for RNA (a) and DNA (b) viruses showing the much greater range of the latter, extending beyond the size of the smallest known bacterial genome (Carsonella ruddii at 160 kb). Data taken from the NCBI genome webpage (http://www.ncbi.nlm.nih.gov).

It is generally thought that RNA viruses are small because of their high mutation rates [34]. As with lethal mutagenesis and mutational robustness, this expectation was derived from early quasispecies models, which suggested an inverse relationship between sequence length (information content) and mutation rate (the fidelity of copying) 35, 36. However, this relationship is also intuitive: genomes experiencing a high mutation rate should not be able to exceed a certain size, given that most mutations are harmful 12, 37. Mutation rate and genome size do in general appear to be inversely related, with the per base mutation rate of a range of DNA microbes varying such that their per genome mutation rate is approximately constant [1]. Consistent with being under such a constraint, RNA viral genomes show signs of compression, with a widespread use of overlapping reading frames (more than one protein being coded for by the same stretch of RNA) [38].

It is not known whether RNA viruses with larger genomes have lower per base mutation rates, as direct measurements of mutation rate exist for only a few species [10]. However, indirect evidence for such a relationship comes from the observation that substitution rates appear to be lower in larger viruses [39] (although substitution rate can also be affected by natural selection and genetic drift). We have also found that RNA virus species with larger genomes tend to have relatively larger polymerases, which we speculate might reflect a higher copying fidelity, whereas the equally essential nucleocapid proteins show no such tendency (Figure 2 ). We also note that parvoviruses (very small DNA viruses) have rates of substitution similar to those of RNA viruses [40]. An unrelated factor that might also play a role in the small size of RNA viruses is a putative limitation in transcription initiation points, which we discuss in the online Supplementary Material.

Figure 2.

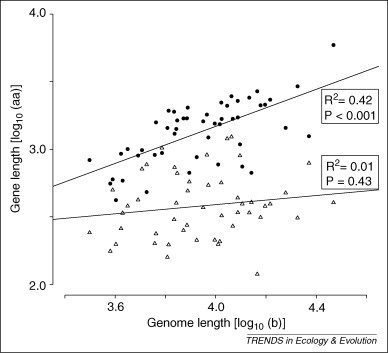
Relationship between mean protein size and genome lengths, showing a significant positive relationship for proteins with replicase activity (closed circles) but not for nucleocapid proteins (open triangles). Each data point represents the mean value for a family of RNA viruses (taken from our web application/database at http://virus.zoo.ox.ac.uk/virus/index.html).

The profound consequences of the limitation on RNA virus genome size imposed by high mutation rates require a reevaluation of the nature of RNA adaptability. The exceptionally high mutation rates of RNA viruses provide, at least theoretically, the potential for rapid molecular adaptation. This has important consequences, such as in the viral adaptation to adaptive immune defences or our acquisition of new diseases through zoonotic transmission. However, such adaptation is, somewhat paradoxically, highly constrained by the nature of RNA virus genomes, which, owing to their small size, must exhibit high levels of pleiotropy, fitness trade-offs, epistasis and convergent evolution [34]. Thus, rather than being infinitely flexible, it is better to view RNA viruses as restless beasts pacing a small cage – they are capable of rapid adaptive switching among a set of limited phenotypes. The high mutation rate that enables swift viral evolutionary change is the same factor that reduces the complexity of potential viral adaptations, owing to the upper limit that it imposes on viral genome size.

Conclusions

Our discussion above points toward several promising research areas in virus evolution. First, it should be possible to test whether genomic properties such as genome size and recombination rate are correlated to viral life-history traits, and to investigate how particular genomic architectures enable viruses to deal with innate and adaptive immune responses. We predict that RNA viruses (and perhaps small DNA viruses) are associated more with hit-and-run and adaptive escape strategies that depend on high replication and high mutation rates, respectively; by contrast, the complex immune sabotage strategies of the large DNA viruses (e.g. murine cytomegalovirus) involve genes dedicated to this function, and we therefore expect them to be associated with larger genomes [5].

Second, experimental evolution approaches, which have proved vital in understanding many aspects of virus evolution, could be extended to address two fundamental questions: (i) are virus mutation rates reduced in larger RNA viruses, and (ii) is there a trade-off between mutation and replication rates?

Third, we suggest that new theoretical work is needed, with a greater emphasis on the integration of model behaviour and empirical data. As we outlined earlier, further theoretical development would assist the development of lethal mutagenesis as an antiviral therapy. In particular, the biological realism of existing model assumptions requires greater consideration. Genomic robustness is another topic that warrants further theoretical exploration and empirical investigation, especially as this incorporates questions of epistasis and genome complexity that apply to all taxa [41]. The simple genomes and experimental tractability of RNA viruses make them an ideal model system for this subject, and there are now methods for selecting experimentally for reduced mutational robustness in viruses [42].

Lastly, we hope that our metaphor of viruses adaptively roaming a small space will help shed light on their sometimes paradoxical nature; similar ideas have already been used to understand the epidemiological and antigenic dynamics of the human influenza A virus [43]. We further note an inescapable corollary of our ‘small cage’ metaphor: because current RNA viruses inhabit different cages, evolutionary events that enable viruses to explore an entirely new set of behaviours must occasionally occur. Although almost certainly rare, these viral ‘paradigm shifts’ are of the greatest importance in viral evolution. Candidate events for such transitions include the acquisition of new accessory genes in large nidoviruses [44] and the recombination event that generated a new alphavirus lineage [45]. Viruses have proved to be invaluable model systems for many evolutionary questions, and there is no reason to suppose that they will be any less revealing in the study of macroevolution and evolutionary transitions.

Glossary

Error catastrophe

in the quasispecies model, the loss of the fittest sequence owing to competition with mutated sequences. The term is also used to describe an accompanying loss of the consensus sequence for the population, which then drifts randomly through sequence space.

Error threshold

in the quasispecies model, the point at which fidelity of sequence replication is too low to prevent the error catastrophe (Box 1).

Lethal mutagenesis

the reduction in growth rate of a virus achieved by artificially increasing its mutation rate.

Mutational robustness

the ability of a genotype to sustain mutations without affecting its phenotype.

Quasispecies

a mathematical representation of population growth where the population is divided into categories that are defined by, and linked via, their number of (deleterious) mutations. There is no necessary conflict between these models and those of traditional population genetics: the quasispecies model can be interpreted in terms of mutation–selection balance [46]. Also, the term refers to a chemical rather than a biological definition of a species (i.e. ‘almost’ a single type or ‘species’ of molecule). Importantly, and perhaps controversially, mutational linkage leads fitness to being seen as an attribute of the population rather than of an individual virus.

Survival of the flattest

under a high mutation rate, the competitive advantage of a genotype with lower replication rate but higher mutational robustness.