Abstract
Co-infections of hosts by multiple pathogen species are ubiquitous, but predicting their impact on disease remains challenging. Interactions between co-infecting pathogens within hosts can alter pathogen transmission, with the impact on transmission typically dependent on the relative arrival order of pathogens within hosts (within-host priority effects). However, it is unclear how these within-host priority effects influence multi-pathogen epidemics, particularly when the arrival order of pathogens at the host-population scale varies. Here, we combined models and experiments with zooplankton and their naturally co-occurring fungal and bacterial pathogens to examine how within-host priority effects influence multi-pathogen epidemics. Epidemiological models parametrized with within-host priority effects measured at the single-host scale predicted that advancing the start date of bacterial epidemics relative to fungal epidemics would decrease the mean bacterial prevalence in a multi-pathogen setting, while models without within-host priority effects predicted the opposite effect. We tested these predictions with experimental multi-pathogen epidemics. Empirical dynamics matched predictions from the model including within-host priority effects, providing evidence that within-host priority effects influenced epidemic dynamics. Overall, within-host priority effects may be a key element of predicting multi-pathogen epidemic dynamics in the future, particularly as shifting disease phenology alters the order of infection within hosts.
Keywords: co-infection, within-host, between-host, priority effects, epidemic, Daphnia
1. Introduction
Epidemics of infectious diseases can strongly influence natural, agricultural and human populations. They can result in rapid degradation of host health, regulate host-population dynamics and even put species at risk of extinction [1–3]. Predicting the dynamics and severity of epidemics ahead of time is therefore imperative for timely public health interventions, such as limiting trade of infected livestock or immunizing at-risk human and wildlife populations. However, the vast majority of host populations is co-infected by multiple pathogen species [4–7], and the epidemics of different pathogens often alter one another's trajectories. For instance, influenza epidemics historically increased population susceptibility to pneumonia [8]. Thus, understanding how co-infecting pathogens interact at the individual and population scales is essential to predict epidemic dynamics and mitigate epidemic severity.
Co-occurring pathogens can increase or decrease one another's epidemic severity by interacting at the individual host scale. Pathogens can interact by competing for resources such as nutrients or body tissue, by directly interfering with or facilitating one another (e.g. by producing bacteriocins), and/or by indirectly interacting via the immune system [9–12]. These within-host interactions alter host susceptibility, pathogen transmission rates and the duration of infections, thus determining the rate at which pathogens transmit through a host population [13,14]. Therefore, the severity of an epidemic may be difficult to predict without knowing the identities of co-infecting pathogens and how they interact within hosts.
While the many ways that pathogens interact within hosts are well documented [15], scaling these interactions up to predict epidemic severity has proven challenging because within-host interactions are influenced by the order of pathogen arrival at multiple spatial scales [16]. Within-host interactions have a deterministic component based on fitness asymmetry between pathogens but can be modified by the order in which pathogens infect hosts, both in multi-strain co-infections [17] and in multi-species co-infections [18]. These within-host priority effects can alter both the strength and direction of within-host interactions [19] and can alter disease risk [20]. Furthermore, the first pathogen to spread through a host population during a multi-pathogen epidemic is likely to be the first pathogen to infect individual hosts [16,21]. Thus, differences in the arrival order of co-occurring epidemics can alter within-host interactions and thereby could change epidemic dynamics. However, large enough interspecific asymmetry in pathogen fitness within and across hosts could override context-dependent within-host priority effects. In this scenario, infection order may not be important and will simply add ‘noise’ to the dynamics of epidemics. Given that variation in the timing of epidemics is common because pathogens typically respond differently to seasonal forcings [22], it is important to understand whether within-host priority effects can alter epidemic severity and whether measuring them will allow us to better predict future epidemic dynamics.
One challenge to understand the role of within-host priority effects in determining epidemic severity is that within-host priority effects may themselves be context-dependent. Many studies have documented within-host priority effects experimentally [18,23–26], but these interactions are often measured in isolated hosts under ideal conditions that do not reflect the complex, stressful and ever-changing environmental conditions hosts and pathogens experience during epidemics. For instance, host and pathogen populations at the start, peak or end of an epidemic experience very different resource conditions [27], population densities [2] and age/stage structures [28] that could all modify within-host interactions and thus alter within-host priority effects. Consequently, measuring within-host interactions and priority effects experimentally in isolated hosts may not allow us to understand their role in determining epidemic dynamics at the host-population scale.
To help fill these conceptual gaps, we asked the following two questions. (1) How does relative epidemic start date interact with within-host priority effects to alter epidemic dynamics? (2) Does measuring within-host priority effects at the individual host scale improve our ability to predict multi-pathogen epidemics? To answer these questions, we used individuals and populations of zooplankton co-infected with naturally co-occurring fungal and bacterial pathogens as a model system. We ran predictive epidemic models parametrized with or without within-host priority effects and then tested the predictions of these models with experimental multi-pathogen epidemics. Predictive models with or without within-host priority effects showed clear qualitative differences in the impact of epidemic arrival order on epidemic dynamics, and our experimental epidemics qualitative matched patterns predicted only by our within-host priority effect model. Together, these results indicate that within-host priority effects interact with a relative epidemic start date to alter multi-pathogen epidemic dynamics in our system and that we might better predict multi-pathogen epidemics by taking within-host priority effects into account.
2. Methods
We predict that epidemic timing will alter epidemic dynamics by creating feedback loops mediated by within-host priority effects. The first pathogen to enter a host population will most likely be the first pathogen to enter individual hosts in the first host generation of a multi-pathogen epidemic. In later generations, an epidemic arrival order will alter the order of infection at the single-host scale indirectly. The arrival order in the first generation of hosts will determine the transmission of pathogens from those hosts and thus the force of infection of both pathogens. When two pathogens circulate in a host population, the pathogen with the higher force of infection will be more likely to infect hosts first [19]. Thus, the relative start dates of co-occurring epidemics can indirectly alter the arrival order of pathogens at the single-host scale several generations after the start of the epidemics.
It is intractable to measure these priority effect-mediated feedback loops directly, as we would need to measure both the infection order of pathogens in each individual host and the transmission of pathogens from those hosts, during an epidemic. Instead, we built predictive epidemic models parametrized with experiments conducted at the single-host scale and ran these models with and without within-host priority-mediated feedback loops. This approach allowed us to understand how these feedback loops influence multi-pathogen dynamics and isolate within-host priority effects from effects arising simply from co-infections. We then tested the qualitative predictions made by our epidemic models by running experimental multi-pathogen epidemics in the laboratory.
(a). Study system
We built models to predict epidemic dynamics in the zooplankton species Daphnia dentifera (henceforth ‘zooplankton’). This zooplankton species is common in lakes in the midwestern USA [29]. In late summer, zooplankton populations commonly host pathogens, including the fungus Metschnikowia bicuspidata and the bacterium Pasteuria ramosa (henceforth ‘fungus’ and ‘bacterium’). While lakes differ in their pathogen communities, the fungus and bacterium do co-occur in some lakes. Zooplankton ingests infectious spores of both pathogens while filtering for algae. After ingestion, spores replicate until host death, at which point they escape into the water column until they are ingested by a new host [30]. For this study, we used a clonal zooplankton line (Mid37) and pathogen isolates that had been grown in laboratory for several years (‘Standard’ fungus and ‘G/18’ bacterium).
(b). Epidemic models
To predict the impact of within-host interactions and within-host priority effects on epidemic severity and to test whether we can predict epidemic severity by measuring within-host interactions experimentally, we ran multi-pathogen epidemic simulations parametrized with experimental measurements of within-host priority effects. We compared models which (i) included within-host interactions, (ii) included within-host interactions but not within-host priority effects, and (iii) did not include any within-host interactions (figure 1). We include a no within-host interaction model to determine whether co-infection and epidemic arrival order alter epidemic dynamics purely by altering host-population dynamics.
Figure 1.
Pathogen fitness in all models: those that contained within-host interactions/priority effects, corresponding to empirical data (full model), those that did not contain within-host priority effects (no priority effects) and those that did not contain any within-host interactions (no interactions). The fitness of pathogens was measured as the average number of infectious spores released from hosts at death [31]. Points indicate the relative spore yield of pathogens in co-infected hosts compared to the mean spore yield of singly infected hosts when the fungus arrived first (fun), when pathogens arrived at the same time (simul) or when the bacterium arrived first (bac). Blue points represent the bacterium and yellow points represent the fungus. The grey shading indicates the likelihood that a pathogen will be competitively excluded, ranging from 0 in the white to 1 in the darkest grey (see electronic supplementary material, for calculation). Bars indicate 95% of posterior estimate for each point. Raw data and relevant methods can be found in Clay et al. [31]. (Online version in colour.)
We parametrized our model with within-host priority effects measured and fully described in [31]. Age-controlled hosts were singly infected, simultaneously co-infected or sequentially infected, with either the bacterium or the fungus arriving 4 days after the other pathogen. Comparing glms with heteroscedasticity using the glht function in R [32], we determined that fungal spore yield (number of infectious spores in the host at death) was significantly lower in co-infected hosts the fungus arrived first when compared with other co-infected host classes. Bacterial spore load was significantly lower in co-infected hosts than singly infected hosts in all cases. To parametrize the within-host priority effects for this study, we used the R2jags package in R [33] to find Bayesian estimates of the mean values of fungal spores (normally distributed) and bacterial spores (Poisson distributed) from each infected host class (figure 1). We used a Bayesian approach to more efficiently carry forward uncertainty through nested layers of modelling (parameters estimated from single hosts were used to estimate parameters in single-pathogen epidemics, which were used to make predictions about multi-pathogen epidemics).
Here, we present our full model that includes both within-host interactions and within-host priority effects (figure 2). See electronic supplementary material, methods for equations describing all models and for discussion of model assumptions. We model epidemics as a discrete-time SI system of environmentally transmitted bacterial and fungal pathogens, with environmental spore pools B and F. Hosts may be susceptible (S), singly infected (IB or IF), co-infected simultaneously (Csim), sequentially infected with the fungus first (CFB) or sequentially infected with the bacterium first (CBF). Further, upon co-infection, pathogens may competitively exclude one another. Hosts in class Xi,sim, Xi,FB or Xi,BF were previously co-infected, but pathogen i competitively excluded its competitor within the host. Once a pathogen has been competitively excluded, it cannot re-infect a host.
Figure 2.

Model flowchart, highlighting most likely transmission pathways for each multi-pathogen experimental treatment, e.g. in our ‘bacterium first’ treatment, we predict susceptible individuals will first become singly infected by the bacterium (IB) and then co-infected (CBF). (Note, however, that all highlighted transmission pathways can occur in all treatments.) Blue is used to indicate state variables and parameters related to the bacterium, including hosts singly infected by the bacterium (IB), bacterial infection (solid blue arrow), bacterial spore release (dashed blue arrow) and bacterium competitively excluding the fungus within hosts (dotted blue arrow). Similarly, yellow represents state variables and parameters related to the fungus, including hosts singly infected by the fungus, fungal infection, fungal spore release and the fungus competitively excluding the fungus within hosts. Green represents co-infected hosts and simultaneous co-infection. Multi-coloured lines mean that hosts can move back and forth between two classes. Line thickness represents relative rate, e.g. bacterial spore release is less from co-infected individuals than from singly infected individuals, and thus, the bacterial spore release line is thinner from co-infected hosts. Note that competitive exclusion happens instantaneously upon co-infection, thus individuals move directly from singly infected individuals to cleared individuals in model equations. (Online version in colour.)
To differentiate between simultaneous co-infections (infections occur on the same day) and sequential co-infections (infections happen on different days), we model dynamics in discrete time, with a time step of 1 day. Dynamics of the susceptible class are given by
| 2.1 |
where b is the number of offspring/host/day at low population density, K is the host carrying capacity and Nt is the total population size at time t. In experimental, single-pathogen epidemics (described below), we observed no developing offspring in the brood chamber of any infected zooplankton. Thus, infected hosts do not give birth in our model. Hosts must go through a juvenile stage, lasting j days, before they are counted as part of the susceptible, adult population. Susceptible hosts become singly infected by feeding on spores in the water column. Thus, θi,t is the proportion of hosts to become infected by pathogen i at time t, given by
| 2.2 |
and
| 2.3 |
where ft is the total proportion of spores in the environment eaten by each host at time step t, and μi is the per spore infectivity of pathogen i (equations (2.2) and (2.3) were established to be mass action processes based on previous experiments, see electronic supplementary material). We assume that pathogens do not alter host susceptibility to one another, as shown in [31]. In these prior experiments, we found that the order of infection of the fungal and bacterial pathogens only altered spore yield. We found no evidence of protection or immune suppression (prior exposure by one pathogen did not reduce or increase the likelihood of infection by the other pathogen). Thus, we assume that infection likelihood is not altered by the infection status of the host. The proportion of susceptible hosts to become simultaneously co-infected at time t is θB,tθF,t, and the proportion of susceptible hosts to become singly infected by pathogen i is the proportion of susceptible hosts to become infected by pathogen i, minus the proportion of those hosts to also become simultaneously co-infected. At no point in our simulations does θB,t or θF,t become greater than one. Finally, dS is the rate of intrinsic host mortality.
Hosts singly infected by the fungus may become co-infected upon ingesting bacterial spores, and vice versa. Upon co-infection, the probability of remaining co-infected until death with no competitive exclusion is ωj, where j is the co-infection class. λB,j is the probability that the fungus will competitively exclude the bacterium, and λF,j is the probability that the bacterium will competitively exclude the fungus. See the electronic supplementary material for the calculation of competitive exclusion probabilities. After the fungus is cleared from infected hosts, the hosts can become reinfected by the fungus, returning to their original co-infected class. Upon reinfection, the bacterium and the fungus may once again competitively exclude one another, with the original probabilities associated with that co-infected class. We assume that once the bacterium is excluded by the fungus, it cannot re-infect hosts, as the time between fungal infection and host death is relatively short. Finally, since fungal infection reduces host lifespan [31], all hosts infected by the fungus die at an increased rate (dF), with their death rate reverting to dS if the bacterium excludes the fungus. Thus, changes in the numbers of infected and co-infected hosts are then given by
| 2.4 |
| 2.5 |
| 2.6 |
| 2.7 |
| 2.8 |
| 2.9 |
| 2.10 |
| 2.11 |
| 2.12 |
| 2.13 |
and
| 2.14 |
Infected hosts transmit spores into environmental spore pools upon death, whose dynamics are given by
| 2.15 |
and
| 2.16 |
where βi(j) represents the number of spores i released from host class j. Thus, all hosts that are infected by a given pathogen add spores of that pathogen to the environment upon death. We assume that if a pathogen is competitively excluded from a host, the host's spore yield reverts to that of a singly infected host. Spores have a loss rate (αi), which represents spore degradation and spores moving out of the system (e.g. due to settling), and fungal spores are removed from the environment by host feeding (f) [34]. Bacterial spores, alternatively, can survive passage through the host gut and thus are not removed by host feeding unless they actively infect the host [35].
Models were parametrized with a combination of three experiments. First, we measured the lifespan and birthrates of uninfected hosts with a life table experiment (electronic supplementary material). We then measured pathogen fitness (infectious spores released upon host death) in singly infected, sequentially infected and simultaneously co-infected hosts [31]. Finally, we estimated carrying capacity and spore degradation from the uninfected and singly infected treatments of our experimental epidemics (electronic supplementary material). All parameters were estimated with the R2jags package in R [33], in order to create Bayesian posterior distributions of parameter value probabilities. See electronic supplementary material for full methods and all parameter values (electronic supplementary material, table S1).
To predict epidemic dynamics under shifting epidemic arrival order, we ran our model under conditions where fungal epidemics started a week before bacterial epidemics, where epidemics started simultaneously and where bacterial epidemics started a week before fungal epidemics, matching our experimental treatments (table 1). We simulated each scenario 1000 times, each time drawing parameters from posterior distributions of Bayesian parameter estimates (electronic supplementary material). Within-host interactions and priority effects in this system primarily impact infectious spore production [31]. Thus, for our model with no within-host interactions, we set the spore release rate from all co-infected hosts equal to the spore release rate from singly infected hosts. For our model which included within-host interactions but no within-host priority effects, we set the spore release rate of sequentially co-infected hosts equal to that of simultaneously co-infected hosts (figure 1; see electronic supplementary material for exact equations for each model).
Table 1.
Treatments in host-population scale experiments.
| treatment no. | treatment day 2 | treatment day 9 |
|---|---|---|
| 1 | control | control |
| 2 | fungus | control |
| 3 | bacterium | control |
| 4 | fungus/bacterium | control |
| 5 | fungus | bacterium |
| 6 | bacterium | fungus |
(c). Testing model predictions
To test our epidemic model predictions empirically, we ran experimental multi-pathogen epidemics. We seeded 1 l beakers of filtered pond water with 100 adult zooplanktons each on day 1 of the experiment. On day 2, we homogenized singly infected zooplankton to create infectious spore slurries and seeded beakers with either 190 fungal spores ml−1, 1000 bacterial spores ml−1, 190 fungal spores ml−1 and 1000 bacterial spores ml−1, or a controlled dosage of ground-up uninfected Daphnia. We repeated this procedure on day 9 to create populations with no epidemics, single-pathogen epidemics or multi-pathogen epidemics with varying epidemic arrival orders (table 1), with eight replicate populations per treatment.
To monitor host–pathogen dynamics, we subsampled 1/10th of each zooplankton population every 5 days, filtering out Daphnia and returning water to each replicate after sampling. Juveniles were counted and discarded. Adult individuals were homogenized and infectious spores inside each adult were identified. We then categorized adult zooplankton as uninfected, singly infected by the fungus, singly infected by the bacterium or co-infected. We ran the experiment for 67 days, ending when the majority of infected populations had gone extinct. We fed each replicate 20 000 Ankistrodesmus sp. cells per millilitre 4 days a week (Monday, Tuesday, Thursday, Friday).
(d). Comparing models predictions and experimental epidemics
To compare model predictions and empirical epidemics, we focused on treatment differences in three key metrics that characterize a different aspect of epidemics: mean prevalence, epidemic length (time between first observed and last observed infected host) and integrated prevalence (the summed prevalence across all sampling dates). For each metric and pathogen, we first calculated significant pairwise differences between single-pathogen epidemics and each multi-pathogen epidemic treatment. Second, for each pathogen, we calculated the relationship between a metric and the relative timing of infection (day of fungal spore introduction − day of bacterial spore introduction) among our co-infected treatments. Residuals of the mean fell under gamma or normal distributions for all variables in each treatment. Thus, all comparisons were performed with the generalized linear model (glm) function in R [36].
Our models predicted that within-host priority effects resulted in testable differences in a key aspect of epidemics (see Results) across arrival treatments. Thus, if our no interaction model (figure 1, ‘no interactions’) correctly predicts epidemic dynamics, then within-host interactions are not important drivers of epidemic dynamics in our system. If our no within-host priority effects model (figure 1, ‘no priority effects’) correctly predicts epidemic dynamics, then within-host interactions, but not within-host priority effects are important drivers of epidemic dynamics in our system. If only our full model (figure 1, ‘full model’) predicts epidemic dynamics, then we can conclude that within-host priority effects alter epidemic dynamics and that by measuring them, we can accurately predict epidemic dynamics a priori. If no models correctly predict epidemic dynamics, then measurements of within-host interactions made experimentally do not necessarily represent within-host interactions that occur during an epidemic.
3. Results
(a). Model predictions
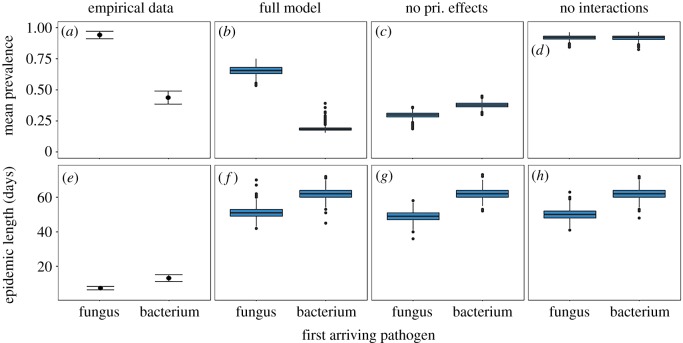
Adding within-host priority effects on our predictive models altered the predicted impact of epidemic arrival order on bacterial epidemic dynamics. In all models, the presence of a fungal epidemic reduced the integrated prevalence, mean prevalence and epidemic length of bacterial epidemics (electronic supplementary material, figure S2). All models also predicted the same impact of epidemic arrival order on bacterial epidemic length, with bacterial epidemics lasting longer when bacterial epidemics start before fungal epidemics. However, models disagreed on the impact of epidemic arrival order on the mean prevalence. Models that did not include within-host interactions predicted no effect of epidemic arrival order on the mean prevalence. Models that accounted for within-host interactions but not within-host priority effects predicted that the mean prevalence would be higher when the bacterial epidemic started before the fungal epidemic than in other treatments. In sharp contrast, our full model (including within-host priority effects) predicted the opposite result: as bacterial epidemic start date moved later and fungal epidemic start date moved earlier, mean bacterial prevalence should decrease (figure 3; electronic supplementary material, figure S2).
Figure 3.
Empirical estimates of the impact of epidemic arrival order on mean bacterial prevalence and epidemic length match predictions made by our full model. The y-axis shows the mean prevalence (a–d) and length (e–h) of bacterial epidemics in experiments (a,e) and in models when the fungal epidemic precedes the bacterial epidemic (fungus), and when the bacterial epidemic precedes the fungal epidemic (bacterium). Points for empirical data represent means with standard error across replicates, while model data are represented by boxplots of 1000 model runs. (Online version in colour.)
All models predicted no change in fungal epidemic dynamics due to co-infection or epidemic arrival order (electronic supplementary material, figure S3).
(b). Empirical single-pathogen epidemic dynamics
Both pathogens spread readily through host populations. In single-pathogen epidemics, the fungus and the bacterium both reached 100% prevalence in all replicates and maintained themselves in host populations until host populations went extinct (figure 4; electronic supplementary material, figure S3). Bacterial epidemics reached 100% prevalence roughly 40 days after epidemic start date and stayed close to 100% prevalence until populations went extinct (figure 4e). Fungal epidemics spread much faster and first peaked near 100% prevalence at day 11 of our experiment, then proceeded to cycle through multiple epidemic peaks of varying intensity (figure 4f).
Figure 4.
Empirical bacterial epidemics (blue, top) changed with co-infection and epidemic arrival order, while fungal epidemics (yellow, bottom) did not. y-axis shows the prevalence (proportion) of hosts infected over the course of the epidemic. Prevalence includes both singly infected and co-infected hosts. Lines represent the mean prevalence across non-extinct replicates, with ribbons representing 95% confidence intervals at each time point. Co-infection reduced the integrated prevalence of all bacterial epidemics (b versus e, p = 0.017; c versus e, p = 0.046; d versus e, p = 0.048). The integrated prevalence did not significantly change with shifting epidemic start date (p = 1.0). As bacterial epidemics shifted earlier and fungal epidemics shifter later, bacterial epidemics became longer (p = 0.036) and had lower average prevalence (p = 0.0015). Fungal epidemics were not significantly different between treatments. (Online version in colour.)
(c). How do co-infection and epidemic timing alter empirical epidemic severity?
Co-infection and relative epidemic start date interacted to change epidemic dynamics. We saw co-infected individuals at a high rate in all co-infected treatments (electronic supplementary material, figure S4). Co-infection reduced the total size of all bacterial epidemics (integrated prevalence of infected individuals over time, hereafter referred to as integrated prevalence: only bacterium versus fungus first p = 0.017, only bacterium versus simultaneous epidemics p = 0.046, only bacterium versus bacterium first p = 0.048; figure 3). The integrated prevalence did not significantly change with shifting epidemic start date (p = 1.0). However, as bacterial epidemics shifted earlier and fungal epidemics shifter later, bacterial epidemics became longer (p = 0.036), and had lower average prevalence (p = 0.0015; figures 3a,e and b–d). Overall, these results indicate that the relative epidemic start date in our system shaped how epidemics were distributed over time, though not their overall size. Fungal epidemics were not significantly different in integrated prevalence, mean prevalence or length across any treatments (electronic supplementary material, table S2; fungal epidemics appear longer in singly infected populations in figure 3f due to a single replicate).
(d). Testing model predictions with empirical dynamics
The dynamics of our experimental epidemics best matched the predictions made by our full model. In cases where models agreed with one another (predicting that co-infection would reduce the integrated size of bacterial epidemics and that bacterial epidemics would become shorter as the bacterial epidemic shifted later and the fungal epidemic shifted earlier), empirical epidemics matched the predictions of all models (figures 3e–h and 4b–e). However, as the bacterial epidemic shifted later and the fungal epidemic shifted earlier, our empirical data rejected the predictions of our no priority effect models that the mean prevalence of bacterial epidemics would increase or stay the same (figures 3c,d and 4b–e), instead supporting the prediction of our full model that the mean prevalence of bacterial epidemics should decrease.
4. Discussion
In natural systems, the arrival order of pathogens within a host can determine the fitness and transmission of those pathogens. However, it is still unclear how these within-host priority effects can alter disease dynamics during multi-pathogen epidemics. Our study shows that in our system, pathogen arrival order at the within-host scale interacts with pathogen arrival order at the host-population scale to determine multi-pathogen epidemic dynamics. Specifically, we show that co-infection reduced epidemic size, while the relative start dates of co-occurring epidemics determined how epidemics were distributed over time. Predictive epidemic models only accurately captured qualitative multi-pathogen dynamics if they included within-host priority effects measured at the single-host scale, indicating that within-host priority effects can be a mechanism through which disease phenology alters multi-pathogen epidemics. Taken together, this evidence suggests that measuring within-host priority effects may increase our ability to predict multi-pathogen epidemics in the future, particularly under shifting disease phenology.
(a). Mechanisms of single-pathogen epidemics dynamics
The two pathogens in our study created large epidemics but exhibited different temporal dynamics. In our single-pathogen treatments, the sustained high prevalence of the bacterium (figure 3e) is probably driven by its low probability of degradation (electronic supplementary material, table S1), and because this bacterium can remain infectious after passing through host digestive tracts [35]. Therefore, the bacterial spore load in the environment, and thus the probability of infection, could remain high throughout our experiment. The cycling pattern in our fungal epidemics (figure 3f) is due to the synchronized infection and mortality of infected host cohorts. After fungal spores are introduced to the environment, hosts will remove most of them via ingestion. A proportion of those hosts will become infected, and then all die roughly 10–12 days later due to fungus-induced mortality, releasing spores back into the environment, and restarting the cycle.
(b). Mechanisms of multi-pathogen epidemics dynamics
Entering host populations before the fungus could have increased the mean bacterial prevalence as the bacterium had time to spread without fungal interference or could have decreased the mean bacterial prevalence as the bacterium had the lowest fitness within co-infected hosts when it arrived first (figure 1). Ultimately, we found that bacterial prevalence was lowest when bacterial epidemics had a head start (figures 3 and 4). Our epidemic models tease apart the mechanics of how relative epidemic start date alters the mean prevalence of the bacterium. The mean bacterial prevalence shrinks when the bacterium arrives first compared to when the fungus arrives first because there is a high probability of competitive exclusion for the bacterium when it infects hosts before the fungus (figure 1). Thus, as the competitive exclusion of the bacterium increases due to within-host priority effects, the mean prevalence of the bacterium during the epidemic decreases. Therefore, in this system, within-host priority effects are strong enough for the epidemic start date to change epidemic severity.
Fungal epidemic dynamics showed no change between treatments, despite our fungal pathogen experiencing stronger within-host priority effects than the bacterium (figure 1). However, this pattern may be driven by epidemic saturation: fungal pathogens reached 100% prevalence very quickly in all single-pathogen treatments. This high prevalence makes it difficult to detect if epidemics facilitate one another, as epidemic prevalence cannot exceed 100%. Furthermore, it suggests that the spore load of the fungus in the environment may have been far greater than necessary to infect all hosts. Under such conditions, fluctuations in infectious spore yield from co-infected hosts would have no effect on epidemic dynamics. This indicates that for pathogens with very high transmission and prevalence, such as some gut helminths in wildlife populations [37], their dynamics may not be impacted by interactions with other pathogens or by relative epidemic timing.
Ultimately, how epidemic timing and within-host priority effects altered experimental epidemics depended on the type of within-host priority effects we observed. In our system, pathogens had the lowest fitness when they infect co-infected hosts first (figure 1). For the fungus, we hypothesize co-infection with the bacterium facilitates the fungus, as the bacterium causes gigantism via castration [38], allowing for hosts to contain more spores. However, if the fungus arrives first, it may disrupt bacterial castration, removing the facilitative effect. Further experiments are needed to confirm this hypothesis. For a system where within-host priority effects take a different form (e.g. where pathogens have a fitness advantage from prior residency in hosts [17]) the impact of shifting epidemic phenology will be different than that seen in our system. However, our results provide evidence that within-host priority effects can scale up by interacting with disease phenology and may do so in other systems.
(c). Role of within-host interactions
Overall, this study experimentally demonstrates that within-host priority effects can alter epidemic dynamics in our system by shifting pathogen fitness in co-infected hosts. Previous studies have demonstrated that sequential infections can alter epidemic severity if early arriving pathogens increase or decrease host susceptibility to further infection [11,16,20,39]. For instance, endemic infection by helminths makes tuberculosis invasion easier as helminths increase host susceptibility to microparasites [11]. Or, in certain grass hosts, the first-arriving pathogen changes the likelihood of co-infection by all other pathogens in the system [16]. The previous theory further shows that within-host priority effects may alter disease dynamics not only by changing the likelihood of infection but also by altering competitive outcomes within hosts, altering the ability of pathogens to spread through a previously infected population [31,40]. Our study adds to this body of work by providing experimental evidence that within-host competitive outcomes driven by infection order scale up to alter epidemic dynamics. These results may apply even when epidemics do not have separate start dates. This is because hosts will usually be infected first by the pathogen with the highest infection risk in a given system [16,21]. Thus, our results emphasize that we should examine the role of within-host priority effects in driving disease dynamics whenever a host population is infected by multiple pathogens.
Though within-host priority effects are important, they are not the only mechanism through which epidemic timing impacts epidemic dynamics in our system. We found that between-host interactions, rather than within-host interactions, determined variation in epidemic length in our experiments. Between-host interactions occur when pathogens decrease the population size of susceptible hosts, decreasing the transmission of density-dependent pathogens [41]. In our experiments, bacterial epidemics were longer when the bacterium entered the population first than when the fungus entered the population first. This is because co-infection greatly decreased population density and drove host populations to extinction (electronic supplementary material, figure S5C–E). In total, the length of a bacterial epidemic was proportional to the time between when bacterium entered the host population and when the host population went extinct. Similarly, in all of our models, bacterial epidemics are longest when the bacterium enters the population first (figures 2 and 4), because epidemics start when the bacterium enters the host population, and end when the host population goes extinct. Thus, within-host interactions are not needed to predict some aspects of how epidemic timing alters epidemic patterns. However, the strength of between-host interactions increases with pathogen prevalence [39], which depends in part on within-host interactions. Therefore, within-host interactions and between-host interactions likely feedback on one another to determine epidemic severity.
(d). Making predictions
Our results demonstrate that we can predict qualitative changes in multi-pathogen epidemic dynamics in our system. Specifically, our models parametrized with within-host priority effects correctly predicted that epidemic start date would alter the length and mean prevalence of bacterial epidemics (figure 3; electronic supplementary material, figure S2) but would not alter fungal epidemics (electronic supplementary material, figure S3). Our models did not predict quantitative epidemic dynamics (e.g. our full model could not predict pathogen prevalence at a specific time point in the epidemic, electronic supplementary material, figure S6) because Daphnia sp. population dynamics are highly stochastic, follow boom and bust cycles, and depend on asymmetric competition between different daphnia age classes [42,43]. We chose a simpler model that would not capture Daphnia population dynamics, but would better show the impact of within-host priority effects at the host-population scale. Further, qualitative disease predictions are highly valuable in identifying areas of concern, such as identifying where shifts in disease phenology will lead to an increase in epidemic severity.
Importantly, our model predicted the qualitative impact of within-host interactions a priori. Previous multi-pathogen epidemic models have accurately predicted epidemic patterns, but these models were parametrized by either observing or inferring within-host interactions during the epidemic the models were predicting [8,44,45]. The value of models with post hoc parametrization lies in predicting multi-pathogen epidemics that occurs in common spatial and temporal combinations. For instance, Abu-Raddad et al. [44] predicted the dynamics of endemic strains of HIV and malaria in Kenya by observing endemic HIV/malaria interactions in Malawi. However, for novel pathogen combinations or arrival orders, experimentally measured within-host interactions must be used to predict how pathogen interactions will alter epidemic dynamics a priori. Our results indicate that this approach can accurately predict qualitative metrics, but also that we must take into account how within-host interactions will translate from a laboratory setting to a field setting, where pathogens face fundamentally different conditions [46]. For instance, for our models to make accurate predictions, we needed to assume that within-host competition between pathogens was higher during experimental epidemics than during the experiments performed on isolated hosts used to parameterize our predictive models (an assumption with empirical support, see electronic supplementary material). How within-host interactions will change from field to laboratory settings will depend on within-host mechanisms. For instance, hosts rarely compete for resources during experimental measurements of within-host interactions [25,26,31,47,48]. Within-host competition for resources may then increase when hosts compete for host resources in the field [49], but apparent competition via the immune system may decrease when hosts compete for resources [50]. Thus, to predict how changing ecology will qualitatively change multi-pathogen epidemics before they occur, researchers should examine the mechanisms underlying within-host priority effects, rather than simply measuring the impact of sequential infection on pathogen fitness in a laboratory setting.
5. Conclusion
Infectious disease research now acknowledges that many pathogens usually circulate within-host populations [51]. Epidemics of these pathogens occur in response to environmental conditions (temperature, rainfall), host-population dynamics (aggregation, dispersal, foraging) or within-host conditions (seasonal weakening of immune systems) [22]. These variables are constantly changing, and as long as pathogens respond differently to environmental or host cues, then epidemics will continue to fluctuate in their relative timing, and thus severity. Further, we expect to see shifts in environmental variables and host-population dynamics under future climate conditions, potentially creating novel timing conditions of co-occurring epidemics. If we do not take both within-host interactions and within-host priority effects into account, we may become increasingly unable to predict epidemic severity in the future.
Supplementary Material
Acknowledgements
We thank Rebecca Bilich, Katie Hunsberger, Laura Lopez, Clara Shaw, Karana Wickens and Khadijah Payne for laboratory support. We further thank Tom E. X. Miller and Amy Dunham for helpful discussions on experimental planning and data analysis.
Data accessibility
All data and code are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.pnvx0k6h6 [52].
Authors' contributions
P.A.C. and V.H.W.R. conceptualized and designed this experiment. M.A.D. provided pathogens and hosts. P.A.C. analysed empirical data and built epidemiological models. All authors contributed to the writing of the manuscript.
Competing interests
We declare we have no competing interests.
Funding
Work was supported by NSF grant nos DEB-1748729 and DEB-1601353.
References
- 1.Roelke-Parker ME, et al. 1996. A canine distemper virus epidemic in Serengeti lions (Panthera leo). Nature 379, 441–445. ( 10.1038/379441a0) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hudson PJ. 1998. Prevention of population cycles by parasite removal. Science 282, 2256–2258. ( 10.1126/science.282.5397.2256) [DOI] [PubMed] [Google Scholar]
- 3.Ezenwa VO, Jolles AE. 2015. Opposite effects of anthelmintic treatment on microbial infection at individual versus population scales. Science 347, 175–177. ( 10.1126/science.1261714) [DOI] [PubMed] [Google Scholar]
- 4.Petney TN, Andrews RH. 1998. Multiparasite communities in animals and humans: frequency, structure and pathogenic significance. Int. J. Parasitol. 28, 377–393. ( 10.1016/S0020-7519(97)00189-6) [DOI] [PubMed] [Google Scholar]
- 5.Brogden KA, Guthmiller JM, Taylor CE. 2005. Human polymicrobial infections. Lancet 365, 253–255. ( 10.1016/S0140-6736(05)17745-9) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Balmer O, Tanner M. 2011. Prevalence and implications of multiple-strain infections. Lancet Infect. Dis. 11, 868–878. ( 10.1016/S1473-3099(11)70241-9) [DOI] [PubMed] [Google Scholar]
- 7.Cox FEG. 2011. Concomitant infections, parasites and immune responses. Parasitology 122, S23–S38. ( 10.1017/S003118200001698X) [DOI] [PubMed] [Google Scholar]
- 8.Shrestha S, Foxman B, Weinberger DM, Steiner C, Viboud C, Rohani P. 2013. Identifying the interaction between influenza and pneumococcal pneumonia using incidence data. Sci. Transl. Med. 5(191r), a84 ( 10.1126/scitranslmed.3005982) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Graham AL. 2008. Ecological rules governing helminth-microparasite coinfection. Proc. Natl Acad. Sci. USA 105, 566–570. ( 10.1073/pnas.0707221105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Inglis RF, Gardner A, Cornelis P, Buckling A. 2009. Spite and virulence in the bacterium Pseudomonas aeruginosa. Proc. Natl Acad. Sci. USA 106, 5703–5707. ( 10.1073/pnas.0810850106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ezenwa VO, Etienne RS, Luikart G, Beja-Pereira A, Jolles AE. 2010. Hidden consequences of living in a wormy world: nematode-induced immune suppression facilitates tuberculosis invasion in African buffalo. Am. Nat. 176, 613–624. ( 10.1086/656496) [DOI] [PubMed] [Google Scholar]
- 12.Wale N, Sim DG, Read AF. 2017. A nutrient mediates intraspecific competition between rodent malaria parasites in vivo. Proc. R. Soc. Lond. B 284, 20171067 ( 10.1098/rspb.2017.1067) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ezenwa VO, Jolles AE. 2011. From host immunity to pathogen invasion: the effects of helminth coinfection on the dynamics of microparasites. Integr. Comp. Biol. 51, 540–551. ( 10.1093/icb/icr058) [DOI] [PubMed] [Google Scholar]
- 14.Clark PR, Ward WT, Lang SA, Saghbini A, Kristan DM. 2013. Order of inoculation during Heligmosomoides bakeri and Hymenolepis microstoma coinfection alters parasite life history and host responses. Pathogens (Basel, Switzerland) 2, 130–152. ( 10.3390/pathogens2010130) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fenton A, Lamb T, Graham AL. 2008. Optimality analysis of Th1/Th2 immune responses during microparasite-macroparasite co-infection, with epidemiological feedbacks. Parasitology 135, 841–853. ( 10.1017/S0031182008000310) [DOI] [PubMed] [Google Scholar]
- 16.Halliday FW, Umbanhowar J, Mitchell CE. 2017. Interactions among symbionts operate across scales to influence parasite epidemics. Ecol. Lett. 20, 1285–1294. ( 10.1111/ele.12825) [DOI] [PubMed] [Google Scholar]
- 17.de Roode JC, Helinski MEH, Anwar MA, Read AF. 2005. Dynamics of multiple infection and within-host competition in genetically diverse malaria infections. Am. Nat. 166, 531–542. ( 10.1086/491659) [DOI] [PubMed] [Google Scholar]
- 18.Hoverman JT, Hoye BJ, Johnson PTJ. 2013. Does timing matter? How priority effects influence the outcome of parasite interactions within hosts. Oecologia 173, 1471–1480. ( 10.1007/s00442-013-2692-x) [DOI] [PubMed] [Google Scholar]
- 19.Clay PA, Cortez MH, Duffy MA, Rudolf VHW. 2019. Priority effects within coinfected hosts can drive unexpected population-scale patterns of parasite prevalence. Oikos 128, 571–583. ( 10.1111/oik.05937) [DOI] [Google Scholar]
- 20.Halliday FW, Umbanhowar J, Mitchell CE. 2018. A host immune hormone modifies parasite species interactions and epidemics: insights from a field manipulation. Proc. R. Soc. B 285, 20182075 ( 10.1098/rspb.2018.2075) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fukami T. 2015. Historical contingency in community assembly: integrating niches, species pools, and priority effects. Annu. Rev. Ecol. Evol. Syst. 46, 1–23. ( 10.1146/annurev-ecolsys-110411-160340) [DOI] [Google Scholar]
- 22.Altizer S, Dobson A, Hosseini P, Hudson P, Pascual M, Rohani P. 2006. Seasonality and the dynamics of infectious diseases. Ecol. Lett. 9, 467–484. ( 10.1111/j.1461-0248.2005.00879.x) [DOI] [PubMed] [Google Scholar]
- 23.Al-Naimi FA, Garrett KA, Bockus WW. 2005. Competition, facilitation, and niche differentiation in two foliar pathogens. Oecologia 143, 449–457. ( 10.1007/s00442-004-1814-x) [DOI] [PubMed] [Google Scholar]
- 24.Lohr JN, Yin M, Wolinska J. 2010. Prior residency does not always pay off—co-infections in Daphnia. Parasitology 137, 1493–1500. ( 10.1017/S0031182010000296) [DOI] [PubMed] [Google Scholar]
- 25.Doublet V, Natsopoulou ME, Zschiesche L, Paxton RJ. 2015. Within-host competition among the honey bees pathogens Nosema ceranae and deformed wing virus is asymmetric and to the disadvantage of the virus. J. Invertebr. Pathol. 124, 31–34. ( 10.1016/J.JIP.2014.10.007) [DOI] [PubMed] [Google Scholar]
- 26.Rynkiewicz EC, Brown J, Tufts DM, Huang C-I, Kampen H, Bent SJ, Fish D, Diuk-Wasser MA. 2017. Closely-related Borrelia burgdorferi (sensu stricto) strains exhibit similar fitness in single infections and asymmetric competition in multiple infections. Parasit. Vectors 10, 64 ( 10.1186/s13071-016-1964-9) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pedersen AB, Greives TJ. 2008. The interaction of parasites and resources cause crashes in a wild mouse population. J. Anim. Ecol. 77, 370–377. ( 10.1111/j.1365-2656.2007.01321.x) [DOI] [PubMed] [Google Scholar]
- 28.Hite JL, Penczykowski RM, Shocket MS, Strauss AT, Orlando PA, Duffy MA, Cáceres CE, Hall SR. 2016. Parasites destabilize host populations by shifting stage-structured interactions. Ecology 97, 439–449. ( 10.1890/15-1065.1) [DOI] [PubMed] [Google Scholar]
- 29.Tessier AJ, Woodruff P. 2002. Trading off the ability to exploit rich versus poor food quality. Ecol. Lett. 5, 685–692. ( 10.1046/j.1461-0248.2002.00373.x) [DOI] [Google Scholar]
- 30.Auld SKJR, Hall SR, Housley Ochs J, Sebastian M, Duffy MA. 2014. Predators and patterns of within-host growth can mediate both among-host competition and evolution of transmission potential of parasites. Am. Nat. 184, S77–S90. ( 10.1086/676927) [DOI] [PubMed] [Google Scholar]
- 31.Clay PA, Dhir K, Rudolf VHW, Duffy MA. 2019. Within-host priority effects systematically alter pathogen coexistence. Am. Nat. 193, 187–199. ( 10.1086/701126) [DOI] [PubMed] [Google Scholar]
- 32.Hothorn T, Bretz F, Westfall P. 2008. Simultaneous inference in general parametric models. Biom. J. 50, 346–363. ( 10.1002/bimj.200810425) [DOI] [PubMed] [Google Scholar]
- 33.Su Y-S, Yajima M. 2015. R2jags: using R to Run ‘JAGS’. R package version 0.5-7. See https://CRAN.R-project.org/package=R2jags.
- 34.Civitello DJ, Pearsall S, Duffy MA, Hall SR. 2013. Parasite consumption and host interference can inhibit disease spread in dense populations. Ecol. Lett. 16, 626–634. ( 10.1111/ele.12089) [DOI] [PubMed] [Google Scholar]
- 35.King KC, Auld SKJR, Wilson PJ, James J, Little TJ. 2013. The bacterial parasite Pasteuria ramosa is not killed if it fails to infect: implications for coevolution. Ecol. Evol. 3, 197–203. ( 10.1002/ece3.438) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.R Core Team. 2017. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- 37.Lotz JM, Font W. 1994. Excess positive associations in communities of intestinal helminths of bats: a refined null hypothesis and a test of the facilitation hypothesis. J. Parisitol. 80, 398–413. [PubMed] [Google Scholar]
- 38.Ebert D. 1996. Development, life cycle, ultrastructure and phylogenetic position of Pasteuria ramosa Metchnikoff 1888: rediscovery of an obligate endoparasite of Daphnia magna Straus. Phil. Trans. R. Soc. Lond. B 351, 1689–1701. ( 10.1098/rstb.1996.0151) [DOI] [Google Scholar]
- 39.Vasco DA, Wearing HJ, Rohani P. 2007. Tracking the dynamics of pathogen interactions: modeling ecological and immune-mediated processes in a two-pathogen single-host system. J. Theor. Biol. 245, 9–25. ( 10.1016/j.jtbi.2006.08.015) [DOI] [PubMed] [Google Scholar]
- 40.Bushman M, Antia R, Udhayakumar V, de Roode JC. 2018. Within-host competition can delay evolution of drug resistance in malaria. PLoS Biol. 16, e2005712 ( 10.1371/journal.pbio.2005712) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Rohani P, Green CJ, Mantilla-Beniers NB, Grenfell BT. 2003. Ecological interference between fatal diseases. Nature 422, 885–888. ( 10.1038/nature01542) [DOI] [PubMed] [Google Scholar]
- 42.Ananthasubramaniam B, Nisbet RM, Nelson WA, McCauley E, Gurney WSC. 2011. Stochastic growth reduces population fluctuations in Daphnia -algal systems. Ecology 92, 362–372. ( 10.1890/09-2346.1) [DOI] [PubMed] [Google Scholar]
- 43.Grover JP, McKee D, Young S, Godfray HCJ, Turchin P. 2000. Periodic dynamics in daphnia populations: biological interactions and external forcings. Ecology 81, 2781–2798. ( 10.1890/0012-9658(2000)081[2781:PDIDPB]2.0.CO;2) [DOI] [Google Scholar]
- 44.Abu-Raddad LJ, Patnaik P, Kublin JG. 2006. Dual infection with HIV and malaria fuels the spread of both diseases in sub-Saharan Africa. Science 314, 1603–1606. ( 10.1126/science.1132338) [DOI] [PubMed] [Google Scholar]
- 45.Abu-Raddad LJ, van der Ventel BIS, Ferguson NM. 2008. Interactions of multiple strain pathogen diseases in the presence of coinfection, cross immunity, and arbitrary strain diversity. Phys. Rev. Lett. 100, 168102 ( 10.1103/PhysRevLett.100.168102) [DOI] [PubMed] [Google Scholar]
- 46.Laine A-L. 2011. Context-dependent effects of induced resistance under co-infection in a plant-pathogen interaction. Evol. Appl. 4, 696–707. ( 10.1111/j.1752-4571.2011.00194.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Natsopoulou ME, McMahon DP, Doublet V, Bryden J, Paxton RJ. 2015. Interspecific competition in honeybee intracellular gut parasites is asymmetric and favours the spread of an emerging infectious disease. Proc. R. Soc. B 282, 20141896 ( 10.1098/rspb.2014.1896) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Marchetto KM, Power AG. 2017. Coinfection timing drives host population dynamics through changes in virulence. Am. Nat. 191, 173–183. ( 10.1086/695316) [DOI] [PubMed] [Google Scholar]
- 49.Budischak SA, Sakamoto K, Megow LC, Cummings KR, Urban JF, Ezenwa VO. 2015. Resource limitation alters the consequences of co-infection for both hosts and parasites. Int. J. Parasitol. 45, 455–463. ( 10.1016/j.ijpara.2015.02.005) [DOI] [PubMed] [Google Scholar]
- 50.Hite JL, Cressler CE. 2018. Resource-driven changes to host population stability alter the evolution of virulence and transmission. Phil. Trans. R. Soc. B 373, 20170087 ( 10.1098/rstb.2017.0087) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Johnson PTJ, de Roode JC, Fenton A. 2015. Why infectious disease research needs community ecology. Science 349, 1259504 ( 10.1126/science.1259504) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Clay PA, Duffy MA, Rudolf VHW. 2020. Data from: Within-host priority effects and epidemic timing determine outbreak severity in co-infected populations Dryad Digital Repository. ( 10.5061/dryad.pnvx0k6h6) [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Clay PA, Duffy MA, Rudolf VHW. 2020. Data from: Within-host priority effects and epidemic timing determine outbreak severity in co-infected populations Dryad Digital Repository. ( 10.5061/dryad.pnvx0k6h6) [DOI] [PMC free article] [PubMed]
Supplementary Materials
Data Availability Statement
All data and code are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.pnvx0k6h6 [52].