Abstract
Many emerging and reemerging viruses, such as rabies, SARS, Marburg, and Ebola have bat populations as disease reservoirs. Understanding the spillover from bats to humans and other animals, and the associated health risks requires an analysis of the disease dynamics in bat populations. Traditional compartmental epizootic models, which are relatively easy to implement and analyze, usually impose unrealistic aggregation assumptions about disease-related structure and depend on parameters that frequently are not measurable in field conditions. We propose a novel combination of computational and adaptive modeling approaches that address the maintenance of emerging diseases in bat colonies through individual (intra-host) models of the response of the host to a viral challenge. The dynamics of the individual models are used to define survival, susceptibility and transmission conditions relevant to epizootics as well as to develop and parametrize models of the disease evolution into uniform and diverse populations. Applications of the proposed approach to modeling the effects of immunological heterogeneity on the dynamics of bat rabies are presented.
Keywords: Immune system, Viral infection, Rabies, Individual heterogeneity, Disease processes and demographics, Bats
1. Introduction
During the past decade many bat species (Order Chiroptera) have been suggested as reservoirs of different emerging and reemerging viral diseases. Since its emergence in 2002, the SARS-like viruses was discovered by two research groups (Li et al., 2005, Lau et al., 2005) in several species of horseshoe bats (genus Rhinolophus) in southern China. Confirmed high levels of seroprevalence suggest that bats may be natural reservoirs for SARS-like coronaviruses. Independently, Poon et al. (2005) report the identification of a novel bat coronavirus, with high prevalence in fecal and respiratory samples from three bat species (Miniopterus spp.) in Hong Kong. Coronavirus RNA was detected in six of 28 fecal specimens from bats in the Rocky Mountain region (Dominguez et al., 2007). The first recorded human outbreak of Ebola virus was in 1976, but a natural reservoir of this virus remains unsubstantiated. Bats have been proposed as potential reservoirs based on circumstantial evidence such as geographic distribution of viral variants and the association between bats and other groups of viruses. Ebola virus specific antibodies have been identified in blood samples from bat species (Hypsignathus monstrosus, Epomops franqueti, and Myonycteris torquata) in central Africa (Leroy et al., 2005). In addition, several species of African fruit bats are the only mammals except humans and apes from which RNA of highly pathogenic filoviruses, such as Ebola (Leroy et al., 2005) and Marburg (Swanepoel et al., 2007) have been detected. Outbreaks of the closely related Nipah and Hendra viruses in Malaysia and Australia have been also connected to specific bat species (Pteropus) (Chua et al., 2002, Breed et al., 2006). Although these viruses have not been isolated from bat tissues, virus-neutralizing antibodies have been detected in 14 different bat species (Johara et al., 2001).
Rabies is the most studied viral disease associated with bats. After the initial discovery of bat rabies in the early 1900s, cases of rabid bats have been reported throughout most of North, Central and South America including all 48 contiguous states of the US and the District of Columbia (Brass, 1994) and in most bat species that have been adequately sampled (Constantine, 1979). More than 90% of human cases in the US during the last 50 years have been attributed to bats. The literature on rabies in the US suggests that rabies is enzootic in some bat species, including Brazilian free-tailed bats (Tadarida brasiliensis), and the disease ecology in those species is characterized by relatively low prevalence of the virus, which varies from less than 1% to 4% (Constantine, 1967, Constantine et al., 1968, Dean et al., 1960, Girard et al., 1965, Steece and Altenbach, 1989) and much higher prevalence of rabies virus-neutralizing antibodies at levels of 65% or more (Burns and Farinacci, 1955, Steece and Altenbach, 1989).
Accurate assessment of the health risks associated with the above agents and other infectious diseases with probable reservoirs in bat populations is not possible without a detailed understanding of the disease dynamics in bats. It is surprising that despite the persistence of different infectious pathogens in bats, population extinctions and massive individual die-offs are uncommon (Pybus et al., 1986), while in other mammalian species significant mortality is well documented. Some of the rare collapses in bat colonies remain unresolved and usually are attributed to non-disease related causes, such as adverse weather or pesticide poisoning (Burns and Farinacci, 1955, Clark and Shore, 2001). Physiological stress has been suggested as a factor that may reduce individual fitness, lead to immunosuppression, and contribute to population die-offs (Constantine, 1967, Constantine et al., 1968).
Disproportion between the high level of seropositivity and low levels of prevalence and disease-related mortality documented in all of the mentioned diseases suggests the possibility of asymptomatic infections. Support for the existence of a subclinical state is provided by a recent report of experimentally infected vampire bats shedding virus in saliva without evidence of virus in brain tissue (Aguilar-Setien et al., 2005), but these results must be interpreted with caution because several aspects of the study are inconsistent (Kuzmin and Rupprecht, 2007). The significance of those subclinical infections for transmission of rabies virus in bats remains unknown.
In this paper we propose a new class of adaptive epizootic models (AEMs) as a tool to provide descriptive and predictive analysis of the disease ecology in bat populations. Our theoretical approach emphasizes the variation in the intra-host viral dynamics driven by individual diversity. The specificity of the disease dynamics is captured through application of adaptive transmission, infectivity and mortality mechanisms at the inter-host level. Our AEM implementation focuses on the variation in immune characteristics of the individuals in bat populations and on pathogen dose-dependence exposure and infectivity. Although motivated by our rabies project, the proposed modeling approach represents a general theoretical framework that can be adapted to other infectious diseases in bats and in other wildlife.
The paper is organized as follows: In Section 2 we present the theoretical framework for modeling viral diseases in bats. In Section 3 we develop an AEM based on the immune system response and its application to bat rabies. We indicate roles of the immune heterogeneity of bat colonies in its influence on the disease ecology in Section 4.
2. Theoretical framework
The development of infectious diseases in wild populations is often simulated and analyzed by traditional compartmental epizootic models, which are defined by classes of individuals aggregated with respect to the infection (susceptible, exposed, infectious, recovered). These SEIR models assume constant population parameters, such as contact rates, transmission rates, and death rates that represent average values over the population. Such parameter values are extremely difficult to measure in field conditions and consequently are estimated indirectly based on additional assumptions about field data. Resulting non-AEMs represent dynamics of the viral infection but require static parameter values in time. This approach does not allow the influences of the environmental factors or influences of disease evolution on population parameters to be analyzed. Equally significant is that the effects on the disease dynamics of the individual differences in susceptibility, immune response efficiency, transmission ability, and subsequent chances of survival cannot be investigated. Therefore, the heterogeneity of the population, which plays an important role in determining the outcome of a viral invasion also needs to be incorporated into the disease dynamics through adaptive modeling techniques. In this section we introduce a multi-level theoretical approach for modeling viral diseases in bats that is founded upon the individual characteristics of bats. The interactions between modeling components at individual and population levels shown in Fig. 1 can be adapted to different viral infections through disease-specific mechanisms and processes (DMP). A description of each component of the conceptual model follows:
Fig. 1.
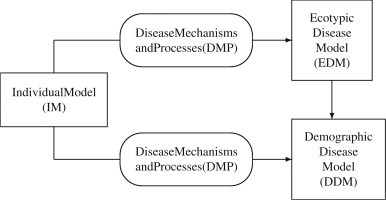
Adaptive epizootic modeling.
Individual (intra-host) models (IM) represent the response of the host to a virus challenge through delineation of the dynamics of the concentrations of the virus and components of the host systems that are involved in interactions with the agent. This broad formulation allows for putting emphasis on disease-specific physiological, biochemical, or biophysical mechanisms through different design techniques. It is important that the implemented IM is able to prescribe all documented outcomes of an exposure to the virus including progression of the disease, immunity, death, subclinical and carrier stages. The design of an IM must be based on and validated by experimental data from field studies and laboratory infections. These models in combination with the disease mechanisms and processes at the inter-host level form the foundation of our modeling approach. The development of the modeling components at the population level is intricately connected to the dynamics of IM. The parameters of IM represent individual characteristics and are used to introduce heterogeneity in response to the infection at the population level.
DMP are critical parts of the theoretical framework in that they describe the disease-specific abilities of the individuals to contract, transmit and clear the virus as well as the disease-related events that occur during effective contacts between naive and diseased bats. Here a contact is an interaction that is sufficient to provide opportunity for a viral transmission, while an effective contact is a contact during which transmission occurs. An effective contact results in a viral exposure. In contrast with the IM which concentrates on the continuous process of interaction between the host and the virus following a viral exposure, DMP delineate specific moments of virus–host association including times of exposure, transmission and clearance of the virus as well as the time of possible disease-related death. The following DMP establish connections between the intra-host and inter-host disease dynamics. The susceptibility mechanism classifies the individuals by their immune reaction to the virus. This mechanism accounts for the immunological memory from previous exposures as well as the strength and duration of the acquired immunity. The infectivity mechanism determines how and when an exposed individual becomes infectious or loses its infectivity. This mechanism describes the effects of individual diversity on the individual's ability to suppress the viral proliferation after a viral exposure. The transmission process determines viral concentrations transmitted by an infectious bat during its contacts with other individuals. This process is affected by the variability in the viral transfer caused by dynamic changes in viral concentrations and by the differences in contact effectiveness. The assimilation process determines the viral concentration that is assimilated by a susceptible bat when it is exposed through a contact with an infectious bat. This process is influenced by the differences in the site of exposure, temperature and other physiological and environmental factors. The recovery mechanism describes the ability of the individual to clear the virus completely. This mechanism specifies the physiological and immunological effects of the viral exposure of the individual's life activities following the recovery, including the strength and duration of the acquired immunity. These effects can be assessed through analysis of the damage caused by the infection (Asachenkov et al., 1994), or by establishing an explicit dependence of the individual's fitness and survival on its current viral concentration (Antia and Lipsitch, 1997). The terminal mechanism determines the combinations between viral concentration, immune response, and physiological status that result in death. This mechanism delineates the variability in the lifespan of infected bats caused by the individual diversity implemented through different dynamic representations of IM.
Ecotypic disease models (EDM) are used to investigate the evolution of the viral infection in uniform populations which are composed of a single “ecotype”. The design of an EDM follows the traditional aggregating approach by assuming that individuals express identical characteristics, defined by a fixed set of parameters for IM. The disease progression in individuals from an “ecotypic” population exposed to the virus is governed by a common IM. However, their intra-host dynamics depend on the assimilated viral dose during a viral exposure. This dependence introduces “parallel” structure in the compartmental diagram of EDM as an epizootic model. In addition, the disease-related parameters of each EDM are estimated based on the dynamics of IM and the predefined DMP. This approach has two major advantages. First, the necessity of highly aggregating data to compute average population parameters is avoided. Second, the traditional assumption that these parameters remain constant throughout the infection is relaxed in that the parameters are functions of the population adaptivity to the viral invasion.
Demographic disease models (DDM) represent the evolution of the viral infection in heterogeneous populations. Population diversity is expressed through variation in selected individual characteristics associated with “structural” parameters of the IM. Those “structural” parameters are identified by their biological significance as determined through experimental data or by their influence on dynamical properties of the IM as determined by sensitivity analysis of the IM. DDMs are structured by continuous, discrete or network integration of multiple EDMs, which cover the full spectrum of realistic sets of “structural” parameters. The disease-related parameters of each DDM are estimated based on the dynamics of IM and the predefined DMP. DDMs provide environments to analyze the effects of the disease on the population dynamics as well as the dynamical changes in the population profile with respect to selected individual characteristics.
The generality of the proposed conceptual framework combined with the adaptivity of its modeling components allows for development of disease- and species-specific AEMs that integrate experimental data at the individual level and yield predictions at the population level.
3. Adaptive modeling of bat rabies
In this section we present an application of the multi-level theoretical approach to rabies in bats. This modeling effort is a part of an integrated project that includes field and laboratory studies to analyze rabies virus exposure, infection and transmission in natural populations of Brazilian free-tailed bats and Big brown bats (Eptesicus fuscus). The proposed AEM implementation is motivated by and realistically extends the three-level modeling setup previously developed (Dimitrov et al., 2007). We emphasize the heterogeneity variations in immunological parameters that determine different DMP and explore dependence of the survival, susceptibility, and transmission on the initial viral dose. The model illustrates the adaptivity of the conceptual framework described in Section 2.
As a specific example of an IM we utilize the immune response model (IRM) (Dimitrov et al., 2007) that represents the immune response of the host to a viral challenge and models the estimated dynamics of the concentrations of the virus and the components of the adaptive immune system (B cells, T cells, virus-neutralizing antibodies) involved in interactions with the antigen. The IRM has the following form:
| (1) |
where B, T, A and V represent concentrations of B cells, T cells, virus-neutralizing antibodies and the virus, respectively. The constants and are non-disease-related production and mortality rates of the corresponding components, parameters and represent the removal rates of antibodies and virus, respectively, through irreversible complex formations, while describe the infection-related rates of production of antibodies, T cells and B cells, as well as the maximum growth rate of the virus in the host. The interactions between immune components are modeled by Type IV sigmoid response functions , defined by
| (2) |
where is a threshold parameter measuring the stimulation effect of the component j on the component i. Parameters of IRM represent major immunological characteristics, such as the lifespan and rates of change of T cells, B cells, and antibodies, as well as rates of activation of the immune mechanisms. The IRM distinguishes the documented consequences of exposure to rabies virus that include development of the disease, followed by death or attainment of a subclinical stage, which results in development of immunity (Fig. 2 ). The model expresses threshold behavior with respect to the infective dose. A bat survives if it assimilates an initial viral dose, which is less than its computed “survival threshold value” (STV). The STV fluctuates during the course of infection following the concentration changes of the immune components. The STV also depends on the immunological characteristics regulated by the parameters of the IRM.
Fig. 2.
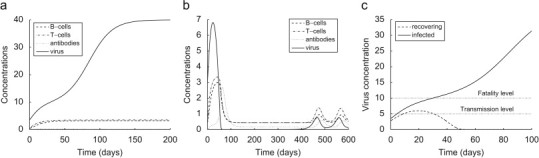
Dynamics of the IRM for a bat with exposed to different viral concentrations. (a) , (b) , (c) transmission diagram.
The reappearance of the infection (Fig. 2b) at potentially infectious levels that correspond to a long asymptomatic carrier state was thoroughly investigated (Dimitrov et al., 2007). However, the existence of such a carrier class is not well documented in field studies nor validated in laboratory experiments. Consequently, many rabies virologists do not accept this paradigm. This modeling effort is focused on formulations which do not support a carrier state by providing a mechanism that allows the disease to manifest but the population does not go to extinction. We assume that during the initial activation of its immune system the recovering host ultimately is able to clear the virus which leads to development of a long-lasting immunity.
The parameter values in IRM are based on estimates from previous publications (Chowdhury, 1993, Kaufman et al., 1985, Kaufman and Thomas, 1987, Bona and Bonilla, 1996). More importantly, they can be obtained by experimental infections in laboratory conditions.
The DMP of rabies in this AEM introduce biologically consistent dose-dependence and connect the transmission and mortality mechanisms to the dynamics of the viral concentration from the IRM. The following concepts and assumptions are novel to this modeling approach:
-
•
(A1) Threshold-based infectivity: An exposed bat is assumed to become infectious when its viral concentration exceeds a predefined “transmission” level (Fig. 2c).
This mechanism explains the existence of an initial (incubation) period of rabies in bats infected in laboratory experiments (Jackson et al., 2008) and its variation throughout the population. During the incubation period the rabies virus replicates within the host and is transported via the central nervous system to the salivary glands. Bats surviving an exposure to the virus can potentially become infectious as demonstrated in (Aguilar-Setien et al., 2005) if their viral concentration reaches the “transmission” level. Variations in individual immune parameters and in the assimilated initial viral doses affect the feasibility of achieving that level.
-
•
(A2) Condition al transmission: Infectious bats transmit only the viral load which exceeds the “transmission” level (Fig. 2c). All contacts are assumed equally effective.
-
•
(A3) Infective-dose-dependence: A naive bat exposed to a viral concentration below the STV assimilates the nearest of n different level doses.
This mechanism initiates “parallel” exposed classes () each of which expresses different intra-host dynamics and periods of temporal infectivity. Similarly, a bat exposed to viral concentration above the STV assimilates the nearest of m level doses defining “parallel” infected classes (). Bats in those classes also have different infectious periods. The version of AEM illustrated below uses five equally distant level doses below and above the STV.
-
•
(A4) Complete immunity upon survival: Once initiated, the immune system of the bats from the exposed classes becomes fully activated against rabies and they cannot be reinfected. The survival of an exposure to rabies virus results in long-lasting complete immunity.
This assumption mirrors the fact that most of those bats that survive experimental inoculations do not succumb after consecutive exposures to high viral concentrations even if they are conducted after a long period of time (Jackson et al., 2008).
-
•
(A5) Threshold-based mortality: Infected bats die when their viral concentration reaches a predefined “lethal” level (Fig. 2c).
This modeling mechanism expresses the lifespan variation observed during experimental infections.
Information about the lethal and transmission levels used in the above mechanisms is not available in the literature. We estimate these thresholds from existing data for the distribution of the incubation period and the lifespan of the infected individuals during experimental infections (Jackson et al., 2008).
At the ecotypic level (EDM), we develop an immunotypic disease model (IDM) of a rabies virus infection in a immunologically homogeneous bat colony that we call an immunotype. Our version of IDM (Fig. 3 ) derives from the dynamic predictions of IRM and utilizes the disease mechanisms (A1–A5). The following assumptions that represent findings about the life history of colonial bats are employed in the model:
-
•
(A6) Both genders are equally represented in the population.
-
•
(A7) Newborn bats are introduced by birth pulses at the rate b once per year and each is susceptible to the virus.
-
•
(A8) The population suffers natural losses at rate d due to dispersal and deaths unrelated to the disease.
Fig. 3.
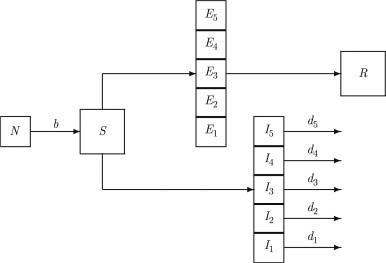
Diagram of immunotypic disease model with susceptible (S), removed (R), and 5 distinct exposed and infected classes that illustrates how viral exposures result in different level of virus assimilation leading to different infectivity and mortality rates . N is the total population size and b is the birth rate.
Using assumptions (A1)–(A8), the IDM takes the form in the diagram of Fig. 3 and can be described by the following system of differential and impulsive equations:
| (3) |
where t is a positive integer, represents the contact rate, transmission coefficients and regulate the flow from the susceptible class to exposed and infected classes following contacts with bats from classes and , respectively, expresses the transfer rate at which individuals leave class with long-lasting immunity, is the rabies-related death rate for the infected class , and N stands for the size of the whole population. Note that IDM considers separately the contact rate from the effective contact rates, which for interactions between classes S and are given by with , and for interactions between classes S and are given by with . Standard non-AEMs do not have the dose-dependent exposed and infective classes and use only effective contact rates that are not directly measurable in the field. One major advantage of an IDM is that it uses the contact rate that can be estimated in natural conditions while the transmission coefficients and as well as the transfer rates and the mortality rates are calculated based on the dynamics of the IRM. They are associated with the particular immunotype.
The computational procedure is influenced by the DMP, introduced through assumptions (A1)–(A8) and could be summarized as follows. First, the transfer rates (, ) are calculated as reciprocal values of the durations of the initial phase of the intra-host infection predicted by the dynamics of the IRM following exposure to a viral concentration in the range that corresponds to the exposed class . Second, the mortality rates (, ) are calculated as reciprocal values of the lifespan predicted by the dynamics of the IRM following exposure to a viral concentration in the range that corresponds to the infected class and decreased by the natural loss rate d. Third, the transmission coefficients (, ) are calculated by computing probabilities that during a contact with an infected bat from class a naive individual assimilates a viral concentration in the ranges which will transfer that bat to the exposed class or the infected class , . These probabilities are computed as portions of time during which the viral concentration of the bats in falls into the ranges that correspond to different infected and exposed classes. Fig. 4 a illustrates the computational procedure for . The solid line presents the viral concentration of bats from in time, the dotted line determines the level that corresponds to the STV while the dashed lines are the level doses between the “transmission” and the “ lethal” levels that separate the ranges that correspond to different exposed and infected classes. The coefficient , where is the time period during which the viral concentration remains in the range between and and is the duration of the initial phase of the infection. Fourth, the transmission coefficients (, , ) are calculated by computing probabilities that during a contact with a bat from class a naive individual assimilates a viral concentration in the ranges which will transfer that bat to the exposed class or the infected class , . Fig. 4b illustrates the computational procedure for . The solid line presents the viral concentration of bats from in time and , where and are the time periods during which the viral concentration remains in the range between and while is the duration of the initial phase of the infection. If the viral dynamics of the IRM that corresponds to the class does not reach the “transmission” level then the bats from that class never become infectious and , .
Fig. 4.
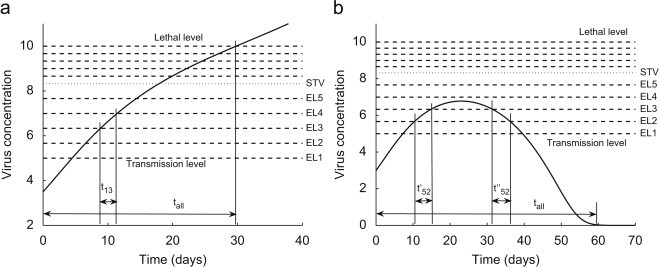
Calculation of the transmission coefficients of IDM with .
Simulations analyzing the introduction of the rabies virus into populations composed of single immunotypes are presented in Fig. 5 . The disease dynamics are strongly influenced by the strength of the bats’ immune system. We distinguish three possible dynamic outcomes of an immunotypic exposure to rabies. Here, a “recovering” population is able to eradicate the disease, i.e., it asymptotically tends to a “naive” population (Fig. 5c). An “endangered” population is not able to survive and steadily declines in time (Fig. 5a and b). A “reservoir” population survives and grows in time but it always includes a small number of infected bats and a significant portion of removed bats (Fig. 5d).
Fig. 5.
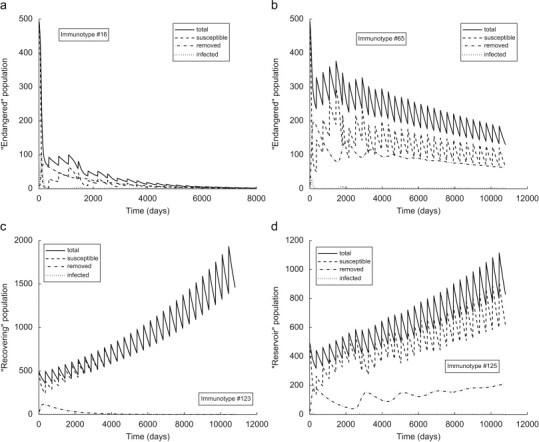
Disease dynamics of immunotypic bat colonies modeled by IDM with . (a) , , , (b) , , (c) , , , and (d) , , .
The calculated parameter values of an IDM for one of the simulated immunotypic populations are presented in Appendix B. Simulations in Fig. 5 show that an IDM (3) is able to represent the observed dynamics of bat rabies which characterize persistence of the infection with a significant portion of exposed and removed individuals and an extremely low level of infected bats. The persistence of the disease is possible even without the presence of a long-lasting carrier state and it is driven by the dose-dependence introduced in IDM.
The final stage of the AEM is the population disease model (PDM) which investigates the rabies dynamics in an immunologically diverse bat population composed of 128 different immunotypes. Each immunotype represents bats with the same immune system governed by seven “structural” parameters of the IRM (1). The parameter values are chosen by taking one of two biologically relevant levels, low and high. The selection of the “structural” parameters is a result of sensitivity analysis of the IRM which determines the influence of each immune characteristic on the individual's ability to clear the rabies infection successfully, i.e., its impact on the individual's STV. Variations in those characteristics affect the duration of the incubation period, the immune activation process, and the lifespan of the infected individuals. In this PDM implementation, a variation of 10% from an average level is introduced in each parameter (see Appendix A). Each immunotype j of PDM with a total density is divided into epizootic classes (; , ; , , ). The dynamics of the PDM is described by a system of differential and 128 impulsive equations:
| (4) |
The birth mechanism of the PDM adds newborns through annual birth pulses to the immunotypes of their mothers. Transmission coefficients and , stored in matrices P and Q, regulate the flow from the susceptible class to the exposed and infected classes of each immunotype. A contact between bats from classes and results in effective transmission with a probability , where represent the portion of the newly exposed individuals moving to the exposed class for or the infected class for . Similarly, a contact between bats from classes and results in effective transmission with a probability , where represent the portion of the newly exposed individuals moving to the exposed class for or the infected class for . Transmission coefficients and are determined by the same procedure as indicated in the description of the IDM, based on the dynamics of the IDM for the different immunotypes and the rabies-specific DMP. The PDM also incorporates the assumption that bats from all immunotypes share a common “transmission” level, which results in equal effective transmission rates of the interactions (, ) and (, ) that we denote with and . The above properties of the transmission coefficients lead to the following features of the matrices P and Q:
In Fig. 6 we simulate the introduction of a small number of infected bats into a naive population of equally represented immunotypes. The predicted dynamics are biologically relevant in that they allow infected bats from a single immunotype to initiate transfers from susceptible classes to all infected and exposed classes. Introduced dose-dependent parallel structure and the competitive coexistence of all three type of ecotypic sub-populations (endangered, reservoir, and recovering) foster the persistence of the infection without the presence of long-lasting carriers. The simulations of the population dynamics show a significant impact of the infection on the immunological profile of the colony over a period of 50 years, even if the total population size remains relatively stable. The AEM framework allows us to examine the change in the population profile with respect to a single “structural” parameter or a group of immunological characteristics (Fig. 6c–f).
Fig. 6.
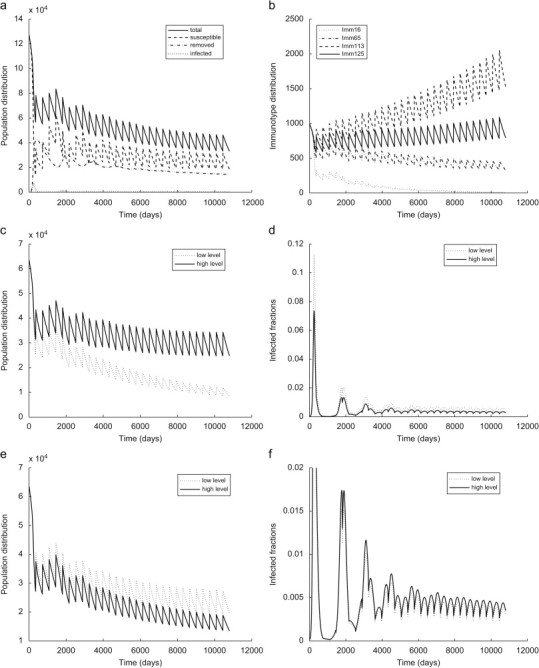
Disease dynamics of an initial colony of equally represented immunotypes. (a) , , , , , (b) , , , , , (c) population distribution with respect to the rate of antibody production , (d) infected portions in population fractions with different rates of antibody production , (e) population distribution with respect to the immune activation parameter , (f) infected portions in population fractions with different immune activation levels .
4. Results
In this section we use the AEM model of bat rabies to investigate the influence of the immunological heterogeneity in bat populations on the disease and population dynamics. We consider several scenarios of rabies virus introduction into bat colonies with different initial population profiles and compare the resulting trends in the population size as well as the portions of infected and exposed bats.
Effects of immunological heterogeneity: One of the main motivations to develop an AEM based on the diversity of the immune response comes from the serious differences in the intra-host dynamics observed during experimental rabies infections. Because the strength of the immune system of each individual bat determines its chances of survival then the disease puts different levels of pressure on each immunotype. The simulations of bat rabies in colonies composed of single immunotypes clearly distinguish three dynamical types of immunotypic populations (Fig. 5). It is natural to expect that the introduction of the virus into a heterogeneous population will initiate a dynamic process of stressor selection eventually leading to a “survival of the fittest immunotype”. However, the results of our simulations predict an alternative outcome. To illustrate the role of the immune response variations we consider bat populations composed of two distinct immunotypes and investigate how immune heterogeneity affects the dynamics of each immunotypic subpopulation and the colony as a whole. The graphs in Fig. 7 present AEM simulations of the disease dynamics of bat colonies that consist of combinations of Immunotypes #16, #113, and #125 as defined in Appendix A. The comparison of those graphs to simulations from Fig. 5 shows that the survival of the immunologically stronger immunotype is not necessarily at the weaker immunotype's expense. To the contrary, an existing infection slows down the growth of the stronger immunotype and improves the performance of the weaker immunotype. This effect is particularly significant in the combination between Immunotypes #16 and #113 where the “endangered” subpopulation turns into a growing “reservoir” type when combined with a stronger “recovering” immunotype. These unexpected dynamics can be explained by the frequency-dependent transmission mechanism of the PDM (4). It implies that after the introduction of the virus into a bi-immunotypic population the portion of the colony belonging to the stronger immunotype increases, the disease pressure on the weaker subpopulation decreases and it is able to overcome the infection. Conversely, the disease pressure on the stronger subpopulation increases and therefore its growth slows compared to the immunotypic population scenario. In addition, the portion of exposed and infected bats is higher among the immunosuppressed subpopulation (Fig. 7b), which supports a hypothesis (Constantine, 1988) that immunodeficient individuals maintain rabies viruses in colonial bat populations.
Fig. 7.
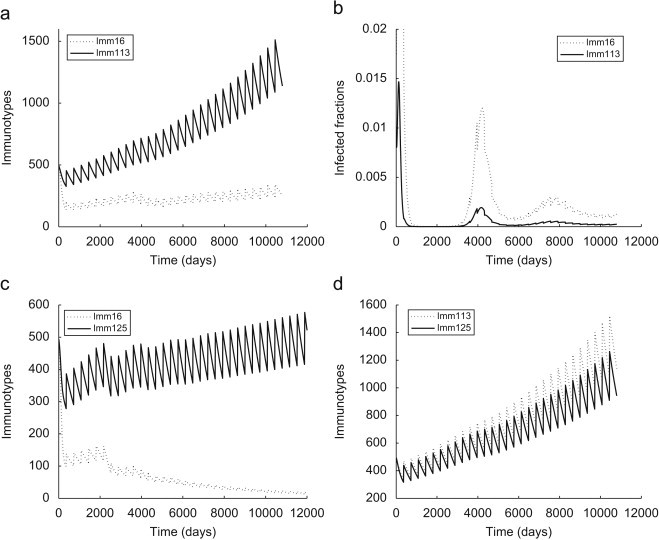
Dynamics of the profile of bi-immunotypic populations. (a) ; ; ; , (b) infected portions of the immunotypes from (a), (c) ; ; ; , (d) ; ; ; .
Infectivity of surviving bats: The existence of an infectious period of bats surviving rabies exposure was discussed (Echevarria et al., 2001, Steece and Altenbach, 1989). However, the vast majority of bat studies dismiss this possibility. A discussion was recently reopened after some experimental infections resulted in a temporal infectiousness tending toward survival (Aguilar-Setien et al., 2005). An AEM allows us to analyze the effect of a possible infectious period on the disease dynamics in immunologically homogeneous and heterogeneous bat populations. For the purpose of that analysis we consider two different versions of the IDM (3) and the PDM (4).“Full” versions, defined in Section 3 assume that the recovering bats can go through a brief infectious period while “subclinical” versions ignore the possibility that exposed individuals are able to initiate effective contacts, i.e., assume that . The two implementations of the IDM are identical for some “endangered” immunotypic populations, such as the one based on Immunotype #16, because the viral concentrations of all exposed classes never reach the transmission threshold. For some “recovering” immunotypic populations the disease dynamics for both versions differ in their epizootic distribution but do not express significant differences in the population dynamics (Fig. 8 a and b). These colonies are immunologically strong, most exposed bats recover, and the colonies clear the disease after a short period. The temporal infectivity of surviving bats has a much stronger effect on the “reservoir” and some of the “endangered” populations. The comparison of simulations of the “subclinical” IDM (Fig. 8c and d) for immunotypic populations #65 and #125 with the corresponding “full” version simulations from Fig. 5b and c shows substantial differences in the population dynamics. The additional infections initiated by recovering bats do not increase the disease pressure on the colonies. Conversely, populations benefit from these infections which contribute mostly to the immunized portion of the colonies. These effects do not change the qualitative disease dynamics, in that the long term fate of those colonies remains unaffected.
Fig. 8.
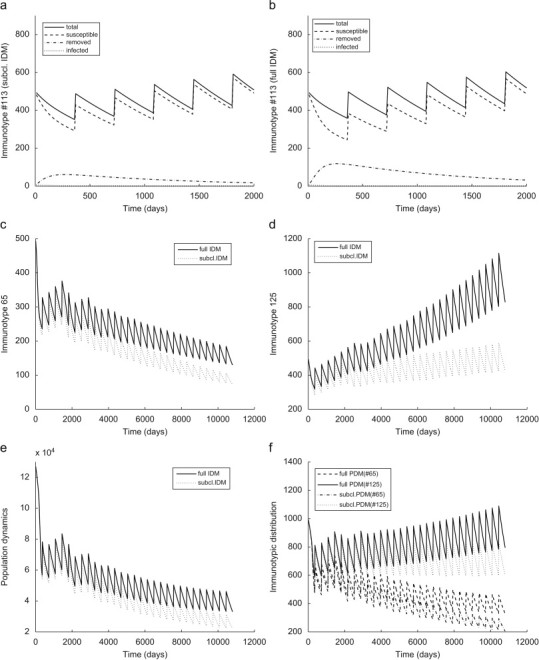
Effects on the existence of infectious period of surviving bats on the disease dynamics. (a) , , , (b) , , , (c) , , , (d) , , , (e) , , , , , and (f) , , , , .
Fig. 8e and f compare the disease dynamics caused by the introduction of the virus into heterogeneous populations simulated with the “full” and “subclinical” PDMs. In addition to the effects of the temporal infectivity of surviving bats on the population dynamics we observe differences in the immunological profile of the colony. Immunotypic subpopulations with intermediate immunocompetence such as #65 and #125 benefit from the increased amount of effective contacts because most of the additionally exposed bats survive and develop immunity. The growth of some subpopulations as a part of the population profile is supported only by the “full” PDM. Based on the calculated transmission coefficients the average portion of effective transmissions caused by infectious recovering bats varies between 2% and 3% of all effective contacts. Our simulations show that even at such low levels they have a serious impact on the disease dynamics by increasing the immunocompetence of the exposed colonies. This fact emphasizes the need for additional investigation of this hypothesis and its significance to the association between rabies and bats.
5. Discussion
Mathematical modeling of viral infections in wild mammals such as bats has often been handled in a way similar to infectious diseases in humans or livestock. This fact underestimates the significant differences in disease dynamics, transmission routes, treatment mechanisms, and possible control strategies. One of the main obstacles in our desire to understand the dynamics of bat diseases lays in the limited extent and the sporadic accessibility of time sensitive information about exposure, transmission and evolution of viral infections in natural habitats. The specifics of bat lifestyles that often include large colony sizes and long-range mobility make individual identification almost impossible and the probability of consecutive encounters low. The theoretical approach presented in this paper emphasizes the intra-host disease dynamics and inter-host DMP that can be studied through experimental infections in laboratory conditions and properly planned field investigations. This approach consists of interconnected components at both individual and population levels adapted to the specifics of different viral infections. The application of the proposed technique in modeling bat rabies highlights the importance of the immunological heterogeneity and the infective-dose-dependence to the persistence of the virus in bat colonies. The IRM presents realistic intra-host dynamics, predicts the possible outcomes for the individual bat, and allows for experimental parametrization. The implemented disease mechanisms are biologically consistent in describing the variations in the incubation period, the infectivity, and the lifespan of infected bats. The disease processes of inter-host transmission and assimilation produce an adaptive modeling environment for investigation of experimentally suggested disease phenomena such as the possibility of temporal infectivity of recovering bats. The components at the population level (IDM and PDM) are conceptually and computationally derived from the dynamic predictions of IDM considered in the context of rabies-specific DMP. They capture the observed population dynamics and disease-related distribution from previous field studies. Moreover, they represent novel theoretical tools for testing ecological hypothesis related to the level of the immune diversity and fluctuations in the immune response due to environmental or physiological factors.
However, some of the modeling decisions in this paper are motivated by more general reasoning about viral infections in bats and other mammals or by the necessity of computational cost optimization. Some limitations of our model at this stage include both the greater complexity of the pathogens related to outcome, as well as the potential role of non-acquired, innate immunity. We fully concentrate on the adaptive immune system because of its substantial role in protection against rabies (Hooper et al., 1998) and because of the insufficient understanding of an innate immune system in bats. However, these immune mechanisms are potentially important for the maintenance of a long-term immunity in bats as suggested by experimental studies showing a high survival rate of repeatedly infected bats with very low antibody titers (Jackson et al., 2008). Therefore, in IRM and PDM we assume that bats surviving an exposure to rabies virus develop a long-term immunity. In addition to the action of the innate functions, this long-term protection is supported through regular consecutive effective contacts with infectious bats in natural conditions which we do not model explicitly. We are currently working on experimental and modeling designs to estimate the duration of the acquired immunity and to investigate its effects on the disease and population dynamics (Dimitrov and King, 2008). Finally, our impulsive birth mechanism assumes that newborn bats are susceptible to rabies virus and they inherit the immunological characteristics of their mothers. Later modeling formulations will consider the possibility of temporal post-natal immunity indicated by some field studies (Shankar et al., 2004). We are not aware of any detailed study that connects the immunology of mothers and pups and we plan to include this question in our future investigations. It is also reasonable at a future stage to integrate host physiology in the proposed framework by modeling the energetic cost of the immune functions and the influence of the current physiological status on the immune activation, especially as may be affected by anthropogenic stress. A further approach involves validating models by testing conformity of their predictions with field data from species such as Big brown bats and Brazilian free-tailed bats where data on exposure, colony size, contact rates, and indices of adaptive innate immune response are becoming available.
Acknowledgments
This project is supported by NSF/NIH-EID Grant 043041. The authors thank two anonymous referees for many useful comments on an earlier draft. The findings and conclusions in this article are those of the authors and do not necessarily represent the views of their Institutions.
Appendix A. Immunotypic distribution
In this appendix we delineate characteristics of the immunotypes are identified. The concept underlying the immunotypic division is in different manifestation of several individual immunological parameters from the IRM. These parameters influence the abilities of the bats to survive exposures to rabies virus, to develop immunity, and to transmit the virus through contacts with other bats. The parameter values of , , and are selected from the ranges proposed previously (Chowdhury, 1993, Kaufman et al., 1985, Kaufman and Thomas, 1987), while are taken from estimated production rates of B and T cells (Bona and Bonilla, 1996).
The dynamic importance of each parameter is determined through sensitivity analysis of IRM that estimates the influence of each parameter on the individual's STV. This analysis identified the characteristics listed in Table A1 as the most significant for the variation of STV. Based on that we were able to rank parameters influence in the following order: , , , , , , and with being positively correlated while and being negatively correlated with STV. The expression of those parameters in the population is assumed at two biologically relevant levels, low and high, that differ by 10% from their basic values (Table A1).
Table A1.
“Structural” immunological parameters and their population levels
| Parameters | Basic level | Low levelbasic level | High levelbasic level | |
|---|---|---|---|---|
| # | Name | |||
| 1 | 0.25 | 0.225 | 0.275 | |
| 2 | 0.25 | 0.225 | 0.275 | |
| 3 | 0.25 | 0.225 | 0.275 | |
| 4 | 0.1 | 0.09 | 0.11 | |
| 5 | 0.1 | 0.09 | 0.11 | |
| 6 | 1.0 | 0.9 | 1.1 | |
| 7 | 1.0 | 0.9 | 1.1 | |
The PDM (4) consists of 128 immunotypes. The “structural” parameter values for Immunotype #N are determined as follows:
Immunotypes defined in this manner express all combinations of feasible parameter values. Individual's STVs in such a heterogeneous population vary from 0.615473 in Immunotype 16 to 3.97759 in Immunotype 113.
Appendix B. Transmission coefficients
Computation of the transmission coefficients as well as the transfer and mortality rates of IDM and PDM based on the dynamical predictions of IRM for each immunotypes is a major part of the modeling setup. Here we present an example of the calculated values of IDM for a single immunotype (Table B1, Table B2, Table B3 ). The other parameter values used in simulations presented in Fig. 5, Fig. 6, Fig. 7, Fig. 8 are , , and .
Table B1.
Calculated transmission coefficients for Immunotype #113
| 0.0843 | 0.0958 | 0.1073 | 0.1341 | 0.1686 | 0.0536 | 0.0575 | 0.0651 | 0.0690 | 0.0728 |
| 0.1010 | 0.1111 | 0.1263 | 0.1414 | 0.1717 | 0.0455 | 0.0505 | 0.0505 | 0.0556 | 0.0556 |
| 0.1145 | 0.1265 | 0.1325 | 0.1446 | 0.1687 | 0.0482 | 0.0422 | 0.0482 | 0.0542 | 0.0482 |
| 0.1241 | 0.1310 | 0.1448 | 0.1517 | 0.1655 | 0.0414 | 0.0483 | 0.0483 | 0.0483 | 0.0483 |
| 0.1406 | 0.1406 | 0.1484 | 0.1563 | 0.1641 | 0.0469 | 0.0483 | 0.0483 | 0.0483 | 0.0483 |
Table B2.
Calculated transmission coefficients for Immunotype #113
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.1012 | 0.1360 | 0.2720 | 0.0945 | 0 | 0 | 0 | 0 | 0 | 0 |
Table B3.
Calculated transfer rates and mortality rates for Immunotype #113
| 0.0140 | 0.0295 | 0.0283 | 0.0232 | 0.0158 | |
|---|---|---|---|---|---|
| 0.0375 | 0.0497 | 0.0594 | 0.0682 | 0.0773 |
References
- Aguilar-Setien A., Loza-Rubio E., Salas-Rojas M., Brisseau N., Cliquet F., Pastoret P.P., Rojas-Dotor S., Tesoro E. Salivary excretion of rabies virus by healthy vampire bats. Epidemiol. Infect. 2005;133(3):517–522. doi: 10.1017/s0950268805003705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antia R., Lipsitch M. Mathematical models of parasite responses to host immune defences. Parasitology. 1997;115:S155–S167. doi: 10.1017/s003118209700200x. [DOI] [PubMed] [Google Scholar]
- Asachenkov A.L., Marchuk G.I., Mohler R.R., Zuev S.M. Immunology and disease-control: a systems-approach. IEEE Trans. Biomed. Eng. 1994;41(10):943–953. doi: 10.1109/10.324526. [DOI] [PubMed] [Google Scholar]
- Bona C., Bonilla F. Harwood Academic Publishers; New York: 1996. Textbook of Immunology. [Google Scholar]
- Brass D. Livia Press; Ridgefield, CT: 1994. Rabies in Bats: Natural History and Public Health Implications. [Google Scholar]
- Breed A.C., Field H.E., Epstein J.H., Daszak P. Emerging henipaviruses and flying foxes—conservation and management perspectives. Biol. Conserv. 2006;131(2):211–220. doi: 10.1016/j.biocon.2006.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burns K.F., Farinacci C.J. Rabies in nonsanguivorous bats of texas. J. Infect. Dis. 1955;97(2):211–218. doi: 10.1093/infdis/97.2.211. [DOI] [PubMed] [Google Scholar]
- Chowdhury D. A unified model of immune response II: continuum approach. J. Theor. Biol. 1993;165:135–159. doi: 10.1006/jtbi.1993.1180. [DOI] [PubMed] [Google Scholar]
- Chua K.B., Koh C.L., Hooi P.S., Wee K.F., Khong J.H., Chua B.H., Chan Y.P., Lim M.E., Lam S.K. Isolation of Nipah virus from Malaysian island flying-foxes. Microb. Infect. 2002;4(2):145–151. doi: 10.1016/s1286-4579(01)01522-2. [DOI] [PubMed] [Google Scholar]
- Clark D., Shore R. Chiroptera. In: Shore R., Rattner B., editors. Ecotoxicology of Wild Mammals. Wiley; New York: 2001. pp. 159–214. [Google Scholar]
- Constantine D. Activity patterns of the Mexican free-tailed bat. University of New Mexico Publications in Biology. 1967;7:1–79. [Google Scholar]
- Constantine D. Health precautions for bat researchers. In: Kunz T., editor. Ecological and Behavioral Methods for the Study of Bats. Smithsonian Institution Press; Washington, DC: 1988. pp. 491–528. [Google Scholar]
- Constantine D., Tierkel E., Kleckner M., Hawkings D. Rabies in New Mexico cavern bats. Public Health Rep. 1968;83:303–316. [PMC free article] [PubMed] [Google Scholar]
- Constantine D.G. Updated list of rabies-infected bats in North America. J. Wildlife Dis. 1979;15(2):347–349. doi: 10.7589/0090-3558-15.2.347. [DOI] [PubMed] [Google Scholar]
- Dean W., Maddy K., Cockrum E., Crecelius H. Rabies in insectivorous bats of Arizona. Ariz. Med. 1960;17:69–77. [PubMed] [Google Scholar]
- Dimitrov, D.T., King, A., 2008. Modeling evolution and persistence of neurological viral diseases in wild populations. Math. Biosci. Eng., accepted for publication. [DOI] [PubMed]
- Dimitrov D.T., Hallam T.G., Rupprecht C.E., Turmelle A.S., McCracken G.F. Integrative models of bat rabies immunology, epizootiology and disease demography. J. Theor. Biol. 2007;245(3):498–509. doi: 10.1016/j.jtbi.2006.11.001. [DOI] [PubMed] [Google Scholar]
- Dominguez S.R., O’Shea T.J., Oko L.M., Holmes K.V. Detection of group 1 coronaviruses in bats in North America. Emerging Infect. Dis. 2007;13(9):1295–1300. doi: 10.3201/eid1309.070491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Echevarria J., Avellon A., Juste J., Vera M., Ibanez C. Screening of active lyssavirus infection in wild bat populations by viral RNA detection on oropharyngeal swabs. J. Clin. Microbiol. 2001;39(10):3678–3683. doi: 10.1128/JCM.39.10.3678-3683.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girard K., Hitchcock H., Edsall G., MacCready R. Rabies in bats in southern New England. N. Engl. J. Med. 1965;272:75–80. doi: 10.1056/NEJM196501142720204. [DOI] [PubMed] [Google Scholar]
- Hooper D., Morimoto K., Bette M., Weihe E., Koprowski H., Dietzschold B. Collaboration of antibody and inflammation in clearance of rabies virus from the central nervous system. J. Virol. 1998;72(5):3711–3719. doi: 10.1128/jvi.72.5.3711-3719.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson F., Turmelle A., Farino D., Franka R., McCracken G., Rupprecht C. Experimental rabies virus infection of big brown bats (Eptesicus fuscus) J. Wildlife Dis. 2008;44:612–621. doi: 10.7589/0090-3558-44.3.612. [DOI] [PubMed] [Google Scholar]
- Johara M.Y., Field H., Rashdi A.M., Morrissy C., van der Heide B., Rota P., bin Adzhar A., White J., Daniels P., Jamaluddin A., Ksiazek T. Nipah virus infection in bats (Order chiroptera) in Peninsular Malaysia. Emerging Infect. Dis. 2001;7(3):439–441. doi: 10.3201/eid0703.010312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman M., Thomas R. Model analysis of the bases of multistationarity in the humoral immune response. J. Theor. Biol. 1987;129:141–162. doi: 10.1016/s0022-5193(87)80009-7. [DOI] [PubMed] [Google Scholar]
- Kaufman M., Urbain J., Thomas R. Towards a logical analysis of the immune-response. J. Theor. Biol. 1985;114(4):527–561. doi: 10.1016/s0022-5193(85)80042-4. [DOI] [PubMed] [Google Scholar]
- Kuzmin I., Rupprecht C. Bat rabies. In: Jackson A., Wunner W., editors. Rabies. second ed. Academic Press; New York: 2007. pp. 259–308. [Google Scholar]
- Lau S.K.P., Woo P.C.Y., Li K.S.M., Huang Y., Tsoi H.W., Wong B.H.L., Wong S.S.Y., Leung S.Y., Chan K.H., Yuen K.Y. Severe acute respiratory syndrome coronavirus-like virus in Chinese horseshoe bats. Proc. Natl. Acad. Sci. USA. 2005;102(39):14040–14045. doi: 10.1073/pnas.0506735102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leroy E.M., Kumulungui B., Pourrut X., Rouquet P., Hassanin A., Yaba P., Delicat A., Paweska J.T., Gonzalez J.P., Swanepoel R. Fruit bats as reservoirs of Ebola virus. Nature. 2005;438(7068):575–576. doi: 10.1038/438575a. [DOI] [PubMed] [Google Scholar]
- Li W.D., Shi Z.L., Yu M., Ren W.Z., Smith C., Epstein J.H., Wang H.Z., Crameri G., Hu Z.H., Zhang H.J., Zhang J.H., McEachern J., Field H., Daszak P., Eaton B.T., Zhang S.Y., Wang L.F. Bats are natural reservoirs of SARS-like coronaviruses. Science. 2005;310(5748):676–679. doi: 10.1126/science.1118391. [DOI] [PubMed] [Google Scholar]
- Poon L.L.M., Chu D.K.W., Chan K.H., Wong O.K., Ellis T.M., Leung Y.H.C., Lau S.K.P., Woo P.C.Y., Suen K.Y., Yuen K.Y., Guan Y., Peiris J.S.M. Identification of a novel coronavirus in bats. J. Virol. 2005;79(4):2001–2009. doi: 10.1128/JVI.79.4.2001-2009.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pybus M., Hobson D., Onderka D. Mass mortality of bats due to probable blue-green algal toxicity. J. Wildlife Dis. 1986;22:449–450. doi: 10.7589/0090-3558-22.3.449. [DOI] [PubMed] [Google Scholar]
- Shankar V., Bowen R.A., Davis A.D., Rupprecht C.E., O’Shea T.J. Rabies in a captive colony of big brown bats (Eptesicus fuscus) J. Wildlife Dis. 2004;40(3):403–413. doi: 10.7589/0090-3558-40.3.403. [DOI] [PubMed] [Google Scholar]
- Steece R., Altenbach J. Prevalence of rabies specific antibodies in the Mexican free-tailed bat (Tadarida brasiliensis mexicana) at lava cave, New Mexico. J. Wildlife Dis. 1989;25:490–496. doi: 10.7589/0090-3558-25.4.490. [DOI] [PubMed] [Google Scholar]
- Swanepoel R., Smit S.B., Rollin P.E., Formenty P., Leman P.A., Kemp A., Burt F.J., Grobbelaar A.A., Croft J., Bausch D.G., Zeller H., Leirs H., Braack L.E.O., Libande M.L., Zaki S., Nichol S.T., Kslazek T.G., Paweska J.T. Studies of reservoir hosts for Marburg virus. Emerging Infect. Dis. 2007;13(12):1847–1851. doi: 10.3201/eid1312.071115. [DOI] [PMC free article] [PubMed] [Google Scholar]


