Strategies for enhancing the analytical performance of nanomaterial-based sensors

Highlights

• •Strategies for enhancing the analytical performance of nanomaterial-based sensors.
• •The influence of nanomaterials characteristics on analytical performance.
• •Appropriate calibration models overcome the device-to-device variation.
• •Advantages and limitations of integrating nanomaterials on sensing platforms.

Abstract

We provide a state-of-the-art review of the main strategies for the enhancement of analytical performance of sensors using nanomaterials, particularly nanowires and carbon-based materials. We emphasize the way to overcome the problem of device-to-device variation. We discuss the study of the influence of nanomaterial characteristics, sensor dimensions and operational conditions on sensing performance, and the application of appropriate calibration models.

1. Introduction

The incorporation of nanomaterials in chemical and biological sensors has been responsible for the development of a wide variety of nanoelectronic systems on environmental, food and clinical applications, since such nanostructures display particular electrical, chemical and transport properties. For example, sensors based on field-effect transistor (FET) configurations with carbon nanotubes (CNTs) [1], [2], [3], graphene [4], [5], [6], [7], and nanowires (NWs) [8], [9], [10] have been widely used for sensing the electric charge of biomolecules (e.g., glucose, proteins and DNA) after their adsorption on the FET surface. The most reported biological interactions with nanomaterial-based FET sensors are enzymatic glucose detection, antibody-antigen binding (immunoreaction) and DNA hybridization [1], [11], [12].

Besides the advantages of applying nanomaterials, it is also known that some nanomaterial characteristics may cause considerable variability in device properties, so affecting the analytical performance of sensing systems, as shown in Fig. 1 . For example, the role played by CNT density in FET-biosensor performance has been reported [11], [13], [14], [15], demonstrating that it is critical in achieving high uniformity and analytical performance. Following that perspective, the influence of NW dimensions and doping levels for the sensitivity of NW-FET devices has also been demonstrated by theoretical and experimental studies [10], [16], [17], [18], [19], [20]. Sensitivity and limit of detection (LOD) are figures of merit that are closely associated with the transduction mechanism and morphological characteristics of sensors [21], being important tools for assessing analytical reliability, capacity, and variability in techniques and devices [22].

Figure 1.

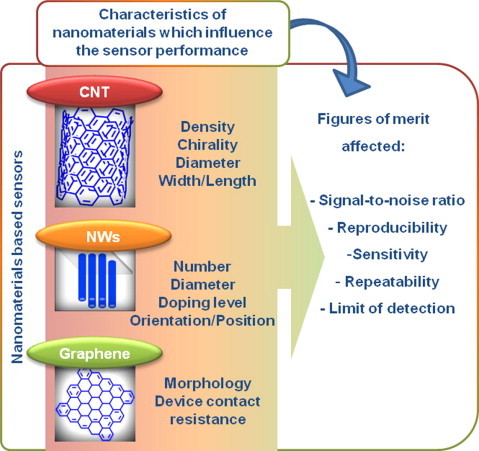
Characteristics of nanomaterials that can influence the analytical performance of chemical and biological sensors.

From such considerations, the main objective of the present review paper is to identify the main factors of sensor fabrication and integration that can influence the final analytical performance. This review therefore discusses recent works on the main strategies for the enhancing the analytical performance of nanomaterial-based sensors, and highlights the way to overcome the problem of device-to-device variation. We also identify the advantages and the limitations of integrating nanomaterials on sensing platforms.

2. Advantages of the integration of nanomaterials in sensors

Of existing nanomaterials, we focus the present review on CNT, graphene and graphene-based materials [e.g., graphene oxide (GO) and reduced GO (rGO)] and Si-NWs and metal-oxide based NWs, since they are the most reported in existing literature. The various physical, chemical and optical properties of such nanomaterials are identified in Table 1 together with their main applications.

Table 1.

Properties of some nanomaterials and potential applications

Nanomaterial	Characteristics	Properties	Potential applications	Ref.
CNTs	•One-dimensional material •Long cylinders of onea or moreb layer(s) of sp2 carbon, originated from the roll-up of graphene	•Mechanical stiffness •High carrier mobility •Thermal conductivity •High surface-to-volume ratio •Improved electron transfer	•Transistors/circuits •Scanning probes •Mechanical composites •Transparent electronics •Chemical and biological sensing devices	[23], [24], [25], [26]
NWs	•One-dimensional material •Various natures: elemental (e.g. Si and Ge) and compound (groups II-VI, III-V, and IV-VI) NWs	•High surface-to-volume ratio •Electrical current carriers	•Nanoelectronic and nanosensing devices	[8], [27], [28]
Graphene	•Two-dimensional material •Layer of a polycyclic hydrocarbon network, with carbon atoms arranged hexagonallyc	•High intrinsic current mobility •High electronic conductivity •Good thermal stability •Excellent mechanical strength	•Chemical and biological sensorsd •Clean energyd •Electronic and photonic devicesd	[12], [29], [30]

^aFor single-walled carbon nanotubes (SWCNTs).

^bFor multi-walled carbon nanotubes (MWCNTs).

^cSuch characteristics are also used to define the graphene-based materials; however, some differences should be considered: graphene has a metallic character and comprises only C and H atoms, graphene oxide (GO) has in addition O groups and the C:O ratio is between 2 and 3, and the reduced graphene oxide (rGO) has an oxygen fraction ⩽10%.

^dApplications of graphene and its derivatives (i.e. GO and rGO).

The development of sensing systems is the main application of nanomaterials, since they can enhance the analytical performance of such devices. CNT and graphene have carbon atoms on all their surfaces, enabling facile interaction with biological molecules. While CNTs have increased chemical reactivity due to large curvatures [24], graphene was also recently used as the transduction surface for chemical sensing [31] and biosensing systems [12], [30], [32], [33] due to its physical and chemical properties [29], [34].

In some works, the incorporation of multiple single-walled CNTs (SWCNTs), also called SWCNT networks, onto FET devices is preferred over individual SWCNTs, due to higher uniformity and higher reproducibility [35], [36], [37]. Such SWCNT networks have been used as the conducting channel of FET-sensing devices for environmental and clinical applications [26], [36], [38], [39], [40], [41], since they average the global properties of large random individual SWCNTs, and provide larger surface area for sensing [14], [35].

Graphene and graphene-based materials (e.g., GO, rGO, and exfoliated graphite) have also been used in various sensing systems, as recently reviewed by Liu et al. [12], Kochmann et al. [30] and He et al. [33]. For example, graphene-based FETs provide significant conductance changes with acceptable signal-to-noise ratio [5], high sensitivity [6] and specificity [7].

Regarding Si-NW-FET devices, their potential for biosensing has been demonstrated – due to their ultrasensitivity, specific, label-free and real-time detection abilities, mainly for biomedical diagnosis and cellular recording investigation, and proteins, DNA sequences, small molecules, cancer biomarkers, and viruses [28]. In addition, the possibility of controlling electrical properties, chemical composition and size of NWs by doping [42], [43] provides an advantage over the carbon-based materials (e.g., graphene and CNTs), since the charge-carrier density in devices can be controlled leading to set the sensor-response magnitude.

Understanding of the sensing-transduction mechanisms of FET sensors will lead to better interpretation of the analytical response, and allow the design of strategies for their improvement before fabrication and application. The sensing mechanism of chemical and biological systems with NWs is based on modulating the NW-surface potential, which is due to the change of charge density of the target analytes after their binding to the receptor groups linked to the NW surface. Thus, the depletion or the accumulation of carriers in the NW structure causes the high sensitivity of the devices [44]. For FET devices with SWCNTs, three possible mechanisms have been proposed and extensively reviewed by Heller et al. [45]. When analyte molecules interact with CNTs, the electronic properties of devices are altered causing changes in the current signal due to:

• •charge transfer between molecules and NTs;
• •scattering potential for mobile charges; or,
• •charge scattering caused by local deformation.

3. Limitations of the integration of nanomaterials in sensors

The principal failure in development and consequent commercialization of nanomaterial-based sensors is related to the unreliable positioning and orienting methodology for individual nanostructures, whether SWCNTs or Si-NWs [35], [46]. The use of aligned arrays of Si-NWs, rather than individual Si-NWs, is more significant in sensing devices, due to the avoidance of positioning and structural control since such devices exhibit the average properties of multiple Si-NWs, which lead to higher stability, repeatability, and better error tolerance [46]. However, irregularities in electrical, chemical and mechanical properties of sensors with CNTs come from the different processes of CNT synthesis. More specifically, the device-to-device variation after the interaction of biomolecules can be due to [14], [47]:

• (1)the random nature of NT networks in terms of their chirality (depending of the way of rolling up the sheet of graphene), which consequently affects the CNT diameter;
• (2)variations in NT density;
• (3)bundling of SWCNT networks; and,
• (4)different ratios of metallic and semiconducting NTs, depending of their chiral angles and diameters.

Such physical features can affect the electronic structure of SWCNTs and consequently their mobility and current on each device (e.g., leading to variations in conductance, ON/OFF ratios, and sensitivity). Also, for NWs, the drawbacks in device fabrication are associated with the failure in reliable control of the number and the diameters of integrated NWs in individual sensing devices [48]. The fluctuation in the position of Si-NWs on the device surface and the difficulty in maintaining the high signal-to-noise ratio in complex nanodevices remain as a challenge to Si-NW-device fabrication [46]. Concerning the graphene-based sensors, the variations in electrical, chemical, and mechanical properties and consequent sensing performance are due to fabrication factors (e.g., contact resistances, and configuration of graphene on metal electrodes) [49].

From the above considerations, it can be concluded that all variations observed in nanomaterial-based sensors, independently of the nature of nanostructures, have repercussions for the analytical performance, and essentially their reproducibility. The variations in nanomaterial characteristics from device-to-device produce great variability in device properties and their analytical performance, hindering further application of such sensors to real samples, and limiting the scale-up potential. In the following sections, we discuss the state of the art of the main strategies to enhance the analytical performance of nanomaterial-based sensors.

4. Strategies to enhance the analytical performance of nanomaterial-based sensors

The device-to-device variation in properties (e.g., drain current, conductance, and transconductance) and analytical performance of nanomaterial-based sensors (e.g., sensitivity, LOD, and signal-to-noise ratio) constitutes a major challenge in the practical application of such sensors. Several strategies have emerged to resolve this analytical barrier and improve sensor performance:

• (1)study of the influence of nanomaterials characteristics, and sensor dimensions and operational conditions; and,
• (2)application of appropriate calibration algorithms.

Such strategies reduce the variability of the analytical response and the properties of sensing devices, independently of the nature of incorporated nanostructures {i.e. NWs [metal-oxide NWs (e.g., In₂O₃ and Si)] and carbon-based materials [e.g., CNTs, graphene and graphene-based materials (e.g., GO, and rGO)]}.

4.1. Study of the influence of nanomaterial characteristics on the analytical performance of integrated sensors

In this sub-section, we discuss the effect of nanomaterial characteristics (e.g., the density of CNTs, and the number, doping density and diameter of NWs) on the analytical performance of integrated chemical and biological sensors. The main results obtained from some recent works are summarized in Table 2 .

Table 2.

Influence of nanomaterials characteristics on the analytical performance of integrated sensors

Sensor description	Nanomaterial characteristics	Enhancement of sensor characteristics	Enhancement of figures of merit	Ref.
FET with SWCNT networks for streptavidin detection	CNT densitya	•ON/OFF ratio from <10, for high CNT density, to ∼104, for low CNT density	•LODs of 100 pM–1 nM for high CNT density and 1–10 pM for low CNT density	[14]
Si-NW sensors for human immunoglobulin G detection	NW number		•∼38 and ∼82% of sensitivity for sensors with one NW, compared to sensors with 4 and 7 NWs, respectively	[48]
	NW diameter		•∼16 and ∼37% of sensitivity for sensors with NW diameter of 60–80 nm compared to sensors with NW diameter of 81–100 nm and 101–120 nm, respectively
	NW-doping density		•∼3.2-fold of sensitivity for sensors with NW doping concentration of 1019  atoms/cm3 compared with 1017  atoms/cm3 •LODs from 10 pg/mL and 10 fg/mL for sensors with NW-doping concentration 1019  atoms/cm3 and 1017  atoms/cm3, respectively
FET with SWCNT networks for DNA detection	CNT density	•ON/OFF ratio from 5 to 2000 with high and low CNT density, respectively	•LODs 10 pM and 0.1 fM with high and low CNT density, respectively	[50]

^aCNT density was classified as low, medium, and high, according to the time of incubation in ferritin solution (i.e. 10, 20, and 60 min for low, medium, and high density, respectively), which is associated to the density of catalyst nanoparticles responsible for the synthesis of nanotubes.

The density of CNTs affects the performance of transistors [13], which is consequently reflected on the analytical performance (sensitivity and reproducibility) of sensing systems. Ishikawa et al. [14] studied the effect of network-SWCNT density on the analytical performance of FET devices, and concluded that, when the density of CNTs is lower, the sensitivity in terms of both LOD and the magnitude of analytical response (defined as normalized conductance) is higher (Table 2), and the reproducibility of such biosensors is better. The enhanced sensitivity associated with a low density of SWCNTs is partly explained by the elimination of direct metallic NT pathways, enhancing the semiconductor behavior of NTs and providing a strong gate dependence, lower capacitance, and high ON/OFF ratios, while the high density of SWCNTs reflects their quasi-metallic behavior [14].

The ultrasensitivity of FET biosensors with SWCNT networks for detection of DNA molecules (0.1 fM) was also verified by Fu et al. [50] (Table 2), where the lower density of NTs improved the ON/OFF ratio and LOD of devices by three and five orders of magnitude, respectively.

The influence of NW number (i.e. the number of bridging NWs incorporated into each device), NW-doping density, and NW diameter was also verified on the sensitivity of Si-NWs FET sensors.

Li et al. [48] developed NW-based sensors for human immunoglobulin G (hIgG) as a model analyte providing the following observations (Table 2) – the device sensitivity (defined as the slope of the normalized current versus hIgG concentration plot) increases with decreasing number of NWs, smaller NW diameters, and decreasing NW-doping concentration. The increase in sensitivity with the decrease in number of NWs reported by Li et al. [48] was attributed to the increase in binding events between NWs and hIgG molecules, which results in higher current changes of sensing devices. The sensitivity increase obtained with smaller NW diameters [48] can be explained by the increase of surface-to-volume ratio in thin NWs, leading to large conductance changes [51]. The sensitivity increase with the decrease in NW-doping concentration [48] can be attributed to the reduced effect of charge screening in NWs at lower doping densities [16]. Li et al. [48] also observed that a lower LOD for hIgG was verified together with such sensitivity increase.

The control of the positioning and the handling of nanomaterials (CNTs, NWs and graphene) remains a challenge for their integration into lab-on-chip systems, interfering in the analytical performance. A wide range of fabrication methods has been proposed to resolve such integration issues. These fabrication methods are based on selective, controlled growth methods, directed-assembly and printing technologies of CNTs and NWs, as recently well reviewed by Lee et al. [52].

Post-processing methodologies could be used to control the number and diameters of NWs {e.g., ion-beam milling for selective NW removal [53] or nanomanipulation [48]}. However, the more adequate technique for producing uniform devices is nanomanipulation (using a piezoelectric nanomanipulator inside an SEM) [48] in order to optimize the number of NWs through the removal of unwanted NWs, while the ion-beam-milling technique [53] can lead to deterioration or alteration of charge-transport properties. That constitutes an advance in the fabrication of sensing devices, thus improving their sensing performance.

As an example, Lee et al. [54] proposed a strategy based on preparing high-performance “textured” network devices to control the connectivity of NTs and NW networks. Such a strategy can overcome the limitations of devices fabricated with NTs and NW networks, which, in many cases, provide low mobility and conductivity due to the nanoscale width of the conducting channel.

Regarding graphene sheets, their suspension in FET devices, rather than their common use on SiO₂ substrates, has demonstrated improvement in the signal-to-noise ratio and sensitivity of devices (e.g., pH sensors in aqueous solutions) [4]. Increased transconductance and reduction of the low-frequency noise from the contact between graphene and metal contacts of FET sensors were observed.

Cheng et al. [4] proposed that such improvements were due to the lack of scattering effect from the SiO₂ substrate, encouraging the application of such strategy for general chemical and biological sensors. Recently, Chang et al. [55] combined the properties of different nanomaterials (SWCNTs and GO) to develop FET devices with improved sensitivity and specificity. SWCNTs were used as the conducting channel, which was covered with a GO membrane in order to preserve the intrinsic electrical properties of the SWCNTs and to avoid the direct attachment of analyte molecules to SWCNTs. The sensitivity of FET devices, applied to the detection of avidin, was improved (∼4.5%) due to the enhancement of current ON/OFF ratio (∼88%) and semiconducting behavior better than devices without GO passivation.

From the above discussion about the influence of nanomaterials characteristics on the analytical performance of nanomaterial-based sensors, it can be concluded that:

• (a)FET sensors with lower CNT density provide higher sensor conductance and ON/OFF ratios leading to enhanced sensitivity, LOD, and reproducibility;
• (b)the sensitivity of FET sensors with Si-NWs can be increased with few NWs, small NW diameters, and low NW-doping concentration;
• (c)control of the number and the diameters of NWs by advanced techniques (e.g., nanomanipulation) and optimization of the way to position nanomaterials on the sensor surface, can lead to better device properties (e.g., conductance) also improving the analytical performance (e.g., sensitivity and signal-to-noise ratio).

4.2. The effects of device dimensions and operational conditions on the analytical performance of sensing systems

The control of the device dimensions, in terms of the width and the length of the conducting channel of nanomaterials can also improve the analytical performance of nanoscale sensors, mainly in sensitivity, LOD and signal-to-noise ratio, as shown in Table 3 .

Table 3.

Influence of device dimensions and operational conditions on the analytical performance of nanomaterial-based sensors

Sensor description	Parameters studied	Enhancement of sensor characteristics	Enhancement of figures of merit	Ref.
Sensor with SWCNT networks for Hg2+ detection	CNT-channel width	•Considering the mathematical relation obtained (width in nm): → Conductivity ∼ width−0.25	•LODs of 10 nM (for 2-μm-wide SWCNT network sensors) and 1 pM (for 100-nm-wide SWCNT network sensors) •Considering mathematical relations obtained (width in nm): → Signal-to-noise ratio ∼ width−1.1 → Sensitivity ∼ width−1.6	[56]
FET devices with Si NWs for prostate specific antigen detection (PSA)	Operational conditions (linear and sub-threshold regimes)	•∼50% of conductance at sub-threshold regime compared to linear regimea	•LODs of ∼0.75 pM and ∼1.5 fM in linear and sub-threshold regimes, respectively •5-fold greater signal-to-noise ratio at sub-threshold regime compared to linear regimea	[18]
FET devices with SWCNT for poly-l-lysine and poly-l-aspartic acid detection			•Increase of signal-to-noise ratio (3-fold) at sub-threshold regime compared to linear regime	[57]

^aWhen sensing 15 pM of PSA.

Regarding SWCNT networks, made of metallic and semiconducting current paths, Lee et al. [56] have verified better signal-to-noise ratio, large conductivity, and higher sensitivity in FET devices with narrower channels (100 nm) rather than with wider channels (2 μm), which may be due to a decrease in effective length of the current paths. Lee et al. [56] have determined mathematical relations between the width of SWCNT channel and the signal-to-noise ratio, conductivity, and sensitivity, as shown in Table 3. Consequently, the improved sensor could be applied to the detection of Hg²⁺ ions (LOD of ∼1 pM) in drinking water [56]. Highest sensitivity with smallest channel dimensions was also reached by Kim et al. [19] when NW-FET devices were applied to prostate specific antigen (PSA) detection (30 aM), due to the easy depletion of Si-NW channels by negatively charged biomolecules in such conditions.

Another attempt to improve the analytical performance of biosensing systems is performing the experiments in specific operational conditions; Gao et al. [18] and Heller et al. [57] have proposed the performing of biosensing experiments on FET devices with Si-NWs and SWCNTs, respectively, at sub-threshold regime (rather than linear regime) to improve the sensitivity of devices. Gao et al. [18] have developed Si-NW-FET devices doped with boron for the PSA detection, and they found that FET devices have the optimal signal-to-noise ratio and LOD at sub-threshold regime (Table 3), which is the zone preceding the higher slope in I_D  −  V_G plot. That could be due to the increase of conductance, leading to a most effective gating effect of analyte molecules, which in turn it is due to the reduced screening of charge carriers of Si-NWs. Heller et al. [57] developed NT-FETs with a liquid gate for the detection of poly-l-lysine and poly-l-aspartic acid, and they also shown that the maximum signal-to-noise ratio (Table 3) was obtained when NT-FET devices are operated in sub-threshold regime.

From the above discussion about the effect of device dimensions and its operational conditions on the analytical performance of nanomaterial-based sensors, it can be concluded that: (a) better signal-to-noise ratio, large conductivity, and higher sensitivity can be obtained in FET devices with smallest SWCNT-network channels; and (b) optimal signal-to-noise ratio and better LOD can be obtained when FET devices with SWCNT and Si-NWs are operated in sub-threshold regime.

4.3. Application of the appropriate calibration model to overcome the device-to-device variation from nanomaterial-based sensors

The choice of the appropriate calibration model for the improvement of sensing performance has been an option proposed by several authors [58], [59], [60], [61], [62]. Table 4 shows the main conclusions of the most significant works where different data analysis approaches are suggested to minimize the variability of nanomaterial-based sensors (i.e. enhancing their reproducibility).

Table 4.

Influence of the calibration model for the improvement of the analytical performance from nanomaterial-based sensors to overcome device-to-device variation

Calibration models	Calibration equation	Parameters from calibration models	Results obtained	Ref.
Calibration model based on the Langmuir adsorption model	$\mathrm{\Delta }{I}_D=\mathrm{\Delta }{I}_{\mathit{sat}}\times \frac{C}{C+\frac{1}{K}}$	ΔID – change in the drain current of devices, when the PSA/anti-PSA is adsorbed onto device surface ΔIsat – current when PSA/anti-PSA reaches the saturation mode C – concentration of the interactant solution (PSA) at equilibrium K – equilibrium constant of adsorption of PSA θ – normalized drain current	•A variability was founda on ΔID values (17.4 ± 11.9 nA) and on transconductance (86.8 ± 68.3 nS)	[58]
Optimized calibration model	$\theta =\frac{C}{C+\frac{1}{K}}=\frac{\mathrm{\Delta }{I}_D}{\mathrm{\Delta }{I}_{\mathit{sat}}}$		•With the application of the optimized calibration model, ΔID values became similar (∼0.87 ± 0.08)a
Calibration model based on the correlation between the biosensor gate dependence (dI/dVg) and the absolute response (ΔID)	$\mathrm{\Delta }{I}_D=\left(\frac{B(V_g-V_T)-B(V_g-(V_T+\mathrm{\Delta }V))}{B}\right)\times \frac{\mathit{dI}}{{\mathit{dV}}_g}$	ΔID – absolute change in drain current B – electrostatic interaction Vg – gate voltage VT – threshold voltage ΔV – equivalence gate potential induced by the biomolecule	•Variability was founda , b in ΔID values (∼113.3 ± 88.9 nA) and a CV of 59% was obtained for absolute response •With application of the calibration model, a similarity in response (∼14 mV)a and an improvement in CV were found for calibrated (19%) and normalizedc (25%) responses over the absolute response (59%)	[59]
Use of normalized response to reduce the device-to-device variation	$\frac{\mathrm{\Delta }{I}_D}{I_0}=A\frac{\alpha \times n}{1+\alpha \times n}$	ΔID – current change I0 – initial current A – coefficient that converts surface coverage into electrical response α – constant n – concentration of analyte (N-protein) gm – transconductance	•The variation of analytical responsea decreased from ∼7.4 ± 6.4 nA to ∼26.3 ± 7.6 nA for absolute and normalized responses, respectivelyd	[60]
Calibration model based on the gate effect induced by the analyte	$\frac{\mathrm{\Delta }I}{g_m}=A\frac{\alpha \times n}{1+\alpha \times x}$		•The variation of analytical responsea decreased from ∼120 ± 40 mV to ∼127 ± 11 mV for normalized and calibrated responses, respectivelye	[61]
Calibration model based on Langmuir adsorption equation	$\frac{\mathrm{\Delta }G}{G_0}=\frac{g_L\times q_A}{G_0\times C_0}\times [B{]}_{\text{max}}\times \frac{[A]}{[A]+\frac{1}{K}}$	ΔG – conductance change G0 – initial conductance gL – liquid transconductance qA – electric charge of adsorbed analyte molecules by unit surface CNT density C0 – coupling constant between the analyte molecules and CNT surfaces [B max] – maximum surface density of binding sites on CNT networks [A] – concentration of analyte α – slope of the fitting curve γ – x-intercept of the fitting curve	•Variation in sensor response (ΔG/G0) was foundf , g (∼21 ± 6)	[62]
Optimized calibration model	$\frac{\mathrm{\Delta }G}{G_0}=\alpha ({\log }_{10}[A]-\gamma )$, where $\alpha =\frac{1}{4\log {}_{10}e}\times \frac{g_L\times q_A}{G_0\times C_0}\times [B{]}_{\text{max}}$, and $\gamma =-\log {}_{10}(e^{2}K)$		•Similar K values (4.8×105  M−1) and similar coupling parameters (−1.9) were obtained on application of the calibration model

CV – Coefficient of variation.

^aVariability between three devices.

^bWhen the analytical response (change in drain current) was plotted as a function of time of exposure to 100 nM streptavidin solution.

^cNormalized response (ΔI/I₀) obtained by the normalization of current by the initial value.

^dAfter exposure of 10 nM of N-protein solution.

^eAfter exposure of 200 ng/mL of IGF-II solution.

^fVariability between six devices.

^gFor concentrations of ${\mathit{NH}}_4^{+}$ higher than 10⁻⁵ M.

The Langmuir adsorption model is the model used most to fit the experimental data obtained from nanomaterial-based sensors in order to minimize the device-to-device variation, and its general concepts should be known. The mechanism of Langmuir adsorption theory was used to relate the monolayer adsorption of an antigen (interactant/adsorbate) on their specific antibodies (ligand/adsorbent) fixed on the top gate of NT-FET devices [63] with specific surface coverage (θ), and the Langmuir isotherm equation is given by

$$\theta =(K\times C)/(1+K\times C)$$

where K is the equilibrium constant, and C is the concentration of adsorbate.

Abe et al. [58] have developed FET biosensors with SWCNTs for the detection of pig-serum albumin (PSA) (interactant) antigens through the reaction with their specific antibodies (ligand), which, in turn, were attached to the top gate of the NT-FET devices by physical adsorption. When the analytical response (ΔI_D) was plotted against the various concentrations of PSA through a calibration model based on the Langmuir isotherm equation, significant differences were observed in the ΔI_D values among individual devices (Table 4). Abe et al. [58] associated such differences with the non-uniformity of CNT channels (i.e. CNTs with different chiralities), which was supported by the different values of transconductance obtained. An optimized equation was then obtained through the normalization of the drain current change (ΔI_D) by ΔI_sat, and a decrease in the variation of analytical signal was found among three individual devices (Table 4).

Another strategy based on a model for the calibration of In₂O₃-NW biosensors was reported by Ishikawa et al. [59]. The calibration model, based on the correlation between the biosensor-gate dependence (dI/dV_G) and the absolute response (ΔI), was proposed to suppress the device-to-device variation in the sensing response significantly when three devices were exposed to a 100-nM solution of streptavidin (Table 4). The applicability of the calibration method developed to real-time biosensing was an advantage, since the absolute response in current (nA units), which led to the large device-to-device variation, was modified for a response in voltage (mV units, calibrated response), reducing such variation. In this way, the calibrated response depends on only the change in the effective gate voltage induced by the binding of streptavidin. Moreover, the calibrated responses from different devices lower the estimated coefficient of variation (CV), compared to the CV obtained from absolute response (Table 4).

A similar strategy, based on the calibrated response as the change of absolute conductance by the device transconductance values (dI/dV_G), was followed by Elnathan et al. [44] in order to normalize the variation among Si-NW-FET devices for biosensing of human cardiac troponin antigens.

The use of normalized response (ΔI/I₀), rather the calibrated response, was also tested by Ishikawa et al. [59] to reduce the device-to-device variation but with no success. The normalization produced a CV higher than that obtained by the calibrated response (Table 4). The same research group [60] has also shown the large device-to-device variation of absolute response over the normalized response when In₂O₃-NW devices were applied to the detection of N-protein of severe acute respiratory syndrome (SARS) [i.e. a biomarker (nucleocapsid protein) for SARS].

The gate effect induced by the analyte was also considered by Chang et al. [61] for the calibration of biosensors with In₂O₃-NWs for the detection of IGF-II (an epithelial ovarian cancer biomarker) in order to suppress the variability in calibrated responses. Such calibrated response was given by ΔI/g_m, similar to the normalized response (ΔI/I ₀), but replacing I₀ by g_m (i.e. the transconductance, which is a measure of switching speed of devices done by dI/dV_G). Chang et al. [61] found that the calibrated response led to a lower device-to-device variation than the normalized response (Table 4).

Another strategy based on the Langmuir adsorption equation [58] was proposed by Lee et al. [62] for the analytical modeling of biosensing devices (Table 4). A universal parameter based on equilibrium constant (1/K) was found to make CNT-network sensors predictable for ion detection, also overcoming the irregularities on their electrical properties. When the analytical response (ΔG/G₀) for various sensors was plotted, a variation was observed for ${\mathit{NH}}_4^{+}$ concentrations higher than 10⁻⁵  M (Table 4), where a linear region was shown. Lee et al. [62] then plotted such a linear region through the optimized calibration model (Table 4) and the values of equilibrium constant (K) and coupling parameter $\left(\frac{q_A}{C_0}\times [B{]}_{\text{max}}\right)$ were similar for all sensor devices (Table 4), since they are estimated from each x intercept and the slope of the fitting curves, respectively. In this way, Lee et al. [62] demonstrated that different CNT sensors can have universal parameters (equilibrium constant and coupling parameter), which are independent of the variations of device properties (e.g., conductance or transconductance) as well as of NT chiralities.

The variation among FET sensors with rGO for gas detection (e.g., NO₂) was also overcome by a strategy based in signal processing and data treatment reported by Lu et al. [49]. When NO₂ was applied to various graphene-based devices, a variation in the sensor response (∼2.8 ± 1.3, dimensionless) was observed, which was explained by differences in contact resistances, and differences in the amount and the configuration of rGO on metal electrodes. The sensor response (R _a/R _g), due to the charge transfer between rGO and adsorbed gas molecules, was assessed by the relation between the device resistance before (R _a, in air) and after (R _g) gas sensing. In order to overcome the device-to-device variation, the signal-processing method proposed suggested that the calibrated sensor response could be a consistent indicator of the analyte concentration.

Schedin et al. [64] reported that the change in the charge-carrier density of graphene in target gas and in air is linearly dependent on the analyte concentration. Then, as the sensing response (R _a/R _g) is due only to the gas adsorption on rGO [49], the correlation of (R _a  −  R _g) versus R _a has a slope dependent on the analyte concentration. Furthermore, a high linear correlation was observed for seven graphene-based devices (R ²  = 0.994), which revealed that the model used for calibration is effective in suppressing the device-to-device variation and makes the graphene-based sensors amenable for further practical applications.

The strategies discussed, based on the choice of the appropriate calibration model to overcome the device-to-device variation in nanomaterial-based sensors and contributing to the enhancement of their reproducibility, were demonstrated as successful in each specific work, since the variability found on the analytical response was resolved by applying an optimized calibration model. Such an optimized calibration model leads to a decrease in the CV (i.e. a decrease in the variability between individual devices applied to the detection of the analyte of interest, and the variation in analytical response) and findings of similar values of device parameters (e.g., equilibrium constant or transconductance).

The various strategies were appropriate and specific for the case studies discussed, but they should be used with caution or adapted in other works when the reproducibility affects the analytical performance of sensors with nanomaterials.

From all considerations in the development of nanomaterial-based sensors described as successful for clinical and environmental applications, a particular issue to be addressed is the mechanistic nature of the calibration models based on the Langmuir adsorption equation, which is used to overcome the variability of sensing systems. The adjusted and optimized calibration models can have some limitations when applied to universal sensors, since the estimated parameters are specific for each set of experimental data (i.e. they can be determined only if the experimental data fit strict mechanistic models). For example, the implementation of the Langmuir isotherm model should take into consideration the following requirements:

• •a monolayer adsorption of analytes on binding sites is employed;
• •all adsorption species interact with one site only and not with another; and,
• •the adsorption energy of all sites is identical and independent of the presence of adsorbed species on neighboring sites.

Moreover, such requirements based on monolayer coverage, adsorption-site equivalence and independence are not met in biosorption because biological molecules have various types of binding site, which contribute to the biosorption process. However, the formation of a monolayer is possible only under low-pressure conditions, and the theoretical homogeneity of binding events requested is not always verified in real surfaces, so limiting application of the model. Then, when the Langmuir isotherm model is applied to the calibration of nanomaterial-based sensors, special care must be taken about the effectiveness of such an application and about the experimental conditions of the sensor development.

5. Conclusion

Although various advantages are associated with the applications of nanomaterials in chemical and biological sensing systems, their challenges need be addressed to improve the analytical performance of such devices. The device-to-device variability verified in various nanomaterial-based sensors is the main cause for hindering their use in practical applications. In this field, the control of the nanomaterial characteristics (e.g., density, chirality and diameter of CNTs, and number, diameter and doping level of NWs) is of paramount importance, since they are critical to the enhancement of various figures of merit (e.g., LOD and sensitivity towards the analyte of interest).

The application of appropriate calibration models has also been highlighted as an important strategy for overcoming the variation of analytical response among individual devices. Such a strategy can be used for further analytical improvement, after the optimization of experimental conditions in individual works. The complementarity of all strategies discussed in this article should be considered in the further development of nanomaterial-based sensors in order to design devices with analytical performance as enhanced as possible and to minimize device-to-device variability.