Constant sub-second cycling between representations of possible futures in the hippocampus

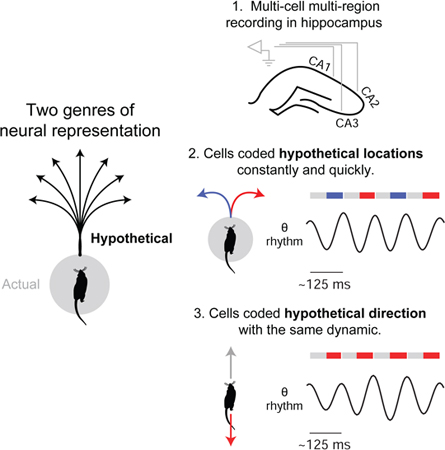
Summary

Cognitive faculties such as imagination, planning, and decision-making entail the ability to represent hypothetical experience. Crucially, animal behavior in natural settings implies that the brain can represent hypothetical future experience not only quickly but also constantly over time, as external events continually unfold. To determine how this is possible, we recorded neural activity in the hippocampus of rats navigating a maze with multiple spatial paths. We found neural activity encoding two possible future scenarios (two upcoming maze paths) in constant alternation at 8 Hz: one scenario per ~125 ms cycle. Further, we found that the underlying dynamics of cycling (both inter- and intra-cycle dynamics) generalized across qualitatively different representational correlates (location and direction). Notably, cycling occurred across moving behaviors, including during running. These findings identify a general dynamic process capable of quickly and continually representing hypothetical experience, including that of multiple possible futures.

Graphical abstract.

eTOC blurb

Imagination, planning, and decision-making require the ability to generate representations of hypothetical experience. Kay et. al. find that neurons in the rat hippocampus can represent alternative hypothetical scenarios both regularly and quickly (every ~125 ms). Further, the underlying activity has a temporal structure that is equivalent across different representational correlates (location and direction), implying a common process.

Introduction

Traditional approaches to cognition have focused on the neural representation of external stimuli (Mountcastle, 1998). In contrast, the ability to construct and simulate hypothetical experience, whether of a counterfactual past, an alternative present, or a possible future, has only more recently begun to be widely understood as fundamental to the brain (Buzsáki, 2006; Buckner and Carroll, 2007; Gilbert and Wilson, 2007; Suddendorf and Corballis, 2007; Seligman et al., 2013; Mullally and Maguire, 2014; Smallwood and Schooler, 2015). This ability – which we here refer to as “generativity” – is essential to a range of cognitive faculties (e.g. planning, imagination, decision-making), indicating a unifying role in cognition. Despite this importance, it remains unclear how generativity is implemented in the brain at the neural level.

Here, behavior and ecology provide direct insight. Generativity contributes to behavior ultimately through projection into the future: future-projection enables outcome prediction, which advantageously guides ongoing behavior. Thus an account of behaviors that entail future-projection can identify biologically necessary properties of generative representation. Crucially, in natural (ecological) settings, high-speed behaviors such as predation and escape are known to require subjects to decide between possible future scenarios not only extremely quickly, but also constantly, as external events continually unfold (Cisek and Kalaska, 2010; Cisek, 2012). This observation implies that the underlying process that generates representations of possible future scenarios has matching properties: sub-second speed and constant operation over time.

Previous work has identified candidate patterns of neural activity encoding possible future scenarios, but these patterns have been found to occur only intermittently and in association with relatively slow (~1 Hz or less), overtly deliberative behaviors, namely head scanning (Johnson and Redish, 2007; Redish, 2016) and immobility (Carr et al., 2011; Pfeiffer and Foster, 2013; Buzsaki, 2015; Foster, 2017; Joo and Frank, 2018). As a consequence, it has remained unknown how the brain is capable of representing possible future scenarios both quickly and constantly.

Cycling firing in the hippocampus

To investigate how generativity is implemented in the brain, we sought first to specify a candidate neural substrate. Importantly, generative thinking has been found to activate and require the hippocampus (Buckner, 2010; McCormick et al., 2018), a brain region traditionally linked to memory and spatial navigation. Indeed, recent work on spatially selective hippocampal neurons (place cells) has found activity patterns encoding single generative scenarios in the form of single hypothetical spatial paths (Johnson and Redish, 2007; Carr et al., 2011; Pfeiffer and Foster, 2013; Buzsaki, 2015; Redish, 2016; Foster, 2017; Joo and Frank, 2018). Yet despite this advance, these generative activity patterns have been found to occur only intermittently (~1 Hz or slower), and thus cannot implement the speed and constant operation required by natural behavior.

We conjectured that identifying a candidate pattern of neural activity might require a methodological approach inspired by natural behavior: specifically, (i) use of a task that requires naturalistic behavior (self-generated locomotion) and can be solved rapidly by means of generative representation, such as of upcoming spatial paths (Figure 1A), and (ii) analysis of neural activity inclusive of periods of high-speed movement. We speculated that these two methods could together prove sufficient if applied to the study of neural substrates implicated in generativity.

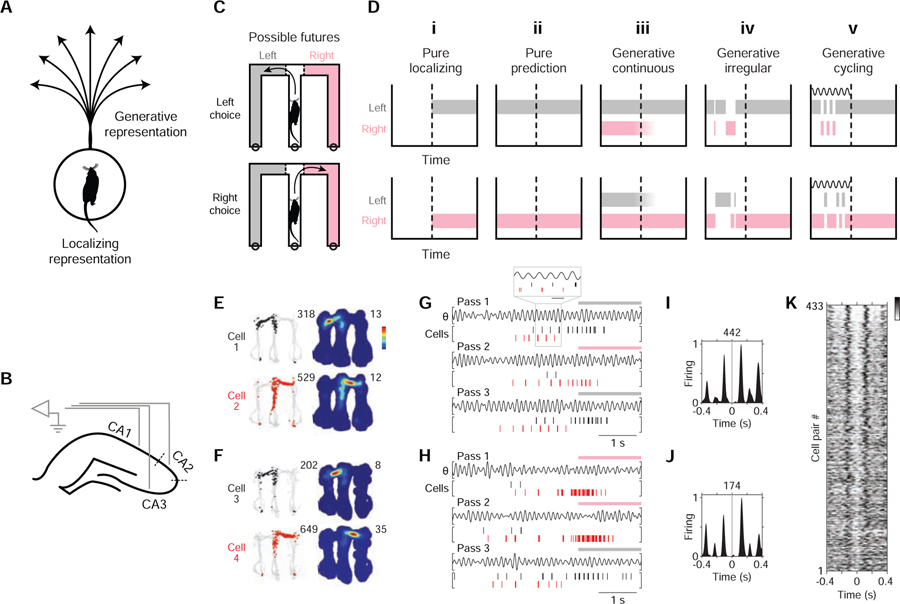
Figure 1. Study rationale and initial observation.

(A) A visualization of two types of representation: localizing vs. generative. For illustration, the representational correlate is here taken to be the animal’s (rat) location. Given this correlate, veridical (localizing) representation refers to actual location, while hypothetical (generative) representation refers to possible locations; for example, spatial paths projecting from the animal’s actual location.

(B) Diagram of hippocampal recording sites. CA2 recording sites were those near the cytoarchitectural locus of CA2 (dotted lines).

(C) Diagram of task maze and generative scenarios (possible futures). Separate diagrams are shown for two types of maze passes: those in which subjects (rats) choose left (L; grey) vs. right (R; pink) maze arms. Actual maze was not colored differently. In the maze task (Figure S1A), subjects were rewarded for choosing correctly between L vs. R. When the subject is located in the center maze arm before crossing the choice boundary (CB, dotted line), the L and R maze arms constitute possible future locations; moreover, for a given maze pass, entry into the maze arm not subsequently chosen necessarily constitutes a possible future scenario.

(D) Identifying generative neural activity: competing hypotheses. For each hypothesis, a schematic of neural activity during a single maze pass is shown; a colored bar indicates neural activity encoding one of two locations: L (grey) vs. R (pink) maze arms. The time at which the subject crosses the choice boundary (CB) is indicated by a dotted line. Neural activity is in reference to a particular brain region of study (e.g. the hippocampus). Note that neural activity is generative only if the unchosen maze arm (alternative) is encoded, as in (iii), (iv), and (v).

(i) Pure localizing. Neural activity encodes no information about possible experience.

(ii) Pure prediction. Before the CB, neural activity only encodes the subsequently chosen maze arm (i.e. fully anticipated experience).

(iii) Generative continuous. Before the CB, neural activity encoding the alternative occurs without interruption.

(iv) Generative irregular. Before the CB, neural activity encoding the alternative occurs only during irregular intervals. Irregularity can be defined as having a wide incident frequency and also lacking entrainment to any narrow-frequency pattern. Two irregular patterns associated with generative neural representation are sharp-wave ripples (Buzsaki, 2015; Joo and Frank, 2018) and behavioral head scanning events (vicarious-trial-and-error (Redish, 2016)).

(v) Generative cycling. Before the CB, neural activity encoding the alternative occurs at regular intervals (in cycles); an internal dynamic process having a characteristic time course (diagrammed as a wave) is implied.

(E and F) Firing maps of two example cell pairs. Each row corresponds to a cell. Data from outbound maze passes. Left column: positions visited (grey) and positions where the cell fired (colored points; cell 1: black; cell 2: red). Total number of spikes is reported at upper right. Right column: time-averaged firing map. Peak firing rate is reported at upper right. Recording regions: cell 1: CA3; cell 2: CA2; cell 3: CA3; cell 4: CA3.

(G and H) Firing rasters of the two cell pairs from (E) and (F), respectively, during three maze passes. Plotted above each pass is theta-filtered LFP (θ, 5–11 Hz from CA3). Periods when subject was located in an outer maze arm are indicated above plots by colored bar (grey: left; pink: right). In (G), a portion of the data is expanded to help show the firing pattern (grey boxing; scale bar: 125 ms). Note the firing alternation between cells at the ~125 ms (8 Hz) timescale.

(I and J) Firing cross-correlogram (XCG) of the two cell pairs from (E) and (F), respectively. Cell 1 (and 3) spikes are aligned to Cell 2 (and 4) spikes (t = 0 s). Each XCG (5-ms bins) is smoothed with a Gaussian kernel (σ = 10 ms) and peak-normalized; total number of spikes in XCG is reported at top.

(K) Firing XCGs of anti-synchronous cell pairs (in rows; see STAR Methods for criteria). Greyscale value indicates firing density. Data from outbound maze passes. Additional cell pair types and data conditions in Figure S2.

Taking this approach, we recorded and analyzed hippocampal place cell activity in simple self-paced task that benefits from generative representation: in a bifurcating maze, subjects (rats) allowed to move at high speeds (~50 cm/s) had to choose correctly between two upcoming locations – the left (L) vs. right (R) maze arm – without relying on external directing cues (spatial alternation task: Figure S1A; recording configuration: Figure 1B; cells analyzed were putative principal cells (n = 1756 cells from 12 subjects; CA1: 978, CA2: 250, CA3: 528) firing at least 100 spikes (mean ± SD: 912 ± 810 spikes) in a ~15 min recording epoch; survey of mean firing rates in Figure S1B) (Karlsson and Frank, 2009; Kim and Frank, 2009; Kay et al., 2016). Importantly, the bifurcation in the task maze enables unambiguous detection of generative neural activity: in the time period prior to the subject’s choice of arm, neural activity encoding the arm not chosen would necessarily constitute neural activity encoding a possible future scenario (schematic in Figures 1C and 1D). Leveraging this experimental paradigm, we examined the activity of place cells encoding either the L or R arm (surveyed in Figures S1D-F), focusing on periods of movement prior to subjects’ overt choice of arm.

Unexpectedly, we found that place cells encoding the L vs. R arms could fire in strikingly regular alternation at ~8 Hz, i.e. a given cell firing on every other 8 Hz cycle (example cell pairs: Figures 1E–J and 2A–F; survey of cell pairs: Figure 1K). This pattern of activity was significant in two ways: first, this pattern was unexpected given the classical description of place cells as firing characteristically on adjacent 8 Hz cycles (O’Keefe and Recce, 1993; Huxter et al., 2003; Zugaro et al., 2005) (examples of classic firing in Figures S1L-O); second, this pattern was the first indication that possible future scenarios (the two upcoming arms) could be encoded with both sub-second speed (i.e. firing within single 8 Hz cycles) and constancy over time (i.e. firing regularly every other 8 Hz cycle).

Figure 2. Constant cycling (8 Hz) in the hippocampus.

Example cell pairs showing constant cycling firing at 8 Hz.

(A-D) Four example cell pairs with differing locational representations (left (grey) vs. right (pink) arm; schematic at far left). Plotting conventions are the same as Figures 1E–J. Data from outbound maze passes, with data from left (grey) vs. right (pink) passes plotted separately. In (A) and (B), a portion of the data is expanded to help show the firing pattern (grey boxing; scale bar: 125 ms).

(E-J) Six example cell pairs with differing directional representations (outbound (grey, Out) vs. inbound (pink, In) direction; schematic at far left). Data from inbound vs. outbound maze passes plotted separately. Plotting conventions are the same as Figures 1E–J but with the following differences: black corresponds to outbound-preferring cells, while red corresponds to inbound-preferring cells; below, linearized (rather than 2D) time-averaged firing maps are plotted (arms plotted in linearized maps correspond to positions plotted as light grey in raw firing maps); in rasters, maze pass times are indicated above plots by colored bars. In (E) and (F), a portion of the data is expanded to help show the firing pattern (grey boxing; scale bar: 125 ms).

(K and L) Two example cell pairs with similar locational and directional representations. Data from inbound (pink) vs. outbound (grey) maze passes (schematic at far left, shared with that of E-J), with passes of each direction plotted separately. Plotting conventions are the same as (E-J), but firing data from cell 26 is shown in dark blue to denote outbound preference (same preference as cell 25), and firing data from cell 27 is colored in dark red to denote inbound preference (same preference as cell 28). In the example in (L), two XCGs are plotted, one for each (directional) condition; notably, anti-synchronous cycling firing is seen only in one condition. Note that (K) and (L) are suggestive of a representational correlate, different from location and direction, that may be associated with cycling firing.

Recording regions: CA1: cells 3–6, 11–14, 16–17, 19; CA2: cells 9, 18, 23; CA3: cells 1–2, 7–8, 10, 15, 20–22, 24.

We further found that place cells encoding opposite heading directions (direction-selective place cells (McNaughton et al., 1983a); surveyed in Figures S1G-I) could fire in regular alternation at 8 Hz (example cell pairs: Figures 2E–J), a finding we revisit later. Overall quantification indicated that regular alternation at 8 Hz was a surprisingly common pattern in the hippocampus (8–9% of cell pair samples; Figure S2). To refer to this dynamic pattern of neural firing, we hereafter use the term “constant cycling,” denoting the combination of regularity and alternation.

Importantly, 8 Hz matches the frequency of hippocampal theta (Buzsaki, 2002; Colgin, 2013), a neural rhythm overtly expressed in the local field potential (LFP) (example raw trace and spectrum in Figure S1J; filtered at 5–11 Hz and shown in plots as θ throughout study, e.g. Figure 1G) and known to entrain hippocampal neural firing (O’Keefe, 2007; Mizuseki et al., 2009; Kay et al., 2016). Indeed theta entrained the firing of the majority of cells in the dataset (90% or 1485 out of 1644 cells; Figure S1K), consistent with theta entrainment of 8 Hz cycling and previous work showing theta entrainment of competing neural populations during spatial foraging (Harris et al., 2003; Deshmukh et al., 2010; Jezek et al., 2011; Brandon et al., 2013). Given these results, we analyzed periods when theta is continuously active: namely periods of locomotor behavior such as walking and running (O’Keefe, 2007; Kay and Frank, 2018).

Two correlates of cycling

Prior work has claimed that anatomical (Marr, 1971; McNaughton and Morris, 1987; Lisman et al., 2005) and behavioral (Buzsaki, 1989; O’Keefe, 2007; Kay and Frank, 2018) correlates of hippocampal neural activity are essential to understand function. We therefore sought to determine whether constant cycling at 8 Hz had any such correlates. To do so, we analyzed single-cell firing (Figure 3), for which constant cycling would manifest as “skipped” cycles (Deshmukh et al., 2010; Brandon et al., 2013) (cycle skipping) (example cells: Figures 3A–E; survey of cells: Figure 3F). Notably, single-cell analysis does not require two particular cells to fire in alternation, thus making fewer assumptions about cell participation from cycle to cycle.

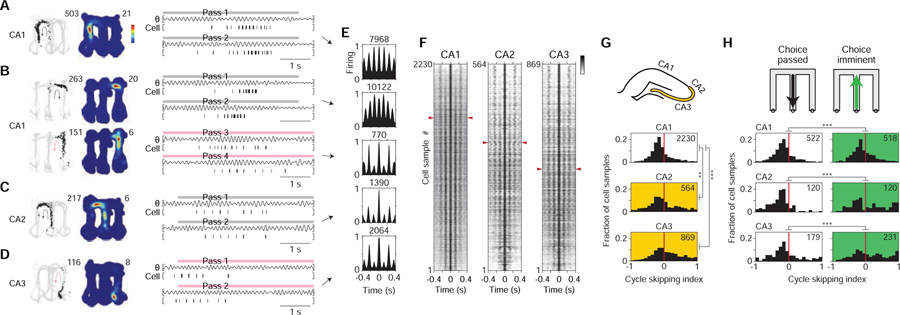
Figure 3. Two correlates of cycling.

(A-D) Time-averaged firing maps (left) and rasters (right) of four example cells (recording regions at far left). Data plotted is from a single type of maze pass (colored arrows; grey: outbound; pink: inbound). In rasters, maze pass times are indicated above plots by colored bars; plotted above each pass is theta-filtered LFP (θ, 5–11 Hz from CA3). Firing maps, left column: positions visited (grey) and positions where the cell fired (black points). Total number of spikes is reported at upper right. Firing maps, right column: time-averaged firing map. Peak firing rate is reported at upper right. For the cell in (B), data from two types of maze passes are shown on separate rows to illustrate that firing patterns for an individual cell could depend on condition.

(E) Firing auto-correlograms (ACGs) of the four cells from (A-D). Each ACG (5-ms bins; zero bin excluded) is smoothed with a Gaussian kernel (σ = 10 ms) and peak-normalized. Total number of spikes in ACG is reported at top. For the cell from (B), data from each of the two types of maze passes are shown on two separate rows.

(F) Firing ACGs of all cell samples (in rows) across recording regions (CA1, CA2, CA3). Greyscale indicates firing density. Each cell sample corresponds to data from a single cell for one type of maze pass. Cell samples are ordered by cycle skipping index (CSI; high to low plotted top to bottom); for each region, red arrowheads indicate division between cell samples with CSI > 0 (above division) vs. < 0 (below division). CSI < 0 corresponds to classical firing (firing on adjacent cycles), while CSI > 0 corresponds to cycle skipping.

(G) Cycle skipping index (CSI) by hippocampal recording region. Top, diagram of sub-regions with higher CSI values (CA2 and CA3; yellow zone). Bottom, histograms of CSI values across cell samples. Total number of cell samples is indicated at upper right. Values in CA2/CA3 were higher than in CA1.

(H) CSI by behavioral condition. Top, schematic of the conditions (choice passed: periods when subject was leaving the choice point; choice imminent: periods when subject was approaching the choice point). Bottom, histograms of CSI values across cell samples. Total number of cell samples is indicated at upper right. For every recording region (CA1, CA2, CA3), CSI values were higher for choice imminent vs. choice passed.

Rank-sum tests.

P-values reported in main text.

**, P < 0.01.

***, P < 0.001.

To quantify cycle skipping in single cells, we calculated a cycle skipping index (CSI) similar to measures used in studies of entorhinal cortex (Deshmukh et al., 2010; Brandon et al., 2013); in particular, the CSI measures the tendency of single cells to fire on adjacent cycles vs. on every other cycle, ranging from −1 (only adjacent) to 1 (only every other).

The subsequent quantification revealed both an anatomical and a behavioral correlate: (1) cycle skipping was more prevalent in cells in subregions CA2 and CA3 than in CA1 (median [interquartile range] (n = # cell samples); CA1: −0.15 [−0.27, 0.01] (n = 2230), CA2: −0.11 [−0.30, 0.21] (n = 564), CA3: 0.01 [−0.21, 0.36] (n = 869); CA2 vs. CA1, P = 0.0039; CA3 vs. CA1, P = 4.5e-33; rank-sum tests) (distributions in Figure 3G), and (2) cycle skipping was more prevalent when subjects approached vs. departed from the choice point (choice imminent vs. choice passed, corresponding to outbound vs. inbound periods in the center maze arm, respectively; diagrammed at the top of Figure 3H) (median [interquartile range] (n = # cell samples); CA1 imminent: −0.13 [−0.29, 0.10] (n = 518), CA1 passed: −0.18 [−0.34, −0.04] (n = 522), CA2 imminent: −0.02 [−0.30, 0.52] (n = 120), CA2 passed: −0.25 [−0.46, −0.12] (n = 120), CA3 imminent: 0.05 [−0.26, 0.50] (n = 231), CA3 passed: −0.16 [−0.35, 0.11] (n = 179); CA1 imminent vs. passed: P = 0.00017, CA2 imminent vs. passed: P = 1.9e-7, CA3 imminent vs. passed: P = 1.1e-5; rank-sum tests) (distributions in Figure 3H).

To assess whether these findings were due to a simple relationship between cycle skipping and overall amount of firing, we also tested whether there was any correlation between CSI and average firing rate. The resulting correlation values were not significant (Spearman’s ρ = 0.01, P = 0.40; n = 3663 path-based cell samples across CA1, CA2, CA3), indicating that enhancement of cycle skipping was not simply due to differing overall firing. The results in Figures 3G and 3H implicate instead structural and behavioral factors, respectively, with the latter suggesting that behavior-level choice (here, between upcoming maze paths) recruits the constant cycling firing pattern globally across hippocampal neurons.

Constant cycling in a neural population

We hypothesized that constant cycling firing, which we first found to encode possible future scenarios in pairs of cells (Figures 1 and 2), might in fact be coherently expressed across entire populations of hippocampal neurons. To test this possibility, we analyzed hippocampal neural firing at the population level (Figure 4). Preliminary inspection of firing across co-recorded cells suggested constant cycling at 8 Hz between possible future locations (L vs. R maze arms) prior to the behavioral choice (example cell population firing in Figure S3). For formal analysis, we used a decoding algorithm that is maximally inclusive of the recorded neural firing data (clusterless decoding (Kloosterman et al., 2013; Deng et al., 2015) of all electrodes (across regions) reporting putative principal cells; see STAR Methods). Given the behavior-level correlates identified above (possible future locations in Figures 1 and 2A–D and choice imminent periods in Figure 3H), we decoded location when subjects approached the choice point (decoding examples in Figures 4A–C and S4A-F). As expected from previously established results showing ~100 ms population firing encoding sequences of locations along a single path (schematized in Figure S1C) (Feng et al., 2015; Wikenheiser and Redish, 2015), the decoded firing data showed ~100 ms periods in which location projected away from the subject (example instances highlighted by open arrowheads in Figures 4A and S4A).

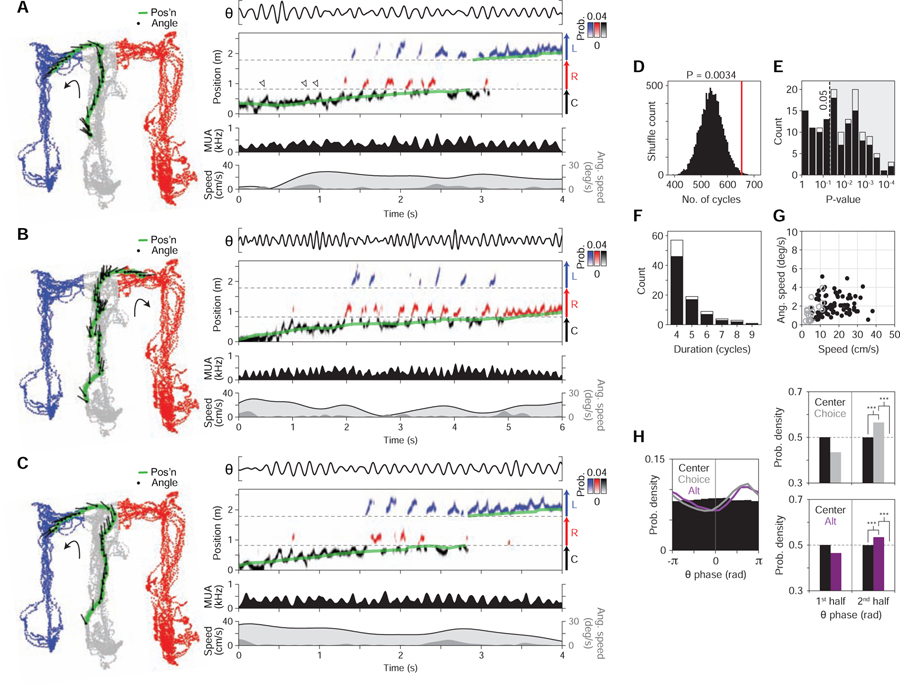
Figure 4. Constant cycling (8 Hz) of possible future locations.

Three example maze passes (A, B, C) from a single recording epoch.

(At left) Behavior plot. Position (green) and head angle (black lines; sampling period in plot: 133 ms) are overlaid on positions visited by the subject in epoch (color-coded by maze arm; grey: C (center); blue: L (left); red: R (right)).

(At right) Data and decoded representation. Top section: LFP (θ, 5–11 Hz; CA3). Second section: decoded output (y-axis: linearized position); probability density is plotted as color values and colored by maze arm (black: C; blue: L; red: R); green line indicates actual position of subject. In (A), several example instances of ~100 ms spatial sequences within the center arm (schematized in Figure S1C) are highlighted by open arrowheads. Third section: multi-unit spiking activity (MUA; smoothed with Gaussian kernel (σ = 20 ms)). Bottom section: linear (light grey fill trace) and angular (dark grey fill) speed.

(D) Prevalence of constant cycling in observed (red line) vs. shuffled data (histogram, 10000 permutations; study-wide shuffle). Plotted is the total number of cycles in detected constant cycling periods. P = 0.0034 (34 out of 10000 shuffles had equal or higher prevalence of cycles).

(E) P-values of individual constant cycling periods (individual period shuffle). Shaded area enclosed by dotted line indicates criterion (P < 0.05) for individual periods analyzed subsequently in (F) and (G). Plotted separately are individual periods that occurred exclusively during movement (>4 cm/s) (black bars) versus those that overlapped with low speed periods (<4 cm/s for <0.5 s) (stacked white bars).

(F) Histogram of durations (in cycles) of individual constant cycling periods. Bar plot convention follows that of panel (E).

(G) Behavioral speed during individual constant cycling periods. Individual periods that occurred exclusively during movement (>4 cm/s) (black dots) versus those that overlapped with low speed periods (<4 cm/s for <0.5 s) (open grey circles) are plotted separately. Observed periods commonly occurred when angular speed was low (<10 deg/s), indicating that constant cycling could occur in the absence of overtly deliberative behavior (e.g. head scanning (Johnson and Redish, 2007; Redish, 2016)).

(H) Theta phase histograms of decoded location representation (n = 1683 maze passes across 7 subjects; SEM omitted from plots due to minimal size). For each maze pass, posterior density (across positions) was pooled across time bins, subdivided into three maze arms (center, choice, and alternative (alt)), then histogramed by theta phase. Decoded data restricted to the center arm. Note that both choice and alternative arms tended to be represented in the second half of theta (0 to π).

(Left) 12-bin histogram: center, choice, and alternative (alt).

(Upper right) 2-bin histogram: center vs. choice.

(Lower right) 2-bin histogram: center vs. alternative (alt).

Signed-rank tests.

P-values reported in main text.

***, P < 0.001.

Remarkably, the decoded output showed periods of constant cycling at 8 Hz between L vs. R maze arms (constant cycling detected as L/R switching across 4 or more successive cycles; seen as alternating periods of L (blue) vs. R (red) decoded locations (color density) in Figures 4A–C and S4A-F), recalling the constant cycling at 8 Hz observed in cell pairs (Figures 1 and 2A–F). To test whether constant cycling between L vs. R representations may have occurred due to random or noisy activity, we carried out two shuffle analyses. First, we shuffled the order of decoded cycles across the dataset (10000 permutations; cycles segregated with respect to the 8 Hz theta rhythm) and measured the frequency (P-value) with which constant cycling occurred in the observed vs. shuffled data (study-wide shuffle). This analysis indicated that the constant cycling pattern was unlikely to have occurred by chance (P = 0.0034, observed (red line) vs. shuffled (black histogram) prevalence of constant cycling shown in Figures 4D and S4G). Second, individual periods of constant cycling were tested by shuffling within each recording epoch (individual period shuffles), thereby identifying particular periods that were unlikely to have occurred by chance (93 (of 141 total) constant cycling periods at P < 0.05; shuffle p-values and period durations in Figures 4E, F and S4H, I).

Previous work has described hippocampal neural activity encoding possible future locations as occurring specifically in association with overtly deliberative behavior such as head scans (vicarious trial-and-error (Johnson and Redish, 2007; Redish, 2016)); this claim led us to ask whether constant cycling at 8 Hz was restricted to such behaviors. We found this not to be the case – constant cycling at 8 Hz commonly occurred during high movement speed in the absence of head scans, and thus did not depend on overtly deliberative behavior (Figures 4G and S4J). We also asked whether decoded activity during movement was reliably associated with future behavior; in particular, the subject’s upcoming choice of L vs. R maze arms. We found that the decoded activity did not reliably predict L vs. R (Figure S5), indicating that the cycling dynamic reflected a flexible underlying process not deterministically controlled by overt choice, at least under the present conditions (maze navigation and learning prior to asymptotic performance).

Intra-cycle coding of hypotheticals

How does the hippocampus represent possible futures as fast as at 8 Hz? The finding that 8 Hz cycling was paced by the theta rhythm (Figures 4, S3, and S4; also evident in Figures 1 and 2) suggested that investigating theta would clarify the underlying dynamic process. We thought that this process might in fact operate at a timescale finer than full theta cycles: the above observation of cycling of future possibilities across theta cycles (inter-cycle coding) suggests a structured process that generates an individual possibility within each theta cycle (intra-cycle coding).

Intriguingly, classic work (O’Keefe and Recce, 1993; Skaggs et al., 1996) has identified an instance of intra-cycle coding: place cells fire at specific phases within theta cycles such that early vs. late phase firing encodes current vs. future location, respectively (O’Keefe and Recce, 1993; Skaggs et al., 1996; Feng et al., 2015; Wikenheiser and Redish, 2015). Importantly, this classic case refers only to neural firing related to a single spatial path; this differs from the present study, in which we initially observed neural firing related to multiple alternative spatial paths (as defined either by the maze bifurcation (Figures 1 and 2A–F) or by heading direction (Figures 2E–J)), indicating encoding of hypothetical scenarios. In light of these findings, we conjectured that the classic correlate of intra-cycle coding – current vs. future location – might in fact be an instantiation of a decidedly more abstract correlate: namely, current vs. hypothetical experience. As such, neural firing encoding any type of hypothetical (whether of location, direction, or other correlates) would occur at the late phase of theta, akin to firing encoding future location in the classic case (O’Keefe and Recce, 1993; Skaggs et al., 1996; Feng et al., 2015; Wikenheiser and Redish, 2015).

To investigate this possibility, we first determined whether intra-cycle coding generalizes to the representation of possible future locations (L vs. R, schematized in Figure S1D) both at the population and single-cell levels. At the population level (Figure 4), we measured the theta phase when decoded position was in one of three locations in the maze: the center arm, the subsequently chosen (choice) arm, or non-chosen (alternative) arm. The resulting phase histograms (Figures 4H and S4K, histograms at two resolutions: 12-bin (at left) and 2-bin (at right); n = 1683 maze passes across 7 subjects) and quantification (referencing 2-bin histograms in Figures 4H and S4K) indicated that the alternative arm was represented selectively on the 2^nd half of theta (alternative (alt, purple) vs. center (black), P = 3.1e-6; alternative (alt, purple) vs. uniform distribution (0.5 proportion; dashed line), P = 3.2e-6; signed-rank tests), equivalently to representation of the choice arm (choice (grey) vs. center (black), P = 4.6e-44; choice (grey) vs. uniform distribution (0.5 proportion; dashed line), P = 2.0e-47; signed-rank tests) and to future location as in the classic single-path case (O’Keefe and Recce, 1993; Skaggs et al., 1996; Feng et al., 2015; Wikenheiser and Redish, 2015).

Importantly, this result yielded further insight into single-cell firing (Figures 5A and 6A–D). Subsets of single place cells are known to fire at different mean rates depending on which path (e.g. L vs. R) the subject subsequently takes (Frank et al., 2000a; Wood et al., 2000; Ferbinteanu and Shapiro, 2003), a pattern we here refer to as outbound path coding. In light of cycling between differing upcoming locations (Figure 4), it would be expected that place cells showing outbound path coding (higher mean firing when preferred path is going to be chosen) fire to some extent even when subjects choose the cells’ non-preferred path; furthermore, such non-preferred firing should occur mainly at later theta phases given the later theta phase specificity of alternative path representation at the population level (Figure 4H). Visual inspection of single-cell firing (examples in Figures 5A and 6A; survey in Figure 6B) and quantification of firing phase confirmed both implications (Figures 6C and 6D, histograms at two resolutions: 12-bin (at left) and 2-bin (at right); quantification references 2^nd half of theta in 2-bin histograms, n = 132 cell samples; non-preferred (non-pref) vs. preferred (pref), P = 1.2e-8; non-preferred (non-pref) vs. uniform distribution (0.5 proportion; dashed line), P = 2.2e-10; signed-rank tests). Thus, firing on the non-preferred path is consistent with representation of a possible future, or hypothetical, location.

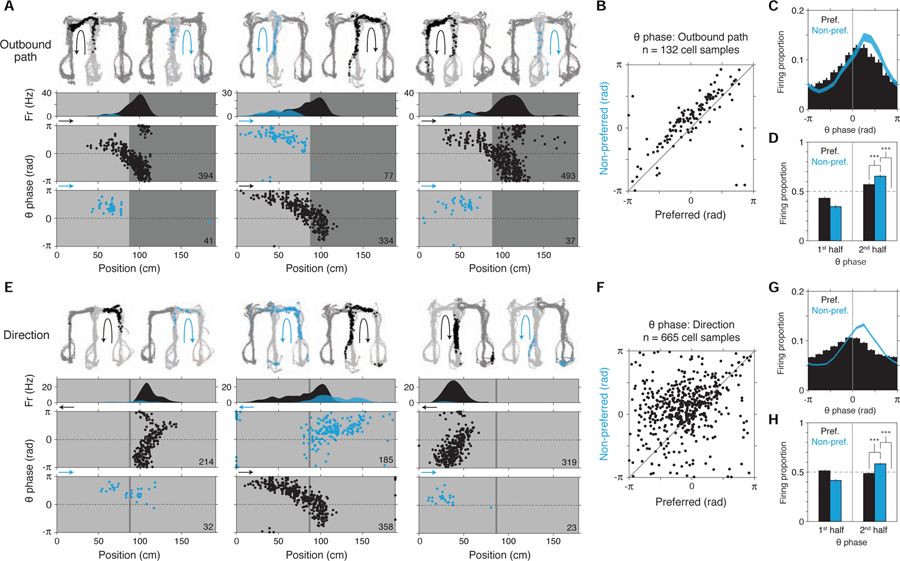
Figure 5. Intra-cycle coding of hypotheticals.

Single-cell examples of hypothetical coding; examples grouped by representational correlate (A, outbound path; B, direction; C, inbound path). Across all plots, firing data are colored based on the condition in which they occurred: preferred (black) vs. non-preferred (blue). Note that, regardless of representational correlate, firing in the non-preferred (vs. preferred) condition is shifted to the second half of theta (0 to π), consistent with encoding of hypothetical (vs. current) experience.

(A) Outbound path-coding cells. Each example cell is plotted in a column. For outbound path coding, preferred vs. non-preferred conditions correspond to whether the maze path subsequently taken by the subject was to the left vs. right. In each plot, maze locations where quantification of theta phase of firing (Figure 6) was performed are indicated (light grey; other locations in dark grey).

Top section, firing maps. Two maps are shown: one from preferred path (black arrow) maze passes and one from non-preferred path (blue arrow) maze passes. Firing locations during each path pass type are shown as colored points (preferred: black; non-preferred: blue).

Second section, time-averaged linearized firing map.

Bottom section, theta phase of firing by position. Firing is plotted separately whether occurring in the preferred (black) vs. non-preferred (blue) condition. Arrow at upper left of plots indicates the subject’s heading direction. Total number of spikes is indicated at lower right.

Recording regions, left to right: CA3, CA2, CA2, CA1.

(B) Direction-coding cells. Plotting conventions are the same as in (A), with total spike counts indicated at lower left. Preferred vs. non-preferred conditions correspond to opposite heading directions.

Recording regions, top row, left to right: CA3, CA3, CA1, CA3; bottom row, left to right: CA3, CA3, CA1, CA1.

(C) Inbound path-coding cells. Plotting conventions are the same as in (A). Preferred vs. non-preferred conditions correspond to whether the path previously taken by the subject was from the left vs. right.

Recording regions, left to right: CA1, CA2, CA1, CA2.

Figure 6. Intra-cycle coding of hypotheticals: summary.

Additional examples and study-wide quantification of outbound path (A-D) and direction (E-H) representation in single cells. Across all plots, firing data are colored based on the condition in which they occurred: preferred (black) vs. non-preferred (blue).

(A) Outbound path-coding cells. Plotting conventions are the same as in Figure 5A. Recording regions, left to right: CA3, CA2, CA1.

(B) Scatter of mean theta phase (n = 132 cell samples). For each cell sample, the theta phases of spikes in the preferred and non-preferred conditions were separately collected and the circular mean calculated. Cell samples analyzed were restricted to those with at least 20 spikes in the non-preferred condition, and with non-uniform phase histograms (Rayleigh tests at P < 0.05) in both conditions.

(C) Theta phase histogram (12-bin). Mean ± SEM (n = 132 cell samples).

(D) Theta phase histogram (2-bin). Mean ± SEM (n = 132 cell samples). (Note that preferred vs. non-preferred comparison would be expected to depend partly on locations of cells’ spatial firing fields.) Firing was higher in the 2^nd half of the theta cycle in the non-preferred condition.

(E) Direction-coding cells. Plotting conventions follow (A). The cell in the middle column is same as that in the middle column in (A), instancing a cell with both location (left vs. right arms; Figures S1D-F) and direction (outbound vs. inbound direction; Figures S1G-I) selectivity. Note that, as in (A), spikes that occur in the non-preferred condition are shifted to the second half of theta (0 to π).

Recording regions, left to right: CA1, CA2, CA1.

(F-H), Directional firing theta phase quantification (n = 665 cell samples). Plotting conventions and comparisons follow (B-D). As in location (B-D), firing was higher in the 2^nd half of the theta cycle in the non-preferred condition. Signed-rank tests.

P-values reported in main text.

***, P < 0.001.

Unexpectedly, single-cell analysis indicated that theta phase also governed the well-established hippocampal representation of heading direction (McNaughton et al., 1983a; Battaglia et al., 2004; Davidson et al., 2009). Visual inspection of single-cell firing (Figures 5B and 6E; survey in Figure 6F) and quantification of firing phase (Figures 6G and 6H, histograms at two resolutions: 12-bin (at left) and 2-bin (at right); quantification references 2^nd half of theta in 2-bin histograms, n = 665 cell samples; non-preferred (non-pref) vs. preferred (pref), P = 1.6e-35; non-preferred (non-pref) vs. uniform distribution (0.5 proportion; dashed line), P = 4.9e-29; signed-rank tests) revealed that firing occurring when subjects traveled in cells’ non-preferred direction occurred at later phases of theta, a pattern echoing the outbound path case (Figures 6A–D). In this way, firing in the non-preferred direction is consistent with representation of the non-current, or hypothetical, direction. It is worth noting that past surveys of directional selectivity in single cells have found a markedly wide distribution of selectivity values (Battaglia et al., 2004) (Figure S1I; unlike that of location, Figure S1F), consistent with the possibility that single-cycle dynamics (not captured by time-averaging) in fact govern the representation of direction.

The generalization of intra-cycle coding to direction suggested that other correlates might be similarly organized via phase. Indeed, extending our analysis, we observed equivalent theta phase coding for additional representational firing patterns in the hippocampus: inbound path coding (Frank et al., 2000a; Wood et al., 2000; Ferbinteanu and Shapiro, 2003) and extra-field firing (Johnson and Redish, 2007) (inbound path examples in Figure 5C; collected results shown in Figure S6A). The finding of equivalent temporal organization across multiple neural codes characterized by alternative hypotheticals – here of location, direction, and path – suggests a single common process that generates representations of hypothetical scenarios, including possible futures, and expresses these representations selectively on later phases of theta.

Lastly, we determined whether there was any direct relationship between intra-cycle structure and the previously observed inter-cycle firing (Figures 1, 2, 3, 4), which had indicated encoding of hypotheticals at a longer timescale. Quantification of inter-cycle firing (cycle skipping in single cells, characterized initially in Figure 3) conditioned on intra-cycle structure (whether firing occurred on the 1^st vs 2^nd half of theta cycles) indicated that inter-cycle firing is stronger for firing from the 2^nd half of theta cycles (Figure S6B), further consistent with a common process that underlies representation of hypotheticals.

Cycling between directions

The finding that theta phase (intra-cycle) coding – long established for the representation of location (O’Keefe and Recce, 1993; Skaggs et al., 1996) – generalizes to non-locational correlates at the single-cell level (Figures 6 and S6A) raises the possibility that theta phase organizes non-locational representations across entire populations of hippocampal neurons.

To determine whether this was the case, we analyzed the hippocampal representation of heading direction, a non-locational variable long known to be a robust correlate of single-cell firing (McNaughton et al., 1983a; Eichenbaum et al., 1999; Battaglia et al., 2004). Initially, we observed instances of population-level activity consistent with intra-cycle organization by inspecting firing in co-recorded place cells grouped by directional selectivity (Figure S7A). For formal analysis, we inferred the representation of direction from population-level hippocampal neural firing using the same decoding approach as applied previously to location (clusterless decoding of all electrodes (across regions) reporting putative principal cells; see STAR Methods). Notably, the decoded output exhibited periods of <100 ms duration within which the decoded representation switched from current to hypothetical direction and back (upper decoded data in Figures S6C and S6D). Quantification with respect to theta phase revealed that current vs. hypothetical direction were preferentially expressed on the first vs. second halves of theta, respectively, indicating phase organization at the population level (Figure S6E). Leveraging this finding, we subsequently decoded in windows that sampled each half of the theta cycle (half-theta cycle windows in middle and lower decoded data in Figures S6C and S6D).

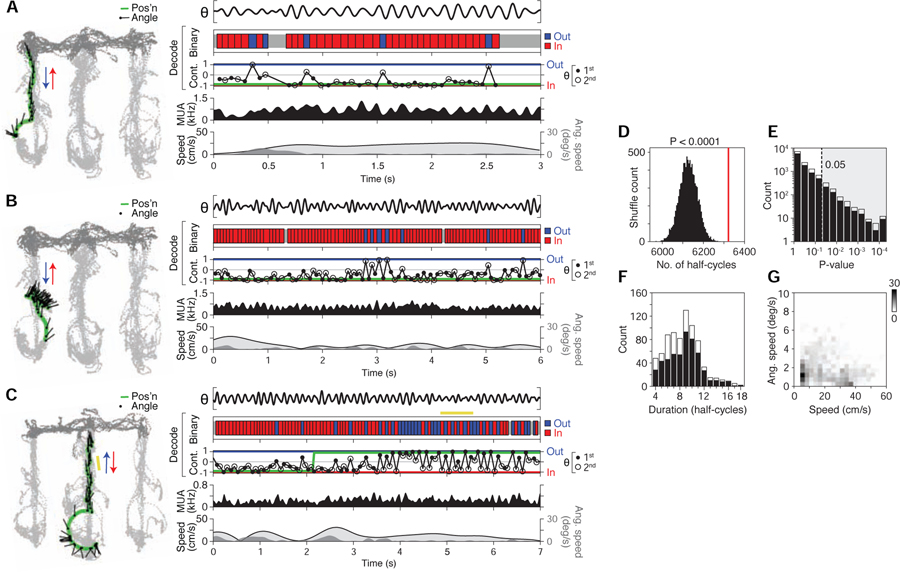
Strikingly, decoding revealed periods of constant half-theta cycling of direction (example decoded data in Figures 7A–C and S7B-E; constant half-theta cycling defined as representational switching across 4 or more successive half-theta cycles, seen as alternating periods of outbound (out, blue) vs. inbound (in, red) in decoded direction). To test whether constant half-theta cycling between outbound vs. inbound may have occurred due to random or noisy activity, we carried out two shuffling analyses. First, we shuffled the order of decoded cycles across the dataset (10000 permutations) and measured the frequency (P-value) with which constant half-theta cycling occurred in the observed vs. shuffled data (study-wide shuffle). This analysis indicated that the constant half-theta cycling activity pattern was unlikely to have occurred by chance (P < 0.0001, the lower bound of the test; observed (red line) vs. shuffled (black histogram) prevalence of constant half-theta cycling shown in Figure 7D). Second, individual periods of constant half-theta cycling were tested by shuffling within each recording epoch (individual period shuffles), thereby identifying particular periods that were unlikely to have occurred by chance (767 (of 12147 total) constant half-theta cycling periods at P < 0.05, shuffle p-values in Figures 7E (4+ half-cycles) and S7F (8+ half-cycles); period durations in Figure 7F). Importantly, as in periods of constant cycling of location (Figures 4G and S4J), periods of constant half-theta cycling of direction could occur at a wide range of linear and angular speeds (Figures 7G and S7G), including during running.

Figure 7. Constant cycling of heading direction.

(A-C) Three example maze passes showing various levels of half-theta cycling. Examples in (A) and (B) are from same recording epoch. In example (C), an individual period of constant half-theta cycling is highlighted (yellow bar).

(Left) Behavior plot. Position (green) and head angle (black lines; sampling period in plot: 133 ms) are overlaid on locations visited by the subject in the recording epoch (light grey: locations analyzed; dark grey: other locations).

(Right) Data and decoded representation.

Top section: LFP (θ, 5–11 Hz from CA3).

Second section: binary decoded output (red: inbound; blue: outbound).

Third section: continuous-valued decoded output (−1: inbound; 0: non-directional; 1: outbound) (filled circle: 1^st half theta; open circle: 2^nd half theta; connecting lines shown for visual clarity); green line denotes actual direction of subject.

Fourth section: multi-unit firing activity (MUA) smoothed with Gaussian kernel (σ = 20 ms).

Fifth section: linear (light grey fill trace) and angular (dark grey fill) speed of rat.

(D) Prevalence of constant (half-theta) cycling in observed (red line) vs. shuffled data (histogram, 10000 permutations; study-wide shuffle). Plotted is the total number of cycles participating in detected constant cycling periods. P < 0.0001 (0 out of 10000 shuffles had equal or greater prevalence of cycles).

(E) P-values of individual constant (half-theta) cycling periods (individual period shuffle). Shaded area enclosed by dotted line indicates criterion (P < 0.05) for individual periods analyzed subsequently in (F) and (G). Individual periods that occurred exclusively during movement (>4 cm/s) (black bars) versus those that overlapped with low speed periods (<4 cm/s for <0.5 s) (stacked white bars) are plotted separately.

(F) Histogram of durations (in half-cycles) of individual constant half-theta cycling periods. Bar plot convention follows that of (E).

(G) Behavioral speed during individual constant (half-theta) cycling periods. Data plotted as a 2D histogram, where greyscale value corresponds to count density (767 total periods plotted). Observed periods commonly occurred when angular speed was low (<10 deg/s), indicating that constant cycling could occur in the absence of overtly deliberative behavior (e.g. head scanning (Redish, 2016)).

Discussion

We present two main findings: (1) neural firing capable of fast and continual representation of multiple possible future scenarios (constant cycling at 8 Hz); (2) generalization of the underlying cycling dynamics (both inter- and intra-cycle dynamics) across qualitatively different representational correlates, here location and direction (cycle coding of hypotheticals). Cycling dynamics were detectable at three levels of neural organization (the single-cell (Figures 3, 5, and 6), cell-pair (Figures 1 and 2), and population (Figures 4 and 7) levels) and, further, had both anatomical (Figure 3G) and behavioral (Figure 3H) correlates.

Recent work has established that high-level cognitive functions such as planning and deliberation rely on the brain’s ability to represent hypothetical (rather than ongoing) experience, an ability we here refer to as “generativity.” Yet unlike stimulus-driven activity as classically described in sensory neural circuits (Mountcastle, 1998), the origins of generative neural activity remain poorly understood. Here, place cells in the hippocampus offer a model system given their known generativity – in particular, their representation of hypothetical spatial paths (Lisman and Redish, 2009; Pfeiffer and Foster, 2013; Wikenheiser and Redish, 2015; Redish, 2016; Foster, 2017).

In this study, we find that the rat place cell representation of possible futures has an unexpected conjunction of four properties: constancy over time, sub-second speed, temporal segmentation (akin to time-division multiplexing (Akam and Kullmann, 2014; Caruso et al., 2018)), and rhythmicity (pacing by the 8 Hz theta rhythm). Further, these temporal properties generalize across (at least) two qualitatively different representational correlates (location and direction). Together, these properties and their generalization specify putative mechanisms of generativity in three ways: time, neural substrates, and generality.

With respect to time, segmentation within theta cycles (an intra-cycle dynamic (Hasselmo et al., 2002; Kunec et al., 2005; Siegle and Wilson, 2014; Wilson et al., 2015)) specifies a mechanism that can switch between representations of current vs. hypothetical experience as fast as twice the frequency of theta (equivalent to 16 Hz); in addition, segmentation across theta cycles (an inter-cycle dynamic (Harris et al., 2003; Deshmukh et al., 2010; Jezek et al., 2011; Brandon et al., 2013)) specifies a mechanism that can switch between representations of hypotheticals as fast as the frequency of theta (8 Hz). The present observation of these two dynamics builds on previous results demonstrating representational switching at the population level in the hippocampus (Johnson and Redish, 2007; Jezek et al., 2011; Kelemen and Fenton, 2016), specifically by showing that sub-second dynamics govern the representation of behaviorally-explicit alternative possibilities (here alternative locations and directions), moreover in constant operation over time.

It is also worth remarking on how these two dynamics elaborate upon previous cycle-based frameworks (Lisman and Redish, 2009; Sanders et al., 2015) for understanding hippocampal neural representation: the intra-cycle dynamic corresponds to transitions from current (in 1^st half-cycle) to hypothetical (in 2^nd half-cycle), while the inter-cycle dynamic corresponds to activation of differing hypotheticals (across successive 2^nd half-cycles). Furthermore, with regard to external input, either dynamic occurred in the absence of inducing sensory stimuli – i.e. spontaneously – and under naturalistic conditions (here self-paced, goal-directed navigation); these dynamics were moreover seen in the absence of overtly deliberative behaviors such as head scans (vicarious trial-and-error (Redish, 2016)). Most immediately, these various properties indicate that models of network-level theta dynamics (Tsodyks et al., 1996; Thurley et al., 2008; Navratilova et al., 2012a; Wang et al., 2015; Chadwick et al., 2016; Mark et al., 2017) require additional or alternative mechanisms.

With respect to neural substrates, the rhythmic entrainment of 8 Hz cycling to the theta rhythm implicates brain regions linked to the generation and expression of theta (Buzsaki, 2002; Colgin, 2013). Indeed, previous work has reported cycling firing at 8 Hz in subpopulations of neurons in several of these regions (medial septum (King et al., 1998) and entorhinal cortex (Jeffery et al., 1995; Deshmukh et al., 2010; Brandon et al., 2013)). Additionally, multiple theta generators have been found within the hippocampus itself (Buzsáki, 2006; Montgomery et al., 2009), reminiscent of the finding that cycling firing is expressed at different levels in CA1 vs. CA2/3 neurons (Figure 3G). These various results suggest privileged roles for structurally defined neural circuits within and beyond the hippocampus. At the same time, the present results implicate a distributed mechanism: cell firing (in single cells or cell pairs) could exhibit cycle skipping in one condition but not another (examples in Figures 1G, 1H, 2, and 3B), indicating that a larger scale of organization is required to explain how cycling is generated.

With respect to generality, the finding that cycling dynamics are shared across the representations of location and direction (intra-cycle: Figures 5 and 6; inter-cycle: Figures 1 and 2) and likely other representations (Figure S6A), indicates that, at least for the rat hippocampus, generative activity for different correlates is produced by a theta-associated common mechanism. Indeed, it may be that such a mechanism may structure additional (and possibly all) hippocampal representational correlates involving hypotheticals. Still, it is important to note that the theta rhythm appears to be expressed in a species-specific manner, with an apparent lack of continuous activation in humans, primates, and bats (Las and Ulanovsky, 2014). One important possibility, suggested by recent findings in bats (Eliav et al., 2018), is that cycle-based dynamics could occur without continuous rhythmicity. Indeed, from an algorithmic viewpoint, constant cycling – defined as a process that regularly represents differing items (e.g. alternative locations) at segregated and internally generated times (cycles) – does not entail any particular spectral bandwidth, much less any particular neural rhythm. Further, intra-cycle coding of hypotheticals – defined as a process that represents a radically abstract correlate (current vs. hypothetical experience) to internally specified times (cycle phases) – likewise does not entail any particular frequency or rhythm. Thus these structured dynamic processes are not only plausibly observable in other neurobiological systems, but also plausibly implementable in artificial representational systems.

Beyond the hippocampus, the present findings imply that neural representation dependent on theta dynamics (intra- and inter-cycle) may be the case in brain regions directly or indirectly connected to the hippocampus (David and Pierre, 2007; Sirota et al., 2008; van Strien et al., 2009), including regions associated with mnemonic, evaluative, and executive function; indeed pacing of neural firing by theta has been observed throughout the brain (Buzsaki, 2002; Berke et al., 2004; Buzsáki, 2006; O’Keefe, 2007; Sirota et al., 2008; Colgin, 2013; Redish, 2016; Alexander et al., 2018; Tingley and Buzsáki, 2018). More generally, these findings suggest that neural representation depends on temporal relationships to fast patterns of activity generated within the brain (Engel et al., 2001; Buzsaki and Draguhn, 2004; Buzsáki, 2006; Rich and Wallis, 2016). Such dependencies may be missed if neural activity is evaluated only over long timescales (e.g. across trials) or only relative to externally observable events (e.g. task cues and behaviors).

The present findings also have vital implications for the neural basis of decision-making. Previous work suggests that a crucial property of decision-making is speed; in natural environments and with natural behaviors (e.g. predation and escape), decision-making requires a representational mechanism capable of responding to rapidly and continually evolving external conditions (e.g. the behavior of other agents) so that behavior can be re-directed with commensurate speed (Cisek and Kalaska, 2010; Cisek, 2012). Constant sub-second cycling dynamics in the hippocampus meet this requirement, raising the possibility that hippocampal activity in particular, and short-timescale neural representation generally, can in fact drive decisions. Consistent with this possibility, single-cell expression of cycling was most prevalent immediately prior to behaviorally reported choice.

Lastly, we note that the present results may help clarify the neural basis of various cognitive faculties characterized by generativity (e.g. recollection, prospection, and imagination; (Schacter et al., 2012; Mullally and Maguire, 2014; Smallwood and Schooler, 2015)). Previous work has found that these memory-based faculties are associated with activity in a subset of brain regions inclusive of the hippocampus (Hassabis et al., 2007; Buckner, 2010; Mullally and Maguire, 2014; Miller et al., 2017; Stachenfeld et al., 2017; McCormick et al., 2018), a foundational observation that refers to activity monitored at longer timescales (seconds to minutes). The present findings highlight that (i) methodologically, monitoring activity at the sub-second timescale in these identified regions may be necessary to resolve competing representations, and (ii) mechanistically, neural representation in these identified regions may be governed by sub-second dynamics of internally generated activity. This mechanistic basis may also extend to strikingly similar internally generated sub-second patterns that govern sensory perception (VanRullen, 2016; Fiebelkorn et al., 2018; Helfrich et al., 2018) and sensorimotor actions (Kepecs et al., 2005; Kleinfeld et al., 2016); these patterns, currently thought to reflect adaptive mechanisms for sampling information from the external world, may be coordinated with the sub-second patterns of generative activity described here, which can in turn be likened to sampling from internal representations. Such internal sampling could implement optimal decision-making using prior knowledge (Fiser et al., 2010; Pouget et al., 2013; Vul et al., 2014; Rich and Wallis, 2016; Shadlen and Shohamy, 2016) or, more generally, be used to construct and simulate hypothetical experience.

STAR Methods

Lead contact and materials availability.

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Loren Frank (loren@phy.ucsf.edu). New reagents were not generated in this study.

Experimental model and subject details.

Neural activity (single-neuron (cell) firing and local field potential (LFP) activity) was recorded from the dorsal hippocampus (regions CA1, CA2, CA3, and DG) of twelve male rats (Rattus norvegicus; 4–9 months old, weighing 500–600 g) performing a spatial alternation task (Karlsson and Frank, 2009; Kim and Frank, 2009; Kay et al., 2016); task described in detail below. Rats were housed in a humidity- and temperature-controlled facility with a 12-hour light-dark cycle. All experiments were conducted during the light cycle. Before the start of experiments, rats from the same breeding cohort were housed in pairs; at the start of experiments, rats were single-housed. All experimental procedures were in accordance with University of California San Francisco Institutional Animal Care and Use Committee and US National Institutes of Health guidelines. Data from all subjects have been reported in earlier studies (Karlsson and Frank, 2008, 2009; Carr et al., 2012; Kay et al., 2016).

Method details.

Behavioral task and neural recordings.

Subjects were food deprived to 85% of their baseline weight and pre-trained to run on a 1-m linear track for liquid reward (sweetened evaporated milk). After subjects alternated reliably, they were implanted with microdrives containing 14 (two subjects), 21 (three subjects), 25 (one subject), or 30 (six subjects) independently movable four-wire electrodes (tetrodes (Wilson and McNaughton, 1993; Gray et al., 1995)) targeting dorsal hippocampus (all subjects) and medial entorhinal cortex (two subjects).

In five subjects, right and left dorsal hippocampus were targeted at AP: −3.7 mm, ML: ± 3.7 mm. In two subjects, dorsal hippocampus was targeted at AP: −3.6 mm, ML: +2.2 mm, in addition to medial entorhinal cortex at AP: −9.1, ML: +5.6, at a 10 degree angle in the sagittal plane. In five subjects, right dorsal hippocampus was targeted at AP: −3.3 to −4.0 mm, ML: +3.5 to +3.9 mm, moreover, in two of these subjects, the septal pole of right hippocampus was targeted with an additional six tetrodes targeted to AP: −2.3 mm, ML: +1.1 mm. Targeting locations were used to position stainless steel cannulae containing 6, 14, 15, or 21 independently driveable tetrodes. The cannulae were circular except in four cases targeting dorsal hippocampus in which they were elongated into ovals (major axis ∼2.5 mm, minor axis ∼1.5 mm; two subjects with major axis 45° relative to midline, along the transverse axis of dorsal hippocampus; two subjects with major axis 135° relative to midline, along the longitudinal axis of dorsal hippocampus). Data from tetrodes targeting both right and left dorsal hippocampus were analysed in this study.

In five subjects, viral vectors with optogenetic transgenes were targeted to either right dorsal CA2 (three subjects, AAV2/5-CaMKII-hChR2(H134R)-EYFP, UNC Vector Core, 135 nl at AP: −3.6 mm, ML: +4.2 mm, DV: −4.5 mm), dorsal DG (one subject, AAV2/5-I12B-ChR2-GFP (see ref. 52 for details about the I12B promoter)), 225 nl at AP: −3.75 mm, ML: +2.2 mm, DV: 3.9 mm and AP: −3.75 mm, ML: +1.8 mm, DV: −4.5 mm), or right supramammilary nucleus (one subject, AAV2/5-hSyn-ChETA-EYFP, Penn Vector Core, 135 nl at AP: −4.3 mm, ML: +1.8 mm, and −8.9 mm along a trajectory angled at 6° in the coronal plane). Viruses were delivered during the implant surgery using a glass micropipette (tip manually cut to ∼25 μm diameter) attached to an injector (Nanoject, Drummond Scientific). In addition, a driveable optical fiber (62.5/125 μm core/cladding) was integrated in the tetrode microdrive assembly to enable light delivery to hippocampus. This fibre was advanced to its final depth (2.5–3 mm) within 7 days of implantation. Data reported in this study were collected before light stimulation. No overt differences in neural activity were observed in subjects that received virus (Kay et al., 2016).

Over the course of two weeks following implantation, the tetrodes were advanced to the principal cell layers of CA1 (all subjects), CA2 (5 subjects), CA3 (11 subjects), and DG (3 subjects). In several subjects, tetrodes were also left in cortex overlying dorsal hippocampus. Neural signals were recorded relative to a reference tetrode positioned in corpus callosum above right dorsal hippocampus. The reference tetrode reported voltage relative to a ground screw installed in skull overlying cerebellum, and local field potential (LFP) from this tetrode was also recorded. All tetrode final locations were histologically verified (see below).

After 5–7 days of recovery after surgery, subjects were once again food deprived to 85% of their baseline weight, and again pre-trained to run on a linear track for liquid reward. At ∼14 days after surgery, six subjects were then introduced to one task W-maze and recorded for 3 to 6 days before being introduced to a second task W-maze, located in a separate part of the recording room and rotated 90° relative to the first. On recording days in which the second task W-maze was used, recordings were also conducted in the first task W-maze. In two subjects, recordings were conducted in both task W-mazes on every recording day. The W-mazes were 76 × 76 cm with 7-cm-wide track sections. The two task W-mazes were separated by an opaque barrier.

In each W-maze, subjects were rewarded for performing a hippocampus-dependent continuous alternation task (Figure S1A). Liquid reward (sweetened evaporated milk) was dispensed via plastic tubing connected to a hole at the bottom of each of the three reward wells, miniature bowls 3 cm in diameter. In eight subjects, reward was dispensed via syringes operated manually by an experimenter who was located in a separate part of the recording room. In five subjects, entry of the subject’s head into reward wells was sensed by an infrared beam break circuit attached to the well, and reward was automatically delivered by syringe pumps (OEM syringe pumps, Braintree Scientific) either immediately or after an imposed delay lasting from 0.5 to 2 s. Task recording epochs (elsewhere also referred to as “recording epochs”) lasting ~15 min were preceded and followed by rest recording epochs lasting ∼20 min in a high-walled black box (floor edges 25–35 cm and height 50 cm), during which rats often groomed, quietly waited, and slept. Two subjects also ran in an open field environment for scattered food (grated cheese) after W-maze recordings, with additional interleaved rest epochs. Tetrode positions were adjusted after each day’s recordings.

Data were collected using the NSpike data acquisition system (L.M.F. and J. MacArthur, Harvard Instrumentation Design Laboratory). During recording, an infrared diode array with a large and a small cluster of diodes was affixed to headstage preamplifiers to enable tracking of head position and head direction. Following recording, position and direction were reconstructed using a semi-automated analysis of digital video (30 Hz) of the experiment. Spike data were recorded relative to the REF tetrode, sampled at 30 kHz, digitally filtered between 600 Hz and 6 kHz (2-pole Bessel for high- and low-pass), and threshold crossing events were saved to disk. Local field potentials (LFPs) were sampled at 1.5 kHz and digitally filtered between 0.5 Hz and 400 Hz. LFPs analysed were relative to the reference tetrode except where otherwise indicated.

Single-cell (unit) neural firing was identified by clustering spikes using peak amplitude, principal components, and spike width as variables (MatClust, M.P.K.). Only well-isolated units with stable spike waveform amplitudes were clustered. A single set of cluster bounds defined in amplitude and width space could often isolate units across an entire recording session. In cases where there was a shift in amplitudes across time, units were clustered only when that shift was coherent across multiple clusters and when plots of amplitude versus time showed a smooth shift. No units were clustered in which part of the cluster was cut off at spike threshold. Units were not tracked across days.

Histology and recording site assignment.

After recordings, subjects were anesthetized with isoflurane, electrolytically lesioned at each tetrode (30 μA of positive current for 3 s applied to two channels of each tetrode), and allowed to recover overnight. In one subject, no electrolytic lesions were made, and tetrode tracks rather than lesions were used to identify recording sites. Subjects were euthanized with pentobarbital and were perfused intracardially with PBS followed by 4% paraformaldehyde in PBS. The brain was post-fixed in situ overnight, after which the tetrodes were retracted and the brain removed, cryoprotected (30% sucrose in PBS), and embedded in OCT compound. Coronal (10 subjects) and sagittal (2 subjects) sections (50 μm) were taken with a cryostat. Sections were either Nissl-stained with cresyl violet or stained with the fluorescent Nissl reagent NeuroTrace Blue (1:200) (Life Technologies, N-21479). In four subjects, the sections were blocked (5% donkey serum in 0.3% Triton-X in TBS, used for all incubations) for 1 h, incubated with RGS14 (Lee et al., 2010; Kohara et al., 2014; Dudek et al., 2016) antibody (1:400) (Antibodies Inc., 75–140) overnight, washed, and subsequently incubated with fluorescent secondary antibody (1:400) (Alexa 568, Life Technologies). CA2 recording sites were designated as those in which the electrolytic lesion or end of tetrode track overlapped with the dispersed cytoarchitectural zone characteristic of CA2 (Lorente de Nó, 1934; David and Pierre, 2007; Lee et al., 2015; Lu et al., 2015; Mankin et al., 2015; Dudek et al., 2016). It is important to note that CA2 sites defined in this way include recording locations that have been designated in previous studies as ‘CA3a’.

Data analysis.

All analyses were carried out using custom software written in Matlab (Mathworks).

Cell inclusion and classification.

Units (single cells) analyzed in the study were those that fired at least 100 spikes in at least one task epoch and had at least 50 spikes in their auto-correlogram (0–40 ms; t = 0 excluded). Across all cells, a scatter plot of mean firing rate (from the task recording epoch with highest mean rate), spike width, and autocorrelation function mean (0–40 ms; low values indicating burst firing) showed two clusters (Ranck, 1973; Fox and Ranck, 1981; Buzsaki et al., 1983; Skaggs and McNaughton, 1996; Csicsvari et al., 1999; Mizuseki et al., 2009; Kay et al., 2016). Putative principal cells corresponded with the cluster showing low firing rate (<4 Hz), large spike width, and low autocorrelation mean, while putative interneurons corresponded to the cluster characterized by high firing rate, small spike width, and high autocorrelation mean. Thirty-seven cells with ambiguous features were left unclassified and not further analyzed.

Total putative principal unit counts across recording sites were CA1: 978, CA2: 250, CA3: 528, DG: 17. Following previous work (Kay et al., 2016; Oliva et al., 2016), a subset of CA2-site putative principal cells were identified by whether they were positively modulated (CA2 P cells) vs. non-positively modulated (CA2 N cells) by the sharp wave-ripple network pattern; since the firing activity of cells of either type can overlap with periods of locomotion (Kay et al., 2016), cells of either type were included in subsequent analyses (as cells recorded in CA2) as long as subsequent relevant criteria were met.

Maze linearization (segments, arms, choice boundary, center zone).

For later analyses, the 2D position of subject was converted into 1D position (linearized position) along the three arms (center, left, and right arms) of the task maze. The three arms meet at the central junction, with the center arm composed of a one linear segment, and the left and right arms composed of two linear segments. Linearization requires specification of the six segment endpoints (2D coordinates; three corresponding to the locations of the three reward wells, and three corresponding to the junctions between linear segments); these endpoints were specified manually prior to analysis of neural data.

Linearized position was obtained by projecting the 2D position of subject onto the nearest linear segment and measuring the distance, along the maze arms, from the center well (defined as 0 cm). Every positional data point was assigned to one of the five maze segments and to one of the three maze arms.

The choice boundary was defined as the linearized position 10 cm beyond the central junction; the choice boundary was interpreted as the position where spatial choice (left vs. right) for outbound maze paths (Figure S1A) was overtly reported by the subjects’ behavior. The center zone was defined as the set of linear positions (largely corresponding to the center arm) prior to choice boundary. Note that the choice boundary refers to the boundary with either the L or R arm (e.g. either of the two interfaces between color-coded regions in behavioral maps of Figure 4).

Behavioral states: movement, maze, and task.

Analyses in this study refer to periods of time defined by subjects’ behavior, whether with regard to movement, position/orientation in the maze, or execution of the spatial alternation task.

Locomotion.

Locomotor periods were defined as times when the subject’s head speed was >4 cm/s. Single-cell and cell-pair analyses were restricted to locomotor periods, while decoding analyses included additional 0.5 s flanking periods, described further below.

Task paths.

Task paths were defined as the four spatial trajectories relevant to the task (two outbound: Center to Left (outbound left) and Center to Right (outbound right); two inbound: Left to Center (inbound left) and Right to Center (inbound right); diagrammed in Figure S1A).

Direction.

Locomotor periods were fully subdivided into two types of periods defined by heading direction: outbound or inbound. Outbound vs. inbound periods were times when the subject’s head direction was aligned to outbound vs. inbound task paths (given the assigned maze segment; see above), respectively; furthermore, alignment was binary: the assigned direction (outbound vs. inbound) was the one yielding the smaller angle (0 to 180°) along the maze segment.

Maze passes and path passes.

Maze passes were defined as single contiguous periods where the animal traveled from one reward well to another (or returned to the same well); these periods were comprised largely of locomotor periods but also included occasional intervening non-locomotor periods (i.e. head scans (Monaco et al., 2014; Redish, 2016) and stops). Maze passes were classified into nine types: four corresponding to the four task paths (path passes; two outbound and two inbound), two corresponding to traversals between the two outer wells (left to right and right to left), and three corresponding to backtracking traversals in which the subject left one of the three wells and returned to that same well without reaching a different well. Backtrack passes were detected only if the pass lasted at least 2 s and the subject traveled at least 20 cm from the well in linearized position. The start and end of maze passes were times when the linear position of the subject diverged from and met the linearized positions of the start and end wells, respectively.

Path periods.

Path periods were defined as the subset of times within path passes when (i) the subject was located in one of the three maze segments defining the current task path and (ii) the subject’s heading direction was the same as (aligned to) the direction defining the current task path.

Spatial firing in single cells.

Spatial firing was quantified using linearized (1D) position; 2D spatial firing maps (e.g. Figure 1) are plotted only for illustration. If data from two unique maze environments were available for a cell, and the cell fired at least 100 spikes in the both environments, then the cell was analyzed in the two unique maze environments independently. Thus cells in the dataset could contribute more than one sample to subsequent analyses (cell samples). If multiple recording epochs in one maze environment were available, then the cell was analyzed in recording epoch for which the cell had the highest mean firing rate.

Given the known direction- (McNaughton et al., 1983a; Battaglia et al., 2004; Foster and Wilson, 2006) and path- (Frank et al., 2000a; Wood et al., 2000; Ferbinteanu and Shapiro, 2003; Ito et al., 2015) selectivity of hippocampal cell firing, analysis was performed on locomotor data subdivided in two ways, either (I) direction or (II) path.

(I) For direction, analysis was performed separately for outbound vs. inbound periods, moreover separately for each of the three maze arms; thus a given cell in a given maze environment could contribute up to three samples in subsequent direction-based analyses (direction-based cell samples; outbound and inbound).

(II) For path, analysis was performed separately for periods corresponding to the four task path types (for which a minimum of five available passes were required for each path type); thus a given cell in a given maze environment could contribute up to four samples in subsequent path-based analyses (path-based cell samples; outbound left, outbound right, inbound left, and inbound right). Two days of recordings for one subject were excluded from analysis for lack of path passes in both outer maze arms.

For each cell sample, a time-averaged firing map was calculated for each period type ((I) direction-based firing map, (II) path-based firing map). First, total spike counts and occupancy durations were tabulated in 2-cm bins. Both occupancy and spike counts per bin were smoothed with a Gaussian window (σ = 4 cm), then spike counts were divided by occupancy to produce the cell’s smoothed occupancy-normalized firing map. In sporadic cases, spatial bins with insufficient occupancy (<50 ms in a 2-cm bin) were excluded from analysis. For each time-averaged firing map, the peak (spatial) firing rate was defined as the maximum value across position bins; spatial firing fields (place fields) were detected as sets of contiguous positions with rate >2 Hz and at least 10 cm large.

Note that in the case of direction-based firing maps (in Figures 2E–L, 5B, and 6E), the spatial bin at the center junction appears as a minimum as a result of the above procedure of calculating firing maps for each of the three maze arms separately. In plots, the value of this spatial bin was linearly interpolated; this value was otherwise excluded from subsequent quantification.

Two-dimensional time-averaged firing maps (plotted for illustration) were calculated with an analogous procedure using 1-cm square bins and a symmetric 2D Gaussian smoothing window (σ = 3 cm).

Selectivity index.

To measure the specificity of representation at the single-cell level, a selectivity index was calculated, specifically one for location (Left (L) vs. Right (R) arms; survey in Figure S1F) and one for heading direction (Outbound (O) vs. Inbound (I); survey in Figure S1I).

If data from two unique maze environments were available for a cell, and the cell fired at least 100 spikes in both environments, then the cell was analyzed (selectivity indices calculated) in the two unique maze environments independently. Thus cells in the dataset could contribute more than one cell sample to subsequent analyses (cell samples). If multiple recording epochs in one maze environment were available, then the cell was analyzed in recording epoch for which the cell had the highest mean firing rate.

The location selectivity index was calculated for cell samples for which the 1D firing maps that had at least one place field in either the L or R maze arm. To assess cell activity directly relevant to the spatial choice critical to the task (outbound approach to the L vs. R maze arm bifurcation, Figures 1C, S1A), analysis was performed only for outbound direction-based cell samples (defined above; inbound cell samples yielded a similar result). Furthermore, two inclusion criteria were imposed to ensure accurate estimates: first, data were only considered from positions beyond the choice boundary (i.e. the L or R arm); second, only cell samples with at least 100 spikes in the L or R arm were considered.

The direction selectivity index was calculated for direction-based cell samples that had at least one place field in either the O or I direction.

The selectivity index was defined as (fr₂ – fr₁)/(fr₁+fr₂), where fr is firing rate and 1, 2 correspond to two alternative conditions: for location, 1: L, 2: R; for direction: 1: O, 2: I. For single-cell surveys in Figures S1F and I, fr was defined as the peak firing rate from the time-averaged spatial firing maps (see above); in other analyses, mean firing rate was also used, and stated explicitly if so.

Theta cycles and theta phase.

For each subject, a tetrode in CA3 yielding clustered putative principal cells (i.e. located in the principal cell layer) was designated as the LFP recording site. In a minority of recording epochs (30 out of 287) for which a tetrode in the principal cell layer of CA3 was not available, a tetrode located in principal cell layer of CA1 was used instead.

To isolate activity in the frequency range of hippocampal theta (Buzsaki, 2002; Mizuseki et al., 2009), LFP from these recording sites was filtered at 5–11 Hz. Peaks and troughs of the filtered LFP were detected and used to define half-cycles (π radians) by linear interpolation (Jezek et al., 2011; Belluscio et al., 2012). To establish a common reference phase, a phase histogram (π/6 or 30° bin size) of aggregate single (principal) cell firing in CA1 was calculated across locomotor periods for each recording day; the phase of maximal CA1 firing was then defined to be 0° (Skaggs et al., 1996), with the half-cycle offset (±π) corresponding to the phase segregating individual cycles. Theta cycles were identified as individual cycles whose duration was consistent with the 5–11 Hz frequency range (<200 ms (5 Hz) and >90 ms (11 Hz)); sporadic cycles not meeting this criterion were disregarded in subsequent analyses that explicitly reference theta cycles or theta phase.

Theta phase locking.

To survey the prevalence and strength of theta rhythmicity in neural firing, theta phase histograms of single-cell firing were calculated. For a given cell, theta phase locking analysis was performed for locomotor periods (>4 cm/s), and moreover only when at least 50 spikes were available in these periods. Firing was combined across all available task recording epochs. For CA2 (Figure S1K, middle column), cells previously classified as N cells (see above) were excluded from this analysis, as theta-locking measures for these cells in the present dataset have been reported previously (Kay et al., 2016).

Firing correlograms.

To identify temporal patterns in neural activity, firing correlograms (CG) (time histograms; ±1.5 s, 5-ms bins) were calculated for single cells (auto-correlograms, ACG; t = 0 bin set to 0) and cell pairs (cross-correlograms, XCG). Data analyzed was restricted to locomotor periods that lasted at least 1.5 s, with further subdivisions described below. When multiple recording epochs for a given maze environment were available, data was pooled across epochs. If data from two unique maze environments were available, then data from the two unique maze environments were analyzed independently; thus a cell pair (XCG) or single cell (ACG) could contribute more than one CG (cell-pair sample and cell sample, respectively).

Two types of CGs were calculated: count and corrected. Count CGs were calculated by summing CGs (spike counts) across all data periods. For corrected CGs, CGs from each individual data period were first triangle-corrected (Bair et al., 2001; Mizuseki et al., 2009) to offset bias due to data periods of variable lengths (corrected spike counts); the corrected CG was then obtained by taking the mean over all individual data period CGs.

CGs (count and corrected) were then processed at two timescales: coarse (±1 s window) and fine (±0.4 s window). At each timescale, CGs were convolved with Gaussian kernels of the appropriate bandwidth (coarse, σ = 50 ms; fine, σ = 10 ms; meant to capture behavior- and theta- timescale activity, respectively (Geisler et al., 2007; Cheng and Frank, 2008; Diba and Buzsaki, 2008)) and then peak-normalized within the respective (coarse or fine) time window. Count CGs thus processed are shown in single example plots (e.g. Figures 1I and 1J) and survey plots (XCG: Figure 1K, Figures S2F-H; ACG: Figure 3F) (example raw count CGs shown in Figure S2E), while corrected CGs thus processed were used for subsequent analyses. Both plots and analyses were restricted to CGs with at least 100 spikes in the fine timescale window (±0.4 s). Cycling firing at 8 Hz (also termed “skip” firing (Deshmukh et al., 2010; Brandon et al., 2013; Jankowski et al., 2014)) was overtly present in both count and corrected CGs.

CGs were calculated from locomotor period data subdivided by either (I) path (II) direction, or (III) choice condition. As with other analyses in this study, locomotor periods were defined as periods of movement speed >4 cm/s; a threshold of >20 cm/s was also used to evaluate whether a firing pattern of interest (cycle skipping, see further below) required low movement speed.

(I) For path, CGs were calculated from data separated by periods corresponding to the four task path types; thus a given cell (or cell pair) in a given maze environment could contribute up to four samples in subsequent path-based analyses (path-based cell (or cell-pair) samples). Path-based CGs were used to survey firing in the dataset (ACG: Figures 3A–F, XCG: Figure S2H) and to compare differences between recording regions (Figure 3G) and differences for an additional subdivision of data (by theta phase, Figure S6B). Note that by subdividing data by path type, both the path- and direction-selectivity of hippocampal place cell firing are respected in the analysis; in this way, firing patterns that may differ between conditions may be distinguished. In the case of differing recording regions, the finding of significant differences in firing patterns (Figure 3G) was also observed with additional analysis variations: namely, without any subdivision of data, by subdividing by direction, and also by using higher movement speed thresholds (e.g. >20 cm/s) (data not presented).

(II) For direction, CGs were calculated from data subdivided into outbound vs. inbound periods; thus a given cell (or cell pair) in a given maze environment could contribute up to two samples in subsequent path-based analyses (direction-based cell (or cell-pair) samples). Direction-based XCGs are shown in Figure 1 (outbound only), Figure 2, Figure S1L-O (outbound only), and Figure S2A-E (outbound only), and also surveyed across all cell pairs in Figures S2F (outbound) and S2G (inbound). Direction-based ACGs (data not presented) were qualitatively similar to path-based ACGs (Figures 2E and F).

(III) For choice condition, CGs were calculated from data (a) recorded from linearized positions within the choice boundary, and (b) subdivided into outbound vs. inbound periods; given (b), a given cell in a given maze environment could contribute up to two samples in subsequent analyses (choice-based cell samples). Choice-based CGs were subsequently analyzed (cycle skipping analysis, see below; Figure 3H) to assess whether choice behavior (choice passed: inbound samples; choice imminent: outbound samples) was a correlate of temporal firing patterns.

Cycle skipping index (CSI).

Cycling firing at 8 Hz was detected and quantified with a cycle skipping index (CSI) that was conceptually equivalent to a previously described theta skipping index (Deshmukh et al., 2010; Brandon et al., 2013); the goal of either approach is to measure the lack of firing on adjacent theta (~8 Hz) cycles. In the present study, the term “cycling” was adopted to refer explicitly to the observation that periods of “skipping” (i.e. lack of firing) in the firing of one group of cells can correspond to periods of firing in another group of cells, furthermore in the case where the two groups encode mutually exclusive scenarios (suggested initially at the cell-pair level; Figures 1, 2).

Two types of CSI were calculated: one for single cells (cell CSI) and one for cell pairs (cell-pair CSI); for both, the calculation was performed on corrected CGs (ACG for cell CSI; XCG for cell-pair CSI) that had at least 100 spikes within the fine timescale window (±0.4 s) and that were smoothed and peak-normalized (see above).

Single-cell cycling (cell CSI).

For each ACG, two local maxima (peaks: p₁ and p₂) within two respective time windows were detected: p₁, the peak nearest t = 0 in the 90–200 ms window; p ₂, the peak nearest t = 0 in the 200–400 ms window. In some cases, a peak was not detected within a time window: for p₁, the maximum value in the window was then used; for p₂, the minimum value in the window was then used.

$$\text{Cell}\hspace{0.17em}\text{CSI}=\left({\text{p}}_{\text{2}}{-\text{p}}_{\text{1}}\right)/\max \left({\text{p}}_{\text{1}}{\text{,p}}_{\text{2}}\right)$$

For two ACGs (path-based samples), the CSI could not be calculated due to an absence of spiking in both the 1^st and 2^nd peak time windows.

To evaluate whether there was a monotonic relationship between cycling firing and the overall amount of firing, Spearman’s correlation was calculated between cell CSI and average firing rate within the sample condition (i.e. firing rate across the same periods used to calculate the CSI).

Cell-pair cycling (cell-pair CSI).

For each XCG, five local maxima (peaks: p₀, p_±1, p_±2) within five respective time windows were detected. First, p₀, the peak nearest t = 0 in the ±90 ms window, was identified (if no peak was detected, then p₀ was taken as the value at t = 0). The four remaining peaks were then detected in time windows relative to the time bin of p₀ as follows: p_±1, the two peaks nearest p ₀ in the ±90–200 ms windows; and p_±2, the two peaks nearest p₀ in the ±200–400 ms windows.

$$\text{Cell-pair CSI }= \left({\text{p}}_{\text{0,2}}–{\text{ p}}_{\text{1}}\right) /\text{ max}\left({\text{p}}_{\text{0,2}},{\text{ p}}_{\text{1}}\right)\text{ where}$$

$${\text{p}}_{\text{0,2}}=\text{ mean}\left(\text{max}\left({\text{p}}_{-2},{\text{p}}_{\text{+2}}\right),{\text{p}}_{\text{0}}\right)$$

$${\text{p}}_{\text{1}}=\text{ mean}\left({\text{p}}_{-1},{\text{p}}_{\text{+1}}\right)$$

Cell pair firing types.

Cell-pair samples having at least 100 spikes in their XCG at the fine timescale (±0.4 s) were classified into one of four types: (1) classic, (2) anti-synchronous cycling (anti), (3) super-synchronous cycling (super), and (4) off cycling (off). Classic corresponds to the pattern of co-firing expected given single-cell firing on adjacent cycles (Figures S1L-O), as previously described in the hippocampus (O’Keefe and Recce, 1993; Skaggs et al., 1996; Huxter et al., 2003; Zugaro et al., 2005; Diba and Buzsaki, 2008). Anti corresponds to a pattern of co-firing in which the two cells consistently fire on alternate 8 Hz cycles; Super corresponds to a pattern of co-firing in which the two cells consistently fire together every other 8 Hz cycle. Off corresponds to a pattern of co-firing showing either relatively more or relatively less firing every other 8 Hz cycle, yet for which synchronization within 8 Hz cycles was ambiguous.

Formal criteria were as follows: classic pairs were those with cell-pair CSI <0.3; anti cell pairs were those with p₀ (see above) detected within the ±40 ms window in the XCG, and had cell-pair CSI <−0.3; super cell pairs were those with p₀ detected in ±40 ms in the XCG, and had cell-pair CSI >0.3; off cell pairs were all other cell pairs that had |cell-pair CSI| >0.3.

The goal of these criteria was primarily to identify cell pairs that unequivocally exhibited cycling firing (Figures S2E-H) rather than to demarcate cell pair types optimally; from informal observations, the cell-pair CSI cutoff value presently chosen (0.3) tends to over-classify cell pairs as classic. Given the adopted criteria, cell pair proportions were tabulated (Figures S2F-H), moreover when cell pairs recorded from the same tetrode were excluded (yielding similar proportions; see caption of Figures S2F-H for all numerical values).

It is important to note that the present analysis approach assumes that cycling dynamics do not exceed two cycle types (A-B-A-B-…), though it is possible that cycling dynamics occur with three or more cycle types. Given this particular limitation, single-cell measures (Figure 3) were also adopted to quantify cycling dynamics; the cell pair results are presented here as an initial simple approach to the observation of constant cycling dynamics in the hippocampus (Figures 1, 2, and S2), and to facilitate comparison to recent results in entorhinal cortex (Deshmukh et al., 2010; Brandon et al., 2013).

Clusterless decoding.

To evaluate neural representation at the population level, Bayesian decoding of unsorted neural spikes (i.e. unassigned by experimenter to single cells) was performed (Kloosterman et al., 2013; Deng et al., 2015). The inclusion of unsorted spikes is advantageous for population-level analysis in that recorded data subject to analysis is maximized: all spike sources monitored by electrodes are analyzed. Furthermore, recent studies report improved decoding performance for hippocampal data (Kloosterman et al., 2013; Deng et al., 2015). This improvement is deducible given that (i) spikes with similar waveforms emanate from the same cells (McNaughton et al., 1983b; Gray et al., 1995; Henze et al., 2000), a correspondence that does not depend on spike sorting, and (ii) multi-tetrode recording in hippocampus routinely yields a substantial number of high-amplitude spikes left unsorted prior to analysis (Davidson et al., 2009). In the present study, two variables were separately decoded: location (Wilson and McNaughton, 1993; Brown et al., 1998; Zhang et al., 1998; Pfeiffer and Foster, 2013) and heading direction (McNaughton et al., 1983a; Battaglia et al., 2004; Foster and Wilson, 2006; Davidson et al., 2009), each variable long established as single-cell representational correlates in the hippocampus (Eichenbaum et al., 1999).

Data criteria.

To limit analysis to population-level activity, decoding was performed only for recording epochs for which there were at least 20 putative principal cells clustered and firing at least 100 spikes, moreover only for subjects with at least three such epochs available (83 epochs across 7 subjects). Within each epoch, spikes included for analysis were required to exceed 60 µV on at least one tetrode channel (ii) be recorded on a tetrode that yielded at least one clustered putative principal cell. Across qualifying epochs, 4–17 (median: 9) tetrodes per epoch met criterion (ii); these tetrodes were predominantly in CA1 and CA3, with a subset of epochs (34 out of 83 epochs) also including tetrodes in CA2 and DG. Restricting decoding to CA1 and CA3 tetrodes yielded qualitatively equivalent findings (data not presented). In example plots (e.g. Figures 4A–C and 7A–C), the unsorted spikes that were analyzed were aggregated across tetrodes and shown as multi-unit activity (MUA).

Analysis times.

For both location and direction, the decoding procedure was performed within each ~15 min recording epoch; data used to construct an encoding model were from locomotor periods while decoded data was from locomotor periods and flanking 0.5 s periods (stopping periods). Flanking stopping periods were included in the analysis since the theta rhythm and associated neural firing are known to continue to be expressed during these times; these periods were also included to assess neural activity possibly associated with head scanning behaviors (Johnson and Redish, 2007; Redish, 2016), which can encompass brief low-speed periods. In plots, neural activity overlapping with stopping periods are shown separately from neural activity that occurred solely during locomotor periods (open bars/circles vs. black bars/points, respectively, in Figures 4E–G, 7E and 7F, and S7F).

For location, spikes were analyzed independently in inbound vs. outbound periods since location encoding in the hippocampus is known to be direction-specific (McNaughton et al., 1983a; Battaglia et al., 2004; Foster and Wilson, 2006; Davidson et al., 2009). For direction, spikes analyzed were restricted to periods when subjects were located in the three parallel longer segments of the maze, specified as linearized positions (defined with respect to the center reward well; see above) that were either less than or more than 40 cm from the linearized position of the central junction (shown as lighter grey positions in example behavioral maps in Figures 7A–C and S7B-E). This restriction was imposed to facilitate comparison to previous studies; in particular, prior work on hippocampal directional coding in mazes (McNaughton et al., 1983a; Battaglia et al., 2004; Foster and Wilson, 2006; Wu and Foster, 2014) has generally referred to straight rather than jointed (e.g. perpendicularly connected) maze tracks.

Decoding time windows.

For location, decoding windows were 20 ms with 4 ms overlap between windows. For direction, two types of decoding windows were used (illustrated in Figures S6C and S6D): (i) 20 ms with 4 ms overlap (sliding window decoder), and (ii) windows correspondent with theta half-cycles (half-cycle decoder; Figures 7 and S7B-G). For (ii), theta phase estimated from LFP (see above) was used to identify windows of duration π/4 (90°) centered on first and second halves of theta (i.e. first-half window: (−3*π/4, -π/4); second-half window: (π/4, 3*π/4)). These windows were chosen on the basis of results at both the single-cell (Figure 5B, 6E–H and S6A) and population (Figure S6E) levels indicating that representation of non-current (hypothetical) direction is systematically weakest and strongest at approximately –π/2 and π/2, respectively.

It is worth noting that decoding is performed in sub-second time windows (20–50 ms) to assess temporal dynamics; in contrast, the encoding model is constructed from data pooled across the ~15 min recording epoch without referencing any temporal dynamics in the epoch.

Algorithm.

A two-stage decoding algorithm described previously (Kloosterman et al., 2013; Deng et al., 2015) was used. In the first stage (encoding), the mapping between spikes and the representational variable (location or direction) was modeled as an N-dimensional probability distribution (mark space, M), where each spike corresponds to an N-dimensional vector (mark). In M, N-1 dimensions correspond to the feature space of spikes while the remaining dimension corresponds to the representational variable. M is estimated from all spikes occurring during encoding periods using kernel density estimation. In the present case, N is 5, where 4 dimensions correspond to the amplitude (µV) of the spike on each of the spike’s 4 parent tetrode channels while the remaining dimension corresponds to the value of the representational variable (X; location: linearized position (cm); direction: −1 for inbound, 1 for outbound) observed from the subject at the time of the spike. Each spike contributed a 5-D Gaussian kernel, with the four amplitude dimensions contributing symmetrically (each σ = 20 µV), symmetric in the amplitude dimensions). For location, the representation dimension of M was linearized position divided into 1-cm bins, with each spike contributing a Gaussian kernel (σ = 8 cm). For direction, the representation dimension of M was two-bin distribution, with each spike contributing a Kronecker delta kernel.

In the second stage, decoding was performed using Bayes’ rule:

$$\text{p}\left(\text{X}|\text{spikes}\right) =\text{ c }*\text{ p}\left(\text{spikes}|\text{X}\right) *\text{ p}\left(\text{X}\right)$$

where spike refers to the set of spike marks observed in the decoding window, and c is a normalization constant. Each p(•) term is a probability density over the representational dimension of M; p(X|spikes) is the posterior (decoded output; estimate of the representational correlate X); p(spikes|X) is the likelihood (encoding model); p(X) is the prior.

To obtain p(spikes|X), the aggregate spiking activity across tetrodes was modeled as a marked point process with mark space M, with spikes in each decoding time window treated as independent and following a Poisson distribution with rate parameter fully characterized by M (derivation and formalism in earlier report (Deng et al., 2015)).

Next, the prior p(X) was taken to be either uniform or history-dependent. For decoding of direction, a uniform p(X) was used given a lack of prior knowledge of population-level representation of direction in the hippocampus. For decoding of location, both uniform (Karlsson and Frank, 2009; Kloosterman et al., 2013; Pfeiffer and Foster, 2013) and history-dependent (Brown et al., 1998; Zhang et al., 1998; Johnson et al., 2006; Johnson and Redish, 2007) priors were used to assess the generality of the population-level result (constant cycling at 8 Hz between alternative locations; history-dependent prior: Figure 4; both priors: Figure S4). The advantage of a uniform prior is that it minimizes assumptions about the decoded activity; the advantage of a history-dependent prior is that it models known properties of the decoded activity.

Taking previous work (Johnson et al., 2006; Johnson and Redish, 2007) as a starting point, the history-dependent prior was designed to model the observation that population-level spiking in the hippocampus regularly encodes locational sequences that evolve at virtual speeds exceeding 1 m/s (Davidson et al., 2009; Gupta et al., 2012; Feng et al., 2015; Zheng et al., 2016). This property can be captured by a Markovian state-space model (Deng et al., 2015) implemented by a prior defined at each time step as the product of a constant 1-step transition matrix and the posterior from the previous time step. To eliminate bias for the decoded output to evolve in a particular direction, state transitions were modeled as a 2D random walk (Brown et al., 1998; Zhang et al., 1998; Johnson et al., 2006) where, for simplicity, the three arms of the maze were treated as locations in a radially symmetric Y shape (120° between arms). Transition probabilities between maze locations were calculated as the value of a Gaussian (σ = 1 cm) evaluated at the Euclidean distance between each location in the Y. To model virtual speeds exceeding 1 m/s, the transition matrix was exponentiated by 10 (Johnson et al., 2006; Johnson and Redish, 2007); thus for decoding windows that shifted every 4 ms, the 1-cm scale of the Gaussian corresponds to a virtual speed of 2.5 m/s, with exponentiation by 10 corresponding to 25 m/s. The resulting prior is approximately an order of magnitude more conservative (diffuse over spatial locations) compared to priors modeling virtual speeds of ~2–5 m/s (Johnson and Redish, 2007). It is also worth noting that since the model (transition matrix) is constant, it cannot impose temporal structure (e.g. cycling dynamics).

Constant cycling of location.

To determine whether constant cycling at 8 Hz between alternative locations (i.e. left (L) vs. right (R) maze arm; observed initially in cell pairs (Figures 1, 2, and S2)) occurred at the population level, the output of the clusterless decoding of location (decoded posteriors; see above) was analyzed. Moreover, to investigate further the finding of elevated cycling dynamics when subjects were approaching the L vs. R spatial choice (Figure 3H, suggesting cycling between L vs. R locations), analysis was restricted to the three types of maze passes (defined above) involving this behavior: outbound Left path passes, outbound Right path passes, and backtrack passes from the center well. Analysis was further restricted to locomotor periods and flanking stopping periods (0.5 s), to periods when the subject was located within the choice boundary (center zone), and to periods when the subject was located at least one-third of the linear distance to the choice boundary along the center arm; the latter two restrictions were imposed to focus analysis on cycling neural activity associated with choice approach (previously identified at the single-cell level (Figure 3H).

First, 8 Hz cycles were segregated on the basis of the ~8 Hz theta rhythm. Prior results suggest that population-level representation of locational sequences occur within individual theta cycles (Skaggs et al., 1996; Davidson et al., 2009; Gupta et al., 2012; Feng et al., 2015; Wikenheiser and Redish, 2015): thus the initial step was to identify an appropriate phase by which to segregate theta cycles. To this end, the theta phase distribution of the representation of alternative locations (L or R maze arm) was calculated for each recording epoch; specifically, the decoded probability density located in either the L or R arm (integrating over position bins) was histogrammed in 30° theta phase bins (linear interpolation of 5–11 Hz LFP, see above). The phase bin having the minimum probability density was then used to segregate all theta cycles in the epoch.

Second, candidate 8 Hz cycles representing the alternative locations (L or R maze arm) were identified and binarized. Candidate cycles were identified as the segregated theta cycles that had probability density >0.1 for either the L or R maze arm (L/R density; the remainder corresponding to the center arm); then, for each candidate cycle, the arm with the higher probability density was designated as the location (L vs. R) represented.

Third, constant cycling periods were detected. In general, constant cycling can be defined as cycle-to-cycle switching of representation across at least 3 successive cycles, i.e. A-B-C-D where B is not A, C is not B, and D is not C. For binary alternatives, constant cycling is defined only for the special case of A-B-A-B; accordingly, for the present case of L vs. R, putative constant cycling periods were detected as cases where the representation switched for at least 3 successive cycles (L-R-L-R… or R-L-R-L…), corresponding to a minimum total duration of 4 cycles. The start and end of single constant cycling periods were defined as the beginning of the first cycle to the end of the last cycle. Note that constant cycling periods were only detected within periods of contiguous candidate theta cycles (contig period).

To evaluate whether constant cycling could have resulted from random activity or noisy data, the observation of constant cycling was tested against a null model in which cycle order was random, i.e. temporal shuffling. Testing was moreover conducted at two different levels: (I) the study-wide level (study-wide shuffle) and (II) at the level of individual periods (individual period shuffles).

(I) The study-wide shuffle (Figures 4D and S4G) was performed to test whether constant cycling was a non-random activity pattern. A P-value was calculated by randomly shuffling (10000 permutations) the order of all candidate theta cycles within every contig period across all recording epochs. For each shuffle, constant cycling periods were then re-detected, after which the total number of cycles participating in the re-detected constant cycling periods was tabulated; the P-value was the proportion of shuffles for which the total number of such cycles (i.e. those belonging to constant cycling periods) was equal or greater to the number in the observed data.

(II) Individual period shuffles (Figures 4E and S4H) were performed to measure how non-random single periods of constant cycling were. In contrast to the study-wide shuffle, the goal was to identify individual constant cycling periods that were not likely to have occurred by chance. A P-value was calculated for each observed constant cycling period by randomly shuffling (10000 permutations) the order of candidate theta cycles within the same recording epoch and within time periods of the same path pass type (outbound Left, outbound Right, or center well backtrack) as that of the observed constant cycling period; the P-value of the constant cycling period was proportion of shuffles for which a constant cycling period of the same or greater cycle duration was detected within the same contig period as the observed constant cycling period. The P-value thus measures the frequency of the representational activity pattern (an individual constant cycling period) with respect to the empirical prevalence of the components of that pattern (L vs. R candidate theta cycles from the same recording epoch and path pass type). A criterion of P < 0.05 was then adopted to identify individual constant cycling periods subject to further analyses (Figures 4F and 4G, S4I and J).

Constant cycling of direction.

To determine whether constant (half-theta) cycling between directions (suggested by initial observations, Figure S7A) could occur at the population level, the output of the clusterless decoding of direction (decoded posteriors; see above) was analyzed. Analysis was conducted for all locomotor periods and flanking stopping periods (0.5 s). Furthermore, analysis was performed on the output of the theta half-cycle decoder, as single-cell and population-level results (single-cell: Figure S6A, third row; population: Figure S6E) suggested that this decoder would be maximally sensitive to representations of alternative directions.

First, the decoded half-cycles were binarized (illustration in Figures S6C and S6D): for each half-cycle, the direction having the higher probability density was designated as the direction represented (outbound (O) vs. inbound (I); see above).

Second, constant cycling periods were detected with a procedure analogous to that of location. In general, constant cycling can be defined as cycle-to-cycle switching of representation that occurs contiguously for least 3 successive cycles, i.e. A-B-C-D where B is not A, C is not B, and D is not C. For binary alternatives, constant cycling is defined only for the special case of A-B-A-B; accordingly, for the present case of O vs. I, putative constant cycling periods were detected as cases where the representation switched for at least 3 successive theta half-cycles (O-I-O-I… or I-O-I-O…), corresponding to a minimum total duration of 4 theta half-cycles. The start and end of single constant cycling periods were defined as the beginning of the first theta half-cycle to the end of the last theta half-cycle. Note that constant cycling periods were only detected within periods of contiguous theta half-cycles (contig period).

Third, constant cycling periods were identified as occurring within three types of directional periods: inbound, outbound, or mixed directional periods. The first two types were identified if the detected constant cycling period occurred entirely within the respective (inbound or outbound) directional period. The mixed period type was identified if the constant cycling period overlapped with both inbound and outbound periods.

As in the case of location (see above), to evaluate whether constant cycling could have resulted from random activity or noisy data, the observation of constant cycling was tested against a null model in which cycle order was random, i.e. temporal shuffling. Testing was moreover conducted at two different levels: (I) the study-wide level (study-wide shuffle) and (II) at the level of individual periods (individual period shuffles).

(I) The study-wide shuffle (Figure 7D) was performed to test whether constant cycling was a non-random activity pattern. A P-value was calculated by randomly shuffling (10000 permutations) the order of all half-theta cycles within every contig period across all recording epochs. For each shuffle, constant cycling periods were then re-detected, after which the total number of half-theta cycles participating in the re-detected constant cycling periods was tabulated; the P-value was the proportion of shuffles for which the total number of such half-theta cycles (i.e. those in constant cycling periods) was equal or greater to the number in the observed data.

(II) Individual period shuffles (Figure 7E) were performed to measure how non-random single periods of constant cycling were. In contrast to the study-wide shuffle, the goal was to identify individual constant cycling periods that were not likely to have occurred by chance. A P-value was calculated for each observed constant cycling period by randomly shuffling (10000 permutations) the order of half-theta cycles within the same recording epoch and within the same directional period type (inbound or outbound) as that of the observed constant cycling period; the P-value of the constant cycling period was proportion of shuffles for which a constant cycling period of the same or greater cycle duration was detected within the same contig period as the observed constant cycling period; for individual constant cycling periods that occurred during mixed directional periods, shuffling was performed simultaneously and separately for the half-theta cycles that occurred respectively within outbound vs. inbound periods. The P-value measures the frequency of the representational activity pattern (an individual constant cycling period) with respect to the empirical prevalence of the components of the pattern (O vs. I half-theta cycles from the same recording epoch and directional period type). A criterion of P < 0.05 was then adopted to identify individual constant cycling periods subject to further analyses (Figures 7F and G). In addition, analysis of individual constant cycling periods lasting at least 8 (half-theta) cycles was also conducted (Figures S7F and G).

Decoding choice.

To assess whether population-level activity in the hippocampus could predict spatial choice (Figure S5), Bayesian decoding of hippocampal neural firing was performed using the clusterless decoding algorithm (see above).

The decoding procedure (data criteria, analysis times, algorithm; see above) was the same as that of location and direction, but with the following specifications: (1) the data analyzed were from outbound path pass periods (left (L) and right (R); each pass treated as a single trial), (2) the representational variable was the path chosen (L vs. R in a two-bin distribution; −1: L path, 1: R path), (3) each spike during outbound path periods (occurring during either a L or R outbound path pass; see above for path period definition) contributed a Kronecker delta kernel to the two-bin choice dimension of the mark space (M; the encoding model), and (4) spikes used to encode and decode were restricted to the windows of duration π/4 (90°) centered on 1^st and 2^nd halves of theta (1^st-half window: (−3*π/4, -π/4); 2^nd-half window: (π/4, 3*π/4)), respectively (half-cycle encoder and half-cycle decoder, respectively). Analysis was restricted to path passes (trials) that had at least 12 2^nd-half windows available for decoding.

To evaluate different frameworks for interpreting hippocampal representation, three approaches to the decoding procedure were taken (described and schematized in Figures S5A-C); each approach stipulates a specific subset of data for encoding and decoding.

The decoded output (posterior probabilities) was analyzed as follows. Within each trial, the probability density corresponding to the R choice was averaged across second-half (decoding) windows. If this average probability exceeded 0.5, then the decoded choice was taken to be R; otherwise, the decoded choice was taken to be L.

Hypothetical representation: single cells.

A body of work (Eichenbaum et al., 1999; O’Keefe, 2007) establishing that single neurons in the hippocampus encode externally observable variables was the basis of the present investigation into the neural representation of hypotheticals. Specifically, past findings indicate that single hippocampal neurons reliably (over single trials, recording epochs, days, and months (Thompson and Best, 1990; Lever et al., 2002; O’Keefe, 2007)) fire more in specific conditions (e.g. a particular location, direction, path, etc.) vs. other conditions (other locations, directions, paths, etc.), establishing that these cells encode the relevant variable (representational correlate). Methodologically, time-averaged tuning curves (e.g. place cell maps (Wilson and McNaughton, 1993; O’Keefe, 2007; Pfeiffer and Foster, 2013)) have been used to estimate single-cell encodings. This analysis approach to single cells was adopted, though with two differences.

The first difference was simply terminological: to make the underlying approach explicit (rather than the particular representational correlate, e.g. location, direction, etc.), the higher vs. lower firing conditions were generically termed the “preferred” (P) vs. “non-preferred” (NP) conditions, respectively.

The second difference was conceptual: in cases where single-cell firing was higher in the P (vs. NP) condition, firing in the NP condition was subsequently interpreted not as noise, but as possibly reflecting covert representation of the P condition, i.e. the non-current, or hypothetical, condition. Thus the goal of analysis was to identify whether cells were tuned to fire more in one condition (P) vs. another (NP) with the provisional interpretation that firing in the P vs. NP condition encodes current vs. hypothetical experience, respectively.

Data from each cell were analyzed as samples (cell samples) with the following criteria. If data from two unique maze environments were available for a cell, and the cell fired at least 100 spikes in the both environments, then the cell was analyzed in the two unique maze environments independently. Thus cells in the dataset could contribute more than one cell sample to subsequent analyses. If multiple recording epochs in one maze environment were available, then the recording epoch with the most recorded spikes was analyzed.

Four types of representational firing patterns were studied: (1) outbound path (Frank et al., 2000a; Wood et al., 2000; Ito et al., 2015) (previously termed prospective trajectory), (2) inbound path (Frank et al., 2000a; Wood et al., 2000; Ito et al., 2015) (previously termed retrospective trajectory), (3) directional (McNaughton et al., 1983a; Battaglia et al., 2004), and (4) a putative type termed “extra-field” (Johnson and Redish, 2007; Rubin et al., 2014). As described above, path- and direction-based 1D firing maps for each cell sample were calculated.

For (1), outbound path-based (outbound left (L) vs. outbound right (R)) firing maps were analyzed; P vs. NP refers to L vs. R (or vice versa) paths. For (2), inbound path-based (inbound left (L) vs. inbound right (R)) firing maps were analyzed; P vs. NP refers to L vs. R (or vice versa) paths. For (3), direction-based (inbound (I) vs. outbound (O)) firing maps from each of the three maze arms were analyzed independently, with firing maps from each arm contributing independent cell samples if satisfying additional criteria specified below; for each cell sample, P vs. NP refers to the I vs. O heading direction, respectively (or vice versa). For (4), all four path-based maps were analyzed (outbound L, outbound R, inbound L, inbound R); P vs. NP refers to the task paths with vs. without at least one detected spatial firing field.

For each firing map, spatial firing fields (place fields), defined as contiguous linear positions of firing rate >2 Hz and at least 10 cm large, were detected separately in the following alternative conditions. For (1), (2), and (3), there were two alternative conditions: namely, for (1) and (2), L vs. R path, while for (3), O vs. I direction. For (4), there were four alternative conditions: outbound L vs. outbound R vs. inbound L vs. inbound R path. The inclusion criteria and identification of P vs. NP conditions for each type of representational correlate are as follows.

(1). Outbound path.

Place field detection was performed separately in two locational zones in the maze: the center zone (see above) and the outer maze arms (L and R). Only cell samples that had at least one place field detected in either of the outer arms (L or R), in addition to at least one place field detected in the center zone, were analyzed (note that since the location zones were contiguous, a place field detected in both zones could correspond to a single place field across the zones). Next, for the outer maze arms, the peak firing rate of all detected place fields were compared; the path type (L or R) corresponding to the maze arm (L or R) with highest peak firing rate place field was designated as the cell’s preferred (P) condition (e.g. L path), with the other condition designated as the cell’s non-preferred (NP) condition (e.g. R path).

(2). Inbound path.

Place field detection was restricted to the center arm. Only cell samples that had at least one place field for either path (L or R) were analyzed. The path type (L or R) with the highest peak firing rate place field was designated as the cell’s preferred (P) condition (e.g. L path), with the other condition designated as the cell’s non-preferred (NP) condition (e.g. R path).

(3). Directional.

Place field detection was performed independently in each maze arm. Only cell samples that had at least one place field for either direction (I or O) were analyzed. The direction (I or O) with the place field with the highest peak firing rate was designated as the cell’s preferred (P) condition (e.g. I direction), with the other condition designated as the non-preferred (NP) condition (e.g. O direction).

(4). Extra-field.

Place field detection was performed separately for each of the four task-based firing maps. Task paths with at least one detected place field were designated as the cell’s preferred (P) condition(s), while task paths for which no place fields were detected were designated as the cell’s non-preferred (NP) condition(s). Note that this definition of extra-field firing (i.e. firing in the NP condition) refers to path- and direction- specific firing, while previous approaches focus on location-specific firing (Johnson and Redish, 2007; Rubin et al., 2014); the approaches are otherwise conceptually similar.

Selective firing (P vs. NP).

Past work indicates that the degree of path- and direction-specific firing exists on a continuum, with some cells firing almost exclusively in the preferred condition, while other cells fire equivalently in either condition (e.g. “bidirectional” cells or “pure” place cells). Since only cells showing differential firing between conditions can encode the relevant variable, it was therefore necessary to measure the selectivity of firing between conditions. To this end, the selectivity index (SI, defined above) was calculated for P vs. NP conditions; the SI was moreover calculated for both peak firing rate (from spatial firing maps) and mean firing rate.

A cell sample was classified as showing differential P vs. NP firing if two criteria were met: (1) the SI was >0.2 (equivalent to 1.5x higher firing rate in the P condition; other threshold values yielded qualitatively equivalent single-cell results) for both peak firing rates and mean firing rates, (2) the cell sample in the NP condition had no more than one detected place field. These criteria were adopted to limit analyses to cases where there was unequivocally higher firing on average in the P (vs. NP) condition.

Theta phase of hypotheticals: single cells.

To determine whether single-cell firing putatively encoding hypothetical experience (selective firing in preferred (P) vs. non-preferred (NP) conditions; see above) showed temporal organization at the sub-second timescale, neural firing in cells that were classified as showing differential firing was analyzed with respect to the phase of the ~8 Hz theta rhythm. Analysis was restricted to locomotor periods. In brief, spikes were subdivided by condition (P vs. NP) then analyzed separately.

The set of spikes analyzed was approximately the same as those used to construct firing maps, but with three differences: (1) a small proportion of spikes (~5%) were ignored if they did not occur within periods in which there was a valid estimate of theta phase (see above), (2) in the case of path firing (L vs. R), spikes were taken from all times during path passes between reward wells, with no exclusion of periods in which the rat was temporarily not within or oriented along the completed path, and (3) in the case of path firing (L vs. R), spikes were limited to those that occurred within the center zone. Criterion (2) was adopted to take an inclusive approach to the spikes analyzed, particularly given prior findings showing that path-selective firing generalizes to instances where the path is behaviorally interrupted (Ferbinteanu and Shapiro, 2003). Criterion (3) was adopted to restrict analysis to locations conventionally analyzed for path-specific firing (i.e. locations that overlap between paths).

Four representational correlates (see above) were analyzed: (1) outbound path, (2) inbound path, (3) direction, (4) extra-field. For each cell sample, the theta phases of the spikes in the P vs. NP conditions were then each used to construct separate theta phase histograms. Phase histograms were then constructed at two resolutions: 12-bin (30° bins) and 2-bin (180° bins; first and second half of cycle); the former (12-bin) solely for plots, while the latter (2-bin) for both plots and statistical testing of the basic hypothesis that representation in the hippocampus differs between the first and second halves of the theta cycle. Cell samples analyzed were restricted to those with at least 20 spikes in the phase histogram in the NP condition and with non-uniform phase histograms (Rayleigh tests at P < 0.05) in both the P and NP conditions.

For these cell samples, spike theta phases were averaged (circular mean) to obtain the mean angle in the P and NP conditions (Figures 6B and 6F; first column in Figure S6A). Second, phase histograms were normalized and then averaged across cell samples (Figures 6C and 6D, 6G and 6H; second and fourth columns in Figure S6A). To evaluate whether firing associated with the alternative (i.e. hypothetical) condition was enhanced on the 2^nd half of the theta cycle, two statistical comparisons were conducted for the 2-bin phase histograms: (a) the proportion of firing on the 2^nd half of theta in the NP condition vs. 0.5 and (b) the proportion of firing on the 2^nd half of theta in the NP condition vs. the proportion of firing on the 2^nd half of theta in the P condition.

Theta phase of hypotheticals: population-level.

To determine whether representation of current vs. hypothetical experience showed temporal organization at the population level, the output of the clusterless decoding algorithm (see above), for both location and direction, was analyzed with respect to the phase of the ~8 Hz theta rhythm. Analysis was performed for locomotor periods. The analysis was analogous to the single-cell analysis (see above) in that theta phase was quantified separately (i.e. separate theta phase histograms) for different conditions; the preferred (P) vs. non-preferred (NP) conditions at the single-cell level correspond, here at the population-level, to current vs. hypothetical conditions, defined as follows.

The current condition is defined as the actual (veridical) state of the subject for a given representational correlate (e.g. the subject’s actual location if the representation is self-location), while the hypothetical condition is defined as the non-current state of the subject (e.g. a location remote from the subject’s actual location, or the direction opposite to that of the subject’s actual direction). The analysis procedure for each representational correlate studied presently (location and direction) is described in turn.

Location.

To evaluate theta phase organization of the locational representation (Figures 4H and S4K), the output of the clusterless decoding of location was analyzed for all outbound path passes (n = 1683 path passes across 7 subjects) when the subject was located in center zone. Two types of current condition were defined: current maze arm (Center) and the maze arm (L or R) chosen by the subject in the path pass (Choice, Figure 4H); the alternative condition (Alt) was defined as the maze arm (L or R) not chosen by the subject in the path pass. Theta histograms were pooled across all decoding windows occurring within each path pass. Path passes were moreover analyzed inclusively, with no exclusion of times in which the subject was temporarily not within or oriented along the completed path; this inclusive approach was adopted given prior findings showing that path-selective firing can generalize even to passes where the path is behaviorally interrupted (Ferbinteanu and Shapiro, 2003).

Direction.

To evaluate theta phase organization of the directional representation (Figure S6E), the output of the clusterless decoding of direction (sliding window decoder; see above) was analyzed for each of the 7 subjects for which decoding was performed. The current condition was the subject’s current heading direction (outbound (O) or inbound (I)), while the hypothetical condition was the other direction (O or I). Theta histograms were constructed from decoding windows pooled across all epochs for each subject.

Phase histograms.

Theta phase histograms (current and alternative/hypothetical) were calculated by first identifying the theta phase at the center time (average of start and end time) of each decoding window. Then, for each decoding window, the posterior probability density corresponding to each condition (current and alternative/hypothetical) was added to the corresponding theta phase histogram.

Phase histograms were constructed at two resolutions: 12-bin (30° bins) and 2-bin (180° bins; first and second half of cycle); the former (12-bin) solely for plots, while the latter (2-bin) for both plots and statistical testing of the basic hypothesis that representation differs between the first and second halves of the theta cycle. Phase histograms were then normalized within condition (current vs. alternative/hypothetical) and averaged across samples (passes or subjects). To evaluate whether population-level representation associated with the alternative/hypothetical condition was enhanced on the 2^nd half of the theta cycle, two statistical comparisons were conducted for the 2-bin phase histograms: (a) the proportion of decoding density of the alternative/hypothetical condition on the 2^nd half of theta vs. 0.5 and (b) the proportion of decoding density of the alternative/hypothetical condition on the 2^nd half of theta vs. the proportion of decoding density of the current condition on the 2^nd half of theta.

Quantification and statistical analyses.

Statistical tests and corresponding p-values are reported within the text of the Results sections; however, for findings presented in Supplementary Figures, this information is instead reported within the correspondent Supplementary Figure legend. Measures of dispersion are reported either in the text of the Results section or in figure legends, as appropriate. All statistical tests were two-sided.

Data and code availability.

All data and custom-written code are available upon request.

Highlights.

• Firing across hippocampal neurons can regularly “take turns” (cycle) every ~125 ms

• Cycle firing is seen at single-cell, cell-pair, and population levels

• Cycle firing encodes hypothetical experience, including multiple possible futures

• Cycle coding generalizes across representational correlates, implying common process