The Relative Age Effect in Professional Futsal Players

Abstract

The objective of this study was to verify the occurrence and effect size of relative age effect in professional futsal players, by observing how its presence and impact change according to the season, team level and player position. The sample was composed of 1873 professional futsal players who played in the First Division of the Spanish National Futsal League between seasons 2006-2007 and 2014-2015. The players’ birthdates were divided into quarters (Q1, Q2, Q3 and Q4). A relative age effect reversal was observed in the professional futsal players for the nine analyzed seasons. A relative age reversal effect was observed in high and medium level teams. Finally, a relative age effect reversal was also found for the goalkeeper and pivot positions. The results could suggest that players that initially experienced maturity disadvantages in major sports, can have a second chance to emerge in professional minor sports (i.e. futsal vs. soccer). However, the underlying mechanisms why a reversal occurs are still unclear, and more studies focusing on the mediators of the effect are needed.

Introduction

Sports institutions have generally opted for annual age-grouping as an organizational strategy in order to maintain competitive parity and a correct development of athletes (Musch and Grondin, 2001). This situation can cause an age difference of nearly 12 months between those born immediately after the cut-off date and those born immediately before. The age difference between players born in the same year is known as the "relative age" (RA) (Barnsley and Thompson, 1988; Barnsley et al., 1992) and the impact of RA on performance and participation (whether being relatively younger or older affects performance and participation) is known as the "relative age effect" (RAE) (Barnsley et al., 1992).

The RAE has been extensively researched as a factor that can influence selection and talent identification in team sports (Rađa et al., 2018). Researchers have studied this phenomenon in various team sports such as soccer (Padrón-Cabo et al., 2016), basketball (García et al., 2014), rugby (McCarthy and Collins, 2014), handball (Schorer et al., 2009, 2013) and cricket (McCarthy et al., 2016); and RAE has been proven to be a potential talent selection bias in different modalities (Schorer et al., 2013). Pre-established models give special importance to physical and conditioning variables (Abbott and Collins, 2002). This might be one of the causes why relatively older players seem to perform better in the selection process in comparison to relatively younger players, leading to a higher selection success rate (Malina et al., 2004).

Different studies have shown that the advantage generated by the RAE during the selection and identification phases seems to be reversed at the end of the development process (McCarthy et al., 2016; McCarthy and Collins, 2014). In this sense, a study by McCarthy et al. (2016) suggests that when athletes are transitioning to elite-level sport, RAE decreases, and it can even be reversed. In this approach, a recent investigation on North American professional leagues observed that younger athletes (players who were born closer to the cutoff date) had longer professional careers when compared to older peers (Steingröver et al., 2016). Likewise, Ashworth and Hendels (2007) presented a theoretical model in which players born closer to the cut-off date earn systematically more money than older peers in the cohort. The RAE reversal during the identification and talent selection phases has been labeled the “underdog effect” (Gibbs et al., 2012) or a “reversal of relative age advantage” (McCarthy et al., 2016). Notwithstanding, the conversion ratio of junior to elite players was greater for those who were born closest to the cut-off date (Q₃ and Q₄).

Despite futsal’s popularity and the media impact of some of its major competitions, little research has been done on it, even more so if compared to the sport it originated from, i.e. soccer. Most research articles have addressed physiological demands during match play showing that futsal, like other team sports, may be classified as an intermittent high-intensity sport with frequent occurrence of short sprints (Beato et al., 2016; Matzenbacher et al., 2014). Some studies have analyzed performance variables such as sprint, jump, repeated sprint ability or kicking performance in youth futsal players (Ayarra et al., 2018), but only with regard to semi-professional players. However, there has been no research yet concentrating on the selection process in youth futsal players.

As mentioned before, the RAE is considered a potential bias in the process of identifying talent. Over the years, research on sporting expertise has consistently been revealing asymmetric birthdate patterns within different team sports (Delorme and Raspaud, 2009; McCarthy and Collins, 2014). Recognizing the RAE has important implications for all sports, due to its influence on talent identification, sport systems, practitioners and athletes (Cobley et al., 2018; Sarmento et al., 2018). In other words, intensive early talent identification processes that put more importance on physical attributes than technical skills could reduce the opportunities of younger players to be selected and reduce the extension of the talent pool. Nevertheless, to the best of our knowledge, previous research has not analyzed the RAE in elite professional futsal players. Spain has a long tradition of futsal: the Spanish National Team has won two World Cups and seven UEFA Futsal Championships, and the Spanish First Division is considered one of the most important futsal leagues in the world. Thus, the aim of this study was to verify the occurrence and effect size of the RA in professional futsal players of the Spanish First Division, by observing how its presence and impact changed according to the season, the team level and the player position.

Methods

Sample

The sample of this study was composed of all players who participated in First Division of the National Futsal League, known by its Spanish acronym LNFS, between the 2006-2007 and the 2014-2015 season. This strategy to pool different seasons together has been widely adopted in previous studies (Bjerke et al., 2017; Fumarco et al., 2017; Medic et al., 2007) in an attempt to increase the statistical power of the analysis. In addition, taking into account that relatively younger players have longer careers (Gibbs et al., 2012), we decided not to consider only one observation per player not to provide more observations for relatively young players than older peers, which could lead to spurious lack of evidence of the RAE. A total of 1873 professional futsal players [1477 (79%) from UEFA (Europe) confederation, 380 (20%) from CONMEBOL (South America) confederation, and 16 (1%) from other confederations] and their dates of birth were recorded (Table 1). The information was collected from various public internet sources and then anonymized; therefore, informed consent from the participants was not required.

Table 1.

Number of players analyzed by season and playing position.

	Playing Position
Season	Goalkeeper	Defender	Winger	Pivot	Total
2006-2007	31	39	68	45	183
2007-2008	42	39	76	49	206
2008-2009	38	43	92	28	201
2009-2010	39	45	86	35	205
2010-2011	40	47	90	42	219
2011-2012	41	43	95	39	218
2012-2013	37	39	92	35	203
2013-2014	41	42	90	38	211
2014-2015	40	40	104	43	227
Total	349	377	793	354	1873

Design and procedures

The present study was observational research. For each professional futsal player, the birthdate, player position and level of their futsal team were recorded. Birthdates were categorized into four age quarters according to their birth months (Helsen et al., 2012; Romann et al., 2018). January 1^st was used as the cut-off date for the competition categories in futsal, thus, the months were split into quarters to calculate the RA as follows: players born during the months of January, February and March constituted the first quarter (Q₁); players born in the months of April, May and June composed the second quarter (Q₂); the third quarter (Q₃) consisted of players born in July, August and September; finally, the fourth quarter (Q₄) was composed of all futsal players born in October, November and December.

The team level made reference to the qualifying position the player’s team reached at the end of each season. Teams were classified into 3 groups according to criteria used by Vogelbein et al. (2014): high (teams that qualified to play-offs during the regular season), medium (teams that did not qualify to playoffs, neither ended in the relegation zone) and low (teams which ended in the relegation zone or were relegated to the Second Division).

As previously proposed (Burdukiewicz et al., 2014), professional futsal players were classified according to their specific position as “defender”, “winger”, “pivot” and “goalkeeper”. The position of players in our sample corresponds to the information provided by the official webpage of LNFS (www.lnfs.es), which classifies players according to their skills and tactical profiles.

The data of this research were obtained from public official websites of participating teams, in combination with information from the official website of LNFS (www.lnfs.es). All players belonging to first teams were included in this study.

Statistical analysis

Data analysis was performed using the SPSS statistical package for Macintosh (version 20.0, Chicago, IL, USA). The chi-squared (χ²) test was carried out to analyze the difference between the birth-date distribution in Q₁, Q₂, Q₃, and Q₄ and a uniform distribution. In addition, the same statistical test was used to investigate the difference in birth-date distribution in relation to each positional role and team level. Due to the fact that a substantial portion of futsal players selected in the present study was foreign, we decided to compare players’ birth-dates with a uniform distribution. At present, various studies adopt the theoretical assumption that births are distributed evenly in all quarters (25 percent per quarter) (Helsen et al., 2005). This hypothesis should be taken as valid, since in most countries dates of births are equally distributed throughout the year, and there are no significant seasonal variations (Roenneberg and Aschof, 1990).

As the chi-squared test appeared to be significant, the corrected residuals (z-value) were calculated according to Beasley and Schumacher (1995). When z-value was less than -1.96 or greater than 1.96 it was considered significant. When the degrees of freedom (df) were above 1 the statistical index to determine the size of the effect was Cramer's V (V) (Aron et al., 2002); in the opposite case the φ coefficient was used. For chi-squared analysis, the magnitude of the effect size was measured by calculating Cramer’s V. According to Cramer (1999), if df = 3 (in all comparisons between birthdate quarters), V = 0.06 to 0.17 described a small effect, V = 0.18 to 0.29 described a medium effect and V ≥ 30 a large effect. Statistical significance was set at p < 0.05.

Results

The distribution across quarters of 1873 futsal players of the 2006-2007 to 2014-2015 seasons of LNFS is depicted in Figure 1. No homogeneous distribution was observed for any of the groups (Q₁, Q₂, Q₃ and Q₄). Consequently, the results showed an overrepresentation of players born during the last quarters of the year (Q₃ = 26.4%; Q₄ = 27.1%), as well as a reduced presence of players born closest to the beginning of the year (Q₁ = 22.0%; Q₂ = 24.6%). Therefore, a RAE reversal was visible for LNFS players χ² (3, N = 1873) =11.525, p = 0.01.

Figure 1.

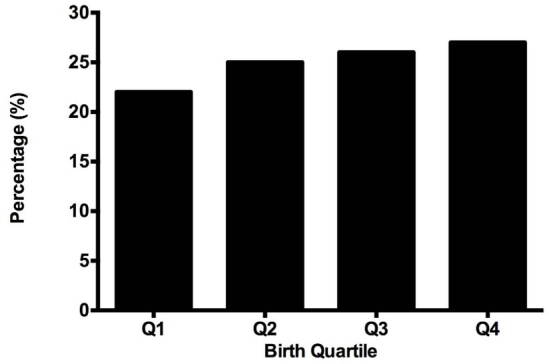
Distribution of birthdates of 1873 futsal players between the 2006-2007 and 2014-2015 seasons.

Table 2 shows the birthdate’s distribution in quarters for each of the nine analyzed seasons. Only the 2007-2008 season showed a significant effect on the RA (p = 0.04). For the 2007-2008 season (V = 0.21), an average effect size on the RA is observed; that is, there was an overrepresentation of players born closer to the end of the year. Furthermore, when the chi-squared (χ²) was significant, Z-values were used. Q₂ from the 2007-2008 season (z-value = -2.0) was far from the average value compared to the rest of the analyzed seasons for this quarter. In the 20072008 season, there were much fewer players born in Q₂ than in any of the other analyzed seasons.

Table 2.

Distribution of birthdates subdivided by season.

		Q1			Q2			Q3			Q4
Variable	n	%	z- value	n	%	z- valu e	n	%	z- valu e	n	%	z-valu e	χ2	df	p	V	OR Q1/Q4
														24		0.08
Season													14.70		0.93
			-0.4			0.9			0.1	46	25.1	-0.6		3		0.10	0.83
2006-2007	38	20.8		50	27.3		49	26.8					1.94		0.59
			-2.0*			0.4			0.8	60	29.1	0.7		3		0.21	0.57
2007-2008	34	16.5		53	25.7		59	28.6					8.49		0.04
			0.0			-0.8			1.0	53	26.4	-0.2		3		0.12	0.83
2008-2009	44	21.9		45	22.4		59	29.4					3.00		0.39
			0.5			0.1			0.7	48	23.4	-1.2		3		0.07	1.00
2009-2010	48	23.4		51	24.9		58	28.3					1.30		0.73
			-0.9			0.5			0.0	61	27.9	0.3		3		0.13	0.70
2010-2011	43	19.6		57	26.0		58	26.5					3.52		0.32
			0.0			-0.1			-0.7	64	29.4	0.8		3		0.11	0.75
2011-2012	48	22.0		53	24.3		53	24.3					2.51		0.47
			1.3			-0.8			-1.4	61	30.0	1.0		3		0.13	0.85
2012-2013	52	25.6		45	22.2		45	22.2					3.40		0.33
			-0.1			0.2			-0.1	57	27.0	0.0		3		0.08	0.81
2013-2014	46	21.8		53	25.1		55	26.1					1.30		0.73
			1.5			-0.5			-0.3	57	25.1	-0.7		3		0.04	1.04
2014-2015	59	26.0		53	23.3		58	25.6					0.37		0.95

Notes: χ² = test value of the chi-square test; p = level of significance; V = Cramer´s V; OR = Odds Ratio; Z-values indicate if the observed count within a specific cell is significantly larger or smaller than the expected count. * Significant difference.

Table 3 presents the distribution of birthdates in quarters according to the team level (high, medium, and low). The chi-squared test determined some statistically significant differences among the distributions in the quarters by the birthdate of players belonging to high, medium and low level teams (p = 0.004, V = 0.10). A significant reverse effect on RA was found for the medium (p = 0.03) and high (p < 0.001) level teams. Likewise, in high (V = 0.14) and medium (V = 0.11) level teams, there was a minor RAE. Nonetheless, the distribution in quarters by date of birth for low level teams (p = 0.29) proved no effect on the RA, hence there was a homogeneous distribution in quarters by birthdate for low level teams. Moreover, z-values show that average values for Q₂ in medium level teams (z-value = 2.8) and for Q₃ in high level teams (z-value = 2.1) are higher than average values for the same quarter for the other level teams. In other words, medium level teams had a greater number of players born in Q₂, and high level teams had a greater number of players born in Q₃. Conversely, atypical values were found regarding the average Q₂ values for high level teams (z-value = -4.2). That is, high level teams had much fewer players born in Q₂ than medium and low level teams, showing the reversal effect for medium level teams.

Table 3.

Distribution of birthdates subdivided by team level.

		Q1			Q2			Q3			Q4
Variable	n	%	z-value	n	%	z-value	n	%	z-value	n	%	z-value	χ2	df	p	V	OR Q1/Q4
															0.00	0.1
Team Level													19.05	6	4	0
			0.0			2.2			-0.9	58	23.	-1.3			0.29	0.1	0.93
Low	54	22. 0		74	30. 2		59	24. 1			7		3.77	3		2
			-1.1			2.8*			-1.6	182	26.	-0.1			0.03	0.1	0.76
Medium	13 9	20. 6		191	28. 3		164	24. 3			9		9.34	3		1
			1.1			-			2.1*	267	28.	-1.0			<0.0	0.1	0.82
High	21 9	23. 0		195	20. 5	4.2*	271	28. 5			0		17.39	3	01	4

Notes: χ² = test value of the chi-square test; p = level of significance; V = Cramer´s V; OR = Odds Ratio; Z-values indicate if the observed count within a specific cell is significantly larger or smaller than the expected count. * Significant difference

This study also examined the distribution in quarters depending on the futsal players’ specific field position. Statistically significant differences, which can be seen in Table 4, were noted (p < 0.001) depending on the futsal players’ field position. An uneven distribution was evident depending on the birthdate quarters for goalkeepers (p < 0.001) and pivots (p = 0.02). Regarding the goalkeeper position, the RAE was average (V = 0.29), while for pivots, a much fewer effect was observed (V = 0.17). For both the goalkeeper and the pivot positions, the obtained average values in Q₁ (z-value = -4.4) and Q₂ (z-value = 3.3) were much higher than the values obtained for these quarters for wingers and defenders.

Table 4.

Distribution of birthdates subdivided by playing position.

		Q1			Q2			Q3			Q4
Variable	n	%	z-value	n	%	z-value	n	%	z-value	n	%	z-value	χ2	df	p	V	OR Q1/Q4
															<0.00	0.1
Playing Position													40.29	9	1	5
			1.0	1		2.3			-0.6	81	21.	-2.7			0.20	0.1	1,12
Defender	91	24. 1		1 0	29. 2		95	25. 2			5		4.61	3		1
			1.0	1		-2.0			0.5	220	27.	0.6			0.06	0.1	0.83
Winger	18 3	23. 1		7 6	22. 2		214	27. 0			7		7.31	3		0
			2.0*			-			0.2	103	29.	1.0			0.02	0.1	0.89
Pivot	92	26. 0		6 4	18. 1	3.1*	95	26. 8			1		9.78	3		7
			-4.4*	1		3.3*			-0.3	103	29.	1.1			<0.00	0.2	0.45
Goalkeeper	46	13. 2		1 0	31. 5		90	25. 8			5		28.36	3	1	9

Notes: χ² = test value of the chi-square test; p = level of significance; V = Cramer´s V; OR = Odds Ratio; Z-values indicate if the observed count within a specific cell is significantly larger or smaller than the expected count. * Significant difference

Discussion

The RAE has been widely studied in team sports (García et al., 2014; Rađa et al., 2018). However, to our knowledge, there have been no previous studies on the RAE in an emergent sport such as futsal. For this reason, the purpose of this study was to analyse the RAE in professional futsal players. The main findings of the present study are the following: (a) a RAE reversal in professional futsal players for the nine analyzed seasons was observed, (b) a RAE reversal was present for high and medium level teams, and (c) a RAE reversal was found for pivots and goalkeepers. This means that professional players who were born closest to the cut-off date were slightly overrepresented in these situations.

The RAE reversal was present among professional players that played in LNFS from the 2006-2007 to the 2014-2015 season, since there was a small overrepresentation of players born in the last quarters of a natural year (Q3 and Q4). Other team sports have also evidenced a RAE reversal in professional players (Gibbs et al., 2012; McCarthy et al., 2016; McCarthy and Collins, 2014). Gibbs et al. (2012) studied the progress of the RAE, by comparing the RAE in junior hockey players, players who were selected in the Entry Draft’s first round, and elite players. Results indicated the presence of RAE in the junior category and in the first Draft’s rounds. However, the RAE was reversed in players who competed for the National Hockey League. Other recent studies on team sports like cricket and rugby (McCarthy et al., 2016; McCarthy and Collins, 2014) evidenced a talent identification phase distorted by RAE. Notwithstanding, the conversion ratio of junior to elite players was greater for those who were born closest to the cut-off date (Q3 and Q4). Therefore, the advantage generated by the RAE during the selection and identification phases seemed to be reversed at the end of the development process.

Previous studies have shown that the RAE reversal, also called the “underdog-effect” (McCarthy and Collins, 2014), could be related to factors such as the sport’s popularity within a concrete region or physiological and psychological conditions (Côté et al., 2006; McCarthy and Collins, 2014; Musch and Grondin, 2001). In Spain, futsal is less popular than soccer, taking into account the broad differences in the number of federated players in both sports. Often, young players are reported to arrive in futsal after a period in soccer. Jovanovic et al. (2011) confirm that most futsal players begin their training in the “big soccer” school and, as the training process progresses, they change to futsal. In this context, the RAE reversal found in the present study may be interpreted as the result of a “strategic adaptation” used by relative younger children (Jovanovic et al., 2011) who change from one sport to another after failing in disciplines in which developed physical attributes are important (Delorme and Raspaud, 2009).

Other compelling justifications have been highlighted in the literature to explain why a RAE reversal might occur. In this regard, psychological mechanisms have been examined in detail so as to find an explanation for the RAE’s presence among professional players. McCarthy and Collins (2014) suggested that players belonging to Q3 and Q4 could perceive more competence, and this perception could act as a mechanism to develop coping strategies that led to greater “mental toughness” and resilience (Collins and MacNamara, 2012). During the initial stages, players belonging to Q1 and Q2 are more advanced at anthropometric and physiological levels (Carling et al., 2009; Helsen et al., 2000). This edge in development may result in a competitive advantage, which gives these players a greater chance of being identified as talented and, consequently, being selected to play for higher level teams (Sherar et al., 2007). Then, the highest RA players will benefit from more resources, better coaches and be able to compete against rivals of higher level (Musch and Grondin, 2001). Nevertheless, the conversion ratio seems to indicate that, although fewer players born in the last quarters of the year are selected during talent identification processes, the total opposite situation occurs in professional categories, where the presence of players born in Q3 and Q4 is higher. This fact could suggest that as differences in the anthropometric and physiological variables fade, so does the advantage of Q1 and Q2 players. At this stage, there is an increase in the number of players belonging to Q3 and Q4 who achieve being part of the elite. A possible cause for this would be that differences in the maturing process between the players who were born at the beginning of the year and those who were born closest to the cut-off date have disappeared by the time players reach the elite. Consequently, they are nonexistent in data samples of players from an elite competition. Nevertheless, considering futsal, Sarmento et al. (2018) suggest other types of constraints, such as popularity, family, coach influences or training time as more influential in the selection process that anthropometric or RA factors. Moreover, talented age-players who were born late may tend to change from an initial interest in soccer to futsal, which is a similar but less popular sport with fewer competitive demands (Romann et al., 2018). Further research on this sport modality should confirm if the RAE reversal is already present in the talent identification phase, if the RAE is reversed when players reach the elite level or if RAE reversal was only a result during these seasons.

Regarding our second finding, previous literature has demonstrated that the RAE could be related to the teams’ performance. The RAE in professional soccer players has been present in the final rounds of the UEFA European Championship and the magnitude of the phenomenon is greater the closer teams reach the final championship rounds (Romann et al., 2018). Nevertheless, other studies with soccer players have positively tested the RAE in all teams regardless of their performance level during a competition (Padrón-Cabo et al., 2016; Williams, 2010). In futsal, our results seem to indicate the existence of an uneven distribution between quarters according to the team level: it seems to be an overrepresentation of players belonging to the last quarters of the year in medium and high level teams. These results are partially in agreement with previous investigations (Fumarco et al., 2017; Gibbs et al., 2012) and might be suggestive of the possibility that relatively younger players perform better, that is the more relatively young players a team has the better is performance of the team (Fumarco et al., 2017). However, future works are necessary to verify this hypothesis.

Players in futsal are assigned a specific position in the field according to their anthropometric characteristics, as well as their technique and tactics, in a similar way to other sports teams (Beato et al., 2016; Matzenbacher et al., 2014). The analysis by field position proves the presence of a RAE reversal in pivots and goalkeepers. In the pivot position, and despite the discovered RAE reversal, there was an overrepresentation of players born in Q1 as compared to the rest of analyzed field positions. In futsal, pivots are usually players with greater weight and body mass index in comparison to the rest of the field positions (Ramos-Campo et al., 2014), thus explaining this overrepresentation. The process of players transition from soccer to futsal might provide a background to the RAE reversal in the goalkeeper position. In soccer, the goalkeeper and defender are the specific positions with greater RAE magnitude (Salinero et al., 2013). In other words, soccer goalkeepers who were born in the beginning of the year have more chances of being selected to higher level teams during the selection and talent identification phases. This trend in soccer might produce the reverse effect in futsal, encouraging goalkeepers who were born closer to the cut-off date, and who are less likely of being selected in soccer, to move to another sport.

Conclusions

The RAE represents a severe problem in team sports because many talented players are lost in selection processes and cannot fulfill their potential. Thus, the influence of RAE must be evaluated for each sport. In the present study, a slight RAE reversal was observed in professional futsal players, with an overrepresentation in players born closest to the cut-off date. This overrepresentation was more evident in medium and high level teams and in specific playing positions such as pivots and goalkeepers. These results may support an ‘underdog effect’ hypothesis, where the relatively younger players were more likely to achieve senior professional status. However, the underlying mechanisms why a RAE reversal occurs are still unclear, and more studies focusing on the mediators of the effect are needed to examine the consistency of the trends observed in this study. For these reasons, our results should be interpreted carefully. Partially, on the basis of our data and the regional context, the present findings may be interpreted as the result of a strategic adaptation used by relatively younger players who move from a more popular sport to another similar one, yet less popular, after failing in the discipline in which developed physical attributes are more advantageous.