Application of Individualized Speed Zones to Quantify External Training Load in Professional Soccer

Abstract

This study aimed to examine the interchangeability of two external training load (ETL) monitoring methods: arbitrary vs. individualized speed zones. Thirteen male outfield players from a professional soccer team were monitored during training sessions using 10-Hz GPS units over an 8-week competitive period (n = 302 observations). Low-speed activities (LSA), moderate-speed running (MSR), high-speed running (HSR) and sprinting were defined using arbitrary speed zones as <14.4, 14.4–19.8, 19.8–25.1 and ≥25.2 km·h-1, and using individualized speed zones based on a combination of maximal aerobic speed (MAS, derived from the Yo-yo Intermittent recovery test level 1), maximal sprinting speed (MSS, derived from the maximal speed reached during training) and anaerobic speed reserve (ASR) as <80% MAS, 80–100% MAS, 100% MAS or 29% ASR and ≥30% ASR. Distance covered in both arbitrary and individualized methods was almost certainly correlated in all speed zones (p < 0.01; r = 0.67-0.78). However, significant differences between methods were observed in all speed zones (p < 0.01). LSA was almost certainly higher when using the arbitrary method than when using the individualized method (p < 0.01; ES = 5.47 [5.18; 5.76], respectively). Conversely, MSR, HSR and sprinting speed were higher in the individualized method than in the arbitrary method (p < 0.01; ES = 5.10 [4.82; 5.37], 0.86 [0.72; 1.00] and 1.22 [1.08; 1.37], respectively). Arbitrary and individualized methods for ETL quantification based on speed zones showed similar sensitivity in depicting player locomotor demands. However, since these methods significantly differ at absolute level (based on measurement bias), arbitrary and individualized speed zones should not be used interchangeably.

Introduction

The use of global positioning system (GPS) technologies for monitoring players’ external training load (ETL) has markedly increased over the last decade among soccer practitioners. A wide range of GPS metrics is currently available from which coaches can be objectively informed and subsequently adjust training programs. The amount of activity performed by the players is commonly quantified using arbitrary (player-independent) speed zones (Akenhead and Nassis, 2016). Despite the inherent information available from distance covered within arbitrary speed zones, this method is biased by the potential players’ diversity within a team (e.g. fitness, age, training experience, injury history), consequently masking individual capacities and thus neglecting ETL imposed on the individual player. The use of individualized (player-dependent) speed zones has recently therefore been proposed for quantifying ETL, reducing the confounding effect of between-player variation in physical capacity (Abbott et al., 2018; Hunter et al., 2015; Mendez-Villanueva et al., 2013).

Individualized speed zones rely on fitness test data, such as measures of cardiorespiratory fitness. Thus, recent studies have adopted incremental field tests to indirectly compute athletes’ maximal aerobic speed (MAS) (Abbott et al., 2017; Fitzpatrick et al., 2018). MAS is very strongly correlated to maximal oxygen uptake and, in conjunction with maximal sprinting speed (MSS), allows calculation of the anaerobic speed reserve (ASR) that accounts for the transition from high-speed running to sprinting (Hunter et al., 2015). However, direct measurements of cardiorespiratory fitness are time-consuming, expensive, require access to equipment uncommon for lower-level clubs and lack ecological validity (Abbott et al., 2018; Lovell and Abt, 2013). The Yo-Yo intermittent recovery test – level 1 (YYIR1) is widely employed by soccer practitioners to profile soccer players’ prolonged intermittent exercise capacity and subsequently estimate MAS. In particular, the YYIR1 involves an essential neuromuscular component imposed by shuttle running, thus better reflecting the physical demands of soccer (Castagna et al., 2006). However, to the best of our knowledge, only one study has attempted to individualize ETL data by deriving individual MAS from the YYIR1 (Scott and Lovell, 2018). In addition, previous studies have predominantly used a single fitness component to adjust ETL data to individual fitness levels, with limited research using a combination of capacities (Abbott et al., 2017, 2018; Fitzpatrick et al., 2018). Considering MSS or MAS independently to analyze ETL data would result in a misunderstanding of TL data (Hunter et al., 2015). Indeed, a combined approach to quantifying ETL data that incorporates fitness data from field-based tests to estimate players’ MAS and MSS provides a more accurate definition of speed zones than a single fitness component (Hunter et al., 2015).

Individualized ETL was shown to give a detailed insight into players’ activity, but there is limited research regarding the validity of this method (Abbott et al., 2018; Hunter et al., 2015). In addition, information regarding the degree of association and agreement between individualized and arbitrary speed zones is still unknown. Previous agreement-type studies in professional soccer have focused on composite ETL variables such as metabolic power (Castagna et al., 2017; Gaudino et al., 2013). Differences between ETL using arbitrary and individualized thresholds have been previously documented using laboratory tests (Abbott et al., 2018; Hunter et al., 2015; Nakamura et al., 2017). Also, previous studies individualizing ETL data have been predominantly conducted in young athletes (Abt and Lovell, 2009; Hunter et al., 2015; Lovell and Abt, 2013; Mendez-Villanueva et al., 2013) with scarce information available for professional players. Moreover, the aforementioned studies focused on competition only and, to the best of our knowledge, only two studies analyzed individualized training ETL (Abbott et al., 2017, 2018). Beyond the well-established importance of accounting for individual capacities when interpreting ETL data, the actual superiority of individualized versus arbitrary ETL has yet to be investigated. With this in mind, it is appealing to analyze ETL in soccer practice sessions taking into consideration individual physical capacity.

Therefore, we aimed to examine the interchangeability of two ETL monitoring methods (arbitrary vs. individualized speed zones) in a group of professional soccer players.

Methods

The present study was conducted under non-experimental conditions as the technical staff and participants did not receive any input from the research team. Training contents were described according to the typical weekly training schedule and associated daily activities. For the description, we considered each training day according to its temporal distance from the match day (MD):

• MD+1 (Sunday): Static stretching and recovery training for starting players (>45 min game-time); dynamic stretching, small-sided games (ball possession) and cardiorespiratory endurance training for non-starting players (≤45 min game-time).

• MD+2 (Monday). Day off.

• MD-4 (Tuesday): Technical skills warm-up, team tactics (e.g. 10 vs. 10 full-sized game), cardiorespiratory endurance exercises, continuous regime small-sided games (pitch was commonly goal to halfway line as length and touchline to touchline as width).

• MD-3 (Wednesday): Dynamic stretching exercises, complex training, intermittent-regime small-sided games (commonly ball-possession without goalkeepers) with reduced pitch sizes (e.g. 3 vs. 3 to 5 vs. 5).

• MD-2 (Thursday): Technical skills warm-up, team tactics (e.g. 11 vs. 11 emphasising specific and expected game situations), free-kicks.

• MD-1 (Friday): Dynamic stretching, corners, free-kicks and pre-match activation (e.g. short skipping session).

• MD (Saturday): Official match.

Participants

During the 2016/17 season, twenty professional male soccer players competing in the Italy’s second-tier league (SerieBwin.it) were regularly monitored in the context of their training routines. Thirteen players (age, body height, body mass and senior experience [mean ± SD]: 25.8 ± 3.5 yrs, 181.5 ± 5.6 cm, 78.3 ± 5.9 kg, 7.3 ± 3.0 yrs) were considered for analysis. The distribution of players by their field position was as follows: central defenders (3), full-backs (2), central midfielders (3), wingers (2) and strikers (3). Goalkeepers and players who did not take part in field tests were excluded. At the end of the season, the club authorised the use of a dataset for research purposes wherever anonymity was ensured. The Ethical Committee of the Faculty of Sports, University of Poro, approved and recorded the study under CEFADE.08.2018.

Measures

Data collection was carried out over an 8-week period of the competitive season between January and March 2017. Physical testing was conducted in September 2016, corresponding to the start of the competitive period. Forty-five training sessions (including three friendly matches) were analyzed, resulting in 302 individual observations (median: 24 training sessions per player; range: 18–28). The quantification method was considered as independent variable, while distance covered within given speed zones were adopted as dependent variable.

Procedures

Testing

The YYIR1 was performed on a natural grass pitch where the team usually conducted its training sessions. The YYIR1 required repeated 2 × 20 m runs (shuttles), separated by a 10 s rest period, between the start and finish line at progressively increased speeds controlled by audio beeps from a tape recorder (Bangsbo et al., 2008). The aim of the test was to perform as many shuttles as possible. When the player twice failed to reach the finish line in time, the distance covered was recorded to estimate MAS using a generic prediction equation (Kuipers et al., 1985), namely:

MAS = speed at the last uncompleted stage (km∙h-¹) + 0.5 × (n/8)

where n = the number of runs completed in the last stage from 14.5 km∙h^-1.

Sprint testing was not part of team assessment. Speed reached during training or matches can be affected by the type of exercise and various situational factors. However, recent findings observed a large relationship (r = 0.84) and trivial bias (~0.30 km∙h^-1) between peak speed obtained by timing gates over a 40 m sprint and peak speed obtained by GPS devices (Massard et al., 2018). MSS was therefore obtained from the GPS by extrapolating raw data for speed and the highest value (in km∙h^-1) recorded throughout the data collection period was retained as individual MSS.

The ASR was determined as the difference between MSS and MAS, and expressed in km∙h^-1, as previously reported (Bundle et al., 2003; Mendez-Villanueva et al., 2013).

External training load monitoring

The ETL was monitored using unobtrusive portable 10-Hz GPS units (BT-Q1000 Ex, QStarz, Taiwan). The mean number of satellites during data collection was 14 ± 1, and the mean horizontal dilution of position was 0.7 ± 0.1. The system used the GPS Doppler data, and distances were calculated from changes in position and, subject to the manufacturer’s proprietary algorithm, integrated to reduce measurement error. A vest was tightly fitted to each player to place the receiver between the scapulae. The accuracy of 10-Hz GPS devices has been previously examined, giving an inter-unit coefficient of variation <5% (Coutts and Duffield, 2010). All devices were always activated 15 min before data collection to allow acquisition of satellite signals in accordance with the manufacturer’s instructions. Also, to avoid inter-unit error, players wore the same GPS device for all training sessions. Total distance and distance covered in each speed zone were calculated using a custom Excel spreadsheet from instantaneous raw data of time, speed and distance available from the manufacturer’s software, and the minimum effort duration was 0.2 s. This analysis process was repeated twice, once applying global speed thresholds and once applying individual speed thresholds.

Arbitrary speed zones were defined in accordance with previous reports for professional soccer players (Akenhead and Nassis, 2016), whereas individualized speed zones were based on a combination of players’ fitness components (Mendez-Villanueva et al., 2013). Four speed zones were established to describe ETL as: low-speed activities (LSA; arbitrary, <14.4; individualized, <80% MAS), moderate-speed running (MSR; arbitrary, 14.4–19.8 km∙h^-1; individualized, 80–99.9% MAS), high-speed running (HSR; arbitrary, 19.9–25.1 km∙h^-1; individualized 100% MAS – 29% ASR) and sprinting (arbitrary, ≥25.2 km∙h^-1; individualized, ≥30% ASR – 100% MSS).

The arbitrary >14.4 km∙h^-1 is supposedly slightly below the average MAS in professional soccer players (~16 km∙h^-1; Osgnach et al., 2010), consequently enabling a direct comparison with the individualized threshold of 80% MAS. To remove the effect of situations in which players were standing (e.g. receiving instructions from coaches, hydration break, static stretching exercises), ETL was reported as a percentage of total distance covered during the training session.

Statistical analysis

To characterize the variability between participants, the coefficient of variation (CV) between players was calculated by dividing SD by the mean and then multiplying by 100, according the different quantification methods. Additionally, in order to provide practical indications of changes in ETL metrics, the smallest worthwhile change (SWC) was calculated by multiplying 0.2 by the within-subjects SD (Hopkins et al., 2009). Average biases were reported as absolute differences between values. Within-participant correlations with associated 90% confidence intervals (90% CI) were calculated between ETL quantification methods for all variables (Bland and Altman, 1995). This approach quantifies the correlation between a covariate and outcome while taking into account the longitudinal nature of the study design removing the variation between participants. The magnitudes of correlations were qualitatively considered as: trivial (r ≤ 0.1), small (r = 0.1–0.3), moderate (r = 0.3–0.5), large (r = 0.5–0.7), very large (r = 0.7–0.9) and almost perfect (r ≥ 0.9) (Hopkins et al., 2009).

Differences between quantification methods were analyzed using a linear mixed model with unstructured covariance, taking into consideration the fact that the participants differed in respect of the number of training sessions in which they participated (Cnaan et al., 1997). The quantification methods were set as fixed effects, individual participants were set as random effects, training contents was set as a covariate, and distance covered in each speed zone was the dependent variable. Differences between methods were quantified using effect sizes (ES) according to Hopkins et al. (2009), namely: trivial (ES < 0.2), small (ES = 0.2–0.6), moderate (ES = 0.6–1.2), large (ES = 1.2–2.0), very large (ES = 2.0–4.0) and huge (ES > 4.0). When 90% confidence intervals overlapped positive and negative values, the effect was deemed to be unclear. Otherwise, the effect was deemed to be the observed magnitude (Batterham and Hopkins, 2006). Quantitative probabilities were evaluated qualitatively as almost certainly not (<1%), very unlikely (1–5%), unlikely (5–25%), possibly (25–75%), likely (75–95%), very likely (95–99%) and almost certainly (>99%) (Batterham and Hopkins, 2006). If the probabilities of the effect being higher or lower than the smallest worthwhile difference were simultaneously >5%, the effect was deemed to be unclear.

Descriptive data were reported as the mean ± SD. Significance was set at p < 0.05. Data analysis was performed using Statistical Package for Social Science software (version 23, IBM SPSS Statistics, Chicago, IL, USA) and a modified statistical Excel spreadsheet (Hopkins, 2007).

Results

Players’ estimated MAS was 17.7 ± 0.6 km∙h^-1 based on distance covered in the YYIR1 of 2289 ± 384 m, and their MSS was 31.1 ± 0.9 km∙h^-1. A detailed representation of individual players’ speed zones is shown in Figure 1. A representation of the within-weekly ETL distribution is shown in Figure 2.

Figure 1.

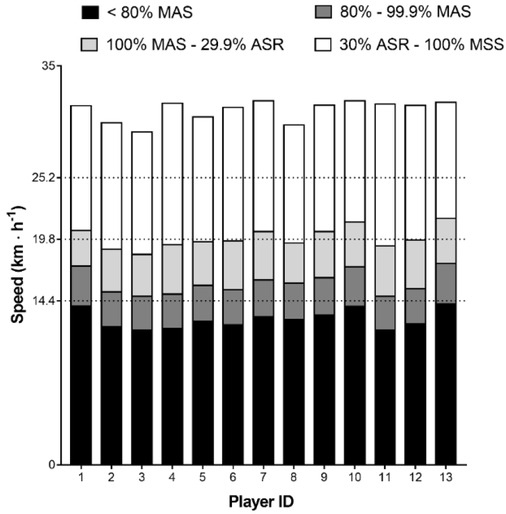
Graphical representation of the arbitrary and individualized speed zone of each player MSS = maximal sprinting speed, ASR = anaerobic speed reserve, MAS = maximal aerobic speed. Dotted lines delimitate arbitrary speed zones.

Figure 2.

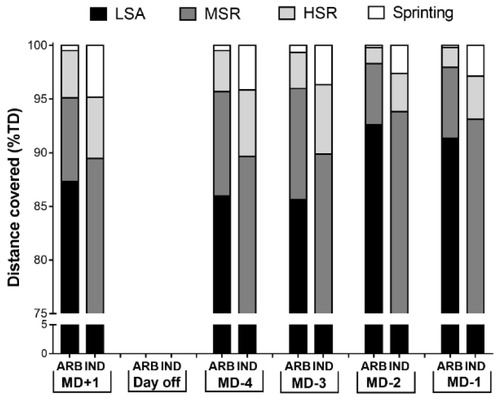
Within-weekly external training load distribution quantified using two methods. ARB = arbitrary speed zones, IND = individualized speed zones, LSA = low-speed activities, MSR = moderate-speed running, HSR = high-speed running, SR = sprinting, MD = match-day, TD = total distance covered

Average total distance covered during training was 6.598 ± 1.136 m (range: 3801–9585 m). In all variables, all measurement biases were higher than the SWC (Table 1). Distance covered in both arbitrary and individualized methods was almost certainly correlated in all speed zones (p < 0.01; r = 0.67-0.78; Figure 3).

Table 1.

External training load calculated using two different quantification methods in professional soccer (n = 302 training observations).

Method	Mean ± SD	Range	CV (%)	SWC
Low-speed activities
Arbitrary (%)	89.1 ± 6.9	54.3; 99.7	7.83	1.2
Individualized (%)	17.6 ± 17.1	1.1; 84.8	96.93	3.6
Bias (90% CI)	70.5 (44.4; 96.7)
Moderate-speed running
Arbitrary (%)	7.9 ± 4.2	0.2; 26.8	53.45	0.8
Individualized (%)	77.2 ± 18.7	14.2; 133.0	24.25	3.7
Bias (90% CI)	69.2 (38.9; 99.5)
High-speed running
Arbitrary (%)	2.6 ± 2.5	0.0; 16.9	96.50	0.5
Individualized (%)	4.9 ± 2.8	0.1; 18.4	56.95	0.5
Bias (90% CI)	2.3 (1.5; 6.2)
Sprinting
Arbitrary (%)	0.3 ± 0.7	0.0; 5.4	193.54	0.1
Individualized (%)	2.8 ± 2.7	0.0; 16.5	97.10	0.5
Bias (90% CI)	2.4 (2.0; 6.9)

CV = coefficient of variation, SWC = smallest worthwhile change.

Figure 3.

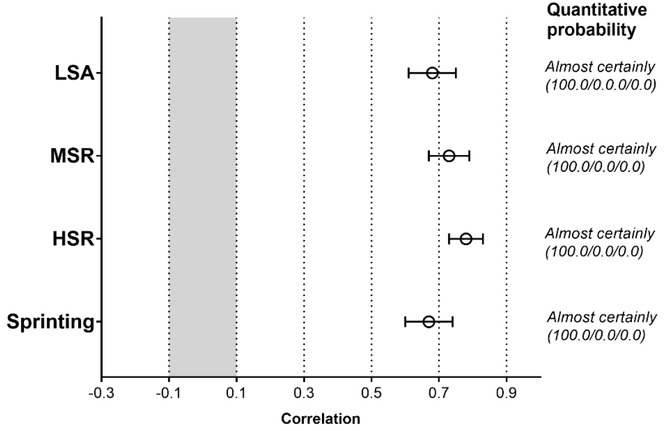
Within-subject correlations between distance covered in arbitrary and individualized speed zones (n = 302 training observations). LSA = low-speed activity, MSR= moderate-speed running, HSR = high-speed running. The grey-filled space represents an unclear correlation (p ≤ 0.05, r < 0.1). Dotted lines delimitate the magnitude of correlations.

There were no significant differences between the models with and without the effect of training contents for all ETL variables (p > 0.05). Significant differences between quantification methods were observed in all variables (p < 0.01). LSAs were almost certainly higher when using the arbitrary method than when using the individualized method (p < 0.01; ES = 5.47 [5.18; 5.76], respectively; Figure 4). Conversely, MSR, HSR and sprinting were higher when using the individualized method than when using the arbitrary method (p < 0.01; ES = 5.10 [4.82; 5.37], 0.86 [0.72; 1.00] and -1.22 [1.0; -1.37], respectively; Figure 4).

Figure 4.

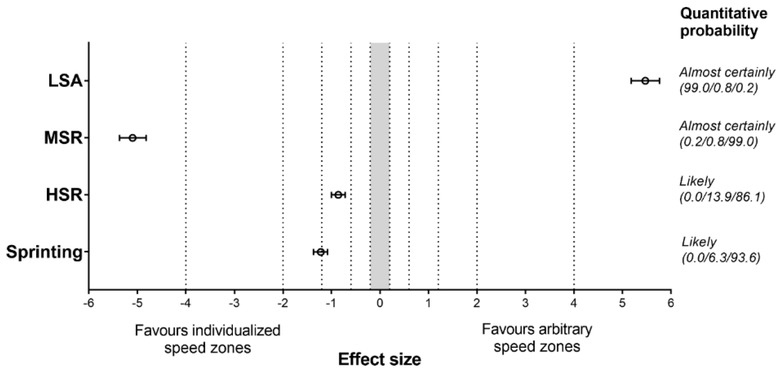
Differences between distance covered using arbitrary and individualized speed zones. LSA = low-speed activity, MSR = moderate-speed running, HSR = high-speed running. The grey-filled space indicates trivial differences (p ≤ 0.05, ES < 0.2). Dotted lines delimitate the magnitude of differences.

Discussion

In the current investigation, we evaluated the interchangeability of two ETL quantification methods in soccer, specifically arbitrary (player-independent) and individualized (player-dependent) speed zones. The main findings were the significant correlation between distance covered in arbitrary and individualized speed zones, although significant measurement bias was found between methods. These results suggest that arbitrary and individualized methods are similarly sensitive in depicting players’ locomotor profiles, but differ when accounting for the amount of activity performed.

Explorative data analysis showed large relationships (r = 0.67 to 0.78) between distance covered within arbitrary and individualized speed zones, indicating the feasibility of interchanging the methods at relative level. However, significant measurement bias (-69 to 70%) was observed between these ETL quantification methods. In fact, except for LSA (<14.4 km∙h^-1 and <80% MAS), distance covered was always higher when calculated with the individualized compared to the arbitrary method. This is in line with previous research conducted in soccer and rugby players, despite the different methodologies adopted (Abbott et al., 2018; Abt and Lovell, 2009; Gabbett, 2015; Hunter et al., 2015; Lovell and Abt, 2013; Nakamura et al., 2017). For instance, Hunter et al. (2015) showed that arbitrary speed zones, with emphasis on sprinting distance, underestimated distance covered compared to individualized speed zones based on laboratory measurements of heart rate deflection point and MSS. Other studies employed laboratory measurements of MAS and ventilatory threshold to individualize ETL characterization (Abt and Lovell, 2009; Lovell and Abt, 2013). The importance of individualizing ETLs taking into consideration MAS can likely be attributed to recent findings in ~17-yr-old soccer players showing that individualized methods based on MAS would solely improve the dose-response relationship between ETLs and cardiorespiratory adaptations (Fitzpatrick et al., 2018). Indeed, the authors showed that time spent above MAS was better associated with changes in MAS (R2 = 0.59) than time spent above 17 km∙h-1 (R2 = 0.37; Fitzpatrick et al., 2018).

Laboratory assessments have the advantage of standardizing measurement conditions, improving their accuracy. However, their employability could be argued as they lack the real-world linkage, being not completely interpretable in relation to the specific physical demands of the sport modality (Foster et al., 2017). It should be also pointed out that the studies above considered MAS per se to adjust ETL data (Abt and Lovell, 2009; Lovell and Abt, 2013). The players’ MAS does not take into account either the players’ capacity to perform short, intense actions or the transition from moderate- to high-intensity exercise domains. For instance, a powerful athlete (e.g. with high MSS) might not sustain high exercise intensity for long, as reflected by their intermittent endurance capacity. By contrast, MSS in isolation from sprint testing might not account for players’ capacity to maintain high velocities for prolonged periods. Indeed, a less powerful athlete may show a comparatively higher intermittent endurance capacity that enables them to run intensively more frequently, enter high-speed zones and recover quicker. To address the limitation associated with considering one fitness component only, we adopted an integrated approach, combining MAS and MSS, as previously documented (Hunter et al., 2015; Mendez-Villanueva et al., 2013).

In this study, the differences detected between methods were more evident in MSR that represented a zone comprising between 14.4 and 19.8 km∙h^-1 or 100% MAS and 29% ASR. Moreover, the results in sprinting suggest that arbitrary thresholds underestimate a significant proportion of distance covered by sprinting, which would represent a limitation when interpreting ETL data. This is supported by recent match-analysis reports in female soccer players, which observed a greater number of repeated sprint sequences using an individualized threshold of 90% MSS compared to an arbitrary threshold of 20 km∙h-1 (Nakamura et al., 2017). This is also supported by large associations between individualized sprinting time (≥30% ASR) and cardiorespiratory adaptations, compared to unclear associations when using an arbitrary threshold (21 km∙h-1; Fitzpatrick et al., 2018). Given that volume of sprinting has been linked to impaired muscle function (decreased isometric force, and increased creatine kinase activity and perceived muscle soreness) (Howatson and Milak, 2009), accurate quantification of sprinting activity would be of importance for assisting neuromuscular recovery monitoring.

Various significant limitations of the current investigation must be pointed out. Firstly, the players could not have attained their actual MSS during training. Indeed, previous studies have evaluated MSS using the best (lower time) 10 m stretch across a 40 m straight sprint (Mendez-Villanueva et al., 2013; Nakamura et al., 2017), which is considered the gold standard for measuring MSS. The relevance of sprint testing in soccer has been questioned in favor of MSS determination using GPS data during matches (Massard et al., 2018). However, those studies failed to include match ETL due to club decisions. Secondly, we analyzed a relatively small sample size (n = 302 training observations) compared to previous research adopting similar designs. For instance, a recent study by Abbott et al. (2018) compared ETL using arbitrary and individualized thresholds over 645 training sessions. Although a large-scale analysis such as one or multiple seasons would be necessary to generalize our findings, the results support previous findings showing that a significantly higher amount of high-intensity activity is accounted for when considering individualized speed zones (Abbott et al., 2018; Hunter et al., 2015). Moreover, it has been suggested that method agreement-type studies should involve at least 40 participants for adequate statistical accuracy (Atkinson et al., 2005). Despite the reduced sample size of this study (n = 13), repeated measurements on individual players increased statistical accuracy (Hopkins, 2000). Thirdly, neither arbitrary nor individualized speed zones account for the transition between speed zones, represented by accelerations and decelerations. This is of utmost importance given the significant physiological strain (e.g. increased blood lactate concentrations, mean heart rate and perception of effort, compared to constant-speed running) associated with changing speed (Akenhead et al., 2015). This provides justification for some previous agreement-type studies in professional soccer having focused on the validity of composite ETL variables (e.g. metabolic power), encompassing a combination of speed and accelerative efforts (Castagna et al., 2017; Gaudino et al., 2013). In this regard, it is a limitation of the current study that both arbitrary and individualized speed zones do not take into consideration efforts imposed by transition between speed zones.

Training load monitoring is considered a pertinent construct in modern soccer. Besides the validity and reliability of ETL monitoring methods, accounting for the specific physical demands imposed on the individual player is vital for subsequent training prescription and recovery. The practical limitations of the use of arbitrary speed zones to calculate ETLs were therefore underlined. However, a recent investigation of common training load monitoring practices revealed that arbitrary speed thresholds are still frequently adopted in professional soccer (Akenhead and Nassis, 2016). However, this approach masks the relative intensity imposed on the individual player (Hunter et al., 2015). This gap is further emphasized when monitoring involves athletes with differing maturity offset (Abbott et al., 2018; Gabbett, 2015). In our view, adopting player-specific intensity zones can add value to the interpretation of GPS data, assisting coaches’ decisions relating to subsequent training dose prescription based on individual capacity and needs, since this is of vital importance for optimizing performance and reducing injury risk.

The practical limitations of the use of arbitrary speed zones to calculate ETL should be taken into consideration when planning monitoring strategies. Based on the significant relationship observed between the researched methods in respect of calculating distance covered, we admit that both methods show similar sensitivity in depicting player’s profiles on high-speed running. However, significant absolute measure differences found between methods indicate that they differ in their ability to account for the number of activities performed. Despite, arbitrary speed zones can be used to monitor seasonal fluctuations in ETL or to compare ETL between drills/sessions. In addition, individualized speed zones provide an insight into players’ physical responses to training and enable comparisons between players’ profiles. Knowledge about players’ locomotor profile would help practitioners understand the cause-effect relationship between the training dose and players’ responses to training.

In summary, this study investigated the interchangeability of two ETL quantification methods in soccer, specifically arbitrary and individualized (based on a combination of maximal aerobic speed and maximal sprinting speed). Our findings indicate that arbitrary and individualized speed thresholds can be interchanged at the relative rank (magnitude level), but not at the absolute rank (measurement error). The descriptive analysis of daily ETL distribution using both methods also provides novel information regarding the interpretation of distance covered in specific speed zones.