Estimating birth weight from observed postnatal weights in a Guatemalan highland community.

Abstract

Objective:

Low birth weight is one of the leading contributors to global perinatal deaths. Detecting this problem close to birth enables the initiation of early intervention, thus reducing the long-term impact on the fetus. However, in low-and middle-income countries, sometimes newborns are weighted days or months after birth, thus challenging the identification of low birth weight. This study aims to estimate birth weight from observed postnatal weights recorded in a Guatemala highland community.

Approach:

With 918 newborns recorded in postpartum visits at a Guatemalan highland community, we fitted traditional infant weight models (Count’s and Reeds models). The model that fitted the observed data best was selected based on typical newborn weight patterns reported in medical literature and previous longitudinal studies. Then, estimated birth weights were determined using the weight gain percentage derived from the fitted weight curve.

Main results:

The best model for both genders was the Reeds2 model, with a mean square error of 0.30 Kg² and 0.23 Kg² for male and female newborns, respectively. The fitted weight curves exhibited similar behavior to those reported in the literature, with a maximum weight loss around three to five days after birth, and birth weight recovery, on average, by day ten. Moreover, the estimated birth weight was consistent with the 2015 Guatemalan National survey, no having a statistically significant difference between the estimated birth weight and the reported survey birth weights (two-sided Wilcoxon rank-sum test; α= 0.05).

Significance:

By estimating birth weight at an opportune time, several days after birth, it may be possible to identify low birth weight more accurately, thus providing timely treatment when is required.

1. Introduction

Guatemala suffers the highest perinatal morbidity and mortality rates in Latin America, particularly affecting Mayan indigenous women in highland rural areas (World Health Organization et al.; 2014). This high burden is a result of barriers, such as economic status, language, and culture, that limit the access to professional medical assistance for performing routine perinatal screening and medical referral. Due to these barriers, pregnant Guatemalan indigenous women are usually attended by traditional birth attendants (TBA), who lack access to adequate medical equipment and sufficient training for the identification of abnormal fetal development.

Low birth weight (LBW) is one of the leading contributors to global perinatal death rates, being the second cause after premature birth (de Bernabé et al.; 2004; Thornton; 2001). LBW could be a consequence of either preterm birth (< 37 weeks) or intrauterine growth restriction (IUGR). However, the former is more common in industrialized countries, whereas the latter commonly occur in low-and middle-income (LMICs) (Ramakrishnan; 2004; Villar and Belizán; 1982), in which around 60% of LBW newborns are due to IUGR (Lee et al.; 2013). In fact, IUGR has a prevalence of around 11% in LMICs (de Onis et al.; 1998).

In an attempt to address IUGR in Guatemala, we have developed a smartphone-mediated affordable perinatal screening system in rural highland Guatemala (Stroux et al.; 2016; Martinez et al.; 2018, 2017). This monitoring system allows Traditional Birth Attendants (TBAs), with minimal training, to use a pictogram- and audio-guided mobile application to assess the maternal and fetal wellbeing during perinatal visits. In these visits, TBAs ask standard symptom questions, take maternal blood pressure, and record One-Dimensional Doppler Ultrasound (1D-DUS) with a low-cost transducer connected to the smartphone.

During postpartum visits, TBAs register the newborn weight, among other parameters. A birth weight lower than 2500 g is an indicator of LBW. Therefore, in countries such as Guatemala, in which recent studies reported an LBW prevalence between 13% (Bose et al.; 2015) and 14.6% (MSPAS/Guatemala et al.; 2017), measuring birth weight is an absolute necessity. Thus, LBW newborns can start early treatment to alleviate short-and long-adverse consequences (de Bernabé et al.; 2004).

Unfortunately, in the Guatemalan rural highland areas is not always possible to register a newborn weight within a few days after birth due to the difficulties in following-up on patients (Unicef and World Health Organization; 2004). Indeed, in our clinical trial, monitoring over 1000 women over two years (Martinez et al.; 2018), some of the postpartum visits were performed days or even weeks after birth. Moreover, the natural drop in body weight in the first week or two after birth, followed by the restoration of birth weight, makes the use of recorded weight problematic. One solution to this challenge is to translate the weight recorded after birth into an estimated birth weight using standardized infant weight charts or curves. However, standard weight charts have been constructed using populations from industrialized countries and may be inaccurate for an LMIC or rural population, particularly of non-European descent (Neufeld et al.; 2004).

The work presented here introduces an approach for estimating newborn birth weights in Guatemalan highland using observed weights recorded days and weeks after birth. To this end, previously reported weight curve models were optimized to fit the observed weights of postpartum visits by using metrics based on infant weight development. The fitted model allows for the characterization of the weight loss and gain behavior of the population used in this study, as well as estimating birth weight.

2. Background

2.1. Infant weight development

After birth, newborns lose weight within the first days due to physiological diuresis and low initial enteral intake (Macdonald et al.; 2003; Chantry et al.; 2011; van Dommelen et al.; 2007). This weight loss is universal regardless of the feeding method (Flaherman et al.; 2018) or the initial birth weight (Shaffer et al.; 1987). However, the maximum percentage of weight loss is not a total agreement, ranging among 7% to 10% (DiTomasso et al.; 2018). After the occurrence of the maximum loss, the weight steady increases during the first months of life (see Figure 1).

Figure 1:

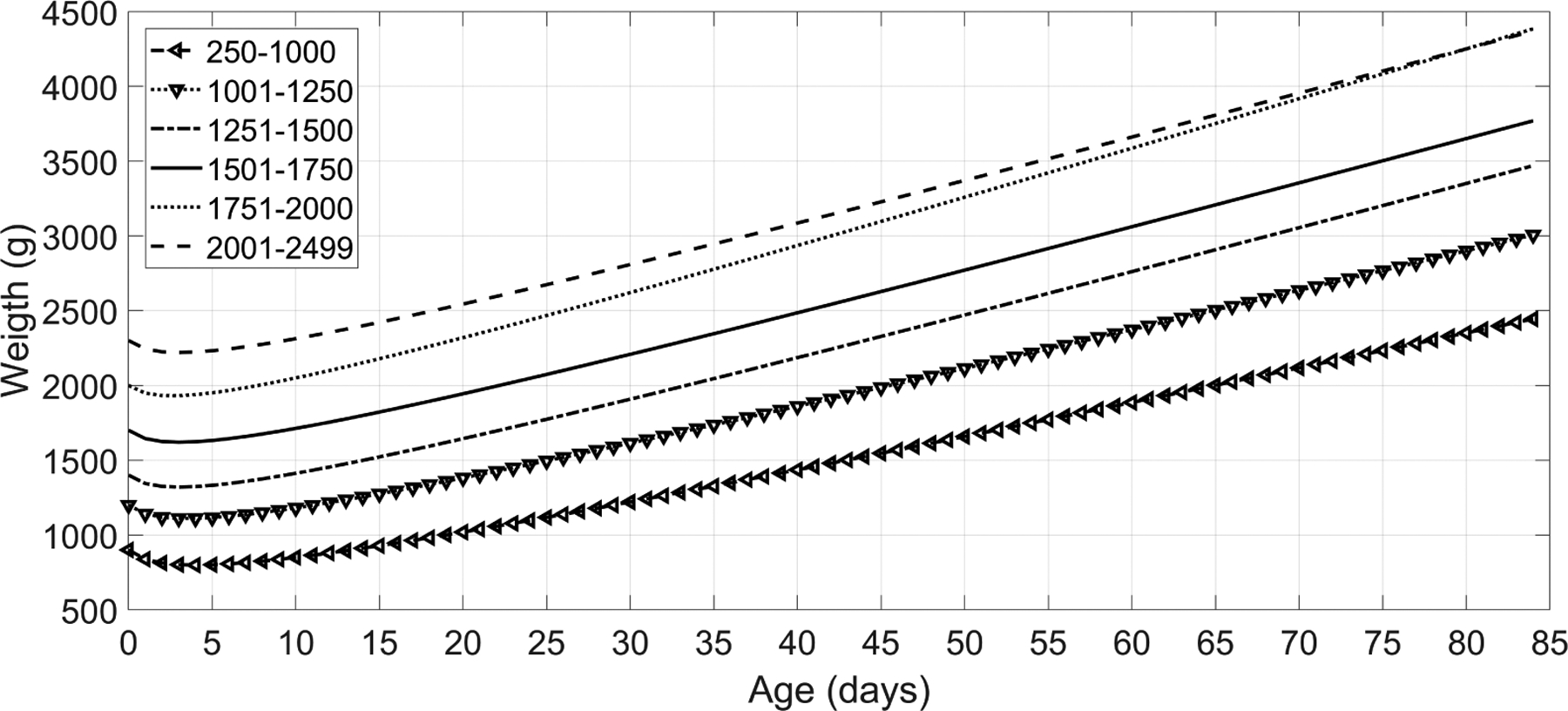
Expected infant weight curves as reported by (Anchieta et al.; 2004), showing a maximum loss weight around the third to fifth days after birth. After this nadir, the weight steady increases during the first months of life.

In order to characterize infant weight patterns, different longitudinal studies have been carried out among different countries. DiTomasso and Paiva (2018) measured weight behavior of 134 newborns in a Rhode Island hospital, observing an average weight loss percentage of 8% around the third and fourth day, whereas the birth weight was recovered by the twelfth day. Likewise, Paul et al. (2016) tracked the weight behavior of a large sample, 143,889 newborns, recorded in California. They found a range for percentage weight between 5.9% and 7.1%, occurring around the 61st and 65th hours after birth. After the loss weight nadir, the weight increased at a rate of 35 to 40 g/day, recovering the birth weight by day 10.

Although no study has been conducted for the Guatemalan population, some studies carried on Latin American LMICs have also reported similar findings than those previously mentioned (Zamorano-Jiménez et al.; 2012; Covas et al.; 2006; Anchieta et al.; 2004; Pais and Gutiérrez; 2003). The reported average weight loss percentage for these studies was around 8% on the third or fourth day after birth. However, there was a variability for the recovery day and the weight increment rate, ranging between 5.7 to 19 days and between 13.9 to 40 g/day, respectively. All details of the previous infant weight development studies are shown in Table 1.

Table 1:

Detail of infant weight development reported by previous published studies.

Study	Location	Sample size	Weight loss percentage (%)	Weight loss day	Recovery day	Weight rate (gr/day)
DiTomasso and Paiva (2018)	Rhode Island	134	[6–9]	[3–4]	[10–12]	39
Paul et al. (2016)	California	143889	[5.9–7.1]	[2.5–2.8]	[9–10]	[35–40]
Zamorano-Jiménez et al.; 2012	Mexico	101	[4.1–13.1]	[2.5–5.9]	[5.7–16.1]	[13.9–21.7]
Covas et al. (2006)	Argentina	810	8	3	[8–10]
Anchieta et al. (2004)	Brazil	340	[5.9–9.7]	[4–5]	[16–19]	[22.8–35.99]
Pais and Gutiérrez (2003)	Uruguay	148	[8–9]	[2–3]	[8–10]	[30–40]

2.2. Weight curve models

Since the middle of the twentieth century, different non-linear models have been introduced for weight gain in infants and children (Hauspie and Molinari; 2004). The first introduced model was the Jenss (Jenss and Bayley; 1937), an exponential model, which showed suitable results for describing head-circumference and length growth, but not for describing the irregularity of weight patterns occurred in the first days after birth.

In addition to the Jenss model, three other non-linear models have been also used for fitting infant weight data. The first one was the Count’s model (Eq. 1) proposed by Count (1942) and modified by Shohoji and Sumiya (2001). The other two models, Reeds1 (Eq. 2) and Reeds2 (Eq. 3), were extensions of the Count’s model developed by Berkey and Reed (1987). All these models were represented by several parameters, including the regression coefficients (a, b, c, d, e); age in months (t); and weight in Kg (y).

$$y=a+bt+c\text{\hspace{0.17em}ln}\left(t+1\right)$$ (1)

$$y=a+bt+c\text{ln}\left(t+1\right)+\frac{d}{t+1}$$ (2)

$$y=a+bt+c\text{ln}\left(t+1\right)+\frac{d}{t+1}+\frac{e}{{\left(t+1\right)}^2}$$ (3)

The weight curve models have been used in different studies to fit collected weight data. Within these studies, the Count’s model has been the most commonly used. Thus, Peter et al. (2002) fitted the Count’s model for a sample of 1931 neonates collected between 1982 and 1990. Similarly, the Count’s model was used in Brazil for describing the weight behavior of 340 newborns from birth to 12 weeks of life (Anchieta et al.; 2004), as well as in Taiwan for examining the weight growth of infants exposed to some specific nutritional and ecological conditions (Kim and Pollitt; 1987).

All the models have also been compared to assess their fitting performance for weight data. Initially, Berkey (1982) compared Jenss and Count’s, reporting that Jenss performed better than Count’s model as the latter challenged to fit data when it was spanned over six years. However, in another study, Peerson et al. (1993) observed that any of these two models were able to fit weight recorded from 70 infants at the University of California Davis during their first 24 months. Nevertheless, in a more extensive study including five different models, Simondon et al. (1992) found that the first-order Reed model was the best model for fitting weight data collected from 95 infants from birth to 13 months of age in rural Congo.

In recent studies, quantile regression has been used over the traditional non-linear weight curve models. Indeed, the majority of weight models fitting after the 2010s applied non-linear quantile regression provided in modern programming languages (Miller et al.; 2015; Paul et al.; 2016; Flaherman et al.; 2015; Williamson et al.; 2018). However, these models assume that the input is a longitudinal dataset, in which multiple samples are recorded for each patient along time.

2.3. Birth weight in Guatemala

Previous works have shown that the average birth weight in Guatemala is lower than the 3.5 Kg of European heritage newborns (Janssen et al.; 2007). In fact, in a global maternity health registry study, Bose et al. (2015) reported an average birth weight of 2,983.2 g (SD = 469.1 g) for a total of 30,262 deliveries. The total percentage of LBW newborns for that sample was 13%.

Similarly, in the Guatemalan national maternal and infant health survey (MSPAS/Guatemala et al.; 2017), the averaged birth weight from 5,604 female newborns was 3,046.6 g (SD = 568.3 g), whereas for 6,071 male was 3,146.5 g (SD = 593.8 g). The percentage of LBW among rural and urban areas was similar, being 14.8% and 14.2%, respectively.

3. Methods

3.1. Database

Data used in this work was collected as a part of a perinatal care program conducted in rural highland Guatemala in the vicinity of Tecpan, Chimaltenango. This program was approved by the Institutional Review Boards of Emory University, the Wuqu’ Kawoq | Maya Health Alliance, and Agnes Scott College (Ref: IRB00076231 - ‘Mobile Health Intervention to Improve Perinatal Continuum of Care in Guatemala’) and registered as a clinical trial (ClinicalTrials.gov identifier NCT02348840). In the program, traditional birth attendants (TBA) were trained to use a mobile app to record perinatal information during regular visits. More details on the design and implementation of the data collection system, and the training of the TBAs can be found in Stroux et al. (2016) and Martinez et al. (2018, 2017).

For this work, data recorded from 918 newborns in postpartum visits were used. For each newborn’s weight measurement was only performed once. These visits occurred on different postnatal days for each case, with an average at 31.36 days after birth (SD=32.86). In addition to measuring the weight, the TBAs also recorded the newborn’s birth date and gender. Moreover, in some cases, TBAs recorded the maternal age at birth, and the number of previous pregnancies (gravity). Table 2 shows available demographic information for the data used in this work.

Table 2:

Average demographics for the data used in this study. For each metric, the standard deviation and the number of samples avaliable for that variable are shown in parenthesis.

Demographic variable	Total
Postnatal visit (days)	31.36 (SD= 32.86; N= 918)
Neonatal weight (Kg)	3.93 (SD= 2.73; N= 918)
Maternal age (years)	26.69 (SD= 8.18; N=903)
Gravidity (count)	3.24 (SD= 2.64; N=683)
Gender(male/female)	467/451

As all data used in this work were recollected in the same rural community, pregnant women and newborns shared maternal nutrition, and delivery and feeding methods among them.

3.2. Preprocessing

As weight recordings were taken manually, prepossessing steps were carried out to ensure that neither measurement errors nor typos were considered into the analysis.

The first preprocessing step was to remove unrealistic observed weights (e.g., 10 Kg). To this end, observed weights higher than the 99th percentile reported in the World Health Organization (2006) were removed (See Table 3).

Table 3:

Maximum weights for each month based on the WHO child growth chart (World Health Organization; 2006).

Month	Days after birth	Maximum weight (kg)
		Male	Female
1st	0 to 30	5.7	5.4
2nd	31 to 60	7.0	6.5
3rd	61 to 90	7.9	7.4
4th	91 to 120	8.6	8.1
5th	121 to 150	9.2	8.7

After removing unrealistic values, the next step was to exclude outliers that could affect the regression fitting. Two different outlier problems were identified in this case. Firstly, as the majority of postnatal visits were done in the first days after birth, the local density of all observed weights after 100 days was low. These points with low density were removed using the local outlier factor (LOF), which was calculated as described in Breunig et al. (2000). Then, using a backtracking search, the last observed point to be considered in the analysis was set as that whose LOF was lower than 1.5.

The second outlier filtering was to remove bivariate extreme points. These outliers were detected using Mahalanobis distance, in which the input matrix was composed of the observed weights and the visit days. The threshold value was set as the chi-square value with a significance level of 0.001 and a degree of freedom of two, ${\chi }_{0.999}^2\left(2\right)=13.82$. Thus, any row with a Mahalanobis distance higher than the threshold was removed.

3.3. Fitting models

Models were fitted for different window lengths (number of days after birth) to find that one that fits the data best. The tested range was from 20 to 150 weeks, increasing by five weeks. For each window length, models were fitted using a two-stage process.

In the first stage, the Count’s (Eq. 1), Reeds1 (Eq. 2), and Reeds2 (Eq. 3) models were applied using non-linear robust regression. For each model, nine different robust weighting functions were used to fit the model, namely: Andrews, bisquare, Cauchy, fair, Huber, logistic, OLS (no weights), Talwar, and Welsch. Consequently, there were a total of 27 regressions, nine per each model.

The assessment of the resulted regression was based on five metrics derived from previous research showed in Table 1. These metrics were: i) the day in which the maximum weight loss occurred (nadir); ii) the maximum percentage of weight loss; iii) the birth weight recovery day; iv) the trend of the fitted model after recovering birth weight, and v) the rate at which weight increases after recovering birth weight.

Based on the average metrics of the Table 1, the reference nadir was set in 3.45 days; the percentage of weight loss in 7.817%; the recovery day in 11.15 days; the trend as monotonically increasing; and the angle at 42.26° (0.9087 Kg/month).

On the other hand, for each regression, the nadir was obtained using the first derivative. The loss percentage was calculated by comparing the origin and nadir weights. The recovery day was set as the day surpassing the origin weight. The trend after weight recovery was set as increasing if the first derivative was positive from that point to the end. Finally, the curve angle was calculated by applying the arc-tangent function to the growth rate.

The comparison between the fitted and reference vectors was performed using mean square error (MSE). Before calculating the MSE, the two vectors were normalized to avoid scale comparison problems. For each model, the weighting function with the lowest MSE was selected.

In the second stage, to reduce the effects of high individual variability reported in longitudinal studies (Berkey; 1982; Shaffer et al.; 1987), the coefficients selected in the first stage were further optimized using non-linear quantile regression. The quantile regression was performed using an interior point algorithm proposed by Koenker and Park (1996), setting the percentile as the median (i.e., 50th percentile), and the initial point as the coefficients found at the first stage.

3.4. Comparison with other models

The obtained fitted curves were compared against those obtained using parameters reported in three previous studies: Kim and Pollitt (1987) and Berkey (1982) for Count’s model, and Simondon et al. (1992) for Count’s, Reeds1 and Reeds2 models. Specifically, as these previous studies fitted a curve for each individual (longitudinal studies), the average value of their parameters was used for generating a curve from the data used in this work.

Additionally, the curves were also compared to the WHO growth charts (World Health Organization; 2006), which includes newborns’ data from the cities of Davis, California, USA; Muscat, Oman; Oslo, Norway; and Pelotas, Brazil; and wealthy neighborhoods of Accra, Ghana, and South Delhi, India. Thus, the fitted curve of each model was plotted against the 5th, 15th, 25th, 50th, 75th, and 95th percentiles of the WHO weight curves. This comparison allowed checking that the fitted model was growing with an inclination within the WHO percentiles.

3.5. Estimating birth weight

The weight gain or loss percentage function was calculated for each fitted models as:

$$g\left(t\right)=\frac{f\left(t\right)-f\left(0\right)}{f\left(0\right)},$$ (4)

where f(t) was the fitted weight value at the t − th week and f(0) was the fitted weight value at birth (t = 0). Then, the birth weight for each newborn was estimated as follows:

$$b\left(i\right)=\frac{o\left(i\right)}{1+g\left(t\left(i\right)\right)},$$ (5)

where o(i) was the observed weight for the i – th newborn recorded in the postpartum visit occurred at t(i) weeks, and g(·) is the gain/loss function (Eq. 4).

3.6. Comparison of the estimated birth weight

The estimated birth weights were compared to the Guatemalan national maternal and infant health survey (MSPAS/Guatemala et al.; 2017). However, as the data used here came from a rural community located in Tecpán, Chimatenalgo, only data with similar characteristics was used for the comparison. Therefore, only 306 birth weights from rural Chimatenalgo newborns, reported in the survey, were considered. From these newborns, 168 were male, whereas 138 were female.

3.7. Identification of low birth weight

A newborn is defined by the WHO to have LBW if the weight at birth is below 2500 g (World Health Organization; 2014). We applied this definition to the Guatemalan national maternal survey, specifically for rural Chimaltenalgo (the region of relevance in our study) (MSPAS/Guatemala et al.; 2017). We found that the lowest 14.3% of male newborns and 16.33% of female newborns satisfied this weight criterion.

4. Results

4.1. Preprocessed data

Figure 2 shows datasets before and after removing unrealistic recorded weights and outliers. In total, 17 and 28 observed weights were discarded for male and females newborns, respectively. For fitting the weight models, male newborns had a total of 450 observed weight ranging from 0 to 3.43 months (103 days), whereas female newborns had a total of 423 weights from 0 to 3.50 months (105 days). The ratio between the retained male and female weight was 1.0638, which is consistent with the 1.06 natural gender ratio reported by (Grech et al.; 2002).

Figure 2:

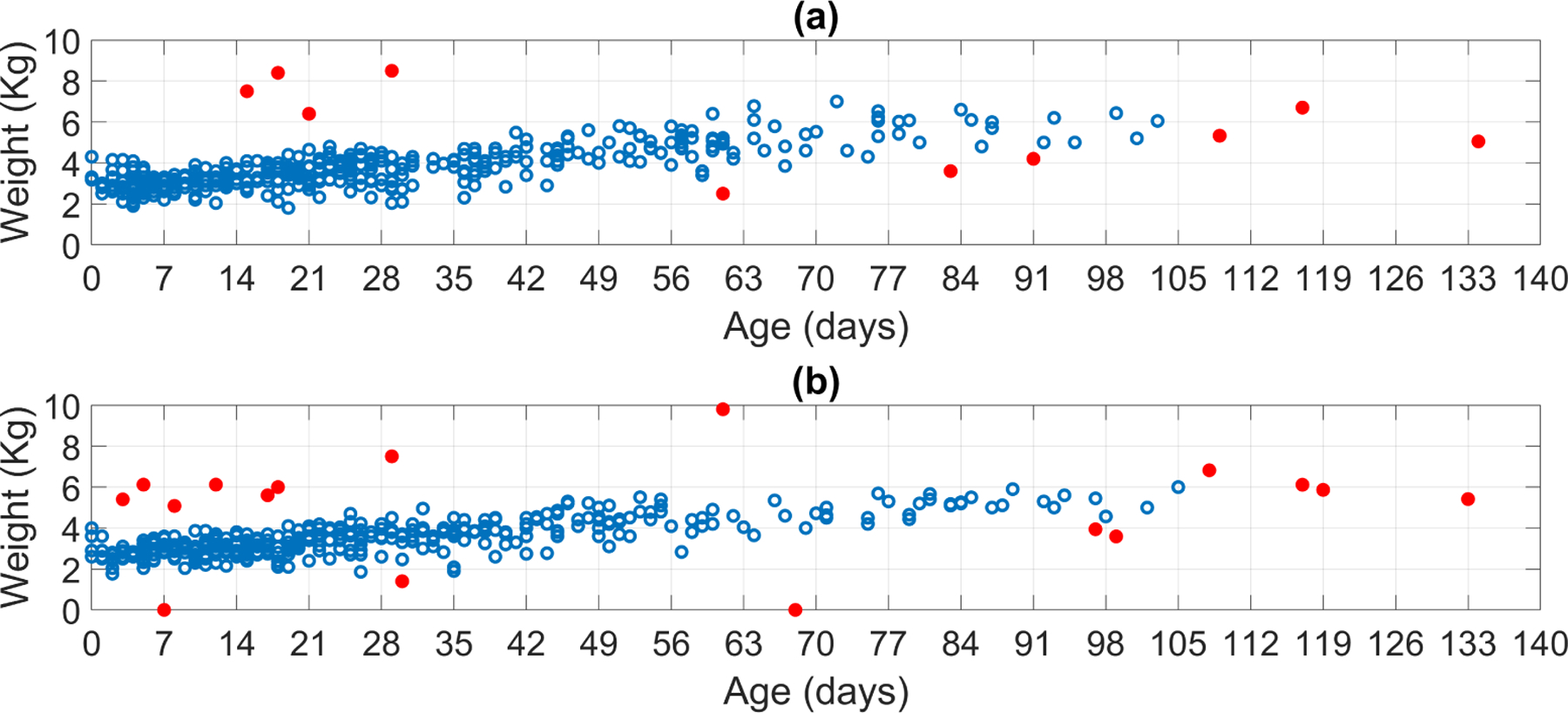
Retained (open circle) and discarded (filled red circle) observed weights for (a) male and(b) female newborns.

4.2. Fitted models

Post-processed data were fed into the two-stage model-fitting using different window lengths (number of days after birth). Table 4 shows the window length that best fitted the observed postnatal weights for each model. The percentage weight loss, the day of lowest weight (nadir), the day at which the neonate recovered their original weight and the rate of weight gain after the recovery day for each of these models were encoded in a vector and compared with the corresponding average metrics reported in previous studies (listed in Table 1) using the L1-norm (see final column in Table 4).

Table 4:

Details of the fitted curves on the observed postnatal weights, grouped by gender. The window length in days and the samples of each fitted curve are provided. The final (9th) column shows the L1-norm between a vector composed of the parameters of each model, (γ), and the target vector given by average of the metrics provided in Table 1, (τ), which corresponds to a nadir of 3.5 days; a weight loss at the nadir of 7.8%; a weight recovery duration of 11.2 days; and a weight gain rate of 30.3 g/day

Gender	Model	Analysis Window (days since birth)	# Samples Used	Weight Loss at Nadir (%)	Nadir (days since birth)	Recovery Day	Weight Recovery Rate (g/day)	‖γ–τ‖1
Male	Count’s	20	209	1.40	0.12	0.25	26.4	24.50
	Reeds1	25	258	4.87	4.52	10.37	32.5	6.84
	Reeds2	60	407	7.34	4.33	11.40	35.2	5.89
Female	Count’s	25	229	1.48	0.13	0.28	27.7	23.07
	Reeds1	62	374	2.23	4.00	8.90	29.1	9.47
	Reeds2	45	332	5.19	3.98	10.38	29.1	5.12

The Reeds2 model provided the best fit to the observations, using a window length of 60 days for males, and 45 days for females. Both genders exhibited a nadir around the fourth day after birth, with a maximum loss of 7.34% for males and 5.19% for females. Both genders recovered birth weights around the tenth day.

Table 5 provides the coefficients derived for the three models being compared in this work, as well as error in the regression (expressed as the MSE). For the Reeds2 model, the MSE between the fitted curve and the observed weights was 0.3 Kg² for males, and 0.2 Kg² for females.

Table 5:

Coefficients for the fitted curves shown in Table 4. The final (10th) column shows the MSE between the fitted curve and the observed postnatal weights.

Gender	Model	Analysis Window (day since birth)	# Samples Used	Coefficients					MSE (Kg2)
				a	b	c	d	e
Male	Count’s	20	209	2.9690	5.6691	−6.3642			0.2213
	Reeds1	25	258	−20.5997	−6.5776	28.1120	23.6392		0.2316
	Reeds2	60	407	112.8610	17.3626	−87.6400	−152.7991	43.0524	0.3018
Female	Count’s	25	229	2.8771	4.7744	−5.4227			0.2079
	Reeds1	62	374	−8.6961	−2.3848	12.9260	11.5857		0.2485
	Reeds2	45	332	116.3558	20.6091	−95.8732	−154.1696	40.7861	0.2277

4.3. Comparison to other models

Figure 3 shows the fitted Reeds2 models against previously reported coefficients (Kim and Pollitt; 1987; Berkey; 1982; Simondon et al.; 1992) for male and female newborns. For both genders, the fitted Reeds models were more accurate than those models generated by coefficients reported in previous research.

Figure 3:

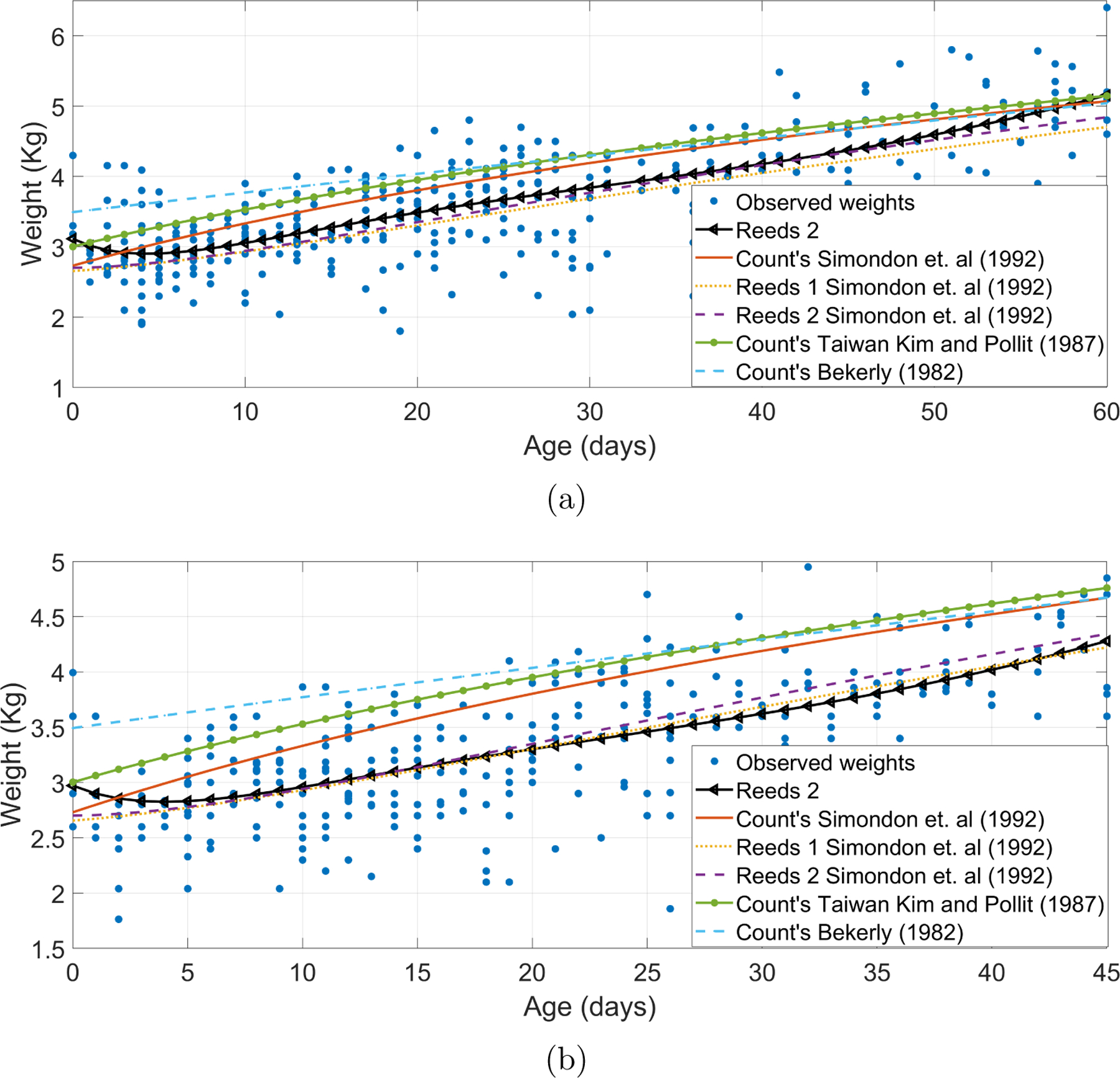
Reeds2 models fitted for (a) male and (b) female newborns against models generated using coefficients reported by Kim and Pollitt (1987) in a Taiwanese population, Berkey (1982) in a Boston hospital sample, and Simondon et al. (1992) in a Congo rural community.

Likewise, Figure 4 compares the fitted models to those corresponding to the weight percentiles of the WHO weight chart. For both genders, the Reeds models grew along with the 25th percentile, which is expected as WHO weight chart includes populations of industrialized countries, as well as affluent neighborhoods in India and Ghana.

Figure 4:

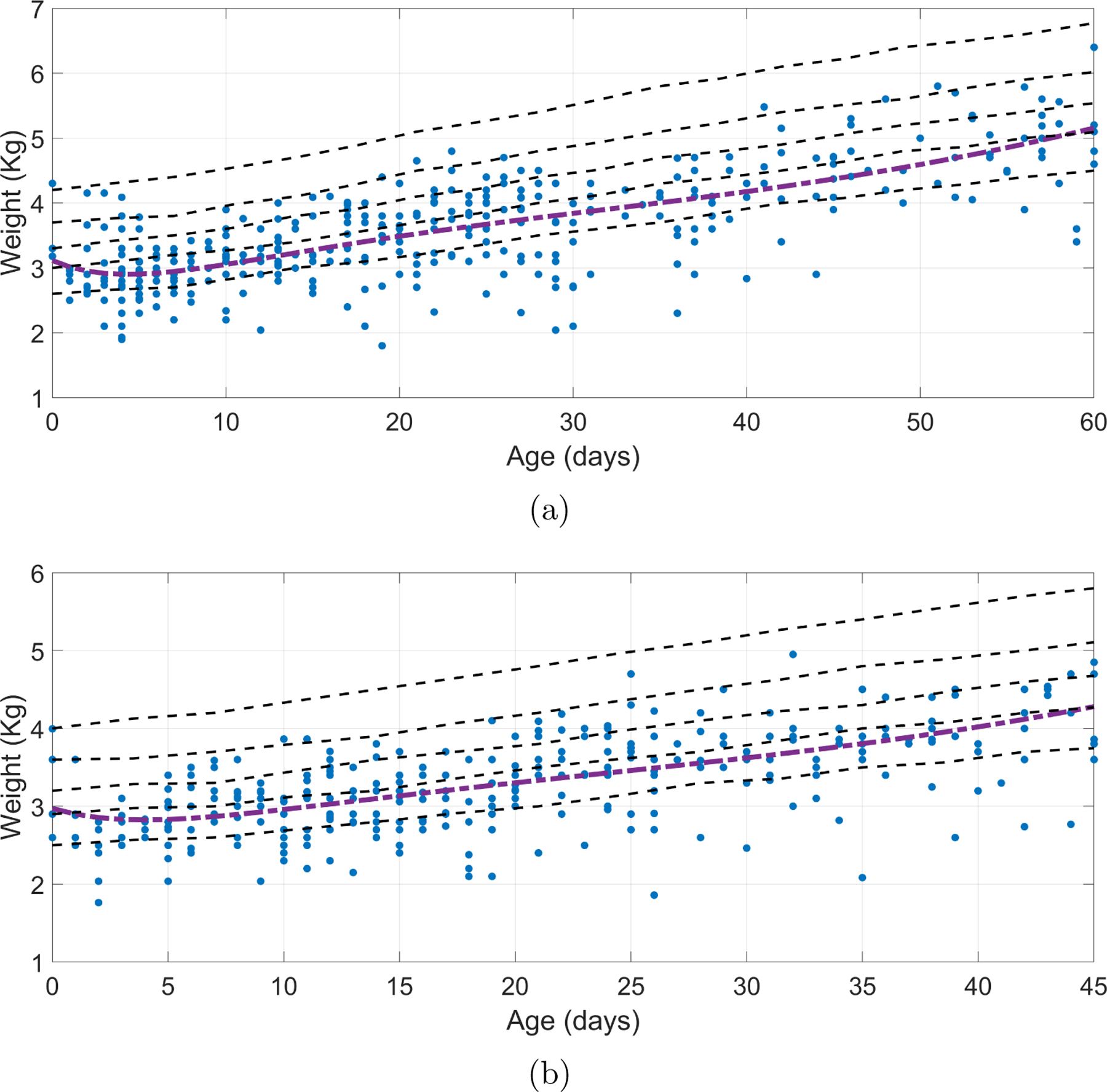
Reeds2 models fitted for (a) male and (b) female in observed weights after birth against WHO weight growth chart percentiles. The percentiles showed for the WHO weight dataset corresponds to the 5th, 25th, 50th, 75th, and 95th.

4.4. Estimation of birth weight and identification of low birth weight

The Reeds2 models were used to estimated birth weight following steps presented in subsection 3.5. Part (a) of the Figures 5 and 6 shows the distributions of estimated birth weight for male and female newborns, respectively. For both genders, the majority of the estimated birth weights were close to 3 Kg, being lower for females. Moreover, the corresponding LBW percentile threshold was located in the estimated birth weights. For male newborns, the weight threshold was found at 2.64 Kg, whereas for females, it was 2.57 Kg.

Figure 5:

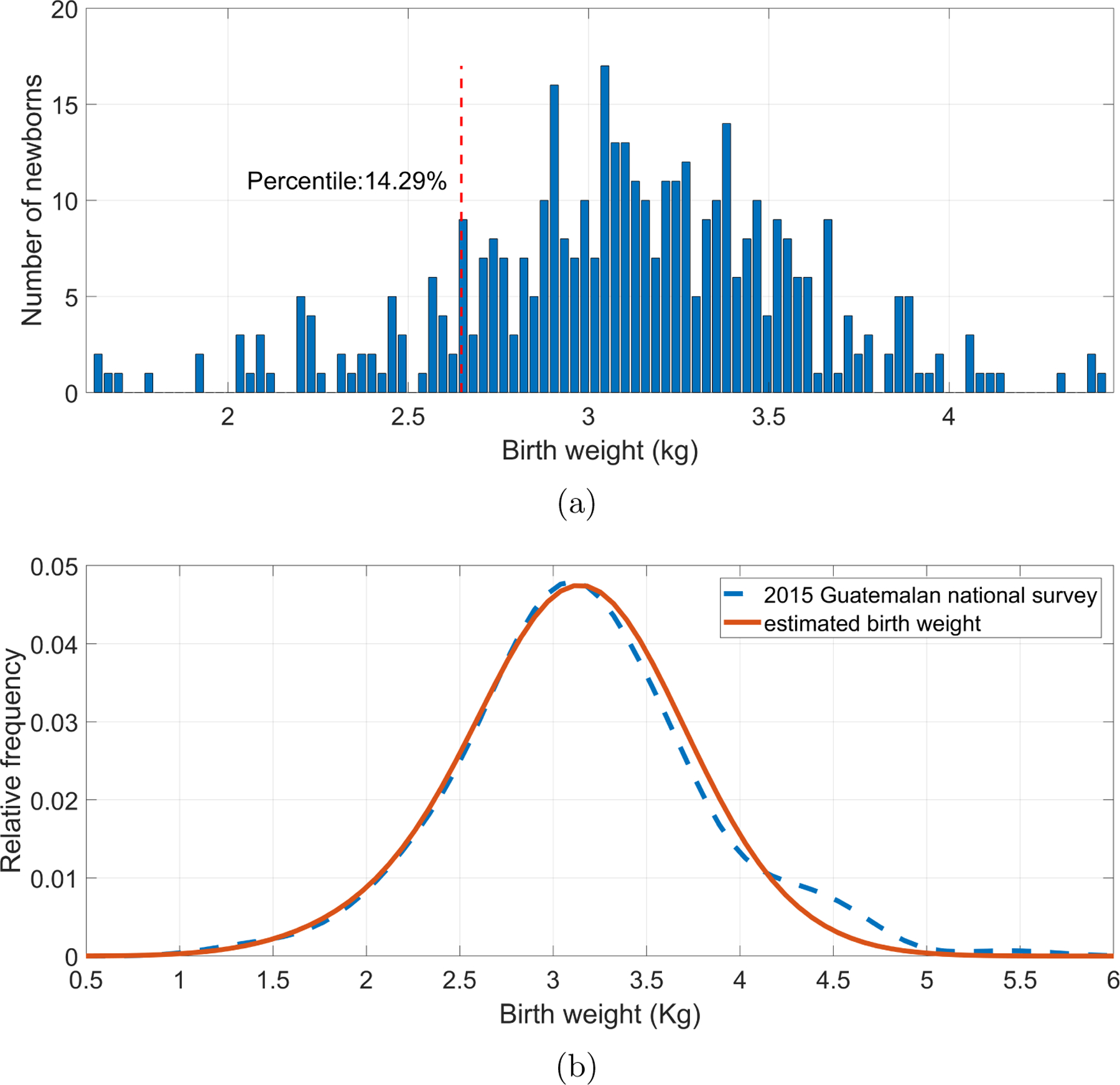
Male newborns’ birth weights estimated using the fitted second-order Reeds model. (a) Histogram of estimated birth weights with the threshold for identifying low birth weight (vertical dotted line), corresponding to the 14.29 percentile, or 2.64 Kg. (b) Comparison of the distribution of estimated birth weights (red) with the measured birth weights in the 2015 Guatemalan national survey for male newborns of rural Chimatenalgo (blue dashed line).

Figure 6:

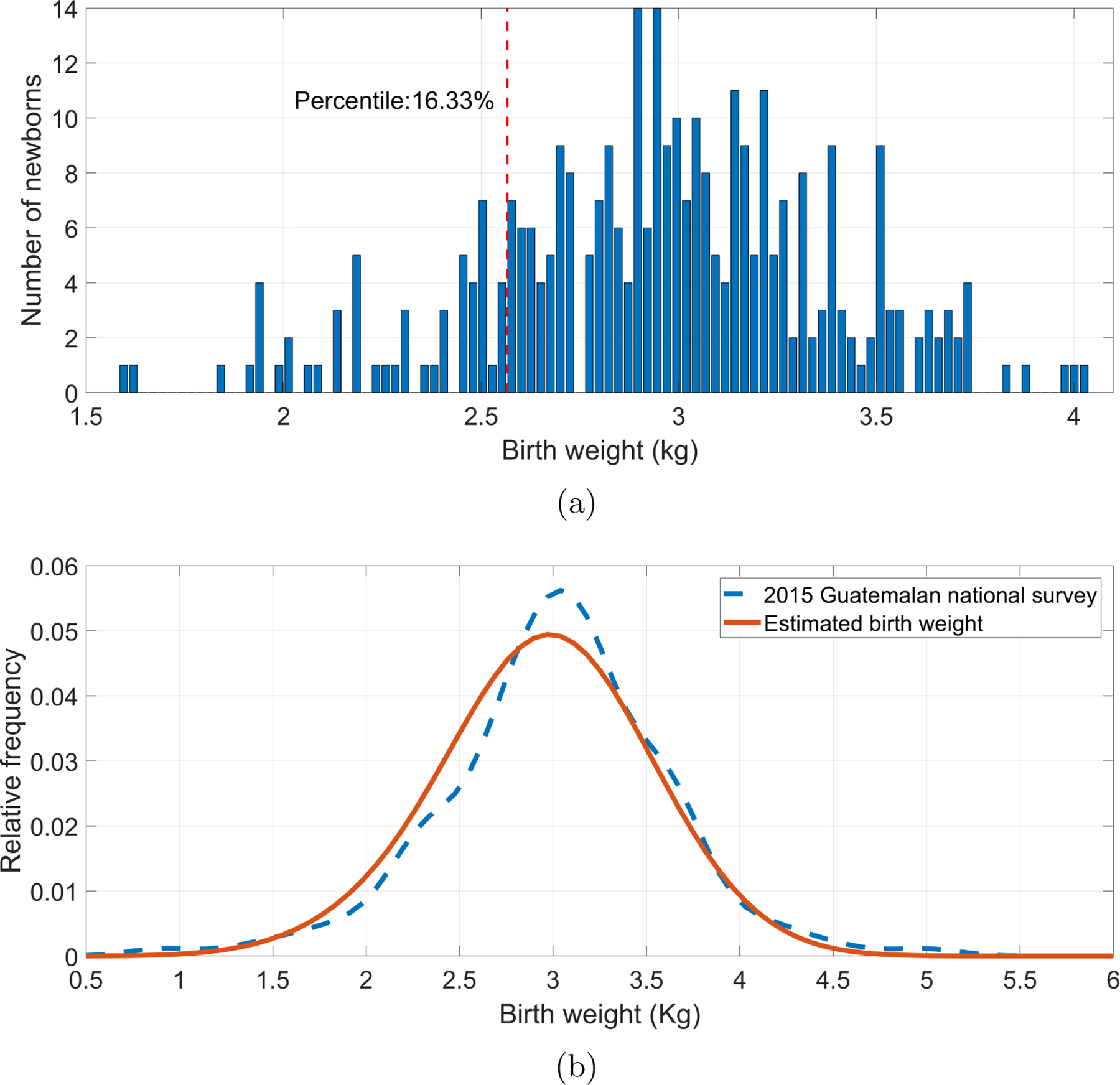
Female newborns’ birth weights estimated using the fitted second-order Reeds model. (a) Histogram of estimated birth weights with the threshold for identifying low birth weight (vertical dotted line), corresponding to the 16.29 percentile, or 2.57 Kg. (b) Comparison of the distribution of estimated birth weights (red) with the measured birth weights in the 2015 Guatemalan national survey for female newborns of rural Chimatenalgo (blue dashed line).

Additionally, Figures 5 and 6, in part (b), shows the distributions of estimated birth weights and those reported in the 2015 Guatemalan national survey for rural Chimatenalgo newborns (MSPAS/Guatemala et al.; 2017). Estimated weight distributions were similar to the surveyed distributions. In fact, in Table 6, it is shown that for any gender, there was no statistically significant difference between the medians of the estimated birth weights and the reported weights for rural Chimatenalgo newborns.

Table 6:

Descriptive statistics of the estimated birth weights and the 2015 Guatemalan national survey reported newborns of rural Chimatenalgo (MSPAS/Guatemala et al.; 2017). Last two columns show the p value of: (i) a two-sample t-test; and (ii) a paired two-sided Wilcoxon signed rank test. Null hypothesis tests were whether the two weight distributions have equal mean and median, respectively.

Gender	Distribution	mean (Kg)	standard deviation (Kg)	kurtosis	skewness	t-test p-value	Wilcoxon signed-rank p-value
Male	Estimated birth weights	3.10	0.47	3.60	−0.32	0.3765	0.7479
	2015 Guatemalan national survey	3.15	0.64	3.89	0.28
Female	Estimated birth weights	2.95	0.43	3.31	−0.32	0.1913	0.1495
	2015 Guatemalan national survey	3.02	0.60	4.43	−0.19

5. Discussion

The fitted weight curves presented here indicates that it is possible to estimate birth weight from observed weight recorded days or months after birth. Notably, our two-stage fitting steps were able to describe a typical newborn weight pattern in a dataset composed of only one sample per newborn rather than multiple points per subject as described in previous research works (Miller et al.; 2015; Flaherman et al.; 2015; Williamson et al.; 2018; Simondon et al.; 1992; Berkey; 1982; Kim and Pollitt; 1987; DiTomasso and Paiva; 2018; Paul et al.; 2016; Zamorano-Jiménez et al.; 2012; Covas et al.; 2006; Anchieta et al.; 2004; Pais and Gutiérrez; 2003). This suitable fitted pattern it is likely explained by the homogeneity of subjects used in this work, in which maternal nutrition, and delivery and feeding methods are common among them.

Within the infant weight models, the Reeds2 model fitted the observed data best, thereby supporting the previous finding reported by Simondon et al. (1992), in which Reeds models resulted in the lowest residuals. As the Reeds2 model has two inflection points (Berkey and Reed; 1987), the curve was able to precisely adjust to the different infant weight patterns than the other models.

In comparison with previous longitudinal (see Table 1), the Reeds2 model obtained similar metrics for both genders, showing a maximum weight loss within the third and fifth day, and recovery the birth weight by ten days after birth. Although the weight percentage loss was lower than the expected 7% for females, it can be explained by the fact that the model was fitted for all subjects, thereby introducing inter-variability in the fitted curve (Paul et al.; 2016; Shaffer et al.; 1987). Nevertheless, the achieved percentage loss, as well as the other model criteria, were within the full ranges reported in previous studies.

The median quantile regression applied to the Reeds model allowed estimating a more robust and less biased trend of the population. Specifically, the second-order Reeds model grew with a feasible rate along with the 25th percentile of the WHO growth chart (Figure 4). Although the fitted median quantile regression was lower than the 50th CDC percentile, there is not any inconsistency as it is expected that Guatemalan newborns have a lower weight than those of a well-equipped-resource environment, such as the US, Norway, and high-income population in New Delhi (Neufeld et al.; 2004). In fact, the WHO 50th quantile birth weight is close to 3.5 Kg, which is the average for European-inheritance newborns.

The average of the estimated birth weights, for both male and female, was consistent with the figures reported by the 2015 Guatemalan national survey in rural Chimatenalgo (MSPAS/Guatemala et al.; 2017), varying less than 20 g. Likewise, the estimated averages were also close to the 2983.2 g reported by Bose et al. (2015) for a Guatemalan sample of 30262 deliveries. Therefore, for both gender, our approach estimated birth weights in a feasible range (see Table 6).

Interestingly, by mapping rural Chimatenalgo LBW percentiles, we obtained a weight threshold for identifying LBW in our estimations. This identification is relevant for TBAs as they may be able to detect any potential LBW cases. Thus, newborns could receive early treatment, thereby reducing short-and long-term complications.

The main limitation of this work is that the observed dataset was not enough to carry on a longitudinal study. Therefore, the weight pattern obtained is an approximation and does not represent a complete characterization of the weight gain pattern of the rural Guatemala population used here. Nevertheless, the simple method used here provides a straightforward way to estimate birth weight, thus helping to identify low birth weight newborns on late postpartum visits.

Future research should perform a longitudinal study by periodically weighing newborns from birth to one year old. Thus, the two-stage method introduced here could be fitted for each newborn, resulting in a more accurate characterization of the newborns’ weight curve for the Guatemalan highland community.

6. Conclusion

In LMICs, timely recording of birth weight is often difficult. This work introduces a simple approach for estimating birth weight from observations recorded after birth. The estimations were consistent with infant weight patterns reported in previous studies conducted in Guatemalan communities. By weighing infants several days after birth, it may, therefore, be possible to identify LBW newborns and initiate treatment to reduce short-and long-term complications. Nevertheless, we note that the neonatal assessment needs to occur in the first few days of life to accurately estimate a birth weight relevant for tracking neonatal health (Lee et al.; 2013).