Method of regulatory network that can explore protein regulations for disease classification

Abstract

Objective

To develop regulatory network to explore and model the regulatory relationships of protein biomarkers and classify different disease groups.

Methods

Regulatory network is constructed to be a hopfield-like network with nodes representing biomarkers and directional connections to be regulations in between. The input to the network is the measured expression levels of biomarkers, and the output is the summation of regulatory strengths from other biomarkers. The network is optimized towards minimizing the energy function that is defined as the measure of the disagreement between the input and output of the network. To simulate more complicated regulations, a sigmoid kernel function is imposed on each node to construct a non-linear regulatory network.

Results

Two datasets have been used as test beds, one dataset includes patients of nasopharyngeal carcinoma with different responses to chemotherapy drug, and the other consists of patients of severe acute respiratory syndrome, influenza, and control normals. The regulatory networks among protein biomarkers were reconstructed for different disease conditions in each dataset. We demonstrated our methods have better classification capability when comparing with conventional methods including Fisher linear discriminant (FLD), K-nearest neighborhood (KNN), linear support vector machines (linSVM) and radial basis function based support vector machines (rbfSVM).

Conclusion

The derived networks can effectively capture the unique regulatory patterns of protein markers associated with different patient groups and hence can be used for disease classification. The discovered regulation relationships can potentially provide insights to revealing the molecular signaling pathways.

In this paper, a novel technique of regulatory network is proposed on purpose of modeling biomarker regulations and classifying different disease groups. The network is composed of a certain number of nodes that are directionally connected in between in which nodes denote predictors and connections to be the regulation relationship. The network is optimized towards minimizing its energy function with biomarker expression data acquired from a specific patient group, thus the optimized network can model the regulatory relationship of biomarkers under the same circumstance. To simulate more complicated regulations, a sigmoid kernel function is imposed on each node to construct a non-linear regulatory network. The regulatory network can extract unique features of each disease condition, thus one immediate application of regulatory network is to classifying different diseases. We demonstrated that regulatory network is capable of performing disease classification through comparing with conventional methods including FLD, KNN, linSVM and rbfSVM on two protein datasets. We believe our method is promising in mining knowledge of protein regulations and be powerful for disease classification.

1. Introduction

High-throughput microarray profiling platform can simultaneously assess expressions of tens of thousands of genes or proteins in biological materials, thus provide biomedical researchers an ideal tool to investigate mechanism of tumor [1], [2], [3], [4], [5], [6], [7], [8]. It has been shown that analyzing microarray data is a challenging task due to its high-dimensionality and small-sample nature. The most popular way to utilize the array data is to identifying biomarkers for specific diseases [3], [5], [6], [8] or building classification models [4], [7], [8]. These conventional approaches only target for achieving highly differentiated biomarkers or signatures, thus the relationships among biomarkers are not of their concern. Biomarker can vary drastically in different circumstances, suggesting it is risky to rely on individual biomarkers without knowing its regulations in between.

Recently there is an obvious trend to discover molecular regulations through analyzing microarray data. Kim et al. [9], Zou and Conzen [10], and Yamaguchi et al. [11] applied Bayesian networks to analyze gene regulations with a probabilistic manner; Curtis and Brand proposed a modular regulation analysis method [14]; Yeung et al. presented the dominant spectral component technique for discovering transcriptional regulations [15]. Some researches devoted to exploring molecular interactions for classification purpose. For instance, Qiu et al. proposed an ensemble dependence model-to-model linear dependence relationships among gene clustering centers [12]. In particular, Antonov et al. believed that molecular patterns vary in different patient groups, and proposed to extract regulatory relationships by using linear programming methods [13]. As a result, by adopting a weighted sum of the logarithms of the expression levels, the authors proposed a classification model based on regulation information. One disadvantage of aforementioned methods is that the regulation relationship is constructed for all groups, thus no unique feature can be extracted for individual patient group [16].

From a biological viewpoint, there exists an underlying regulatory network which is responsible for tumor genesis [17], [18]. In this paper, we propose to construct a regulatory network (RN) to model the biological regulations. In brief, a RN is constructed to be a hopfield-like network with nodes representing biomarkers and directional connections to be regulations in between. The input to the network is the measured expression levels of biomarkers, and the output is the summation of regulatory strengths from other biomarkers. An energy function is defined as the measure of the disagreement between the input and output of the network. Minimizing the energy function can thus reconstruct the regulatory relationships among biomarkers. Since RN can extract unique features of each disease condition, one immediate application of RN is to classify different diseases. To simulate more complicated regulations, a sigmoid kernel function is imposed on each node to construct a non-linear regulatory network (NRN), which will be shown can enjoy higher stability and accuracy in disease classification.

Our methods were applied to model protein regulations in different disease conditions. Unlike genome, which is relatively constant and simple, proteome is much more complicated due to its extensive interactions with other molecules and environmental conditions. For instance, many proteins only function in the presence of other molecules, and some proteins may cooperatively form complexes that could be involved in the translational modification of other proteins. Proteinchip of SELDI-TOF-MS (surface-enhanced laser desorption/ionization time-of-flight mass spectrometry) is a high-throughput technique that can simultaneously interrogate thousands of proteins, thus providing abundant information of protein expressions in an organism. Two datasets have been used as test beds, one dataset includes patients of nasopharyngeal carcinoma (NPC) with different responses to chemotherapy drug, and the other consists of patients of severe acute respiratory syndrome (SARS), influenza, and control normals. The regulatory networks among protein biomarkers were reconstructed for different disease conditions in each dataset. We demonstrated our methods have better classification capability when comparing with conventional methods including Fisher linear discriminant (FLD), K-nearest neighborhood (KNN), linear support vector machines (linSVM) and radial basis function based support vector machines (rbfSVM)).

2. Methods and materials

2.1. Data sets

Our approach was validated through two real-world protein profiling datasets. The NPC dataset [19] includes 54 patients that are categorized into two groups: 10 chemo-responders (RS) and 44 nonresponders (NR). The SARS dataset [20] includes 74 patients from three disease groups: 44 SARS patients, 20 IFZ (influenza-infected) patients, and 10 control normals. These data sets were acquired by the department of oncology of Hong Kong Queen Elizabeth Hospital using SELDI-TOF-MS technology.

For both two datasets, ProteinChip profiling spectra were generated from each serum fraction with proteins/peptides displayed as unique peaks based on their mass-to-charge ratio (m/z) as analyzed by Ciphergen ProteinChip Software 3.0.2. Each peak was first baseline subtracted, then normalized with mean total ion current and included for analysis with a cutoff signal-to-noise ratio >5 for the 1st pass and >2 for the 2nd. After preprocessing, the NPC dataset contains 530 proteins, and the SARS dataset contains 103 proteins.

2.2. Construction and optimization of regulatory networks

In brief, the RN is constructed by employing a hopfield-like network to highlight the mutual relationships among biomarkers, as shown in Fig. 1 . Each node represents a biomarker and arrow lines denote the regulatory relationships. Without loss of generality, assume that there are p biomarkers whose expression levels are denoted by a vector x  = [x ₁,  x ₂, …,  x _p]^T and the regulatory matrix of the RN is denoted as A  = {a _ij  ∈  R; i,  j  = 1, 2, …,  p} with the element a _ij representing the regulatory coefficient from the jth node to the ith node. Let x and y  = [y ₁,  y ₂, …,  y _p]^T be the input and output of the network, the RN can be modeled as

$$\left\{\begin{array}{c}\hfill y_1=a_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1p}{x}_p+b_1\hfill \\ \hfill y_2=a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2p}{x}_p+b_2\hfill \\ \hfill ⋮\hfill \\ \hfill y_p=a_{p1}{x}_1+a_{p2}{x}_2+\cdots +a_{pp}{x}_p+b_p\hfill \end{array}\right),\text{or}\text{written}\text{as}y=Ax+B,B={[b_1,b_2,\cdots b_p]}^{\text{T}}$$ (1)

where b _i, i  = 1, 2, …,  p, is a constant bias.

Fig. 1.

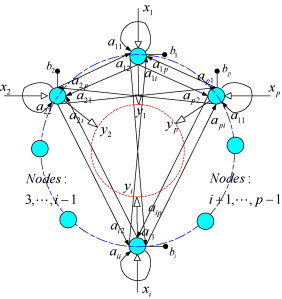
Structure of regulatory network.

For the matrix A, since interaction of a biomarker to itself is meaningless, the following constraint is naturally imposed:

$$a_{ii}=0,i=\mathrm{1,2},\dots ,p$$ (2)

Although some classic neural networks (such as Hopfield network [21]) assume the connection matrix is symmetrical, no assumption is made to the regulation matrix of the RN because two biomarkers incline to regulate each other with different strengths from a biological viewpoint.

A critical issue of building the RN is how to characterize and analyze the RN. To this end, we define an energy function for the RN. The energy function can be formulated as the measurement of the disagreement between the network input and output as follows:

$$E=\frac{1}{2}{(y-x)}^T(y-x)$$ (3)

By substituting Eq. (1) into Eq. (3), the energy function can be rewritten as the following form:

$$E=\frac{1}{2}{(Ax+B-x)}^{\text{T}}(Ax+B-x)$$ (4)

The definition of the energy function indicates that lower energy status corresponds to higher agreement between input and output. If high agreement state remains true for all of the samples in a specific patient group, then the connection matrix of the network can reflect the consistent patterns of biomarker interactions specific to the patient group. The unique patterns of interactions can be used for disease classification. What follows presents the obtainment and optimization of the regulation matrix.

Let X  = [x ₁,  x ₂, …,  x _l] be the biomarker profiling observations of a specific group of patients. The optimal connection matrix A can be achieved through solving the following objective function upon the data X:

$$\begin{array}{l}\text{Minimize}f=E(A,X)=\frac{1}{2}\sum _{j=1}^l{((A-I){\text{x}}_j+B)}^{\text{T}}((A-I){\text{x}}_j+B)\hfill \\ \text{s.t.}{a}_{ii}=0,i=\mathrm{1,2},\dots ,p\hfill \end{array}$$ (5)

where I is the identity matrix. Let $\tilde{A}=(A-I)$, the objective function can be rewritten as

$$f=\frac{1}{2}\sum _{x\in X}{(\tilde{A}x+B)}^{\text{T}}(\tilde{A}x+B)$$ (6)

where the diagonal elements ${\tilde{a}}_{ii}$ of $\tilde{A}$ satisfy:

$${\tilde{a}}_{ii}=-1$$ (7)

By rewriting $\tilde{A}$ as $[{\tilde{A}}_1,{\tilde{A}}_2,\dots ,{\tilde{A}}_p]$, Eq. (6) is expanded to the following form:

$$f=\frac{1}{2}({\tilde{A}}_{1}X+b_1\text{e}){({\tilde{A}}_{1}X+b_1\text{e})}^{\text{T}}+\frac{1}{2}({\tilde{A}}_{2}X+b_2\text{e}){({\tilde{A}}_{2}X+b_2\text{e})}^{\text{T}}+\cdots +\frac{1}{2}({\tilde{A}}_{p}X+b_p\text{e}){({\tilde{A}}_{p}X+b_p\text{e})}^{\text{T}}$$ (8)

where e is a l-dimensional row vector whose elements equal one. The present work only considers the simple case of zero bias, i.e., b _i  = 0, i  = 1, 2, …,  p. In this case, the objective function becomes

$$f=\frac{1}{2}({\tilde{A}}_{1}X){({\tilde{A}}_{1}X)}^{\text{T}}+\frac{1}{2}({\tilde{A}}_{2}X){({\tilde{A}}_{2}X)}^{\text{T}}+\cdots +\frac{1}{2}({\tilde{A}}_{p}X){({\tilde{A}}_{p}X)}^{\text{T}}$$ (9)

By rewriting the ith row vector of X as $U_i={\left[x_{i1},x_{i2},\dots ,x_{il}\right]}^{\text{T}}$ and creating $Z_i=\{x_{jk};k=1,\dots ,i-1,i+1,\dots ,p,j=1,\dots ,l\}$, Eq. (9) is then converted into

$$f=\frac{1}{2}{(U_1-Z_1{\varphi }_1)}^{\text{T}}(U_1-Z_1{\varphi }_1)+\frac{1}{2}{(U_2-Z_2{\varphi }_2)}^{\text{T}}(U_2-Z_2{\varphi }_2)+\cdots +\frac{1}{2}{(U_p-Z_p{\varphi }_p)}^{\text{T}}(U_p-Z_p{\varphi }_p)$$ (10)

where ${\varphi }_i={\left[a_{i1},a_{i2},\dots ,a_{i(i-1)},a_{i(i+1)},\dots ,a_{ip}\right]}^{\text{T}}$ is unknown. Let the derivatives of the objective function in Eq. (10) toward ϕ _i be zero, we have:

$$\frac{\partial f}{\partial {\varphi }_i}=-{Z_i}^{\text{T}}{U}_i+{Z_i}^{\text{T}}{Z}_i{\varphi }_i=0,i=\mathrm{1,2},\dots ,p$$ (11)

By solving Eq. (11), the regulatory coefficients can be obtained as follows:

$${\varphi }_i={(Z_i^{\text{T}}{Z}_i)}^{-1}{Z_i}^{\text{T}}{U}_i,i=\mathrm{1,2},\dots ,p$$ (12)

In case that the inverse of $Z_i^{\text{T}}{Z}_i$ does not exists, the pseudo-inverse can be used to compute the solution.

Although the linear RN is straightforward and easy to explain, the solution may hardly converge in a robust way due to the large variations existed in the data points (especially in marginal data points). To further improve the robustness of the algorithm, we propose to construct the NRN (non-linear regulatory networks) based on the linear RN: adding a sigmoid kernel transformation unit between the input and output of the RN. The sigmoid unit takes x as input and outputs the following vector:

$$v={[v_1,v_2,\dots ,v_p]}^{\text{T}},v_i=s(x_i)={\left(1+e^{-\beta {(x_i-{\mu }_i/{\sigma }_i)}^2}\right)}^{-1},i=\mathrm{1,2},\dots ,p$$ (13)

where β  ∈ (0, 1] is a tunable sigmoid parameter, and ${\mu }_i=\left(\sum x_{ij}\right)/n$ and ${\sigma }_i=\sqrt{\left(\sum {(x_{ij}-{\mu }_i)}^2\right)/(n-1)}$ are the mean and standard deviation of the expression data of ith biomarkers, respectively. Then, the new vector v is fed to the linear RN unit to form the NRN. For NRN, in terms of Eqs. (4), (13), the corresponding energy function becomes

$$E=\frac{1}{2}{(A\text{v}+B-\text{v})}^{\text{T}}(A\text{v}+B-\text{v})$$ (14)

With this new energy function, the structure of the non-linear network can be determined similar to that of the linear network. In addition, the NRN can be optimized by tuning the sigmoid parameter β in Eq. (13).

2.3. Disease classification with the regulatory network and biomarker selection

The information of mutual regulations among biomarkers is stored in the connection matrix of RN. As described above, since the network is optimized towards minimizing its energy function for all the training samples in a group of patients, the connection matrix reserves the unique pattern of this specific group. In other words, for a sample belonging to this group the network will approach a low energy status, and otherwise, the network has high energy. The regulatory networks can be used to predict disease status. Without loss of generality, consider a G-class disease classification problem, we can first obtain G RNs using the network modeling algorithm as described above, which correspond to the G groups. Based on the G RNs, a classification function can be designed as follows:

$$D_{\text{u}}=\arg \{\underset{g}{\min }(E_g(\text{u}),g=\mathrm{1,2},\dots ,G)\}$$ (15)

where u represents an unknown sample, D _u  ∈ {1, 2, …,  G} is the predicted class label, and E _g is the energy function of the gth RN. Fig. 2 illustrates the classification framework.

Fig. 2.

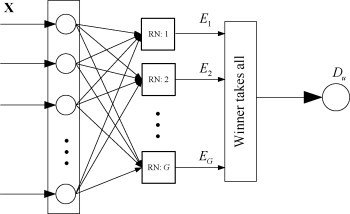
Classification framework based on regulatory networks.

For the designed classifier, selecting significantly regulated biomarkers to construct regulatory networks is essential to achieve good classification ability. We develop a three-step selection procedure to select key proteins. First, the regulation probability method (RPM) [22], [23] is used to pre-select a number of discriminative biomarker candidates to form a biomarker panel. Second, different numbers (p  = 2, 3, 4, …) of biomarkers from the panel are exhaustively combined, and based on each combination, the RN classification algorithm is applied. All the combinations are then evaluated by leave-one-out-cross-validation (LOOCV) accuracy. In the evaluation, to eliminate the influence of the unbalance of sample sizes of different groups the following LOOCV accuracy (Accu) is adopted:

$$Accu=\frac{1}{G}\sum _{g=1}^G\frac{t_g}{l_g}$$ (16)

where t _g is the number of correctly classified samples and l _g is the sample number in gth class. Finally, the biomarker combination with highest accuracy is picked up as the final biomarker set. Based on the biomarker set, the final RN classifier is constructed using all training samples.

3. Results and discussion

3.1. Analysis on the NPC dataset

The NPC dataset was randomly divided into training set and validation set, each with 22 nonresponders and 5 responders. Firstly, we performed the three-step selection procedure on the training data to select differently expressed proteins. To determine the size of the biomarker panel, based on the regulation probability method introduced in [23], a permutation test experiment with 50 permutations was performed to calculate the significance level for each protein. As a result, 20 significant proteins with the significance of <0.1 were picked out to form the panel of biomarker. After that, we implemented the linear and non-linear regulatory network approaches to the NPC data, respectively. For the NRN classifier, the parameter β of the sigmoid function was optimized in the set of {0.001, 0.01, 0.1, 0.5 and 1} through leave-one-out cross-validation. Since small-scale network is more computationally preferable, the number of network nodes p was initially set to 2, and then was gradually increased. Considering increasingly heavy computational burden, our experiments were performed with no more than 6 nodes.

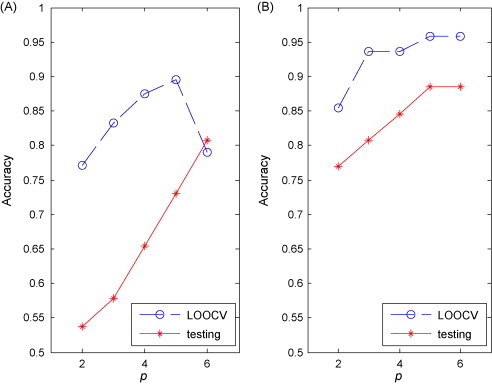
Fig. 3 (A) and (B) shows the changing curves of the classification performances of the RN and NRN classifiers while p is increasing. From the two figures, it can be found that the accuracies of both RN and NRN tend to increase with more proteins were involved, suggesting that more regulatory information is available with more biomarkers for NPC classification. Moreover, the testing accuracies of RN and NRN reached their peaks while 5 biomarkers used, indicating that five proteins can stably support the feature space to distinguish the two groups of patients. The figures also illustrate that NRN achieved a higher testing accuracy of 93% (2 errors among 27 testing samples) compared to RN (89%, 3 errors among 27 testing samples), which suggests that NRN tends to have better classification capability. Fig. 3 also shows that the testing accuracies were consistent with the LOOCV accuracies for both RN and NRN classifiers, which further indicated RN and NRN have the good generalization ability. Fig. 4 illustrates the expression levels of the 5 proteins derived by 5-node NRN in RS and NR groups, it can be seen that two proteins are down-regulated and three are up-regulated. Although proteins are distinctly expressed, their expression ranges over two groups have quite large overlap. This further indicates that the regulatory network can wisely merge noisy information to produce a quality prediction.

Fig. 3.

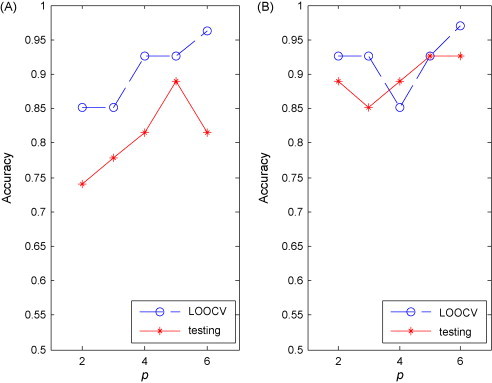
Performances of our RN (A) and NRN (B) classifiers for the NPC dataset.

Fig. 4.

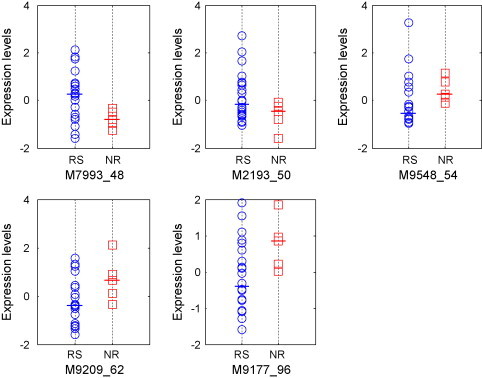
The expression levels of the selected proteins in chemo-responders (RS) and nonresponders (NR).

Fig. 5 illustrates the two NRNs derived from RS and NR groups. The positive interaction strengths represent promotional regulation and the negative ones represent repressive regulation. It can be found that the connection metric of the two networks is remarkably different, suggesting the regulation patterns varied in the different chemo-response groups. For example, interaction coefficients between protein M7993_48 and M2193_50 in RS group are 0.26 and 0.32, suggesting mutual promotion between the two proteins. However, the regulatory strengths become negative, suggesting mutual repression between them. Moreover, in the network of RS group, the mutual regulations between M7993_48 and M9209_62 are very weak (0.035, 0.025), but the regulation from protein M9209_62 to M7993_48 becomes very strong (12.15). Furthermore, both of the NRNs have different dominant biomarkers with greater regulatory coefficients than any others, as marked in the hexagon nodes in Fig. 5(A) and (B). Such dominant biomarkers may dominate the networks associated with cancer and are the hub biomarkers of the networks, which play a crucial role in cancer development [24]. The biomarkers having smaller regulatory coefficients than others are marked in the smaller circle nodes in Fig. 5(A) and (B), which may locate at the far end of the cancer regulation pathway. These differences of regulative patterns captured by our regulatory networks play crucial roles in the RN classifier, which could be potentially meaningful in revealing the molecular mechanism of proteins in cancer development.

Fig. 5.

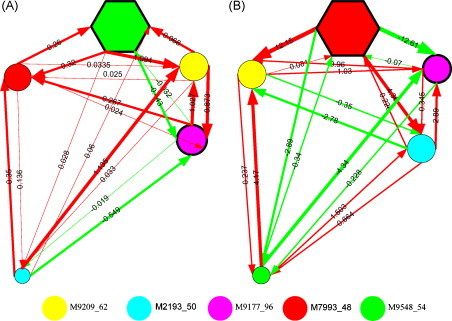
Optimized non-linear regulatory networks with five nodes for the NPC dataset. Subfigure A is for RS; subfigure B is for NR.

We then compared the classification performance of the NRN classifiers with those of conventional methods including FLD, KNN with k  = 3, linSVM and rbfSVM. These methods are either linear or non-linear, and are widely used in bioinformatics and pattern recognition [25], [26], [27], [28], [29], among them SVM has been demonstrated to have superior classification performance in various application areas [30]. In this comparison analysis, rbfSVM parameters, namely the regularization and kernel width, were optimized via two-dimensional grid search and leave-one-out cross-validation. Fig. 6 shows the classification results of NRN and other methods on the independent test set while different numbers of proteins (p) were selected. It can be seen that when p  = 2 or 3, the results of NRN, KNN and rbfSVM were really close. When p is increased to 4, 5, and 6, NRN consistently outperform other methods. NRN classifier got its best accuracy of 93% when p  = 5.

Fig. 6.

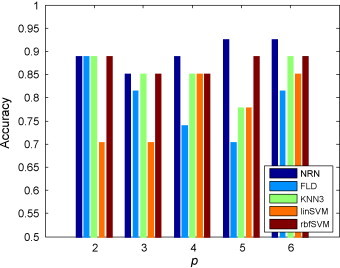
Comparison of the performance of our NRN classifiers with several conventional classification methods on the NPC dataset.

3.2. Analysis on the SARS data

The SARS dataset was split to training set and test set and each with 37 samples including 22 SARS, 10 IFZ, and 5 control normals. Similar to NPC data analysis, a panel of significant proteins was first picked out by using regulation probability methods. Best protein combinations were sought through searching the panel with cross-validation training RN and NRN on the training data. Fig. 7 shows the classification performances with different number of biomarkers (p). It can be seen that both for RN and NRN, the testing accuracies increased when more proteins were involved and similar trend on LOOCV accuracies. This again confirmed that the regulatory network approach can perform very robustly with excellent generalization power. The best test accuracy of 89% was achieved by NRN when 5 proteins were involved. Fig. 8 illustrates the expression range of the 5 proteins, in which it can be seen that C03278_7 and C08131_5 highly expressed for SARS group, C08989_3 and C08954_7 highly expressed for IFZ group, and all the proteins down-regulated for control normals.

Fig. 7.

Performances of our RN and NRN classifiers for the SARS dataset.

Fig. 8.

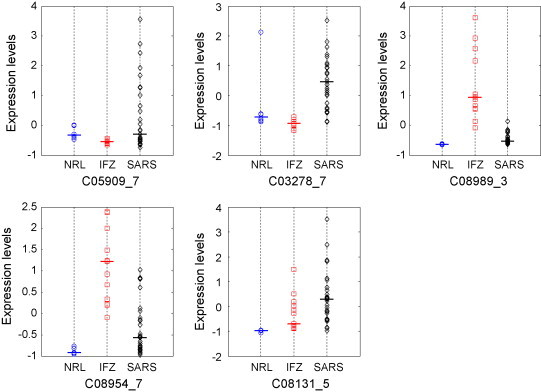
Comparison of the expression levels of the 5 proteins used by the 5-biomarker NRN classifier in normals, IFZ and SARS groups.

Fig. 9 illustrates the three NRNs captured by the 5-node NRN classifier. It can be found that the connection metrics of the three networks are remarkably different, suggesting the regulation patterns change in the three patient groups. For example, the regulations between C08989_3 and C3278_7 are weak in SARS (−0.10, −0.12) and normal (0.09, 0.14), while in IFZ group, the repression strength from C3278_7 to C08989_3 becomes very strong. Also in SARS group, regulatory coefficients between protein C05909_7 and C08989_3 are 0.23 and 0.30, suggesting mutual promotion between the two proteins; while in normal and IFZ groups, their regulatory coefficients become negative, suggesting mutual repression in between. Similar to the analysis on the NPC data, the dominant and minor biomarkers of the regulatory network of each patient group are marked in hexagon and smaller circle nodes respectively. It is observed that the three NRNs have different dominant and minor biomarkers. In summary, the obtained NRNs can remarkably discriminate the three groups from the aspect of protein regulations.

Fig. 9.

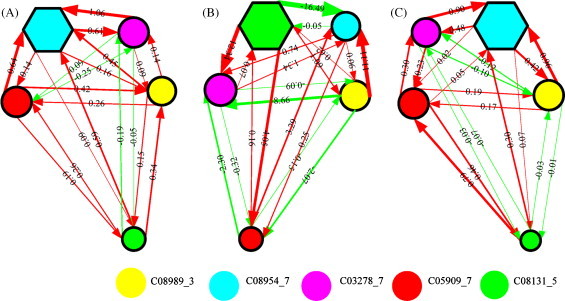
Optimized non-linear regulatory networks with five nodes. Red and green lines represent positive and negative regulations, respectively, and the width of lines indicates the strength of regulations. A is for normal group; B is for influenza-infected group; C is for SARS group. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of the article.)

We then compared the results of our NRN classifier with those of conventional approaches. Similar to that in the NPC experiment, the regularization parameter and the width of the radial basis function kernel of rbfSVM were optimized through two-dimensional grid search and cross-validation. Fig. 10 shows the comparison results, from which it can be found that NRN can always enjoy the best testing accuracies for different number of biomarkers compared to other methods, and it reached its best accuracy of 89% when p  = 5. rbfSVM classifier achieved its best accuracy of 84% when 6 proteins were involved.

Fig. 10.

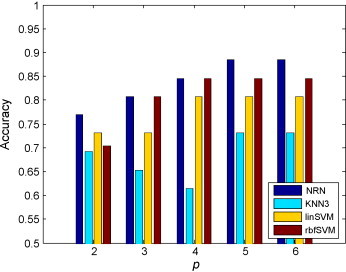
Comparison of the performance of our NRN classifiers with several conventional classification methods on the SARS dataset.

3.3. Stability of the algorithm

From the above two applications, it can be seen that the non-linear regulatory network performs better than its linear version. Hence we believe that the non-linear transformation in the NRN classifiers plays a crucial role in improving the performance. The sigmoid coefficient β is an important parameter of the sigmoid function, which controls the non-linear transformation and can improve the separability of the original data by reducing noise. To investigate the impact of this coefficient, we check the classification performance of the NRN classifier under different values of β on the NPC dataset. As a result, it is observed that even when the coefficient is fixed in range of [0.00, 10.1], similar classification performances can still be obtained, which shows NRN is not sensitive to the sigmoid parameter. We then check the optimized non-linear regulatory coefficients for the NR and RS groups with different values of β. Fig. 11 shows the Pearson relation values between obtained regulatory matrices for the two groups under the setting of β  = {0.001, 0.01, 0.1, 0.5}, of which subfigure (A) is for NR, (B) is for RS, and (C) is between NR and RS. In these subfigures, the different colors represent different Pearson relation values, as shown in the color bar (right panel) (For interpretation of the references to colour in the text, the reader is referred to the web version of the article.). From Fig. 11(A) and (B), it can be found that for the same patient group, the relation values between the regulatory matrices obtained for different values of β are very high (>0.8), while those for different groups are very low (<0.4), as shown in subfigure (C). To check more details, we further compute the deviations of the five regulatory coefficient values of a protein relation. Fig. 12 shows the probability distribution of the deviations for each patient group, indicating that the deviations approach zero. The results suggest that our proposed regulatory network approach can obtain the stable and reliable regulatory relationships as long as the sigmoid parameter is properly set.

Fig. 11.

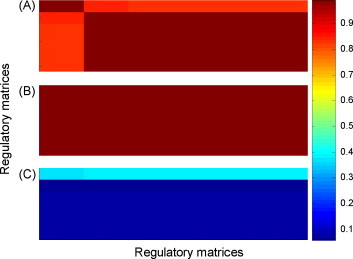
Pearson relations of regulatory matrices by different sigmoid factors. (A) and (B) is for the 5 regulatory matrices of the RS and NR classes, respectively, and (C) is between the regulatory matrices of RS and those of NR.

Fig. 12.

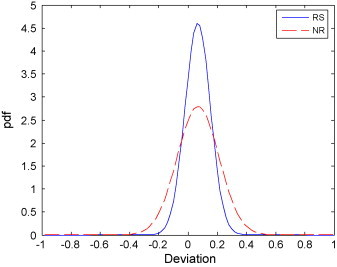
Probability distributions of the deviations of regulatory coefficients by different sigmoid factor for the RS and NR class.

3.4. Sensitivity and specificity analysis

Sensitivity and specificity are another two important criteria for the evaluation of classification performance. In general, sensitivity is considered to be capable of reflecting how good a test is at picking out patients with a disease, and specificity refers to the ability of the test to pick out patients who do not have the disease. As an example, for the NPC dataset, we set the nonresponder group as the positive class and responder group to be negative. For SARS dataset, we take one class as the positive class and the left two classes as negative in turn to make evaluation. As a result, the sensitivities and specificities of our NRN classifiers and the three methods, KNN, linSVM and rbfSVM, are shown in Table 1 . It can be found that all sensitivity and specificity values of our NRN classifier are higher than 80%, which are better than those of the three previous approaches. It is also observed that irrespective the NPC dataset or the SARS dataset, the NRN classifier has less variation between sensitivity and specificity than any of the three previous approaches. This advantage should be due to the capsulation of the optimized regulatory networks for each group in the NRN classifier.

Table 1.

Comparison of sensitivity and specificity of the NRN classification approach with those of several conventional approaches.

Datasets			NRN	KNN3	LinSVM	RbfSVM
NPC	RS	Sensitivity	95%	86%	86%	95%
		Specificity	80%	40%	40%	60%
SARS	SARS	Sensitivity	100%	80%	86%	93%
		Specificity	81%	90%	90%	72%
	IFZ	Sensitivity	100%	100%	86%	86%
		Specificity	94%	89%	94%	100%
	Normals	Sensitivity	25%	25%	50%	50%
		Specificity	100%	86%	86%	95%

The best results of different methods upon the two datasets (NPC and SARS) are shown in bold values.

4. Conclusions

In this paper, we proposed a novel approach of regulatory network for regulatory pattern extraction and disease classification. The derived networks can effectively capture the unique regulatory patterns of protein markers associated with different patient groups and hence can be used for disease classification. In the experimental section, the proposed regulatory networks have been validated on two real-world protein profiling dataset, NPC and SARS. The comparisons of our method and the conventional methods, including FLD, KNN, linSVM and rbfSVM have been made as well. Experimental results showed the effectiveness and efficiency of our networks in capturing the regulatory patterns of various diseases as well as the excellent discriminative power. In contrast to conventional methods, the proposed approach can characterize complex regulation relationships and perform disease classification in an accurate manner. The regulatory patterns of disease classes were encapsulated in the regulatory coefficients of the RNs. From a biological viewpoint, the positive coefficients represent up-regulation which promotes the expression of the regulated genes, while the negative coefficients represent down-regulation which represses the expression of the regulated genes, and the absolute values of the coefficients indicate the corresponding regulation strengths. The discovered regulation relationships can potentially provide insights to revealing the molecular signaling pathways.