Coupling infectious diseases, human preventive behavior, and networks – A conceptual framework for epidemic modeling

Abstract

Human-disease interactions involve the transmission of infectious diseases among individuals and the practice of preventive behavior by individuals. Both infectious diseases and preventive behavior diffuse simultaneously through human networks and interact with one another, but few existing models have coupled them together. This article proposes a conceptual framework to fill this knowledge gap and illustrates the model establishment. The conceptual model consists of two networks and two diffusion processes. The two networks include: an infection network that transmits diseases and a communication network that channels inter-personal influence regarding preventive behavior. Both networks are composed of same individuals but different types of interactions. This article further introduces modeling approaches to formulize such a framework, including the individual-based modeling approach, network theory, disease transmission models and behavioral models. An illustrative model was implemented to simulate a coupled-diffusion process during an influenza epidemic. The simulation outcomes suggest that the transmission probability of a disease and the structure of infection network have profound effects on the dynamics of coupled-diffusion. The results imply that current models may underestimate disease transmissibility parameters, because human preventive behavior has not been considered. This issue calls for a new interdisciplinary study that incorporates theories from epidemiology, social science, behavioral science, and health psychology.

Highlights

► A modeling framework to couple the diffusion of infectious diseases and preventive behavior based on human networks. ► The first attempt to investigate the coupled-diffusion under scale-free and small-world networks. ► Infection networks play a more important role than communication networks in the coupled-diffusion. ► Previous studies may underestimate parameters regarding disease transmissibility, such as the R₀.

Introduction

Despite outstanding advance in medical sciences, infectious diseases remain a major cause of death in the world, claiming millions of lives every year (WHO, 2002). Particularly in the past decade, emerging infectious diseases have obtained remarkable attention due to worldwide pandemics of severe acute respiratory syndrome (SARS), bird flu and new H1N1 flu. Although vaccination is a principal strategy to protect individuals from infection, new vaccines often need a long time to develop, test, and manufacture (Stohr & Esveld, 2004). Before sufficient vaccines are available, the best protection for individuals is to adopt preventive behavior, such as wearing facemasks, washing hands frequently, taking pharmaceutical drugs, and avoiding contact with sick people, etc. (Centers for Disease Control and Prevention, 2008).

It has been widely recognized that both infectious diseases and human behaviors can diffuse through human networks (Keeling and Eames, 2005, Valente, 1996). Infectious diseases often spread through direct or indirect human contacts, which form infection networks. For example, influenza spreads through droplet/physical contacts among individuals, and malaria transmits via mosquitoes between human hosts. Human behavior also propagates through inter-personal influence that fashions communication networks. This is commonly known as the ‘social learning’ or ‘social contagion’ effect in behavioral science, i.e., people can learn by observing behaviors of others and the outcomes of those behaviors (Hill et al., 2010, Rosenstock et al., 1988). In the current literature, models of disease transmission and behavioral diffusion have been developed separately for decades, both based on human networks (Deffuant et al., 2005, Keeling and Eames, 2005, Valente, 1996, Watts and Strogatz, 1998). Few efforts, however, have been devoted to integrating infectious diseases and human behaviors together. In reality, when a disease breaks out in a population, it is natural that individuals may voluntarily adopt some preventive behavior to respond, which in turn limits the spread of disease. Failing to consider these two interactive processes, current epidemic models may under-represent human-disease interactions and bias policy making in public health.

This article aims to propose a conceptual framework that integrates infectious diseases, human preventive behavior, and networks together. The focus of this article is on issues that arise in establishing a conceptual framework, including basic principles, assumptions, and approaches for model formulization. The following section (Section 2) describes the conceptual framework and basic assumptions, which abstract essential aspects of a disease epidemic. The third section discusses approaches to formulize the model framework into a design. The fourth illustrates a computing model upon various human network structures and compares the simulation results. The last section concludes the article with implications.

Conceptual model and basic assumptions

The conceptual model consists of two networks and two diffusion processes (Fig. 1 ). The two networks include an infection network that transmits disease agents (dark dash lines), and a communication network that channels inter-personal influence regarding preventive behavior (gray dash lines). Both networks are composed of same individuals but different types of interactions. These two networks could be non-overlapping, partially or completely overlapping with one another. The two diffusion processes refer to the diffusion of infectious diseases (dark arrows) and that of preventive behavior (gray arrows) through the respective network. As illustrated in Fig. 1, if individual #1 is initially infected, the disease can be transmitted to individual #2 and #3, and then to individual #4, following the routes of infection network. Meanwhile, individual #2 may perceive the risk of being infected from individual #1, and then voluntarily adopt preventive behavior for protection, known as the effects of ‘perceived risks’ (Becker, 1976). Further, the preventive behavior of individual #2 may be perceived as a ‘social standard’ by individual #4 and motivate him/her toward adoption, i.e., the ‘social contagion’. In such a manner, the preventive behavior diffuses on the communication network through inter-personal influence. During an epidemic, these two diffusion processes take place simultaneously and interact in opposite directions. The diffusion of diseases motivates individuals to adopt preventive behavior, which, in turn, limits the diffusion of diseases. This two-network two diffusion framework is dubbed as a ‘coupled diffusion’ in the subsequent discussion.

Fig. 1.

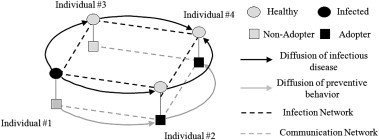
Conceptual model of the coupled-diffusion processes through two networks.

The conceptual framework entails five assumptions. First, individuals differ in their characteristics and behaviors, such as their infection status, adoption status, and individualized interactions. Second, both infection and communication networks are formed by interactions among individuals. Third, the development of infectious diseases follows disease natural history, such as the incubation, latent, and infectious periods. Fourth, individuals voluntarily adopt preventive behavior, dependent on their own personality, experiences, and inter-personal influence from family members, colleagues, as well as friends (Glanz, Rimer, & Lewis, 2002). Fifth and lastly, the infection status of surrounding people or their behavior may motivate individuals to adopt preventive behavior, which then reduces the likelihood of infection. Of the five assumptions, the first two provide networks as a basis for modeling. The third and fourth assumptions are relevant to the two diffusion processes, respectively. The last assumption represents the interactions between the two processes.

Model formulization

Corresponding to the five assumptions, this article introduces a number of approaches to represent individuals, networks, infectious diseases, and preventive behavior, as four model components, and depicts the relationships between the four.

Individuals

The first model assumption requires a representation of discrete individuals, their unique characteristics and behaviors. This requirement can be well addressed by an individual-based modeling approach. In the last decade, this modeling approach has gained momentum in the research community of both epidemiology and behavioral science (Judson, 1994, Koopman and Lynch, 1999). Specifically, the individual-based approach views a population as discrete individuals, i.e., every individual is a basic modeling unit and has a number of characteristics and behaviors. The characteristics indicate states of individuals, e.g., the infection status, adoption status, and the number of contacts, while the behaviors change these states, e.g., receiving infection and adopting preventive behavior. By simulating at an individual level, this approach allows to understand how the population characteristics, such as the total number of infections and adopters, emerge from collective behaviors of individuals (Grimm & Railsback, 2005). From an implementation perspective, the characteristics and behaviors of individuals can be easily accommodated by object-oriented languages, a mainstream paradigm of programming technologies. Various tools are also available to facilitate the design and implementation of individual-based approach, such as the NetLog and Repast (Robertson, 2005).

Networks

With regard to the second assumption, both the infection and communication networks can be abstracted as a finite number of nodes and links. Nodes represent individuals and links represent interactions among individuals. The network structure is compatible with the aforementioned individual-based approach, in that the individual nodes directly correspond to the basic modeling units, while links can be treated as a characteristic of individuals. Interactions between individuals (through links) can be represented as behaviors of individuals. To be realistic in modeling, both networks can be generated to fit observed characteristics and structures of real-world networks.

Important characteristics of networks include: the number of links attached to a node (the node degree), the minimum number of links between any pair of nodes (the path length), the ratio between the existing number of links and the maximum possible number of links among certain nodes (the level of clustering), and so on (Scott, 2000). Particularly for human networks of social contacts, empirical studies showed that the average node degree often varies from 10 to 20, dependent on occupation, race, geography, etc (Edmunds et al., 2006, Fu, 2005). The average path length was estimated to be around 6, popularly known as the ‘six degrees of separation’ (Milgram, 1967). The level of clustering has typical values in the range of 0.1–0.5 (Girvan & Newman, 2002). Besides these characteristics, studies on human networks have also disclosed two generic structures: “small-world” and “scale-free” structures. The “small-world” structure is named after the ‘small-world’ phenomena, arguing that people are all connected by short chains of acquaintances (Travers & Milgram, 1969). Theoretically, the small-world structure is a transition state between regular networks and random networks (Watts & Strogatz, 1998). The regular networks represent one extreme that all nodes are linked to their nearest neighbors, resulting in highly clustered networks. The random networks are the other extreme that all nodes are randomly linked with each other regardless of their closeness, resulting in short path lengths. A typical small-world structure has characteristics from both extremes, i.e., most nodes are directly linked to others nearby (highly clustered), but can be indirectly connected to any distant node through a few links (short path lengths). The “scale-free” structure has also been commonly observed in social, biological, disease, and computer networks, etc. (Cohen et al., 2001, Jeong et al., 2000, Liljeros et al., 2001). It depicts a network with highly heterogeneous degrees of nodes, whose distribution follows a power-law decay function, p < k > ∼k ^{− γ} (k denotes the node degree and empirically 2 < γ < 3). In other words, a few individuals have a significantly large number of links, while the rest of individuals only have a few (Albert, Jeong, & Barabasi, 2000). All of these observed characteristics and structures can be used to calibrate the modeled networks, which then serve as a reliable basis to simulate the coupled-diffusion process.

Infectious diseases

In epidemiology, the development of infectious diseases has been characterized by a series of infection statuses, events, and periods, often referred to as the natural history of diseases (Gordis, 2000). The progress of an infectious disease often starts with a susceptible individual. After having contact with an infectious individual, this susceptible individual may receive disease agents and develop infection based on a transmission probability. The receipt of infection triggers a latent period, during which the disease agents develop internally in the body and are not emitted. The end of the latent period initiates an infectious period, in which this individual is able to infect other susceptible contacts and may manifest disease symptoms. After the infectious period, this individual either recovers or dies from the disease. Among these disease characteristics, the transmission probability is critical for bridging infectious diseases to the other model components: individuals, networks, and preventive behavior. This probability controls the chance that the disease agents can be transmitted between individuals through network links. Meanwhile, the reduction of transmission probability reflects the efficacy of preventive behavior.

The individual-based modeling approach enables the representation of disease progress for each individual. The infection statuses, periods, and transmission probability per contact can be associated with individuals as their characteristics, while infection events (e.g., receipt of infection and emission of agents) can be modeled as behaviors of individuals. Each individual has one of four infection statuses at a time point, either susceptible, latent, infectious, or recovered (Kermack & McKendrick, 1927). The infection status changes when infection events are triggered by behaviors of this individual or surrounding individuals. The simulation of disease transmission often starts with an introduction of a few infectious individuals (infectious seeds) into a susceptible population. Then, the first generation of infections can be identified by searching susceptible contacts of these seeds. Stochastic methods, such as the Monte Carlo method, could be used to determine who will be infected or not. Subsequently, the first generation of infections may further infect their contacts, and over time leads to a cascade diffusion of disease over the network. To parameterize the simulation, the transmission probability of a disease, the lengths of latent period and infectious period can be derived from the established literature or from observational disease records.

Preventive behavior

Like other human behaviors, the adoption of preventive behavior depends on the individual’s own characteristics (e.g., knowledge, experience, and personal traits) and inter-personal influence from surrounding individuals (e.g., family supports and role model effects) (Glanz et al., 2002). Because individuals vary in their willingness to adopt, human behaviors often diffuse from a few early adopters to the early majority, and then over time throughout the social networks (Rogers, 1995). A number of individual-based models have been developed by sociologists and geographers to represent such behavioral diffusion processes, e.g., the Mean-Information-Field (MIF) model (Hägerstrand, 1967), the threshold model (Granovetter, 1978), the relative agreement model (Deffuant et al., 2005), etc. The MIF model populates individuals on a regular network (or a grid), and assumes that a behavior diffuses through the ‘word-of-mouth’ communication between an adopter and his/her neighbors. The MIF is a moving window that defines the size of neighborhood and the likelihood of human communications to every adopter. The simulation centers the MIF on every adopter and uses the Monte Carlo method to identify a new generation of adopters (Hägerstrand, 1967). The threshold model assumes that individuals observe their surroundings and adopt a behavior based on a threshold effect (Granovetter, 1978, Valente, 1996). The threshold is the proportion of adopters in an individual’s social contacts necessary to convince this individual to adopt. The behavioral diffusion begins with a small number of adopters, and spreads from the low-threshold population to the high-threshold population. The recently proposed relative agreement model assumes that every individual holds an initial attitude, which is a value range specified by a mean value, maximum and minimum. Based on the value ranges, individuals’ attitudes are categorized as positive, neutral, and negative. Individuals communicate through a social network, and influence their attitudes (value ranges) reciprocally according to mathematical rules of relative agreement. If individuals can hold positive attitudes for a certain time period, they will decide to adopt a behavior (Deffuant et al., 2005). Due to the individual-based nature of all these models, they can be easily incorporated under the proposed conceptual framework. To further discuss the individual-based design of behavioral models, this research chose the threshold model for illustrations. In terms of complexity, the threshold model lies midway between the MIF model and the relative agreement model, and its parameters can be feasibly estimated through social surveys. The MIF model has been criticized for its simplicity in that it assumes an immediate adoption after a communication and oversimplifies the decision process of individuals (Shannon, Bashshur, & Metzner, 1971). By contrast, the relative agreement model is too sophisticated: many parameters are difficult to estimate, for example, the ranges of individual attitudes.

The threshold model can be formulized as follows so as to become an integral part of the coupled-diffusion framework. First, individuals are assumed to spontaneously evaluate the proportion of adopters among their contacts, and perceive the pressure of adoption. Once the perceived pressure reaches a threshold (hereinafter called the threshold of adoption pressure), an individual will decide to adopt preventive behavior. Second, in order to relate the preventive behavior to infectious diseases, individuals also evaluate the proportion of infected individuals (with disease symptoms) among their contacts, and perceive the risks of infection. Once the perceived risk reaches another threshold (hereinafter called the threshold of infection risk), an individual will also adopt preventive behavior. These two threshold effects can be further formulized as three characteristics and two behaviors of individuals. The three characteristics include an adoption status (adopter or non-adopter) and two individualized thresholds toward adoption. The two behaviors represent the individual’s evaluation of adoption pressure and infection risk from surrounding contacts, which in turn determines their adoption status. The individualized thresholds toward adoption reflect personal characteristics of individuals, while the behaviors of evaluation represent the inter-personal influence between individuals. To build a working model, the individualized thresholds toward adoption can be best estimated by health behavior surveys as illustrated below.

Relationships between components

Based on the discussion above, the conceptual framework (Fig. 1) can be transformed into a formative design with four model components and their relationships (Fig. 2 ). Individuals are building blocks of the proposed model, and their interactions compose networks as a core of the model. Through the infection network, individuals may receive infection from others and have their infection status changed, propelling the diffusion of diseases. Meanwhile, individuals may perceive risks and pressure from the communication network, and gradually adopt preventive behavior, resulting in the behavioral diffusion. The adoption of preventive behavior reduces the disease transmission probability, thus controlling and preventing the disease transmission. In this manner, the diffusion of diseases and preventive behavior in a population are coupled together.

Fig. 2.

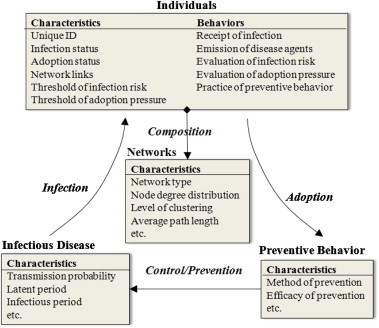
Four model components (boxes), associated characteristics and behaviors (inside boxes), and relationships between components (arrows).

Model illustrations

Model implementation

To illustrate the proposed coupled-diffusion model, an influenza epidemic was simulated in a hypothetic population of 5000 individuals (N = 5000), each with characteristics and behaviors as described in Fig. 2. Influenza was chosen because it is common and readily transmissible between individuals. The simulation simply assumes that the population is closed, i.e., no births, deaths, or migrations. With regard to the network component, the average number of links per individuals was set to 12, reasonably assuming that an individual on average has contact with 2 family members and 10 colleagues. For the purpose of sensitivity analysis, the illustrative model allowed the disease and communication networks to take either a small-world (SW) structure or a scale-free (SF) structure. The generation of SW structures started with a regular network where all individuals were linked to their nearest neighbors. Then, each individual’s existing links were rewired with a probability to randomly selected individuals (Watts & Strogatz, 1998). The rewiring probability p ranged from 0 to 1, and governed the clustering level and average path lengths of resultant networks (Fig. 3 a). The SF structures were created by a preferential attachment algorithm, which linked each new individual preferentially to those who already have a large number of contacts (Pastor-Satorras & Vespignani, 2001). This algorithm produces a power-law degree distribution, p < k > ∼k ^{− γ} (k is the node degree), with various exponents γ (Fig. 3b). Based on Fig. 3a and b, the rewiring probabilities p were set to 0.005, 0.05, and 0.5 to typically represent the regular, small-world, and random networks, respectively (Fig. 3c–e). The exponent γ were set to 3, 5, and 7 to represent three scale-free networks with high, medium, and low levels of node heterogeneity (Fig. 3f–h). A sensitivity analysis was performed to examine every possible pair of <p, p>, <γ, γ>, <p, γ> and <γ, p> as a network combination (3 p-values × 3 γ-values × 4 = 36 combinations in total), where the first parameter indicates the structure of infection network and the second specifies the structure of communication network.

Fig. 3.

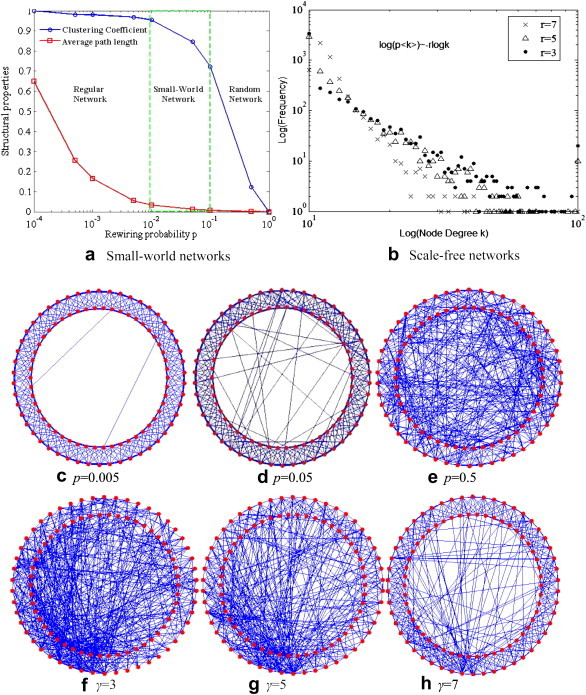
(a) Standardized network properties (average path length and clustering coefficient) as a function of rewiring probability p from 0 to 1, given N = 5000; (b) The power-law degree distributions given γ = 3, 5 and 7, given N = 5000; (c–e) an illustration of generated SW networks for three p values, given N = 100 for figure clarity; (f–h) an illustration of SF networks for three γ values, given N = 100.

To simulate the diffusion of influenza, the latent period and infectious period were specified as 1 day and 4 days, respectively, based on published estimates (Heymann, 2004). The transmission probability per contact was varied from 0.01 to 0.1 (with a 0.01 increment) to test its effects on the coupled-diffusion processes. 50% of infected individuals was assumed to manifest symptoms, following the assumption made by Ferguson et al. (2006). Only these symptomatic individuals could be perceived by their surrounding individuals as infection risks. Recovered individuals were deemed to be immune to further infection during the rest of the epidemic.

With respect to the diffusion of preventive behavior, the use of flu antiviral drugs (e.g., Tami flu and Relenza) was taken as a typical example because its efficacy is more conclusive than other preventive behavior, such as hand washing and facemask wearing. For symptomatic individuals, the probability of taking antiviral drugs was set to 75% (McIsaac et al., 1998, Stoller et al., 1993), and the consequent probability of infecting others was set to be reduced by 40% (Longini, Halloran, Nizam, & Yang, 2004). Susceptible individuals may also take antiviral drugs due to the perceived infection risk or adoption pressure. If they use antiviral drugs, the probability of being infected was set to be reduced by 70% (Hayden, 2001).

The key to simulate the diffusion of preventive behavior was to estimate thresholds of infection risk and that of adoption pressure for individuals. A health behavior survey was conducted online for one month (March 12–April 12, 2010) to recruit participants. Voluntary participants were invited to answer two questions: 1) “Suppose you have 10 close contacts, including household members, colleagues, and close friends, after how many of them GET INFLUENZA would you consider using flu drugs?”, and 2) “Suppose you have 10 close contacts, including household members, colleagues, and close friends, after how many of them start to USE FLU DRUGS would you consider using flu drugs, too?”. The first question was designed to estimate the threshold of infection risks, while the second was for the threshold of adoption pressure. The survey ended up with 262 respondents out of 273 participants (a 96% response rate), and their answers were summarized into two threshold-frequency distributions (Fig. 4 ). The Monte Carlo method was then performed to assign threshold values to the 5000 modeled individuals based on the two distributions. This survey was approved by the IRB in University at Buffalo.

Fig. 4.

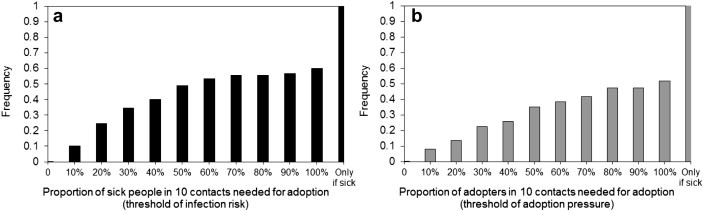
Cumulative frequency distributions of the two adoption thresholds estimated from the online health behavior survey. The category ‘Only-if-sick’ means that surveyed individuals will use flu drugs only if they were sick (symptomatic).

To initialize the simulation, all 5000 individuals were set to be non-adopters and susceptible to influenza. One individual was randomly chosen to be infectious on the first day. The model took a daily time step and simulated the two diffusion processes simultaneously over 200 days. The simulation results were presented as disease attack rates (total percent of symptomatic individuals in the population), and adoption rates (total percent of adopters in the population). Another two characteristics were derived to indicate the speed of coupled-diffusion: the epidemic slope and the adoption slope. The former is defined as the total number of symptomatic individuals divided by the duration of an epidemic (in day). Similarly, the latter is defined as the total number of adopters divided by the duration of behavioral diffusion (in day). They are called slopes because graphically they approximate the slopes of cumulative diffusion curves. A higher slope implies a faster diffusion because of more infections/adoptions (the numerator) in a shorter time period (the denominator). All simulation results were averaged by 50 model realizations to average out the randomness.

Simulation results and discussion

Simulation results were presented in two parts. First, the coupled-diffusion process under various transmission probabilities was analyzed, and compared to an influenza-only process that is widely seen in the literature. The influenza-only process was simulated with the same parameters in the coupled-diffusion process except that individual preventive behavior was not considered. For the ease of comparison, a typical “small-world” network (p = 0.05), was chosen for both infection and communication networks, assuming the two are overlapping. The second part examined the dynamics of coupled-diffusion under various structures of infection and communication networks, i.e., the 36 pairs of network parameters <p, p>, <γ, γ>, <p, γ> and <γ, p> while fixing the influenza transmission probability to 0.05 (resultant basic reproductive number R₀ = 1–1.3).

Fig. 5 a indicates that the diffusion of influenza with and without the preventive behavior differs significantly, particularly for medium transmission probabilities (0.04–0.06). For the influenza-only process (the black curve with triangles), the disease attack rate rises dramatically as the transmission probability exceeds 0.03, and reaches a plateau of 50% when the probability increases to 0.07. The coupled-diffusion process (the black curve with squares) produces lower attack rates, which slowly incline to the maximum of 45%. This is because individuals gradually adopt preventive behavior, thereby inhibiting disease transmission from infectious individuals to the susceptible. Meanwhile, the adoption rate (the gray curve with squares) also increases with the transmission probability, and can achieve a 65% of the population as the maximum. This is not surprising because the more individuals get infected, the greater risks and pressure other individuals may perceive, motivating them to adopt preventive behavior. Individuals who have not adopted eventually may have extremely high-threshold of adoption (see Fig. 4), and thus resist adopting preventive behavior. Fig. 5b displays an example of the coupled-diffusion process (transmission probability = 0.05), ending up with nearly 2000 symptomatic cases and approximately 3000 adopters of flu antiviral drugs. Despite differences in magnitude, the two diffusion curves exhibit a similar trend that follows the 5-phase S-shaped curve of innovation diffusion (Rogers, 1995). The ‘innovation’ phase occurs from the beginning to Day 30, followed by the ‘early acceptance’ phase (Day31–50), ‘early majority’ (Day 51–70), ‘late majority’ (Day 71–90) and ‘laggards’ (after Day 90). This simulated similarity in temporal trend is consistent with many empirical studies regarding flu infection and flu drug usage. For example, Das et al. (2005) and Magruder (2003) had compared the temporal variation of both influenza incidence and over-the-counter flu drug sales in the New York City and the Washington DC metropolitan area, respectively. Both studies reported a high correlation between over-the-counter drug sales and cases of diagnosed influenza, and thus suggested that over-the-counter drug sales could be a possible early detector of disease outbreaks. The consistency with the observed facts, to some extent, reflects the validity of the proposed model.

Fig. 5.

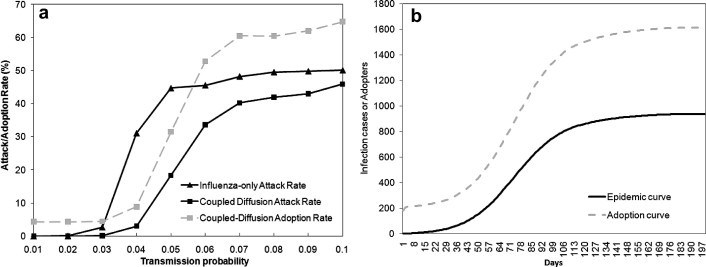
(a) Effects of transmission probability (0.01–0.1) on the influenza-only diffusion process and the coupled-diffusion process; (b) A simulated dynamics of coupled-diffusion processes, given the transmission probability = 0.05 (R₀ = 1–1.3). The epidemic curve depicts the cumulative number of symptomatic individuals in the population throughout the course of the epidemic, while the adoption curve indicates the cumulative number of adopter in the population during the behavioral diffusion.

In addition to the transmission probability, the coupled-diffusion process is also sensitive to various combinations of network structures, i.e., 36 pairs of network parameters <p, p>, <γ, γ>, <p, γ> and <γ, p> (Fig. 6 ). The Z axis represents either the epidemic or adoption slope, and a greater value indicates a faster diffusion process. In general, both epidemic and adoption slopes change dramatically with the structure of infection network, while they are less sensitive to the variation of communication networks. Given the small-world infection network (Fig. 6a–b and e-f), the epidemic and adoption slopes increase quickly as the rewiring probability p rises from 0.005 to 0.5. When p = 0.005 (a regular network), almost all individuals are linked to their nearest neighbors, and influenza transmission between two distant individuals needs to go through a large number of intermediate individuals. The slow spread of influenza induces a low perception of infection risks among individuals, thereby decelerating the dissemination of preventive behavior. As p increases to 0.5 (a random network), a large number of shortcuts exist in the network, and the transmission of influenza is greatly speeded by shortcuts. As a result, the diffusion of preventive behavior is also accelerated, because individuals may perceive more risks of infection and take actions quickly. Likewise, given a scale-free infection network (Fig. 6c–d and g-h), both influenza and preventive behavior diffuse much faster in a highly heterogeneous network (γ = 3) than in a relatively homogeneous network (γ = 7). This is because a highly heterogeneous network has a few super-spreaders who have numerous direct contacts. Super-spreaders act as hubs directly distributing the influenza virus to a large number of susceptible individuals, thus speeding the disease diffusion. As individuals perceived more risks of infection in their surroundings, they will adopt preventive behavior faster.

Fig. 6.

The sensitivity of coupled-diffusion processes to various network structures, including SW_Infection−SW_{Communication} as <p_Infection, p_{Communication} >, SF_infection−SF_{Communication} as <γ_Infection,γ_{Communication} > SW_Infection−SF_{Communication} as <p_Infection, γ_{Communication} > and SF_Infection−SW_{Communication} as <γ_Infection, p_{Communication} >. Each combination is displayed in one row from top to bottom. The SW and SF denote the network structure, while the subscripts indicate the network function. Parameter p is the rewiring probability of a SW network, taking values (0.005, 0.05, 0.5), while parameter γ is the exponent of a SF network, taking values (3, 5, 7). The Z axis denotes epidemic slopes (the left column) and adoption slopes (the right column) as a result of a network structure. A greater Z value indicates a faster diffusion process.

Conclusions and implications

Human networks, infectious diseases, and human preventive behavior are intrinsically inter-related, but little attention has been paid to simulating the three together. This article proposes a conceptual framework to fill this knowledge gap and offer a more comprehensive representation of the disease system. This two-network two diffusion framework is composed of four components, including individuals, networks, infectious diseases, and preventive behavior of individuals. The individual-based modeling approach can be employed to represent discrete individuals, while network structures support the formulization of individual interactions, including infection and communication. Disease transmission models and behavioral models can be embedded into the network structures, and simulate disease infection and adoptive behavior, respectively. The collective changes in individuals’ infection and adoption status represent the coupled-diffusion process at the population level. Compared to the widely used influenza-only models, the proposed model produces a lower percent of infection, because preventive behavior protects certain individuals from being infected. Sensitivity analysis identifies that the structure of infection network is a dominant factor in the coupled-diffusion, while the variation of communication network produces fewer effects.

This research implies that current predictions about disease impacts might be under-estimating the transmissibility of the disease, e.g., the transmission probability per contact. Modelers fit to observed data in which populations are presumably performing preventive behavior, while the models they create do not account for the preventive behavior. When they match their modeled infection levels to those in these populations, the disease transmissibility needs to be lower than its true value so as to compensate for the effects of preventive behavior. This issue has been mentioned in a number of recent research, such as Ferguson et al. (2006), but the literature contains few in-depth studies. This article moves the issue towards its solution, and stresses the importance of understanding human preventive behavior before policy making. The study raises an additional research question concerning social-distancing interventions for disease control, such as the household quarantine and workplace/school closure. Admittedly, these interventions decompose the infection network for disease transmission, but they may also break down the communication network and limit the propagation of preventive behavior. The costs and benefits of these interventions remain unclear and a comprehensive evaluation is needed.

The proposed framework also suggests several directions for future research. First, although the illustrative model is based on a hypothetical population, the representation principles outlined in this article can be applied to a real population. More realistic models can be established based on the census data, workplace data, and health survey data. Second, the proposed framework focuses on inter-personal influence on human behavior, but has not included the effects of mass media, another channel of behavioral diffusion. The reason is that the effects of mass media remain inconclusive and difficult to quantify, while the effects of inter-personal influence have been extensively studied before. Third, the proposed framework has not considered the ‘risk compensation’ effect, i.e., individuals will behave less cautiously in situations where they feel safer or more protected (Cassell, Halperin, Shelton, & Stanton, 2006). In the context of infectious diseases, the risk compensation can be interpreted as individuals being less cautious of the disease if they have taken antiviral drugs, which may facilitate the disease transmission. This health psychological effect could also be incorporated to refine the framework.

To summarize, this article proposes a synergy between epidemiology, social sciences, and human behavioral sciences. For a broader view, the conceptual framework could be easily expanded to include more theories, for instance, from communications, psychology, and public health, thus forming a new interdisciplinary area. Further exploration in this area would offer a better understanding of complex human-disease systems. The knowledge acquired would be of a great significance given that vaccines and manpower may be insufficient to combat emerging infectious diseases.