Abstract
The importance of the promoter sequences in the function regulation of several important mycobacterial pathogens creates the necessity to design simple and fast theoretical models that can predict them. This work proposes two DNA promoter QSAR models based on pseudo-folding lattice network (LN) and star-graphs (SG) topological indices. In addition, a comparative study with the previous RNA electrostatic parameters of thermodynamically-driven secondary structure folding representations has been carried out. The best model of this work was obtained with only two LN stochastic electrostatic potentials and it is characterized by accuracy, selectivity and specificity of 90.87%, 82.96% and 92.95%, respectively. In addition, we pointed out the SG result dependence on the DNA sequence codification and we proposed a QSAR model based on codons and only three SG spectral moments.
Keywords: QSAR, Markov model, Mycobacterial promoters, Star-graph, Lattice network, Topological indices
1. Introduction
Protein synthesis promoter sequences play an important role in the function regulation of several important mycobacterial pathogens (Levine and Tjian, 2003; Wyrick and Young, 2002). In this sense, the prediction of the mycobacterial promoter sequences (Mps) could be interesting for the future discovery of new anti-mycobacterial drug targets or for the study of protein metabolism. Mycobacteria have a low transcription rate and a low RNA content per DNA unit. Thus, the transcription and translation signals in Mycobacteria may be different from those in other bacteria such as Esccherichia coli. The large variations among the characterized mycobacterial promoters suggest that the consensus sequences are not representative of these promoters. Consequently, a number of conflicting opinions regarding the presence and characteristics of consensus promoter sequences in the Mycobacteria have been presented in the literature (Mulder et al., 1997). Therefore, understanding the factors responsible for the low level of transcription and the possible mechanisms of regulation of gene expression in Mycobacteria, involves the examination of the mycobacterial promoter structure and the promoter transcription machinery, including chemical information about the involved RNA molecules (Arnvig et al., 2005; Harshey and Ramakrishnan, 1977). Efforts have been made to develop statistical algorithms for the sequence analysis and motif prediction by searching for homologous regions or by comparing the sequence information with a consensus sequence (O’Neill and Chiafari, 1989). Wide variations existing within individual promoter sequences are primarily responsible for the unsatisfactory results yielded by the promoter-site-searching algorithms that in essence perform statistical analysis (Mulligan and McClure, 1986; Mulligan et al., 1984). Therefore, it can be inferred that the recognition of Mps requires a powerful technique capable of unravelling those hidden patterns in the promoter regions, which are difficult to identify directly by sequence alignment.
The bioinformatics methods, based on sequence alignment, may fail in general in cases of low sequence homology between the database query and the template sequences. The lack of function annotation (defined biological function) of the sequences used as template for function prediction constitutes another weakness of the alignment approaches (Dobson and Doig, 2005; Dobson et al., 2004, Dobson et al., 2005). In addition, Chou demonstrated that the 3D structures developed, based on homology modelling are very sensitive to the sequence alignment of the query protein with the structure-known protein (Chou, 2004). A group of researchers shows the growing importance of machine learning methods for predicting protein functional class, independently of sequence similarity (Han et al., 2006). These methods often use the input the 1D sequence numerical parameters, specifically defined to seek sequence–function relationships. For instance, the so-called pseudo amino acid composition approach (Chou, 2001a, Chou, 2005), based on 1D sequence coupling numbers, has been widely used to predict subcellular localization, enzyme family class, structural class, as well as other attributes of proteins based on their sequence similarity (Caballero et al., 2006; Chou and Shen, 2006; Du et al., 2008). Alternatively, the molecular indices that are classically used for small molecules (Aguero-Chapin et al., 2006; Liao and Wang, 2004a, Liao and Wang, 2004b, Liao and Wang, 2004c; Liao and Ding, 2005; Liao et al., 2005, Liao et al., 2006; Liu et al., 2002; Nandy, 1994, Nandy, 1996; Nandy and Basak, 2000; Randic and Vracko, 2000; Randic and Balaban, 2003; Randic and Zupan, 2004; Randic et al., 2000; Song and Tang, 2005; Woodcock et al., 1992; Zupan and Randic, 2005) have been adapted to describe the protein sequences. On the other hand, many authors have introduced 2D or higher dimension representations of sequences prior to the calculation of numerical parameters. This is an important step in order to uncover useful higher-order information not encoded by 1D sequence parameters (Randic, 2004). An example of the 2D representations is the graphs used for proteins and DNA sequences. For instance, the spectral-like and zigzag representations have been used in order to suggest an algorithm to enclose long strings of building blocks (like four DNA bases, 20 natural amino acids, or all 64 possible base triplets) (Aguero-Chapin et al., 2006). The use of the graphic approaches to study biological systems can provide useful insights, as indicated by many previous studies on a series of important biological topics, such as enzyme-catalyzed reactions (Andraos, 2008; Chou, 1981, Chou, 1989; Chou and Forsen, 1980; Chou and Liu, 1981; Chou et al., 1979; Cornish-Bowden, 1979; King and Altman, 1956; Kuzmic et al., 1992; Myers and Palmer, 1985; Zhou and Deng, 1984), protein folding kinetics (Chou, 1990), inhibition kinetics of processive nucleic acid polymerases and nucleases (Althaus et al., 1993a, Althaus et al., 1993b, Althaus et al., 1993c; Chou et al., 1994), analysis of codon usage (Chou and Zhang, 1992; Zhang and Chou, 1993, Zhang and Chou, 1994), analysis of DNA sequence (Qi et al., 2007). Moreover, graphical methods have been introduced for the quantitative structure-activity relationships (QSAR) study (Gonzalez-Diaz et al., 2006c, González-Díaz et al., 2007b; Prado-Prado et al., 2008) as well as used to deal with complicated network systems (Diao et al., 2007; González-Díaz et al., 2007a., González-Díaz et al., 2008). Recently, the “cellular automaton image” (Wolfram, 1984, Wolfram, 2002) has also been applied to study hepatitis B viral infections (Xiao et al., 2006a), HBV virus gene missense mutation (Xiao et al., 2005b), and visual analysis of SARS-CoV (Gao et al., 2006; Wang et al., 2005), as well as to represent complicated biological sequences (Xiao et al., 2005a) and help to identify protein attributes (Xiao and Chou, 2007; Xiao et al., 2006b).
In this work, we are proposing a comparative study of the Mycobacterial DNA promoter prediction using pseudo-folding lattice network (LN) and star-graph (SG) topological indices. The first group of indices contains the mean stochastic electrostatic potential (LN ξk), Markov spectral moments (LN πk) and Markov entropies (LN θk) of a Markov model (MM) associated to a 2D network that numerically characterize DNA sequences and build a QSAR model to predict Mps. The lattice-like representations (also called maps or graphs) for Mps and control group sequences (Cgs) were derived (González-Díaz et al., 2003a, González-Díaz et al., 2006a, González-Díaz et al., 2005c; González-Díaz, 2007d). The ξk, πk and θk values of several types of graphs/networks have been the base for different QSAR studies of DNA/RNA and protein sequences (Du et al., 2007a, Du et al., 2007b; Garcia-Garcia et al., 2004; Marrero-Ponce et al., 2004a, Marrero-Ponce et al., 2004b, Marrero-Ponce et al., 2005b; Meneses-Marcel et al., 2005; Santana et al., 2006). The second group of TIs is derived from the SG representations (Harary, 1969). We subsequently developed a classifier to connect Mps information (represented by the ξk, πk, θk and SG TIs values) with the prediction of Cgs as Mps. The Linear Discriminant Analysis (LDA) was selected as a simple but powerful technique (González-Díaz et al., 2006b; González-Díaz, 2003a).
2. Materials and methods
2.1. Pseudo-folding LN
The first MM, also called MARCH-INSIDE, was used to codify the information of 135 Mps (González-Díaz et al., 2005a, González-Díaz et al., 2006a, González-Díaz et al., 2007d) and 511 random Cgs (see Table S.1 in the Supplementary material). Our methodology considers as states of the Markov Chain (MC) any atom, nucleotide or amino acid depending on the class of molecule to be described (González-Díaz et al., 2005e, González-Díaz et al., 2003c). Therefore, MM deals with the calculation of the probabilities (k pij) where the charge distribution of nucleotide moves from any nucleotide in the vicinity i at time t 0 to another nucleotide j along the protein backbone in discrete time periods, until a stationary state is achieved (Yuan, 1999). As seen from the discussion above, we selected LN ξk , LN πk and LN θk based on the utility of non-stochastic (González-Díaz and Uriarte, 2005; González-Díaz et al., 2005d; Ramos de Armas et al., 2004) and stochastic parameters (Randic and Vracko, 2000). Many researchers have demonstrated the possibility of predicting RNA from sequences (Aguero-Chapin et al., 2006) and we used 2D graphs to encode information about Mps sequences (Estrada, 2000, Estrada, 2002; Estrada and González-Díaz, 2003; González-Díaz et al., 2005b; González and Moldes del Carmen Teran, 2004; González et al., 2005, González et al., 2006; Vilar et al., 2005, Vilar et al., 2006). This RNA 2D graphical representation is similar to those previously reported for DNA (Jacchieri, 2000; Nandy, 1994, Nandy, 1996) using four different nucleotides. The construction of the 2D lattice graph corresponding to the Mps of the gene Alpha in Mycobacterum bovis (BCG) is shown in Table 1 and Fig. 1 . Each nucleotide in the sequence is placed in a Cartesian 2D space starting with the first monomer at the (0, 0) coordinates. The coordinates of the successive nucleotide are calculated according to with the following rules:
-
(a)
Increase by +1 the abscissa axis coordinate for thymine (rightwards-step) or
-
(b)
Decrease by –1 the abscissa axis coordinate for cytosine (leftwards-step) or
-
(c)
Increase by +1 the ordinate axis coordinate for adenine (upwards-step) or
-
(d)
Decrease by –1 the ordinate axis coordinate for guanine (downwards-step).
Table 1.
LN construction rules for the Mps of the gene Alpha in Mycobacterum bovis (BCG)
| DNA LN | |||
|---|---|---|---|
| c1g2a3c4t5t6t7c8g9c10c11c12g13a14a15t16c17g18a19c20 | |||
| a21t22t23t24g25g26c27c28t29c30c31a32c33a34c35a36c37g38g39t40 | |||
| a41t42g43t44t45c46t47g48g49c50c51c52g53a54g55c56a57c58a59c60 | |||
| g61a62c63g64a65 | |||
| n | Nucleotide | x | y |
| 1 | c1a3t5g25 | 0 | 0 |
| 2 | g2c10g26 | 0 | −1 |
| 3 | c4t16 | −1 | 0 |
| 4 | t6c8 | 1 | 0 |
| 5 | t7 | 2 | 0 |
| 6 | g9 | 1 | −1 |
| 7 | c11c27t29 | −1 | -1 |
| 8 | c12a14g18c28c30g48 | −2 | −1 |
| 9 | g13g49 | −2 | −2 |
| 10 | a15c17a19t45t47 | −2 | 0 |
| 11 | c20a32t44c46 | −3 | 0 |
| 12 | a21 | −3 | 1 |
| 13 | t22 | −2 | 1 |
| 14 | t23 | −1 | 1 |
| 15 | t24 | 0 | 1 |
| 16 | c31 | −3 | −1 |
| 17 | c33g43 | −4 | 0 |
| 18 | a34t42 | −4 | 1 |
| 19 | c35a41 | −5 | 1 |
| 20 | a36 | −5 | 2 |
| 21 | c37 | −6 | 2 |
| 22 | g38 | −6 | 1 |
| 23 | g39 | −6 | 0 |
| 24 | t40 | −5 | 0 |
| 25 | c50 | −3 | −2 |
| 26 | c51 | −4 | −2 |
| 27 | c52a54 | −5 | −2 |
| 28 | g53g55 | −5 | −3 |
| 29 | c56 | −6 | −3 |
| 30 | a57 | −6 | −2 |
| 31 | c58 | −7 | −2 |
| 32 | a59 | −7 | −1 |
| 33 | c60a62 | −8 | −1 |
| 34 | g61 | −8 | −2 |
| 35 | c63a65 | −9 | −1 |
| 36 | g64 | −9 | −2 |
Fig. 1.
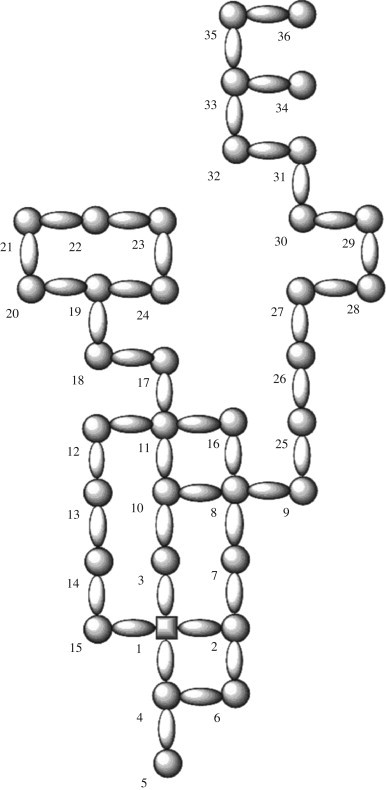
LN for the Mps of the gene Alpha in Mycobacterum bovis (BCG).
In the next step, we assigned a stochastic matrix 1 Π to each graph. The elements of 1 Π are the probabilities 1 pij of reaching a node ni with the charge Qi moving through a walk of length of k=1 from another node nj with charge Qj (Aguero-Chapin et al., 2006):
| (1) |
| (2) |
where αij equals to 1 if the nodes ni and nj are adjacent in the graph or equal to 0 otherwise; Qj is equal to the sum of the electrostatic charges of all nucleotides placed at this node. Note that the number of nodes (n) in the graph is equal to the number of rows and columns in 1 Π but it may be equal or even smaller than the number of DNA bases in the sequence. It then becomes straightforward to calculate different types of invariant parameters for 1 Π in order to numerically characterize the DNA sequence. In this work we calculated the following invariants:
| (3) |
| (4) |
| (5) |
where LN πk are the Markov spectral moments and indicate that we sum all the values in the main diagonal of the matrices LN πk=tr(k Π)=tr[(1 Π)k] (tr is the trace operator), LN ξk are the mean values of electrostatic potentials and LN θk are the Markov entropies (González-Díaz et al., 2007e). All calculations of the LN ξk , LN πk and LN θk values for the DNA sequences of both groups (Mps and Cgs) were carried out with our in-house software MARCH-INSIDE, version 2.0® (González-Díaz et al., 2007e), including sequence representation.
2.2. SG topological indices
Each DNA sequence is a real network where the nucleotides are the vertices/nodes, connected in a specific sequence by the phosphodiester bonds. SG is an abstract representation of the real network that has a dummy non-nucleotide centre and a number of “rays” equal with the nucleotide types. In the case of DNA, we can consider two codifications: the nucleotide code (as in the case of the amino acid protein sequences) and the DNA codons (the final incomplete codons are ignored). In the first codification, there are only four branches (“rays”) of the star corresponding to the four types of nucleotides: adenosine (a), thymidine (t), cytidine (c) and guanosine (g). Using the codons, the DNA sequences are virtually translated into amino acid sequences that generate 21 branches, 20 standard amino acids and an extra X non-amino acid corresponding to the STOP DNA codons (Griffiths et al., 1999). Even if the promoters are not naturally translated in proteins, the second codification is useful for a comparison with the protein SG calculations. The same DNA/protein can be represented by different forms associated to distinct distance matrices (Randic et al., 2007). Standard SG were constructed for each DNA promoter: each nucleotide/vertex holds the position in the original sequence and the branches are labelled by the standard letters of the nucleotides (a, t, c and g). If the initial connectivity in the DNA sequence is included, the graph is embedded. In order to qualitatively evaluate the graphs, it is necessary to transform the graphical representation into correspondent connectivity matrix, distance matrix and degree matrix. In the case of embedded graph, the matrices of the connectivity in the sequence and in the SG are combined. These matrices and the normalized ones are the base of the calculation of the topological indices.
For a visual comparison of the lattice and SG representations, the same promoter sequence from Table 1 was used to generate a standard SG based on codons that are virtually translated to amino acids (see Table 2 and Fig. 2 ).
Table 2.
SG codifications for the virtually translated Mps of the gene Alpha in Mycobacterum bovis (BCG)
| DNA codon SG | |
|---|---|
| DNA nucleotide sequence | c1g2a3c4t5t6t7c8g9c10c11c12g13a14a15t16c17g18a19c20a21 |
| t22t23t24g25g26c27c28t29c30c31a32c33a34c35a36c37g38g39 | |
| t40a41t42g43t44t45c46t47g48g49c50c51c52g53a54g55c56a57c58a59c60g61a62c63 | |
| DNA codons sequence | cga1ctt2tcg3ccc4gaa5tcg6aca7 |
| ttt8ggc9ctc10cac11aca12cgg13 | |
| tat14gtt15ctg16gcc17cga18gca19cac20gac21 | |
| Virtually translated amino acid sequence | R1L2S3P4E5S6T7F8G9L10H11T12R13Y14V15L16A17R18A19H20D21 |
Fig. 2.
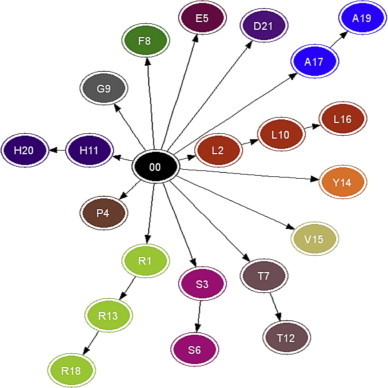
SG for the Mps of the gene Alpha in Mycobacterum bovis (BCG).
The SG topological indices are obtained with the in-house sequence to star networks (S2SNet) python application. This tool can transform any character string in SG topological indices. Our recent works (Munteanu et al., 2008a, Munteanu et al., 2008b) proved the potential of S2SNet in protein QSAR models. The calculations presented in this work are characterized by embedded (E) and non-embedded (nE) TIs, non-weights, Markov normalization and power of matrices/indices (n) up to 5. The result file contains the following embedded (super index “e”) or non-embedded TIs (Todeschini and Consonni, 2002):
Shannon Entropy of the n powered Markov matrices (SG θn):
| (6) |
where pi are the ni elements of the p vector, resulted from the matrix multiplication of the powered Markov normalized matrix (ni×ni) and a vector (ni×1) with each element equal to 1/ni;
The trace of the n connectivity matrices (SG πn):
| (7) |
where n=0−power limit, SG M=SG connectivity matrix (i*i dimension); ii=ith diagonal element;
Harary number (H):
| (8) |
where dij are the elements of the distance matrix and mij are the elements of the M connectivity matrix;
Wiener index (W):
| (9) |
Gutman topological index (S 6):
| (10) |
where degi are the elements of the degree matrix;
Schultz topological index (non-trivial part) (S):
| (11) |
Balaban distance connectivity index (J):
| (12) |
where nodes+1=AA numbers/node number in the SG+origin, ∑k dik is the node distance degree;
Kier–Hall connectivity indices (n X):
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
Randic connectivity index (1 XR):
| (18) |
The embedded and non-embedded SG TIs are used to construct a DNA promoter classification model using the LDA statistical methods.
2.3. Linear discriminant analysis
LDA forward stepwise analysis from STATISTICA (StatSoft.Inc., 2002) was carried out for a variable selection to build up the model (Garcia-Garcia et al., 2004; Kutner et al., 2005; Marrero-Ponce et al., 2004a, Marrero-Ponce et al., 2004b, Marrero-Ponce et al., 2005b; Meneses-Marcel et al., 2005; Santana et al., 2006). In order to decide whether a DNA sequence is classified as a mycobacterial promoter (Prom) or not (nProm), we added an extra dummy variable named Prom/nProm (binary values of 1/−1 for LN and 1/0 for SG) and a cross-validation variable (CV). The best cross-validation methods in practice are the independent dataset test, the subsampling test and the jackknife test (Chou and Zhang, 1995). The jackknife test has been increasingly used by investigators to examine the accuracy of various predictors (Chen and Li, 2007; Chou and Shen, 2007a, Chou and Shen, 2008; Diao et al., 2007; Ding et al., 2007; Lin, 2008; Xiao and Chou, 2007). In the actual work, the independent data test is used by splitting the data at random in a training series (train, 75%) used for model construction and a prediction one (val, 25%) for model validation (the CV column is filled by repeating 3 train and 1 val). All the variables included in the models were standardized in order to bring them onto the same scale. Subsequently, standardized linear discriminant equations that allow comparison of their coefficients were obtained (Chiti et al., 2003; Pawar et al., 2005).
In the case of LN, the general QSAR formula is the following:
| (19) |
where LNMps-score is the continue score value for the DNA mycobacterial promoter classification corresponding to the lattice representation, LN πk are Markov spectral moments (traces), LN θk are the Markov entropies, LN ξk the mean stochastic electrostatic potential, bk, ck, dk are the coefficients of the previous indices and a 0 is the independent term. A similar formula defines the SG QSAR model in Eq. (20).
| (20) |
where SGMps-score is the continue score value for the DNA mycobacterial promoter classification corresponding to the SG representation, SG πk e/SG πk and SG θk e/SG θk are embedded/non-embedded traces (Markov spectral moments) and the Shannon entropies, TIk e/TIk are the other 22 standard SG embedded and non-embedded TIs (H, W, S 6, S, J, 0 X, 2 − 5 X, 1 XR, H e, W e, S 6 e, S e, J e, 0 X e, 2 − 5 X e, 1 XR e), fk e/fk, gk e/gk and ek e/ek are the TIs coefficients and e 0 is the independent term. Accuracy, specificity, sensitivity, F, Wilk's (λ) statistic (λ=0 perfect discrimination, being 0<λ<1) were examined in order to assess the discriminatory power of the model.
3. Results and discussion
Many different parameters can be used to encode RNA sequence information and further assign or predict the function or physical properties (González-Díaz and Uriarte, 2005). The present approach involves the calculation of different sequence parameters, which can be applied to different types of molecular graphs (Aguero-Chapin et al., 2006), including DNA, RNA and proteins (Di Francesco, 1999; González-Díaz et al., 2005c). MM has been applied successfully to Genomics and Proteomics and represents an important tool to analyse biological sequence data. In particular, MM has been used for protein folding recognition (Chou, 2001b) and for prediction of protein signal sequences (Chou and Shen, 2007b; Van Waterbeemd, 1995). This work compared two models based on different TIs including πk and θk values of the stochastic matrices 1 Π(LN) and 1 Π(SG) (SGM) associated with LN and SG, LN ξk parameters of 1 Π(LN) as well as classic TIs for 1 Π(SG). These parameters describe the distribution of the nucleotides of the DNA sequence in the above graphs/networks. This calculation was carried out for two groups of DNA sequences, one made up of Mps and the other formed by Cgs. In addition, previous results of the RNA secondary structure (2S) QSAR are compared.
3.1. Results for DNA LN indices
In the first study of the DNA LN representations, the best QSAR equation that classifies a novel sequence as Mps or not is the following (Table 3 ):
| (21) |
The statistical parameters of this equation were Wilk's statistic (λ=0.95) and the error level (p-level<0.001). This discriminant function misclassified only 36 cases out of 511 Cgs used, reaching a high level of accuracy (90.87%). More specifically, the model classified correctly 112/135 (82.9%) of Mps and 475/511 (92.9%) of the control group. Conversely, the remaining four descriptors LN ξ 0, LN ξ 2, LN ξ 3 and LN ξ 4 do not have a significant relationship with the Mps characteristic. The use of only six molecular descriptors to model a data set of 585 sequences prevents us by large from chance correlation. In physical terms, the above results confirm other studies about the relationship between the electrostatic potential of the DNA molecule and its biological activity. However, in this case, not all the electrostatic interactions affect the activity in the same way. Finally, long-term electrostatic interaction potentials (LN ξ 0, LN ξ 2, LN ξ 3 and LN ξ 4) do not correlate with the Mps activity. The detailed results of the forward stepwise analysis are given in Table 3.
Table 3.
Summary of the LDA results for DNA LN and SG models vs. RNA 2S folding representations
| TI | Ac (%) | Se (%) | Sp (%) | Final TIs | Vars. | λ | F | p | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| Primary structure of DNA nucleotide & LN | |||||||||
| LNθk | 78.33 | 72.59 | 79.84 | LNθ0 | 1 | 0.74 | 230.5 | 0.0001 | a |
| LNπk | 81.73 | 78.52 | 82.58 | LNπ0, LNπ1, LNπ5, | 3 | 0.89 | 76.3 | 0.0001 | a |
| LNξk | 90.87 | 82.96 | 92.95 | LNξ1, LNξ5 | 2 | 0.82 | 142.1 | 0.0001 | a |
| Pool | 92.88 | 75.56 | 97.46 | LNθ0, LNπ0, LNξ1, LNξ5 | 4 | 0.83 | 130.8 | 0.0001 | a |
| Primary structure of DNA nucleotide sequences & SG | |||||||||
| SGθk | 66.25 | 81.48 | 62.23 | SGθ1e, SGθ4e | 2 | 0.78 | 69.62 | 0.001 | a |
| SGπk | 71.21 | 85.19 | 67.51 | SGπ0e, SGπ2e, SGπ5e | 3 | 0.76 | 49.54 | 0.001 | a |
| TIk | 75.39 | 68.15 | 77.30 | W, Je, 0Xe | 3 | 0.73 | 58.19 | 0.001 | a |
| Pool | 81.58 | 68.15 | 85.13 | SGπ5e, H, 1XRe | 3 | 0.67 | 79.94 | 0.001 | a |
| Primary structure of DNA codon sequences & SG | |||||||||
| SGθk | 70.43 | 76.30 | 68.88 | SGθ0, SGθ1, SGθ4e | 3 | 0.75 | 52.31 | 0.001 | a |
| SGπk | 74.77 | 82.96 | 72.60 | SGπ4, SGπ4e, SGπ5e | 3 | 0.74 | 56.37 | 0.001 | a |
| TIk | 76.16 | 59.26 | 80.63 | S, 0X, 1XRe | 3 | 0.72 | 60.98 | 0.001 | a |
| Pool | 80.80 | 74.81 | 82.39 | SGθ0, SGθ4e, SGπ4e, SGπ5e, W | 5 | 0.67 | 47.04 | 0.001 | a |
| RNA electrostatic parameter of thermodynamically-driven 2S folding | |||||||||
| 2Sθk | 97.60 | 93.30 | 100.00 | 2Sθ0 | 1 | 0.34 | 724.47 | 0.001 | b |
| 2Sπk | 93.83 | 83.70 | 98.89 | 2Sπ0, 2Sπ2 | 2 | 0.44 | 515.03 | 0.05 | c |
| 2Sξk | 96.58 | 85.19 | 100.00 | 2Sξ0, 2Sξ1 | 2 | 0.41 | 38.8 | 0.001 | d |
Note: the terms Ac, Se, and Sp mean accuracy, sensitivity and specificity, and measure the ratio of the number of total, Mps, or Cgs sequences correctly classified by the model with respect to the real classification; Vars.=no of variables in the QSAR equations; SG=star-graph; LN=lattice network; 2S=secondary structure; super index “e” represents the embedded calculations; references (Ref.) are a: this work, b: (González-Díaz et al., 2007c), c: (González-Díaz et al., 2005a) and d: (González-Díaz et al., 2006a).
Analyzing the above equations, it is important to highlight that, the combination of a negative contribution of LN ξ 1 and a positive contribution of LN ξ 5 in Eq. (21) point to a pseudo-folding rule for the biological activity. A validation procedure was subsequently performed in order to assess the model predictability. This validation was carried out with an external series of Mps and randomized Cgs. The present model showed an accuracy of 90.87%, which is similar in comparison to results obtained by other researchers when using the LDA method in QSAR studies (González-Díaz et al., 2007f). These results are also consistent with many others that we have recently reviewed in-depth and published as a review article where we used different network-like indices in small-sized, nucleic acid, and protein QSAR (González-Díaz et al., 2005d, González-Díaz et al., 2007d, González-Díaz et al., 2007f; Marrero-Ponce et al., 2005a, Marrero-Ponce et al., 2005b; Van Waterbeemd, 1995).
3.2. Results for DNA SG indices
The second study used the SG–QSAR models in order to evaluate the same mycobacterial DNA promoter property (see Table 3). The grouping of the embedded and non-embedded TIs was done similar to the lattice models: the traces (SG πk e/SG πk), the Shannon entropies (SG θk e/SG θk), the rest of embedded and non-embedded TIs (H, W, S 6, S, J, 0 X, 2 − 5 X, 1 XR, H e, W e, S 6 e, S e, J e, 0 X e, 2 − 5 X e, 1 XR e) and all SG TIs (pool). The forward stepwise selection variable method, conjugated with the nE & E TIs of the virtually translated DNA sequences, provides better results for the codon grouping of the nucleotides, with accuracy, sensitivity and specificity greater than 70% for the SG πk e/SG πk and for the pool (Table 3). Even if the accuracy of the simple nucleotide sequences are up to 81.58% (pool), the selectivity and the specificity have values lower than 70%. The best QSAR model using the SG based on the codon sequences is defined with the SG πk e/SG πk group of indices in Eq. (22) and is characterized by 74.77% accuracy, 82.96% sensitivity and 72.60% specificity.
| (22) |
Despite the good values of accuracy, sensitivity and specificity (80.80%, 74.81%, 82.39%) for the pool group of TIs (SG θ 0, SG θ 4 e, SG π 4 e, SG π 5 e, W), the QSAR model cannot be considered due to the low sensitivity for the CV set (66.67%). Thus, the results based on the traces (spectral moments) are similar in the case of LN and SG representations, maintaining the SG π 5 e/LN π 5 in the equations.
3.3. Comparison with RNA 2S and other indices
In previous works, we have published QSAR models to predict Mps using RNA electrostatic parameters of thermodynamically-driven 2S folding representations. These models were based on the 2S θk (González-Díaz et al., 2007c), 2S πk (González-Díaz et al., 2005a) and 2S ξk (González-Díaz et al., 2006a) values for the 1 Π(2S) matrix associated to RNA 2S folding representations. In Table 3 we illustrate that the best values of accuracy, sensitivity and specificity of 97.60%, 93.30% and 100% were found for 2S θ 0. This TI is present in the QSAR equations for DNA LN/SG and RNA 2S folding representations. All these observations pointed out the importance of the spectral moments, entropies and in the stochastic electrostatic potentials in the DNA/RNA QSAR models. In general, the results for RNA 2S folding representation are better, but they require additional calculations for the optimization of RNA 2S. Therefore, several RNA 2S are possible for the same DNA sequence (theoretically because the promoters have no correspondent RNA) by introducing an indeterminacy in the final model prediction. In Fig. 3 we depict a possible 2S for the RNA sequence corresponding to the DNA sequences used in Fig. 1, Fig. 2 (dG is the free energy). This RNA 2S was obtained with the online DINAMelt server (Markham and Zuker, 2005). The SG TIs that show to not be important for the DNA/RNA models (H, W, S, J) can successfully describe protein QSAR models (Munteanu et al., 2008b). This work pointed out the conclusion that the models based on SG, LN, as well as 2S, which are linear and have few variables, can be compared very favourably in terms of complexity with other models previously reported by Kalate et al. (2003). These authors used a non-linear artificial neural network and a large parameter space.
Fig. 3.
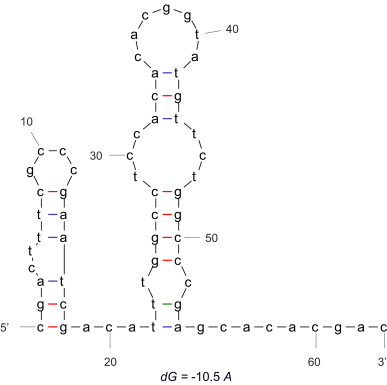
RNA 2S for the Mps of the gene Alpha in Mycobacterum bovis (BCG).
5. Conclusions
The work presents a comparative study of the parameters associated with LN and SG representations in order to predict the mycobacterial DNA promoters. LN QSAR classifier successfully discriminates between Mps and a control group, with values significantly better than the SG-QSAR results based on the DNA codon sequences. In addition, the DNA nucleotide sequences (used for LN) were not able to create a good model based on SG representations. The work promotes the use of the experience accumulated in small-molecules QSAR with spectral moments and other kind of indices (entropies and spectral moments) in new types of DNA QSAR studies, today in the focus of attention of many researchers worldwide.
Acknowledgements
Cristian R. Munteanu thanks the FCT (Portugal) for support from grant SFRH/BPD/24997/2005. González-Díaz H. acknowledges the program Isidro Parga Pondal of Xunta de Galicia for the financial support of a tenure-eligible research position at the Faculty of Pharmacy, University of Santiago de Compostela (Spain). The authors thank financial support from grant INCITE07PXI203141ES, Conselleria de Industria, Xunta de Galicia, Spain.
Footnotes
Supplementary data associated with this article can be found in the online version at doi:10.1016/j.jtbi.2008.09.035.
Appendix A. Supporting Information
Supporting Information A
References
- Aguero-Chapin G., González-Díaz H., Molina R., Varona-Santos J., Uriarte E., González-Diaz Y. Novel 2D maps and coupling numbers for protein sequences. The first QSAR study of polygalacturonases; isolation and prediction of a novel sequence from psidium guajava L. FEBS Lett. 2006;580:723–730. doi: 10.1016/j.febslet.2005.12.072. [DOI] [PubMed] [Google Scholar]
- Althaus I.W., Chou J.J., Gonzales A.J., Diebel M.R., Chou K.C., Kezdy F.J., Romero D.L., Aristoff P.A., Tarpley W.G., Reusser F. Steady-state kinetic studies with the non-nucleoside HIV-1 reverse transcriptase inhibitor U-87201E. J. Biol. Chem. 1993;268:6119–6124. [PubMed] [Google Scholar]
- Althaus I.W., Gonzales A.J., Chou J.J., Diebel M.R., Chou K.C., Kezdy F.J., Romero D.L., Aristoff P.A., Tarpley W.G., Reusser F. The quinoline U-78036 is a potent inhibitor of HIV-1 reverse transcriptase. J. Biol. Chem. 1993;268:14875–14880. [PubMed] [Google Scholar]
- Althaus I.W., Chou J.J., Gonzales A.J., Diebel M.R., Chou K.C., Kezdy F.J., Romero D.L., Aristoff P.A., Tarpley W.G., Reusser F. Kinetic studies with the nonnucleoside HIV-1 reverse transcriptase inhibitor U-88204E. Biochemistry. 1993;32:6548–6554. doi: 10.1021/bi00077a008. [DOI] [PubMed] [Google Scholar]
- Andraos J. Kinetic plasticity and the determination of product ratios for kinetic schemes leading to multiple products without rate laws: new methods based on directed graphs. Can. J. Chem. 2008;86:342–357. [Google Scholar]
- Arnvig K.B., Gopal B., Papavinasasundaram K.G., Cox R.A., Colston M.J. The mechanism of upstream activation in the rrnB operon of Mycobacterium smegmatis is different from the Escherichia coli paradigm. Microbiology. 2005;151:467–473. doi: 10.1099/mic.0.27597-0. [DOI] [PubMed] [Google Scholar]
- Caballero J., Fernandez L., Abreu J.I., Fernandez M. Amino acid sequence autocorrelation vectors and ensembles of Bayesian-regularized genetic neural networks for prediction of conformational stability of human lysozyme mutants. J. Chem. Inf. Model. 2006;46:1255–1268. doi: 10.1021/ci050507z. [DOI] [PubMed] [Google Scholar]
- Chen Y.L., Li Q.Z. Prediction of apoptosis protein subcellular location using improved hybrid approach and pseudo amino acid composition. J. Theor. Biol. 2007;248:377–381. doi: 10.1016/j.jtbi.2007.05.019. [DOI] [PubMed] [Google Scholar]
- Chiti F., Stefani M., Taddei N., Ramponi G., Dobson C.M. Rationalization of the effects of mutations on peptide and protein aggregation rates. Nature. 2003;424:805–808. doi: 10.1038/nature01891. [DOI] [PubMed] [Google Scholar]
- Chou K.C. Two new schematic rules for rate laws of enzyme-catalyzed reactions. J. Theor. Biol. 1981;89:581–592. doi: 10.1016/0022-5193(81)90030-8. [DOI] [PubMed] [Google Scholar]
- Chou K.C. Graphical rules in steady and non-steady enzyme kinetics. J. Biol. Chem. 1989;264:12074–12079. [PubMed] [Google Scholar]
- Chou K.C. Review: applications of graph theory to enzyme kinetics and protein folding kinetics. Steady and non-steady state systems. Biophys. Chem. 1990;35:1–24. doi: 10.1016/0301-4622(90)80056-d. [DOI] [PubMed] [Google Scholar]
- Chou K.C. Prediction of protein cellular attributes using pseudo-amino acid composition. Proteins. 2001;43:246–255. doi: 10.1002/prot.1035. [DOI] [PubMed] [Google Scholar]
- Chou K.C. Prediction of signal peptides using scaled window. Peptides. 2001;22:1973–1979. doi: 10.1016/s0196-9781(01)00540-x. [DOI] [PubMed] [Google Scholar]
- Chou K.C. Review: structural bioinformatics and its impact to biomedical science. Curr. Med. Chem. 2004;11:2105–2134. doi: 10.2174/0929867043364667. [DOI] [PubMed] [Google Scholar]
- Chou K.C. Using amphiphilic pseudo amino acid composition to predict enzyme subfamily classes. Bioinformatics. 2005;21:10–19. doi: 10.1093/bioinformatics/bth466. [DOI] [PubMed] [Google Scholar]
- Chou K.C., Forsen S. Graphical rules for enzyme-catalyzed rate laws. Biochem. J. 1980;187:829–835. doi: 10.1042/bj1870829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou K.C., Liu W.M. Graphical rules for non-steady state enzyme kinetics. J. Theor. Biol. 1981;91:637–654. doi: 10.1016/0022-5193(81)90215-0. [DOI] [PubMed] [Google Scholar]
- Chou K.C., Shen H.B. Hum-PLoc: a novel ensemble classifier for predicting human protein subcellular localization. Biochem. Biophys. Res. Commun. 2006;347:150–157. doi: 10.1016/j.bbrc.2006.06.059. [DOI] [PubMed] [Google Scholar]
- Chou K.C., Shen H.B. Recent progress in protein subcellular location prediction. Anal. Biochem. 2007;370:1–16. doi: 10.1016/j.ab.2007.07.006. [DOI] [PubMed] [Google Scholar]
- Chou K.C., Shen H.B. Signal-CF: a subsite-coupled and window-fusing approach for predicting signal peptides. Biochem. Biophys. Res. Commun. 2007;357:633–640. doi: 10.1016/j.bbrc.2007.03.162. [DOI] [PubMed] [Google Scholar]
- Chou K.C., Shen H.B. Cell-PLoc: a package of web-servers for predicting subcellular localization of proteins in various organisms. Nat. Protocols. 2008;3:153–162. doi: 10.1038/nprot.2007.494. [DOI] [PubMed] [Google Scholar]
- Chou K.C., Zhang C.T. Diagrammatization of codon usage in 339 HIV proteins and its biological implication. AIDS Res. Hum. Retroviruses. 1992;8:1967–1976. doi: 10.1089/aid.1992.8.1967. [DOI] [PubMed] [Google Scholar]
- Chou K.C., Zhang C.T. Prediction of protein structural classes. Crit. Rev. Biochem. Mol. Biol. 1995;30:275–349. doi: 10.3109/10409239509083488. [DOI] [PubMed] [Google Scholar]
- Chou K.C., Jiang S.P., Liu W.M., Fee C.H. Graph theory of enzyme kinetics: 1. Steady-state reaction system. Scientia Sinica. 1979;22:341–358. [Google Scholar]
- Chou K.C., Kezdy F.J., Reusser F. Review: steady-state inhibition kinetics of processive nucleic acid polymerases and nucleases. Anal. Biochem. 1994;221:217–230. doi: 10.1006/abio.1994.1405. [DOI] [PubMed] [Google Scholar]
- Cornish-Bowden A. Butterworths; London: 1979. Fundamentals of Enzyme Kinetics. (Chapter 4) [Google Scholar]
- Di Francesco V., Munson P.J., Garnier J. FORESST: fold recognition from secondary structure predictions of proteins. Bioinformatics. 1999;15:131–140. doi: 10.1093/bioinformatics/15.2.131. [DOI] [PubMed] [Google Scholar]
- Diao Y., Li M., Feng Z., Yin J., Pan Y. The community structure of human cellular signaling network. J. Theor. Biol. 2007;247:608–615. doi: 10.1016/j.jtbi.2007.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding Y.S., Zhang T.L., Chou K.C. Prediction of protein structure classes with pseudo amino acid composition and fuzzy support vector machine network. Protein. Pept. Lett. 2007;14:811–815. doi: 10.2174/092986607781483778. [DOI] [PubMed] [Google Scholar]
- Dobson P.D., Doig A.J. Predicting enzyme class from protein structure without alignments. J. Mol. Biol. 2005;345:187–199. doi: 10.1016/j.jmb.2004.10.024. [DOI] [PubMed] [Google Scholar]
- Dobson P.M., Boyle M., Loewenthal M. Home intravenous antibiotic therapy and allergic drug reactions: is there a case for routine supply of anaphylaxis kits? J. Infus. Nurs. 2004;27:425–430. doi: 10.1097/00129804-200411000-00008. [DOI] [PubMed] [Google Scholar]
- Dobson P.S., Weaver J.M., Holder M.N., Unwin P.R., Macpherson J.V. Characterization of batch-microfabricated scanning electrochemical-atomic force microscopy probes. Anal. Chem. 2005;77:424–434. doi: 10.1021/ac048930e. [DOI] [PubMed] [Google Scholar]
- Du Q.S., Wei Y.T., Pang Z.W., Chou K.C., Huang R.B. Predicting the affinity of epitope-peptides with class I MHC molecule HLA-A*0201: an application of amino acid-based peptide prediction. Protein Eng. Des. Sel. 2007;20:417–423. doi: 10.1093/protein/gzm036. [DOI] [PubMed] [Google Scholar]
- Du Q.S., Huang R.B., Wei Y.T., Wang C.H., Chou K.C. Peptide reagent design based on physical and chemical properties of amino acid residues. J. Comput. Chem. 2007;28:2043–2050. doi: 10.1002/jcc.20732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Q.S., Huang R.B., Wei Y.T., Du L.Q., Chou K.C. Multiple field three dimensional quantitative structure–activity relationship (MF-3D-QSAR) J. Comput. Chem. 2008;29:211–219. doi: 10.1002/jcc.20776. [DOI] [PubMed] [Google Scholar]
- Estrada E. On the topological sub-structural molecular design (TOSS-MODE) in QSPR/QSAR and drug design research. SAR QSAR Environ. Res. 2000;11:55–73. doi: 10.1080/10629360008033229. [DOI] [PubMed] [Google Scholar]
- Estrada E. Characterization of the folding degree of proteins. Bioinformatics. 2002;18:697–704. doi: 10.1093/bioinformatics/18.5.697. [DOI] [PubMed] [Google Scholar]
- Estrada E., González-Díaz H. What are the limits of applicability for graph theoretic descriptors in QSPR/QSAR? Modeling dipole moments of aromatic compounds with TOPS-MODE descriptors. J. Chem. Inf. Comput. Sci. 2003;43:75–84. doi: 10.1021/ci025604w. [DOI] [PubMed] [Google Scholar]
- Gao L., Ding Y.S., Dai H., Shao S.H., Huang Z.D., Chou K.C. A novel fingerprint map for detecting SARS-CoV. J. Pharm. Biomed. Anal. 2006;41:246–250. doi: 10.1016/j.jpba.2005.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia-Garcia A., Galvez J., de Julian-Ortiz J.V., Garcia-Domenech R., Munoz C., Guna R., Borras R. New agents active against Mycobacterium avium complex selected by molecular topology: a virtual screening method. J. Antimicrob. Chemother. 2004;53:65–73. doi: 10.1093/jac/dkh014. [DOI] [PubMed] [Google Scholar]
- González M.P., Moldes del Carmen Teran M. A TOPS-MODE approach to predict adenosine kinase inhibition. Bioorg. Med. Chem. Lett. 2004;14:3077–3079. doi: 10.1016/j.bmcl.2004.04.040. [DOI] [PubMed] [Google Scholar]
- González M.P., Helguera A.M., Cabrera M.A. Quantitative structure–activity relationship to predict toxicological properties of benzene derivative compounds. Bioorg. Med. Chem. 2005;13:1775–1781. doi: 10.1016/j.bmc.2004.11.059. [DOI] [PubMed] [Google Scholar]
- González M.P., Teran C., Teijeira M. A topological function based on spectral moments for predicting affinity toward A3 adenosine receptors. Bioorg. Med. Chem. Lett. 2006;16:1291–1296. doi: 10.1016/j.bmcl.2005.11.063. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., Uriarte E. Biopolymer stochastic moments. I. Modeling human rhinovirus cellular recognition with protein surface electrostatic moments. Biopolymers. 2005;77:296–303. doi: 10.1002/bip.20234. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., de Armas R.R., Molina R. Markovian negentropies in bioinformatics. 1. A picture of footprints after the interaction of the HIV-1 Psi-RNA packaging region with drugs. Bioinformatics. 2003;19:2079–2087. doi: 10.1093/bioinformatics/btg285. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., Molina R.R., Uriarte E. Stochastic molecular descriptors for polymers. 1. Modelling the properties of icosahedral viruses with 3D-Markovian negentropies. Polymer. 2003:3845–3853. [Google Scholar]
- González-Díaz H., de Armas R.R., Molina R. Vibrational Markovian modelling of footprints after the interaction of antibiotics with the packaging region of HIV type 1. Bull. Math. Biol. 2003;65:991–1002. doi: 10.1016/s0092-8240(03)00064-8. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., Pérez-Bello A., Uriarte E. Stochastic molecular descriptors for polymers. 3. Markov electrostatic moments as polymer 2D-folding descriptors: RNA–QSAR for mycobacterial promoters. Polymer. 2005;46:6461–6473. [Google Scholar]
- González-Díaz H., Cruz-Monteagudo M., Molina R., Tenorio E., Uriarte E. Predicting multiple drugs side effects with a general drug-target interaction thermodynamic Markov model. Bioorg. Med. Chem. 2005;13:1119–1129. doi: 10.1016/j.bmc.2004.11.030. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., Aguero-Chapin G., Varona-Santos J., Molina R., de la Riva G., Uriarte E. 2D RNA-QSAR: assigning ACC oxidase family membership with stochastic molecular descriptors; isolation and prediction of a sequence from Psidium guajava L. Bioorg. Med. Chem. Lett. 2005;15:2932–2937. doi: 10.1016/j.bmcl.2005.03.017. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., Cruz-Monteagudo M., Vina D., Santana L., Uriarte E., De Clercq E. QSAR for anti-RNA-virus activity, synthesis, and assay of anti-RSV carbonucleosides given a unified representation of spectral moments, quadratic, and topologic indices. Bioorg. Med. Chem. Lett. 2005;15:1651–1657. doi: 10.1016/j.bmcl.2005.01.047. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., Aguero G., Cabrera M.A., Molina R., Santana L., Uriarte E., Delogu G., Castanedo N. Unified Markov thermodynamics based on stochastic forms to classify drugs considering molecular structure, partition system, and biological species: distribution of the antimicrobial G1 on rat tissues. Bioorg. Med. Chem. Lett. 2005;15:551–557. doi: 10.1016/j.bmcl.2004.11.059. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., Perez-Bello A., Uriarte E., González-Diaz Y. QSAR study for mycobacterial promoters with low sequence homology. Bioorg. Med. Chem. Lett. 2006;16:547–553. doi: 10.1016/j.bmcl.2005.10.057. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., Vina D., Santana L., de Clercq E., Uriarte E. Stochastic entropy QSAR for the in silico discovery of anticancer compounds: prediction, synthesis, and in vitro assay of new purine carbanucleosides. Bioorg. Med. Chem. 2006;14:1095–1107. doi: 10.1016/j.bmc.2005.09.039. [DOI] [PubMed] [Google Scholar]
- González-Diaz H., Sanchez-González A., González-Diaz Y. 3D-QSAR study for DNA cleavage proteins with a potential anti-tumor ATCUN-like motif. J. Inorg. Biochem. 2006;100:1290–1297. doi: 10.1016/j.jinorgbio.2006.02.019. [DOI] [PubMed] [Google Scholar]
- González-Díaz, H., Molina-Ruiz, R., and Hernandez, I., 2007a. MARCH-INSIDE version 3.0 (MARkov CHains INvariants for SImulation & DEsign); Windows supported version under request to the main author contact email: gonzalezdiazh@yahoo.es.
- González-Díaz H., Vilar S., Santana L., Uriarte E. Medicinal chemistry and bioinformatics—current trends in drugs discovery with networks topological indices. Curr. Top. Med. Chem. 2007;7:1025–1039. doi: 10.2174/156802607780906771. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., Pérez-Bello A., Cruz-Monteagudo M., González-Díaz Y., Santana L., Uriarte E. Chemometrics for QSAR with low sequence homology: Mycobacterial promoter sequences recognition with 2D-RNA entropies. Chemom. Intell. Lab. Syst. 2007;85:20–26. [Google Scholar]
- González-Díaz H., Agüero-Chapin G., Varona J., Molina R., Delogu G., Santana L., Uriarte E., Gianni P. 2D-RNA-coupling numbers: a new computational chemistry approach to link secondary structure topology with biological function. J. Comput. Chem. 2007;28:1049–1056. doi: 10.1002/jcc.20576. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., Vilar S., Santana L., Uriarte E. Medicinal chemistry and bioinformatics—current trends in drugs discovery with networks topological indices. Curr. Top. Med. Chem. 2007;10:1015–1029. doi: 10.2174/156802607780906771. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., Bonet I., Teran C., De Clercq E., Bello R., Garcia M.M., Santana L., Uriarte E. ANN-QSAR model for selection of anticancer leads from structurally heterogeneous series of compounds. Eur. J. Med. Chem. 2007;42:580–585. doi: 10.1016/j.ejmech.2006.11.016. [DOI] [PubMed] [Google Scholar]
- González-Díaz H., González-Díaz Y., Santana L., Ubeira F.M., Uriarte E. Proteomics, networks, and connectivity indices. Proteomics. 2008;8:750–778. doi: 10.1002/pmic.200700638. [DOI] [PubMed] [Google Scholar]
- Griffiths A.J.F., Miller J.H., Suzuki D.T., Lewontin R.C., Gelbart W.M. Freeman; New York: 1999. Introduction to Genetic Analysis. [Google Scholar]
- Han L., Cui J., Lin H., Ji Z., Cao Z., Li Y., Chen Y. Recent progresses in the application of machine learning approach for predicting protein functional class independent of sequence similarity. Proteomics. 2006;6:4023–4037. doi: 10.1002/pmic.200500938. [DOI] [PubMed] [Google Scholar]
- Harary, F., 1969. Graph theory, MA.
- Harshey R.M., Ramakrishnan T. Rate of ribonucleic acid chain growth in Mycobacterium tuberculosis H37Rv. J. Bacteriol. 1977;129:616–622. doi: 10.1128/jb.129.2.616-622.1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacchieri S.G. Mining combinatorial data in protein sequences and structures. Mol. Divers. 2000;5:145–152. doi: 10.1023/a:1016286720984. [DOI] [PubMed] [Google Scholar]
- Kalate R.N., Tambe S.S., Kulkarni B.D. Artificial neural networks for prediction of mycobacterial promoter sequences. Comput. Biol. Chem. 2003;27:555–564. doi: 10.1016/j.compbiolchem.2003.09.004. [DOI] [PubMed] [Google Scholar]
- King E.L., Altman C. A schematic method of deriving the rate laws for enzyme-catalyzed reactions. J. Phys. Chem. 1956;60:1375–1378. [Google Scholar]
- Kutner M.H., Nachtsheim C.J., Neter J., Li W. McGraw-Hill; New York: 2005. Standardized Multiple Regression Model, Applied Linear Statistical Models. pp. 271-277. [Google Scholar]
- Kuzmic P., Ng K.Y., Heath T.D. Mixtures of tight-binding enzyme inhibitors. Kinetic analysis by a recursive rate equation. Anal. Biochem. 1992;200:68–73. doi: 10.1016/0003-2697(92)90278-f. [DOI] [PubMed] [Google Scholar]
- Levine M., Tjian R. Transcription regulation and animal diversity. Nature. 2003;424:147–151. doi: 10.1038/nature01763. [DOI] [PubMed] [Google Scholar]
- Liao B., Ding K. Graphical approach to analyzing DNA sequences. J. Comput. Chem. 2005;26:1519–1523. doi: 10.1002/jcc.20287. [DOI] [PubMed] [Google Scholar]
- Liao B., Wang T.M. Analysis of similarity/dissimilarity of DNA sequences based on nonoverlapping triplets of nucleotide bases. J. Chem. Inf. Comput. Sci. 2004;44:1666–1670. doi: 10.1021/ci034271f. [DOI] [PubMed] [Google Scholar]
- Liao B., Wang T.M. New 2D graphical representation of DNA sequences. J. Comput. Chem. 2004;25:1364–1368. doi: 10.1002/jcc.20060. [DOI] [PubMed] [Google Scholar]
- Liao B., Wang T.M. A 3D graphical representation of RNA secondary structures. J. Biomol. Struct. Dyn. 2004;21:827–832. doi: 10.1080/07391102.2004.10506972. [DOI] [PubMed] [Google Scholar]
- Liao B., Ding K., Wang T.M. On a six-dimensional representation of RNA secondary structures. J. Biomol. Struct. Dyn. 2005;22:455–463. doi: 10.1080/07391102.2005.10507016. [DOI] [PubMed] [Google Scholar]
- Liao B., Xiang X., Zhu W. Coronavirus phylogeny based on 2D graphical representation of DNA sequence. J. Comput. Chem. 2006;27:1196–1202. doi: 10.1002/jcc.20439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin H. The modified Mahalanobis discriminant for predicting outer membrane proteins by using Chou's pseudo amino acid composition. J. Theor. Biol. 2008;252:350–356. doi: 10.1016/j.jtbi.2008.02.004. [DOI] [PubMed] [Google Scholar]
- Liu Y., Guo X., Xu J., Pan L., Wang S. Some notes on 2-D graphical representation of DNA sequence. J. Chem. Inf. Comput. Sci. 2002;42:529–533. doi: 10.1021/ci010017g. [DOI] [PubMed] [Google Scholar]
- Markham N.R., Zuker M. DINAMelt web server for nucleic acid melting prediction. Nucleic Acids Res. 2005;33:W577–W581. doi: 10.1093/nar/gki591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrero-Ponce Y., Diaz H.G., Zaldivar V.R., Torrens F., Castro E.A. 3D-chiral quadratic indices of the ‘molecular pseudograph's atom adjacency matrix’ and their application to central chirality codification: classification of ACE inhibitors and prediction of sigma-receptor antagonist activities. Bioorg. Med. Chem. 2004;12:5331–5342. doi: 10.1016/j.bmc.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Marrero-Ponce Y., Castillo-Garit J.A., Olazabal E., Serrano H.S., Morales A., Castanedo N., Ibarra-Velarde F., Huesca-Guillen A., Jorge E., del Valle A., Torrens F., Castro E.A. TOMOCOMD-CARDD, a novel approach for computer-aided ‘rational’ drug design: I. Theoretical and experimental assessment of a promising method for computational screening and in silico design of new anthelmintic compounds. J. Comput. Aided Mol. Des. 2004;18:615–634. doi: 10.1007/s10822-004-5171-y. [DOI] [PubMed] [Google Scholar]
- Marrero-Ponce Y., Medina-Marrero R., Castillo-Garit J.A., Romero-Zaldivar V., Torrens F., Castro E.A. Protein linear indices of the ‘macromolecular pseudograph alpha-carbon atom adjacency matrix’ in bioinformatics. Part 1: prediction of protein stability effects of a complete set of alanine substitutions in arc repressor. Bioorg. Med. Chem. 2005;13:3003–3015. doi: 10.1016/j.bmc.2005.01.062. [DOI] [PubMed] [Google Scholar]
- Marrero-Ponce Y., Castillo-Garit J.A., Olazabal E., Serrano H.S., Morales A., Castanedo N., Ibarra-Velarde F., Huesca-Guillen A., Sanchez A.M., Torrens F., Castro E.A. Atom, atom-type and total molecular linear indices as a promising approach for bioorganic and medicinal chemistry: theoretical and experimental assessment of a novel method for virtual screening and rational design of new lead anthelmintic. Bioorg. Med. Chem. 2005;13:1005–1020. doi: 10.1016/j.bmc.2004.11.040. [DOI] [PubMed] [Google Scholar]
- Meneses-Marcel A., Marrero-Ponce Y., Machado-Tugores Y., Montero-Torres A., Pereira D.M., Escario J.A., Nogal-Ruiz J.J., Ochoa C., Aran V.J., Martinez-Fernandez A.R., Garcia Sanchez R.N. A linear discrimination analysis based virtual screening of trichomonacidal lead-like compounds: outcomes of in silico studies supported by experimental results. Bioorg. Med. Chem. Lett. 2005;15:3838–3843. doi: 10.1016/j.bmcl.2005.05.124. [DOI] [PubMed] [Google Scholar]
- Mulder M.A., Zappe H., Steyn L.M. Mycobacterial promoters. Tuber. Lung Dis. 1997;78:211–223. doi: 10.1016/s0962-8479(97)90001-0. [DOI] [PubMed] [Google Scholar]
- Mulligan M.E., McClure W.R. Analysis of the occurrence of promoter-sites in DNA. Nucleic Acids Res. 1986;14:109–126. doi: 10.1093/nar/14.1.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulligan M.E., Hawley D.K., Entriken R., McClure W.R. Escherichia coli promoter sequences predict in vitro RNA polymerase selectivity. Nucleic Acids Res. 1984;12:789–800. doi: 10.1093/nar/12.1part2.789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munteanu C.R., González-Diaz H., Magalhaes A.L. Enzymes/non-enzymes classification model complexity based on composition, sequence, 3D and topological indices. J. Theor. Biol. 2008;254:476–482. doi: 10.1016/j.jtbi.2008.06.003. [DOI] [PubMed] [Google Scholar]
- Munteanu, C.R., González-Díaz, H., Borges, F., and Magalhães, A.L., 2008b. Natural/random protein classification models based on star network topological indices. J. Theor. Biol. 〈 10.1016/j.jtbi.2008.07.018〉. [DOI] [PMC free article] [PubMed]
- Myers D., Palmer G. Microcomputer tools for steady-state enzyme kinetics. Bioinformatics (original: Comput. Appl. Biosci.) 1985;1:105–110. [PubMed] [Google Scholar]
- Nandy A. Recent investigations into global characteristics of long DNA sequences. Indian J. Biochem. Biophys. 1994;31:149–155. [PubMed] [Google Scholar]
- Nandy A. Two-dimensional graphical representation of DNA sequences and intron-exon discrimination in intron-rich sequences. Comput. Appl. Biosci. 1996;12:55–62. doi: 10.1093/bioinformatics/12.1.55. [DOI] [PubMed] [Google Scholar]
- Nandy A., Basak S.C. Simple numerical descriptor for quantifying effect of toxic substances on DNA sequences. J. Chem. Inf. Comput. Sci. 2000;40:915–919. doi: 10.1021/ci990117a. [DOI] [PubMed] [Google Scholar]
- O’Neill M.C., Chiafari F. Escherichia coli promoters. II. A spacing class-dependent promoter search protocol. J. Biol. Chem. 1989;264:5531–5534. [PubMed] [Google Scholar]
- Pawar A.P., Dubay K.F., Zurdo J., Chiti F., Vendruscolo M., Dobson C.M. Prediction of “aggregation-prone” and “aggregation-susceptible” regions in proteins associated with neurodegenerative diseases. J. Mol. Biol. 2005;350:379–392. doi: 10.1016/j.jmb.2005.04.016. [DOI] [PubMed] [Google Scholar]
- Prado-Prado F.J., González-Diaz H., de la Vega O.M., Ubeira F.M., Chou K.C. Unified QSAR approach to antimicrobials. Part 3: first multi-tasking QSAR model for input-coded prediction, structural back-projection, and complex networks clustering of antiprotozoal compounds. Bioorg. Med. Chem. 2008;16:5871–5880. doi: 10.1016/j.bmc.2008.04.068. [DOI] [PubMed] [Google Scholar]
- Qi X.Q., Wen J., Qi Z.H. New 3D graphical representation of DNA sequence based on dual nucleotides. J. Theor. Biol. 2007;249:681–690. doi: 10.1016/j.jtbi.2007.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramos de Armas R., González-Díaz H., Molina R., Perez Gonzalez M., Uriarte E. Stochastic-based descriptors studying peptides biological properties: modeling the bitter tasting threshold of dipeptides. Bioorg. Med. Chem. 2004;12:4815–4822. doi: 10.1016/j.bmc.2004.07.017. [DOI] [PubMed] [Google Scholar]
- Randic M. 2-D graphical representation of proteins based on virtual genetic code. SAR QSAR Environ. Res. 2004;15:147–157. doi: 10.1080/10629360410001697744. [DOI] [PubMed] [Google Scholar]
- Randic M., Balaban A.T. On a four-dimensional representation of DNA primary sequences. J. Chem. Inf. Comput. Sci. 2003;43:532–539. doi: 10.1021/ci020051a. [DOI] [PubMed] [Google Scholar]
- Randic M., Vracko M. On the similarity of DNA primary sequences. J. Chem. Inf. Comput. Sci. 2000;40:599–606. doi: 10.1021/ci9901082. [DOI] [PubMed] [Google Scholar]
- Randic M., Zupan J. Highly compact 2D graphical representation of DNA sequences. SAR QSAR Environ. Res. 2004;15:191–205. doi: 10.1080/10629360410001697753. [DOI] [PubMed] [Google Scholar]
- Randic M., Vracko M., Nandy A., Basak S.C. On 3-D graphical representation of DNA primary sequences and their numerical characterization. J. Chem. Inf. Comput. Sci. 2000;40:1235–1244. doi: 10.1021/ci000034q. [DOI] [PubMed] [Google Scholar]
- Randic M., Zupan J., Vikic-Topic D. On representation of proteins by star-like graphs. J. Mol. Graph Model. 2007;290-305 doi: 10.1016/j.jmgm.2006.12.006. [DOI] [PubMed] [Google Scholar]
- Santana L., Uriarte E., González-Diaz H., Zagotto G., Soto-Otero R., Mendez-Alvarez E. A QSAR model for in silico screening of MAO-A inhibitors. Prediction, synthesis, and biological assay of novel coumarins. J. Med. Chem. 2006;49:1149–1156. doi: 10.1021/jm0509849. [DOI] [PubMed] [Google Scholar]
- Song J., Tang H. A new 2-D graphical representation of DNA sequences and their numerical characterization. J. Biochem. Biophys. Meth. 2005;63:228–239. doi: 10.1016/j.jbbm.2005.04.004. [DOI] [PubMed] [Google Scholar]
- StatSoft.Inc., STATISTICA (data analysis software system), version 6.0, 〈www.statsoft.com〉 Statsoft, 2002.
- Todeschini R., Consonni V. Wiley-VCH; New York: 2002. Handbook of Molecular Descriptors. [Google Scholar]
- Van Waterbeemd H. Wiley-VCH; New York: 1995. Chemometric Methods in Molecular Design. [Google Scholar]
- Vilar S., Estrada E., Uriarte E., Santana L., Gutierrez Y. In silico studies toward the discovery of new anti-HIV nucleoside compounds through the use of TOPS-MODE and 2D/3D connectivity indices. 2. Purine derivatives. J. Chem. Inf. Model. 2005;45:502–514. doi: 10.1021/ci049662o. [DOI] [PubMed] [Google Scholar]
- Vilar S., Santana L., Uriarte E. Probabilistic neural network model for the in silico evaluation of anti-HIV activity and mechanism of action. J. Med. Chem. 2006;49:1118–1124. doi: 10.1021/jm050932j. [DOI] [PubMed] [Google Scholar]
- Wang M., Yao J.S., Huang Z.D., Xu Z.J., Liu G.P., Zhao H.Y., Wang X.Y., Yang J., Zhu Y.S., Chou K.C. A new nucleotide-composition based fingerprint of SARS-CoV with visualization analysis. Med. Chem. 2005;1:39–47. doi: 10.2174/1573406053402505. [DOI] [PubMed] [Google Scholar]
- Wolfram S. Cellular automation as models of complexity. Nature. 1984;311:419–424. [Google Scholar]
- Wolfram S. Wolfram Media Inc.; Champaign, IL: 2002. A New Kind of Science. [Google Scholar]
- Woodcock S., Mornon J.P., Henrissat B. Detection of secondary structure elements in proteins by hydrophobic cluster analysis. Protein Eng. 1992;5:629–635. doi: 10.1093/protein/5.7.629. [DOI] [PubMed] [Google Scholar]
- Wyrick J.J., Young R.A. Deciphering gene expression regulatory networks. Curr. Opin. Genet. Dev. 2002;12:130–136. doi: 10.1016/s0959-437x(02)00277-0. [DOI] [PubMed] [Google Scholar]
- Xiao X., Chou K.C. Digital coding of amino acids based on hydrophobic index. Protein Pept. Lett. 2007;14:871–875. doi: 10.2174/092986607782110293. [DOI] [PubMed] [Google Scholar]
- Xiao X., Shao S., Ding Y., Huang Z., Chen X., Chou K.C. Using cellular automata to generate Image representation for biological sequences. Amino Acids. 2005;28:29–35. doi: 10.1007/s00726-004-0154-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao X., Shao S., Ding Y., Huang Z., Chen X., Chou K.C. An application of gene comparative image for predicting the effect on replication ratio by HBV virus gene Missense mutation. J. Theor. Biol. 2005;235:555–565. doi: 10.1016/j.jtbi.2005.02.008. [DOI] [PubMed] [Google Scholar]
- Xiao X., Shao S.H., Chou K.C. A probability cellular automaton model for hepatitis B viral infections. Biochem. Biophys. Res. Comm. 2006;342:605–610. doi: 10.1016/j.bbrc.2006.01.166. [DOI] [PubMed] [Google Scholar]
- Xiao X., Shao S.H., Ding Y.S., Huang Z.D., Chou K.C. Using cellular automata images and pseudo amino acid composition to predict protein subcellular location. Amino Acids. 2006;30:49–54. doi: 10.1007/s00726-005-0225-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan Z. Prediction of protein subcellular locations using Markov chain models. FEBS Lett. 1999;451:23–26. doi: 10.1016/s0014-5793(99)00506-2. [DOI] [PubMed] [Google Scholar]
- Zhang C.T., Chou K.C. Graphic analysis of codon usage strategy in 1490 human proteins. J. Protein Chem. 1993;12:329–335. doi: 10.1007/BF01028195. [DOI] [PubMed] [Google Scholar]
- Zhang C.T., Chou K.C. Analysis of codon usage in 1562 E. Coli protein coding sequences. J. Mol. Biol. 1994;238:1–8. doi: 10.1006/jmbi.1994.1263. [DOI] [PubMed] [Google Scholar]
- Zhou G.P., Deng M.H. An extension of Chou's graphical rules for deriving enzyme kinetic equations to system involving parallel reaction pathways. Biochem. J. 1984;222:169–176. doi: 10.1042/bj2220169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zupan J., Randic M. Algorithm for coding DNA sequences into “spectrum-like” and “zigzag” representations. J. Chem. Inf. Model. 2005;45:309–313. doi: 10.1021/ci040104j. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information A


