Abstract
A novel air dehumidification system is proposed. The proposed system incorporates a membrane-based total heat exchanger into a mechanical air dehumidification system, where the fresh air flows through the enthalpy exchanger, the evaporator and the condenser subsequently. Thermodynamic model for the performance estimation of the combined system is investigated. Processes of the fresh air and the refrigerant are studied. Two additional specific programs are devised to calculate the psychrometrics and the thermodynamic properties of the refrigerant R134a. Annual energy requirement is 4.15 × 106 kJ per person, or 33% saving from a system without energy saving measures.
Keywords: Air dehumidification, Enthalpy exchanger, Membrane, Cooling coils
List of symbols
- Atot
total exchange area (m2)
- C0
constants in sorption curves
- COP
coefficient of performance
- cp
specific heat (kJ kg−1 K−1)
- Dwm
water diffusivity in membrane (kg m−1 s−1)
- h
specific enthalpy (kJ/kg)
- ks
convective mass transfer coefficient in supply side (kg m−2 s−1)
mass flow rate (kg/s)
- Δp
total pressure rise (Pa)
- q
heat (kW)
- T
temperature (K)
- U
total heat transfer coefficient (kW m−2 K−1),
- Va
air (water) volumetric flow rate (m3/h)
- wmax
constants in sorption curves
- x
degree of dryness
Greek letters
- η
efficiency
- ɛ
effectiveness
- ϕ
relative humidity
- ω
humidity (kg vapor/kg air)
- δ
membrane thickness (m)
Subscripts
- a
air stream
- c
condenser
- com
compressor
- e
evaporator
- f
refrigerant
- fan
fan
- motor
motor
- s
isentropic
1. Introduction
It is often necessary to control and modify the water vapor content in the air: the operation is quite usual in air conditioning. Normally the water vapor content of atmospheric air is small, some tens of grams per kilo of air; nonetheless, due to the very high heat of vaporization, the latent heat content in air conditioning is of the same order of the sensible one. The relative importance of latent load increases with the ventilation rates to buildings. Higher ventilation rates are dictated both by better comfort requirements and by the most recent standards such as the ASHRAE 62/99 [1].
More recently, people’s concern on indoor air quality has been greatly deepened since the outbreak of the severe acute respiratory syndrome (SARS) epidemic that molested South China and some other parts of the world in this Spring and caused a loss of 17.9 billion US$ (or 1.3% GDP) in China alone and 59 billion US$ globally [2]. The mechanisms of SARS virus spreading is complex and remains a mystery till now. However, it is believed that enough fresh air ventilation is helpful in decreasing the possibility of being infected by the disease.
Ventilation air is the major source of moisture load in air conditioning. As shown in Fig. 1 for a moisture load estimation of a medium size retail store [3], ventilation air constitutes about 68% of the total moisture load in most commercial buildings. As a consequence, treatment of the latent load from the ventilation air is a difficult and imminent task for HVAC engineers, especially in hot and humid climates like South China.
Fig. 1.
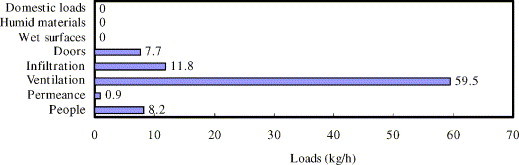
Sources of moisture loads in a medium size retail store.
Traditionally, latent load and sensible load are treated in a coupled way. Because air is not only for ventilation, but also a heat transfer medium, and large quantities of air is needed to extract the sensible load, energy requirements are very high. Another problem with this technique is that in transit seasons, humidity will lose control [4].
There is an increasing trend to separate the treatment of sensible and latent load by using an independent humidity control system. According to this concept, the latent load of a room is treated by an independent humidity control system, while the sensible load is treated with some other alternative cooling techniques such as chilled-ceiling panels. Since the circulating air is dramatically reduced, energy consumption can be reduced substantially. Another benefit is that chilled water or suction temperatures can be raised, resulting in increased equipment efficiency and decreased operating costs. It is estimated that 30% of the energy used could be saved with chilled-ceiling panels combined with independent humidity control system, in comparison to a traditional coupled system [5], [6]. Nevertheless, due to the hot and humid climates in south China, energy for moisture control with an independent humidity control system still accounts for 25% of the total energy for air conditioning. Thus, energy recovery measures must be combined to an independent humidity control system.
In this study, a novel air dehumidification system, namely, mechanical dehumidification with membrane-based total heat exchanger, is proposed. The thermodynamic modeling of the system is performed. Through hour-by-hour analysis, the annual primary energy consumptions for the systems proposed are discussed.
2. Mathematical model
A schematic of the new air dehumidification system modeled in this work is shown in Fig. 2 (a) and its psychrometrics are shown in Fig. 2(b). In this system, a membrane based total heat exchanger is used to pre-cool the fresh air before it is pumped to a refrigeration system for air dehumidification. The total heat exchanger has a membrane core where the incoming fresh air exchanges moisture and temperature simultaneously with the exhaust air. In this manner, the total heat or enthalpy from the exhaust is recovered, and both the temperature and the humidity of the fresh air are decreased, which results in energy saving. Then the cooled and dehumidified fresh air is flowed through the condenser of the refrigeration system, to satisfy the requirements of supply air: 7 g/kg humidity and 20 °C in temperature. This system is relatively simple, since the membrane system has no moving parts, and is compact. Desiccant wheels may be another choice, however, in some circumstances, gas or other thermal heat may be difficult to find. The control of the new system is easier than a conventional compression dehumidification system, because no other components except a membrane system is added to the system. The differences are the operating parameters are changed, and much fan power is needed. The membrane system operated in near atmospheric pressure condition, the maintenance is easy.
Fig. 2.
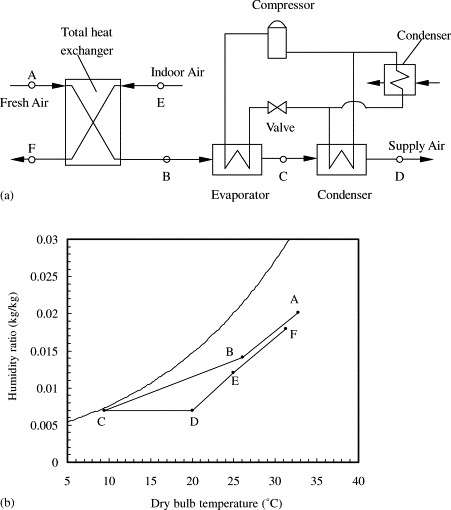
Schematics (a) and psychrometrics (b) of the air dehumidification system.
This study is to estimate the energy performance of a novel air dehumidification system by thermodynamic analysis. The modeling methodology of the refrigeration cycle is a steady-state one. They are sufficient to reflect the coefficient of performance or the energy performance of the refrigeration cycle. Even though more detailed models are proposed by some authors, see [7], [8], they are complicated and case-sensitive. In other words, the distributed parameter models in such studies are strongly based on design parameters of a specific refrigeration system. Those detailed models just gave very generalized equations for the calculation of heat and mass transport in each component and rely heavily on manufacturers’ product empirical data. Further, this study gives a general view of energy savings in sub-tropical regions, which do not rely on a specific system. Furthermoreover, the more detailed partial difference models in other studies are difficult and slow in finding a solution. It is difficult to use such models in a whole-year-hour-by-hour simulation. Those more complicated models are usually necessary to study transient responses and start-up characters of a refrigeration cycle, which is beyond the scope of this study.
2.1. The refrigeration cycle
The effects of the refrigeration cycle on the whole system are demonstrable. A thermodynamic model of the refrigeration system is formulated based on the processes of refrigerant R134a shown in Fig. 3 . Saturated R134a liquid at point 4 flows through an expansion valve and becomes wet vapor at point 5. Refrigerant at this state flows to the evaporator (also the dehumidifier) where it chills and dehumidifies the fresh air and evaporates to point 6 and further superheats to point 1. Then the refrigerant vapor is pumped by a compressor to point 2 where the vapor is displaced to the condenser and condensates from state 2 to 4 through 3. The superheat is set to 5 °C. It should be noted that the exact degree of superheating may be affected by many factors, such as evaporator, expansion valve, and compressor, and are strongly related to operating conditions, control strategies. Experiments found superheating are in the range of 2–16 °C; and the superheating increases with air temperature in the evaporator, from 3 to 14 °C when the expansion valve is fully open. From viewpoint of energy use, too large superheating is not good. Generally, 3–14 °C superheating are possible. Refrigerant superheating refers to the superheating in the evaporator. Superheating from tubes can be neglected with well tube-insulating, since superheating from such sources is harmful to energy performance and should be prevented. The effects of heating in the compressor are included in the compressor’s isentropic efficiency.
Fig. 3.
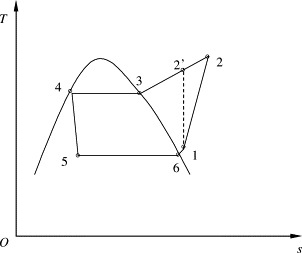
T–s diagram of the refrigeration system.
The specific enthalpy of the refrigerant at the compressor exit is calculated by
| (1) |
where η s is the isentropic efficiency; h 2, is the specific enthalpy at the condensing pressure by isentropic compression from the evaporating pressure. Experimental results have shown that the isentropic efficiency is a weak function of the displacement volume, and varies linearly with the compressor speed. In this analysis, a constant isentropic efficiency of 0.75 is assumed, neglecting the rotational speed of the compressor.
The specific enthalpy after the expansion valve is calculated by
| (2) |
The degree of dryness at the inlet of the evaporator
| (3) |
where h 5, is the specific enthalpy of the saturated liquid refrigerant at the evaporating pressure.
The electricity consumed by the compressor
| (4) |
where is the mass flow rate of refrigerant (kg/s); η motor is the motor efficiency, which is considered as 0.75.
The energy load of the evaporator
| (5) |
Heat rejected in the condenser
| (6) |
Refrigeration efficiency
| (7) |
2.2. Evaporator and condenser
Cooling and dehumidification of the incoming fresh air are performed in the evaporator. A detailed modeling of the evaporator and the condenser are rather complicated [7], [8]. Usually, they are divided into regions associated to the phase of the refrigerant. Each region constitutes a separate heat exchanger. In the case of the condenser, the superheated vapor, the condensation and subcooled liquid regions are considered, whereas for the evaporator it is divided into the evaporating and superheated vapor regions. For each region, the refrigerant side and air side convective heat transfer coefficients need be calculated from the established correlations for single-phase and two-phase flow. For the evaporator, when the average fin surface temperature is calculated to be less than the local water dew point of the air stream, moisture condensation will occur. Under these conditions, the air heat transfer coefficients can no longer be calculated as in dry conditions, and a water mass balance must be carried out. In this case, the enthalpic method, proposed by Threlkeld [9] and introduced in ASHRAE Handbook [10] was most adequate for use. According to this procedure, the driving force for heat transfer is assumed to be the difference between the saturated enthalpy of the air flowing over the fins and a fictitious saturated air enthalpy evaluated at the refrigerant temperature.
The analysis of air cooling and dehumidifying coils requires coupled, non-linear heat mass transfer relationships. While the complex heat mass transfer theory that is presented in many textbooks is often required for cooling coil design, simpler models based on effectiveness concepts are usually more appropriate for energy estimation. These techniques are resulted from basic heat and moisture transfer equations for simultaneous heat and moisture transport. Therefore, in this study, to ease the analysis, thermal performance of the heat exchangers regions is evaluated by the (ɛ, NTU) method. According to this procedure, the heat exchanger effectiveness is defined as
| (8) |
where T hi and T ci are the inlet temperatures of the hot and cold fluids, respectively (K). Because the operations are set to fluctuate around the design points, constant evaporator and condenser effectiveness are assumed in the simulations. Then the air states at the outlets of evaporator and condenser could be obtained.
The heat extracted in the evaporator is calculated by
| (9) |
where is the mass flow rate of fresh air stream (kg/s); h aB and h aC are the specific enthalpies of air at point B and C, respectively.
Similarly, heat rejected at this portion of the condenser is governed by
| (10) |
It should be noted that an energy balance requires that Eq. (9) equals to Eq. (5); while q c1 calculated from Eq. (10) is only a portion of that calculated by Eq. (6). In the study, the evaporating temperature is fixed to 5 °C, while the refrigerant flow rate and the condensing temperature varies according to the cooling load of the evaporator and the outside weather conditions. Usually, a 10 °C log mean temperature difference between the condensing refrigerant and the air flowing through it is required.
2.3. The membrane-based enthalpy exchanger
Energy saving for conditioning fresh air can be achieved by the application of heat recovery ventilators, in which a fraction of energy is recovered from the exhaust air to the supply air. There are presently two kinds of techniques available for heat recovery ventilators: sensible heat exchangers and energy wheels. The sensible heat exchangers are simple and reliable, but they cannot recover latent energy. Energy wheels, which could save latent energy, are problematic due to rotating moving parts.
Hydrophilic polymer membranes provide a new alternative. Some membranes such as polyethersulphone, cellulose triacetate, and polyvinylchloride, are useful in separating moisture from the vapor/air mixture, due to their strong affinity to the water molecule. The strong affinity also leads to the high permeation difference between water and air. The permeability ratio of water to air ranges from 460 to 30,000. In other words, gases other than vapor can hardly permeate through the membrane. These features have led to the development of a novel ventilator, the so-called membrane based enthalpy exchanger in which both the sensible heat and the moisture are transferred simultaneously through the membrane. Since the membranes are very thin, both the heat and the moisture transfer rates can be very high. Furthermore, no water condensation happens in the membrane system, which prevents hygienic problems of micro-organism growth that is common for cooling coils.
In this study, a membrane-based enthalpy recovery ventilator developed in the laboratory is used [11]. Two effectiveness: sensible effectiveness (ɛ S) and latent effectiveness (ɛ L) are defined. Air state at point B in Fig. 2 is calculated by:
| (11) |
| (12) |
The membrane-based energy recovery ventilator is just like a traditional plate-type heat recuperator. The only difference is that hydrophilic membranes are used in place of metal plates.
A total number of transfer units is used to reflect the sensible heat transfer in an exchanger. For the membrane exchanger that has equal area on both sides of the air streams, the total number of transfer units for sensible heat is [12]:
| (13) |
where U is the total heat transfer coefficient (kW m−2 K−1), A tot is the total exchange area (m2), is the mass flow rate (kg/s), and c pa is the specific heat of air (kJ kg−1 K−1).
The sensible effectiveness is a function of two dimensionless parameters, NTU and , the ratio of minimum to maximum heat capacity rate of the two air streams. For un-mixed cross flows, it can be expressed as [11], [12]
| (14) |
Moisture transfer is more complicated due to the couplings between moisture transfer and operating conditions, as well as membrane materials. By clarification of moisture resistance in membrane, a form similar to Eq. (14) for latent effectiveness has been proposed and validated by the authors as
| (15) |
and
| (16) |
where
| (17) |
| (18) |
| (19) |
and
| (20) |
where k s is convective mass transfer coefficient in supply side (kg m−2 s−1); δ the membrane thickness, and D wm is the water diffusivity in membrane (kg m−1 s−1); C 0 and w max are constants in sorption curves, which determine the equilibrium between the membrane and moisture at its surface by
| (21) |
where θ is the moisture uptake in membrane at two surfaces (kg kg−1).
The convective mass transfer coefficient k can be estimated from convective heat transfer coefficient by
| (22) |
A sensible effectiveness of 0.8 is easily obtained with a membrane system, and the latent effectiveness is about 0.9 of the sensible effectiveness according to a case study in [11], [12].
Fan energy is an important factor in the annual energy consumption of an HVAC system. Fan (pump) performance can be characterized by its efficiency, which itself is dependent on operational air flow rate. Mostly, rated volumetric flow rate, pressure rise and efficiency are available from the manufacturer. Then rated power can be calculated as
| (23) |
where V a is air (water) volumetric flow rate (m3/h), Δp is total pressure rise (Pa), η fan is fan (pump) efficiency.
The simulations are conducted on an hour-by-hour basis. The air flow rates are dictated as 45kg/h per person. The operating hours are from 9:00 to 18:00. Fan efficiency is selected as 0.6. For the convenience of comparison, energy consumed in the form of electricity is converted to primary energy by a factor of 3.3. In addition, two specific programs was written to calculate the psychrometrics and the thermodynamic properties of R134a. It is based on a cubic equation of state [13]. The calculations are on a per person basis. It is recommended that each person has 45 kg/h of fresh air.
3. Results and discussions
3.1. Variations of COP
The COP varies with both the evaporating temperature and the condensing temperature. The influence of the condensing temperatures on the COP is shown in Fig. 4 . As can be seen, the COP decreases with increasing condensing temperatures. When the condensing temperature increases from 20 to 50 °C, the system COP decreases from around 8.0–2.5. Following correlation could be formulated for the relation for the refrigeration evaporating at 5 °C:
| (24) |
The effects of the evaporating temperature on the COP are shown in Fig. 5 . The system COP rises with increasing evaporating temperatures. In fact, when the evaporating temperature increases from −10 to 25 °C, COP is improved from 2.0 to 6.5. A correlation has been formulated for the analysis of the system performance:
| (25) |
where the condensing temperature is fixed as 45 °C.
Fig. 4.
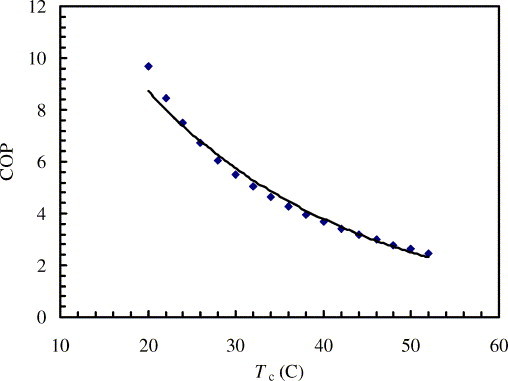
Variations of COP vs. condensing temperature, when Te = 5 °C.
Fig. 5.
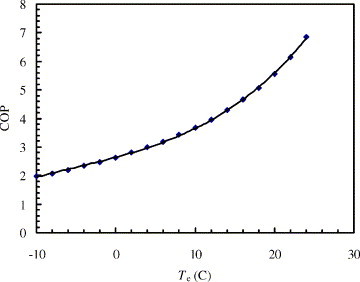
Variations of COP vs. evaporating temperature, when Tc = 45 °C.
Fig. 6 shows the distribution of the COP of the refrigeration system during a year. As indicated, in winter, the system has higher performance, in contrast, when it’s hot in summer, the system COP decreases, which will in return deteriorate the energy requirements.
Fig. 6.
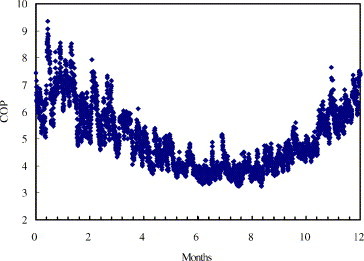
Distribution of COP of the refrigeration cycle in a year.
3.2. Annual primary energy requirements
In the analysis, the system is used to treat the latent load solely, and the sensible load of the room is around 50 W/m2, which will be extracted by chilled-ceiling panels. Results indicate that the annual total energy requirement is 4.15 × 106 kJ per person. In comparison, an air dehumidification with no energy recovery measures would consume more than 6.2 × 106 kJ per person of primary energy. In other words, energy saving is 33%. Considering local primary energy price of 0.007USD/MJ, the annual economic return for each person would be 15USD, which is not a small amount, considering China is still a developing country and the energy price is low. With oil prices growing very fast now, we believe the savings potential could be higher in future.
Fig. 7 plots the primary energy requirements by the dehumidification system for each person in each month in a year. In hot and humid regions like Guangzhou, air dehumidification is required most of the year. The energy values vary from 1.5 × 105 to 4.3 × 105 kJ per month per person. In January and February, when it is the dry season, energy requirements are the least. In August, it is the most humid season, required energy is the largest. In office buildings, the moisture load from ventilation air comprises almost all the moisture load.
Fig. 7.
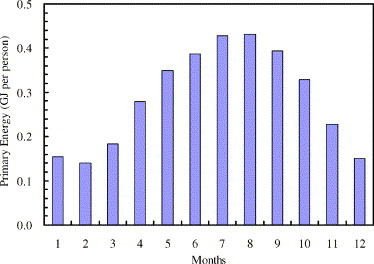
Primary energy consumptions of the air dehumidification system in each month.
The percentages of the energy required in each month to the annual total energy are shown in Fig. 8 . Five months from May to September account for 60.5% of the yearly energy load. Other 7 months account for the rest 39.5%. South China has a long hot and humid summer. The energy for air dehumidification is substantially large. To save energy while ensuring a healthy built environment with enough fresh air ventilation, an independent air dehumidification system with energy recovery is necessary.
Fig. 8.
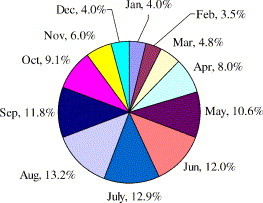
Percentages of primary energy consumed in each month in a year.
4. Conclusions
Concerns on indoor air quality have prompted the researches of novel air dehumidification techniques. This study proposed a new air dehumidification system in which a mechanical dehumidification is combined with a membrane-based enthalpy exchanger. An hour-by-hour simulation reveals that the novel independent air dehumidification system could save 33% of primary energy. With this system, the annual total primary energy used for independent air dehumidification is around 4.2×106 kJ per person.
Acknowledgements
This Project 50306005 is supported by National Natural Science Foundation of China. This project is also supported by the Natural Science Foundation of South China University of Technology.
References
- 1.ASHRAE, ANSI/ASHRAE Standard 62–1999, Ventilation for acceptable indoor air quality. American Society of Heating, Refrigerating and Air-Conditioning Engineers Inc., Atlanta, 1999.
- 2.Hu Angang, Economic toll of SARS, China Youth Daily, 11 November 2003 (in Chinese).
- 3.Harriman L.G., Judge J. Dehumidification equipment advances. ASHRAE J. 2002;44(8):22–29. [Google Scholar]
- 4.Niu J.L., Zhang L.Z., Zuo H.G. Energy savings potential of chilled-ceiling combined with desiccant cooling in hot and humid climates. Energy and Buildings. 2002;34(5):487–495. [Google Scholar]
- 5.Zhang L.Z., Niu J.L. Indoor humidity behaviors associated with decoupled cooling in hot and humid climates. Building and Environment. 2002;38(1):99–107. [Google Scholar]
- 6.Imanari T., Omori T., Bogaki K. Thermal comfort and energy consumption of the radiant ceiling panel system, comparison with the conventional all-air system. Energy and Buildings. 1999;30:167–175. [Google Scholar]
- 7.Bensafi A., Borg S., Parent D. Cyrano: a computational model for the detailed design of plate-fin-and-tube heat exchangers using pure and mixed refrigerants. International Journal of Refrigeration. 1997;20(3):218–228. [Google Scholar]
- 8.Koury R.N.N., Machado L., Ismail K.A.R. Numerical simulation of a variable speed refrigeration system. International Journal of Refrigeration. 2001;24:192–200. [Google Scholar]
- 9.Threlkeld J.L. second ed. Prentice-Hall Inc.; 1970. Thermal Environmental Engineering. [Google Scholar]
- 10.ASHRAE Handbook: Energy Estimating and Modeling methods. American Society of Heating, Refrigerating and Air-Conditioning Engineers Inc.; Atlanta: 1997. (Chapter 30) [Google Scholar]
- 11.Niu J.L., Zhang L.Z. Membrane-based enthalpy exchanger: material considerations and clarification of moisture resistance. Journal of Membrane Science. 2001;189(2):179–191. [Google Scholar]
- 12.Zhang L.Z., Niu J.L. Effectiveness correlations for heat and moisture transfer processes in an enthalpy exchanger with membrane cores. ASME Journal of Heat Transfer. 2002;122(5):922–929. [Google Scholar]
- 13.Basu R.S., Wilson D.P. Thermophysical properties of 1,1,1,2-tetrafluoroethane (R134a) International Journal of Thermophysics. 1989;10(3):591–603. [Google Scholar]


